「また、更新をサボってしまったな」
「そうよ。DERIVEの発売から、2008年9月で、2年よ。しっかりして下さいよ！ ところで、VISTAパソコンでもDERIVEは動くのかしら？」
「ははは、ともちゃんにしかられてしまったのう。
ところで、数式処理ソフト DERIVE（デライブ）の日本での発売元の「Naoco」のページ（http://www.naoco.com）では、対象OSは、XPまでしか書いとらんのじゃが、インストール自体は、VISTAでも大丈夫のようじゃ。ただ、ヘルプの起動には、失敗するの。マイクロソフトのページに説明がある。修正も可能だが、副作用もあり得るようじゃ。となると、VISTAでの利用は、あくまでも自己責任でということになるのかな」
「「図形の面積と重心」については、2002年3月の今月のご挨拶「図形の面積と重心」で取り上げてるわね」
「そうじゃな。あれは、わしが、昔、測量会社に勤めておった頃の経験を元に、2次元平面上の多角形の面積と重心の計算方法を書いてみたのじゃが、なつかしいのう・・」
「ちょっと、ちょっと！ 昔のことをすぐ口にするのは、老化現象よ。で、今回は、どんなことを考えているの？」
「うん。今回は、3次元空間の平面上の多角形の面積を考えてみようということじゃ。できれば、さらに、多面体の体積や重心についても発展して考えてみようという心づもりなのじゃ」
「じゃ、前回の復習をしてみるよ。
平面上にn個の点からなる多角形があり、各頂点を時計回りにPi（xi、yi）とする。PからX軸へ下ろした垂線の交点をRとすると、Ri－Pi－Pi+1－Ri+1という台形の面積は、(1/2）（yi＋yi+1）（xi+1－xi）なので、多角形の面積をSとしたとき、2S＝Σ（yixi+1－yi+1xi）となるわね」
「そうじゃ。xとyは、適当な直角座標系から見た各点の座標値じゃ。最後では、Σ（－yｉxｉ＋yi+1xi+1）＝0をつかう。
この2Sの式をよく見ると、Pの位置ベクトルri（xi、yi、0）を元にして、ri×ri+1のZ軸方向の成分の符号を変えたものに等しいことが分かる。ここで、×はベクトル積じゃ」
「ということは、頂点の番号を多角形の上から見て、反時計回りに番号を振り、多角形の法線方向の面積ベクトルをS（0,0,S）とすれば、2S＝Σri×ri+1な訳ね」
「そう。以下では、数学や物理での原則に従って、多角形から外向きの法線を考えて、外から見て反時計回りに多角形の頂点に番号を振って考えることにしよう。別の表現では、頂点の番号に沿って右ねじをねじったときに、ねじが飛び出す方向が外向きになるように番号を振るということじゃ」
「ベクトルと行列については、第23回で触れているわね。でも、DERIVEでのベクトルの外積の記法について、はっきりと書いていないわね」
「いや。うっかりしておったな。では、ここで、あらためて、説明しよう。
位置ベクトルを、3次元ベクトルとして、［x↓i，y↓i，0］のように書く。ベクトル積は、右下の演算記号パレットの中の「×」（外積）を使う。
結果は、([0, 0, x↓iy↓(i + 1) － x↓(i + 1)y↓i])となって、法線方向の成分が面積の2倍の式と一致しておる」
「変な下向きの矢印は何だたっけ？」
「↓は、下の添え字を表すのじゃ。すなわち、x↓iは、xiということじゃよ」
「2002年3月の「図形の面積と重心」でも「ストークスの定理」が出てくるわね」
「一般に閉曲面における面積分、∫▽×A ・dSと線積分、∫A・dt が等しいというのがベクトル解析で習う、ストークスの定理じゃ。
▽＝（∂/∂x,∂/∂y,∂/∂z）であるのじゃが、xy平面上で考えると、ベクトル関数Aを特に（－y，x，0）とすれば、左辺の面積分は、∫［0,0,2］・[0,0,1］dS＝2Sとなる。
一方、右辺は、dt＝［dx，dy，0］として、∫（xdy－ydx）となるので、Σ（xi（yi+1－yi）－yi（xi+1－xi））＝Σ（xiyi+1－yixi+1）。」
「するってぇーと。3次元の任意の多角形の面積は、面の法線ベクトルを（nx，ny，nz）として、特に、A＝（nyz－nzy，nzx－nxz，nxy－nyx）と選べば、
面積分は、∫[2nx，2ny，2nz］・［nx，ny，nz］dS＝2Sとなる。
問題の右辺は、∫（nyz－nzy）dx＋（nzx－nxz）dy＋（nxy－nyx）dz＝Σ（（nyzi－nzyi）（xi+1－xi）＋（nzxi－nxzi）（yi+1－yi）＋（nxyi－nyxi）（zi+1－zi））。
整理すると、nxΣ（yizi+1－ziyi+1）＋nyΣ（zixi+1－xizi+1）＋nzΣ（xiyi+1－yixi+1）となる。
xy平面上では、nz＝1、それ以外はゼロなので、前式に一致するわね」
「Aのテスト関数によう、気がついたな。
ただ、法線ベクトルの成分は、頂点の座標値で決定できるはずじゃ。
今、多角形の載っている平面を考えて、その方程式をαx＋βy＋γz＋δ＝0としよう。
平面は、3点の頂点を持つ多角形があれば、決定できるので、α、β、γ、δのうち3つが独立なのじゃが、測定誤差を考えると、∂/∂αΣ（αxi＋βyi＋γzi＋δ）2＝0などと置き、これらの4つの式から、α、β、γ、δを決定するのが良いじゃろうな」
「αなどが決定できると、nxなどが決定できる訳ね。でも、具体的には、どうすれば、いいのかしら」
「場合を分けて、考えてみよう。まず、γ＝0のときは、どうじゃな」
「γ＝0のときは、αx＋βy＋δ＝0で、平面は、z軸に平行である。更に、β＝0のときは、x＝－δ/αというx軸に垂直な平面であるので、nx＝1、ny＝nz＝0。
同様に、α＝0の時は、ny＝1、nx＝nz＝0。
で、問題は、αβ≠0のときね」
「α、βがいずれもゼロでないときは、平面上の1点（x，y）は、αx＋βy＋δ＝0を満たす。
同一平面上のQ（x＋dx、y＋dy）を考えると、ベクトルPQと法線ベクトル（nx，ny）は、垂直である。（z軸に平行なので、nz＝0）
となると、nxdx＋nydy＝0、一方、平面の方程式から、αdx＋βdy＝0なので、dy/dx＝－α/βから、ny＝β/αnx、nx2＋ny2＝1を使うと、
nx = ±α/√(α2 + β2)、 ny =± β/√(α2 + β2))、ここで、符号同順となる」
「これを見ると、γ＝0の時は、α、βのいずれかがゼロの場合も含めて、この式で表せるのね」
「次は、γ≠0の時じゃな。このとき、平面の式は、γで割って、z＝－（α/γ）x－（β/γ）y－（δ/γ）となる。先ほどと同様に考えるとどうじゃな」
「う～ん。Qとして、（x＋dx、y＋dy、z＋dz）を取ると、nxdx＋nydy＋nzdz＝0となる。dz＝－（α/γ）dx－（β/γ）dyなので、dx、dyの任意性を利用すると、
nx = ±α/√(α2 + β2 + γ2) 、 ny = ±β/√(α2 + β2 + γ2)、nz=±γ/√(α2 + β2 + γ2)となる。」
「そのとおりじゃな。結果を見ると、α、β、γのすべてがゼロでない限り、これらの式で良いことになるの。ま、もっとも、すべてがゼロでは平面にはならない」
「符号はどう取ればよいのかしら」
「実は、先ほどの条件式のうち、2つの式から、nx、nyが求まるが、3つ目の式から、この2つは、同符号でなくてはならないことが分かる。そして、その符号が正の場合は、nzも正号、負の場合は、負号をとる必要があるのじゃ」
「すると、整理すると、
nx = α/√(α2 + β2 + γ2) 、 ny = β/√(α2 + β2 + γ2)、nz=γ/√(α2 + β2 + γ2)
または、nx = －α/√(α2 + β2 + γ2) 、 ny =－β/√(α2 + β2 + γ2)、nz=－γ/√(α2 + β2 + γ2) ということなのね」
「そういうことじゃ。もっとも、今の場合、この平面のどちら側が外部なのか、これだけでは、分からないので、2組の解があるのじゃが、次のように考えると、どちらなのかを判断できる。
内側から見て、右ねじを回す方向に番号付けがなされているとすれば、Σri×ri+1と同方向のnxの組を選択すればよい」
「空間上の任意の3角形を考える。頂点をP1などと決めるが、見やすいように原点をP1に選ぶ。面積はどうなるかの」
「ヘロンの公式（注）を使うと、長さだけで面積Sが表せるけど、6つのパラメータ（座標）を持つので、ちょっと長い式にはなるわね」
「前節のストークスの定理から導いた式ではどうなるかの」
「まずは、平面の方程式の係数を決めなきゃということで、∂/∂αΣ（αxi＋βyi＋γzi＋δ）2＝0などだけど、原点を通るので、最初から、δ＝0と置いていいわね。
γがゼロでないと仮定すると、αx＋βy＋γz＝0で、全体をγで割ったとして、新しい係数を改めて、αなどと書くことにすれば、あるいは、同じ事だけど、γ＝1とすれば、α
= (y2z3 － y3z2)/(x2y3 － x3y2)、β = (x3z2 － x2z3)/(x2y3 － x3y2)、γ＝1となる。
nx = α/√(α2 + β2 + γ2) などから、分かる。
なお、添え字は、DERIVEの式をそのまま貼り付ける関係で、nxと書くべきところをnxなどと書くことにすれば、
nx＝ (y2z3 － y3z2)SIGN(x2y3 － x3y2)/√(x2^2(y3^2 + z3^2) － 2x2x3(y2y3 + z2z3)
+ x3^2(y2^2 + z2^2) + (y2z3 － y3z2)^2) などが求められる」
「一方、2S＝nxΣ（yizi+1－ziyi+1）＋nyΣ（zixi+1－xizi+1）＋nzΣ（xiyi+1－yixi+1）なので、この式に代入する必要があるの」
「第1項のΣは、（y2z3－z2y3）、第2項のΣは、（z2x3－x2z3）、第3項のΣは、（x2y3－y2x3）である。代入すると、
2S＝√(x2^2(y3^2 + z3^2) － 2x2x3(y2y3 + z2z3) + x3^2(y2^2 + z2^2) + (y2z3
－ y3z2)^2)SIGN(x2y3 － x3y2) 。
ヘロンの公式との一致は、双方を2乗して引き算をすることにより、ゼロとなったことで確認できたわ」
「うん。複雑にはなるが、ヘロンの公式は3角形しか適用できんからな。
さて、本題の、Σri×ri+1の値が気になるところじゃが」
「この場合は、ABS（Σri×ri+1）/2 と上で求めた面積Sの式は、一致したわ」
「一般にはどうなるかじゃな」
（注）ヘロンの公式
s＝（a＋b＋c）/2 と置くとき、三角形の面積は、√s（s－a）（s－b）（s－c） で表すことができる。ここで、a、b、cは三角形の3辺の長さ。
「上記で分かったと思うのじゃが、Σri×ri+1を座標で表すと、実は、［Σ（yizi+1－ziyi+1），Σ（zixi+1－xizi+1），Σ（xiyi+1－yixi+1）］となるのじゃな。
これを簡単に X＝［ｕ，v，w］と表してみよう。u＝Σ（yizi+1－ziyi+1）などじゃ。
一方、4節のストークスの定理から求めた式では、2S＝nxu＋nyv＋nzw であるが、これを ［nx，ny，nz］・［ｕ，v，w］とベクトルの内積で書き直すと、2S＝n・X と書けることに気がつくじゃろう。ここで、「・」は、内積を表す。
よく知っているように、内積の別の表現では、2S＝ABS（n）ABS（X）cosθ＝ABS（X）cosθ 。θは、法線ベクトルnとXがなす角度じゃ。
そこでじゃ、その大きさはともかくとして、ri×ri+1の方向だが、たとえば、始点P1を原点に考えれば、平面上のベクトル同士の外積ベクトルの方向は、平面に垂直な成分しか持たないことが分かる。従って、そのベクトル和も垂直成分のみから、θが0となるので、2S＝ABS（X）cosθ＝ABS（X）。
すなわち、Xの大きさは、2Sであることが証明できたというわけじゃよ」
「なるほど。でも、原点が別の場所にあれば、どうかしら」
「r1からの相対ベクトルをRi＝ri－r1 で、定義すると、Σri×ri+1＝Σ（Ri＋r1）×（Ri+1＋r1）＝ΣRi×Ri+1＋r1×Σ（Ri+1－Ri） 。
第2項のΣは、恒等的にゼロとなるので、相対ベクトルで書いても同一の表式となることが分かり、原点をP1に移すという便宜的な証明方法で問題は、ないのじゃよ」
「となると、3次元空間上の多角形の面積公式としては、結局のところは、S＝ABS（Σri×ri+1）/2 として、良い訳ね」
「そうじゃ。ストークスの定理をそのまま、利用する方法では、あとで消去する、α、βなどやnxなどを経由するので、手間がかかるからの。ま、もっとも、実数の座標値だけであれば、計算そのものは、大した手間ではないとも言えるが」
「幾何学的には、証明できないのかしらね」
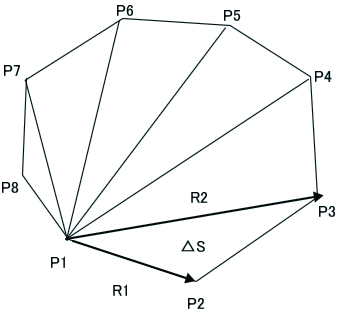
「そうじゃな。凸多角形ならば、分かりやすいの。相対ベクトルで考えると、Ri×Ri+1＝nRiRi+1sinθi＝（P1－Pi－Pi+1で形作る小三角形の倍面積）n 。
ここで、nは、法線ベクトル。その和が凸多角形の倍面積になることは、直感的にも明らかじゃな」
※ サイト内リンク（2020/11/8追記）
多角形及び多面体の重心と高次のモーメント（1）
多角形の面積と重心を求めるExcelブックをダウンロードできます。
多角形及び多面体の重心と高次のモーメント（2）
多面体の体積と重心を求めるExcelブックをダウンロードできます。
多角形及び多面体の重心と高次のモーメント（3）
慣性モーメント、慣性乗積について、解説しています。
最終更新日：2008/8/20
リンク追加：2020/11/8
リンク追加：2022/1/7
※ 2008/10/25 ヘロンの公式に関する注の係数が間違っていましたので、修正しました。
