
2014年の年賀状から
「続きはウェブにて」の続き
道中双六
宿場数が1の場合
宿場数が2の場合
宿場数が2の場合(別解その1)
宿場数が2の場合の別解2(2014/1/4追記)
終わりにあたって
「さあ、寄ってらっしゃい、見てらっしゃい。昔懐かしい「道中双六」だよ。
日本橋を振り出しに東海道最初の宿場は、品川宿。間を端折って、五十三個目が大津宿、上がりは花の都は京の三条大橋だ。
今年は午年、馬と宿場は縁があるんだ。元は駅と言っていた。電車じゃないのよ。停まるのは。
昔、中国で馬を置き通信の便にあてそれを驛と言った。驛の字が馬偏だ。簡単に言えば、馬の乗り継ぎ所。五十三「次」や「駅伝」にいわれが残る。
なに、この双六は、宿場の数が少ないとな。なんと、賢い、お客様。お客様は神様だ。
ここからが肝心だ。急に難しくなっちゃうよ。
この双六の宿場では、確率 Pで一つ進み、確率(1-P)で一つ戻る。
振り出しは常に一つ進み、上がりは双六から消えちゃうよ。
さあ、そうすると、どうなるか。ドウと鳴らなきゃ、カンと鳴る。カントは、ドイツの哲学者。
P=1ならば宿場毎に1日を費やすと最短で宿場の数に一を加えた日数だ。
P=0ならば、上がらない。誰もやらないよ。つまらないから。
しかれども、その刻遅く、彼の刻早く、Pが0と1の間の値を取ったなら、平均、最短の何倍で上がれるかが問題と、言ってるそばから日が暮れる。
蕎麦は長いが日は短い。カラスと一緒に帰ります。
続きは、ウェブにてと、向後万端よろしくお願い申し上げます。」
(2014年年賀状から)
目次に戻る
 「あけましておめでとうございます」
「あけましておめでとうございます」
「おう、ともちゃんか。
おめでとうさん。今年もよろしくな」
「おじさん、年賀状、ありがとうございます。
スゴロクって、「双六」なのね。カタカナ感覚だったけど」
「元は、2つのサイコロを振ったから、その和が最大になるのは、両方が6の場合じゃ。それを「双六」と呼んだという説があるそうじゃ。
2011年のNHK大河ドラマの「平清盛」に、「双六」をやる場面がしばしば出てきたな」
「なんか、チェスみたいなやつね」
「盤を使うゲームを今では、「盤双六」、道中双六のような現代に言うところの双六を「絵双六」というそうじゃ。
平安の昔に流行った「盤双六」の正確なルールは、伝わっておらんらしいが、「バックギャモン」と似ているらしい。
道中双六のような「絵双六」は、江戸時代前期に、「盤双六」から分かれて誕生したということのようじゃな。
バックギャモンは、Windowsの「ゲーム」にも、入っているところを見ると、西洋では、親しまれているようじゃ。
とは言いつつ、わしは、バックギャモンを知らんがの」
「あたしは、人生ゲームで遊んだ記憶があるわ」
「まあ、そうかも知れん。
タカラトミーのホームページでは、「人世ゲーム」の歴史について、説明している。http://www.takaratomy.co.jp/
アメリカ生まれのゲーム「THE GAME OF LIFE」は、1968年に日本で「人世ゲーム」として、発売されたということじゃ」
「人世ゲームがアメリカの「ミルトン・ブラッドレー」という若い人がキリスト教の教えを示すゲームとして1860年に作ったことは、知らなかったわ」
「1860年(万延元年)というと、日本では、幕末じゃな。
人世ゲームにそんな歴史があることは、知らなかった。日本に古くからある絵双六と類似していたため、分かりやすいこともあり流行したとあるな」
「なるほどね。
投資とか不動産の売買とか、プレイヤーの選択手段が豊富だったこともあると人気が出た理由だと思うわ」
目次に戻る
「絵双六は、日本でも、昔は、仏教などの教えを面白く広める目的で工夫されたらしい。
徐々に、ゲームとしての面白さを増す仕組みを取り入れていったとのことじゃ。
わしが子供の頃に遊んだ双六がどんな絵柄だったかは、とても記憶がないが、特定のマス目に「1が出たら振り出しに戻る」とあるのに、そこで 1を出してしまったときの残念!感は、しっかりと覚えているな」
 「今回の双六では、振り出しから、1つずつ進み、1つずつ戻る、という単純なルールなのね」
「今回の双六では、振り出しから、1つずつ進み、1つずつ戻る、という単純なルールなのね」
「そうじゃな。ゲームとしての面白みには欠けるがの。その分、解析しやすいじゃろう。
また、双六を離れて、通信路などのエラーと読み替えるのも面白いのではないかと思う」
「なるほど。
TCPの通信では、バケットのエラーが発生すると再送する仕組みがあるからね」
「さて、ここで、今回の道中双六の問題(以下「双六の問題」という)のルールをおさらいしておこう。
1.駒は、振り出しから、必ず、1番目の宿場に進める。
2.駒は、各宿場で、確率Pで、次の宿場に進み、確率(1-P)で1つ戻るものとする。
3.駒が最後の宿場から上がりに進んだときは、双六上から消える。
4.駒どおしの関係は、無いものとする。
5.振り出しから、1番目の宿場まで、及び、各宿場間、並びに、最後の宿場と上がりまでの所要時間は、同一とし、1日と勘定する」
「付け加えると、少なくとも、1つの宿場があるとする訳ね。
双六の問題では、振り出しから上がりまでの日数の平均値が最短日数の何倍かを答えよ、ということね」
 「まあ、そういうことじゃな。
「まあ、そういうことじゃな。
昨年のお正月の今月のご挨拶のテーマは、覚えているかな?」
「干支拳でお正月でしょう。2012年1月のテーマは、「じゃんけん」だった」
「そう。干支拳で・・では、じゃんけんの「手」を、グー、チョキ、パー以外にも増やした時のあいこの確率やゲームの種類の総数などの問題を扱ったのじゃな。
あれから、もう1年が経ったということかの」
「今回の問題では、確率Pで、勝つと、1つ進めることは、じゃんけんなどと同じね」
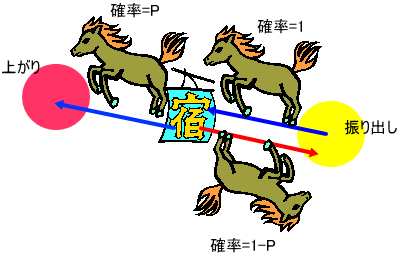
「上の図は、宿場数が1の時の図じゃ。
宿場数が、sのとき、最短日数で上がれる確率を求めよという問題であれば、答えは、p^s、となって、(広義の)じゃんけんで勝ち続ける確率の問題と同様だ。
しかし、今回の双六では、確率1-Pで、1つ戻ることに注意する必要がある」
「そうね。じゃんけんと同一視は出来ないということになるわね」
「似て非なる問題というわけじゃ。
勝ち数の合計が駒を進めることができた宿場数に等しいとは限らない。
なお、双六の問題では、振り出しから上がりまでの日数の平均値(期待値)が最短日数の何倍かを問うていて、最短日数を単位としているが、それは、本質的なことではない。
平均値が宿場数sにどのように依存しているかを分かりやすくしたかっただけのことじゃ」
目次に戻る
「宿場数が1の場合の双六の問題の答えを先に言うてしまうと、振り出しから上がりまでの日数の平均値は、2/p、となるので、答えは、最短日数(2日)の1/p倍ということになるの」
 「じゃ、あたしが説明するけど、宿場数は、s=1ね。
「じゃ、あたしが説明するけど、宿場数は、s=1ね。
ここで、確率pは、0<p<=1として、最短で上がれる場合を、2=+1+1、と略記するわよ。
この最短日数で上がれる確率は、p、に等しい。左辺の2は、所要日数を表し、右辺の+は、pで次へ1つ進めたことを表します。
また、右辺の太字は、確率1で進むことを意味すると約束する。(右辺の式は、左端を先頭として、振り出しから始める)
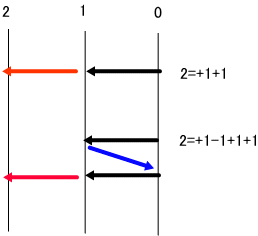 1の個数が上がりまでの日数を表します。
1の個数が上がりまでの日数を表します。
そして、2日の次は、3日はなくて、4日ということになるけど、
2=+1-1+1+1、ここで、-は、(1-p)で1つ戻ることを意味する。
(ここでは、宿場から振り出しに戻り、また、出発して宿場まで、計2日)
この確率は、p(1-p)となる。
※上図で、0は、振り出し、1は宿場、2は、上がりを示す。
※黒線は、確率1での推移、赤線は、確率P、青線は、確率(1-P)での推移をそれぞれ表す。
以下、6日は、2=+1-1+1-1+1+1、これは、確率 p(1-p)^2、などとなるので、
結局、2m+2日で上がれる確率は、p(1-p)^m、である。(m=0~の整数)
これから、求めたい平均日数(振り出しから上がりまでの日数の期待値)は、
Σ(2m+2)p(1-p)^m=2/p - 2(1 - p)^(n + 1)(np + p + 1)/p、m=0、1・・n。
0<p<=1なので、n→∞とすると、この値は、2/p、となる」
「念のため、Σp(1-p)^m=1 - (1 - p)^(n + 1)、なので、0<P<=1 ならば1に収束する事が分かる。
確率密度関数の近似など、興味のあるところは、あるが、今は、これくらいにして、宿場数が2の場合に進もう」
目次に戻る
 「じゃ、宿場数sが2の場合を考えてみるよ。
「じゃ、宿場数sが2の場合を考えてみるよ。
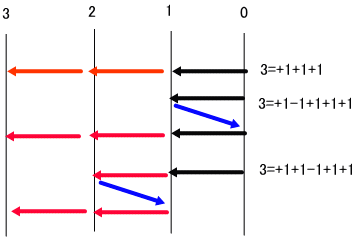
※上図で、0は、振り出し、1と2は宿場、3は、上がりを示す。
※黒線は、確率1での推移、赤線は、確率P、青線は、確率(1-P)での推移をそれぞれ表す。
まずは、最短日数は、3で、確率は、p^2。
次に短い日数は、5で、これには、2とおりがあるの。
一つは、上図の2番目の経路で、3=+1-1+1+1+1であり、確率は、(1-p)p^2。
もう一つは、図の3番目の経路で、3=+1+1-1+1+1であり、確率は、p^3(1-p)。
次の日数は、7。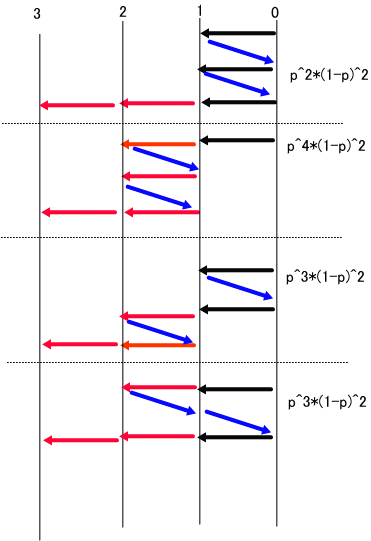
これには、上図のように、4とおりがある。(異なる確率の組としては、3とおり)
右側の、p^2(1-p)^2などは、確率。
更に、9の場合は、下図のように8とおりとなる。(異なる確率の組としては、4とおり)
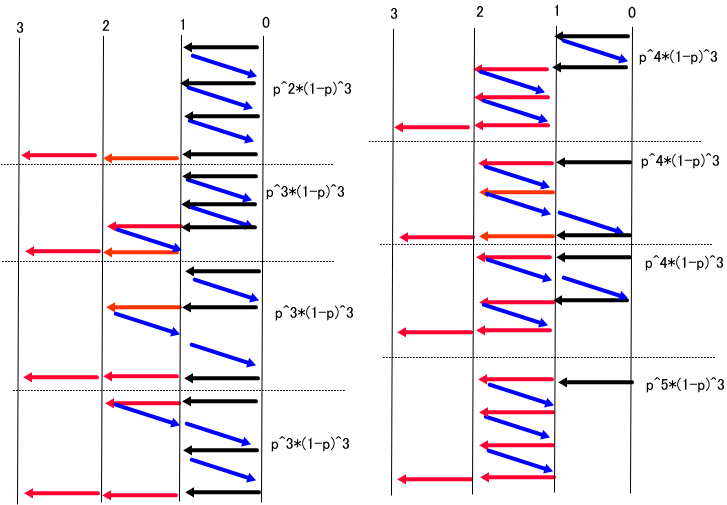
これらから、一般に、0と1の間で折り返す組数をAとし、1と2の間での折り返し組数をBと書くと、
m=0、1、・・の整数として、2m+3=3+2A+2B、ここで、左辺の2m+3は、日数の計である。
これから、A+B=m。
m=0の場合は、A+B=0 → A=B=0、確率は、p^2。
m=1の場合は、A+B=1 → A=1 ∩ B=0、又は、A=0 ∩ B=1。確率は、(1-p)p^2+p^3(1-p)。
一般のmの場合の確率は、Σ(A=0~m)Comb(m,A)×(1-p)^m×p^(m-A+2)、となる。
よって、宿場数2の場合の日数の平均値は、
Σ(m=0~∞)(2m+3)(Σ(A=0~m)Comb(m,A)×(1-p)^m×p^(m-A+2))、となるんだけど。
この先がきれいにいかないの」
「計算はあっているがの。
ついでに言うておくと、Comb(a,b)は、おなじみの組合せ、aCb を示す「DERIVE」の記号じゃな。
ところで、ともちゃんが示してくれた、2m+3日の確率の式、
Σ(A=0~m)Comb(m,A)×(1-p)^m×p^(m-A+2)、は次のように変形出来る。
p^2ΣComb(m,A)×(1-p)^m×p^(m-A)=p^2×(1-p)^m×(1+p)^m、これから、
p^2(1-p^2)^m、と簡単になって、
平均値は、Σ(m=0~∞)(2m+3)×p^2(1-p^2)^m=(p^2+2)/p^2となる」
「なるほど。
そうすると、宿場数が2の場合の双六の問題の答えは、(p^2+2)/(3p^2)で、例えば、p=1/2のときは、3(倍)となる訳ね。
おじさんは、どんな風に考えたの?」
「それでは、次節で、そのあたりを説明してみよう」
目次に戻る
「ともちゃんの結果を見て、実は、ぎくっとしたのじゃよ。
と言っても、ぎっくり腰ではないぞ。
それは、確率の式がわしのと違っているように見えたからじゃが、前節のように、変形出来るので等しいことが分かったので、安心した。
では、わしの考えを説明しようかの。
宿場を含めて、場所を、j=0~s+1で表す。これまでと同様に、j=0は、振り出し、j=s+1は、上がりじゃ。
j=jにk日で到達する確率を、f(j,k)で表す。k>0の整数じゃ。
このとき、以下の式が成り立つと考えられる。
f(s+1,k+1)=p*f(s,k)、上がり側
f(s,k+1)=p*f(s-1,k)、上がり側の最後の宿場
f(1,k+2)=(1-p)*f(1,k)+(1-p)*f(2,k+1)、振り出し側の最初の宿場(1)
f(1,1)=1、f(2,2)=p、振り出し側の最初の宿場(2)
途中の宿場の式(略)
s=2の場合は、以下となる。
f(3,k+1)=p*f(2,k)
f(2,k+1)=p*f(1,k)
f(1,k+2)=(1-p)*f(1,k)+(1-p)*f(2,k+1)
f(1,1)=1、f(2,2)=p
これらから、f(3,2m+3)=p^2*(1-p^2)^m、を導くことが出来る。
ただし、m=0、1、・・」
 「s>2の一般の場合は、どうなるかよね。
「s>2の一般の場合は、どうなるかよね。
途中の式を省略したのは、どうしてかしら?」
「宿場の数が3以上の場合は、実例で確かめていないのでな。(ちょっと自信がないからな)
それにもうすぐ、大晦日の除夜の鐘も鳴ってしまいそうなので、この続きは、次回の今月のご挨拶に回させてもらうことにしたいのう」
「分かりました。
勘弁してあげましょう。
では、みなさま、今年も、よい1年になりますことを、お祈り申し上げます」
目次に戻る
「お正月休みの間に少し考えましたぞ」
 「ははあ、双六をやりながらですか」
「ははあ、双六をやりながらですか」
「そういうわけじゃないがな。
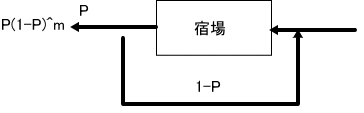
もっとエレガントな解答がありそうなものだと思ってな。
こう考えてみたのじゃ」
「なるほど」
「まだ、何も言っておらんじゃろうが。
上の図で、宿場数が1の場合じゃが、宿場に1回寄る度に確率Pで上がることが出来た。
ところが、2つ目の宿場があることにより、最短で上がる確率がPからP^2に変わったと考えられる。
さすれば、宿場数が1つの確率の式のPをp^2で置き換えたものが宿場数2の場合の確率密度であると思われる。
従って、P(1-P)^m → P^2(1-P^2)^m 、
ただし、最短日数が1日増えることにより、日数 2m+2に1を加えて、2m+3日の時の確率、となるのではないかとな」
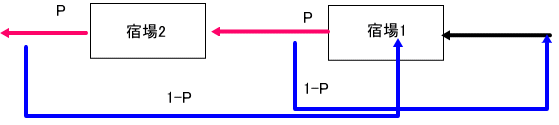
「ううう。それだとすごいけど。
でも、それは、まだ証明ではないでしょ。
上のダイアグラムを下図のように変形出来ることを意味しているものね」
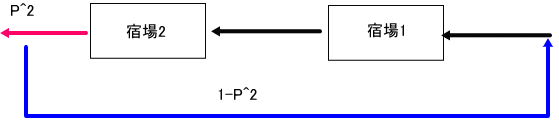
「まあ、そう言われると、少し、自信がないな」
目次に戻る
今回もご覧いただき、ありがとうございました。
本年、2014年4月9日に、いよいよ、Windows XPとOffice 2003 に対するマイクロソフト社のサポートが終了を迎えます。
それまでに3ヶ月となったわけです。Office 2002までのサポートは、すでに終了しています。
サポート終了後、インターネットに接続して利用するパソコンでは、セキュリティが厳しい状態になります。
Windows 7、または、Windows 8、Windows 8.1 搭載のパソコンに買い換えましょう。もはや、考えている時間は、ありません。
特に、Windows 7のプリインストールパソコンは、量販店では、既に販売されておりませんので、通販サイト等を利用する必要があります。年度末が近づくとこれらは、品薄となり得ますので、早めに対処する必要があるでしょう。(参考URL:http://www.nikkeibp.co.jp/xp2014/)
なお、当教室でも、Office2003関係コースの新規受講受付を2013/12末で終了いたしました。
ご了承下さいますようお願い申し上げます。
では、次回も、また、本欄で元気にお会いできますことを願っています。
目次に戻る
作成日 2014/1、目次を追加 2019/5/5