数式処理ソフト DERIVE(デライブ) de ドライブ
76.多角形及び多面体の重心と高次のモーメント(2)
(0)目次
(1)反省会
(2)多面体の重心 (多面体の重心を求める公式を推測)
(3)例題1 凸多面体 ((2)の方法を適用して確認)
(4)多面体の重心(ガウスの定理) (ガウスの定理を使用して重心公式を導く)
(5)例題2 原点から離れた位置にある三角錐 ((2)の方法と(4)の方法とを併用して比較)
(6)例題3 凹んだ多面体 ((2)の方法と(4)の方法とを併用して比較)
(7)多面体の体積・重心のまとめ ((2)と(4)の方法とは、同一であることを説明。併せて、多面体の体積公式も簡単化)
(8)多面体の高次のモーメント (体積、重心、慣性モーメント等の高次のモーメント)
(9)多面体の体積と重心位置を求めるExcelブック (多面体の体積と重心を計算するExcelブックをダウンロードできます)
(1)反省会
 「何なの、反省会って?
「何なの、反省会って?
忘年会の間違いじゃないの」
「おう、ともちゃんか。
前回、第75回「多角形及び多面体の重心と高次のモーメント(1)」の(6)節の反省会じゃよ。
ほれ、3次元空間上の多角形の重心を求めるところに後から手を入れたじゃろう」
「ああ、そのことね。
頂点の座標値から多角形が存在する平面の方程式の係数を求める順序ね」
「そうじゃ。当初は、第39回にならって、
平面の方程式をαx+βy+γz+δ=0とした際、α等の4つのパラメーターについては、
∂/∂αΣ(αxi+βyi+γzi+δ)2=0、から、Σxi(αxi+βyi+γzi+δ)=0、
∂/∂βΣ(αxi+βyi+γzi+δ)2=0、から、Σyi(αxi+βyi+γzi+δ)=0、
∂/∂γΣ(αxi+βyi+γzi+δ)2=0、から、Σzi(αxi+βyi+γzi+δ)=0、
∂/∂δΣ(αxi+βyi+γzi+δ)2=0、から、Σ(αxi+βyi+γzi+δ)=0、
という「観測方程式」から決定すると書いたんじゃ。
最初の3つの方程式は、DERIVE画面では、
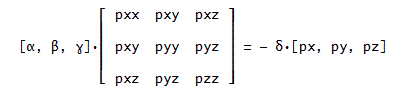
と整理できる。
ここで、
Pxx=Σx(i)^2、Pxy=Σx(i)y(i)、Pxz=Σx(i)z(i)、
Pyy=Σy(i)^2、Pyz=Σy(i)z(i)、Pzz=Σz(i)^2、
Px=Σx(i)、Py=Σy(i)、Pz=Σz(i)。
3つの方程式は、丁寧に書くと、次のようになる。
pxx α + pxy β + pxz γ = - px δ、
pxy α + pyy β + pyz γ = - py δ、
pxz α + pyz β + pzz γ = - pz δ、
そして、α等は、4つの内3つまでが独立なので、δ<>0の場合は、δ=1と置いてよいから、
結局、α等は、[α,β,γ]=-[px,py,pz]T ^-1、と求められる。(T^-1は、Tの逆行列)。
その後、面の法線方向の単位ベクトル n=[nx,ny,nz]を、
nx = ±α/√(α2 + β2 + γ2) 、
ny = ±β/√(α2 + β2 + γ2)、
nz=±γ/√(α2 + β2 + γ2)、
から、決めるつもりじゃったんだがな」
「例題では、うまくいっていたんだけど?」
「そこなんじゃ。そこと入っても、井戸の底ではないぞ。(何度も言っている気がするのう。年のせいかな)
例題では、偶々、多角形の乗る平面が普通というか、xy平面などに平行だったり、原点を通ったりするものではなかったのが幸いして、δを1と置いた場合に、α、β、γが3つとも決定できた。
ところが、座標値から、面積、重心を計算するExcelブックを作成して、テストしたところ、頂点総数が3点のような単純な例でも、うまく求められない場合があることに気がついたんじゃ」
「それが、xy平面に平行などの場合なのね」
「ま、そうじゃ。
実は、白状すると、α、β、γのいずれか1つがゼロとなる場合は、考えていたんじゃがな。
Tの対角要素である、pxx=Σx(i)^2、pyy=Σy(i)^2、pzz=Σz(i)^2 のいずれもゼロでない場合にも、行列式がゼロとなる(正則行列ではない)ケースがあったわけじゃ。
線形代数の基礎じゃなぁ。その辺の認識が甘かったと。まずは、1つめの反省点じゃ」
「ふ~ん。
まあ、ハンセイは、結構なんじゃないの。
しかし、面積ベクトルが面の法線方向を与えることは、わかりきってたことなのにね。
と言っても、あたしも、気がつかなかったから大きな事は言えないわね。
コロンブスのたまご的」
「2つめの反省点じゃ。
Excel計算表でうまく重心位置が算出できない例も含めて、α等を正しく計算しようと、1日~2日、うろうろと、ExcelのVBAをいじってみたんじゃ。
正則行列でない場合の処理が意外と面倒でな。ますます深みにはまった。
しかし、立ち止まって、よく考えてみると、答えは、面積計算の段階で、すでに出ていたのじゃ。
そこで、uvw系のw軸の単位ベクトルを面積ベクトルを基に決定とα等の決定→u軸の単位ベクトルの決定→v軸の単位ベクトルの決定→残差の計算、
という順序に変更したんじゃ。
δも、α、β、γを求めてから、4つめの方程式から、αΣx(i)+βΣy(i)+γΣz(i)+δ×頂点総数=0、
すなわち、δ=-(α Px+β Py+γ Pz)/頂点総数、としたため、δ=0 とδ<>0の場合を分けて考える必要もなくなった」
「最初は、α等の決定→uvw系のw軸の決定→面積ベクトルとの一致具合の判定→u軸の単位ベクトルの決定→v軸の単位ベクトルの決定、だったものね」
「連立方程式を解く必要もなかった。これで、VBAのコードも短く、非常に単純になった。
方程式が出てくると、まずは、解いてからと、考えるのは、盲点になるなあ。先入観を持ってはダメだと言うことだな。
まあ、全体の道筋は、合っていても、プログラムに実装すると、問題が出てくるのは、これまでの経験で分かっていても、あらためて、勉強になった」
「パチパチ。以上、反省会、おしまい」
目次へ戻る
(2)多面体の重心
「第75回の(7)節で、多角錘の重心位置を計算した。
図を再掲しよう。
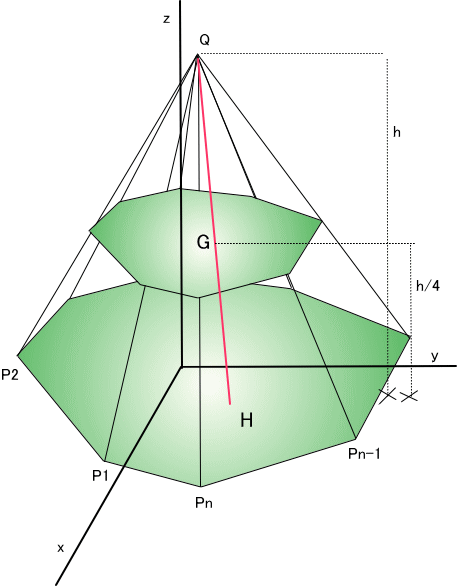
図のような、底辺が多角形の多角錘がある。底辺の多角形の重心をHで表す。
多角錘の重心 G は、HからQへの直線上にあり、HG=HQ×1/4である。
Hの位置は、第75回の方法で、多角形の頂点の座標値から、求めることができる
そこで、多角錘の重心位置は、原点を Oとすると、OG=OH+HQ×1/4=OH+(OQ-OH)/4=(1/4)(OQ+3*OH) と書くことができるじゃろう」
 「だけど、Qの位置が、面の法線方向にある場合、具体的には、下の図のような場合はどうなるのかしら?
「だけど、Qの位置が、面の法線方向にある場合、具体的には、下の図のような場合はどうなるのかしら?
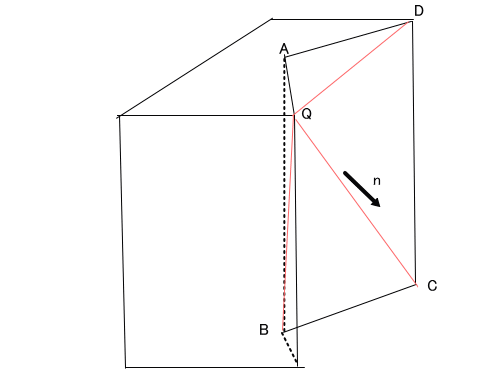
長方形 A-B-C-Dの面積法線 n は、図の矢印の向きでしょ。
このとき、Qが図の点であるとすると、この多角錘の重心寄与分は、マイナスになるべきでしょう」
「その部分は、多面体全体から見てへこんでいるのじゃから、体積の計算でマイナスとなればよいのではないか。
まとめると、OG= 1/(多面体の全体積)Σ(各面の和)((1/4)(OQ+3*OH))*多角錘の体積)、
となりそうじゃ。早速、次節の例題で検証してみよう」
目次へ戻る
(3)例題1 凸多面体
「第61回の「多面体の体積公式」で取り上げた例題じゃ。
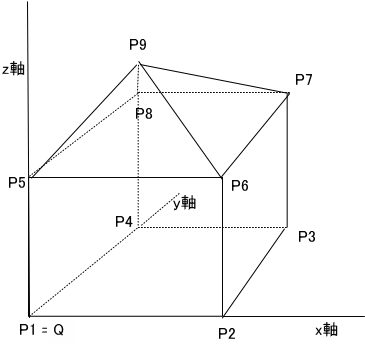
※第61回の記号の内、A をQに変えてあります。
各点の座標は、
P1:[0,0,0]、P2: [a,0,0]、P3: [a,b,0]、P4: [0,b,0]、P5: [0,0,c]、P6: [a,0,c]、P7:
[a,b,c]、P8: [0,b,c]、P9: [a/2,b/3,c+d]
ここで、パラメーター a,b,c,d は、正の実数とする。
この立体の体積Vは、V=abc + abd/3=ab(c+d/3)となる。
V=Σ(各面の和)(1/6)(r(1)-rq )・Σ(i=1~n)(ri×ri+1)、
なお、rqは、Q点の位置ベクトルじゃ。
各面を回る向きは、本稿に合わせて、多面体を外から見て、反時計回りになるように変えてあります。
1面:P1-P4-P3-P2 -> 0
2面:P1-P2-P6-P5 -> 0
3面:P1-P5-P8-P4 -> 0
4面:P3-P4-P8-P7 -> abc/3
5面:P2-P3-P7-P6 -> abc/3
6面:P5-P6-P9 -> abc/18
7面:P6-P7-P9 -> ab(c+2d)/12
8面:P7-P8-P9 -> ab(2c+3d)/18
9面:P5-P9-P8 -> abc/12
合計で、ab(3c+d)/3、となる。
というのが、第61回の結果じゃった。
とはいえ、重心まで含めると手計算では、間違えそうじゃ。
ともちゃん、DERIVEで、確かめてみてくれんかの」
 「分かりやした。
「分かりやした。
各面を別々に計算する方法でやってみるよ。
たとえば、1面では、x:=[0, 0, 0, 0, 0]、y:= [0, 0, 0, 0,0]、z:= [0, 0, 0, 0,0]、とする。
そして、rq:= [0, 0, 0]、
また、r(i):= [x↓i, y↓i, z↓i]、と定義する。
このとき、1面の体積分は、
Fv(n):= 1/6(r(1)- rq) ・ (∑(r(i) ⨯ r(i + 1), i, 1, n - 1) + r(n) ⨯ r(1))、で、n=4として、計算できる。
問題は、多角形と違って、頂点の番号が不規則なことよね。
そこで、
Px := [0, a, a, 0, 0, a, a, 0, a/2, 0]、
Py:= [0, 0, b, b, 0, 0, b, b, b/3, 0]、
Pz:= [0, 0, 0, 0, c, c, c, c, c + d, 0]、
とP1~P9までの座標値を、あらかじめ、Px、Py、Pzという3つのベクトルにセットしておく。
そして、関数 Fp(n1,n2,n3,n4,n5)を次のように定義する。(とりあえず、多角形の頂点が5個まで)
これは、Px ↓n1をx ↓1にセットすることにより、たとえば、1面であれば、Fp(1,4,3,2,0)とすることで、1面の頂点の座標値をx,y,zのベクトルの値として代入することができる。
Fp(n1, n2, n3, n4, n5):=
PROG(
IF(n1_ > 0,
PROG(x↓1 ≔ Px↓n1_, y↓1 ≔ Py↓n1_, z↓1 ≔ Pz↓n1_)),
IF(n2_ > 0,
PROG(x↓2 ≔ Px↓n2_, y↓2 ≔ Py↓n2_, z↓2 ≔ Pz↓n2_)),
IF(n3_ > 0,
PROG(x↓3 ≔ Px↓n3_, y↓3 ≔ Py↓n3_, z↓3 ≔ Pz↓n3_)),
IF(n4_ > 0,
PROG(x↓4 ≔ Px↓n4_, y↓4 ≔ Py↓n4_, z↓4 ≔ Pz↓n4_)),
IF(n5_ > 0,
PROG(x↓5 ≔ Px↓n5_, y↓5 ≔ Py↓n5_, z↓5 ≔ Pz↓n5_)),
true))、
※青字個所の一部に誤りがありましたので、2015/10/19に修正しました。
このように、「Prog」命令を使うと、複数の命令を列挙できる。
Prog(命令1,命令2,・・・)、これは、第69回の「方程式の数値解法(4)」で紹介されている。
これらを使って、例題の多面体の体積をあらためて、計算してみた。
下の表にまとめた。
| 面 |
多角形の頂点順 |
Fp() |
頂点総数 n |
体積 Fv(n) |
| 1 |
P1-P4-P3-P2 |
Fp(1,4,3,2,0) |
4 |
0 |
| 2 |
P1-P2-P6-P5 |
Fp(1,2,6,5,0) |
4 |
0 |
| 3 |
P1-P5-P8-P4 |
Fp(1,5,8,4,0) |
4 |
0 |
| 4 |
P3-P4-P8-P7 |
Fp(3,4,8,7,0) |
4 |
(a*b*c/3) |
| 5 |
P2-P3-P7-P6 |
Fp(2,3,7,6,0) |
4 |
(a*b*c/3) |
| 6 |
P5-P6-P9 |
Fp(5,6,9,0,0) |
3 |
(a*b*c/18) |
| 7 |
P6-P7-P9 |
Fp(6,7,9) |
3 |
(a*b*(c/12 + d/6)) |
| 8 |
P7-P8-P9 |
Fp(7,8,9) |
3 |
(a*b*(c/9 + d/6)) |
| 9 |
P5-P9-P8 |
Fp(5,9,8,0,0) |
3 |
(a*b*c/12) |
| 合計 |
|
|
|
(a*b*(c + d/3)) |
「なるほど。
この表に面積ベクトル、多角形のxyz系の重心、多角錘のxyz系の重心、を追加して欲しいのう」
「じゃ、まず、面積ベクトルを与える関数を、Fs(n)(nは、頂点総数)として、
Fs(n):= 1/2(∑(r(i) ⨯ r(i + 1), i, 1, n - 1) + r(n) ⨯ r(1))、
たとえば、6面では、Fp(6,7,9,0,0)、としてから、Fs(3)=[b*d/2, 0, a*b/4]、と求められる。
xyz座標系からuvw座標系に変換するには、[u,v,w]=([x,y,z]-r(1))*T、
ここで、Tは、回転行列なんだけど、これを決めるには、w軸の単位ベクトルを、s(n)=Fs(n)/ABS(Fs(n)、とする。
次に、u軸の単位ベクトルをpとして、p(n)∝(1/n)Σ(r(i)-r(1)、
最後に、v軸の単位ベクトルをq(n)として、q(n)=s(n)×p(n)とする。
まとめると、
s(n):= Fs(n)/ABS(Fs(n))、
p(n):=(1/n*∑(r(i), i, 1, n) - r(1))/ABS(1/n*∑(r(i), i, 1, n) - r(1))、
q(n):= s(n) ⨯ p(n)、
T(n):= [(p(n))↓1, (q(n))↓1, (s(n))↓1; (p(n))↓2, (q(n))↓2, (s(n))↓2; (p(n))↓3, (q(n))↓3, (s(n))↓3]、となる。
これらから、r(i)のuvw系の位置ベクトルを Fr(i,n)と書くと、
Fr(i,n):=(r(i) - r(1))*T(n)、と求められる。
更に、、x、y、z、に対応して、uvw系の座標値を格納するためのベクトルとして、u、v、w を定義する。
そして、r(i)↓1 → u↓iなどと代入する関数 Fuvw(n)を次のように定義する。
Fuvw(n):= PROG(VECTOR(u↓k ≔ (Fr(k, n))↓1, k, 1, n, 1), VECTOR(v↓k ≔ (Fr(k, n))↓2, k, 1, n, 1), VECTOR(w↓k ≔ (Fr(k, n))↓3, k, 1, n, 1))、
こうすると、多角形の重心Hのuvw系の座標は、[Hu(n),Hv(n),Hw(n)]、は、
Hu(n):= 1/6*ABS(Fs(n))*(∑((u↓i + u↓(i + 1))*(u↓i*v↓(i + 1) - u↓(i + 1)*v↓i), i, 1, n - 1) + (u↓n + u↓1)*(u↓n*v↓1 - u↓1*v↓n))、
Hv(n):= 1/6*ABS(Fs(n))*(∑((v↓i + v↓(i + 1))*(u↓i*v↓(i + 1) - u↓(i + 1)*v↓i), i, 1, n - 1) + (v↓n + v↓1)*(u↓n*v↓1 - u↓1*v↓n))、
Hw(n):=0、
と定義できる。
最後に、多角形のxyz系の重心 Hの位置ベクトル OHは、
OH:=[Hx(n),Hy(n),Hz(n)]として、
OH=[Hu(n),Hv(n),Hw(n)]]*T(n)` + r(1))、
Hx(n):=OH↓1、
Hy(n):=OH↓2、
Hz(n):=OH↓3、であ~る。 しんど」
「ようやってくれた。
あと少しじゃ。がんばれ」
「あんたは、言うだけかいな。
さてと、Qの位置は、多面体全体で固定しておかないといけないので、rq:=[Px↓1,Py↓1,Pz↓1]とする。
1/(多面体の全体積)Σ(多面体のすべての面についての和をとる)((1/4)(rq+3*OH))*多角錘の体積)において、
多角錘の重心のxyz系の位置は、OG:=[Gx(n),Gy(n),Gz(n)]、として、
OG(n):=1/4(rq + 3 OH(n))、
Gx(n):=OG(n)↓1、
Gy(n):=OG(n)↓2、
Gz(n):=OG(n)↓3、
と求められたのだ。
結果を下の表にまとめた」
| 面 |
頂点順 |
頂点数 n |
体積 Fv(n) |
面積ベクトル Fs(n) |
重心 OH(n) |
重心 OG(n) |
OG(n)×Fv(n) |
| |
多角形 |
多角錘 |
多角形 xyz系 |
多角形 xyz系 |
多角錘 xyz系 |
|
| 1 |
1-4-3-2 |
4 |
0 |
([0, 0, - a*b]) |
([a/2, b/2, 0]) |
([3*a/8, 3*b/8, 0]) |
([0, 0, 0]) |
| 2 |
1-2-6-5 |
4 |
0 |
([0, - a*c, 0]) |
([a/2, 0, c/2]) |
([3*a/8, 0, 3*c/8]) |
([0, 0, 0]) |
| 3 |
1-5-8-4 |
4 |
0 |
([- b*c, 0, 0]) |
([0, b/2, c/2]) |
([0, 3*b/8, 3*c/8]) |
([0, 0, 0]) |
| 4 |
3-4-8-7 |
4 |
(a*b*c/3) |
([0, a*c, 0]) |
([a/2, b, c/2]) |
([3*a/8, 3*b/4, 3*c/8]) |
([a^2*b*c/8, a*b^2*c/4, a*b*c^2/8]) |
| 5 |
2-3-7-6 |
4 |
(a*b*c/3) |
([b*c, 0, 0]) |
([a, b/2, c/2]) |
([3*a/4, 3*b/8, 3*c/8]) |
([a^2*b*c/4, a*b^2*c/8, a*b*c^2/8]) |
| 6 |
5-6-9 |
3 |
(a*b*c/18) |
([0, - a*d/2, a*b/6]) |
([a/2, b/9, c + d/3]) |
([3*a/8, b/12, (3*c + d)/4]) |
([a^2*b*c/48, a*b^2*c/216, a*b*c*(3*c + d)/72]) |
| 7 |
6-7-9 |
3 |
(a*b*(c/12 + d/6)) |
([b*d/2, 0, a*b/4]) |
([5*a/6, 4*b/9, c + d/3]) |
([5*a/8, b/3, (3*c + d)/4]) |
([5*a^2*b*(c + 2*d)/96, a*b^2*(c + 2*d)/36, a*b*(c + 2*d)*(3*c + d)/48]) |
| 8 |
7-8-9 |
3 |
(a*b*(c/9 + d/6)) |
([0, a*d/2, a*b/3]) |
([a/2, 7*b/9, c + d/3]) |
([3*a/8, 7*b/12, (3*c + d)/4]) |
([a^2*b*(2*c + 3*d)/48, 7*a*b^2*(2*c + 3*d)/216, a*b*(2*c + 3*d)*(3*c + d)/72]) |
| 9 |
5-9-8 |
3 |
(a*b*c/12) |
([- b*d/2, 0, a*b/4]) |
([a/6, 4*b/9, c + d/3]) |
([a/8, b/3, (3*c + d)/4]) |
([a^2*b*c/96, a*b^2*c/36, a*b*c*(3*c + d)/48]) |
| 合計 |
|
32 |
(a*b*(c + d/3)) |
([0, 0, 0]) |
|
|
([a^2*b*(3*c + d)/6, a*b^2*(36*c + 11*d)/72, a*b*(6*c^2 + 4*c*d + d^2)/12]) |
| 重心 |
|
|
|
|
|
|
([a/2,
b*(36*c + 11*d)/(24*(3*c + d)),
(6*c^2 + 4*c*d + d^2)/(4*(3*c + d))]) |
「どれどれ、これは、労作じゃな。
お疲れ様。
面積ベクトルの和は、常にゼロとなることに注意して欲しい。
さてと、正解を計算してみよう。
この例題の立体は、V1:直方体(底辺 a×b、高さ c)の上に、V2:四角錐(底辺 a×b、高さ d)を積み上げた形じゃ。
v1は、簡単じゃ。体積 abc、重心は、[a/2,b/2,c/2]、
V2は、体積は、簡単じゃが、重心は、ちょと、面倒だな。
V2の底辺の重心 Hは、OH=[a/2,b/2,c]、頂点 P9は、OP9=[a/2,b/3,c+d]、となるので、
ここで、V2の重心をG とすると、OG =(1/4)(OP9+3*OH)=([a/2, 11*b/24, c + d/4])、
これらを下の表に整理すると、多面体(V1+V2)の体積及び重心は、ともちゃんの計算してくれた表の値とピタリと一致したぞ」
| 立体 |
体積 |
重心 |
重心×体積 |
| V1 |
abc |
[a/2,b/2,c/2] |
([a^2*b*c/2, a*b^2*c/2, a*b*c^2/2]) |
| V2 |
abd/3 |
([a/2, 11*b/24, c + d/4]) |
([a^2*b*d/6, 11*a*b^2*d/72, a*b*d*(4*c + d)/12]) |
| 計 |
ab(c+d/3) |
|
([a^2*b*(c/2 + d/6), a*b^2*(c/2 + 11*d/72), a*b*(6*c^2 + 4*c*d + d^2)/12]) |
| 重心 |
|
|
([a/2,
b*(36*c + 11*d)/(24*(3*c + d)),
(6*c^2 + 4*c*d + d^2)/(4*(3*c + d))]) |
「まずは、めでたし、めでたし、というところかしら」
「次節で、別な角度から、研究してみよう」
目次へ戻る
(4)多面体の重心 (ガウスの定理)
「ガウスの定理を使ってみようというわけじゃ。
ベクトル点関数 F=[x^2,xy,xz]とすると、ガウスの定理、∫∫∫div(F)dV=∫∫F・dS、の左辺は、
div(F)=4 x、から、左辺=4∫∫∫x dV=4 V Gx、じゃ。
ここで、Gx=∫∫∫x dV/V、なる多面体の重心のx座標値、また、Vは、多面体の体積であることは、言うまでもない。
そこで、右辺が、問題となるのう」
 「右辺の積分内は、各面毎の和とする訳ね。
「右辺の積分内は、各面毎の和とする訳ね。
∫∫F・dS=Σ∫∫(x^2 Sx +xy Sy+xz Sz) dS、となる。
ここで、面積ベクトル S=[Sx,Sy,Sz]、また、その大きさを S =|S|と書いている。
今、ある面のみを考えて、Σの内部だけを取り上げると、面の方程式を、αx+βy+γz+δ=0と書くとき、
積分内、x^2 Sx +xy Sy+xz Sz =x(x Sx+y Sy+z Sz)、ここで、α=Sx/S、β=Sy/S、γ=Sz/S、とすることができるので、
積分内は、x(αx+βy+γz)となる。
よって、∫∫x^2 Sx +xy Sy+xz Sz dS=∫∫x (x(αx+βy+γz)dS=∫∫x (-δ)dS=-δ∫∫x dS、
ここで、∫∫x dS=S Hx、の関係を使うと、(OH=[Hx,Hy,Hz]は、面の重心)、
-δ∫∫x dS=-δ Hx S、となることが分かる」
「まとめると、
4∫∫∫x dV=4 V Gx=Σ(各面の和)(-δ Hx S)、から、
Gx=(1/4V)Σ(各面の和)(-δ Hx S)、となる。(δやHx、Sは、各面で一般には異なる)
一方、αx+βy+γz+δ=0 から、面の重心 H も当然、同じ面上にあるので、-δ=αHx+βHy+γHz、より、
Gx=(1/4V)Σ(各面の和)(-δ Hx S)=(1/4V)Σ(各面の和)(αHx+βHy+γHz)Hx S、
ここで再び、α=Sx/S、β=Sy/S、γ=Sz/S を使うと、
Gx=(1/V)Σ(各面の和)(Sx Hx+Sy Hy+Sz Hz)Hx / 4、
かっこ内の (Sx x1+Sy y1+Sz z1)=[Sx,Sy,Sz]・OH、であることに注意する。
同様のことを、y、zについても、行うと、
OG=[Gx,Gy,Gz]=(1/V)Σ(各面の和)(1/4)(S・OH)OH 、と綺麗な形となる」
「へー。
じゃ、例題で確認してみるよ。
| 面 |
頂点順 |
頂点数 n |
体積 Fv(n) |
面積ベクトル Fs(n) |
重心 OH(n) |
ガウスの定理による (S・OH)OH/4 |
| |
多角形 |
多角錘 |
多角形 xyz系 |
多角形 xyz系 |
|
| 1 |
1-4-3-2 |
4 |
0 |
([0, 0, - a*b]) |
([a/2, b/2, 0]) |
0 |
| 2 |
1-2-6-5 |
4 |
0 |
([0, - a*c, 0]) |
([a/2, 0, c/2]) |
0 |
| 3 |
1-5-8-4 |
4 |
0 |
([- b*c, 0, 0]) |
([0, b/2, c/2]) |
0 |
| 4 |
3-4-8-7 |
4 |
(a*b*c/3) |
([0, a*c, 0]) |
([a/2, b, c/2]) |
([a^2*b*c/8, a*b^2*c/4, a*b*c^2/8]) |
| 5 |
2-3-7-6 |
4 |
(a*b*c/3) |
([b*c, 0, 0]) |
([a, b/2, c/2]) |
([a^2*b*c/4, a*b^2*c/8, a*b*c^2/8]) |
| 6 |
5-6-9 |
3 |
(a*b*c/18) |
([0, - a*d/2, a*b/6]) |
([a/2, b/9, c + d/3]) |
([a^2*b*c/48, a*b^2*c/216, a*b*c*(3*c + d)/72]) |
| 7 |
6-7-9 |
3 |
(a*b*(c/12 + d/6)) |
([b*d/2, 0, a*b/4]) |
([5*a/6, 4*b/9, c + d/3]) |
([5*a^2*b*(c + 2*d)/96, a*b^2*(c + 2*d)/36, a*b*(c + 2*d)*(3*c + d)/48]) |
| 8 |
7-8-9 |
3 |
(a*b*(c/9 + d/6)) |
([0, a*d/2, a*b/3]) |
([a/2, 7*b/9, c + d/3]) |
([a^2*b*(2*c + 3*d)/48, 7*a*b^2*(2*c + 3*d)/216, a*b*(2*c + 3*d)*(3*c + d)/72]) |
| 9 |
5-9-8 |
3 |
(a*b*c/12) |
([- b*d/2, 0, a*b/4]) |
([a/6, 4*b/9, c + d/3]) |
([a^2*b*c/96, a*b^2*c/36, a*b*c*(3*c + d)/48]) |
| 合計 |
|
32 |
(a*b*(c + d/3)) |
([0, 0, 0]) |
|
([a^2*b*(3*c + d)/6, a*b^2*(36*c + 11*d)/72, a*b*(6*c^2 + 4*c*d + d^2)/12]) |
| 重心 |
|
|
|
|
|
([a/2,
b*(36*c + 11*d)/(24*(3*c + d)),
(6*c^2 + 4*c*d + d^2)/(4*(3*c + d))]) |
結果は、上表の通り。
合っているじゃん」
「なんと、なんと、ナントの勅令じゃ。
ただ、ガウスの定理を使って前節の方法を証明したことになるのかどうか?、という点じゃ。
すなわち、前節の方法は、
OG=1/VΣ(各面の和)((1/4)(OQ+3*OH))*多角錘の体積)、
一方、本節の方法は、
OG=1/VΣ(各面の和)((1/4)(S・OH)OH)、
となる」
「後の方法には、多角錘の体積の項がないわね」
「そうじゃ。
しかし、前者で、OQ=[0,0,0]と置くことができれば、OG=1/VΣ(各面の和)((1/4)(OQ+3*OH))*多角錘の体積)は、
=1/VΣ(各面の和)(1/4)(3*多角錘の体積)OH、
これと、後者の式を比較すると、一致するためには、3*多角錘の体積と(S・OH)が等しい必要がある。
仮に、等値すると、多角錘の体積=(1/3)(S・OH)、となるが、
右辺は、(1/3)|S||OH|cosθであり、底面積 |S|、高さ |OH|cosθの多角錘の体積を意味する。
|OH|は、原点と面の重心との距離であり、原点を頂点とし、面を底辺とする多角錘を表していることが分かる」
「あ、本当だ!
だけど、前節の OQのQは、多面体の表面又は内部の点と仮定してきたんだけど、後者の方法では、Qが原点で決め打ちは、いいのかな?」
「確かに、その点は、少し気になるな。
前節の例題では、多面体の頂点 P1は、原点でもあるので、違いが出てきていないかもしれん。
次節で別の問題に適用して、比較してみよう」
目次へ戻る
(5)例題2 原点から離れた位置にある三角錐
「例題1では、凸多面体の例を考えたが、頂点の一つを原点に置いていた。
今回の例題2では。原点から離れた位置にある下図のような三角錐を考えてみよう。
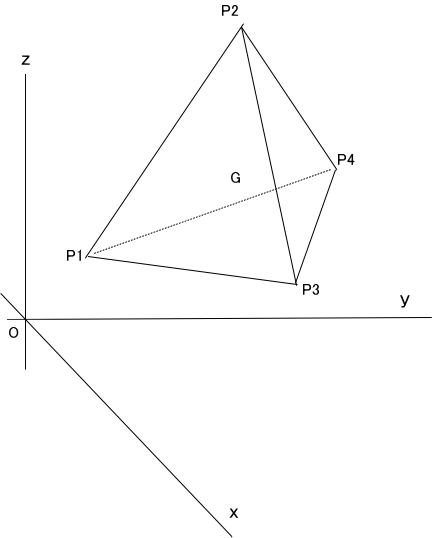
頂点の座標値は、P1[1,2,3]、P2[5,7,11]、P3[19,13,6]、P4[3,17,8]、とし、重心を Gで表す」
 「この三角錐の体積 Vは、V=((OP3-OP1)×(OP4-OP1))・(OP2-OP1)/6、となることは、第61回「多面体の体積公式」で説明している。
「この三角錐の体積 Vは、V=((OP3-OP1)×(OP4-OP1))・(OP2-OP1)/6、となることは、第61回「多面体の体積公式」で説明している。
また、重心 Gは、面(P1-P4-P3)の重心H から頂点 P2に引いたベクトルOH+(OP2-OH)/4、の位置にある。
すなわち、OG=(OP2-OH)/4、
具体的には、
V=802/3、
OH=(1/3)(OP1+OP3+OP4)、から、([23/3, 32/3, 17/3]、
OG=[7, 39/4, 7]、となる」
「よっしゃ。
まずは、(2)節の方法で検証してみよう。
Q点は、P1としている。
| 面 |
頂点順 |
頂点数 n |
体積 Fv(n) |
面積ベクトル Fs(n) |
重心 OH(n) |
重心 OG(n) |
OG(n)×Fv(n) |
| |
多角形 |
多角錘 |
多角形 xyz系 |
多角形 xyz系 |
多角錘 xyz系 |
|
| 1 |
1-4-3 |
3 |
0 |
([-5, 42, -124]) |
([23/3, 32/3, 17/3]) |
([6, 17/2, 5]) |
0 |
| 2 |
1-2-4 |
3 |
0 |
([- 95/2, -2, 25]) |
([3, 26/3, 22/3]) |
([5/2, 7, 25/4]) |
0 |
| 3 |
2-3-4 |
3 |
(802/3) |
([16, 26, 76]) |
([9, 37/3, 25/3]) |
([7, 39/4, 7]) |
([5614/3, 5213/2, 5614/3]) |
| 4 |
1-3-2 |
3 |
0 |
([73/2, -66, 23]) |
([25/3, 22/3, 20/3]) |
([13/2, 6, 23/4]) |
0 |
| 合計 |
|
12 |
(802/3) |
([0, 0, 0]) |
|
|
([5614/3, 5213/2, 5614/3]) |
| 重心 |
|
|
|
|
|
|
([7, 39/4, 7]) |
結果を見ると、体積及び重心とも一致した。
実は、最初、頂点の位置座標を文字にしていたのじゃが、どうも結果がおかしいので、数値で与えてみて分かった。
それで、調べて見ると、関数内の引数や変数が他の関数の計算に影響を与えている可能性があった。
関数の引数と関数内で使用している引数、変数をすべて、n_ のように、アンダーバー付きとした。
あらためて、使用した関数を修正して、列挙してみる。
1.ベクトル x、y、z に ベクトル Px、Py、Pzから、値をセットする--------
Fp(n1_, n2_, n3_, n4_, n5_) ≔
PROG(IF(n1_ > 0, PROG(x↓1 ≔ Px↓n1_, y↓1 ≔ Py↓n1_, z↓1 ≔ Pz↓n1_)),
IF(n2_ > 0, PROG(x↓2 ≔ Px↓n2_, y↓2 ≔ Py↓n2_, z↓2 ≔ Pz↓n2_)), IF(n3_
> 0, PROG(x↓3 ≔ Px↓n3_, y↓3 ≔ Py↓n3_, z↓3 ≔ Pz↓n3_)), IF(n4_ > 0,
PROG(x↓4 ≔ Px↓n4_, y↓4 ≔ Py↓n4_, z↓4 ≔ Pz↓n4_)), IF(n5_ > 0, PROG(x↓5
≔ Px↓n5_, y↓5 ≔ Py↓n5_, z↓5 ≔ Pz↓n5_)), true))、
2.x、y、z を基に頂点の位置ベクトルr(i)---------
r(i_) ≔ [x↓i_, y↓i_, z↓i_]、
3.多面体全体で共通の点 Q-----------
rq ≔ [0↓1, Py↓1, Pz↓1]、 (必要なくなりました)
4.底辺:r(1)~r(n)の多角形、頂点 原点の多角錘の体積---
Fv(n_) ≔ 1/3(r(1) ・Fs(n_))、(修正しました)
5.底辺:r(1)~r(n)の多角形の面積ベクトル--------
Fs(n_) ≔ 1/2*(∑(r(i_) ⨯ r(i_ + 1), i_, 1, n_ - 1) + r(n_) ⨯ r(1))、
6.面のw軸の単位ベクトル(法線)-------------
s(n) ≔ Fs(n)/ABS(Fs(n_))、
7.面のu軸の単位ベクトル----------------
p(n_) ≔ (1/n_*∑(r(i_), i_, 1, n_) - r(1))/ABS(1/n_*∑(r(i_), i_, 1, n_) - r(1))、
8.面のv軸の単位ベクトル-----------------
q(n_) ≔ s(n_) ⨯ p(n_)、
9.xyz系からuvw系への変換するための回転行列--------
T(n_) ≔
[(p(n_))↓1, (q(n_))↓1, (s(n_))↓1; (p(n_))↓2, (q(n_))↓2, (s(n_))↓2; (p(n_))↓3,
(q(n_))↓3, (s(n_))↓3]、
10.xyz系の座標からuvw系の座標を定義------------
Fr(i_, n_) ≔ (r(i_) - r(1))*T(n_)、 (19番の関数内に右辺を書き込んだので必要なくなりました)
11.面の重心のuvw系のu座標値---------------
Hu(n_) ≔
1/(6*ABS(Fs(n_)))*(∑((u↓i_ + u↓(i_ + 1))*(u↓i_*v↓(i_ + 1) - u↓(i_ + 1)*v↓i_), i_, 1, n_ - 1) + (u↓n_ + u↓1)*(u↓n_*v↓1 - u↓1*v↓n_))、
12.面の重心のuvw系のv座標値---------------
Hv(n_) ≔
1/(6*ABS(Fs(n_)))*(∑((v↓i_ + v↓(i_ + 1))*(u↓i_*v↓(i_ + 1) - u↓(i_ + 1)*v↓i_), i_, 1, n_ - 1) + (v↓n_ + v↓1)*(u↓n_*v↓1 - u↓1*v↓n_))、
13.面の重心のuvw系のw座標値---------------
Hw(n_) ≔ 0、
14.面の重心のxyz系の座標-----------------
OH(n_) ≔ [Hu(n_), Hv(n_), Hw(n_)]*T(n_)` + r(1)、
15.面の重心のxyz系のx座標値-----------------
Hx(n_) ≔ (OH(n_))↓1、
16.面の重心のxyz系のy座標値-----------------
Hy(n_) ≔ (OH(n_))↓2、
17.面の重心のxyz系のz座標値-----------------
Hz(n_) ≔ (OH(n_))↓3、
18.多角錘の重心のxyz系の座標-----------------
OG(n_) ≔1/4*(Fs(n_) ・ OH(n_))*OH(n_)、
19.xyz系の座標からuvw系の座標をセット-------------
Fuvw(n_) ≔
PROG(VECTOR(u↓k_ ≔ ((r(k_) - r(1))*T(n_))↓1, k_, 1, n_, 1), VECTOR(v↓k_ ≔ ((r(k_) - r(1))*T(n_))↓2, k_, 1, n_, 1), VECTOR(w↓k_ ≔ ((r(k_) - r(1))*T(n_))↓3, k_, 1, n_, 1))、
20.ガウスの定理から導いたxyz系の重心-------------
OGauss(n_) ≔ 1/4*(Fs(n_) ⋅ OH(n_))*OH(n_)、 (18番と統一しました)
となっている」
「なるほど。
複数の関数を使う場合は、気をつけないといけないわね。
ローカル変数とグローバル変数との区別がないみたい」
「そのようじゃな。
以前にも、この点を指摘したことがあったが、時間が経つと忘れてしまうな。
さて、ガウスの定理に基づいた方法を検証してみよう。
| 面 |
頂点順 |
頂点数 n |
面積ベクトル Fs(n) |
重心 OH(n) |
OG(ガウスの定理) |
| |
多角形 |
多角形 xyz系 |
多角形 xyz系 |
|
| 1 |
1-4-3 |
3 |
([-5, 42, -124]) |
([23/3, 32/3, 17/3]) |
([- 6739/12, - 2344/3, - 4981/12]) |
| 2 |
1-2-4 |
3 |
([- 95/2, -2, 25]) |
([3, 26/3, 22/3]) |
([141/8, 611/12, 517/12]) |
| 3 |
2-3-4 |
3 |
([16, 26, 76]) |
([9, 37/3, 25/3]) |
([4941/2, 6771/2, 4575/2]) |
| 4 |
1-3-2 |
3 |
([73/2, -66, 23]) |
([25/3, 22/3, 20/3]) |
([- 1325/24, - 583/12, - 265/6]) |
| 合計 |
|
12 |
([0, 0, 0]) |
|
([5614/3, 5213/2, 5614/3]) |
| 重心 |
|
|
|
|
([7, 39/4, 7]) |
ガウスの定理から導いた重心は、OG=1/VΣ(各面の和)((1/4)(S・OH)OH)、じゃった。
上の表では、OG(ガウスの定理)に各面の計算結果を記入した。結果は、一致した
これに伴い、新しい関数として、OGauss(n)を20番目として、前段の関数に追加しておいた」
「これで、ガウスの定理に基づく方法の信頼度は、グーンとアップしたね」
「確かにな。
次節では、へこんだ個所がある多面体に適用してみよう」
目次へ戻る
(6)例題3 凹んだ多面体
「凹んだ多面体を考えてみよう。
図のような三角柱の上部にくぼみのある多面体となる。
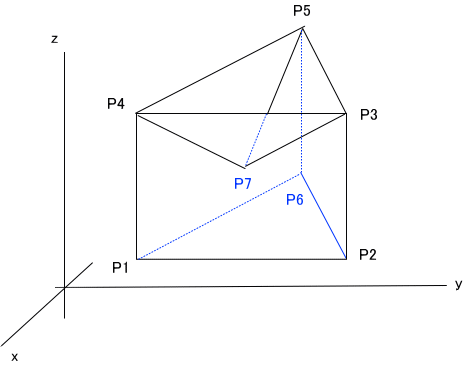
各点の座標じゃ。
P1[x1,y1,z1]、P2[x1,y1+a,z1]、P3[x1,y1+a,z1+b]、P4[x1,y1,z1+b]、
P5[x1-c,y1+a/2,z1+b]、P6[x1-c,y1+a/2,z1]、P7[x1-c/3,y1+a/3,z1+2b/3]、とする」
 「じゃ、あたしは、(2)節の方法でトライしてみるよ。(rq=[x1,y1,z1])
「じゃ、あたしは、(2)節の方法でトライしてみるよ。(rq=[x1,y1,z1])
| 面 |
頂点順 |
頂点数 n |
体積 Fv(n) |
面積ベクトル Fs(n) |
重心 OH(n) |
重心 OG(n) |
OG(n)×Fv(n) |
| |
多角形 |
多角錘 |
多角形 xyz系 |
多角形 xyz系 |
多角錘 xyz系 |
|
| 1 |
1-2-3-4 |
4 |
0 |
([a*b, 0, 0]) |
([x1, a/2 + y1, b/2 + z1]) |
([x1, (3*a + 8*y1)/8, (3*b + 8*z1)/8]) |
0 |
| 2 |
2-6-5-3 |
4 |
(a*b*c/3) |
([- a*b/2, b*c, 0]) |
([x1 - c/2, 3*a/4 + y1, b/2 + z1]) |
([(8*x1 - 3*c)/8, (9*a + 16*y1)/16, (3*b + 8*z1)/8]) |
([a*b*c*(8*x1 - 3*c)/24, a*b*c*(9*a + 16*y1)/48, a*b*c*(3*b + 8*z1)/24]) |
| 3 |
1-4-5-6 |
4 |
0 |
([- a*b/2, - b*c, 0]) |
([x1 - c/2, a/4 + y1, b/2 + z1]) |
([(8*x1 - 3*c)/8, (3*a + 16*y1)/16, (3*b + 8*z1)/8]) |
0 |
| 4 |
1-6-2 |
3 |
0 |
([0, 0, - a*c/2]) |
([x1 - c/3, a/2 + y1, z1]) |
([(4*x1 - c)/4, (3*a + 8*y1)/8, z1]) |
0 |
| 5 |
3-7-4 |
3 |
(a*b*c/18) |
([- a*b/6, 0, a*c/6]) |
([x1 - c/9, 4*a/9 + y1, 8*b/9 + z1]) |
([(12*x1 - c)/12, (a + 3*y1)/3, (2*b + 3*z1)/3]) |
([a*b*c*(12*x1 - c)/216, a*b*c*(a + 3*y1)/54, a*b*c*(2*b + 3*z1)/54]) |
| 6 |
3-5-7 |
3 |
(a*b*c/36) |
([a*b/12, - b*c/6, a*c/4]) |
([x1 - 4*c/9, 11*a/18 + y1, 8*b/9 + z1]) |
([(3*x1 - c)/3, (11*a + 24*y1)/24, (2*b + 3*z1)/3]) |
([a*b*c*(3*x1 - c)/108, a*b*c*(11*a + 24*y1)/864, a*b*c*(2*b + 3*z1)/108]) |
| 7 |
4-7-5 |
3 |
(a*b*c/36) |
([a*b/12, b*c/6, a*c/12]) |
([x1 - 4*c/9, 5*a/18 + y1, 8*b/9 + z1]) |
([(3*x1 - c)/3, (5*a + 24*y1)/24, (2*b + 3*z1)/3]) |
([a*b*c*(3*x1 - c)/108, a*b*c*(5*a + 24*y1)/864, a*b*c*(2*b + 3*z1)/108]) |
| 合計 |
|
|
(4*a*b*c/9) |
([0, 0, 0]) |
|
|
([4*a*b*c*(3*x1 - c)/27, a*b*c*(97*a + 192*y1)/432, a*b*c*(43*b + 96*z1)/216]) |
| 重心 |
|
|
|
|
|
|
([(3*x1 - c)/3,
(97*a + 192*y1)/192,
(43*b + 96*z1)/96]) |
結果は、上の表のようになった」
※青字部分に誤りがありましたので、訂正しました。2015/10/16。
「では、ガウスの定理による方法を試みる前に、正解を計算してみよう。
V1:三角柱、(底面積 a c/2、高さ b)、
V2:三角錐(くぼんでいる個所:底面積 a c/2、深さ b/3)、
V1の重心のx、y 座標は、(P1+P2+P6)/3、とz座標は、b/2+z1、
V2の重心は、H[(P1+P2+P6)/3,z1+b]からP7へのベクトルの1/4+OH、となる。
結果は、下の表のようになって、体積、重心とも、一致したのう」
| 立体 |
体積 |
重心 |
重心×体積 |
| V1 |
abc/2 |
([(3*x1 - c)/3, (a + 2*y1)/2, z1 + b/2]) |
([a*b*c*(3*x1 - c)/6, a*b*c*(a + 2*y1)/4, a*b*c*(b + 2*z1)/4]) |
| V2 |
-a*b*c/18 |
([(3*x1 - c)/3, (11*a + 24*y1)/24, 11*b/12 + z1]) |
([a*b*c*(c - 3*x1)/54, - a*b*c*(11*a + 24*y1)/432, - a*b*c*(11*b + 12*z1)/216]) |
| 計 |
(4*a*b*c/9) |
|
([a*b*c*(3*x1 - c)/6, a*b*c*(a + 2*y1)/4, a*b*c*(b + 2*z1)/4]) |
| 重心 |
|
|
([(3*x1 - c)/3,
(97*a + 192*y1)/192,
(43*b + 96*z1)/96]) |
「やったね。
じゃ、あたしは、ガウスの定理による方法で、計算してみよう。
| 面 |
頂点順 |
頂点数 n |
面積ベクトル Fs(n) |
重心 OH(n) |
OG(ガウスの定理) |
| |
多角形 |
多角形 xyz系 |
多角形 xyz系 |
xyz系 |
| 1 |
1-2-3-4 |
4 |
([a*b, 0, 0]) |
([x1, a/2 + y1, b/2 + z1]) |
([a*b*x1^2/4, a*b*x1*(a + 2*y1)/8, a*b*x1*(b + 2*z1)/8]) |
| 2 |
2-6-5-3 |
4 |
([- a*b/2, b*c, 0]) |
([x1 - c/2, 3*a/4 + y1, b/2 + z1]) |
([b*(2*x1 - c)*(a*(2*c - x1) + 2*c*y1)/16, b*(3*a + 4*y1)*(a*(2*c - x1) + 2*c*y1)/32, b*(b + 2*z1)*(a*(2*c - x1) + 2*c*y1)/16]) |
| 3 |
1-4-5-6 |
4 |
([- a*b/2, - b*c, 0]) |
([x1 - c/2, a/4 + y1, b/2 + z1]) |
([b*(c - 2*x1)*(a*x1 + 2*c*y1)/16, - b*(a + 4*y1)*(a*x1 + 2*c*y1)/32, - b*(b + 2*z1)*(a*x1 + 2*c*y1)/16]) |
| 4 |
1-6-2 |
3 |
([0, 0, - a*c/2]) |
([x1 - c/3, a/2 + y1, z1]) |
([a*c*z1*(c - 3*x1)/24, - a*c*z1*(a + 2*y1)/16, - a*c*z1^2/8]) |
| 5 |
3-7-4 |
3 |
([- a*b/6, 0, a*c/6]) |
([x1 - c/9, 4*a/9 + y1, 8*b/9 + z1]) |
([a*(9*x1 - c)*(b*(c - x1) + c*z1)/216, a*(4*a + 9*y1)*(b*(c - x1) + c*z1)/216, a*(8*b + 9*z1)*(b*(c - x1) + c*z1)/216]) |
| 6 |
3-5-7 |
3 |
([a*b/12, - b*c/6, a*c/4]) |
([x1 - 4*c/9, 11*a/18 + y1, 8*b/9 + z1]) |
([(9*x1 - 4*c)*(a*(b*(c + x1) + 3*c*z1) - 2*b*c*y1)/432, (11*a + 18*y1)*(a*(b*(c + x1) + 3*c*z1) - 2*b*c*y1)/864, (8*b + 9*z1)*(a*(b*(c + x1) + 3*c*z1) - 2*b*c*y1)/432]) |
| 7 |
4-7-5 |
3 |
([a*b/12, b*c/6, a*c/12]) |
([x1 - 4*c/9, 5*a/18 + y1, 8*b/9 + z1]) |
([(9*x1 - 4*c)*(a*(b*(c + x1) + c*z1) + 2*b*c*y1)/432, (5*a + 18*y1)*(a*(b*(c + x1) + c*z1) + 2*b*c*y1)/864, (8*b + 9*z1)*(a*(b*(c + x1) + c*z1) + 2*b*c*y1)/432]) |
| 合計 |
|
|
([0, 0, 0]) |
|
([4*a*b*c*(3*x1 - c)/27, a*b*c*(97*a + 192*y1)/432, a*b*c*(43*b + 96*z1)/216]) |
| 重心 |
|
|
|
|
([(3*x1 - c)/3,
(97*a + 192*y1)/192,
(43*b + 96*z1)/96]) |
結果は、上の表の通り。
ガウスの定理による方法でも、重心の計算結果は、正解と一致したわ」
「やはり、予想通りと言ったところじゃな。
これは、(4)節で記載したように、両者の方法が同一の結果を与えることは、ほぼ、間違いないようじゃな。
Excelブックによる、計算表は、いずれ後日として、とりあえず、多面体の重心については、これで、仕舞いにしよう」(Excelブックを(9)に追加しました。)
「おじさんも、お疲れ様でした」
目次へ戻る
(7)多面体の体積・重心のまとめ (2015/10/17追記)
(6)節の多角錘の体積及び重心位置の値を2015/10/16に青字部分を修正した。
この修正の原因は、rq が本来の値でなかったためであるが、修正前でも、多面体の全体積と多面体全体の重心は、正しく計算されていた。
このことは、多面体の体積: V=Σ(各面の和)(1/6)(r1-rq)・Σ(i=1~n)(ri×ri+1))、及び
多面体の重心 OG=1/V Σ(各面の和)((1/4)(rq+3*OH))*多角錘の体積)、の2つの式において、
rq=[0,0,,0]、としても、正しいことを暗示している。
まず、体積の方は、
第61回「多面体の体積公式」で説明したように、ベクトル点関数 F=[x,y,z]と置けば、∫∫∫div(F) dV=∫∫F・dS、である。
左辺は、3 V、となり、右辺、∫∫F・dS=∫∫(x nx+y ny+z nz)dS、(n=[nx,ny,nz]は、面の法線ベクトル)、
ここで、面の方程式(α x+β y+γ z+δ=0)の係数 α=nx、β=ny、γ=nz を使えば、(ここが今回気がついたポイント)
∫∫(α x+β y+γ z)dS=∫∫-δ dS=-δ∫dS=-δS、となる。
そして、頂点の最初の点の位置ベクトル r1を使えば、α x1+β y1+γ z1+δ=0、であるので、α=Sx/S等により、
-δSは、(α x1+β y1+γ z1)S=[x1,y1,z1]・[α,β,γ]S=r1・[Sx/S,Sy/S,Sz/S]S=(r1・S)、となる。
すなわち、
体積 V=(1/3)Σ(各面の和)(r1・S)、と簡潔にまとまった。(Sは、面の面積ベクトル。S=(1/2)Σ(i=1~n)(ri×ri+1))))、
同様に、多面体の重心も、(4)節に記載したように、ガウスの定理により導かれた方法と(2)節の方法は、同一のものであり、
重心 OG=(1/4)Σ(各面の和)((OH・S)OH)、でよいことになる。(OHは、面の重心の位置ベクトル)
このように書けば、多面体の体積と重心の式は、似通った綺麗な形となった。
なお、(5)節に掲げた関数を上記に沿って、rqは、削除し、Fv(n)は、修正し、OG(n)は、OGauss(n)の表式に内容を変え、OGaussは、削除しました。
目次へ戻る
(8)多面体の高次のモーメント (2015/10/17追記)
(7)節の内容を一般化すると、ベクトル点関数 F=(x^k y^m z^n)[x,y,z]とすれば、
k、m、nをゼロ又は正の整数として、
(k+m+n+3)∫∫∫(x^k y^m z^n)dV=∫∫(x^k y^m z^n)(x nx+y ny+z nz)dS
=∫∫(x^k y^m z^n)(α x+β y+γ z)dS=∫∫(x^k y^m z^n)(-δ)dS
=Σ(各面の和)([x1,y1,z1]・[α,β,γ]∫∫(x^k y^m z^n)dS)
=Σ(各面の和)(r1・[Sx/S,Sy/S,Sz/S]∫∫(x^k y^m z^n)dS)
=Σ(各面の和)(r1・S)(1/S)∫∫(x^k y^m z^n)dS)、
∫∫∫(x^k y^m z^n)dV=(1/(k+m+n+3))Σ(各面の和)(r1・S)(1/S)∫∫(x^k y^m z^n)dS)、
となることが分かる。
ここで、r1は、各面の最初の頂点の位置ベクトル、Sは、各面の面積ベクトルを表すものとする。
k=m=n=0の場合が、多面体の体積、
k=1、 かつ、m=n=0 のように、k+m+n=1の場合は、多面体の重心の関係式を与える。
k=2、かつ、m=n=0、または、k=1、m=1、n=0のように、k+m+n=2の場合は、慣性モーメントの関係式を与える。
※青字部分が抜けていましたので、2015/10/18に修正しました。
目次へ戻る
(9)多面体の体積と重心位置を求めるExcelブック (2015/10/21 追記)
3次元空間上における多面体の体積と重心を求めるExcelブックを作成しました。
TamentaiVer2.xlsm です。(クリックして名前を付けて保存してください)
ブックは、Excel 2013で作成し、計算には、Excel VBAを使用しています。(Excel 2007、2010、365等でも動作します)
ダウンロードしたものは、適当な場所に保存してから開いてください。
開く際、セキュリティの警告が表示された場合は、適宜、「コンテンツの有効化」等(Windows
あるいはOfficeのバージョンによって警告等の内容と動作は変わります)を選択してください。
なお、すでに4点のデータが入力・計算されています。これらのデータは、(5)節のものです。
使い方は、次の通りです。
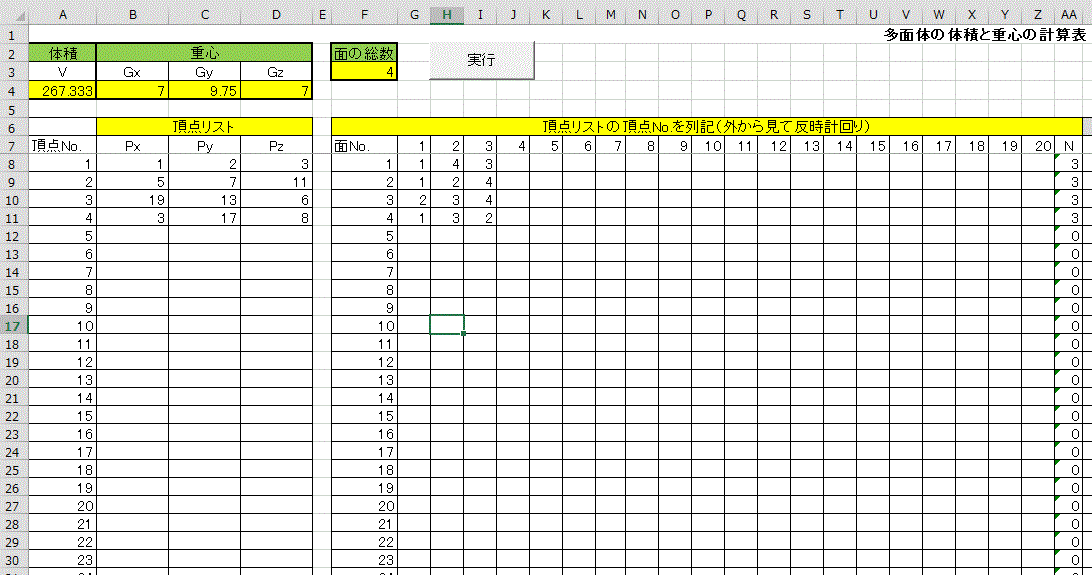
1.すべての頂点の座標値をB列のPx C列のPy, D列のPz蘭に入力します。
頂点総数は、100点まで利用できます。(無関係のセルは、空白にしてください。)
2.各面の頂点の番号をG列~Z列まで水平方向に入力してください。
各面の頂点の数は、20個まで入力できます。無関係のセルは、空白にしてください。(ゼロではありません)
3.「実行」ボタンをクリックしてください。
4.A4に体積、B4~D4にxyz座標系の重心位置、が表示されます。
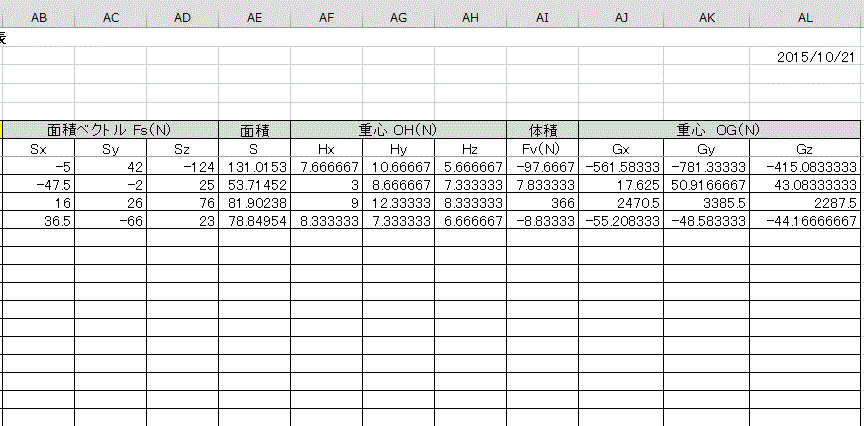
AB列からAL列には、各面毎の面積ベクトル、面積、面のxyz系の重心、多角錘の体積、多角錘のxyz系の重心が表示されます。
計算には、倍精度浮動小数点型の変数を使用しています。
シートは、保護していますので、入出力用のセル以外の編集はできませんが、「シートの保護を解除」することで編集は、可能となります。
なお、動作の保証は、できかねますので、自己責任にて、ご利用ください。(改変は自由です)
下図は、Excel画面の左側と、右側の部分です。
目次へ戻る
最終更新日 2015/10/22



 「何なの、反省会って?
「何なの、反省会って?




