数式処理ソフト　DERIVE（デライブ） de ドライブ

７７．多角形及び多面体の重心と高次のモーメント（3）

（1）はじめに

「まだ、続きがあるの？」

「おお。ともちゃんかい。
　たしかに、体積と重心については、前々回「第76回　多角形及び多面体の重心と高次のモーメント（1）」、前回「第77回　多角形及び多面体の重心と高次のモーメント（2）」で終わったな。
　しかし、2次のモーメント（たとえば、慣性モーメント）について、まだ終わってないのう」

「タイトルでは、「・・高次のモーメント」とうたっているのだからね。
　第75回で、xy平面上で、k, m をゼロ又は正の整数としたとき、
∫∫x^k y^m dx dy=（1/（k+m+2））（∫－（y^（m+1）（x^k））dx＋∫x^（k+1）（y^m））dy）、について、
k+m=0～3の範囲で、右辺の具体的な表式を示しているけど、3次元空間の多角形でも、xyz座標系からuvw座標系に移らないと、そのままでは、右辺の計算が難しい。
　とはいえ、計算後に、その量をxyz座標系にどのように変換したら良いかが分からない」

「そうじゃったな。
　数式処理ソフト DERIVE（デライブ）の第76回では、上式を一般化し、k, m, nをゼロ又は正の整数としたとき、
∫∫∫（x^k y^m z^n）dV=（1/（k＋m＋n＋3））Σ（各面の和）（r1・S）（1/S）∫∫（x^k y^m z^n）dS）、を示している。
　ここで、各面毎に、r1は、面上の点を表す位置ベクトル（第76回では、最初の頂点とした）、Sは、面の面積ベクトル、Sは、その大きさじゃ。
　上の式において、k=m=n=0、の場合が体積、k+m+n=1、の場合が重心に当たるわけだな。
　そして、k+m+n=2（あるいはその組み合わせ）が慣性モーメントに代表される2次のモーメントの関係式となる。
　まず、次節で、慣性モーメントについて、おさらいしてみよう」

（2）慣性モーメントのおさらい（1）　（定義・慣性テンソルと座標回転）

「力学で「慣性モーメント」にお目にかかるのは、質点系の力学が最初で、その中でも、特に「剛体の力学」で重要な役割を果たしている。
　まあ、質点の力学での質量と同じような感じじゃな」

「慣性モーメントの定義では、ある回転軸の回りの慣性モーメントは、I=Σm（i）r（i）^2、となっているわね。
　ここで、m（i）は、i番目の質点の質量、r（i）は、i番目の質点と軸との最短の直線距離を表す。　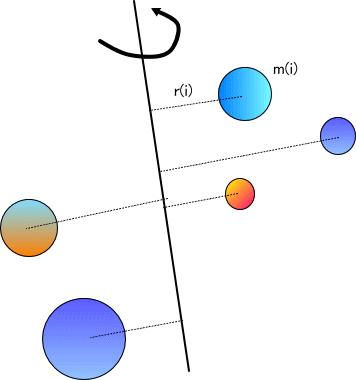左の図のようなイメージね」

「慣性とは、英語では、inertia なので、慣性モーメントは、 moment of inertia、といわれる。
そこで、英字の頭文字をとり、I と表すことが多い。
　図では、質点に大きさがあるように描いてあるが、実際は、大きさが無視できる程度と考えて欲しい。
　また、結びあわされているなどにより、お互いの位置関係を変えないものとする。。
　　さて、m（i）>0、r（i）^2>0 なので、I は、正のスカラー量である。
　　次に、今、一つの質点が系に追加された場合は、その質点の m r^2 をI に加算すれば良いことが分かる。
　　ところで、質点系全体の重心を考えたとき、重心を通り、当該軸と平行で、最短距離 L だけ離れた軸がある。
　この新しい軸の回りの慣性モーメントは、どうなるかな？」

「元の軸をz軸とすれば、I=Σm（i）r（i）^2=Σ（m（i）（x（i）^2＋y（i）^2）、と書けるよね。
　ま、x、y軸の方向は、特にこだわらないけどさ。
　ところで、重心のこの座標系における座標を［Gx，Gy，Gz］と書く。
　すると、元の軸からの最短距離 L は、Gx^2＋Gy^2=L^2、である。
　一方、重心の定義から、Gx=Σm（i）x（i）/M、Gy=Σm（i）y（i）/M、Gz=m（i）z（i）/M、だわね。
ここで、M=Σm（i）、と、全質量とします。
　さて、Gを通る軸の回りの慣性モーメントをIGとすれば、左下図を参照して、
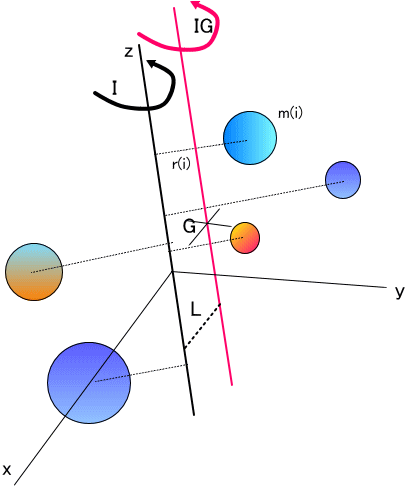　IG=Σm（i）（（x（i）－Gx）^2＋（y（i）－Gy）^2）、
　=Σm（i）（x（i）^2＋y（i）^2）－2GxΣm（i）x（i）－2GyΣm（i）y（i）＋（Gx^2＋Gy^2）Σm（i）、
　ここで、M=Σm（i）、Gx=Σm（i）x（i）/M などを使うと、
　IG=Σ（m（i）（x（i）^2＋y（i）^2））－2MGx^2－2MGy^2＋M（Gx^2＋Gy^2）、
　ところで、Σm（i）（x（i）^2＋y（i）^2）=Iなので、、
　IG=I－M（Gx）^2＋（Gy）^2=I－M L^2、と求められた」

「 I=IG＋ML^2、の形で記載されていることが多い。
　気をつけないといけないのは、片方の軸が重心を通り、軸同士が平行という条件が付いていることじゃ」

「なるほどね。
　今は、z軸の回りの慣性モーメントを考えたけど、x軸、y軸の回りの慣性モーメントについても同様のことが言えるわけね。
　じゃ、一般には、どうなるのかしら？」

「そのあたりを探るために、ここからは、座標系をXYZ系と原点 Oは、同一であるがXYZ系から見て回転した座標系をuvw系としよう。
　これまで見て来たように、［u，v，w］=［X，Y，Z］*T、の関係がある。
　ここで、Tは、座標の回転行列じゃな。
　逆に、［X，Y，Z］=［u，v，w］T '、とも書ける。T ' は、Tの転置行列。
　XYZ系で各軸の回りの慣性モーメントを次の記号で表す。
　Ixx=Σm（i）（Y（i）^2＋Z（i）^2）、
　Iyy=Σm（i）（X（i）^2＋Z（i）^2）、
　Izz=Σm（i）（X（i）^2＋Y（i）^2）、
　ここで、Ixxなどは、Σm（i）x（i）^2、などではないことに注意して欲しい。
　次に、XYZ系で、原点を通り、ベクトルA=［AX，AY，AZ］方向の軸の回りの慣性モーメントを求めることを考えてみよう。
　ここで、|A|=1、じゃ。
　この軸と質点r（i）との最短距離の2乗は、（r sinθ）^2=｜A×r（i）｜^2、である。

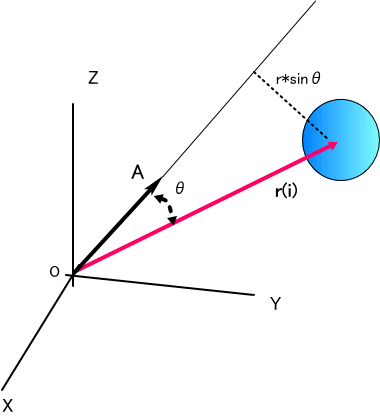
　右辺の｜A×r（i）｜^2、の成分で添え字 i を省略して書くと、
　AX^2·Y^2 + AY^2·X^2 + AX^2·Z^2 + AZ^2·Y^2+ AY^2·Z^2 + AZ^2·X^2－2·AX·AY·X·Y － 2·AX·AZ·X·Z －2·AY·AZ·Y·Z 、
　A方向の軸の回りの慣性モーメント IAは、質点系全体では、上式にm（i）を掛けて和を取り、
　Ixx=Σm（i）（Y（i）^2＋Z（i）^2）、などを使うと、、
　IA=AX^2*Ixx＋AY^2*Iyy＋AZ^2*Izz－2（AXAY Σm（i）X（i）Y（i）＋AXAZΣm（i） X（i）Z（i）＋AYAZYΣm（i）（i）Z（i））、と表される。
　ここで、
　Ixy=－Σm（i）X（i）Y（i）、
　Ixz=－Σm（i）X（i）Z（i）、
　Iyz=－Σm（i）Y（i）Z（i）、
　を新しく定義する。
　この3つの量は、「慣性乗積」あるいは「慣性相乗モーメント」と呼ばれ、マイナスの符号を付けている点に注意して欲しい。
　慣性乗積の符号を負にしてあるのは、後述のように座標変換に対してこの定義がはなはだ都合が良いためである。
　すると、IA=AX^2*Ixx＋AY^2*Iyy＋AZ^2*Izz＋2（AXAY *Ixy＋AXAZ*Ixz）＋AYAZ*Iyz）、とまとめられる。
　今、A=［AX，AY，AZ］は、既知なので、Iの要素（Ixx、Ixyなど6つの量）が分かっていれば、原点を同じくする任意の直線の回りの慣性モーメントを求められる。
　ともちゃん、ところで、［X，Y，Z］’*［X，Y，Z］を作ると、3行3列の行列が得られるのをヒントに、I を、uvw系で見るとどう簡潔に表現できるかを考えて欲しい」

「あれれ、DERIVEで、［X，Y，Z］’* ［X，Y，Z］は、X^2+Y^2+Z^2 とベクトル同士の内積になっちゃうよ」

「そうなんじゃな。
　DERIVEでは、ベクトルとしては、行ベクトル（横ベクトル：row vector）のみが許されていて、列ベクトル（縦ベクトル：column vector）は、ベクトルとしては、使えないのじゃ。
　なお、横ベクトル×行列、は、許される。
　そこで、便宜上、縦ベクトルを使う必要があるときは、［［X，Y，Z］］と入力した後に転置し、1行3列の行列として扱えばよい」
※後述のOUTER（ベクトルa，ベクトルb）関数は、同様の働き（全く同じではない）である。

「へー。今まで、気がつかなかったよ。
　ベクトルと行列については、第23回「ベクトルと行列」で取り上げたんだけども。
　あと、DERIVEで、大文字で入力しても、小文字で演算結果が表示されてしまうのは、どうしてなのかな？」
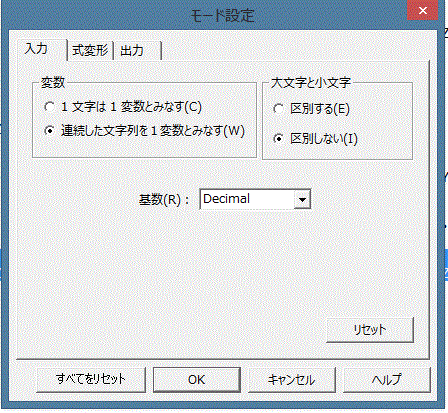
「これは、オプションメニューのモード設定の入力タブで、下図のように、「大文字と小文字」の「区別する」方にチェックを付ければ良い。
　ただ、必要がなければ、間違いの元とじゃから、どちらも、余りお勧めはせんがな」

　
「たしかにね。
　こうすれば、下図のように、3行×1列と1行×3列の積が3行3列の行列となったわ。

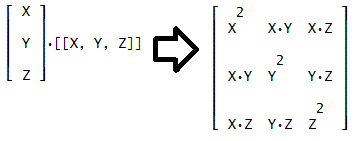
　ただし、図中の⇒は、後から書き加えたものよ。
　で、肝心のテーマを忘れてしまいそうだけど、こいつと、さっきの、
　Ixx=Σm（i）（Y（i）^2＋Z（i）^2）、Iyy=Σm（i）（X（i）^2＋Z（i）^2）、Izz=Σm（i）（X（i）^2＋Y（i）^2）、
　Ixy=－Σm（i）X（i）Y（i）、Ixz=－Σm（i） X（i）Z（i）、Iyz=－Σm（i）Y（i）Z（i）、
　を結びつけることが必要なんだよね。
　行列にスカラーを掛けるのは、行列の要素にスカラーを掛けるのと同じ。
　また、同じサイズの行列の和は、個々の要素の和でもある。
　しかし、上で得た行列と求めようとしている行列（下図）とは、少し、離れているんだな、これが。

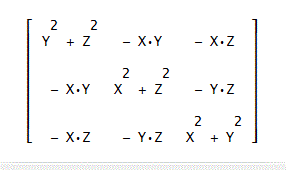
　そこで、［X，Y，Z］・　［X，Y，Z］=r^2=X^2＋Y^2＋Z^2、と、3行3列の単位行列 E とを組み合わせて、
　r^2*E－r ' * r、を作ると、これは、下図のように、3行3列の行列となる。（r=［X，Y，Z］）
　

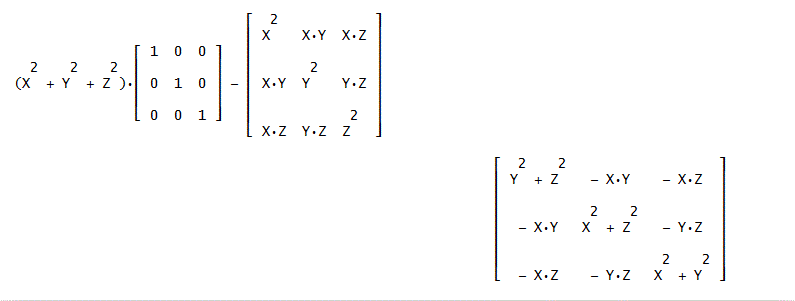
　この行列の各要素のX等をX（i）に置き換えて、m（i）を乗じて、行列の和をとると、各要素が慣性モーメント、慣性乗積となることが分かる。
　この行列 I は、下の通り。
　

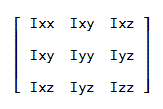
　すなわち、式で書けば、I=Σm（i）（r（i）^2）*E－Σm（i）r（i） ' * r（i）、
　一方、［u，v，w］=［X，Y，Z］T、の関係から、添え字 i を略して書くと、r =［X，Y，Z］、R=［u，v，w］として、
　uvw系の行列は、Σm（R^2）*E－Σm R ' * R、となる。
　R=r Tの関係を使うと、R^2=r^2、及び、R ' * R=T '（r ' * r）T、から、
　Σm（R^2）*E－Σm R ' * R=T' * T（Σm（r^2））－T'（Σm r ' * r）T=T ' （（Σm（r^2）－（Σm r ' * r））T
　これを見ると、赤字の部分が、I であることから、uvw系では、I は、T' I T、と表せることが分かる」

「ようできたのう。
　Tは、直交変換なので、r^2=R^2、なのじゃな。
　慣性乗積（Ixy=－Σm（i）X（i）Y（i）など）の符号を変えたご利益で、座標変換に対して、このように、簡潔に表すことができた。
　これは、「物理学への数学的序説」（荒木源太郎著：1967年（昭和42年）11月30日：みすず書房）の134ページの定義に倣ったものじゃ。
　手元のいくつかの参考書でも、このような定義となっておる。
　これで、一度、ある座標系で慣性モーメントなどを要素に持つ行列が得られれば、同一原点を持つ座標系であれば、再計算せずに、その行列を計算することができる。
　ところで、いちいち、慣性モーメントなどを要素とする行列というのは、回りくどいので、「慣性テンソル」ということにする。
　ここで出てくるテンソルは、2階のテンソルということになる。※
　さて、最後に、IAの表現を簡潔に表すことを考えてみよう。
　IA=AX^2*Ixx＋AY^2*Iyy＋AZ^2*Izz＋2（AXAY *Ixy＋AXAZ*Ixz）＋AYAZ*Iyz）、
　これは、XYZ系で、I という慣性テンソルが与えられているときに、原点を起点とする単位長さのベクトルA=［AX，AY，AZ］上の直線の回りの慣性モーメントじゃ。
これを簡潔に表してみよう」

「えーと、
　さっきの、T' I Tをまねて、A I A' を作ってみると、
　A I A' =IA、となることが分かった」

「その通りじゃな。
　いや、実は、荒木先生の本で、IAがA I A' のように変形出来ると記載されていたのじゃが、どうも、できんかった。
　一方、IAの式そのものは、合っているように思えた。ここで、悩んだんだな。
　再度、「物理学への数学的序説」の慣性乗積の定義を見直してみると、「慣性乗積」を「慣性相乗モーメント」と呼び、名前だけでなく、符号も負に変えてあることに気がついた。
　些細な点のように思えたが、この符号が正のままであると、任意のベクトルの方向の軸の回りの慣性モーメント IAをA I A' 、のように書き表すことができない。
　また、座標変換後の慣性テンソルを、T ' I T、のように表すこともできない。
　さて、慣性モーメントのおさらいも、だいぶ、長くなった。
　次節では、2次元の3角形を例にとり、慣性テンソルの計算をしてみよう」
※　2階のテンソルとは、座標変換に対して「共傾」に変換されるものをいう。2つの添え字で表される要素を持つ行列すべてではない。

（3）慣性モーメントのおさらい（2）　（例：2次元空間の3角形）

「例を挙げよう。
　たとえば、下図のような三角形では、どうなるかな。

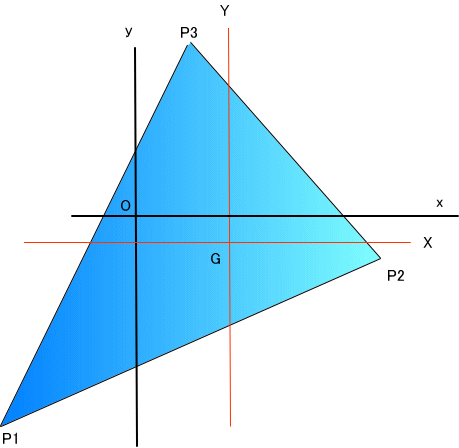
　xyz座標系で測定した、各頂点の座標値は、すべてz=0の平面上なので、2次元と限定する。、
P1　［－3，－5/2］、
P2　［7/2，－2］
P3　［1，5］
とする。
　面積：187/8=23.375、重心Gは、[1/2，1/6]、である」

「まずは、2次元で考えて慣性テンソルの独立な要素は、Ixx、Iyy、Ixy、なので、
　Ixx=∫∫y^2 dx dy、なんだけど、　
　第75回の（2）節の補足で、
　∫∫x^k y^m dx dy=（1/（k+m+2））（∫－（y^（m+1）（x^k））dx＋∫x^（k+1）（y^m））dy） 、
　の具体的な表現を求めてるから、
、Ixx=∫∫y^2 dxdy、は、上式で、k=0、m=2の場合より、Ixx=（1/4）（∫x y^2 dy－ y^3 dx）、
　補足に従うと、P1～P2の表現は、(y1^2 + y1·y2 + y2^2)·(x1·y2 － x2·y1)/12、であるので、添え字1をiに、2をi+1に変えて、
　Ixx=（1/12）Σ((y(i)^2 + y(i)y(i+1) + y(i+1)^2)(x(i)y(i+1) － x(i+1)y(i))）、を得る。
　あらかじめ、x:=［r1↓1，r2↓1，r3↓1］、y:=［r1↓2，r2↓2，r3↓2］、と置く。
　M（n_）:=1/12·∑((y↓i_^2 + y↓i_·y↓(i_ + 1) + y↓(i_ + 1)^2)·(x↓i_·y↓(i_ + 1) － x↓(i_ + 1)·y↓i_), i_, 1, n_ － 1) + （1/12）(y↓n_^2 + y↓n_·y↓1 + y↓1^2)·(x↓n_·y↓1 － x↓1·y↓n_)、
　と定義すれば、
Ixx=M（3）=13277/192≒69.15104166、
　同様に、Iyy=∫∫x^2 dx dyは、k=2、m=0の場合なので、Iyy=（1/4）（∫x^3 dy －y x^2 dx）、
　そのP1～P2の表現は、(x1^2 + x1·x2 + x2^2)·(x1·y2 － x2·y1)/12、、であるので、添え字1をiに、2をi+1に変えて、
　Iyy=（1/12）Σ（((x(i)^2 + x(i)x(i+1) + x(i+1)^2)(x(i)y(i+1) － x(i+1)y(i))）、を得る。
　N(n_):= 1/12·∑((x↓i_^2 + x↓i_·x↓(i_ + 1) + x↓(i_ + 1)^2)·(x↓i_·y↓(i_ + 1) － x↓(i_ + 1)·y↓i_), i_, 1, n_ － 1) + 1/12·(x↓n_^2 + x↓n_·x↓1 + x↓1^2)·(x↓n_·y↓1 － x↓1·y↓n_))、
　と定義すれば、
Iyy=N（3）=(9163/192)≒47.72395833、を得る。
　最後に、Ixy=－∫∫x y dxdy は、k=m=1の場合なので、－（1/4）（∫x^2 y dy－∫y^2 x dx）、
　補則に従うと、P1～P2の表現は、－((x1·y2 － x2·y1)·(x1·(2·y1 + y2) + x2·(y1 + 2·y2))/24)、であるので、添え字1をiに、2をi+1に変えて、
MN(n_):= － 1/24·∑((x↓i_·y↓(i_ + 1) － x↓(i_ + 1)·y↓i_)·(x↓i_·(2·y↓i_ + y↓(i_ + 1)) + x↓(i_ + 1)·(y↓i_ + 2·y↓(i_ + 1))), i_, 1, n_ － 1) － 1/24·(x↓n_·y↓1 － x↓1·y↓n_)·(x↓n_·(2·y↓n_ + y↓1) + x↓1·(y↓n_ + 2·y↓1))、
　と定義して、
Ixy=MN(3)=(－ 4675/384)≒－12.17447916、
これで、慣性テンソル IのIxx、Iyy、Ixy と3つの要素が求まった。
　行列の形で書くと、こんな感じ」

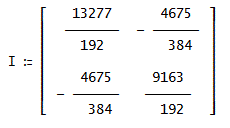
「では、わしは、重心Gを通るXYZ座標系で考えてみよう。
　P1、P2、P3は、それぞれ、xyz系でのOGの位置ベクトル［1/2, 1/6］を引いた値となるので、XYZ系で表した位置ベクトルは、
P1　[－7/2, － 8/3]、
P2　([3, －13/6])、
P3　([1/2, 29/6])、となる。
　これから、重心を原点とする慣性テンソルIGの要素は、
IGXX=(39457/576)≒68.50173611、
IGYY=(8041/192)≒41.88020833、
IGXY=(－ 1309/128)≒－10.2265625、となる。
　行列の形に整理すると、

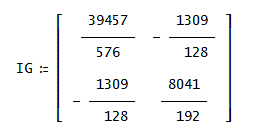
　ところで、x軸とX軸との最短距離、Lxは、重心のy座標値なので、その2乗は、Lx^2=Gy^2=（1/6）^2=1/36、であるので、
　IGxx＋面積×Lx^2=39457/576＋（1/36）*(8/187）=13277/192であるが、この値は、ともちゃんが計算してくれた、Ixx=13277/192、と一致する。
　これは、（2）節で導いたI=IG＋ML^2、と同様の法則 Ixx=IGXX＋MLx^2 が成り立つことを示している。
　なお、ここでは、全質量Mは、面密度が一定であるとして、面積で置き換えている。
　同様に、y軸とY軸との最短距離 Lyは、重心のx座標（=1/2）なので、2乗（=1/4)、から、
　IGyy＋面積×Ly^2=8041/192 + 1/4·(187/8)=9163/192、となる。
　これは、Iyyと一致する。すなわち、Iyy=IGYY＋MLy^2、じゃ。
　さて、残ったのは、慣性乗積 IGXYとIxy の関係じゃが、どうなるかな」

「IGXY=－Σm（i）X（i）Y（i）、X（i）=x（i）－Gx、Y（i）=y（i）－Gyを使って、
IGXY=－Σm（i）（x（i）－Gx）（y（i）－Gy）=－Σm（i）x（i）y（i）＋GxΣm（i）y（i）＋GyΣm（i）x（i）－Gx*GyΣm（i）、
　ここで、Gx=Σm（i）x（i）/M、Gy=Σm（i）y（i）/M、の関係から、
IGXY=－Σm（i）x（i）y（i）＋M*Gx*Gy＋M*Gx*Gy－M*Gx*Gy=Ixy＋M*Gx*Gy、
　よって、Ixy=IGXY－M*Gx*Gy、である」

「そのようじゃな。
　では、確認してみよう。
　IGXY－M*Gx*Gy=－1309/128)－(187/8)(1/2)(1/6)=－4675/384、で、これは、Ixyと等しい。
　ここから、主軸変換となるのじゃが、（3）節もだいぶ、長くなったので、次節に移ろう」　

（4）慣性モーメントのおさらい（3）　（慣性楕円体と主軸変換）

「慣性楕円体について、触れておこうかの。
　（2）節で、任意の軸の回りの慣性モーメント IA は、次のように表すことができた。
　IA=AX^2*Ixx＋AY^2*Iyy＋AZ^2*Izz＋2（AXAY *Ixy＋AXAZ*Ixz）＋AYAZ*Iyz）、
　ここで、A=［AX，AY，AZ］は、任意の軸上の単位ベクトルじゃ。
　IAは、（2）節でともちゃんが示してくれたように、IA=A I A ' と簡潔に書くこともできる。
　さて、ここで、XYZ座標系の任意の点［X，Y，Z］までの距離を r で表すと、X=r* AX、Y=r*AY、Z=r*AZ、であるので、
IAの式のAX等をrとX等に置き換えると、
　IA*r^2=Ixx*X^2＋Iyy*Y^2＋Izz*Z^2＋2（Ixy*XY＋Ixz*XZ＋Iyz*YZ）、となる。
　今、慣性モーメントは、非負なので、r=1/√IA と置くことにより、
　Ixx*X^2＋Iyy*Y^2＋Izz*Z^2＋2（Ixy*XY＋Ixz*XZ＋Iyz*YZ）=1、と［X，Y，Z］の満たす方程式が得られる。
　これは、どんな曲面となっているじゃろうか」

「そうね。
　たとえば、Ixxなどがすべてゼロである場合、これは、点ね。このときは、質点が原点に集中しているんだけど。
　そこまで、極端でなくとも、質点がX軸上にのみ存在するときは、Ixx=Ixy=Ixz=0、となるので、Iyy*Y^2＋Izz*Z^2=1となり、YZ平面上の楕円となる。
　同様に、Y軸上にのみ存在する場合は、XZ平面上の楕円、Z軸上にのみ存在する場合は、XY平面上の楕円（左下図の赤い図形）となる。
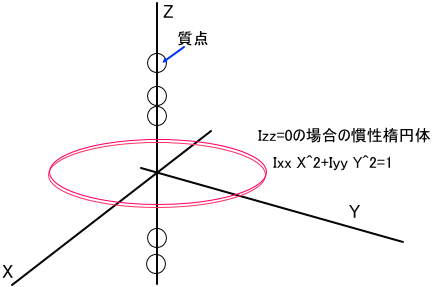　Ixx、Iyy、Izzのいずれもゼロでない場合は、これらの係数が正であることを考えると、楕円体（楕円曲面）ということかしら」

「点は、楕円体の主軸の長さがすべてゼロの場合、平面上の楕円は、ある主軸のみ長さがゼロの場合と認めれば、すべて楕円体と言い切ってもよいじゃろう。
　この楕円体を「慣性楕円体」という。
　原点から慣性楕円体上の点までの距離 r は、その方向の慣性モーメントの逆数の平方根（r=1/√IA）となっている」

「線形代数をかじっていれば、r I r ' で表される「2次形式」と対称行列 I の性質を調べることは、数学的には、同等であるから。
（「行列と行列式」：古屋茂著：培風館：昭和45年3月のP83）。
　rを変換 R=r Pにより、Rに変えて I が、Jになったとすると、J=P ' I P、であり、適切なPを選択すれば、
　R J R ' を J11 u1^2＋J22 u2^2＋・・＋Jkk uk^2、のように「平方項」のみの数列に変形することができる。ここで、kは、行列 I のランクである」

「えーと、ランクとは、行列の小行列式の中でゼロでないものの最大次数じゃったかな」

「そうね。
　要素がすべて実数の対称行列では、変換行列 Pとして、直交行列（回転行列） T をとることができる訳ね」

「そこで、直交行列により、I の対角成分をゼロとすることを主軸変換というわけじゃ。
　I が低次元、たとえば、2次行列の場合は、固有値や固有ベクトルなどの概念を説明しなくても、Tを求めることはできる。
　T ' I T=［［λ1，0］，［0，λ2］］、と変換できたものとする。
　なお、Ixy=0の場合は、すでに非対角要素がゼロなので除外して考える。
　ここで、T=［［p1，q1］，［p2，q2］］、T '=［［p1，p2］，［q1，q2］］、I=［［Ixx，Ixy］，［Ixy，Iyy］］、である。
　Tが直交行列であることから、
　p1^2 + p2^2 = 1、
　q1^2 + q2^2 = 1、
　p1·q1 + p2·q2 = 0、が成り立つ。
　さらに、Z軸の方向を保つためには、［p1，p2，0］×［q1，q2，0］=［0，0，1］が必要。これから、p1·q2 － p2·q1=1、を満たす解に絞る。
　そこで、p1=COS（s）、p2=SIN（s）、q1=－SIN（s）、q2=COS（s）と置くと、これらの補助の4つの方程式を満たしていることが分かる。
　T ' I T=［［λ1，0］，［0，λ2］］を具体的に計算すると、
　Ixx·COS(s)^2 + 2·Ixy·SIN(s)·COS(s) + Iyy·SIN(s)^2 = λ1、
　 Iyy·COS(s)^2 － 2·Ixy·SIN(s)·COS(s) + Ixx·SIN(s)^2 = λ2、
　2·Ixy·COS(s)^2 + (Iyy － Ixx)·SIN(s)·COS(s) － Ixy = 0、
　3番目の式から、TAN（2s）=2*Ixy/（Ixx－Iyy）、と求められる。
　COS（s）^2=（1＋COS（2s））/2、SIN（s）^2=（1－COS（2s））/2 などを使うと、
　λ1=(√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) + Ixx + Iyy)/2、
　λ2=(－√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) ＋ Ixx ＋ Iyy)/2、が求められる。
　なお、λ1＋λ2=Ixx＋Iyy、となることに注意。
　一方、直交行列 Tは、
　
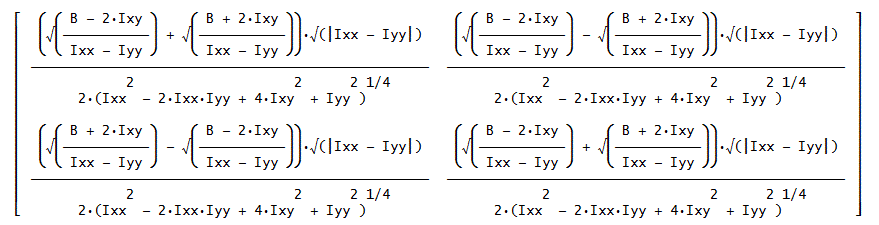
　ここで、B=√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2)·SIGN(Ixx － Iyy)、
　実際、T ' I T=［［λ1，0］，［0，λ2］］、を確認することができる」

「2次元の場合でも、結構ごちゃごちゃした式になってしまうのね」

「そうじゃな。
　数値でなくて、文字記号で表しているからな。
　実際は、主軸変換は、行列の固有値問題として扱うのじゃが、すなわち、
　T ' I T=［［λ1，0］，［0，λ2］］、の右から、T ' =［［p1，p2］，［q1，q2］］を掛けると、
　［［p1，p2］，［q1，q2］］ I=［［λ1，0］，［0，λ2］］［［p1，p2］，［q1，q2］］、となるが、
　これは、p=［p1，p2］、q=［q1，q2］、と書けば、
　p I=λ1 p、と q I=λ2 q、と分解できることに注意する。
　これは、慣性テンソルの主軸変換は、行列の固有値と固有ベクトルを求める問題と同一であることを示している」

「固有値を求めるためには、固有方程式（特性多項式）、｜I －λE｜=0、を解けばいいのね。
　ここで、Eは、単位行列。
　上の2次元の問題をDERIVEで確認してみると、
　I －λ*IDENTITY_MATRIX（2）=0、から、
　λ^2 － λ·(Ixx + Iyy) + Ixx·Iyy － Ixy^2=0、となるので、
　λ =（√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) + Ixx + Iyy)/2、
　λ = （－√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) ＋ Ixx ＋ Iyy)/2、
　の2根が得られる」

「そうじゃな。
　結果は同じでも、計算の見通しが良くなる。
　DERIVEにおける行列の固有値と固有ベクトルについては、次節で扱うことにしよう」

（5）行列の固有値と固有ベクトル

「さて、I またはIG においては、一般には、下図のように、Ixyなどの非対角成分が存在する。

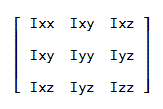
　主軸変換は、座標軸を回転して、非対角成分をゼロにする。
　そのためには、固有方程式、｜I －λE｜=0、を解いて、p I =λp、から、固有ベクトルpを求める必要がある。
　DERIVEには、そのための関数が備えられておる。
　ともちゃん、紹介してくれんかの」

「分かりやした。
　第23回「ベクトルと行列」や第40回「ベクトル解析（1）」では、紹介していなかった組み込み関数の一部を説明するわね。
　たくさんあるので、連立方程式の解法に特に関連する関数などは、省くわ。

　単位行列：IDENTITY_MATRIX（n）⇒n次元の単位行列、
　　　　　　　例：IDENTITY_MATRIX（2）

　
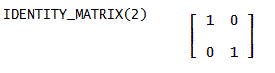
　行列の要素を取り出す：ELEMENT（M，i，j）⇒行列Mのi行j列の要素を取り出す
　　　　　　　例：ELEMENT（I，1，2）
　
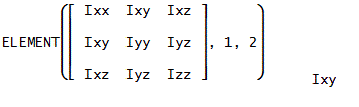
　なお、ELEMENT（ベクトル，数値）の場合は、ベクトルの数値番目の要素を与える。
　
　行列の行数を与える：DIMENSION（M）⇒正方行列では、行数と列数は一致、

　正方行列の対角成分の和：TRACE（M）⇒M11～Mnnの対角成分の和を与える
　　　　　　例：TRACE（I）

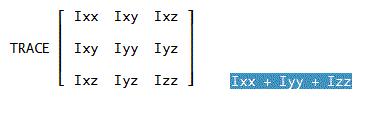
　固有方程式（特性多項式）：CHARPOLY（M，λ）⇒｜M－λE｜を与える。
　　　　　　例：(CHARPOLY([2, 3; a, b], λ))

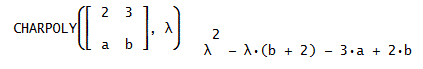
　固有値：EIGENVALUES（M，λ）⇒正方行列Mの固有値を求める
　　例：EIGENVALUES([2, 3; a, b], λ)

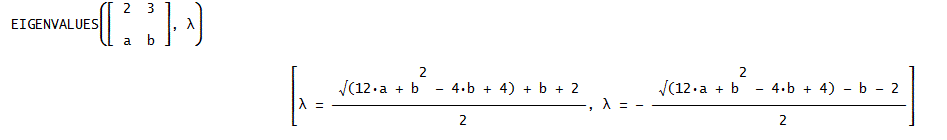
　ベクトルのテンソル積：OUTER（v，w）⇒v ' * w、という行列を与える
　　　　　例：　OUTER([1, 2], [3, 4])

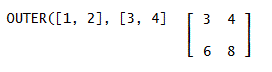
　固有ベクトルの厳密解：EXACT_EIGENVECTOR（M，λ）⇒厳密な固有値λに対応する固有ベクトルを与える
　　　　　例：EXACT_EIGENVECTOR([2, 3; a, b], (√(12·a + b^2 － 4·b + 4) + b + 2)/2)、

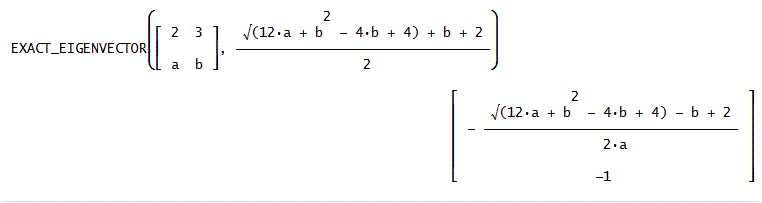
　固有ベクトルの近似解：APPROX_EIGENVECTOR（M，λ）⇒Mの固有値の近似値（数値に限る）に対応する固有ベクトルを与える
　　　　　　例：APPROX_EIGENVECTOR([2, 3; 5, 8], 9.898979485)、（前出の行列のa=5、b=8とした場合）

　なお、EXACT_EIGENVECTOR関数とは異なり、1行n列のベクトルを返す。

　ベクトルの反転：REVERSE_VECTOR（v）⇒ベクトル vの要素を逆にする
　　　　　　例：REVERSE_VECTOR([1,2,3])

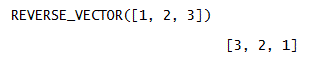
　以上で、今回の問題には、対応できるでしょ」

「いや、ご苦労様じゃったな。
　では、（4）節の問題に適用してみよう。
　特性多項式は、すでに、ともちゃんが解説してくれたが、CHARPOLY(I,λ)=λ^2 － λ·(Ixx + Iyy) + Ixx·Iyy － Ixy^2、となることを確かめることができる。
　固有値は、EIGENVALUES(I)、から、（特性多項式を呼び出す必要はない）
　([(√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) + Ixx + Iyy)/2, － (√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) － Ixx － Iyy)/2])、と求められる。
　固有ベクトルは、EXACT_EIGENVECTOR（I，固有値）から、
　([－ (√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) + Ixx － Iyy)/(2·Ixy); －1])、
　([(√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) － Ixx + Iyy)/(2·Ixy); －1])、
　ただし、その大きさを1にしして、（ここでは）これらのベクトルを横ベクトルにする必要がある。
　p ≔ [－ √2·√(√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) + Ixx － Iyy)·SIGN(Ixy)/(2·(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2)^(1/4)), － √2·ABS(Ixy)/√((Ixx － Iyy)·√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) + Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2)]、
　q ≔ [√2·(√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2) － Ixx + Iyy)·SIGN(Ixy)/(2·√(√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2)·(Iyy － Ixx) + Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2)), － √2·ABS(Ixy)/√(√(Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2)·(Iyy － Ixx) + Ixx^2 － 2·Ixx·Iyy + 4·Ixy^2 + Iyy^2)]、
　これらから、直交行列は、T=［p，q］とすれば、求められる」

「（3）節の I、に適用してみるよ。

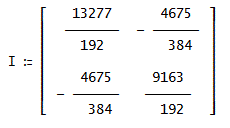
　まず、固有値は、EIGENVALUES（I）から、
　([187·√1109/384 + 935/16, 935/16 － 187·√1109/384])、
　固有ベクトルは、([√1109/25 + 22/25; －1])及び([22/25 － √1109/25; －1])となる。
　固有ベクトルについては、絶対値を1にして、横ベクトルにすると、
　p=([√(48796·√1109 + 2459762)/2218, － √(2459762 － 48796·√1109)/2218])、
　q=([－ √(2459762 － 48796·√1109)/2218, － √(48796·√1109 + 2459762)/2218])、
　直交行列は、
　([√(48796·√1109 + 2459762)/2218, － √(2459762 － 48796·√1109)/2218; － √(2459762 － 48796·√1109)/2218, － √(48796·√1109 + 2459762)/2218])、
　DERIVE画面のコピーは、下図の通り。

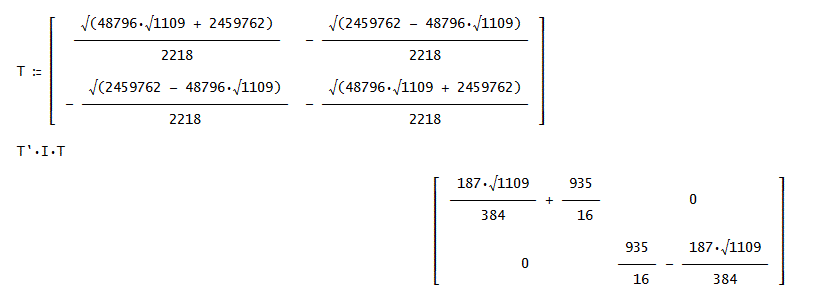
　TとTによる対角化を合わせて表示している」

「4次行列までの固有値の厳密解は、求められるので、固有ベクトルを求めるためには、EXACT_EIGENVECTOR関数を使えばよい。
　しかし、5次以上の行列の固有値は、一般には、近似値が得られるだけなので、その固有ベクトルを求める際は、APPROX_EIGENVECTOR関数を利用する必要がある。
　EXACT_EIGENVECTOR関数に固有値の近似値を使うと、固有ベクトルとして、ゼロベクトルが返ってくるだけなのでな。
　以上で、慣性モーメント、慣性テンソル及び主軸変換のおさらいは、一応、終わりにしよう。
　だいぶ、紙数が多くなったので、本来の目的であった3次元空間上の多面体の慣性テンソルの具体的な計算については、次回に回すことにしよう。
　ともちゃんも、お疲れさんじゃった」　　