そのフォームは、次のとおりである。
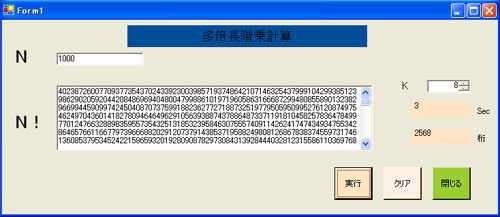
名称は、TabaichoKaijyo.Lzh。今回は、実行形式ファイルのみの公開である。
更新日:2003/9/8
前回で乗算関数ができたので、階乗の多倍長計算を試みた。
ロジックは、簡単で、a=N、b=Nとおいておき
b=b-1、a=a×bを計算する。
これをb=2になるまで繰り返す。
短いので全文を掲げる。
Function Power(ByRef strw As String, ByRef kw As Integer) As String
'多倍長階乗計算ルーチン : TA : 2003/9/8
Dim strw1, strw2 As String
strw1 = strw : strw2 = strw
k = kw
If strw = "0" Or strw = "1" Then
strw1 = "1"
GoTo Power_1
End If
Do Until strw2 = "2"
strw2 = FMN(strw2, "1", k) ’減算関数の利用
strw1 = FMU(strw1, strw2, k) ’乗算関数の利用
Loop
Power_1:
Power = strw1
End Function
上記では、扱う数が正の数であるので、乗算、減算とも符号を考慮しない関数を使用した。
| N | N! | k | 計算時間 | 計算時間2 |
| 15 | 1307674368000 | 8 | 0~ | 0~ |
| 20 | 2432902008176640000 | 8 | 0~ | 0~ |
| 2000 | 5736桁の数 | 8 | 57秒 | 10秒 |
| 同上 | 同上 | 4 | 97秒 | 20秒 |
| 同上 | 同上 | 2 | 178秒 | 38秒 |
| 4000 | 12674桁の数 | 8 | 417秒 | 71秒 |
上表で「計算時間」は、Celelon 766 MHzのパソコンにおける計算結果である。
これは、フィボナッチ数列等の計算の際に使用したパソコンと同等のもの。
「計算時間2」は、Pentium4 2.4 GHzでの計算時間。現在のところ、当方で最速のマシンである。
また、kは、これまでと同様にまとめ計算の数であり、たとえば、N=2000での
結果を見ると、kの効果は、大きいことが分かる。
多倍長の階乗計算を自作ものコーナーに追加した。
そのフォームは、次のとおりである。

名称は、TabaichoKaijyo.Lzh。今回は、実行形式ファイルのみの公開である。