
0.始めにお読みください
1.新型コロナウイルス(COVID-19)感染の拡大
(1)概要
(2)日本の感染状況
(3)日本政府の対応
2.感染曲線1(潜伏期間・回復・免疫無視)
(1)感染率=1
(2)感染率=0.5
(3)微分方程式で解析
3.感染曲線2(回復・免疫無視、潜伏期間を考慮)
(1)感染率=1、潜伏期間=7
(2)感染率=1、潜伏期間=3
(3)感染率=0.5、潜伏期間=3
4.感染曲線3(潜伏期間・回復・免疫を考慮)
(1)感染率=1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=0.2
(2)感染率=0.5、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫率=0、重症率=0.2
(3)感染率=1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫率=0.2、重症率=0.2
(4)感染率=1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫率=0.5、重症率=0.2
(5)感染率=1、潜伏期間=7、軽症者回復=14、初期免疫率=0、重症率=0
5.モデルの検討
(1)新規感染者数
(2)新規免疫者数
(3)初期免疫率
(4)重症者の隔離
(5)死亡率
(6)地域の広がりを考慮
6.軽症者の準隔離の効果 2020/3/22訂正
(1)軽症者の準隔離を取り入れない場合
(2)準隔離時期=20、期間=7
(3)準隔離時期=20、期間=14
(4)準隔離時期=30、期間=7
(5)準隔離時期=30、期間=14
(6)準隔離時期=40、期間=7
(7)準隔離時期=40、期間=14
(8)準隔離時期と期間のまとめ
7.感染拡大防止策
(1)感染率を低くする
(2)マスクや消毒液等の供給量の確保
(3)コロナウイルスの検査の簡便化
(4)重症者の入院と隔離
(5)発症者集中地域の隔離
(6)情報提供の拡充
(7)治療薬の開発と治験 2021/9/8追記
8.終わりにあたって
9.感染(流行)曲線を描くExcel表(2020/3/23~3/28)
(1)分類と名称
(2)分類の時間推移
(3)用語の簡易標記
(4)Excel表とグラフ
(5)計算例1(4.(1)の例)
(6)計算例2(重症者の完全隔離+土日のみ感染率を抑制)
(7)計算例3(感染率が低く死亡率を考慮)
(8)計算例4(感染率が比較的高く死亡率を考慮)
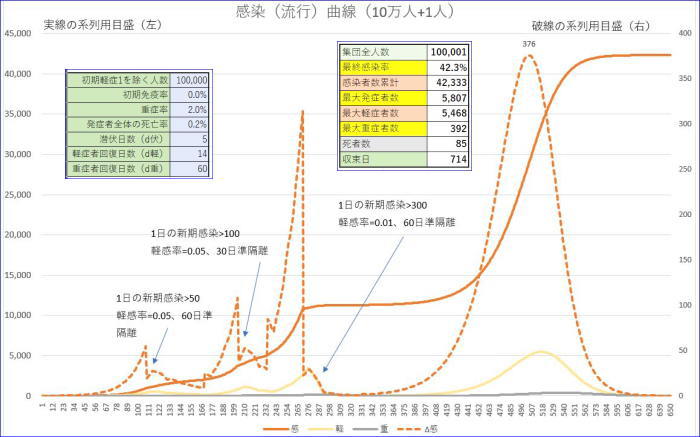
(9)計算例5(10万+1、準隔離=16日または24日)3/28訂正
(10)計算例6(10万+1,準隔離を間隔を空け複数回)3/28訂正
(11)計算例7(週末2日のみ準隔離連続60回)2020/3/30追記
(12)計算例8(10万+1,重症率・死亡率が従来値の1/10)2020/4/30追記
日本では、2020年1月より国内で『新型コロナウイルス』感染者が発生するようになりました。その後、2月に入るとテレビのニュース番組などで盛んに取り上げられるようになったのですが、厚労省は、もとより、一部の専門家の奥歯に物が挟まったような発言やピントの少し外れたコメンテーターのコメントなど、かみ合わないやりとりに終始もやもやした感じが残り続けました。
また、『正しく怖れよ』という言葉も一人歩きしてして、2月半ばまでは、新型コロナは、中国では、大流行しているが、日本では、たいしたことにはならないだろうという楽観ムードが一部に漂っていたようです。
この状況に、たまりかねて、もやもや感を払拭するため、感染症には、素人ですが、Excelを道具として、自己解決を図った過程を紹介しました。感染症の伝播については、(連立の)微分方程式で扱われると思いますが、ここでは、差分(方程式)の考えを使い、Excelの数値計算とグラフで感染の伝わり方をイメージできるようにと考えました。以下に内容をざっくりとご紹介します。
1.『新型コロナウイルス(COVID-19)感染の拡大』では、3/5頃までの現状をまとめています。ただ、その後、状況が日々、変化していますので、最新のデータで更新していません。最新の状況は、厚労省、それぞれの地元の自治体、NHKの特設サイトなどでご確認ください。
差分方程式の組み立て方について、扱いの易しい場合からやや一般的な段階に拡大し、計算したのが、2.『感染曲線1(潜伏期間・回復・免疫無視)』、3.『感染曲線2(回復・免疫無視、潜伏期間を考慮)』、4.『感染曲線3(潜伏期間・回復・免疫を考慮)』です。
その後、一度、5.『モデルの検討』で考えているモデルを検証し、重症者の隔離を取り入れたものが5.(4)『重症者の隔離』です。さらに、6.『軽症者の準隔離の効果』では、軽症者の準隔離(完全ではないが自宅待機などできるだけ人と接触しない生活を送る)を取り入れてみました。軽症者の準隔離が大切であることが分かります。
7.『感染症拡大防止策』では、一般的な防止策などをまとめてみました。外出自粛や交通の減便などにも触れています。
9.『感染(流行)曲線を描くExcel表』では、死亡率も取り入れて、モデルの対象を、より正確に定義して、Excel表の画面の説明と、ダウンロード方法、使い方並びに計算例を記載しています。手っ取り早く、試してご覧になりたい方は、この9節からお読みいただくこともできます。
なお、9節で公開しているExcel表は、6節で使用したExcel表(公開していません)とは異なり、毎日の軽症者感染率、重症者感染率を必要に応じて日ごとにでも変更できるように作り直しました。
目次に戻る
新型コロナウイルス(後日『COVID-19』とWHOが命名)感染症は、2019年11月末頃~12月初めに中国湖北省の武漢市を中心に流行がはじまったとされています。当初、地元政府からは『武漢市内の海鮮市場の動物から人へ感染したもので人から人への感染はない』というゆがんだ情報が内外に発信されましたが、2019年12月31日に武漢市が数十名の肺炎患者が発生していることを認めました。
その後、謎の感染症を引き起こす病原体が通常のインフルエンザ、鳥インフルエンザ、Sars(サーズ:重症急性呼吸器症候群)、Mers(マーズ:中東呼吸器症候群)とも異なる新型の『コロナウイルス』によるものと確定し、1月23日に習近平主席の指導の下、中央政府により武漢市の交通の制限等の措置が実施されるに至りました。
一方、この感染拡大に対して、世界保健機関(WHO)の1月23日~24日の国際会議では、公衆衛生上の脅威とは認められないとの見解を示しましたが、中国国内のさらなる感染拡大を受けて、2020年1月31日(日本時間)、『公衆衛生上の緊急事態』を宣言しました。
日本における最初の感染者は、武漢市からの帰国者であり、2020年1月15日に発生を確認して以降、各地で散発的な感染例が見られるようになりました。これらは、武漢市あるいはそれを含む湖北省に何らかのつながりがある方の感染が中心でした。
さらに、封鎖された武漢市及び近郊に残る日本人及びその家族を帰国させるため、日本政府は、チャーター便を、都合、5回にわたり運航しました。チャーター便による帰国者で症状のない方も施設等での14日間の隔離観察を行うなどの措置が取られました。その結果、828名の帰国者のうち、感染された方は、14名でした。
これだけでも、異例の事態でしたが、並行して思いがけないアクシデントが発生。それは、新型コロナウイルスに感染した乗客が乗船していたクルーズ船の寄港です。この船は、日本及び多くの国の乗客(約2700名)及び乗員(約1000名)が乗船する豪華客船『ダイヤモンド・プリンセス号』(船籍:英国、運営会社:米国、以下『クルーズ船』という)でした。
船内における新型肺炎の発症者1名が1月31日に香港で下船し、その後、一度、沖縄那覇港で日本の検疫を受けた後、乗客の一部は、沖縄の観光を行い、最終的に2月3日に横浜港沖に到着しました。
ここで、異例の2度目の検疫を受けることになりました。この後の細かい経緯は、略しますが、多くの感染者はいないだろうとの当初の予測は、大きく外れ、多くの体調不良者、陽性者の発見が相次ぐようになりました。この3700名という1つの町の人口に相当する膨大な人員に対しての検疫・検査の実施は、困難を極めました。
結局、2/21現在、コロナウイルスに感染していた陽性者は、634名、検査を受けた方は、述べ3063名(複数回の検査を受けた方もあります)でした。これらの方々のうち、4名が亡くなられ、また、検疫官、DMATの看護師、厚生労働省の職員などにも計7名の感染者が出る事態となりました。なお、今後も陰性の乗客、乗員から陽性に転じる方が出る可能性もあり、上の数字も変わる可能性があります。このクルーズ船の出現により、国立感染症研究所や各地の衛生研究所の人手と時間が大幅に割かれた結果、対コロナウイルスに対する日本の戦略に大きな狂いが出たことは、確かでしょう。
上に述べた『クルーズ船』と『チャーター機で帰国した方』を除き、3月3日正午現在、246名が発症し、6名が死亡、また、陽性であるが無症状の方が23名となっています。クルーズ船下船者やチャーター機での帰国者を含めて、発症者は、日々、増え続けています。(赤字数字は、3/5に最新の数字に置き換え)
厚生労働省報道発表一覧は、下のページです。
https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000121431_00086.html
なお、付け加えると、新型コロナウイルスは、乳幼児や10代の感染者や重症者が少ないことことは、通常のインフルエンザとは、大きく異なる特徴とされています。その一方、高齢者や持病のある方などの成人に時として、重症者が出ている点は、大いに危惧すべきことです。(2/15頃の報道では、中国の武漢市を除く地域の発症者のうち、80%は、軽症、20%が重症化するもの17%は、回復し、全体の3%が死亡するとされています)
※各国に感染が広がっています。最近、中国国内の新規感染者増加数より、中国以外の新規感染者の増加数が多くなりました。コロナウイルスによる新型肺炎は、アジアからヨーロッパ、アメリカ、南米、中東、アフリカにも広がりつつあります。WHOが世界的な感染爆発を意味する『パンデミック』(pandemic)を宣言するのも、あるいは、時間の問題かも知れません。
2020/3/11にWHOが『新型コロナウイルスはパンデミックと言える』と発表しました。(2020/3/13追記)
目次に戻る
日本で最初に感染者が発見された1/31から2/24までの感染者の増加を表すグラフを描いてみました。厚生労働省のサイトの報道資料を基にしています。チャーター機で帰国された方の隔離終了後やクルーズ船から陰性とされて下船後に発症した方がいらっしゃるなどしているため、クルーズ船・チャーター機を除く、というタイトルの注意書きを変更しています。
なお、陽性でも統計時点で発症されてない方が除かれているため、ニュース等の報道の数字よりやや少なくなっています。これは、発症者が周囲に感染を広げるリスクがあるため集計の対象にするという見解に基づくものと考えられます。
とは言え、発症しているか否かを厳密に判定するのは難しく、まして、何日に発症したのかは、あいまいにならざるを得ず、さらには、感染後、発症する1または2日前に他人に感染させたと考えられるケースも中国で観察されるなど、無症状者数が増えた場合、発症者と分けて集計することにどれほどの意味があるのかは、疑問に感じられる点です。
従いまして、下のグラフの元になった数字は、やや控えめな値とお考えください。それでも、このまま増え続けると空恐ろしい値ですが・・
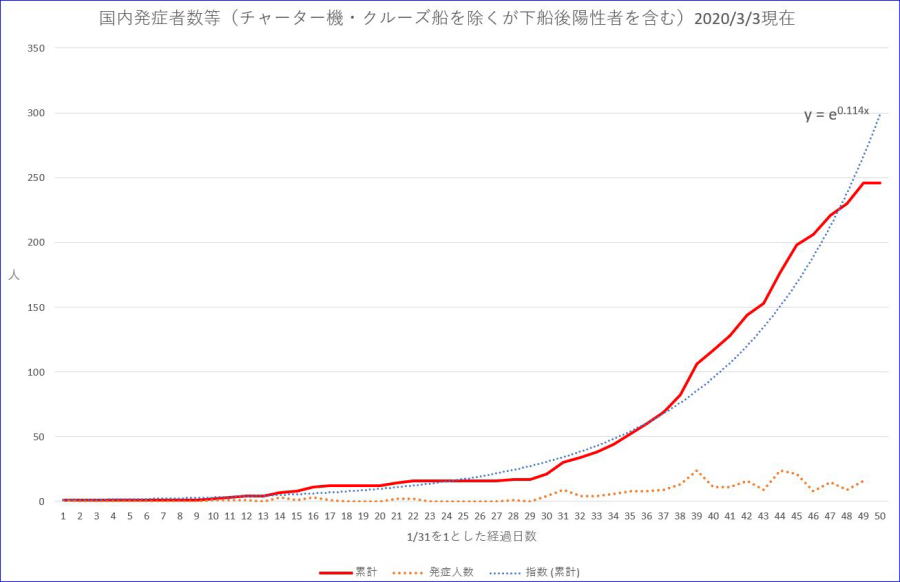
オレンジは、発症者累計数、オレンジの破線は、新規発症者数、青い破線は、累計に指数関数を当てはめた近似式。
※近似式は、あくまでも当該区間のデータにフィットする指数型の近似曲線の一例です。
※近似式の外挿は、意味が乏しいですが、仮に行うと3/31で約6000、4/30で約20万、5/31で約700万!の累計発症者となります。
※上の近似式の外挿の意味が乏しいことは、6月半ばで日本の総人口を軽く超えてしまうことから分かります。
コロナについては、軽症者が多いので、短期間で回復し、回復により免疫ができれば、感染しにくくなるのは、良いことです。また、全体の発症者数を少なくできれば、発症者の約20%と言われる重症者を少なくできるため、医療機関のベッド数は、足ります。
一方、発症者が多いと約80%の軽症者のために医療機関の受診窓口がパンクします。実際、2009年(2009年夏~2010年春)に日本でも流行した新型インフルエンザは、医療機関の受診者数が約2000万人となりましたが、死者は、通常のインフルエンザによるものと大差がなく、これは、抗ウイルス薬の投与も効果があったと言われています。(青字部分は、ウィキペディアによる)
目次に戻る
政府は、2020/2/25にコロナウイルスに対する基本方針を発表しました。非常にざっくりとしたもので、明らかに誤りと指摘できる個所はないものの、具体的な内容が乏しく、ここ2週間ほど以前より、広く国民に呼びかけてきたものと大きく変わっていませんでした。(明治天皇の『五箇条の御誓文』(1868年)かと思いましたな)
この基本方針の下に1年間ほど時間をかけて具体的な対策を練って行こうというのであれば、これでもよいかとも思いましたが、現況は、そのような甘いものではなく、一日の遅滞を許さない厳しい状態です。比喩ではなく、東京が第2の武漢市になりかねません。
コロナウイルス対策という利益のなさそうで、失敗すれば、世間の批判を浴びるであろう事案について、消極的抵抗というべき諸官庁の責任の押しつけ合いの結果、無色透明で無難な『基本方針』が出てきたものと拝察いたします。
テレビ映像に流れる政府の新型コロナウイルスによる感染症対策会議の重々しい映像とそれに見合わない内容の乏しい基本方針は、かつての東宝映画『シン・ゴジラ』の既視感ある映像とシンクロしすぎて、正直、驚きました。優れた作品は、時代を予見するということは、本当かも知れません。
映画で暴れ回ったのは、怪獣『ゴジラ』で、口から放射能の炎を吐きましたが、今回の怪獣『コロナ』は、感染妖怪(姿が見えない!)で、ウイルスをばらまいて回り、ウイルスを取り込んだ人も、また、『コロナ』になってしまうという点がさらにやっかいです。まさにねずみ算ならぬコロナ算で増えてしまうのです。
閑話休題
さすがに、政府も、インターネット上を含めて、多くの指摘や批判を受け、2020/2/26に大きなイベントの中止の要請を行うこととし、翌2020/2/27夕刻に全国の小中学校、高校、特別支援学校を所管する機関等に対して、2020/3/2から春休みまで休校(実質的に4月10日頃までの休み)を呼びかけることになりました。また、卒業式、入学試験等の規模縮小や延期、中止なども併せて要請しました。
一方、幼稚園、保育園、学童保育などの一斉休業は、呼びかけないということになりました。いずれにしても、今後、感染の広がりが続けば、その対応は、一段と厳しく、また、選択肢が乏しいものとなっていきそうです。
さらに困ったことに、マスクや手指の消毒薬などの品不足は、依然として続いており、政府も関係業界に要請を行い、企業も昼夜を問わず生産を続けるものの、医療現場に優先して供給されるため、一般の店頭に行き渡るまでには、まだ、1ヶ月以上かかりそうです。
なお、新型コロナウイルスに対する効果のある治療薬は、今のところ明らかになっておらず、各国で開発や治験が進められています。厚労省は、備蓄されている鳥インフルエンザ対策用のアビガンなどの抗ウイルス薬の新型コロナウイルス感染症に対する治験を3月にも開始するとのことです。
手指の消毒は、石けんによる20秒以上の洗浄やアルコール消毒が有効ですが、アルコールも一部で品薄になっているとの報道もありました。無水エタノール(エチルアルコール)や純エタノール(エチルアルコール)を体積比8に水2を混ぜて用いることで代替可能です。(エチルアルコールのみでも消毒効果はありますが、すぐ蒸発するため手指にある程度の時間残るようにして効果を高めるためと手荒れ防止のため水を混ぜています。なお、エタノール(エチルアルコール)とメタノール(メチルアルコール)=劇物・毒物を間違えないでください。命に関わります)。
ただし、アルコール消毒で強いアレルギーが出る方には、アルコールは、使えませんので、みだりに他人にアルコール消毒を強制することは、お控えください。アレルギーをお持ちの方は、他の薬品や石けんで自らご対応いただくようお願いします。
※2020年4月7日、7都府県(東京都、埼玉県、千葉県、神奈川県、大阪府、兵庫県、福岡県)を対象として、『新型インフルエンザ等対策特別措置法』に基づき緊急事態宣言が出されました。期間は、2020年4月7日から5月6日までとなっています。(2020/4/8追記)
※2020年4月16日、7都府県に続き、緊急事態宣言をそれ以外の全国の道府県を対象に拡大して、5月6日まで適用することになりました。なお、4月7日の7都府県(東京都、埼玉県、千葉県、神奈川県、大阪府、兵庫県、福岡県)に北海道、茨城県、石川県、岐阜県、愛知県、京都府を加えた13都道府県を『特定警戒都道府県』と位置づけています。さらに国民1人当たり10万円の給付を行う方向で補正予算案を組み替えることになりました。(2020/4/17追記)
※2020年5月4日に5月6日までの期限で全国に出されている緊急事態宣言を5月末まで延長する旨が発表されました。
(2020/5/8追記)
※2020年5月14日に8都道府県を除く39県の緊急事態宣言が解除されました。残る地域(東京、埼玉、千葉、神奈川、大阪、京都、兵庫、北海道)は、5月21日前後に再検討し、解除できる場合は、5月末を待たずに解除される可能性もあります。(2020/5/15追記)
※2020年5月21日に大阪、京都、兵庫に出されていた緊急事態宣言が解除されました。残る地域(東京、神奈川、千葉、埼玉、北海道)は、1週間後に再度、検討することで、当面は、そのまま緊急事態宣言が継続されます。(2020/5/21追記)
※2020年5月25日、緊急事態解除宣言が出され、5/21に解除されていなかった地域(東京、神奈川、千葉、埼玉、北海道)も解除され、これで全国に出されていた緊急事態宣言は、すべて解除されました。(2020/5/26追記)
※2021/1/8、緊急事態宣言が東京都、埼玉県、神奈川県、千葉県に再発出されました。今後、関西、中部等の大都市を中心とした地域にも拡大される可能性があります。(2021/1/8追記)
※2021/1/14、緊急事態宣言が2021年1月8日の1都3県に続いて以下の7つの地域に出されました。大阪府、兵庫県、京都府、愛知県、岐阜県、栃木県、福岡県。期間は。2021年2月7日までとされています。
※2021/2/2、緊急事態宣言が出されている11都府県のうち、栃木県のみは、2月7日までで解除するが、その他の10都府県については、3月7日まで延長することになりました。これは、宣言の効果は、一定程度見られるものの、新規感染者数、医療提供体制等からみて、仮に宣言を解除した場合、早期に3度目の緊急事態を宣言せざるを得なくなることを懸念したものです。(2021/2/4追記)
※2021/4/25、3回目の緊急事態宣言が4都府県(東京、大阪、兵庫、京都)に5/11まで出されました。5/12から、福岡、愛知を追加しました。期限は、5/31までとなりました。「まん延防止等重点措置」も、5月9日から北海道、岐阜県、三重県が追加されて8道県に拡大しました。
※2021/5/14には、北海道、岡山、広島の3道県を対象に、5/16から5/31までの期間、緊急事態宣言を出すことを決定。また「まん延防止等重点措置」を群馬、石川、熊本の3県にも適用し、期間は5/16から6/13までとしています。これで緊急事態宣言が出されているのは合わせて9都道府県になりました。
※2021/5/29には、北海道、東京、愛知、大阪、兵庫、京都、岡山、広島、福岡の9都道府県に出されている緊急事態宣言について、5/31の期限を沖縄への宣言と同じ6/20まで延長することを決定しました。
※2021/6/17には、沖縄県を除く、9都道府県は、「まん延防止等重点措置」に移行を決定しました。
※2021/7/8には、東京都のまん延防止等重点措置を4回目となる非常事態宣言(7/12~8/22)に切り替え、沖縄県の非常事態宣言期間を8/22まで延長することを決定しました。また、千葉、神奈川、埼玉、大阪のまん延防止等重点措置を8/22まで延長しました。一方、北海道、愛知、京都、兵庫、福岡のまん延防止等重点措置は、7/11で解除します。
※2021/7/23に『東京2020 オリンピック競技大会』の開会式が新国立競技場で行われました。競技を含めて、ほぼ、無観客で行われています。
※2021/7/30には、東京と沖縄に出されている緊急事態宣言の期間を8/31まで延長するとともに、千葉、神奈川、、埼玉、大阪に4回目の緊急事態宣言を発出(期間は、8/2~8/31)することを決定しました。また、北海道、石川、兵庫、京都、福岡については、まん延防止等措置を適用することになりました。
※2021/8/5には、まん延防止等措置地域に福島、茨城、栃木、群馬、静岡、愛知、滋賀、熊本の8県を追加し、期間は、2021年8月8日から2021年8月31日までとすることを決めました。
※2021/8/17には、緊急事態宣言の対象地域の東京、沖縄、千葉、神奈川、埼玉、大阪に加えて、茨城、栃木、群馬、静岡、京都、兵庫、福岡の7府県を追加し、期間は、2021年8月20日から2021年9月12日までとすることになりました。また、同じ期間、まん延防止等重点措置の対象地域の北海道、石川、兵庫、京都、福岡、愛知、滋賀、熊本に加えて、宮城、山梨、富山、岐阜、三重、岡山、広島、香川、愛媛、鹿児島の10県に新たに適用するほか、これに合わせて、2021年8月31日までの期限の6都府県の宣言と6道県の重点措置を延長することになりました。
※2021/8/25には、すでに出されている緊急事態宣言地域に、北海道、宮城、岐阜、愛知、三重、滋賀、岡山、広島の8道県を追加し、まん延防止等重点措置についても、高知、佐賀、長崎、宮崎を追加することになりました。期間は、8/27から9/12までとします。これにより、緊急事態宣言地域は、東京、沖縄、千葉、神奈川、埼玉、大阪、茨城、栃木、群馬、静岡、京都、兵庫、福岡、北海道、宮城、岐阜、愛知、三重、滋賀、岡山、広島の21都道府県となります。また、まん延防止等重点措置地域は、福島、石川、富山、山梨、香川、愛媛、高知、宮崎、長崎、佐賀、熊本、鹿児島の12県となります。
※2021/9/9には、9月12日までとなっている緊急事態宣言について、宮城県と岡山県は、まん防止等重点措置に移行し、残りの19都道府県を含めて、9月30日まで、期間を延長することになりました。また、9月12日まで、まん延防止等重点措置が適用されている、富山、山梨、愛媛、高知、佐賀、長崎県は、期限となる9月12日で解除することになりました。これにより、9月13日~9月30日まで適用されるのは、緊急事態宣言が、北海道、栃木、群馬、埼玉、茨城、東京、千葉、神奈川、静岡、岐阜、愛知、滋賀、三重、京都、大阪、兵庫、広島、福岡、沖縄の19都道府県、まん延防止等重点措置は、宮城、福島、石川、岡山、香川、熊本、宮崎、鹿児島の8県となります。(2021/9/11追記)
※2021/10/1には、国内のすべての緊急事態宣言、及び、まん延防止等重点措置の指定が解除されました。(2021/10/1追記)
※2021/11/27、南アフリカで見つかった変異ウイルスをWHOが、懸念される変異株に指定しました。新変異ウイルスは、『オミクロン』(ο)というギリシャ文字が割り振られました。
※2021/11/29、これを受けて、日本政府は、外国人の新規入国を30日から禁止する措置をとりました。
※2021/12/1、日本では、ナミビアの外交官及びペルーから入国した方の2人がオミクロン株に感染していることが明らかになりました。また、日本人を含めて、航空便の新規予約の停止を航空会社に要請するも、12/2になり、日本人の帰国者に十分な配慮をするようにと一部、撤回するなど、慌ただしい対応に追われています。
※2021/12/1、新型コロナワクチンの3回目の接種が、2回目の接種から、原則として、8ヶ月経過した医療従事者を対象として開始されました。今後、2022年1月からは、これに加えて、高齢者等への接種も始まる予定です。
※2022/1/7、政府は、新型コロナウイルスのオミクロン株の感染拡大を受けて、沖縄県、山口県、広島県について、2022/1/9から2022/1/31までの間、まん延防止等重点措置を適用することを決めました。
※2022/1/18、政府は、新型コロナウイルスのオミクロン株の感染拡大を受けて、2022/1/17に東京都、埼玉県、神奈川県、千葉県の1都3県から要請があった、まん延防止等重点措置を2022/1/19にも、決定する模様です。期間は、2022年1月21日から2022年2月13日を予定しています。また、同時に、愛知県、岐阜県、三重県の東海3県、群馬県、新潟県、香川県、長崎県、熊本県、宮崎県についても、適用する方向で調整しています。これにより、すでにまん延防止等重点措置が適用されている沖縄、広島、山口を含めて、1都15県に拡大され、今後も対象地域が増加する見込みです。
※ 2022/1/25、政府は、新型コロナウイルスのオミクロン株の感染急拡大を受け、要請のあった、次の18道府県に対して、2022年1月27日から2022年2月20日まで、まん延防止等重点措置を適用することを決定しました。新規に追加されるのは、北海道、青森、山形、福島、茨城、栃木、石川、長野、静岡、京都、大阪、兵庫、島根、岡山、福岡、佐賀、大分、鹿児島県です。また、すでに先行して適用されている、沖縄、広島、山口県の3県の期限を2022年1月31日から、2022年2月20日まで延長することも、併せて、決定しました。これにより、すでにまん延防止等重点措置が適用されている16都県と合わせ、34の都道府県に拡大される結果となります。
※ 2022年2月5日、政府は、新型コロナウイルスのオミクロン株の感染拡大を受け、要請のあった和歌山県にまん延防止等重点措置を適用することを決定しました。期間は、2022年2月5日から2月27日までとなります。これで、まん延防止等重点措置が適用されている都道府県は、35となりました。また、2月13日までとなっている東京都など13都県について、期間を延長する方向で検討しています。
※ 2022年2月10日、政府は、2022年2月13日までとなっていた東京都など13都県に対するまん延防止等重点措置について、2022年3月6日まで期間を延長する方針を政府分科会に諮りました。また、新たに要請のあった高知県について、2022年2月12日から3月6日まで、まん延防止等重点措置を適用することも諮りました。これで、まん延防止等重点措置が出るのは、36都道府県となります。
※ 2022年2月18日、政府は、36都道府県に対して発令中のまん延防止等重点措置について、5県を除き、期限を2022年3月6日まで延長する方針を決定しました。また、沖縄、山形、島根、山口、大分の5つの県は、2022年2月20日で解除することにしました。
※ 2022年3月4日、31の都道府県に発令中のまん延防止等重点措置について、福島、新潟、長野、三重、和歌山、岡山、広島、高知、福岡、佐賀、長崎、宮崎、鹿児島の13の県は、2022年3月6日で解除することにしました。一方、北海道、青森、茨城、栃木、群馬、埼玉、千葉、東京、神奈川、石川、岐阜、静岡、愛知、京都、大阪、兵庫、香川、熊本の18の都道府県は、2022年3月21日まで延長することになりました。
※ 2022年3月21日に13都道府県に発令されていました、まん延防止等重点措置は、すべて解除されました。
※ 2023年1月27日に政府は、2023年5月8日から、新型コロナウイルスの感染症法上の扱いを現在の「2類」相当から、、季節性インフルエンザなどと同じ「5類」に移行する方針を正式に決めました。5類に移行した場合、行動制限(緊急事態宣言、まん延防止等重点措置、強制隔離、検疫等)ができなくなり、医療費やワクチンの自己負担分が発生し、感染者数把握が定点観測になるなどが変化が生じます。ただし、当面、医療費やワクチンの公費負担は、続け、診察や入院可能な医療機関も段階的に広げていく方針です。また、市町村や保健所などが差配している入院調整なども段階的に縮小される見込みです。マスクの着用、三密回避などの感染対策は、個人の判断に委ねられる方向で検討されています。
※ 2023年2月10日に政府は、マスクの着用について、次のような方針を決定しました。
「3月13日から屋内・屋外を問わず個人の判断に委ねる方針を決定しました。なお、医療機関を受診する際や通勤ラッシュ時といった混雑した電車やバスに乗る際などには、マスクの着用を推奨するなどとしました。また新型コロナの流行期に、重症化リスクの高い人が混雑した場所に行く際には、感染対策としてマスクの着用が効果的であると周知するとしたほか、症状がある人や同居家族に陽性者がいる人などは、外出を控え、通院などでやむをえず外出する際には、人混みを避けマスクを着用するよう求めています。重症化リスクの高い人が多くいる医療機関や高齢者施設などの職員については勤務中のマスクの着用を推奨するとしています。このほか、企業などの事業者については、感染対策上の理由や業務の内容などによっては利用者や従業員に対してマスクの着用を求めることは許容されるとした上で、各業界団体にマスク着用に関するガイドラインの見直しを行うよう求めています。」
※ 基本的対処方針分科会の尾身茂 会長は「今後のマスク着用の考え方について「国や専門家が一つ一つの場面でのマスク着用の必要性の有無を『箸の上げ下ろし』まで細かく示すというのは今ではふさわしくなく、基本的には人々の判断や選択に任せることが重要だというのが専門家の一致した意見だ」と説明しました。
そして尾身会長は「マスクは万能ではないが、感染対策には一定の効果がある。高齢化が進んだ日本で高齢者の間でクラスターなど大きく感染が広がれば多くの人が亡くなってしまう。こうした重症化リスクの高い人たちが感染する機会をなるべく減らしたほうがよく、そのために配慮することが重要だ」と述べ、他人に感染させない配慮を持ってマスクの着用を判断してほしいという考えを示しました。
※ 政府の分科会メンバーで東邦大学の舘田一博 教授は「大事な感染対策は維持しつつ緩和できることはないか、マスクの使い方も含めて考え方を変えていく時期にさしかかっている。コロナに感染してもワクチンや治療薬によって、多くの人はかぜのような症状ですむようになったが、高齢者や基礎疾患がある人は死亡のリスクが高まることを1人1人が理解し、周りの人を感染させてしまうとどんなことが起きるのか想像しながら、場合に応じてマスクを使うことが大事だ」と話しています。そして「マスク着用をめぐって、緩和する方向ばかり注目されがちだが、強調したい最も重要なことはマスクは今でも一定の効果がある大事な感染対策だということだ。効果がない、必要ないから外してよい、ということではない。たとえば高齢者や持病がある人も含めた不特定多数の人と密になるような電車内や、重症化リスクが高い人が多い医療機関などでは、自分を感染から守るためだけでなく、周りを感染させず、不安を与えないためにマスクを使っていくことが必要になる」と強調しました。
(緑字部分は、NHK Webニュース 2023/2/10から抜粋)
2023/4/28、「政府は28日の閣議で、新型コロナの感染症法上の位置づけが5月8日に「5類」に移行されるのに伴い、3年あまりにわたって設置されていた対策本部を廃止することを決めました。」
NHK https://www3.nhk.or.jp/news/html/20230428/k10014051951000.html
この報道によると、2023/5/8以降の主な変更点は、以下の通りです。
・ 検査や医療費に自己負担分が発生。
・ 入院・治療費用についても、同様。
・ 外出自粛期間は、発症の翌日から5日間程度を目安として推奨
・ 軽症者用の宿泊施設などは、終了
・ ワクチン接種は、高齢者・ハイリスク者・医療関係者等は、2023/5以降と9月以降に各1回、その他は、9月以降に1回。
2024年3月までは、ワクチンの無料接種は、継続される予定
・ 海外からの空港や港における入国者に対するワクチン証明書等の提出や検査は、終了。(4/29からに前倒しの予定)
・ 感染者、重症者、死亡者の全数把握は、終了し、感染者数は、全国の定められた医療機関からの「定点観測」に変更。
・ マスクや手洗いなどは、有効だが、個人や組織の判断に委ねる。
目次に戻る
手始めに、一番単純なモデルについてExcelで計算してみましょう。時間単位を1日で考えます。(初日を1としています)
合計人数、感染率(1日あたり感染者から非感染者にどのくらい感染させるかの目安)、ただし、感染と発症との違いや免疫、回復、死亡は、考えません。
このとき、当日の新規感染者数=感染率×前日の感染者数×(前日の非感染者数/初日の非感染者数)と仮定します。後述のようにこの分数は、『飽和』を考慮していると言うことになります。
また、当日の感染者数=前日の感染者数+当日の新規感染者数、ただし、感染者数が初期合計数以上となる場合は、初期合計数としましょう。でないと、合計数を超えて感染者が増加してしまいます。
当日の非感染者数=前日の非感染者数-当日の新規感染者数、ただし、負となる場合は、ゼロとする点も同様の考えです。
さて、簡単のために初期には、感染者が1であるとします。下に示すグラフでは、合計数を1000+1としています。
まずは、感染率が1の場合です。
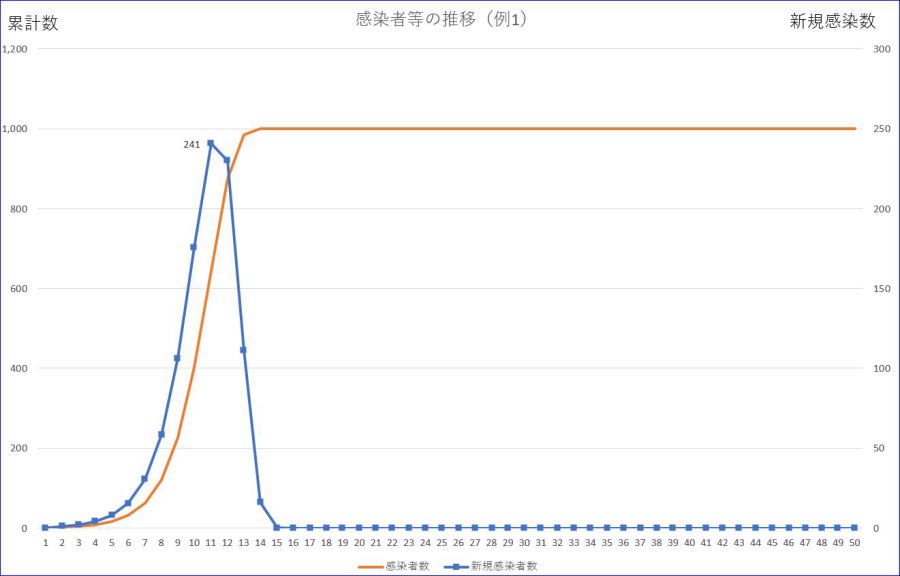
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者累計、右縦軸は、新規感染者数の目盛です。
※オレンジが感染者累計、ブルーが新規感染者数です。
目次に戻る
次に感染率が0.5の場合です。
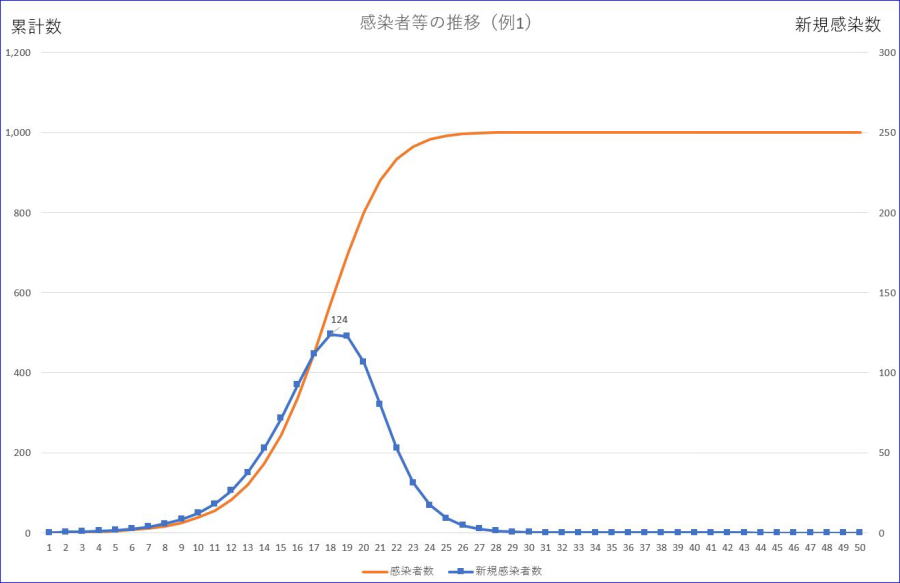
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者累計、右縦軸は、新規感染者数の目盛です。
※オレンジが感染者累計、ブルーが新規感染者数です。
いずれの場合も、当然ながら、時間の経過とともに感染者が1001に達します。その意味では、全員が感染してしまうモデルなので、現実的ではありませんが、注目すべきは、そこではありません。こんな簡単なモデルでも、感染率を低くする効果として、次のような大切な3つのことが分かります。
感染者の増え方を抑制できます。例えば、感染者が全体の50%の500となる日数を調べますと、感染率が1の場合は、10日~11日ですが、感染率が0.5と半分に低下すると、17日~18日までに伸びることが分かります。
また、新規感染者がピークとなる日数を先延ばしにできます。すなわち、新規感染者のピークは、感染率が1の場合、10日~11日であり、感染率が0.5の場合は、19日目であることもわかります。
さらに、新規感染者の最大数を抑えることができます。すなわち、感染率が1の場合は、241であるのに対して、感染率が0.5の場合は、124と約半数に抑えられることが分かります。
この3点目がもっとも、大切な点であると言えます。死亡率が低くても、一定の割合で重症化する方がいれば、現在、発症者の2割と言われていますが、その2割の方を収容する医療施設が足りない可能性があります。その場合、どのような悲劇が起きるかは、武漢市の例を見ると分かります。そのためには、軽症者の方からの感染を如何に防ぐかが重要なポイントとなります。
目次に戻る
上のような簡単なモデルは、感染者累計をy(t)として、dy/dt∝k×y×(a-y)と微分方程式で解析できます。これは、『成長曲線』と呼ばれる曲線の例になります。成長曲線については、『普遍化と専門化』(2017年7月)で取り上げています。
解は、y(t)=a/(1+exp(-m(t-t0)))、ここで、aは、初期の合計、mは、感染率相当、t0は、y=a/2となるときの時間です。
下図は、a=1000、y(1)=1、として、t0を10~20まで変化させて描いてグラフです。最初は、ゆっくりと変化しますが、次第に急激に増加し、最大値の半分まで増加すると、増加は、ゆっくりとなり、最後は、最大値に収束します。
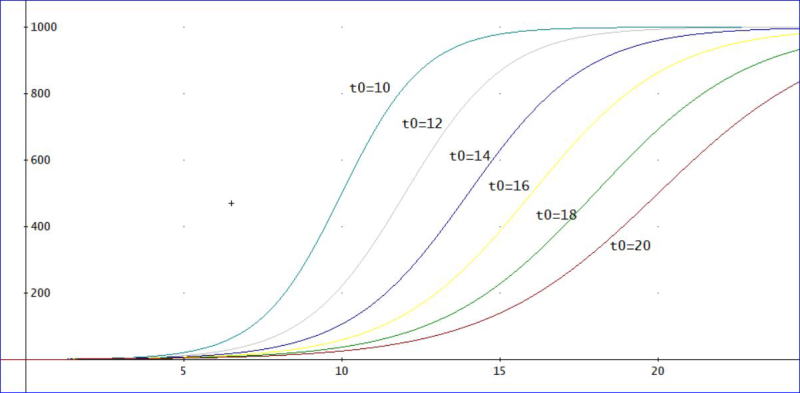
なお、この微分方程式の解と先のExcelの計算との比較など面白いのですが、本題と離れすぎますので、今後、取り上げる機会があれば、その機会にしておきましょう。
なお、伝染病の伝播に関する微分方程式による扱いは、『自然の数理と社会の数理(微分方程式で解析する)Ⅱ』(佐藤總夫著:日本評論社:1987年6月10日第1版第1刷)の第7話『伝染病の伝播-流行と閾値』、第8話『ペスト-閾値定理とペストの流行曲線』、第9話『はしか、インフルエンザの流行-再帰性流行病の数理』、第10話『性病の蔓延-天国から地獄へ』に詳述されています。
しかし、以下では、微分方程式による扱いは、あまりに専門的になりますので行わず、Excelで一日ごとの変化を差分として追跡する方法により、観察します。基本となるのは、加減乗除だけなので、Excelの数式を組み立てられる方であれば、誰でも理解できます。佐藤先生の本のように一般的な定理を導くことは、できませんが、伝染病の流行により感染者がどのように増加するかのイメージは、つかむことができるでしょう。特に初期の流行の段階では、指数関数的な急激な上昇が見られます。指数関数的な増大のイメージは、普通の人間には、とらえにくいものです。身近なところでは、味噌やお酒の醸造などの微生物の活用では、お世話になっているのですが、目に見えないので、激増する様が実感できないのでしょう。
なお、以下の点を予めお断りしておきます。
本稿で使用している用語は、公衆衛生統計等で使われている用語とは、必ずしも一致しません。感染率や非免疫者数等がそれです。また、あくまでも簡易な仮定に基づいていますので、これを実際の統計数字とそのまま比較するのは、無理があります。ご留意願います。
目次に戻る
この節では、潜伏期間を考慮したモデル(例2)について、考えてみましょう。2節との違いは、感染後、一定期間の潜伏期間を経て発症するというモデルとなります。潜伏期間は、ゼロから日単位で数えます。なお、潜伏期間をゼロとした場合は、2節と同一の結果となります。
新規感染者数は、前日の発症者数×(前日の非感染者数/初日の非感染者数)に比例します。
ただし、このモデルでは、回復や免疫を考えていませんので、2節のモデルと同様に時間の経過とともにすべて感染します。
Excelにて、次の算式に基づいて計算します。
新規感染者数=感染率×前日の発症者数×(前日の非感染者数/初日の非感染者数)
発症者数=前日の発症者数+当日の新規発症者数
新規発症者数=潜伏日数前の新規感染者数、
ただし潜伏日数がゼロは、前日の感染者数、前日-潜伏日数が2未満となる場合は、ゼロと見なす。
非感染者数=前日の非感染者数-新規感染者数
ただし、負となる場合は、ゼロとする
重症者数=発症者数×重症率
まずは、合計数1001、初期感染及び発症者=1、感染率=1、潜伏期間=7、の場合のグラフです。
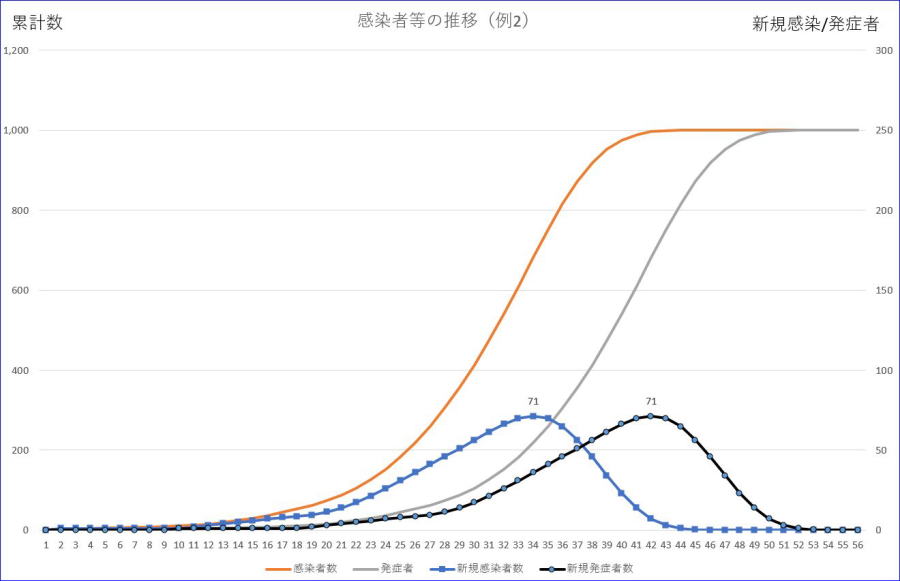
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者累計、右縦軸は、新規感染者/発症者数の目盛です。
※オレンジが感染者累計、ブルーが新規感染者数です。
※グレーは、発症者数、黒は、新規発症者数です。
2節との違いを挙げると、潜伏期間がゼロでないと、当然、発症者がその分、遅れて発生します。また、新規感染者や新規発症者のピークの高さが低くなり、その時期も遅くなることが分かります。
目次に戻る
次に、潜伏期間が、より短くなった場合、合計数1001、初期感染及び発症者=1、感染率=1、潜伏期間=3、の場合のグラフです。
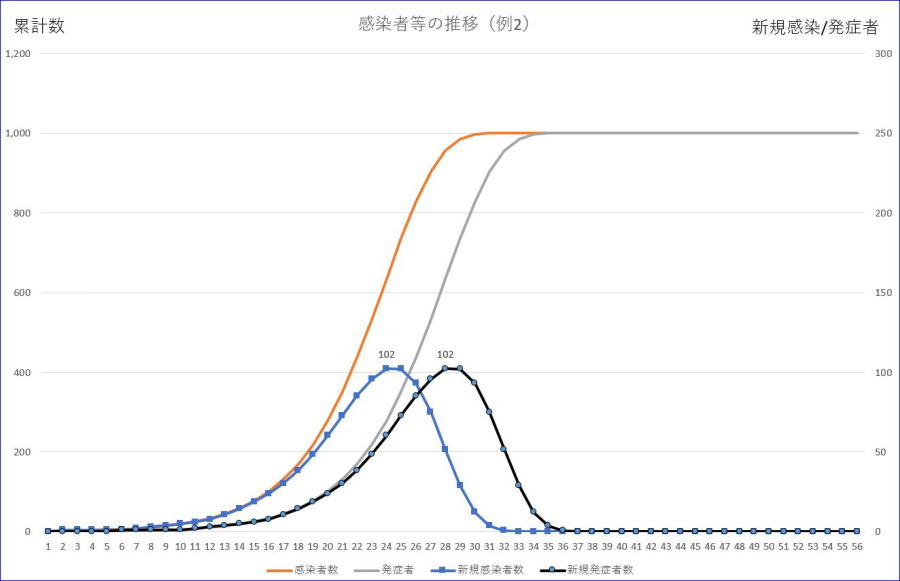
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者累計、右縦軸は、新規感染者/発症者数の目盛です。
※オレンジが感染者累計、ブルーが新規感染者数です。
※グレーは、発症者数、黒は、新規発症者数です。
潜伏日数が7から3に短くなると新規感染者や新規発症者のピークの位置が早まり、ピークの高さも高くなることが分かります。これは、感染から発症までの期間が短くなると感染が劇症化するという直感と一致します。
目次に戻る
最後に挙げるのは、潜伏期間が(2)と同様に短い場合でも、感染率を下げると改善できるという例となります。合計数1001、初期感染及び発症者=1、感染率=0.5、潜伏期間=3、の場合のグラフです。感染率が0.5になっています。
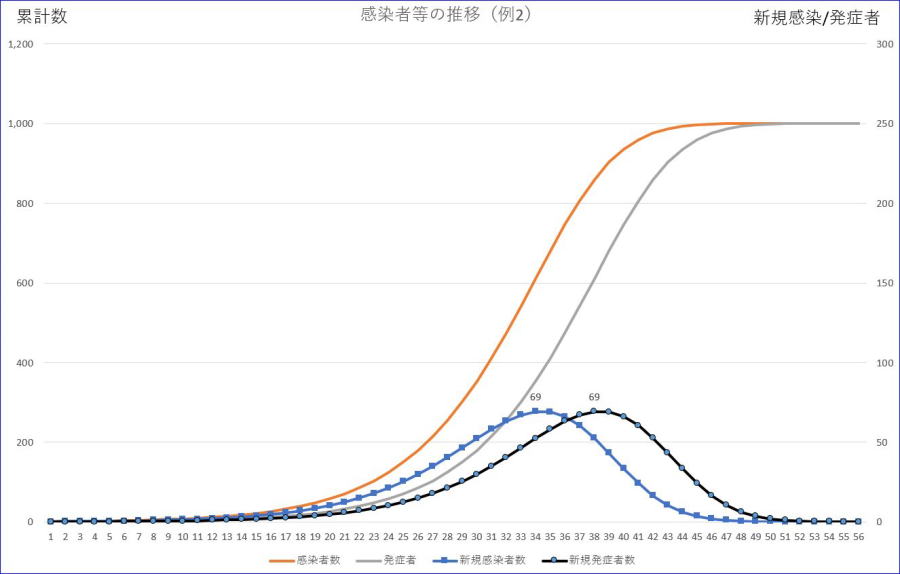
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者累計、右縦軸は、新規感染者/発症者数の目盛です。
※オレンジが感染者累計、ブルーが新規感染者数です。
※グレーは、発症者数、黒は、新規発症者数です。
感染率が0.5になると、潜伏期間が3の場合でも、潜伏期間が7の場合とほぼ同様に新規感染/発症者のピークの位置が遅くなり、高さも低くなることが分かります。
目次に戻る
この節では、潜伏期間の他に、回復と免疫を考慮したモデル(例3)について、考えてみます。3節との違いは、感染後、一定期間の潜伏期間を経て、免疫を持たない人(非免疫者)のみに感染します。
また、発症者のうち(1-重症率)の軽症者は、軽症者の回復期間で完治し、また、重症者も重症者の回復期間で完治します。その後、いずれも免疫を得るというモデルとなります。潜伏期間、回復期間は、ゼロから日単位で数えます。
Excelにて、次の算式に基づいて計算します。赤字部分は、3節との違いを示す。
新規感染者数=感染率×前日の発症者数×((前日の非感染者数-前日の免疫者数)/初日の非感染者数)
ただし、負となる場合は、ゼロと見なす
新規発症者数=(潜伏日数+1)前の新規感染者数
ただし潜伏日数がゼロは、前日の感染者数、潜伏日数+1が初日以前は、ゼロと見なす。
新規免疫者数=(軽症者の回復日数+1)前の新規発症者数×(1-重症率)+(重症者の回復日数+1)前の新規発症者数×重症率
感染者数=前日の感染者数+新規感染者数
発症者数=前日の発症者数+新規発症者数-新規免疫者数
ただし、初期の発症者が軽症と仮定して、軽症者の回復期間と等しくなった日に1を差し引くことにする。
免疫者数=前日の免疫者数+新規免疫者数
非感染者数=前日の非感染者数-新規感染者数
ただし、負となる場合は、ゼロとする
まずは、合計数1001、初期感染及び発症者=1、感染率=1、潜伏期間=7、重症率=0.2、軽症者の回復期間=14、重症者の回復期間=60、初期免疫率=0、の場合のグラフです。
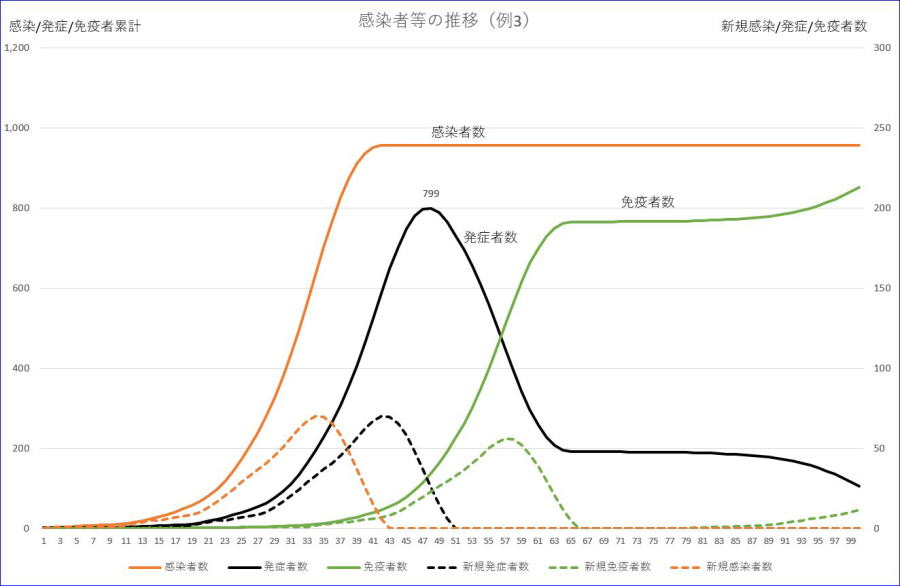
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者/免疫者数累計、右縦軸は、新規感染/発症/免疫者数の目盛です。
※オレンジが感染者累計、オレンジの破線が新規感染者数です。
※黒は、発症者数、黒の破線は、新規発症者数です。
※緑は、免疫者数、緑の破線は、新規免疫者数です。
前節の3節に比較して大きな違いは、免疫を考えているため、発症者数が最大でも1000に届かず799となり、その後低下してゼロとなる点でしょう。なお、新規免疫者がグラフでは、80日目以降に上昇していますが、これは、重症者の回復に伴うものです。
目次に戻る
次に合計数1001、初期感染及び発症者=1、感染率=0.5、潜伏期間=7、重症率=0.2、軽症者の回復期間=14、重症者の回復期間=60、初期免疫率=0、の場合のグラフです。
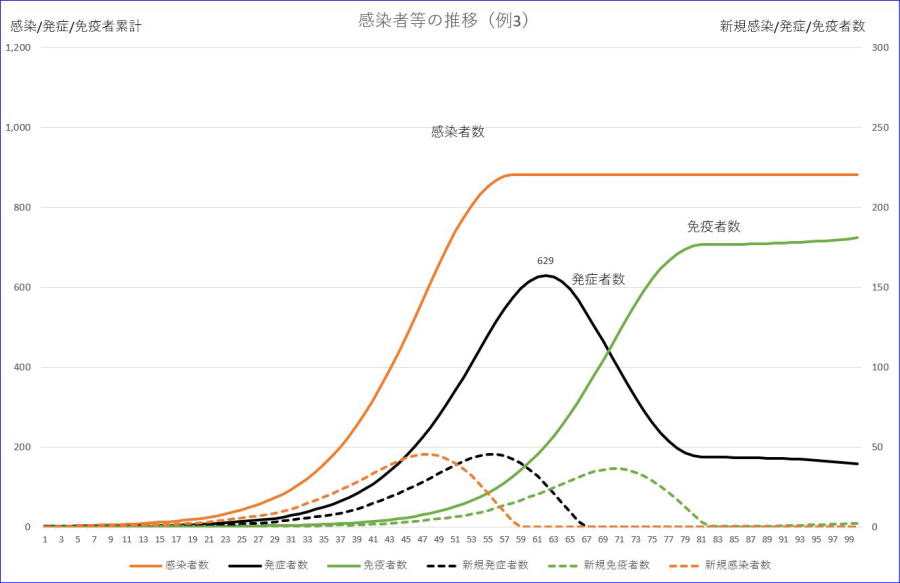
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者/免疫者数累計、右縦軸は、新規感染/発症/免疫者数の目盛です。
※オレンジが感染者累計、オレンジの破線が新規感染者数です。
※黒は、発症者数、黒の破線は、新規発症者数です。
※緑は、免疫者数、緑の破線は、新規免疫者数です。
感染率が1から0.5に変化した場合は、発症者数の最大を799から629と約22%低下させることができました。
目次に戻る
次は、初期免疫がある場合です。合計数1001、初期感染及び発症者=1、感染率=1、潜伏期間=7、重症率=0.2、軽症者の回復期間=14、重症者の回復期間=60、初期免疫率=0.2の場合のグラフです。
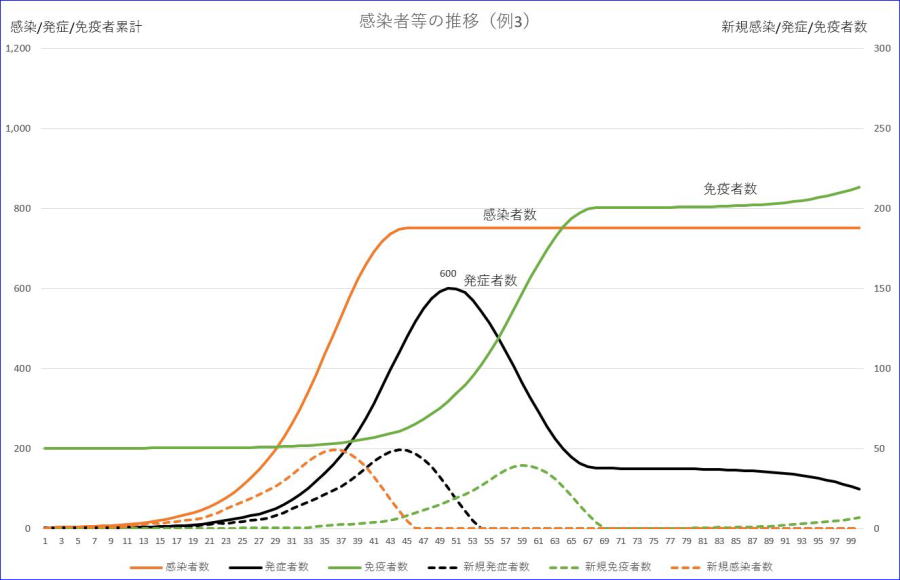
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者/免疫者数累計、右縦軸は、新規感染/発症/免疫者数の目盛です。
※オレンジが感染者累計、オレンジの破線が新規感染者数です。
※黒は、発症者数、黒の破線は、新規発症者数です。
※緑は、免疫者数、緑の破線は、新規免疫者数です。
初期免疫率が20%程度でも、発症者の最大値とピークの時間は、遅らせる効果は、認められます。
目次に戻る
次に初期免疫率が大きい場合です。合計数1001、初期感染及び発症者=1、感染率=1、潜伏期間=7、重症率=0.2、軽症者の回復期間=14、重症者の回復期間=60、初期免疫率=0.5の場合のグラフです。
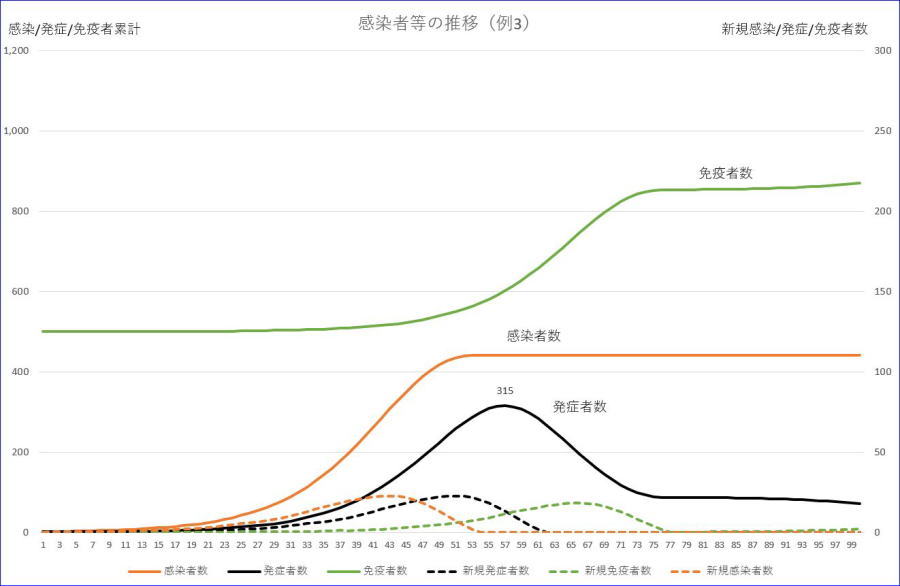
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者/免疫者数累計、右縦軸は、新規感染/発症/免疫者数の目盛です。
※オレンジが感染者累計、オレンジの破線が新規感染者数です。
※黒は、発症者数、黒の破線は、新規発症者数です。
※緑は、免疫者数、緑の破線は、新規免疫者数です。
初期免疫率が50%もあると、発症者の最大値も315と半減します。コロナにはワクチンがまだありませんが、通常のインフルエンザのようにワクチンがある場合は、接種することにより免疫が得られるとすれば、如何に予防接種が大切であるかが実感できる結果となります。
目次に戻る
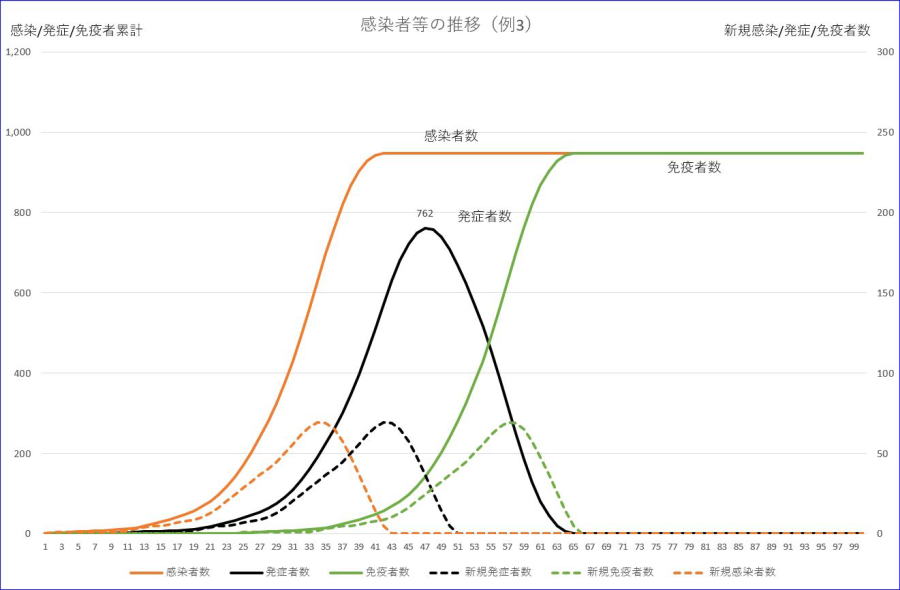
最後に重症率がゼロの場合を参考としてあげておきます。合計数1001、初期感染及び発症者=1、感染率=1、潜伏期間=7、重症率=0、軽症者の回復期間=14、(重症者の回復期間=60)、初期免疫率=0の場合のグラフです。
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者/免疫者数累計、右縦軸は、新規感染/発症/免疫者数の目盛です。
※オレンジが感染者累計、オレンジの破線が新規感染者数です。
※黒は、発症者数、黒の破線は、新規発症者数です。
※緑は、免疫者数、緑の破線は、新規免疫者数です。
この重症者が出ないケースでは、免疫を得た方と感染した方の数がやがて70日程度で一致するようになりました。普通の風邪と呼ばれるものでは、こんな感じなのかなと思われます。
目次に戻る
2、3、4節のモデルでは、新規に感染する数を、新規感染者数=前日の発症者数×感染率×(前日の非感染者数-前日の免疫者数)/(初期の非感染者数)、と計算しています。
なお、新規感染者に対する感染させる働きでは、軽症者と重症者の区別をしていません。重症者が医療機関等に入院して一般とは隔離されるため、この点は、実態にそぐわないと考えられますので、後述します。
さて、背景には、いくつかの仮定があります。一つは、新規感染数が発症者数に比例するという考え方です。感染者数ではなく、発症者数としているのは、感染しても発症していなければ、他人に感染を及ぼす力がないとの考えからです。
もっとも、コロナウイルスの場合、発症前に感染力がゼロなのかというのは、明確には、分かっていません。臨床的には、そういうケースがあると困るわけですが、モデルの計算の上では、潜伏期間が短くなると考えれば、対応可能でしょう。
次の仮定は、(前日の非感染者数-前日の免疫者数)/(初期の非感染者数)の分数です。これは、免疫を持たない人のみに発症者からのウイルスが当たる確率を表しています。発症者がいても感染できる人数がゼロになってしまえば、それ以上、新規感染者が出ない『飽和』を起こすので、そのために必要な係数となります。初日の分数の値は、1ですが、時間の経過とともに感染が広がり発症し、回復後に免疫を持つ人が増えてくると分数は、1より徐々に小さい値となっていき、ついには、ゼロとなる訳です。
最後に、感染率は、なにかということになりますが、1日あたり、一人の発症者がウイルスを渡せる人数といっても良いでしょう。感染率が1の場合は、単純に言えば、1日に濃厚接触する人が1人と言い換えることもできるでしょう。
ですので、発症者が厳密に隔離されたり、自主的に他人に会わずに家にいる場合では、感染率がゼロ又は極度に小さくなります。従いまして、政府の方針に示されているように発症者が可能な範囲で出歩くことがなければ、相当程度、感染率を低く抑える効果が期待できるというわけです。逆に、発症していることに気がつかずに多くの人と濃厚接触してしまうと感染率が相当高くなり、そのような方が多数いらっしゃると武漢市のような局地的な感染爆発が起きます。
目次に戻る
4.のモデルでは、発症して回復後は、すべて、免疫を獲得するとしています。実際は、免疫を100%得られない可能性は、あります。その場合、モデルに新しく、免疫獲得率のようなパラメーターを追加する必要があるでしょう。
実際、大阪の40代女性は、1/29に発症し、PCR検査で陽性となり、入院していました。その後、症状が治まり、PCR検査でも陰性となり退院しましたが、発症し、2/26にPCR検査で陽性と判定されました。体内に残っていたウイルスの再燃か、あるいは、新たにウイルスに感染したのか、いずれかだと考えられています。
このようなケースが多く出てくると免疫獲得率も取り入れる必要があります。
※新型コロナウイルスに感染後、治癒した方が免疫を得たとして、1年以上の長期間の免疫が得られるのか?、あるいは、新型コロナウイルスの変異スピードや型(最近の報道では、少なくとも、武漢型、アジア型、ヨーロッパ型とでも称すべき遺伝子の型が異なるウイルスがあることが分かったようです)により、来年以降の感染拡大を抑えられるかどうかが不安視される点です。(2020/4/17追記)
目次に戻る
これは、未知です。実際、どの程度の人が感染していて、感染しない人がどの程度いるのか推定できないうちは、ゼロと考えて対処するしかありません。
※新型コロナ感染症では、子どもの重症度合いが低いという特徴があります。これについて、読売新聞の2020年5月19日付の記事に興味深いものがありました。『米国ラホイヤ免疫研究所の研究チームが近く米科学誌セルで発表する』もので、この中で、『流行が始まる前の2015~2018年に米国で収集された20~60才の保存血液20人分を調べたところ、約半数から新型ウイルスを認識する免疫細胞「ヘルパーT細胞」を検出した。』という。研究チームは、『風邪の原因となる通常のコロナウイルスに感染した経験によって、免疫系が新型ウイルスも認識できるようになる「交差免疫」が起きたと考えている。』としています。これについて、順天堂大学の奥村特任教授(免疫学)は、『コロナウイルスに感染することが多い子供が、新型に対して重症化しにくいことも、交差免疫で説明できるのではないか』とコメントしていると言うことです。(2020/5/21追記)
目次に戻る
発症者がゼロとなるまでの日数となる収束には、相当の時間がかかることが分かります。たとえば、4.(2)に挙げた例、合計数1001、初期感染及び発症者=1、感染率=0.5、潜伏期間=7、重症率=0.2、軽症者の回復期間=14、重症者の回復期間=60、初期免疫率=0、の場合は、発症者がゼロとなったのは、127日目でした。
しかし、振り返りますと、重症者は、少なくとも入院するなどして隔離されると思われますので、その場合は、感染力が大きく下がります。このように重症者を隔離する仕組みをモデルに取り入れないと、現実に当てはめにくいと思われます。
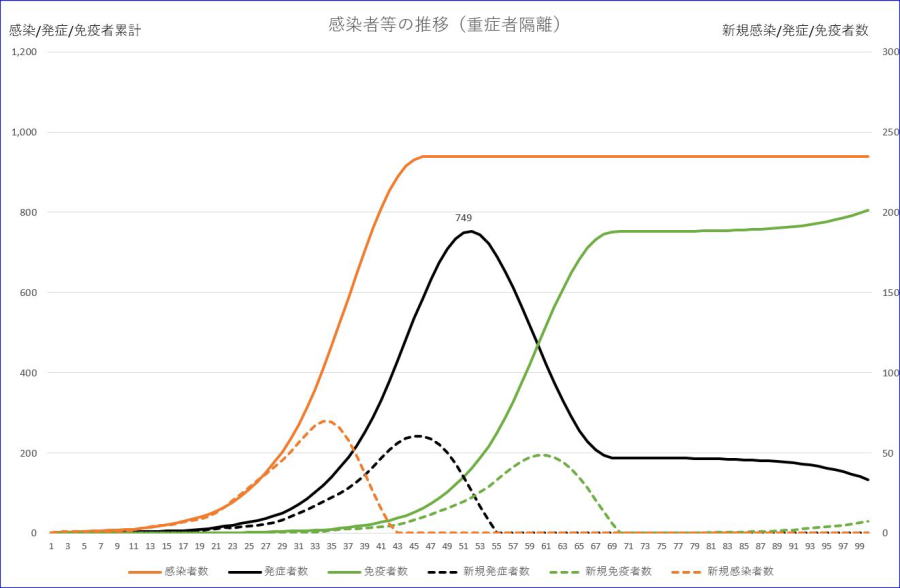
そこで、重症者が入院するなど隔離されて、重症者が新規感染者を生み出さない理想的な場合を計算してみます。4.(1)と同じ、合計数=1001,初期感染/発症者=1、感染率=1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=0.2の場合です。
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者/発症者/免疫者数累計、右縦軸は、新規感染/発症/免疫者数の目盛です。
※オレンジが感染者累計、オレンジの破線が新規感染者数です。
※黒は、発症者数、黒の破線は、新規発症者数です。
※緑は、免疫者数、緑の破線は、新規免疫者数です。
これに対して、重症者も軽症者と同様の感染率で新規感染者を作るという4.(1)の場合は、再掲すると下図の通りです。

一見しても、違いが分かりにくいので、発症者数のみに着目して、同じグラフに表示してみましょう。
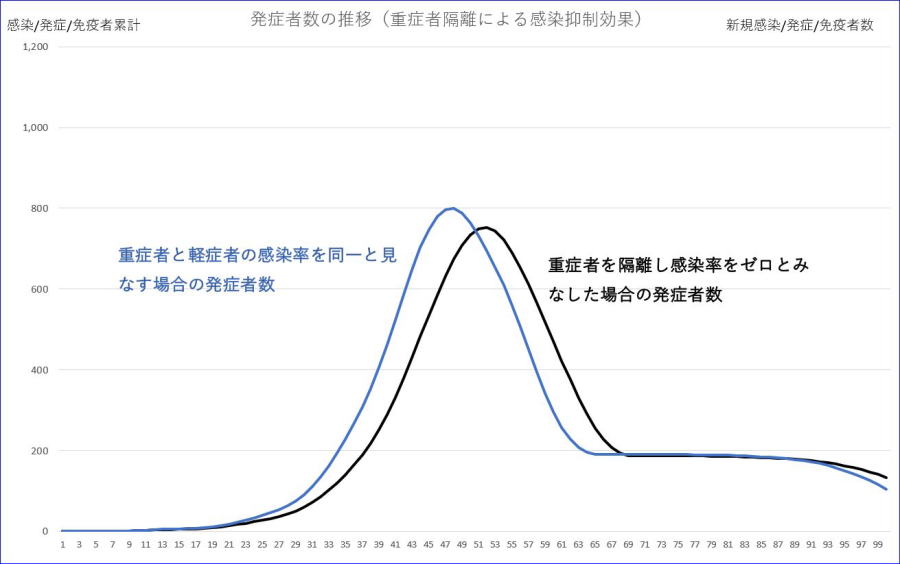
※青い曲線が4.(1)の発症者数、黒い曲線が重症者を隔離して感染率をゼロと見なせる場合
黒い方がピークが下がり、時期も後ろに移動します。ただ、期待したほどの効果は、出てきません。重症者の隔離だけでは、効果が限定的であることが分かります。
重症率が大きいと、違いは、当然ながら顕著になります。重症率が0.5の場合の両者の違いです。

※青い曲線が重症者と軽症者との感染率に違いがない場合、黒い曲線は、重症者が隔離されて感染率がゼロと見なせる場合
このように重症率が高くなると隔離される割合が高まるため、隔離の効果は、大きくなります。
目次に戻る
これまでのモデルでは、亡くなる方を織り込んでいません。コロナウイルスによる感染症の死亡率は、2%程度とかなり低いと考えられていますので、先に挙げた重症者の隔離をモデルに取り込む方が重要性が高いと考えられます。なお、死亡数を取り入れる原理的な困難さは、ありませんが、どの程度の重症期間後に亡くなるかという新しいパラメーターが入ることになります。
目次に戻る
発症者が濃厚接触する活動範囲を日本全国とするのは、さすがに、オーバーだと思われます。たしかに、ごく一部の発症者が新幹線、航空機、長距離バスなどを利用して、長い距離を移動した例もあったことは、事実です。しかし、一般には、そこまでは、広くならず、通勤や通学の範囲に収まるでしょう。さらに発熱などの症状があれば、あまり遠くまでは、移動しないと考えられます。
そのため、初期人口を1億などとするのは、無謀です。多くて、一つの町程度の1万~10万人程度と考えられます。仮に10万として、そのメッシュ(1000個で1億)の一つ一つに1名の発症者がいると仮定するのは、初期状態を過大に評価しすぎていると考えられます。
そこで、初期には、全国の1000個のメッシュのうち数個に1名ずつの発症者がいたとして、メッシュ内で増加し、次第に近隣のメッシュに発症者が移動して、感染が拡大するというモデルが必要でしょう。数学的に言えば、これまでは、人数と時間との関係を差分方程式で近似してきましたが、2次元の広がりを表す空間軸を変数に取り組むモデルに拡張していくのが妥当と考えられます。言い換えれば、常微分方程式から偏微分方程式への拡張のようなものです。
目次に戻る
流行の中途において、軽症者が一定期間、隔離に準ずる形で過ごす(以下『準隔離』という)効果について調べてみました。モデルは、5.(4)で取り上げた重症者の隔離を組み込んだモデルについて、一定期間内の感染率を変化させたものを計算してみました。
準隔離期間の日数に錯誤がありましたので、グラフ及び本文の一部を差し替えました。ここに記して、お詫び申し上げます。なお、この6節以降の計算において使用したExcelブックは、5節までのものと異なります。そのため多少の数値の違いが出ています。(2020/3/22追記)
合計数=1001,初期感染/発症者=1、感染率=1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=0.2の場合で、重症者の隔離は、行われています。
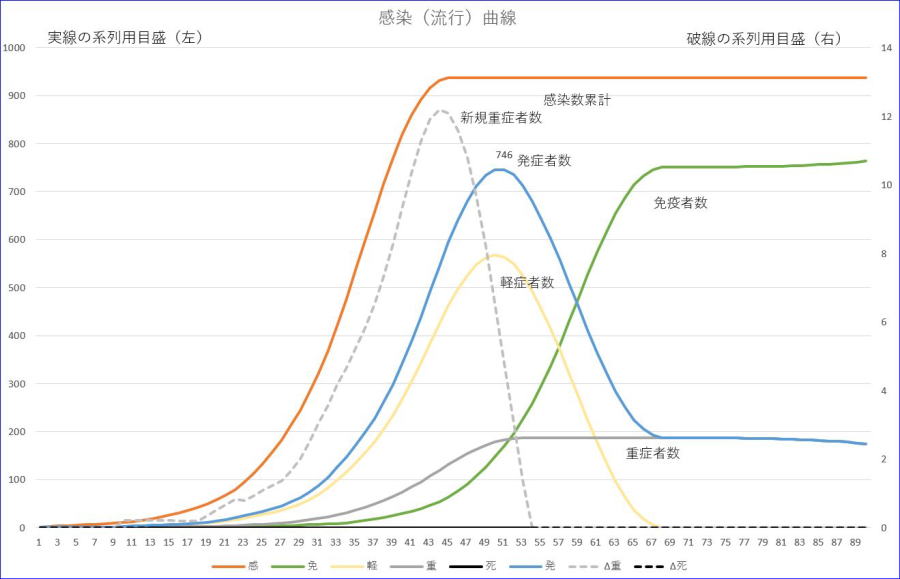
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者数累計/発症者数/軽症者数/重症者数/免疫者数、右縦軸は、新規重症者数の目盛です。
※オレンジが感染者数累計、青は、発症者数、黄色は、軽症者数、緑は、免疫者数、
※グレーは、重症者数、グレーの破線は、新規重症者数です。
発症者の最大値は、51日目頃に746、重症者の最大値は、53日目に187となりました。
目次に戻る
(1)と同じ条件です。ただし、日数が19~25までの期間の感染率は、0.1として、それ以外では、1のままとします。
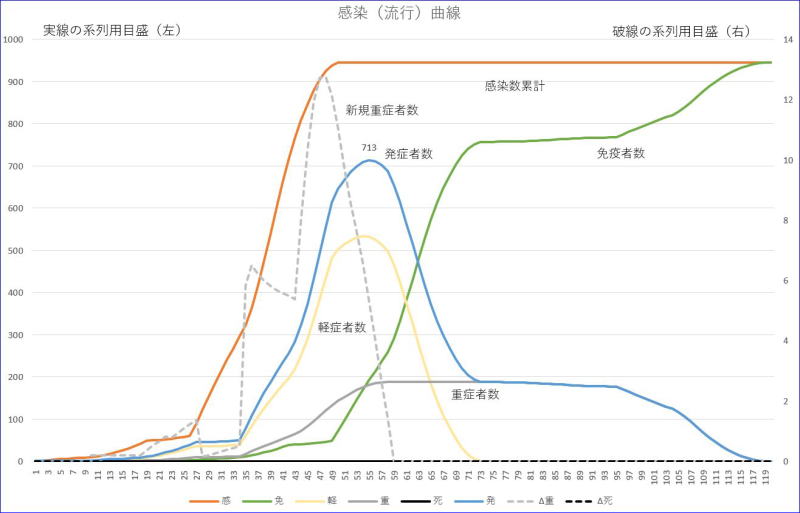
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者数累計/発症者数/軽症者数/重症者数/免疫者数、右縦軸は、新規重症者数の目盛です。
※オレンジが感染者数累計、青は、発症者数、黄色は、軽症者数、緑は、免疫者数、
※グレーは、重症者数、グレーの破線は、新規重症者数です。
この際の発症者の最大値は、約55日目に713となりました。準隔離を行わない場合より4%ほど発症者数を低くできました。また、新規発症者数が27日頃から35日頃まで低く抑えられているのが分かります。しかし、その後、急に増加し、また、減少するなど複雑な動きを示します。
目次に戻る
(1)と同じ条件です。ただし、日数が19~32までの期間の感染率は、0.1として、それ以外では、1のままとします。
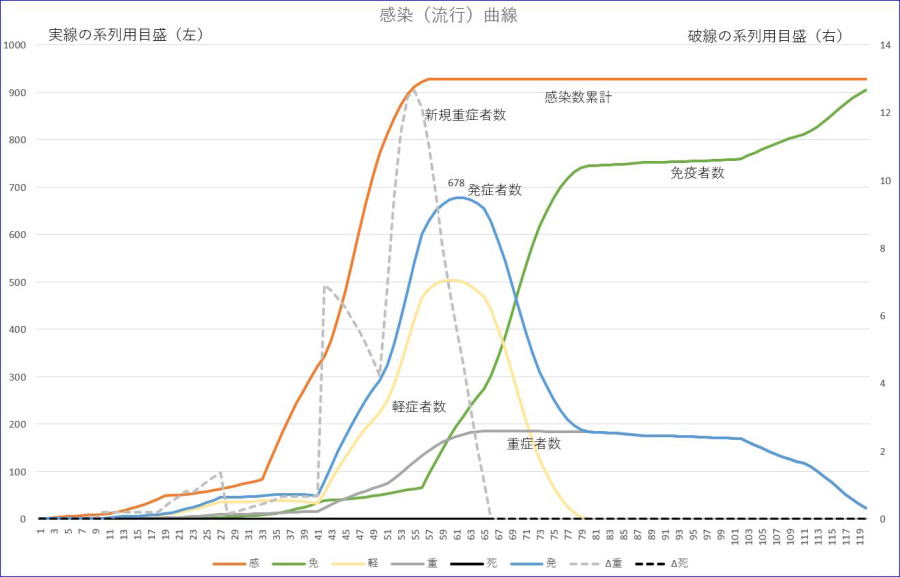
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者数累計/発症者数/軽症者数/重症者数/免疫者数、右縦軸は、新規重症者数の目盛です。
※オレンジが感染者数累計、青は、発症者数、黄色は、軽症者数、緑は、免疫者数、
※グレーは、重症者数、グレーの破線は、新規重症者数です。
この場合は、発症者の最大値は、約62日目頃に678となりました。(1)と比較して、約10%弱の減少となりました。最大時期も、約12日ほど遅くなります。
目次に戻る
(1)と同じ条件です。ただし、日数が29~35までの期間の感染率は、0.1として、それ以外では、1のままとします。
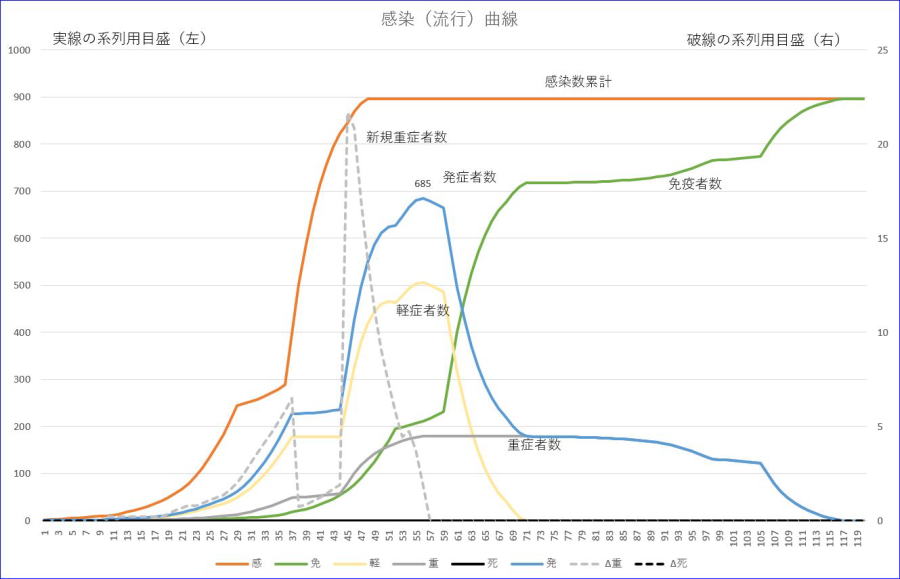
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者数累計/発症者数/軽症者数/重症者数/免疫者数、右縦軸は、新規重症者数の目盛です。
※オレンジが感染者数累計、青は、発症者数、黄色は、軽症者数、緑は、免疫者数、
※グレーは、重症者数、グレーの破線は、新規重症者数です。
発症者の最大値は、56日目頃に685でした。最大重症者数は、準隔離を行わないときより、少し減少しています。
目次に戻る
(1)と同じ条件です。ただし、日数が29~42までの期間の感染率は、0.1として、それ以外では、1のままとします。
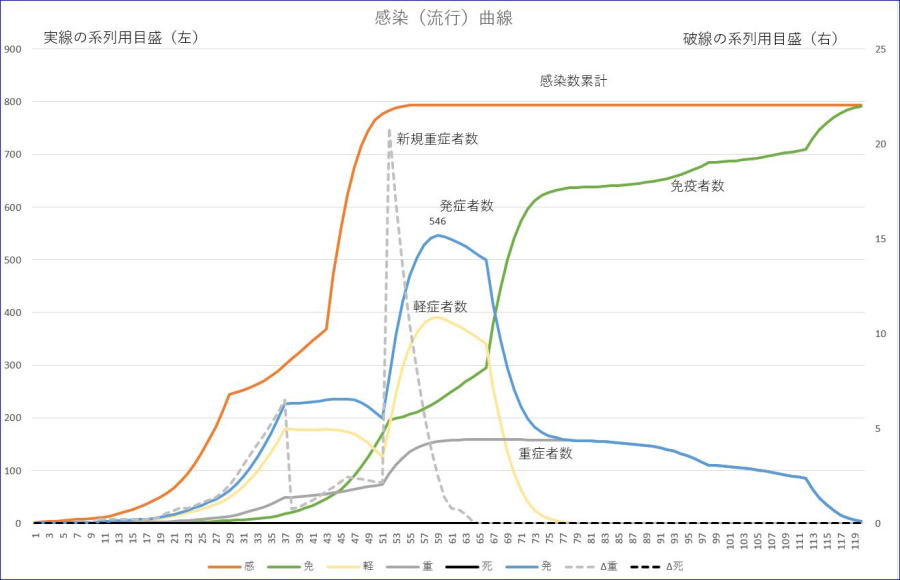
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者数累計/発症者数/軽症者数/重症者数/免疫者数、右縦軸は、新規重症者数の目盛です。
※オレンジが感染者数累計、青は、発症者数、黄色は、軽症者数、緑は、免疫者数、
※グレーは、重症者数、グレーの破線は、新規重症者数です。
発症者の最大値は、約63日目頃に546とこれまででもっとも低くなりました。(1)の746と比較して、実に27%の低下となりました。また、最大重症者数も15%減少しています。
目次に戻る
(1)と同じ条件です。ただし、日数が39~45までの期間の感染率は、0.1として、それ以外では、1のままとします。
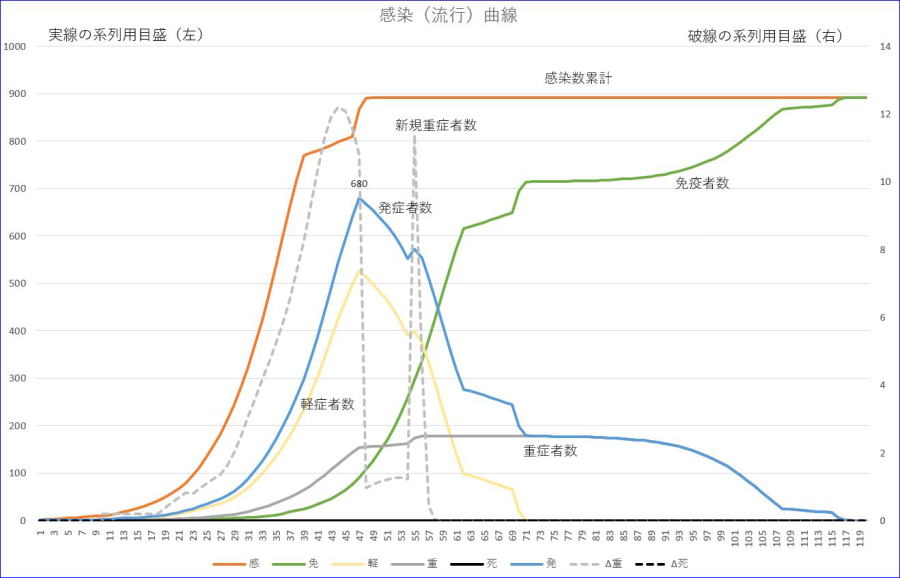
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者数累計/発症者数/軽症者数/重症者数/免疫者数、右縦軸は、新規重症者数の目盛です。
※オレンジが感染者数累計、青は、発症者数、黄色は、軽症者数、緑は、免疫者数、
※グレーは、重症者数、グレーの破線は、新規重症者数です。
発症者の最大値は、約67日目頃に680となります。(3)と同程度でしたが、最大重症者数は、少し小さくなりました。
目次に戻る
(1)と同じ条件です。ただし、日数が39~52までの期間の感染率は、0.1として、それ以外では、1のままとします。
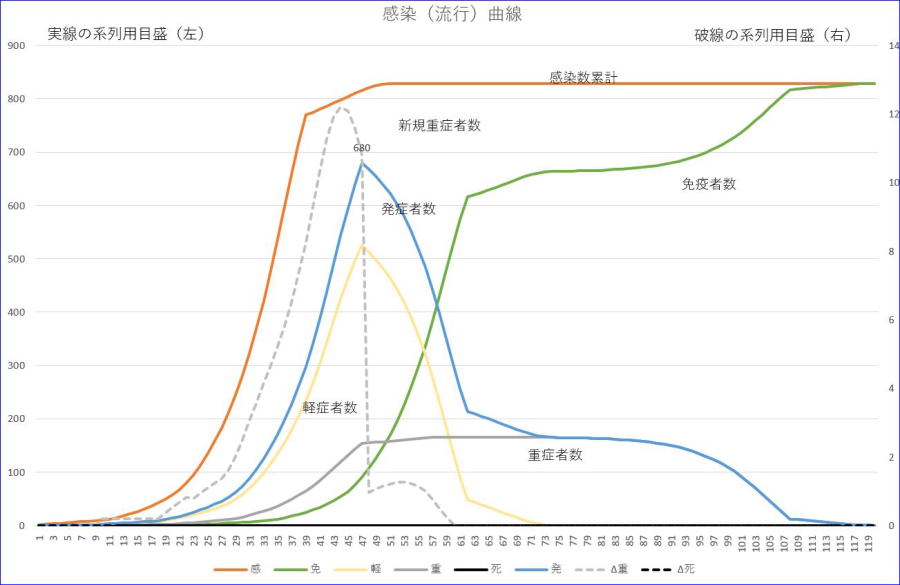
※グラフの横軸の数値は、初日を1とした数字です。
※左縦軸は感染者数累計/発症者数/軽症者数/重症者数/免疫者数、右縦軸は、新規重症者数の目盛です。
※オレンジが感染者数累計、青は、発症者数、黄色は、軽症者数、緑は、免疫者数、
※グレーは、重症者数、グレーの破線は、新規重症者数です。
発症者の最大値は、約47日目頃に680と(6)と同じ値になりました。準隔離の期間を14日と(6)の倍にした割りには、効果が薄いと言えます。最大重症者数は、少し小さくなりました。
目次に戻る
表にまとめますと、下のようになります。
隔離期間が7では、準隔離開始を39日目とした場合が680ともっとも、低くなりました。
一方、隔離期間が14では、準隔離時期を29とした場合の546が今回の中では、最も低くなり、(1)の746から約27%の低下となり顕著な改善が見られました。
軽症者の準隔離を7日間行うだけでも、行わない場合より、発症者の最大値を低く抑えられました。ただし、今回の試算では、準隔離期間の感染率を0.1とかなり低く仮定していますので、これが1に近いようでは、効果がないことは、明白です。
なお、実施時期については、19日目から実施した場合と39日目から実施した場合を比較すると、大きな差は、見られず準隔離を早くやれば、遅くやるよりも効果があるとは、一概に言えない結果となりました。
※準隔離の効果については、9節(9)以降でも、シミュレートしていますので、ご参照ください。
目次に戻る
2~6節までの結果を踏まえて、感染拡大の防止策を検討してみましょう。
具体的には、発症者との濃厚接触を避けることですが、展開すると、
・ 人になるべく会わない、
・ 電話やネットで用件を済ませる
・ テレワークや在宅勤務を行う
・ 人に会って話をする際は、距離を置く、
・ マスクをして、相手に飛沫を浴びせたり、相手からの飛沫を浴びないようにする
・ 不急の回覧板等は、できるだけ、回さないようにする
発症者の隔離が有効、展開すると、
・ 重症者は、入院していると思われるが検査を行い、早期に厳重な感染予防策をとる
・ 軽症者も、自宅等でなるべく、他人に接触しないようにする、
自身が発症者になったことを検知する、を展開すると、
・ 体温を毎日測る、
・ 息苦しさ(呼吸困難)、強いだるさ(倦怠感)、高熱等の強い症状のいずれかがある場合
☆ 重症化しやすい方(※)で、発熱や咳などの比較的軽い風邪の症状がある場合
※高齢者をはじめ、基礎疾患(糖尿病、心不全、呼吸器疾患(慢性閉塞性肺疾患など)など)がある方や透析を受けている方、免疫抑制剤や抗がん剤などを用いている方
☆ 上記以外の方で発熱や咳など比較的軽い風邪の症状が続く場合
(症状が4日以上続く場合は必ずご相談ください。症状には個人差がありますので、強い症状と思う場合にはすぐに相談してください。解熱剤などを飲み続けなければならない方も同様です。)
ご相談は、最寄りの保健所などに設置される「帰国者・接触者相談センター」(地域により名称が異なることがあります。)や、地域によっては、医師会や診療所等で相談を受け付けている場合もありますので、ご活用ください。赤字個所は、厚労省Q&Aから引用。
・ 体調の変化に敏感になる、
・ 味覚や臭覚が効かなくなることがあるので異常を感じた場合は、相談する、(2020/3/30追記)
手指を洗う、消毒を行う、展開すると、
・ 通勤や通学時にマスクをしたり、メガネをかけたりすることは、手で不用意に顔を触らないためにも有効
・ 通勤先や通学先、帰宅時にまっさきに手指を洗う、このためには、それぞれの玄関に消毒薬を常備してまず行う
・ 学校、会社、自宅等のドアノブ、インターフォン、エレベーター等、手で触る場所の消毒
・ ゴム製の手袋は、有効ですが、外すときによほど注意しないと手にウイルスが移ってしまいます。使い捨てが望ましいでしょう。
イベント、集会等の延期や中止、展開すると、
・ 卒業式、入学式の中止や規模の縮小、
・ 遊園地、映画館、劇場、スポーツ施設、博物館、水族館、動物園、図書館、公共のホールや展示会場等の休業や入場者数の制限
・ 国内外の旅行や視察の中止、
・ 全世界への不要不急の旅行の延期(2020/3/25外務省より発表)
※ 詳細は、外務省海外安全HP(https://www.anzen.mofa.go.jp/)
他国からの入国を制限、展開すると、すでに行われていますが、
・ 感染者が多くなっている国や地域からの入国制限、
・ 検疫の強化、
靴などに付着している可能性があるウイルスを室内に持ち込まない、展開すると、
・ 家庭やオフィス、学校等では、建物の入り口に室外用玄関マットを配置し、靴底の汚れを拭う、
・ オフィスの入り口が建物内にある場合は、その入り口にも室内用玄関マットを置き靴底を拭う、
・ 玄関マットは、家庭では、こまめに、中性洗剤等で洗浄し、オフィス等では、業者に洗浄・交換してもらう
・ 家庭では、玄関で靴を脱ぎ、脱いだ靴を72時間程度、タタキに放置して、靴箱などにしまわない、
・ 玄関のタタキは、定期的に中性洗剤等で洗うか、拭き取る、
・ オフィスに着いたとき、職員や学生は、可能ならば、室内履きに履き替えるのが望ましい、
※私見ですが、日本人の生活では、事務所やホテルなどを除いて、一戸建、マンションかを問わず、ほぼ、100%に玄関があり、そこで靴を脱ぐという習慣があります。日本の感染者数、死者数が少ない原因として、検査数が少ないという根本的な原因は、ありますが、それ以外に『玄関で靴を脱ぐ』という(日本人には当たり前の)生活が、感染防止のためのゾーン制御を考えたとき、室内をグリーンゾーンに保つ上で、良い効果を上げていると考えられます。(2020/5/21追記)
目次に戻る
品不足が続いています。医療機関も含めて、これらがないと困ります。備蓄が十分でなかったことは、明白です。
消毒用アルコール(エタノール)の不足が続いています。ついに厚労省は、臨時の措置として、アルコール濃度の高い一部の酒について、消毒用として、病院で使用することを認めることにしました。(2020/4/17追記)
目次に戻る
感染者が軽症であっても、感染を広げてしまうために、コロナウイルスの陽性の有無を調べる検査が一般の医療機関でインフルエンザ並みに可能になることが必要です。できるだけ、早く、完成して欲しいものです。
抗原検査キットが開発され、PCR検査より、精度は低いものの、検査用サンプルの取得も簡便で、所要時間も短時間でコロナ感染の有無が判定できるようになりました。
『抗原検査とは、新型コロナウイルスの構成成分であるタンパク質を、ウイルスに特異的な抗体を用いて検出する検査方法です。ウイルスの遺伝子を特異的に増幅するPCR検査(核酸検出検査)と同様に、陽性の場合はウイルスが検体中に存在することを示します。特別な検査機器を使わず、自宅で簡単に検査ができます。』(神奈川県のHPより)
抗原定性検査キットが一般の薬局でも、購入可能となりました。厚生労働省・消費者庁は、日本で承認された製品には、新型コロナウイルス『体外診断用医薬品』と表示されていることを確認して購入するように注意を呼びかけています。市販価格は、1回分で2000円~となっているようです。(2022/1/18追記)
目次に戻る
感染率を低くするためにも必要です。重症者が多くなりすぎると、入院先が見つからない事態が発生します。病院の新規設置も考えておかないと間に合わないおそれも出てきているのではないでしょうか。
残念ながら、日本では、武漢市に新設された2棟の病院のようにとても短期間で建設もできないでしょう。まずは、建設場所を見つけることも難しく、さらには、そこで働く医療従事者を確保するのが難しそうです。
目次に戻る
新規発症者が百人単位で増える前にテレビやネット上で、コロナ感染集中地域を表示し、集中地域を公開し、なるべく、その地区との濃厚接触を避ける、展開すると、
・ 集中地域と隣接地区では、イベント、集会、飲食等をなるべく行わない、
・ 学校等は、他地区より長く休校する、
・ 交通機関は、状況次第で減便や休止する、
・ 東京都などの大都市を中心に平日の自宅での仕事や週末・夜間の不要不急の外出自粛を強く呼びかけ、(2020/3/26)
目次に戻る
情報が少ないと市民が不安に駆られて、マスクや消毒薬等の買い占めを起こしやいでしょう。また、不心得者が転売、抱き合わせ販売などを行うことがあるようで、取り締まることも大切です。
また、感染拡大モデルがあれば、シミュレーション結果を公開して、今の時点は、どの程度の広がりなのかを市民に広く周知してもらう。天気予報などに準じて、考えれば、良いでしょう。先の見えない不安で、市民や施設等の防止対策が十分に行われず、効果が上がらない可能性が高いです。
放送局や新聞社も注意していただきたい点があります。『あらたに○○人の・・』という常套句を止めていただきたい。当該の報道機関としては、既報の続報だよ、という気分は、分かるのですが、前回の報道を見ていなかったり、覚えていない者からすると、何が『あらたに』なのか分かりにくいです。そして、たいていは、『計○○人となりました』で終わるのですね。途中の経過が分かりません。せめて、表かグラフがあればと良いと思います。
厚労省のサイトも一件一件の内容は、細かく掲載されています。また、地域別や国別合計表はあります。最近、データの一覧表も掲載されるようになりました。コピーすれば、手元のExcel表に落とし込めます。とは言え、折角のExcel表で作られていても、1件に2行使っていたりするので、手作業の修正が必要なのは、困ります。以前は、『2/1に発症した東京都の50代の男性のケース』などと長い枕詞を付けないと対象者を特定できなかった頃と比較すると番号が統一されている点は、一歩前進です。※
しかし、個別の状況と合計数は分かるのですが、時系列で増加数が分かる表は、ありません。結局は、一覧表から独自に集計してみないと分からないのです。そして、なにより、報道機関も含めて、グラフがありません。どの程度の速さで発症者が見つかっているのかを時系列で折れ線グラフ等で表示して、ビジュアルに訴えることが大切では、ないかと思います。
厚労省のページに記載されていた表は、3/10頃より掲載されなくなりました。推測ですが、おそらく個別の発症者毎に整理して掲載できる状態ではなくなってきたためではないかと思われます。
代わって、NHKの特設サイト『新型コロナウイルス』に日別の新規感染者またはその累計を棒グラフで表示できる画面が追加されています。その感染者数が感染者=陽性者なのか、厚労省のページにあったような発症者ベースなのかは、あいまいですが、おそらくは、感染者ベースかと思われます。
○ラジオボタンで累計か新規数かの切り替えができます。
https://www3.nhk.or.jp/news/special/coronavirus/ 青字個所を2020/3/13に追記、NHKの画面のスナップショット画像を削除。(2020/3/30)
目次に戻る
冒頭にも書きましたが、コロナウイルスに対する治療薬の開発や治験を進めることは、大切です。ワクチンも大切ですが、当面は、期待できません。
※ 治療薬については、以下の4つが承認されています。(2021/9/5現在)
「レムデシブル」(2020年5月に特例承認。点滴で投与。当初、対象となる患者は、人工呼吸器や人工心肺装置(ECMO)をつける重症患者などに限定されていましたが、2021年1月からは肺炎になった中等症の患者にも投与が認められました)
「デキサメタゾン」(2020年7月に推奨。重度の肺炎やリウマチなどの治療に使われてきた炎症やアレルギーを抑える作用のあるステロイド剤)
「バリシチニブ」(2021年4月、関節リウマチなどの薬で炎症を抑える効果がある薬として承認されました。この薬は錠剤で、酸素投与が必要な中等症以上の入院患者に対してレムデシビルと併用して服用することが条件となっています)
「抗体カクテル療法」(2021年7月に承認。「カシリビマブ」と「イムデビマブ」という2種類の抗体を混ぜ合わせて点滴で投与することで新型コロナウイルスの働きを抑える効果があります。軽症患者に使用できる治療薬としては初めてのものです。発症から7日間以内に投与すると軽傷者の重症化を防ぐ効果が高いとされます。) 2021/9/8追記
※ 日本におけるワクチン接種は、ファイザー社、モデルナ社、アストラゼネカ社の3つが認可されています。このうち、アストラゼネカ社のものは、まれに血栓ができるとの海外のデータがあったため、当初は、使用を見合わせました。その後、2021年夏にワクチンの枯渇が生じるようになり、40代以上の方向けに地域によっては、使用されるようになっています。
時系列的には、2021年2月17日から、医療従事者への先行接種が始まり、同年3月1日から医療従事者への優先接種開始、同年4月12日から高齢者向け接種が開始されました。同年6月21日からは、職場や大学などでの職域接種も開始されました。
2021年9月7日現在、1回目接種が終了した方が全人口の60%、2回目までが終了した方が48.3%となっています。特に、65才以上の高齢者に限っては、1回目までが、高齢者人口の89.3%、2回目までが、87.4%と(なりました。一方、50代以下の世代に対する接種率は、まだ、50%に届かない状態です。(NHKのまとめサイトより) 2021/9/8追記
2022年1月7日現在、1回目終了が全人口の79.9%、2回目まで終了が78.6%、3回目を終了が1.1%となっています。全人口には、接種対象でない子どもの人数も含みます。(NHKのまとめサイトより) 2022/1/18追記
目次に戻る
今回もご覧いただきありがとうございました。次回も、本欄で元気にお会いできますことを願っています。
余談ですが、2019年のOECDの国際学力調査で日本の15才の中学生の読解力の評価が芳しくなかったですね。NHKの2019年12月5日の解説記事では、『今回の読解力の問題のうち、自由記述式の問題で、「自分の考えを他の人に伝わるような記述ができない」、「問題文から語句を引用するだけで、説明が不十分」といった理由で正答にならない例が多く見られた』とのことです。 厚労省のサイトなどを見ると、日本人の大人も笑えない状況であると痛感します。
今回の記事を書くのに際して、薄型テレビを例にとって、『成長曲線』の説明をしようと一時、準備をしていたのですが、年度別の日本の世帯数をぱっと一覧できる表にたどり着けませんでした。結局、年度別の一つ一つの表をみて数字を抜き出すしかありませんでした。また、この表も総務省の統計資料一覧から見つけるのは、なかなか困難で、Googleで検索した方が早かったという結果でした。
もっとも、肝心の薄型テレビの出荷台数を成長曲線の類似で説明するのは、難しいことがわかり、時間がかかりそうで、結局、省きました。しかし、日本では、統計が重視されていないことを、あらためて(おっといけない。あらたにと言ってしまいそうでしたな)実感しました。
Windows 7(SP1)は、2020年1月14日にマイクロソフト社のサポートが終了しました、また、Office 2010も、2020年10月13日にサポートが終了します。インターネットに接続してお使いの皆さまは、早めの更新をご検討ください。
※旧ドメインは、2017/6/1で閉鎖いたしました。お気に入り、スタートページ等の変更をお願い申し上げます。
目次に戻る
7節までで宿題になっていた死亡率も勘案して、感染(流行)曲線を描く方法を追記しましょう。併せて、これまで、やや、あいまいであった感染者等の分類名とその定義を整理しておきましょう。
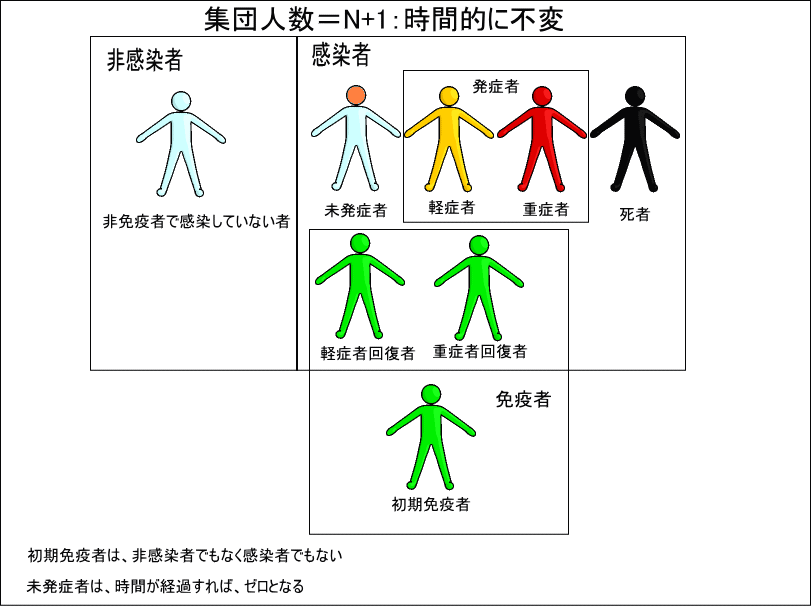
上の図は、基本的な人の分類/集まり(集合)です。死者以外は、これまでも使用してきました。図にも書きましたが、これらの集まりの要素の合計が時間とともに変わらないことを仮定しています。言い換えれば、集団外からの人の流入や集団外への人の流出がありません。
次にもう少し用語の説明をします。
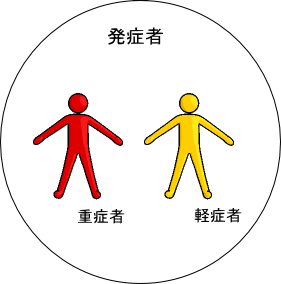
発症者は、上の図のように『軽症者』と『重症者』の集まりです。これまでと同様、本稿では、免疫を持たない者=『非免疫者』であって、感染していない者が感染した場合、一定日数=潜伏日数+1後(潜伏日数がゼロの場合は、翌日)に必ず発症し、発症した時点で軽症者か重症者のいずれかに分類されると仮定します。それまでの間、それらの人達を上の図では、『未発症者』と呼んでいます。
未発症者は、長時間の経過後に必ずゼロとなります。同様に長時間経過後に、軽症者と重症者も軽症者回復者と重症者回復者及び死亡率がゼロでない場合は、重症者回復者となるべき人の一部は、死者に分かれることになります。
従いまして、最終的には、死者+免疫者(初期免疫者+軽症者回復者+重症者回復者)+非感染者は、集団の合計=N+1に丸め誤差の範囲で一致するはずです。
実際は、発症時点で軽症であっても後に重症化したり、重症者も回復に伴い軽症とみなせるようになるわけですが、複雑になるため、発症した時点で指定された重症率に見合うように軽症者と重症者に分類しています。
次は、『感染者』です。
最初の図に示す『感染者』は、一度、感染した者の集まりです。初期免疫者を除いている理由は、t=1以降で感染していないためです。なお、これまで、明確にしていませんでしたが、本稿の中では、『感染者』は、t=1以降に感染した者を示します。このため、その者が回復したり、あるいは、死亡しても、感染者数が減少することは、ありません。そのため、免疫を考えない場合は、十分に時間が経過すれば、感染者数は、常に初期(t=1)の人数=N+1、に等しくなります。
しかし、免疫を考えると、時間が十分に経過した後の最終的な感染者数の初期人数(N+1)に対する割合=『最終感染率』は、『感染率』を低くすればするほど1よりも低下させられます。感染率→0の極限では、最終感染率もゼロに近づくと期待されます。また、感染率がいかに大きくても最終感染率が1以下になるのは、当然です。
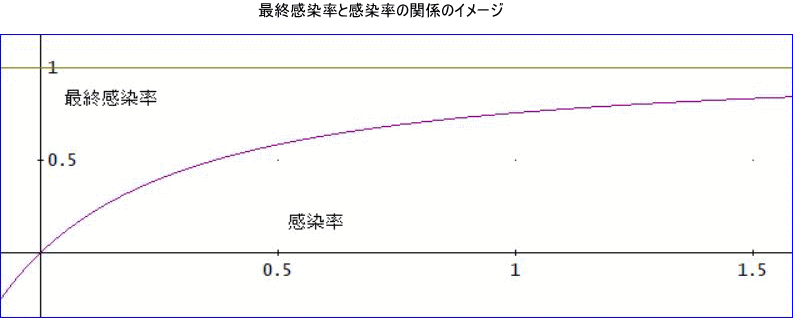
上の図は、そのイメージを表したものです。実際の曲線は、感染率だけでなく、潜伏日数や回復日数により変化します。
ちなみに、6節から利用したExcel表で重症率をゼロ(発症者がすべて軽症者である)と仮定し、軽症者感染率を変化させて、最終感染率を計算したのが下の図です。(数値に誤りがありましたので、再計算して訂正しました。2020/3/25追記)
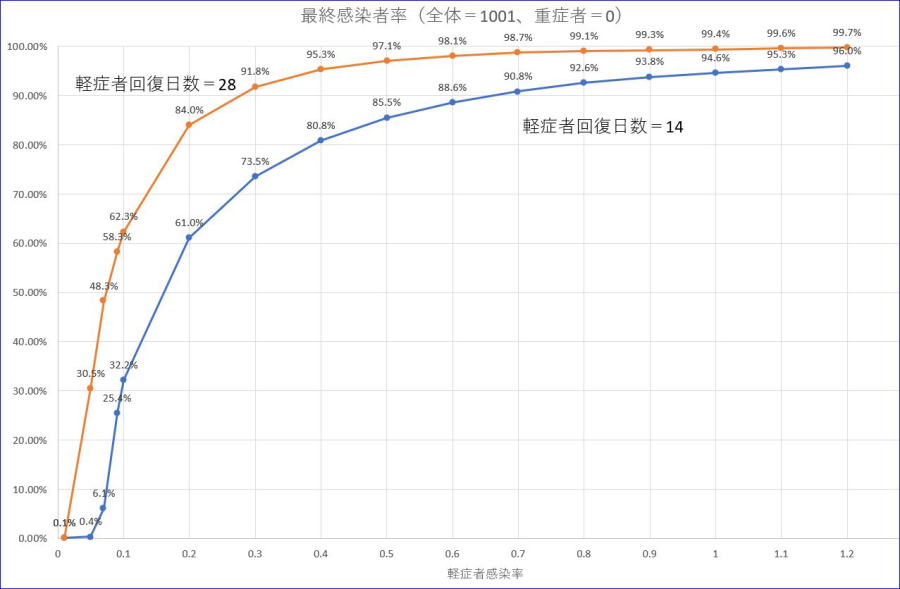
グラフで縦軸は、最終感染率です。青い線は、潜伏日数=7、回復日数=14、の場合、オレンジは、潜伏日数=7、回復日数=28の場合です。
回復日数が長くなると、すなわち、発症から治癒までの期間が長い場合は、最終感染率が増加するのが見て取れます。これは、集団全体への感染が拡大することであり、逆に、治療方法が開発されて、回復日数が短くなれば、全体への感染が低く抑えられることも意味します。
グラフからも分かるように最終感染率は、感染率がゼロに近い付近では、急激に変化しています。ごくわずかな『感染率』の変化が『最終感染率』に大きく影響することが分かります。すなわち、少数の者の油断でも集団全体の最終感染率に大きく影響するのです。
一方、感染率がある程度大きくなると、最終感染率は、それほど敏感に影響されなくなります。たとえば、7節までで多く取り上げた潜伏日数=7,かつ、回復日数が14で、『感染率』が1のケースでは、最終感染率が95%近くになります。この95%は、潜伏期間=7,回復日数=28の場合のほぼ100%と比較して、もはや、大きな違いでは、なくなります。言い換えれば、回復日数が比較的短い感染症でも、『感染率』を相当程度低く抑えないと、回復日数が短いというご利益を受けづらくなることが分かります。
次に『免疫者』です。
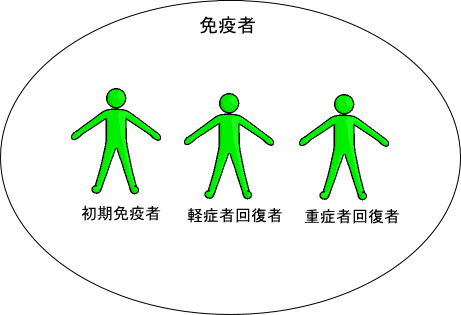
免疫者は、免疫を持っている者の集まりです。上図のように初期免疫者(=N×初期免疫率)、軽症者回復者(軽症から『軽症者回復日数』+1を経て回復した人)、重症者回復者(重症から『重症者回復日数』+1を経て回復した人)の3種類の人の集まりから構成されています。なお、初期免疫率がゼロの場合は、初期免疫者は、いないことになります。
最後に『死者』です。死者については、当日から『重症者回復日数』+1前の新規重症者数×『死亡率』/『重症率』を新規死者数と考えることにします。今回のモデルでは、死者は、重症者から出ると考えています。このため、死亡率(発症者全体に対するもの)は、重症率以下である必要があります。なお、重症率がゼロの場合は、死亡率/重症率は、ゼロとみなします。新型コロナ感染症の場合は、発症者の数パーセントと言われてきたため、これまでは、無視してきたものです。(後述しますが、今回のExcel表では、便宜的に『死亡日数』を『重症者回復日数』と等しいと置いています。青字個所を2020/4/3追記)
目次に戻る
t=1の初期状態では、N+1人のうち、軽症者1名を除くN人については、感染しておらず、また、初期免疫者を除き、免疫者はゼロです。同様にN人について、軽症者、重症者、死者もゼロです。
t=1以降の推移は、下図の通りとなります。
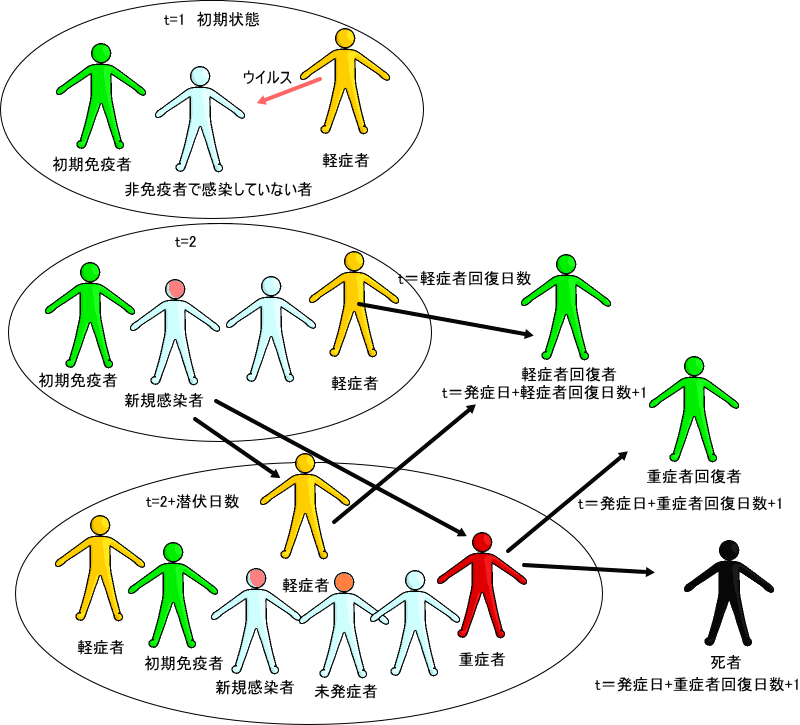
最初は、1名の軽症者から感染が始まると仮定しています。なお、この最初の1名の軽症者の発症日は、0日目と仮定し、日付が『軽症者回復日数』に等しくなった日に新規の軽症者回復者数に1を加えます。
その1名からのウイルスが非免疫者に対して、ウイルス感染を起こさせます。それがt=2での新規感染者(頭を赤くしている者)です。この新規感染者は、発症者または非免疫者で感染していない者のいずれかがゼロとならなければ、t>2以降も継続して発生します。新規感染者は、潜伏日数がゼロでなければ、発症までの間、『未発症者』となります。
t=2の新規感染者は、t=1+潜伏日数+1後に発症すると仮定します。発症者は、前述のように発症した時点で発症者として、重症率に合わせて、新規の軽症者と新規の重症者に計算上、分割します。
発症者のうち、軽症者は、発症日より軽症者回復日数+1後に軽症者回復者となります。
一方、新規死者は、重症者回復日数+1前の新規重症者数×死亡率/重症率とします。すなわち、死者は、重症者から出ることとし、そのタイミングは、『重症者回復日数』と等しくおきます。その理由は、死亡日数を任意に入力できるようにすると、時として、重症者回復者となった人の一部が後日、死者になるというような不自然な動きが起きる場合もありますので、このように便宜的に決めました。なお、前述のように、死者以外の重症者回復者は、免疫者の一部となります。
目次に戻る
Excel表を作る上で前節までの『感染者数計』などと長い名前は、冗長に過ぎて、分かりにくくなると思われます。かといって、アルファベット1~2文字に代表させるのも、筆者も分からなってしまいますので、以下の表に示す略称を使うことにします。なお、時間は、1日を単位とし、1から整数で変化するのに対し、感染者数などは、計算上は、実数と考えます。
なお、名前の頭にΔ(デルタ)が付いているものは、一日の新規の数を、Δの付かないものは、その時点の数を表し、いずれも時間の関数です。また、dで始まるものは、潜伏日数などの日数を表すもの定数(パラメーター)です。
| 略称 | 意味(t>=2の整数) | 算式(Nは、最初の軽症者を除く集団の人数) |
| Δ感(t) | t日目の新規感染者数 軽症者、重症者から感染する |
(軽(t-1)×軽感率(t-1)+重(t-1)×重感率(t-1))×割合(t-1) ただし、割合(t)=(非感(t)-免(t))/(N+1)、負はゼロとする。 添え字の値がゼロ以下は、その関数の値をゼロ(以下同様) |
| 軽感率(t) | t日目の軽症者感染率 | 軽症者から感染する割合、正の実数 |
| 重感率(t) | t日目の重症者感染率 | 重症者から感染する割合、正の実数 |
| 感(t) | t日目の感染者数計 | 感(t-1)+Δ感(t) ただし、N+1を超える場合は、N+1とする |
| 免(t) | t日目の免疫者数 | 初免+軽回(t)+重回(t) 初免は、初期免疫者数=N×初期免疫率 ただし、N+1を超える場合は、N+1とする |
| Δ軽回(t) | t日目の新規の軽症者回復者数 | Δ軽(t-d軽-1) ※t=軽症者回復日数のとき1を加える(初期軽症者1名分) |
| d軽 | 軽症者回復日数 | ゼロ以上の整数、ゼロの時は、翌日回復 |
| Δ重回(t) | t日目の新規の重症者回復者数 | Δ重(t-d重-1)-Δ死(t) ※死者は、すべて重症者から出るとする |
| d重 | 重症者回復日数 | ゼロ以上の整数、ゼロの時は翌日回復 |
| 軽(t) | t日目の軽症者数 | 軽(t-1)+Δ軽(t)-Δ軽回(t) ただし、負はゼロとする |
| Δ軽(t) | t日目の新規軽症者数 | Δ発(t)×(1-重症率) |
| 重(t) | t日目の重症者数 | 重(t-1)+Δ重(t)-Δ重回(t)-Δ死(t) ただし、負はゼロとする |
| Δ重(t) | t日目の新規重症者数 | Δ発(t)×重症率 |
| Δ発(t) | t日目の新規発症者数 | Δ感(t-d伏-1) 収束判定で、収束の場合は、ゼロ。2020/5/9追記 |
| d伏 | 潜伏日数 | ゼロ以上の整数、ゼロの場合は、翌日発症 |
| 死(t) | t日目の死者数 | 死(t-1)+Δ死(t) |
| Δ死(t) | t日目の新規死者数 | Δ重(t-d重-1)×(死亡率/重症率) ただし、重症率がゼロの時はゼロとする d重としたのは重症者回復と同時に死者発生と仮定のため |
| 非感(t) | t日目の非感染者数 | 非感(t-1)-Δ感(t) ただし、非感(1)=N-初免、初免=N×初期免疫率 負はゼロとする |
(1)~(3)までに基づき下記のExcel表を作成しました。自作ものコーナーにアップしてあります。VBAは、使用していません。なお、セル内の数式を保護するためにシートの保護を使っています。パスワードは、空ですので、シートの保護を解除すれば、修正が可能です。
Excelブックの名は、『KansenKyokusenNew4.xlsx』です。Excel 365で作成していますが、Excel 2007以降では、そのまま動作すると思います。なお、ファイルは、ZIP形式で圧縮しています。こちらからダウンロードできます。(2020/3/29に機能を追加して、Ver1.4としています。このため、ファイル名を変更し、本節の図と説明を適宜変更しました。2020/4/30に比率の表示桁数を変更して、Ver1.41としました)
下の部分は、『シート』の上部1行目から11行目までです。パラメーター等の設定と計算結果の概要が表示されます。利用者の方が変更できるのは、B4~B11、D9、E9、F9の値です。なお、前述のように潜伏日数等の日数は、ゼロ以上の整数で、死亡率は、重症率以下でないと入力規則により入力エラーが表示されます。
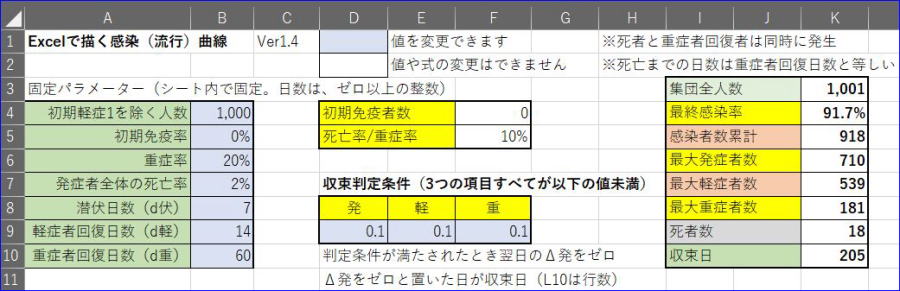
Ver1と比較して、収束判定条件を追加しました。これにより、条件に合致した場合、収束として、収束日を表示しました。収束した場合、翌日以降、H列のΔ発(新規発症者数)をゼロとしています。最終感染率等のセル範囲も当該収束日のセル番地(正確には、収束日+13=L10の値)までとしています。ただし、後述する検算用データに差が大きい場合は、判定条件を見直してください。(赤字部分を補足しました。2020/5/9)
13行目の各列の略称は、(3)の説明を参照してください。たとえば、『感』は、感染者数累計、『Δ感』は、新規感染者数の略です。


上の図は、13行目の表本体の見出し、14行目が1日目の初期状態です。14行以下で利用者が変更できるのは、軽感率(軽症者感染率)と重感率(重症者感染率)のみです。Ver1.4で収束判定用としてU列を追加しました。
なお、13行目の行にフィルターが設定してありますので、グラフシートでご覧になる際に適切な日数以下になるようにB13のセルのフィルターで日付を一定の値以下に絞っていただくとよいと思います。
オートフィルターで絞り込んでいる際は、必ず、絞り込みを解除してから、軽症者感染率、重症者感染率の変更をダブルクリックのオートフィルで適用してください。絞り込んだ状態では、絞り込まれている行以降のセルの値が変更されません。
ちなみに、計算日数は、2200日までを利用し、K4~K9に『最終感染率』等を表示しています。また、計算の確認のため、検算用として下のデータも表記しています。
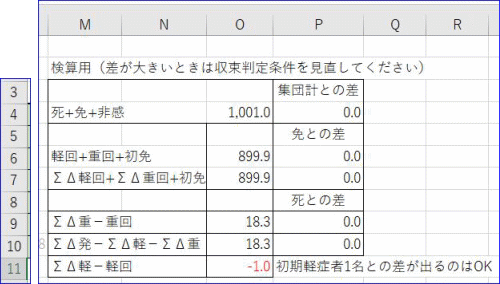
上図の例では、丸め誤差の範囲に収まっていることが分かります。
Excel表の勉強をされている方向けに表の1日目(C14~U14)~2日目(C15~U15)と3日目の一つ(F16)に設定されている式をまとめてみました。F列の『Δ感』のみ3日目(16行)が15行目とは異なるほかは、他の列の3日目(16行)以降は、2日目(15行)のセルの式のコピーとなっています。(F列の4日以降は、3日目(16行)の式のコピーです。)
| 列 | 略称 | 1日目(14行) | 2日目(15行) |
| C | 感 | 1 | =IF(C14+F15>$K$3,$K$3,C14+F15) |
| D | 軽感率 | 入力 | 同左 |
| E | 重感率 | 入力 | 同左 |
| F | Δ感 | 0 | =D14*I14+E14*K14 |
| F | Δ感 | F16(3日目)⇒ | =IF((D15*I15+E15*K15)*(T15-S15)/($K$3)<0,0,(D15*I15+E15*K15)*(T15-S15)/($K$3)) |
| G | 発 | 1 | =I15+K15 |
| H | Δ発 | 0 | =IF(U14=1,0,IF(IF(B15-$B$8<2,0,OFFSET(F15,-$B$8-1,0,1,1))<0,0,IF(B15-$B$8<2,0,OFFSET(F15,-$B$8-1,0,1,1)))) ※U列(収束判定)が1のときは、Δ発は、ゼロとしています。(2020/5/9補足) |
| I | 軽 | 1 | =IF(I14+J15-P15<0,0,I14+J15-P15) |
| J | Δ軽 | 0 | =H15*(1-$B$6) |
| K | 重 | 0 | =IF(K14+L15-R15-N15<0,0,K14+L15-R15-N15) |
| L | Δ重 | 0 | =H15*$B$6 |
| M | 死 | 0 | =M14+N15 |
| N | Δ死 | 0 | =IF(B15-$B$10<2,0,OFFSET(L15,-$B$10-1,0,1,1)*$F$5) |
| O | 軽回 | 0 | =O14+P15 |
| P | Δ軽回 | 0 | =IF(B15=$B$9,1+IF(B15-$B$9<2,0,OFFSET(J15,-$B$9-1,0,1,1)),IF(B15-$B$9<2,0,OFFSET(J15,-$B$9-1,0,1,1))) |
| Q | 重回 | 0 | =Q14+R15 |
| R | Δ重回 | 0 | =IF(B15-$B$10<2,0,OFFSET(L15,-$B$10-1,0,1,1))-N15 |
| S | 免 | =F4 | =IF($F$4+Q15+O15>$K$3,$K$3,$F$4+Q15+O15) |
| T | 非感 | =B4-F4 | =IF(T14-F15<0,0,T14-F15) |
| U | 収束判定 | 0 | =IF(AND(G14<$D$9,I14<$E$9,K14<$F$9),1,0) |
4節の(1)感染率=1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=0.2、死亡率=0の場合で検証してみます。
この例では、感染率に軽症者と重症者との区別をしていないので、D14とE14の値を1としてそれぞれの右下隅のフィルハンドルをダブルクリックして2213行目(日付は2200日)まで一瞬でオートフィルしてください。
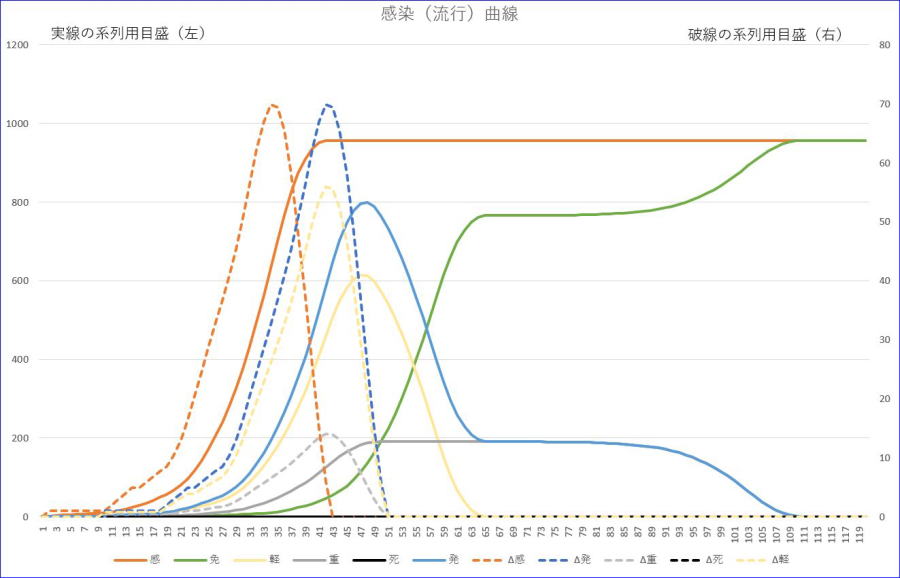
※橙は、感染者数累計、青は、発症者数、緑は、免疫者数、薄い黄色は、軽症者数、灰色は、重症者数です。
※それぞれの色の破線は、新規発生数で、その値の目盛は、右縦軸です。
※死亡率がゼロですので死者数、新規死者数は、ゼロです。
※表示範囲は、120日以下としています。
※最終感染率等は、次の通りです。
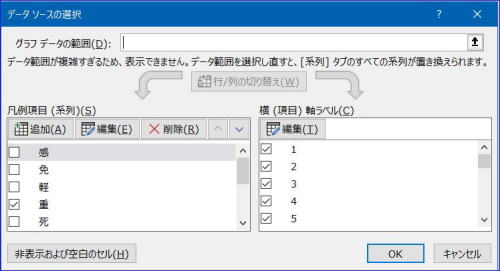
なお、グラフでは、すべての系列を表示させていますが、見づらい場合は、グラフのデザインからデータの選択をクリックして、下図のようなダイアログボックスで不要な系列のレ点(チェック)を外せば、非表示とすることができます。
さて、比較のために、4節の(1)のグラフを挙げると、下図のようになります。

※オレンジが感染者計、オレンジの破線が新規感染者数です。
※黒は、発症者数、黒の破線は、新規発症者数です。
※緑は、免疫者数、緑の破線は、新規免疫者数です。
この場合は、最終感染率は、95.5%、最大発症者数は、799人でした。
目次に戻る
6節(2)~(7)では、重症者は、完全に隔離されるであろうという想定で、重症者感染率(重感率)をゼロにして、かつ、軽症者が7日または14日間、軽症者の感染率を1から0.1に低下させたという想定で計算してみました。
今回は、合計数=1001,初期感染/発症者=1、感染率=1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=0.2について、軽症者感染率を日付が7日、8日を0.1、以降、7の倍数日毎に2日間ずつ0.1に変化させて計算しています。ちなみに、70日と71日までの10セット続けてみました。
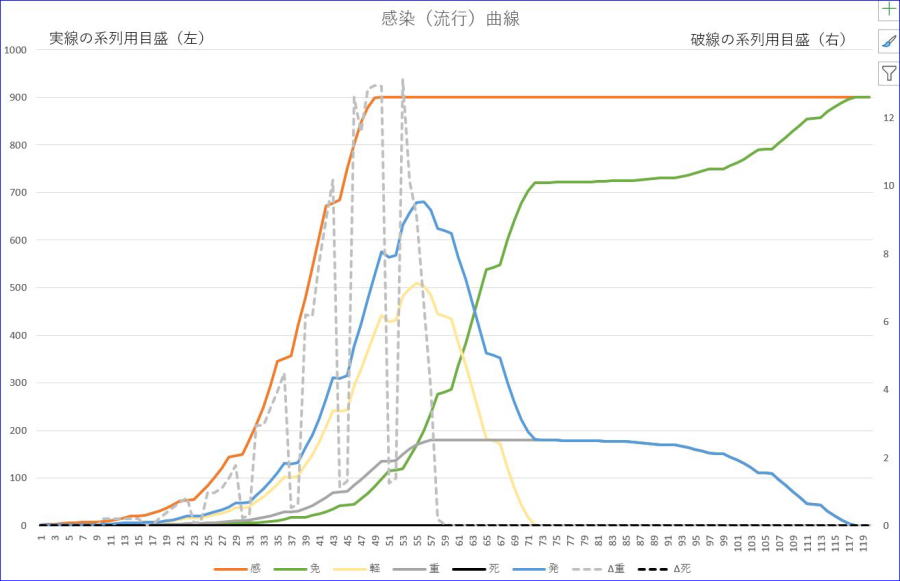
※橙は、感染者数累計、青は、発症者数、緑は、免疫者数、薄い黄色は、軽症者数、灰色は、重症者数です。
※灰色の破線は、新規重症者数で目盛は、右縦軸です。
※死亡率がゼロですので死者数、新規死者数は、ゼロです。
※表示範囲は、120日以下としています。
最終感染率等は、次の通りです。
7日ごとの2日間ずつの準隔離を行わない場合は、下図のようになります。
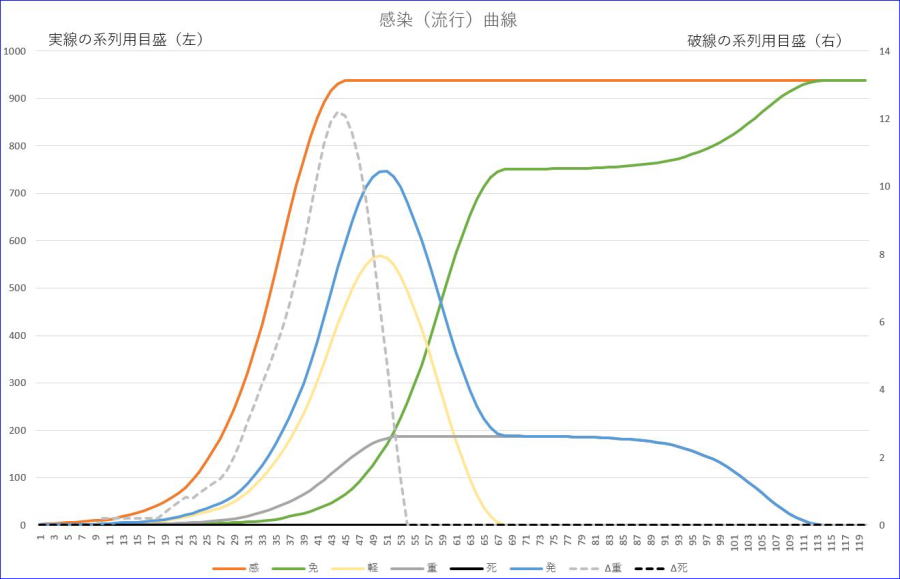
週末毎2日間×10セットの準隔離により、
最終感染率が93.7%から89.9%、
最大発症者数が746から679、
最大重症者数が187から180に減少していることが分かります。
ただ、この計算例では、2日間×10セット=のべ20日間の準隔離にもかかわらず、7日間や14日間の連続した準隔離ほどの大きな効果は、発揮できていないようです。
目次に戻る
軽症者感染率が0.1、重症者感染率が0.05のように非常に小さい場合を計算してみました。パラメーターは、合計数=1001,初期感染/軽症者=1、軽症者感染率=0.1、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=20%、死亡率=2%の例です。
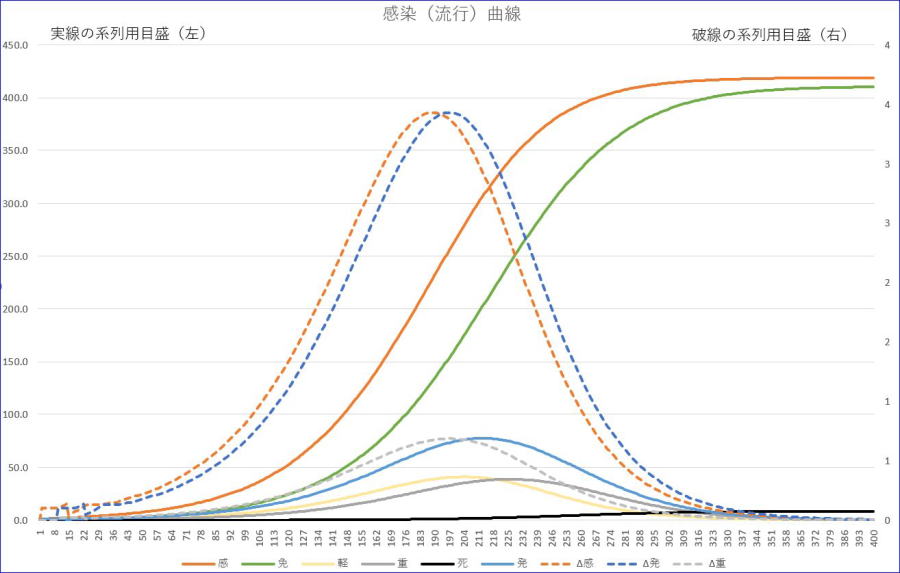
※橙は、感染者数累計、青は、発症者数、緑は、免疫者数、薄い黄色は、軽症者数、灰色は、重症者数、黒は、死者数です。
※橙の破線は、新規感染者数、灰色の破線は、新規重症者数であり、いずれも目盛は、右縦軸です。
※表示範囲は、400日以下としています。
この場合、最終感染率は、41.7%と半数以下の感染に留めることができます。最大重症者は、39名と死亡率がゼロであった前節の例187名よりも大幅に抑えられ、また、死者数も約8名となり、全員が感染した場合(1000名)の2%の20名を大きく下げることができました。ただし、代償として、収束までに約1年以上という長期間を要しますが、医療崩壊を招きにくい理想的な感染曲線と言えるでしょう。
※集団人数を1000+1人としていることに注意してください。集団が、10万人+1名の場合であれば、このような低い感染率で推移しても、感染者総数は、41,830名、最大重症者数は、約3,851名、死者数は、837名などとなります。
目次に戻る
軽症者感染率が0.5、重症者感染率が0.1のように、特に軽症者感染率があまり小さくない場合を計算してみましょう。パラメーターは、合計数=1001,初期感染/軽症者=1、軽症者感染率=0.5、潜伏期間=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=20%、死亡率=2%の例です。
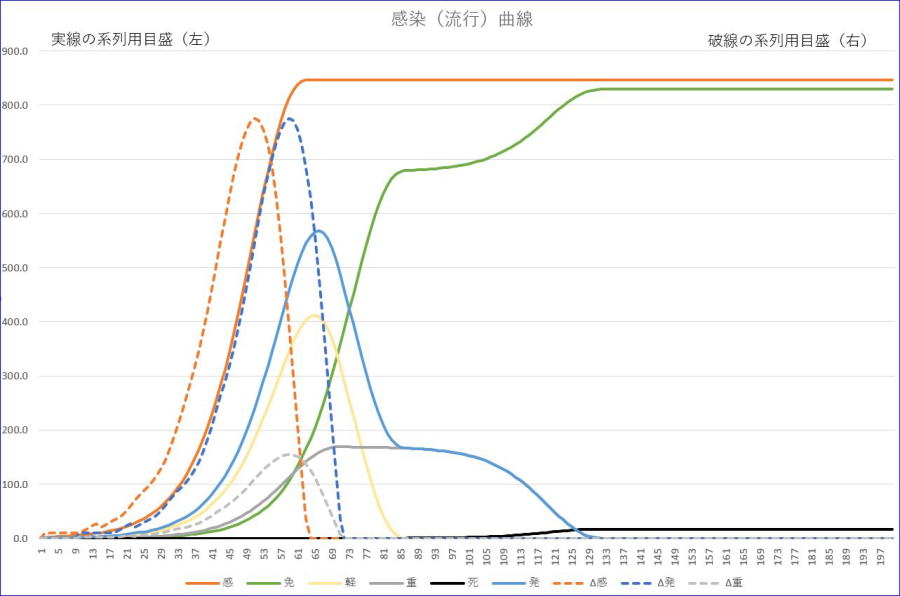
※橙は、感染者数累計、青は、発症者数、緑は、免疫者数、薄い黄色は、軽症者数、灰色は、重症者数、黒は、死者数です。
※橙の破線は、新規感染者数、灰色の破線は、新規重症者数であり、いずれも目盛は、右縦軸です。
※表示範囲は、200日以下としています。
この場合は、収束期間は、約半年になりますが、最終感染率は、84.5%となり、8割以上の人が感染します。感染と治癒に伴い免疫者数も前例の倍に達します。しかし、最大重症者数も169と前例の約4倍になり、計算上の死者数も約2倍となります。しかし、17名ではたいしたことはないと考えられた方は、下の段落をご確認ください。
前例の最後に記載しましたように集団が10万人+1名と仮定すれば、100倍となると考えると、最大重症者数が約1万6千名に達し、その時点で高度な治療を施すための病院が足りなくなることでしょう。不足する医療により、死者数も上の表の17×100=1700人では、収まらなくなり、1万人以上になることも十分にあり得ると思われます。如何に感染率、特に軽症者感染率を可能な限り低く抑えられるかが、この2つの計算例で明白です。
目次に戻る
東京都の感染者数が連日40人以上に増えていることに伴い、東京都及び隣接する千葉県、神奈川県、埼玉県、山梨県が共同で可能な範囲での外出自粛を呼びかける事態になりました(2020/3/26)。本節は、2020/3/27に追記し、3/28に修正しました。
あくまでも試算ではありますが、実態を知っておく必要があるでしょう。本来は、全体のおおまかな流れをグラフを交えて、わかりやすく伝えることが望ましいでしょう。そのことにより、徹底して人との接触を避けないと、とんでもない事態になるということが十分に伝わらないでしょう。特に若い方の大半が症状の軽いこともあり、周知されていないように思われます。
3/26の小池都知事の話も残念ながら、丁寧な語り口で『感染爆発の重大局面にある』とお話になっていました。若いみなさんには、『なんのことなの?』とピンとこないであろう難しい漢語が多かったですね。(ドイツ語のアウフヘーベンよりは良いけど)
推測すると、いくらシミュレーションの数値であると言っても、責任者が一度口にした数字というのは、一人歩きしがちであるので、パニックを怖れて、多くの政治家が慎重になるのは、分かります。しかし、結局のところ、『重大局面』に入れば、隠しておくことは、できません。
マスコミのなかにも、中国やイタリアの感染者数や死者数を話題にして日本は、よく頑張っているという論調がいまだに目に付きます。しかし、ことわざに曰く、『子ども笑うな、昔の自分、年寄り笑うな、明日の自分』です。
昨日の武漢市や今日のバルセロナは、明日の東京や大阪である可能性に耳目を開いていて欲しいです。そこで、集団人数がN=10万人+1名の軽症者の計算例を挙げておきましょう。100倍すれば、1000万人です。
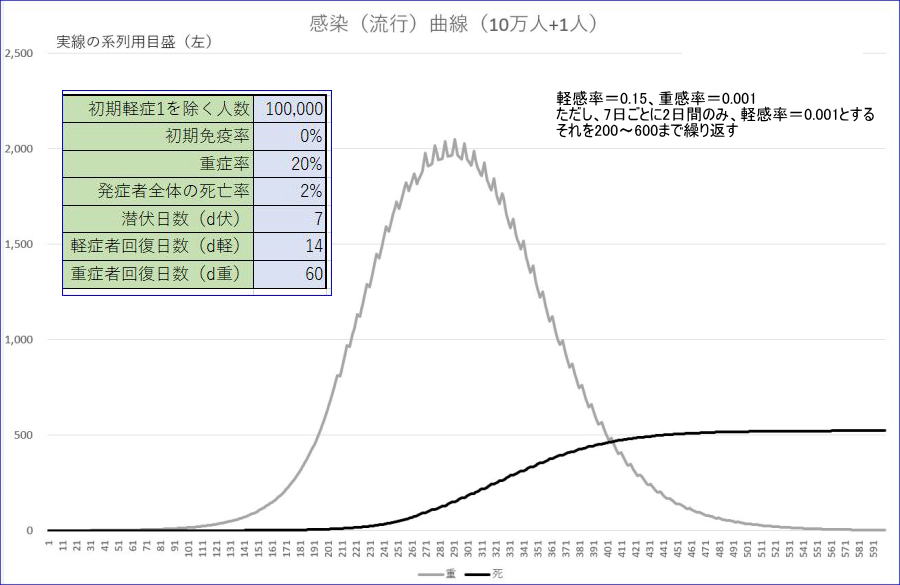
集団人数=10万+1名、軽症者感染率が0.15、重症者感染率=0.001、潜伏日数=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=20%、死亡率=2%の例です。前節までより、軽感率をかなり小さくしています。
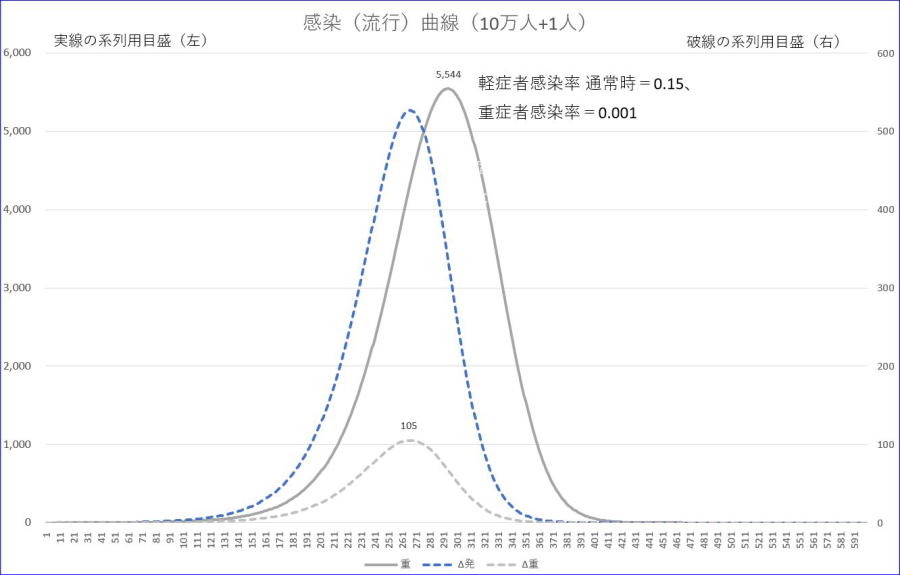
※灰色は、重症者数です。
※青の破線は、新規発症者数、灰色の破線は、新規重症者数であり、いずれも目盛は、右縦軸です。
※表示範囲は、600日以下としています。
最終感染率は、軽感率が低いため、44%程度と良い線を行っているようにも思えますが、最大重症者数が5500人、新規重症者数が1日あたり105人となっています。さらに、この数字は、10万人あたりなので、100倍すると、最大重症者数が55万人、新規発症者が1万人と、まさに感染爆発です。桁違いの大きい数です。
東京都で用意できる重症者用のベッドは、最大でも、5千以下と思われるので、重症者の多くは、収容先の医療施設を見つけられないでしょう。そのため、多くの重症者が亡くなり、上表の死者と合わせて、最大で、60万人という恐るべき数字になってしまいます。 感染者数444万人の14%にあたります。
では、どうすれば、良いのでしょうか? 東京から逃げ出しますか?
それは、『疎開』ですね。太平洋戦争中の日本で、唯一、比較的うまく実行できたと言われるのが、学童疎開であると言われています。今回、子どもや若い方ではなく、年寄りの疎開という考えになるのですが、悪いことでは、ありません。地方に実家や縁戚があるリタイアされている健康な方は、1年程度、東京を離れることも一案ですが、無症状の方が地方に感染を広げるリスクも存在します。2020/4/8赤字を追記。
冷静になって考えると、なかなか、多くの方には、当てはまらないでしょう。高齢者は、持病を抱えていたり、かかりつけの病院、常用している薬があるなど簡単ではありません。
そこで、結局のところ、軽症者の準隔離となるわけです。軽症者と書きましたが、症状のない軽症者のみに限ることができません。検査が行えていないからです。
もし、気軽に検査ができれば、無症状の感染者と濃厚接触者に限って、準隔離をしてもらえばよいのですが、今のところ、不明のままほぼ全員が準隔離を実行していただく必要があります。
試算してみると、もっとも、効果が大きかったのは、250日~265日まで、軽感率=0.001と通常の0.15と比較して、その0.7%という驚異の低さで16日間生活していただくことです。ほとんど、平安時代の『物忌み』に近いかもしれませんね。
これで、最大重症者数を3600にまで下げることができました。さきほどの5400に比べれば、とても小さくなりましたが、下げ幅が、まだまだ足りません。これ以上日数を増やしても効果があまり変わりません。
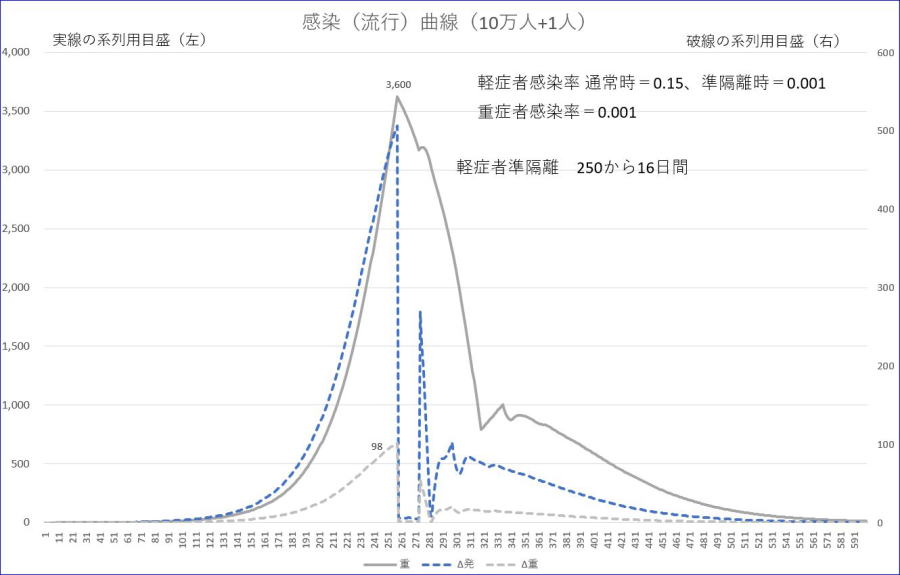
※灰色は、重症者数です。
※青の破線は、新規発症者数、灰色の破線は、新規重症者数であり、いずれも目盛は、右縦軸です。
※表示範囲は、600日以下としています。
それでも、準隔離を行わない場合と比較すると、最終感染率は、44%→21%と23%も低く抑えられますが、最大重症者数が3600人、新規重症者数が1日あたり最大95人となりました。
あくまでも、この数字は、10万人あたりなので、100倍すると、最大重症者数が36万人、新規の重症者数が1日あたり9500人と、まさに感染爆発です。桁違いの大きい数ですが、準隔離を行わない場合と比較して。重症者の多くを失うとして、死者数と合わせて、最大死者数を60→42万人とやや低く抑えられました。
では、準隔離中の軽感率を0.001から文字通りゼロと置いた場合は、どうでしょうか? 実は、16日間(の物忌み)では、ほとんど、変わりません。なぜかというと、16日より以前に感染した者からの発症者が現れるからです。
結局、重症者の回復期間60日間を超える日数、80日間、すなわち、250~329日までが必要となります。この際、重感率もゼロとします。それを行うと下図のように330日頃にようやくゼロとすることができます。
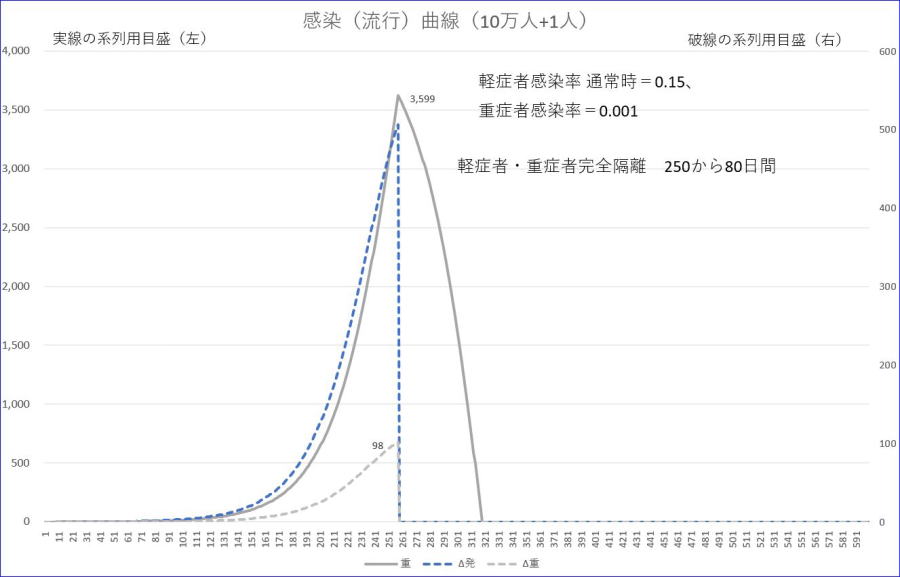
※灰色は、重症者数です。
※青の破線は、新規発症者数、灰色の破線は、新規重症者数であり、いずれも目盛は、右縦軸です。
※表示範囲は、600日以下としています。
このようにすると、準隔離を行わない場合と比較して、最終感染率は、44%→21%と23%も低く抑えられます。また、最大重症者数が3600人、新規重症者数が1日あたり最大98人となります。
あくまでも、この数字は、10万人あたりなので、100倍すると、最大重症者数が36万人、新規の重症者数が1日あたり1万人と、やはり途方もない数字ですが・・。
目次に戻る
それでは、準隔離24日間を複数回、実施するというのは、どうかと言うことで調べてみました。ためしに、新規発症者数が100を超えて切りの良い100日目から準隔離(軽感率=0.001)を24日、その後、200日から再度、24日間の準隔離、のように起点を100日おき、24日間の準隔離を繰り返すと下図のようになりました。
下のグラフでは、準隔離を100、200、300、400、500日目からの5セット繰り返しました。なお、本節は、2020/3/27に追記し、3/28に修正しました。
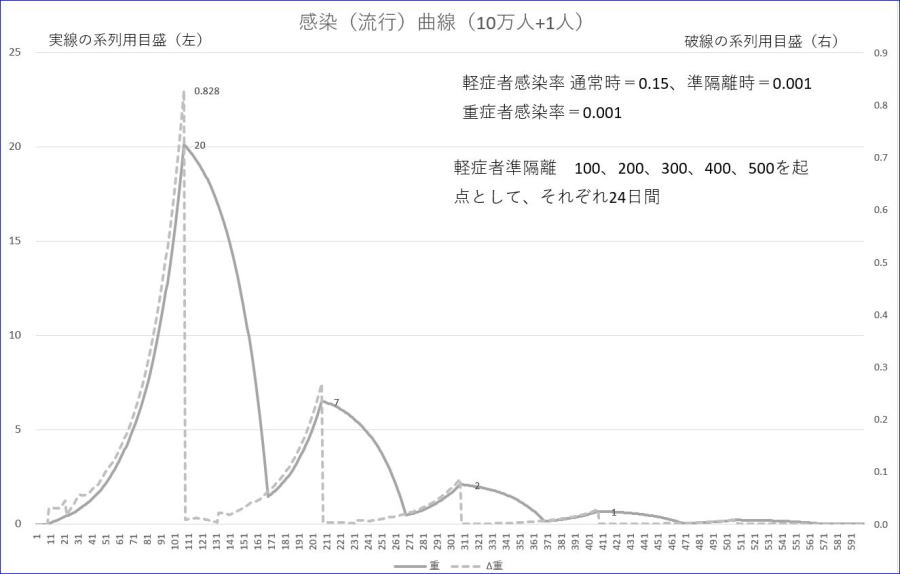
※灰色は、重症者数です。
※灰色の破線は、新規重症者数であり、目盛は、右縦軸です。
※表示範囲は、600日以下としています。
上表でもわかりますが、最大重症者数等は、準隔離1回と比較して、大きく変化しています。この例では、最大重症者数は、20人、これらは、1000万人に換算して、2000人程度と考えられます。対処可能な数字に落ち着いてきました。
Ver1.4から、Excelの計算において、次のような変更を施しています。Δ発(新規発症者数)は、軽(軽症者数)<0.1、重(重症者数)<0.1、発(発症者数)<0.1の全てが満たされた場合は、翌日のΔ発をゼロとします。収束判定条件(上の0.1)は、変更可能です。この修正により、小数点1桁未満の数字が積み重なって、時間が経つと、再度上昇に転ずる、いわば、計算によるゴーストがなくなりました。
※『自作もの』に置いてあるExcel表(KansenKyokusenNew4.xlsx)は、この修正を行ったバージョンです。
さて、現実の問題として、24日休んで、76日生活して、また、24日休んで、という繰り返しが可能かどうか?です。Excelの計算上は、いくらでも実行可能ですが、多くの繰り返しは難しいでしょう。数セット実施すると、しばらくの間は、新規の発症者がゼロに近づきますので、いちはやく、新規発症者を完全に隔離すれば、定常的にゼロとすることができるでしょう。それを行ったのが武漢市だったかと思われます。
準隔離により、ピークが遅くなれば、治療薬の本格適用などにより、軽症者の回復期間を14日から短くできたり、重症者から軽症者へ症状が改善できると思われます。そうすれば、上表の死者数の3人/10万人×1000万人=300人という計算値以下に抑えることができるでしょう。(訂正前の8万人は、300人の記載ミスでした。お詫びして訂正します。2020/4/4)
何も対策を取らないときの死者数最大54万人や準隔離16日間1回の最大41万人という衝撃的な数値よりは、受け入れ可能な範囲内に収められる可能性は、残されていると思います。
なお、24日間という数字は、潜伏日数7日+1日(ここでは、潜伏日数=0の場合は、翌日発症と計算しているため、1を足しています)、これに軽症者の回復日数=14日+1日(やはり、軽症者回復日数の翌日に免疫者の仲間入りをするという仮定を置いているため1を足しています)の和である23日に1を加えた数です。
目次に戻る
計算例(9)や(10)と同様に、集団人数=10万+1名、軽症者感染率が0.15、重症者感染率=0.001、潜伏日数=7、軽症者回復=14、重症者回復=60、初期免疫=0、重症率=20%、死亡率=2%とします。
ただし、週末の7日ごと2日間は、軽感率(軽症者感染率)を0.001と重感率と同一とします。この繰り返しを約60回近く行いました。
※灰色は、重症者数、黒は、死者数です。
※表示範囲は、600日以下としています。
これと比較するために、(9)での計算結果のみを再掲しますと下図の通りです。
最大重症者数は、何もしない場合より、5545→2050と64%減少、死者数も894→523と42%減少します。また、最終感染率も44%から26%と18%の減少するので、発症者数も11306→4060と3分の1近くに減少しています。一方、収束期間は、477日→971日と2倍以上に増加します。
200~600日までの約400日間の間、7日ごとに2日ずつの準隔離を繰り返す(約60回)とこのような効果がありました。まあ、これでも、100倍すると、最大重症者数が20万人となるので、この対策だけでは、前節(10)のような鮮やかな効果には、なりません。やはり、もう少し、長期間の準隔離と組み合わせないといけないでしょう。
目次に戻る
最近になり、アメリカのニューヨーク州などの抗体率が10%程度と発表され、これは、従来、推定されていた値よりも、かなり大きいとの報道がありました。
また、日本においては、従来から、PCR検査を理由はともかくとして、絞っているため、諸外国に比較して感染者数が少なくなっているとの指摘もありました。もちろん、発症者のすべてを検査できないので、発表されている感染者数よりも実際の感染者数が大きいことは、確かでしたが、これほどの差があると従来の計算の見直しが必要となります。
そこで、潜在的な感染者数が発表値の約10倍と仮定して、従来から言われていた重症率20%や死亡率2%という数値も大幅に見直してみました。
まずは、初期人数=10万人+1、初期免疫率=0、重症率=2%、死亡率=0.2%、潜伏日数=7、軽症者回復日数=14,重症者回復日数=60、として、軽症者感染率(軽感率)=0.15、重症者感染率(重感率)=0.01として、準隔離を一切行わないケース。
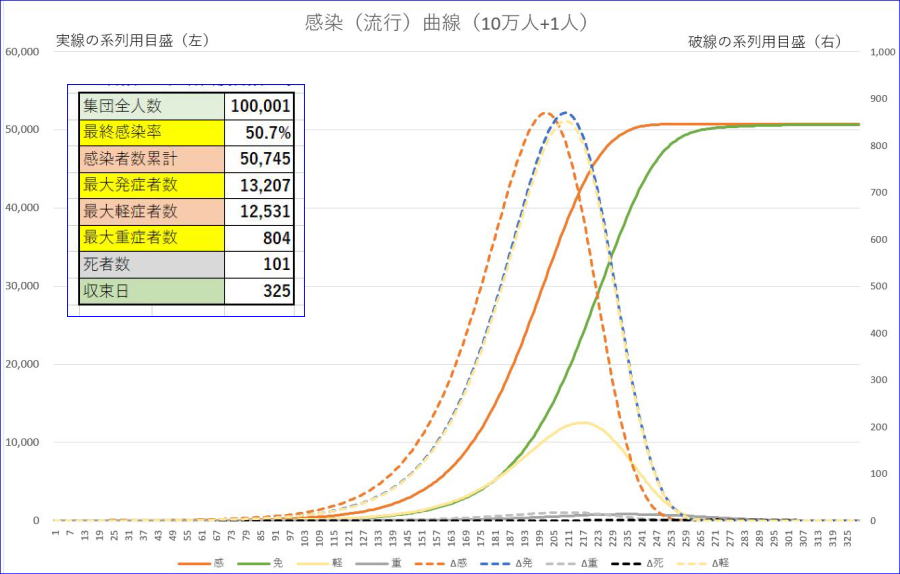
※橙は、感染者数累計、青は、発症者数、緑は、免疫者数、薄い黄色は、軽症者数、灰色は、重症者数、黒は、死者数です。
※破線は、それぞれの新規の数であり、目盛は、右縦軸です。
※表示範囲は、330日以下としています。
これを見ると、死者数は、10万人あたり100人、100倍して1000万人あたりにすると1万人という数字になります。最大重症者数は、同様に10万人あたり800人、1000万人に対して、8万人となりますので、当然ながら、医療崩壊は、避けられません。
ただし、最大重症者を多くを失うとしても、これまでの重症率、死亡率を元にして計算した場合の最大死者数が数十万人という規模には、至りません。これは、この2つの数値が1/10になっている効果がそのまま出ていると考えられます。
次に、2020年4月7日から、東京都他に非常事態宣言がでたことから、98日目(1日目を1/1として4/7に相当)から127日目(5月6日)まで、軽症者の準隔離と考えて、軽感率を1/10の0.015にしたケース。他の条件は同じ。
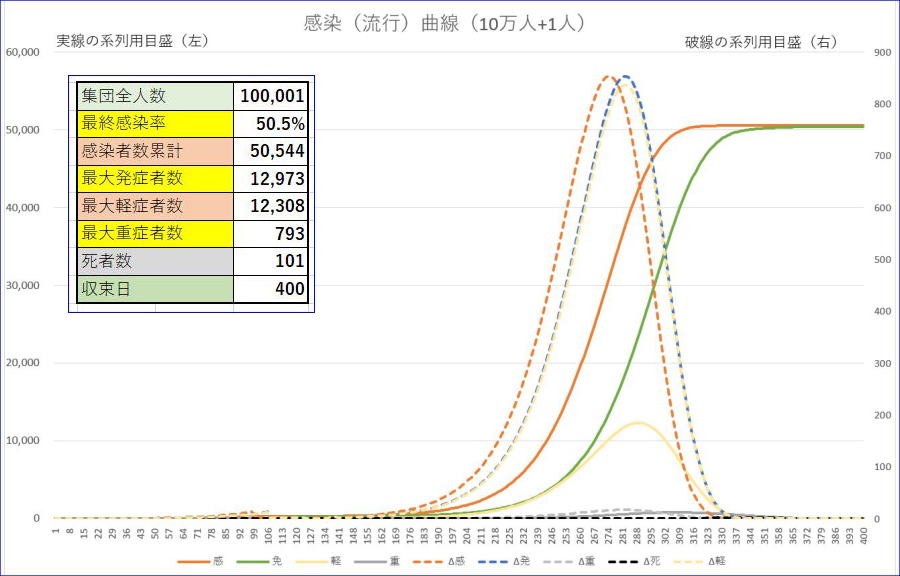
最大重症者数は、少し減少するものの、最終感染率の低下もわずかに留まり、収束日も延びています。5/6まででは、効果は乏しいと言わざるを得ません。
では、5/31まで延長した場合は、どうでしょうか。98日目(1日目を1/1として4/7に相当)から152日目(5月31日)までの軽症者の準隔離を行い、軽感率を1/10の0.015にしたケース。他の条件は同じ。
グラフは、略して、計算結果は、下図の通り。
大きな変化は、ありません。
そこで、さらに準隔離の期間を7/23まで延長した場合、すなわち、98日目(1日目を1/1として4/7に相当)から205日目(7月23日)まで、軽症者の準隔離を行い、軽感率を1/10の0.015にしたケース。他の条件は同じ。
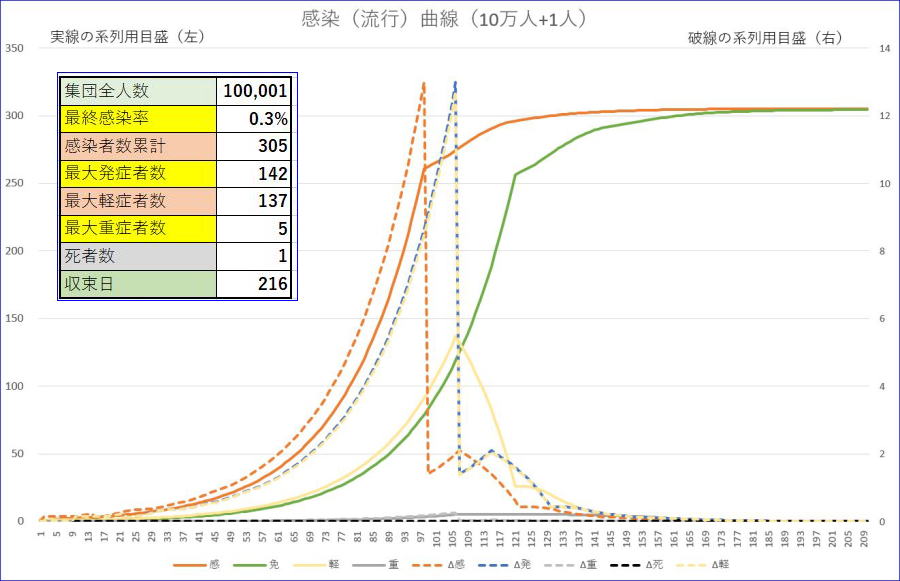
準隔離の効果が最大に発揮されました。10万人あたりの死者数1人、最大重症者数も5人と信じられないほどの効果です。1000万人あたりに換算しても、死者数が100人、最大重症者数が500人です。特に最終感染率が0.3%という結果は、(10)計算例6の準隔離24日を100日周期で5回実施した場合に匹敵します。
目次に戻る
作成日 2020/2/28
一部の文言を修正加除 2020/2/29
一部訂正 2020/3/1、2020/3/4
WHOのパンデミック宣言、NHKの特設サイトを追記 2020/3/13
6節を訂正して再計算 20203/23
『感染(流行)曲線をExcelで描く』を9節に追記 2020/3/23
9節の一部を修正しExcel表をアップ 2020/3/24~3/25
9節に(9)と(10)を追記 2020/3/27
9節の修正 2020/3/28
Excel表をバージョンアップ 2020/3/29
一部を微修正 2020/3/30
9節に(11)を追記 2020/3/30
『始めにお読み下さい』を追記・文を微修正 2020/4/1~4/3
9節(10)の数値の誤りを訂正 2020/4/4
緊急事態宣言等を追記 2020/4/8
緊急事態宣言対象を全国拡大を追記 2020/4/17
重症率、死亡率を従来値の1/10とした試算を追記 2020/4/30
緊急事態宣言の5月末までの延長を追記 2020/5/8
9節の収束判定条件について補足 2020/5/9
39県の緊急事態宣言解除を追記 2020/5/15
3府県の緊急事態宣言解除を追記 2020/5/21
玄関で靴を脱ぐ生活に関するコメントを追記 2020/5/21
緊急事態解除宣言を追記 2020/5/26
タイトルに『差分方程式を立てる・Excelで解く』を追加:2020/10/7
首都圏1都3県に緊急事態宣言再発出:2021/1/8
ページトップの図を準隔離3回繰返しに差替え:2021/1/8
緊急事態宣言を7地域に拡大:2021/1/14
緊急事態宣言を一部を除き延長:2021/2/4
緊急事態宣言の状況を更新:2021/6/1
タイトル図内の誤字を訂正:2021/8/1
緊急事態宣言の近況を追記:2021/8/1
緊急事態宣言等の近況を追記:2021/8/17
治療薬、ワクチンの現状を追記:2021/9/8
緊急事態宣言等の近況を追記:2021/9/11
緊急事態宣言・まん延防止等重点措置解除を追記:2021/10/1
オミクロン株の出現と対応を追記:2021/12/5
抗原検査、ワクチンの接種状況を追記:2022/1/18
オミクロン株による感染急拡大へのまん延防止を追記:2022/1/18
まん延防止等重点措置の追加を追記:2022/1/25
和歌山県のまん延防止等重点措置を追加:2022/2/8
高知県のまん延防止と東京都等の延長を追加:2022/2/10
まん延防止等重点措置の延長と一部解除を追記:2022/2/21
まん延防止等重点措置の一部解除と延長:2022/3/9
まん延防止等重点措置の全面解除を追記:2022/3/30
2類から5類への移行決定を追記:2023/2/3
マスク着用の指針を追記:2023/2/12
5/8から感染症法の5類に移行:2023/4/28