数式処理ソフト　DERIVE（デライブ） de ドライブ

4４．積分（４）（高速ラプラス逆変換）

１．計算尺と数表

「何なの？　計算尺（けいさんじゃく）って」

「あはは。その昔、わしの親父さんが働いていた頃は、コンピュータや電卓など便利な計算道具は、無かったので、対数の性質を利用した「計算尺」という計算道具を使っていたことがあるんじゃ。わしも学生の頃は、少しは、お世話になったものじゃ」

「へー。算盤（そろばん）とは違うんだ。どんな形なの。それにしても、「尺」って古！」

「残念じゃが、計算尺の現物は、もう、わしの手元にはないのう。しばらく前までは、どっかにあったのじゃがな。
「尺」が古いか。まー、1尺は、33cmじゃから、だいたいそのくらいの大きさじゃったかな。全体が「竹」で出来ていて、自分の力でこれを動かしていたんじゃからな。
ホント、エコロジーではあったな。竹に振った目盛りで、かけ算、割り算を行うので、どうしても多少の誤差があるんじゃ。
その意味では、そろばんは、デジタルなので、手間さえいとわにゃ、原理的には、任意精度で計算できる面では、優れているんじゃが、使いこなすためには、修練が必要じゃからの。
計算尺は、専門の技術者などは、1mもあるような大きなものを使っていたということじゃ。長さが長いほど、目盛りが細かく振れて精度が高くなったからの」

「もう一つの「数表」というのは、なんとなく分かるけど」

「「吉田洋一監修　新数学シリーズ　数表　培風館　昭和33年」というものが、手元にある。わしの学生時代は、こちらもお世話になったからな。
今もExcelなどの関数で「引数」（ひきすう）という用語が出てくるじゃろう。引数というのは、元々、数表を引くための元になる数（今風に言えば、検索値）じゃから、こう呼ぶようになったんじゃ。
こういった数表もふだん使う関数は、関数電卓やパソコンで計算できてしまうので、使わなくなってしまったな」

「へー、赤くて意外に、おしゃれなね。最初は、常用対数（5桁）から始まってるんだ！」

「まあ、月並みな言葉じゃが、隔世の感があるのう。対数を発明したネピア（またはネイピアとも書く。スコットランドの人：1550年～1617年　［ウィキペディア］による）が今、よみがえったら、何と言うかのう。
この数表でも、対数を使った計算方法が巻末に丁寧に説明してある。
対数は、ともちゃんも知っているように「かけ算」・「割り算」を「足し算」・「引き算」で済ますために使われたのじゃ。さっきの計算尺もその原理の元に作られたわけじゃからな。当時も今も、10進法が主だから、常用対数（底が10の対数）が計算上、便利だということで、まずは、巻頭に配置されたということじゃろうが、そのことにも今更ながら驚くのう」

「オホン、こういう先人の苦労の上にわしらの生活があることを忘れてはならんぞよ！」

「おいおい、ともちゃん、それは、わしが言う台詞じゃろうが」

「えへへ・・」

２．ヘビサイドと演算子法

「ヘビサイドさんという人が演算子法を作った人なんだ」

「そうじゃ。イギリス人のOliver Heaviside （1850－1925）氏じゃな。対数の発明が複雑な数値計算を足し算・引き算の組み合わせに還元したように、演算子法により微分方程式等を代数計算に帰着させて解くという発想がヘビサイドにあったのじゃろうな。
彼は、数学の専門家ではなかったので、厳密性という点では、当時、いろいろと批判されたようじゃがの。パイオニアの宿命かもしれん」

「じゃ、最初は、ラプラス変換を使っていなかったの？」

「うん。ラプラス変換を使った方法では、「演算子」という言葉がピンとこないじゃろう。元々のヘビサイドの方法では、微分演算子をpで表し、積分を1/pで表したりしていたので、演算子という感じがするじゃろうな。この辺のことは、以前挙げた、近藤次郎先生の本（演算子法　培風館）に書かれておる。
それによると、ラプラス変換による基礎付けや拡張などは、後生の多くの学者の手で行われたのじゃ。
彼は、不遇な生涯を送ったようじゃが、彼の死後、著名な数学者の「ヴィッタッカー（Whittaker）が、『19世紀の最後の四半世紀における3つの最も重要な数学上の進歩として、ポアンカレ（Poincare）の保型関数の発見、リッチ（Ricchi）のテンソル解析と並んで、Heavisideの演算子法の発見をあげるべきである』と1929年に述べた」と記されている。この言葉こそ、冥界へ旅だったヘビサイドへの最上の贈り物と言えるじゃろうの」

３．数値計算によるラプラス逆変換

「さて、ようやく本題に入った来たわけじゃ。ラプラス逆変換結果を数値的に求めよう、ということじゃ」

「でも、複素積分が必要なんでしょ」

「確かにそうじゃが、前回挙げた、「Basicによる高速ラプラス変換」（細野敏夫著：共立出版）によれば、注意点はあるものの関数論を振り回さなくても済みそうじゃ」

「たとえば、どんな感じなのかしら」

「同書では、冒頭に、F（s）＝1/√（s2+1）が例に取り上げられているが、これは、原関数がベッセル関数なので、ここでは、まずは、簡単な例として、
F（s）＝1/（s2+1）を使ってみよう。この原関数は、f（t）＝sin（t）じゃ。
高速ラプラス逆変換（以下、同書にならって「FILT」と書くことにする）の、まずは、Euler変換を使わない方法では、f（t）の任意のt（＞＝0）の値を像関数 F（s）から、次のように近似計算する。
f（t）≒exp（a）/t×Σ（－1）nFn　、和は、n＝1～∞、ここで、Fn＝Im（F（（a＋i（n－1/2）π）/t））
なお、a は、正数で近似の度合いを表す正のパラメータ（大きいほど精度が高いがその分、項数をたくさん加算する必要がある）、i は、虚数単位、Im（　）は、虚数部を取り出す関数とする。
ともちゃんなら、どのようにDERIVEで計算させるかのう」

「Im（ ）関数は、DERIVEでは、IM（ ）関数だわ。これは、昔のDOS版の解説書（Ver2.5版）に書いてあるの。虚数単位は、#i で入力できる。
（下のパレットから、i （ちょっと曲がったアイね）を選んでもいいけどさ）
複素関数関係には、実数部分を取り出す、RE（ ）関数、CONJ（ ）は、前も出てきた共役複素関数、ABS（ ）は絶対値などがあるわ。
ということで、まずは、f((a + i(n － 1/2)π/t)　から、IM関数で、虚数部を取り出して、n＝1～mまで和を定義する。それをg（t,a,m）と書く。
試しに、g（t，3、10）とg（t，3,100）、として、下のグラフにしてみたわ。こんな感じ。



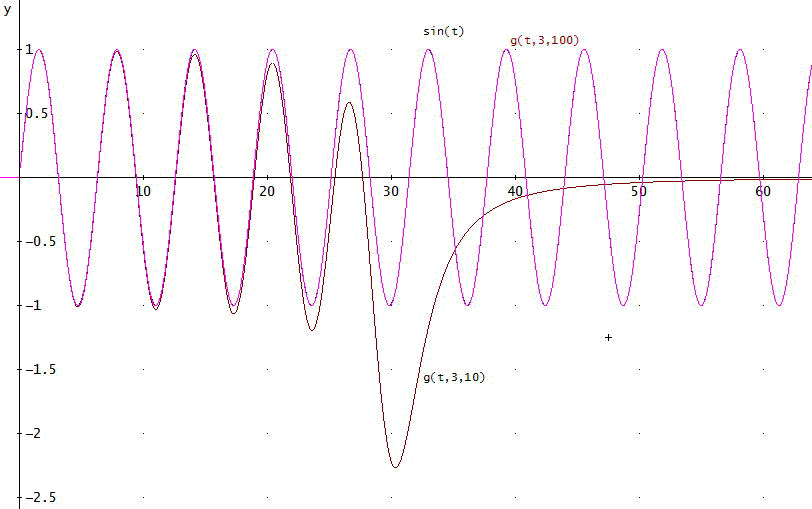
　グラフでは、t＝0～20ぐらいまでは、sin(t)とg(t,3,10）もほとんど、変わらない。ただ、t＝20を過ぎると、さすがに、g(t,3,10)は、大きく、ずれてしまうわ。
でも、g(t,3,100)は、t＝0～300ぐらいまでは、sin(t)とほぼ、一致している！」

「そうじゃの。数値的な精度は、どうじゃな」

「g(t,3,10)＝[0, 0.8392302975, 0.9061947413, 0.1343590227, －0.7632302249, －0.9704146367, －0.2896751143, 0.6404018425, 0.9745124892, 0.3898332674, －0.5646093683, －1.028982014, －0.5645295496, 0.3829308933, 0.9529353838, 0.6023154512, －0.3387996276, －1.024079493, －0.8204927871, 0.06588786666, 0.8159554804]、t＝0～20まで1刻みで計算。
一方、sin(t)も同じ範囲で計算すると、（有効桁数10桁）、
sin（t）＝([0, 0.8414709848, 0.9092974268, 0.1411200080, －0.7568024953, －0.9589242746, －0.2794154982, 0.6569865987, 0.9893582466, 0.4121184852, －0.5440211108, －0.9999902065, －0.5365729180, 0.4201670368, 0.9906073556, 0.6502878401, －0.2879033166, －0.9613974918, －0.7509872467, 0.1498772096, 0.9129452507])
そして、sin(1)で小数点以下1桁目まで一致、相対誤差（%単位）を計算すると、
100*（g(t,3,10)－sin(t)）/sin(t)＝
[?, －0.2662821820, －0.3412178876, －4.790947397, 0.8493272213, 1.198255416, 3.671813563, －2.524367505, －1.500544161, －5.407478320, 3.784459291, 2.899209155, 5.210220411, －8.862223872, －3.802916623, －7.377100719, 17.67826491, 6.519884002, 9.255222470, －56.03876879, －10.62383206]
このように、10項までしか計算しないと、t＝2ぐらいまでは、5%以下の相対誤差であるが、tが大きくなると、10%を超えてしまう。
同じく、
g（t,3,100）＝([0, 0.8411133386, 0.9099827851, 0.1400966220, －0.7554746322, －0.9605467022, －0.2775717085, 0.6548965076, 0.9915919747, 0.4097355786, －0.5415931153, －1.002496320, －0.5341398083, 0.4177577631, 0.9928566421, 0.6481470190, －0.2860363416, －0.9630931194, －0.7496318587, 0.1487630668, 0.9136585015])
なので、sin(1)では、小数点以下3桁まで、一致。相対誤差は、
100*（g(t,3,100)－sin(t))/sin(t)＝
[?, －0.04250248911, 0.07537229312, －0.7251884501, －0.1754570094, 0.1691924614, －0.6598738062, －0.3181329816, 0.2257754637, －0.5782091047, －0.4463053821, 0.2506138134, －0.4534536902, －0.5734085525, 0.2270613485, －0.3292113111, －0.6484729089, 0.1763711266, －0.1804808353, －0.7433704180, 0.07812635175] となって、n＝1～100まで計算した方は、さすがに相対誤差で1%未満に収まるみたい」

４．Fnの振る舞い

「前節で、見たように原関数がsin(t)の場合、a＝3であれば、100項ぐらいの和をとれば、相対誤差が1%未満に収まることが分かった。
しかし、Euler変換を利用できれば、もっと、ずっと少ない項数で済ますことが出来るんじゃな」

「でも、Euler変換を使うには、交代級数である必要があるんでしょ」

「そうじゃ。近似式：f（t）≒exp（a）/t×Σ（－1）nFn で、Fnが定符号であれば、（－1）n を掛けているため、交代級数になるので、その条件は、満たされるの。
Fnの符号を調べてご覧」

「Fn＝16πat^2(1 － 2n)/((4a^2 + (2πn + 2t － π)^2)(4a^2 + (2πn － 2t － π)^2))
と、なって、a＞0、t>=0、n>=1のとき、明らかに、常に、分子は負、分母は、正となるわ」

「すなわち、Fn＜0じゃな。ということは、Euler変換を利用できるということじゃ。
Euler変換を利用すると、f（t）≒exp（a）/t×Σ（－1）nFn≒exp（a）/t×Σ（－1）（m+2）ΔmF1/（2m+1）
＝exp（a）/t×｛Σ（n=1～k）（－1）nFn＋Σ（m=0～）（－1）（k+m+1）ΔmFk+1/2^(m+1)｝
ここで、Δは、階差演算子。
Euler変換を使った近似式のうち、2番目は、Ci（t）の時と同様に、1～kまでは、普通に加算して、k+1以降をEuler変換するのじゃな」

「前回と同様にk＝10として、10項までは、普通に計算してみるわ。階差の上限は、3、5、7として、計算した結果は、次のとおりよ。
sin(t)≒EXP(a)/t∑(f(n, 0)(－1)^n, n, 1, 10) + EXP(a)/t∑((－1)^(m + 11)g(m)/2^(m + 1), m, 0, 3))　、末尾の3は、5又は7となる。
ここで、g(m)：＝ f(11, m) だわ。


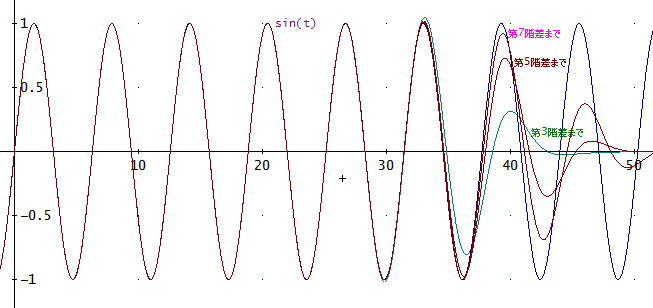
すごいわね。第3階差までで、すでに、効果が出ている」

「数値的に見ると、sin(1)≒0.8414709848、に対して、第3階差までで、0.8411141059 （相対誤差：－0.04241131464 %)
第5階差までで、0.8411152233 （－0.04227852331 %)　、第7階差までで、0.8411152777 （－0.04227205854 %)
ちなみに、第1項のΣは、0.8392302975 となっている。
なので、a＝3では、3桁まで、一致し、第3階差までで、ほぼ、十分ということじゃな。
それ以上階差をとっても、数値は、ほとんど良くならない。
そこで、a＝6として、第6階差までとってみると、0.8414697049　となり、相対誤差は、－0.0001521035559 % となって、5桁まで一致する。
さらに、a＝6のまま、第7階差までとると、0.8414700183 （相対誤差：－0.0001148592572 %）、6桁まで一致する。
第8階差までだと、0.8414700938 （－0.0001058868786 %）、やや、良くなる。
第9階差まででは、0.8414701130 （－0.0001036051378 %)、となって、改善は、ほぼ飽和状態になる。
というように、「Basicによる高速ラプラス変換」（細野敏夫著：共立出版）に記載されているように、aが有効数字の桁数の目安と考えて良いようじゃ。また、おおまかに言えば、aよりいくらか大きく階差の上限をとれば、十分と言えるのう。
なお、数式処理ソフト DERIVE（デライブ）の今回の計算は、有効数字10桁、DERIVEのモードは、近似計算モードで行った」

最終更新日　2008/9/14