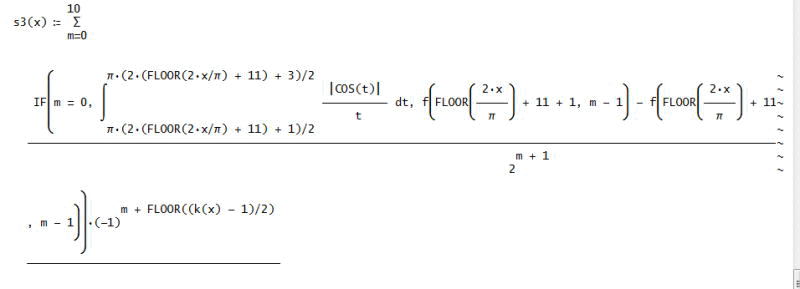数式処理ソフト　DERIVE（デライブ） de ドライブ

43．積分（３）（演算子法の応用）

１．演算子法

「数式処理ソフト DERIVE（デライブ）の第33回の記事で、常微分方程式を扱った際に、演算子法を紹介したのう」

「うん。そうだったわね。演算子法でも積分を扱えるんだ？」

「そうじゃな。ラプラス変換を使った演算子法では、原関数をf(t)、像関数をF(s)として、F(s)＝∫₀^∞ f(t) exp(－st) dt のように変換して、計算する。
積分に関係する役立ちそうな公式は、次のようなものがある。
　（「演算子法　近藤次郎著　培風館 昭和45年6月 第13刷より）
∫f(t) dt　（不定積分）　→　1/sF(s)＋1/s×limt→0（∫f(t)dt）
∫f(t)/t dt、積分範囲　t～∞ →　1/s∫F(s) ds　積分範囲　0～s
∫f(t)/t dt、積分範囲　0～t　→　1/s∫F(s) ds　積分範囲　s～∞
∫f(t)/t dt、積分範囲　0～∞→　∫F(s) ds　　　積分範囲　0～∞ 」

「すると～。第41回で出てきた余弦積分 Ci(t)＝－∫cos(t)/t dt、積分範囲　t～∞ に早速、応用できそうね。
まず、上の2番目の公式を使うと、Ci(t)の像関数は、F(s)＝－1/s∫s/(s²+1）、積分範囲は、0～s と変換できる。
これは、積分できて、F(s)＝－1/2s LN（s²+1）となる。
一方、Ci(x)は、別の表現で、次のように書ける、Ci（t）＝C（オイラー定数）＋Ln(t)－∫（1－cos(t)）/t dt、積分範囲　0～t、
この方の像関数は、C/s＋（－1/s）（C＋LN（s））－（1/s）∫（1/s－s/（s²+1））ds＝－LN（s）/s－（1/s）［LN（s）－1/2LN（s²+1）］（∞～s）
となって、第2項の積分上端は、極限をとるとゼロとなり、結局、像関数は、－1/2LN（s²+1） と求まるので、定義式から直接、ラプラス変換した像関数と一致したわ」

「うん。そのとおり。Ci（x）に関する恒等式が像関数が等しいことで間接的に証明できた感じじゃな」

２．Ci（x）の計算の見直し

「第41回で扱ったCi（x）の計算は、x＝1の計算だけじゃから、Ci（x）の計算という意味では、汎用性がないので、ここで見直しをしてみよう」

「そうね。それに計算時間もそれなりにかかるので、Ci（x）のグラフを描こうとすると大変だものね」

「うん、そういうことじゃ。まず、0＜x＜π/2 と仮定しよう。
まずは、Ci（x）＝－（S1＋S2＋Ｓ３）、S1＝∫cos(t)/t、積分範囲は、x～π/2とする。
第2項のS2＝Σ∫(COS(t)/t, t,π(2n + 1)/2,π(2n + 3)/2) で、n＝0～10までを計算すると、S2≒－0.4996377414
第3項のS3＝Σ(f(11, m)(－1)^m/2^(m + 1)) 、
ただし、f(n, m) ：＝ IF(m = 0, ∫(ABS(COS(t))/t, t, π(2n + 1)/2, π(2n + 3)/2), f(n + 1, m － 1) － f(n, m － 1)) であり、
n=11、m＝0～10として、S3≒0.02763709003 、
すると、Ci（x）≒－（S1－0.4720006513)＝－S1＋0.4720006513 となる」

「0＜x で、xがあまり大きくなければ、k＝2［2x/π］＋1、［ ］は、かっこ内の数値を超えない最大の整数を表すとして、
S1＝S1＝∫cos(t)/t、積分範囲は、x～kπ/2とする。
S2＝Σ∫(COS(t)/t, t,π(2n + 1)/2,π(2n + 3)/2) で、n＝［（k－1）/2］～［（k－1）/2］＋10
S3＝Σ(f(n, m)(－1)^m/2^(m + 1))
ただし、f(n, m) ：＝ IF(m = 0, ∫(ABS(COS(t))/t, t, π(2n + 1)/2, π(2n + 3)/2), f(n + 1, m － 1) － f(n, m － 1)) であり、
n=［（k－1）/2］＋11、m＝0～10
とすれば、いいのかしら」

「S3＝Σ(f(n, m)(－1)^（m＋［（k－1）/2］）/2^(m + 1)) とする必要があるようじゃな。c（x）＝－（S1＋S2＋S3）と定義して、
Ci（x）を1～10まで計算させてみた
([0.3374039228, 0.4229808287, 0.1196297859, －0.1409816978, －0.1900297497, －0.06805724390, 0.07669527847, 0.1224338825, 0.05534753131, －0.04545643295])
一方、Ci（x）＝γ＋LN（x）－∫（（1－cos(t)）/t dt、積分範囲は、0～xの方からCi（x）をx＝0～10まで、1刻みで計算すると、
([0.3374039228, 0.4229808287, 0.1196297860, －0.1409816978, －0.1900297496, －0.06805724390, 0.07669527847, 0.1224338825, 0.05534753132, －0.04545643302])
その差は、([0, 0, － 9.954310306×10^(－11), 0, － 1.000150654×10^(－10), 0, 0, 0, － 1.027323136×10^(－11), 7.014612131×10^(－11)])と
極めて、僅少じゃな」

「計算時間も早くなったわね。1.5秒程度でるわ。以前は、数十秒～100秒程度待たされたものね」

「そうじゃな。階差を0～10と固定する場合は、あらかじめ、下記のS3の定義式を＝で展開しておくと、毎回、再帰的関数の計算を行わずに各項の積分計算を行うだけじゃからな。ただし、展開した式は、ここには、ちょと、書ききれないぐらい長い式になるがの」


　

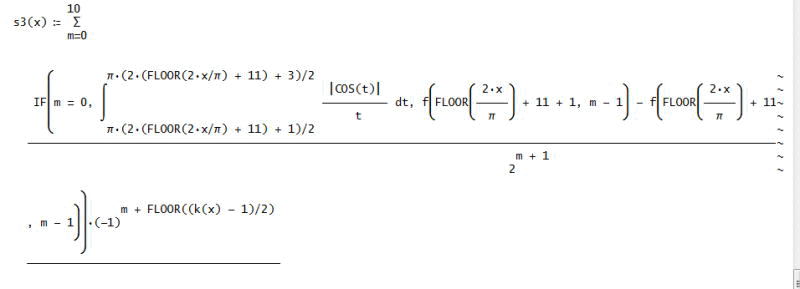
３．計算機によるラプラス逆変換

「演算子法を使って、せっかく、Ci（x）の像関数がF（s）＝－（1/2）LN（1＋s²）と求まってるのに、原関数に戻してしまうと、当然だけど、Ci（x）の式に戻るだけなのは、残念ね。
たとえば、Ci（a×x）→（1/a）F（s/a）などと、いろいろなF（s）を計算できるのに」

「そうじゃな。ラプラス逆変換は、以前書いたように、ブロムウィッチ（Bromwich）積分という複素積分になる。これを利用すると、原関数が求められるのじゃが、複素積分を自由に扱うには、関数論の知識が必須で、なかなかやっかいじゃからな。
そこでじゃ、数値的計算により原関数値を直接、求めてしまおうというのが、計算機によるラプラス逆変換という方法じゃよ」

「へ～。そんなことができるの」

「「Basicによる高速ラプラス変換」（細野敏夫著：共立出版：1984年4月　初版）に書かれているのじゃ。
ちょと、古い本じゃが、といっても、前回のベクトル解析ほど古い本ではないがの。ただし、Basic言語で計算プログラムが書かれているので、そのあたりを今回、少し、DERIVEでやってみようという訳じゃ」

「「高速」とわざわざ書いてあるということは、早いのね」

「今回、わしも驚いたのじゃが、ここでもEuler変換が高速化に活躍しているのじゃよ」

「すごいわね、Euler様は！」

「それと、Euler変換は、交代級数に適用できるのじゃが、符号が正又は負で一定している級数には適用できないのだ。
そこがなんとかならんかと思っていたのじゃが、この本の中で、ある変換を級数に施すと、交代級数に変わり、Euler変換で高速化できるという「術」が紹介されているのじゃ。
この「術」は、Wijngaarden（オランダの数学者ヴァインハーデン）変換というものじゃ」

「期待が高くなるわね」

「そうじゃのう。この本も1984年6月に購入して以来、しっかりと読んでいなかったので、ちょうど良い機会かと思うのじゃ。ただし、次回まで準備をしておきたいので、この回は、ひとまず終了したい。ともちゃん、ご苦労さんじゃった」

「じゃ、さぼらないでね」

最終更新日　2008/9/11