「重積分は、普通、大学の教養課程で出てくるので、高校ではやらないのじゃな」
「そうね。普通の積分の拡張なのね」
「まあ、そうじゃな。一次元上の積分は、単積分と呼ばれている。
ただ、単積分だから簡単とはいかない。前回に見たように計算結果が初等関数にならずに「特殊関数」になることもある。また、そもそも、そのような知られている関数が得られずに（あるいは、計算者が気がつかないこともあるじゃろうが）、数値計算のみに頼ることもある。
重積分（2重積分、3重積分・・）は、2つ以上の変数を持つ被積分関数の積分じゃな。重積分は、単積分に帰着できれば、解析的または数値的な計算が容易になる。単積分に帰着できない場合は、数値計算になるが、メッシュが多くなるので、変数の数が多い多重積分では、「モンテカルロ法」などで計算する方が計算時間と計算資源を節約できることが多いようじゃ」
「具体例で説明しようかの。3次元空間上で、関数、z（x,y）がある。これが、xy平面からのz方向の高さを表すとすると、zは、1つの曲面を表すじゃろう。
ただし、z（x,y）は、xy平面上の曲線、y＝g（x）、y＝h（x）で囲まれた領域で一意に計算可能とする。口で説明すると、わかりにくいが、下図のような範囲じゃな。
この範囲を、S と呼ぼう。
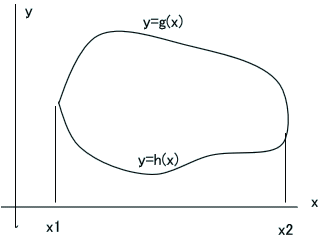
ここで、上図のようにSが定義されていたとすると、この2重積分は、∫x1x2（∫h(x)g(x) z(x,y) dy）dx と単積分に帰着できるのじゃ。
なお、このとき、範囲 Sで、常にzが非負ならば、∫∫z（x,y）dx dy は、xy平面の範囲Sと曲面との間の体積を表す」
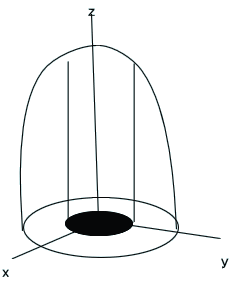
「すると、下図のような、回転楕円体、x2＋y2＋z2/h2＝1、ここで、hは、楕円体の高さとする。
このとき、原点を中心とする半径a（＜1）の円が積分範囲Sであるとき、Sの上部の回転楕円体との間の体積 V は、g(x)＝√（a2－x2）、h(x)＝0、として、対称性から、xの積分範囲を0～aとして、
V/4＝∫0a（∫0√a^2－x^2 h√（1－x2－y2） dy）dx＝πh/6 －πh(1 － a2)(3/2)/6 となるのね。DERIVEで計算すると、
yの積分がゴチャゴチャするけど、xで積分すると、きれいになって、結局、V＝（2πh/3）(1 － (1 － a2)(3/2)） と求められるという訳ね。
試しに、a＝1とすると、V＝（回転楕円体の体積の半分）＝2πh/3 で合っているわ。
「DERIVEでの計算の際、hは正実数、aは、0～1であると、「入力」メニューの「変数の変域」から定義しておくと良いの」
「2節の例のように、積分範囲が円のような場合は、円柱座標を利用すると簡単じゃ。円柱座標は、3次元空間上の点を（r，θ，z）で表すものじゃ。
平面上の座標（x,y）が（r,θ）で表すと、dxdy＝dr r dθで、x＝rcosθ、y＝rsinθから、zの式は、z＝h√(1 － r2) と単純化されるので、
V＝∫dθ∫0a h√(1 － r2) rdr＝2π×(h(1 － (1 － a2)(3/2))/3)＝（2πh/3）(1 － (1 － a2)(3/2)） と簡単に求められじゃろう」
「な～るほど。対称性をうまく利用するところがポイントね。合点です。」
「2節のような立体の重心位置を求めてご覧」
「一般的に考えて、積分範囲Sと曲面zとの間の立体の重心Gの位置をGx、Gy、Gzとすると、（立体の密度は一定として）、
Gx＝（1/V）∫∫x×z（x,y）dxdy、Gy＝（1/V）∫∫y×z（x,y）dxdy、Gz＝（1/2V）∫∫z×z（x,y）dxdy と書けるわ」
「Gzだけ、2で割っとるのは、どうしてかな？」
「それは、底面積が微小な柱（dxdy）、高さzの四角柱の重心のz座標は、z/2だから」
「そうじゃな。2節の例では、Gx＝（1/V）∫∫x×z（x,y）dxdy＝（1/V）∫cosθdθ∫0a h√(1 － r2) r2dr＝0、同様にGy＝0、
Gz＝（1/2V）∫∫z×z（x,y）dxdy＝（1/2V）∫dθ∫0a h2(1 － r2) rdr＝（1/2V）πa2h2(2 － a2)/2＝（3/8）a2h(2－a2)/(1－(1 － a2)(3/2)) 、
ここで、a＝1とすると、Gz＝3h/8 となる」
「第38回の記事の球欠の重心位置の計算の中に出てきた半球の場合（3r/8：ここでrは、半径）の結果と一致するわね」
「体積、重心と来ると、次は、表面積というのが自然じゃな」
「xy平面上の微小長方形 （x，y）－（x+dx，y）－（x+dx，y+dy）－（x，y+dy）を底面とする四角柱の曲面zとの交点をP、Q、R、Tとすると、
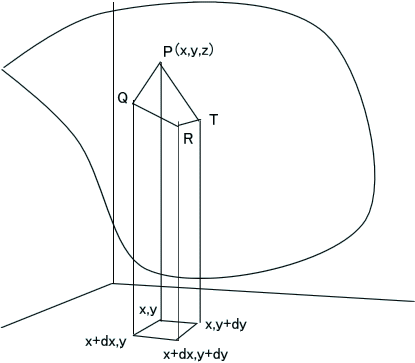
P：z（x,y）、Q：z（x+dx，y）＝z＋（∂z/∂x）dx、R：z（x+dx，y+dy）＝z＋（∂z/∂x）dx＋（∂z/∂y）dy、T：z（x，y+dy）＝z＋（∂z/∂y）dy なので、
3次元空間座標は、P（x,y,z）、Q（x+dx,y,z＋（∂z/∂x）dx）、R（x+dx,y+dy,z＋（∂z/∂x）dx＋（∂z/∂y）dy）、T（x,y+dy,z＋（∂z/∂y）dy）と決定され、
微小曲面PQRTの倍面積は、ベクトル｜PQ×PR｜＋｜PR×PT｜であることが、第39回の記事から分かる。
具体的に計算すると、｜PQ×PR｜＝｜PR×PT｜＝√(（∂z/∂x）2 + （∂z/∂y）2 + 1) dxdy となるので、
結局、表面積は、∫∫√(（∂z/∂x）2 + （∂z/∂y）2 + 1) dxdy 」
「よっしゃ。OKじゃな。
数式処理ソフト DERIVE（デライブ）の第39回の記事が役に立ったな」
最終更新日 2008/9/13
