数式処理ソフト DERIVE(デライブ) de ドライブ
41.積分(1)(単積分、数値積分とEuler変換)
1.「ベクトル」解析って何?
「数式処理ソフト DERIVE(デライブ)の前回は、「ともちゃん大活躍の巻」じゃったな。ほほ」
 「おかしくはないわよ! ところで、ベクトル解析って、なにに役立つの?」
「おかしくはないわよ! ところで、ベクトル解析って、なにに役立つの?」
「そうじゃのう。そもそも、高校数学で習う「微積分」を大学では、「解析学」というような名前で、ε-δ論法のような基礎的なことから、あらためて学ぶことになるんじゃ。そこでじゃ。高校での微積分の対象は、何じゃな?」
「関数でしょ」
「そう。「ベクトル解析」というのは、関数の代わりにベクトルを対象として、その微積分を扱うものなんじゃ」
「でも、ベクトルというのは、その要素が関数(ただの数字もあるけどさ)でしょ。
関数の微積分を知っていれば、用が足りるのじゃないかしら」
「うん。ともちゃんのいうことにも一理あるがの。
このHPでは、数学というより、おもに物理的なことを中心に考えてるから、余計にそうなるのじゃが、法則をベクトルとその微分、積分を含む方程式で表現すると「美しい」というかじゃ。何というか、法則の見通しが良くなるという御利益が感じられるということはあるじゃろうな」
「ふ~ん。久々に「ゴリヤク」登場ね。で、ベクトル解析(2)の内容は何にするの?」
「ベクトルの微分は、前にもいくつか出てきたので、積分を取り上げようかの」
2.積分
 「ちょっと待って。あたし、今、気がついたんだけど、このHP、積分って、あんまり、出てこなかったわね」
「ちょっと待って。あたし、今、気がついたんだけど、このHP、積分って、あんまり、出てこなかったわね」
「う~ん。なるほど、そう言われると、わしとしたことが、うっかりしておったな。
ではじゃ、遅ればせながら、今回は、DERIVEで、ベクトルでない(普通の)関数の積分を調べることにしよう」
「積分には、不定積分と定積分があるわね」
「そうじゃな。一般に1変数関数f(x)の不定積分を∫f(x)dxと書くと、DERIVEでは、f(x)を入力後に、解析メニューから「積分」を指示すると、∫(f(x),
x, c) のようになる。ここで、cは、積分定数じゃ。∫(関数、変数、積分定数)という新しい記法が出てきたの。
たとえば、関数が、x2+1でやってごらん」
「x3/3 + x + c になったわ。正しいわね。定積分の場合も、ほとんど、同じね」
「そういうことじゃ。解析メニューから積分を選択して、ダイアログボックスで定積分を選んでから、積分範囲を入力することになる。1/(x2+1)を0~1で積分してご覧」
「そうすると、π/4≒0.7853981633 となった。積分範囲が無限大の場合は、どうするのかしら」
「同じ関数の例で、1/(x2+1)を0~+∞の範囲で積分するときはじゃ。上限の∞は、下部のパレットから∞を選べばいいんじゃよ」
「こんどは、π/2≒1.570796326 と出たわ。じゃ、-∞~+∞とすると、確かにπになる。な~るほど。カンタン、カンタン、という感じね」
「ただの、微分と違って、初等関数であっても、その積分は、初等関数にならない場合があるんで、困るのじゃな」
「具体的にはどんなのかしら」
「ガウスの正規分布関数、(1/√2π)exp(-x2/2)などは、典型的な例じゃな。積分範囲、-∞~+∞で、この値は、1となる」
「なるほど。その積分範囲での値は、出るけど、不定積分だと、ERF(√2x/2)/2 となって、知らない関数が出てくるのね」
「ERF(x)は、∫(2/√π)exp(-x2)dx、積分範囲は、0~x じゃ。ERF(∞)=1となる。
ただ、こういう特殊関数は、ほとんど同じじゃが係数等が違っている定義があるので、注意が必要じゃ。
DERIVEでは、このERF()を error function といっておるが、「岩波数学辞典」では、∫exp(-x2)dx 、積分範囲 0~x を誤差関数と呼んでいて、今回の積分は、「確率積分」と呼んでいる」
「他に、どんな関数があるのかしら?」
「たとえば、正弦積分 Si(x)=∫(SIN(t)/t, t, 0, x)、余弦積分Ci(x)=-∫(cos(t)/t,t,x,∞)など、多くあるの。
こういった「特殊関数」は、たいてい、ある種の微分方程式を満たしている。逆に、微分方程式からこういった特殊関数が定義されるとも言えるようだの。詳しくは説明できんがの。
さっき挙げた、岩波の数学辞典などの公式表を見ると、めまいがしそうなほどの数の関数が分類されているじゃろう」
「ホント。オドロキ!」
3.数値積分
「で、こういった積分は、特殊関数で表現できる場合も、できない場合も、数値が必要になれば、数値計算に頼る必要があるのは分かるじゃろう」
 「DERIVEでは、=ではなくて、≒の方のボタンね」
「DERIVEでは、=ではなくて、≒の方のボタンね」
「そうじゃ。ただ、積分する関数が単調な関数ではなくて、正負の値で激しく振動したり、積分範囲が∞を含んだりしているときは、正しい値が得られない場合もあるのじゃ。よって、注意が必要じゃな。たとえば、先のCi(x)じゃな。Ci(1)を求めてご覧」
「Ci(1)≒-1.249134221 となったわ。でも、約40秒かかったわ」
「公式集によれば、Ci(x)=-∫(cos(t)/t,t,x,∞)は、次のように変換できる。C+Ln(x)-∫((1-cos(t))/t,t,0,x)、ここでCは、オイラー定数≒0.5772156649
じゃ。
オイラー定数は、DERIVEでは、γで表しているが、これを使うと、Ci(1)≒0.3374039228 となって、全然違うことが分かるじゃろう」
「えー! じゃ、DERIVEで直接求める時は、どうしたらいいのかしら?」
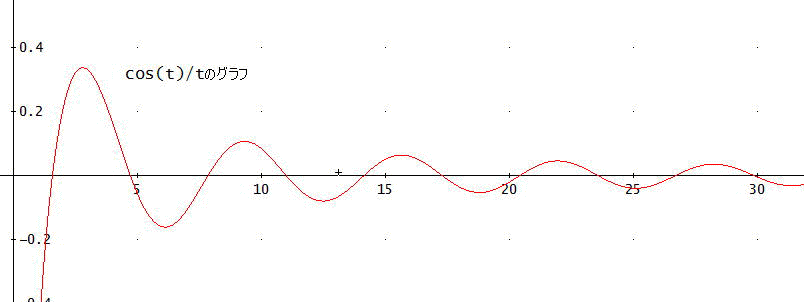
「今回のケースでは、Ci(1)=-((1~π/2の積分)+(π/2~3π/2の積分)+(3π/2~5π/2の積分)+・・)と考えた時、cos(t)が周期πで正負が交代するので、第2項目以降は、正負の交代級数となることに注目する事じゃな。
交代級数は、一般に収束が遅いので、加速する必要がある」
4.正負の交代級数の和を加速して求めるEuler 変換
 「Euler (オイラー)変換って、聞いたことがないわ」
「Euler (オイラー)変換って、聞いたことがないわ」
「まずは、「計算数学夜話(森口繁一著:日本評論社刊:昭和53年4月10日初版)」に従って、Euler変換を紹介しつつ、無限級数 S=1-1/2+1/3-1/4・・を求めることで、その方法と加速を試してみることにしよう。
なお、原理は、同書に委ねるとするが、
Euler 変換とは、S=a0/2-Δa0/4+Δ2a0/8-Δ3a0/16+Δ4a0/32・・として交代級数an(正実数と考えている)の和を求める方法をいうのじゃ。
ここで、a0=1(級数の初項)、Δは、差分演算子じゃ」
「差分演算子って何?」
「Δa0=a1-a0、Δ2a0=Δa1-Δa0=a2-2a1+a0、・・と定義されるものじゃよ。
ベクトル解析で出てきたナブラ ▽やラプラシアン △とはまったく関係がないので誤解のないようにな」
「これをDERIVEでどう計算すればいいのかしらね」
「まずは、f(n,m)という関数を定義するのじゃが、m=0のときは、an であり、そうでないときは、f(n+1,m-1)-f(n,m-1) のように再帰的に定義するところがポイントじゃな、mを階差と呼ぶ。Δmanと書いて、anの第m階差と呼ぶのじゃな。
第ゼロ階差は、級数の各項それ自身じゃ」
「以前出てきた、再帰的定義関数の応用ね。f(n,m):=IF(m = 0,1/n,f(n + 1, m - 1) - f(n, m - 1))、今回は、nが1から始まるのね」
「そう、そこで、S≒Σ(-1)mf(n, m)/2(m + 1)) と近似する。試しに、n=1、Σの範囲を m=0~10として計算してご覧」
「S≒0.6931092453 となったわ」
「真の値は、Ln(2)≒0.69314718055994530941 じゃから、4桁まで、合っている。今は、初項からいきなり、Euler変換を使ったが、森口先生の本では、第11項目からEuler変換を適用している。(ここでは、計算桁数を20桁としている)
このときは、まず、正直にΣ(-1)(n+1)f(n,0)でn=1~10を求める。それは、S1≒0.64563492063492063492 となる。次にS2=Σ(-1)mf(n, m)/2(m + 1)) で、n=11と置いて、m=0~10までを計算する。その値は、S2≒0.047512259882253109807 、よって、S=S1+S2≒0.69314718051717374472となる。青字の部分までが真値と一致しておる。初項から21項までしか使用していないにもかかわらず、10桁の精度が出ておるのじゃ」
「ははぁ。恐れ入谷の鬼子母神(あたしとしたことがこの言い方 古!)。
試しに1000項までを正直に計算しても、0.69264743055982030966 で、2桁しか合わないものね」
「同書によると、100万項まで計算しないと10桁の精度は出ないそうじゃよ」
※ 「Eulerの変換」については、岩波数学辞典 第3版 級数の項、P213にも記載があります。
5.Ci(x)の計算にEuler変換を利用
「さて、お待ちかねの Ci(1)を計算してみよう。Ci(1)=-(S1+S2+S3)として、
まずは、S1=∫cos(t)/t dt で、積分範囲を1~π/2とすると、S1≒0.1345967285 。
S2=Σ∫(COS(t)/t, t,π(2n + 1)/2,π(2n + 3)/2) で、n=0~10までを計算すると、S2≒-0.4996377414
となる。
最後にS3を計算するのじゃが、ともちゃん、やってご覧」
 「えーと。まず、f(n, m):= IF(m = 0, ∫(COS(t)/t, t, π(2n + 1)/2, π(2n + 3)/2), f(n + 1, m - 1) - f(n, m - 1)) と定義して、n=11で計算するとして、S3=Σ(f(11, m)(-1)^m/2^(m + 1)) でどうかしら、ここで、mは、0~10までを動くとする」
「えーと。まず、f(n, m):= IF(m = 0, ∫(COS(t)/t, t, π(2n + 1)/2, π(2n + 3)/2), f(n + 1, m - 1) - f(n, m - 1)) と定義して、n=11で計算するとして、S3=Σ(f(11, m)(-1)^m/2^(m + 1)) でどうかしら、ここで、mは、0~10までを動くとする」
「惜しいのう。わしも、そこで引っかかったのじゃが、先のEuler変換の式は、交代級数の各項自身を「正」という前提で書いてあるので、正しくは、
f(n, m):= IF(m = 0, ∫ABS(COS(t)/t, t, π(2n + 1)/2,π(2n + 3)/2))), f(n +
1, m - 1) - f(n, m - 1)) のように、cos(t)の絶対値をとる必要があるのじゃ」
「はぁ、すると、上式で、n=11として、S3≒0.02763709003 となるので、Ci(1)=-(S1+S2+S3)≒0.3374039228 となる!」
「Ci(1)=C+Ln(x)-∫((1-cos(t))/t,t,0,x)から計算した値と最後の桁まで、合っておるな」
「これぞ、Euler変換の威力!だわ」
6.計算値のチェック
 「でも、あれね。今回のCi(x)のような例があると、DERIVEの計算結果を頭から信用できなくなるわね」
「でも、あれね。今回のCi(x)のような例があると、DERIVEの計算結果を頭から信用できなくなるわね」
「残念ながら、そのようじゃな」
「じゃ、どうしたらいいのかしら?」
「一番良い方法は、2通りの方法で計算してみるのが良いじゃろうな。先ほどの例のようにな」
「でも、普通は、そうは、いかないわよね」
「うん。そのときは、積分範囲を少しずつ、変化させて、値の変化をみるとかを考えることじゃな。先ほどの積分余弦では、積分上端の∞の代わりに、1~1000まで、100ずつ変化させて、計算値を数列にしてみた。
[0, 0.3330166880, 0.3377365200, 0.3392693938, 0.3396553987, 0.3393925381,
0.3387613486, 0.3379900455, 0.3372701290, 0.3367427122]
どうじゃな。最後の積分上端が1001の計算値は、真値と2桁目までは、合っているの」
「変ねー。無限大にすると、-1.249134221 となってしまうのに」
「そうじゃな。同程度の正負の数値の引き算による丸め誤差の累積の結果じゃないかな。詳しくは分からないが。いずれにしても、被積分関数のグラフを描いてみて、検討することも役に立つの」
最終更新日 2008/9/10



 「おかしくはないわよ! ところで、ベクトル解析って、なにに役立つの?」
「おかしくはないわよ! ところで、ベクトル解析って、なにに役立つの?」
