「数式処理ソフト DERIVE（デライブ）では、原関数 sin（t）を例題にして、FILT（高速ラプラス逆変換）を試みてきたが、ここで、あらためて、ラプラス変換について、まとめておこうと思うのじゃ。まずは、極限値じゃ」
「つまり、像関数から、原関数のt＝∞の状態が分かるってこと？」
「そうじゃ。「演算子法」（近藤次郎著：培風館：昭和45年初版第13刷）（以下「近藤本」と呼ぶ）によれば、
lim（t→∞） f（t）が存在すれば、それは、lim（s→0） s×F（s）
lim（t→+0） f（t）が存在すれば、それは、lim（s→∞） s×F（s）
なのじゃ」
「でも、前回まで取り上げているsin（t）では、像関数は、F（s）＝1/（s^2+1）なので、lim（s→0） s×F（s）＝0になってしまうじゃないの。
そうか、lim（t→∞）sin（t）は、一つに定まらないからか」
「そのようじゃな。近藤本のP62には、F（s）の極について、分類している。
（１）すべての極が虚軸の左側にあれば、lim（t→∞） f（t）＝0
（２）すべての極が虚軸上または左側にあり、かつ、虚軸上に極があっても単極ならば、lim（t→∞） f（t）＝有界
（３）極のうち虚軸上に重複極があるか、または、虚軸の右側に一つでも極があれば、lim（t→∞） f（t）＝∞」
「その「極（きょく）」って、何なの？」
「やっぱり、というか、案の定というか、ここは、すこしは、複素関数について、調べておく必要が出てきたようじゃな」
「うっそぉ！ 複素関数は、必要ないって、最初に言ってたんじゃないの」
「ま、できるだけ、触れないでいきたいな、という願望だったんじゃが。結局は、そうは問屋が卸さなかったということじゃな。
さて、複素数や複素平面は知っているとみなして進めよう。複素関数とは、簡単に言うと、複素数（慣例に従って、zで表す）の関数ω（z）をいう。
これに対し、今までの関数を区別して、「実関数」と呼ぶことがある。
ところで、これ以降、考える複素関数は、任意のω（z）ではなくて、「正則」な関数だけとするので、まずは、「正則（せいそく）」ということを説明せねばならんの」
「つまり、なんでもいいってもんじゃない訳ね。えーと。まさのり、じゃない！「正則」って、いったい、どんな条件なの？」
「ω（z）の実部をuで、虚部をvで表す。ω（z）＝u（x，y）＋#i v（x，y） じゃ。虚数単位 i は、このままでは、見にくいので、DERIVEにならって、#i
と書くことにしよう。
ここで、ωのzによる「微分」（全微分）を定義する。
dω/dz＝lim（δ→0）（ω（z＋δ）－ω（z））/δ、ただし、ここで、δは、複素数とする。
複素平面上の任意の方向から、点zに近づけていくというようなイメージじゃな。
たとえば、ω＝z^2+1では、z＝x＋y #i、δ＝α＋β #i として、（x、y等は実数）
dω/dz＝lim（α→0、β→0）（2αx － 2βy + α^2 － β^2 + 2 #i (βx + α(y + β))/（α＋β #i）
＝lim（α→0、β→0の順序に関わりなく）（2x + α + #i(2y + β)＝2x＋2 #i y＝2z となる。
ここで、一般には、極限をとる順序で、その値が変わることがある。変わらない場合、ω（z）は、点zで「正則」である、というのじゃ。
また、正則な点を「正則点」、正則点でない点を「特異点」と呼ぶ」
「ふ～ん。じゃ、いったい、どんな関数が正則じゃないの？」
「具体例を挙げる前に注意しておくと、実関数でも微分可能でない点を持つものもあったのじゃ。
たとえば、y＝｜x｜のようなものは、連続関数ではあるが、x＝0で異なる微分係数を持つ。
さらに、連続関数で、しかも、至るところ微分可能でない点を持つ関数もある。しかし、普通は、そのような「病的な」関数は、考えないがの。
ところで、複素関数で、正則でない点を持つ関数の例を挙げると、たとえば、ω＝x－#i y のようなものじゃな。
dω/dz＝lim（α→0、β→0）（(x + α － #i(y + β)－（x－#i y））/（α＋β #i）
＝lim（α→0、β→0）（(α^2 － β^2)/(α^2 + β^2) － 2#iαβ/(α^2 + β^2)）
ところが、容易に分かるが、α→0では、－1、β→0では、＋1と違うのじゃ。
z＝x＋#i yには、何の条件も付けていないので、このω（z）＝x－#i y は、至る所、「正則」ではない、ということになる」
「そんな簡単な関数が正則じゃないなんて、信じられないわ。
ところで、もっと、簡単に見分ける方法はないものなの？」
「その見分け方じゃ。
前節に述べたように、ω（z）を実部と虚部に分けて、ω＝u（x，y）＋#i v（x，y）としたとき、
dω/dz＝lim（α→0、β→0）（u（x＋α，y＋β）－u（x，y））＋#i （v（x＋α，y＋β）－v（x，y））/（α＋β #i））
＝lim（α→0、β→0）
（（αu（x＋α，y＋β）－αu（x，y）＋βv（x＋α，y＋β）－βv（x，y））－#i（βu（x＋α，y＋β）
－βu（x，y）＋αv（x＋α，y＋β）－αv（x，y））/（α2＋β2）
lim（β→0→α→0）与式＝（α∂u/∂x×α＋#i α∂v/∂x×α）/（α2）＝∂u/∂x＋#i ∂v/∂x
一方、同様に、
lim（α→0→β→0）与式＝∂v/∂y－#i ∂u/∂y となる。
このとき、ωがzで正則ならば、双方が等しい必要があるので、
∂u/∂x＝∂v/∂y
∂u/∂y＝－∂v/∂x
が成立する。この関係式を「コーシー・リーマンの関係式（または微分方程式）」という呼ぶのじゃ。
たとえば、ω＝z2+1ならば、u＝x^2 － y^2 + 1、v＝2xy なので、∂u/∂x＝2x＝∂v/∂y、∂u/∂y＝－2y＝－∂v/∂x
となるから、確かに、この関係式が満たされていることが確認できるじゃろう。
一般に、ω（z）がzの複素平面上の一部又は全部の点で正則であるとき、その領域で正則であるといい、ωを正則関数という」
「なるほど。さっきの、ω＝ｘ－#i yは、∂u/∂x＝1≠∂v/∂y＝－1、∂u/∂y＝0＝－∂v/∂x となって、関係式の一部が満たされないのね」
「ちなみに、コーシーとは、フランスの数学者「Cauchy 1789－1857」、リーマンはドイツの数学者「Riemann 1826－1866」の名前から来ているのじゃ」
「「コーシーの積分定理」を書く前に、「線積分」、「面積分」について、説明しよう。
この節では、複素平面ではない、一般の2次元 xy平面を考える。
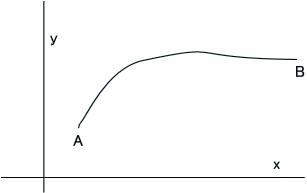
下図のように、点Aから点Bまで、曲線があるとする。この曲線をCと呼ぼう。Cは、x＝α（t）、y＝β（t）のようにtの一価関数で、考えている範囲内で微分可能な連続関数とする。t＝t1～t2で、点AからBまでを動くとする。
また、同じ平面上で定義された任意のスカラー関数をf＝f（x，y）とする。
このとき、∫（t＝t1～t2）f（α（t），β（t））（dα/dt）dt が存在すれば、これを 曲線C上のf（x，y）の線積分と呼ぶ。
これは、∫f（x，y）dx とも書かれる。
また、同様に、∫（t＝t1～t2）f（α（t），β（t））（dβ/dt）dt＝∫f（x，y）dy も曲線C上のf（x，y）の線積分と呼ばれる。
なお、曲線Cは、両端が閉じた曲線でも、下図のように開いた曲線でもよい
上の定義は、（「物理学への数学的序説」（荒木源太郎著：みすず書房：昭和42年）（以下「荒木本」という。）による」
「なんとなく、イメージが湧かないわね。
そもそも、その2つの定義式に従って計算した値は、A、B、Cが同じならば、同じものになるのかしら？」
「一般のf（x，y）では、x＝yでない限りは、違う値になるのう」
「前にベクトル解析でやった「線積分」とは違うの？」
「ベクトル解析で出てきた「線積分」は、「（接線）線積分」というものじゃ。ベクトル関数F（x，y）＝［U（x，y），V（x，y）］に対して、
下図のように、∫F・ds＝∫Fcosθds＝∫［U（x，y），V（x，y）］・［dx，dy］＝∫（U（x，y）dx＋V（x，y））dy と定義されるものじゃ。
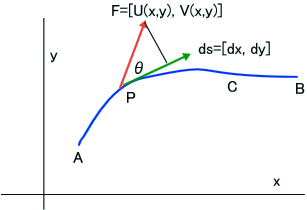
もちろん、先に出てきた、「線積分」のようにパラメータ t を使って、∫（U（x，y）（dx/dt）＋V（x，y）（dy/dt））dt と計算してもよい。実用上は、パラメータを使った方が計算しやすいことも多いじゃろう」
「何か、例を出して欲しいよね」
「接線線積分の例で一番分かりやすいのは、ベクトルFを曲線C上の質点に加わる「力」として、Fに抗して、質点をC上でゆっくり動かすときに要するエネルギーとの関係じゃろうな。
このとき、質点には、接線方向の力（F ｃｏｓθ）と曲線に垂直方向の力（F sinθ）とが働くが、曲線と質点との摩擦が無視できれば、接線方向の力のみを考えればよいので、エネルギーをE、dsを接線ベクトルとして、dE＝－F・ds＝－（Udx＋Vdy） じゃ。
Fに負号が付いているのは、Fとは逆方向に力を加えるためじゃな。（作用－反作用の法則）
ゆえに、E＝－∫（Udx＋Vdy）が点AからBまで移動する際に必要なエネルギーじゃ。
このEは、F、A、Bが同じでも、一般に、曲線Cによって値が異なるが、もし、力 Fがスカラーポテンシャルφから、F＝－▽φと導かれる場合は、
dE＝（∂φ/∂x dx＋∂φ/∂y dy） となるので、この線積分は、Cによらずに計算できて、
∫（点A～B）（∂φ/∂x dx＋∂φ/∂y dy）＝φ（B）－φ（A） となり、始点と終点のポテンシャルだけで、要するエネルギーが求まるのじゃ。
これを、山にたとえれば、富士山に登るのに、人体に働く力は重力のみとすれば、力は、重力ポテンシャルから導かれるため、特定の登山口から頂上へのどの道をたどっても要するエネルギーは同じということじゃ。ま、実際は、急勾配の道やものすごく遠回りの道の方がくたびれるとは思うがの。
なお、2次元平面上では、以前出てきた「ストークスの定理」は、次の形になるのじゃ。∫（Udx＋Vdy）＝∫∫（∂V/∂x －∂U/∂y）dxdy
」
「前節で最初に出てきた「線積分」の定義は、次のようなものじゃった。
∫（t＝t1～t2）f（α（t），β（t））（dα/dt）dt＝∫f（x，y）dx、∫（t＝t1～t2）f（α（t），β（t））（dβ/dt）dt＝∫f（x，y）dy
これを真似て、複素関数ω＝u（x，y）＋#i v（x，y）の線積分を、
∫ωdz＝∫ωdx＋∫ω（#i dy）＝∫（u＋#i v）dx＋∫（u＋#i v）（#i dy）＝∫（u dx－v dy）＋#i ∫（v dx＋u ｄｙ）、
と定義し、これを曲線Cに沿ってのωの複素積分という。
形式的には、ω×（dx＋#i dy）として、複素数同士の乗算により、＝（u dx－v dy）＋#i ∫（v dx＋u ｄｙ）としても、導かれる。
この定義は、Cが閉曲線の場合、次節に記載する「コーシーの積分定理」により積分値がゼロとなるように（うまく）定義されていると言っても良いじゃろうな」
「さて、ここで、特別ではあるけれど、実用上重要な場合、すなわち、曲線Cが閉曲線の時を考える。
このとき、第4節末に記載の2次元のストークスの定理（グリーンの定理ともいう）、
∫（Udx＋Vdy）＝∫∫（∂V/∂x －∂U/∂y）dxdyから、∫ωdzは、
∫（u dx－v dy）＋#i∫（v dx＋u ｄｙ）＝－∫∫（∂v/∂x＋∂u/∂y）dxdy＋#i∫∫（∂v/∂x－∂u/∂y）dxdy
となるが、
第1項、第2項とも、コーシー・リーマンの関係式からゼロとなる。
すなわち、Cが閉曲線の時は、Cの形状や位置によらずに、線積分∫ω（z）dz＝0 となる。これを「コーシーの積分定理」と呼ぶのじゃ。
ただし、特異点が領域に含まれているときは、一般には、ゼロにはならない。なぜならば、面積分において、被積分関数の∂v/∂xなどが定義できないので、線積分の値がゼロとなるとは必ずしも言えないからじゃな」
「へー。大変なものね。で、まいど、なんだけど、例題を出してね」
「たとえば、ω＝z2を考えると、zの全域で正則じゃ。今、原点を中心とした円（半径a）を閉曲線Cとしたとき、線積分 ∫ωdzは、どうなるか」
「∫ωdzで、z＝x＋#i y＝a×exp（#i θ）として、dz＝a #i exp（#i θ）dθ、
∫ωdz＝∫a2exp(#i 2θ）×a#i exp（#i θ）dθ＝∫a3#i exp（#i 3θ）dθ＝0 だわ」
「もし、曲線Cが、原点を中心とする楕円の場合は、どうなるかの」
「そうね。z＝x＋#i y＝aｃｏｓθ＋#i bsinθ、dz＝（－asinθ＋#i bｃｏｓθ） dθより、
∫ωdz＝∫(－ (a^3 + 2ab^2)SIN(θ)COS(θ)^2 + ab^2SIN(θ)^3 + #i(3a^2bCOS(θ)^3
－ COS(θ)(b^3SIN(θ)^2 + 2a^2b)))＝0 となって、やっぱり、0となるわ」
「では、原点を中心とした円（半径a）を閉曲線Cとしたとき、ω＝1/zではどうなるかの」
「うんと、∫ωdz＝∫（1/a）exp（－#iθ）×a#i exp（#i θ）dθ＝2π#i となって、ゼロにはならないわ。
変ね？、そうか、z＝0は正則点ではないからね」
「そうじゃな。下図でC1を半径aの円として、C2を半径b（<a）の円とする。このとき、積分路を（a，0）からC1に沿って反時計回りにとり（a，0）に戻り、さらにC2を時計回りに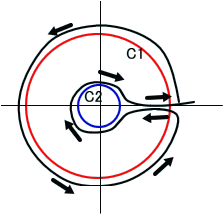
回って、（a，0）に戻るようにとる。C1に沿っての部分は、#i である。一方、C2に沿っての部分は、∫（1/b）exp（－#iθ）×b#i exp（#i
θ）dθ、ただし、θは、－2π～0で積分すると、－2π#iとなり、さらに、C1とC2を結ぶ積分路では、往復のため、打ち消し合ってしまうため、ゼロなので、bは、いくらでも小さく取れるので、原点をのぞいた正則領域では、∫ωdz＝0
となる。」
「ついでだけど、ω＝1/zは、コーシー・リーマンの関係式をしっかりと満たしているわね」
「と、まあ、ここまで、やってきたんじゃが、ラプラス逆変換までは、まだ、道は遠いのう。
ここらで、いったんお開きにして、次回、この続きをやっていくことにしよう。
ともちゃんも、お疲れさんじゃったな」
最終更新日 2008/9/25
