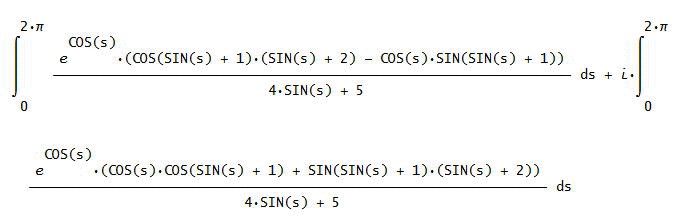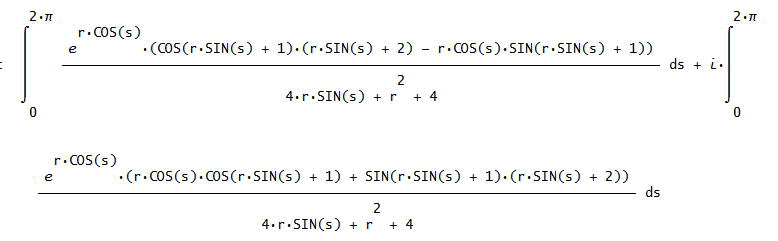数式処理ソフト　DERIVE（デライブ） de ドライブ

４７．複素関数（２）（正則、特異点、極、コーシーの積分公式）

１．正則関数

「ω（z）＝u（x，y）＋#i v（x，y） が正則関数であるとき、 zω（z）も正則関数であるか、どうかを確認してご覧」

「∂(u(x, y), x, 1) － ∂(v(x, y), y, 1) = 0、∂(u(x, y), y, 1) + ∂(v(x, y), x, 1) = 0　：　コーシー・リーマンの関係式から
容易に、∂（u（x，y），x，2）＋∂（u(x, y), y,2）＝0、∂（v（x，y），x，2）＋∂（v(x, y), y,2）＝0 ：「ラプラスの方程式」が得られる。
zω（z）＝（x u（x，y）－y v（x，y））＋#i（x v（x，y）＋y u（x，y））なので、上記の方程式のu（x，y）、v（x，y）をそれぞれ、
x u（x，y）－y v（x，y）、x v（x，y）＋y u（x，y） に置き換えると、いずれも、恒等的にゼロとなることが分かるので、
zω（z）もコーシー・リーマンの関係式を満たすっていのうはどう」

「そうじゃな。ω×定数も正則、また、η（z）をω（z）と同一の領域で正則関数であるとすると、ω（z）±η（z）もまた、正則であることが明らかじゃ。
このことと、上で証明してもらった、zω（z）が正則であることから、任意のzの整次式をa₀＋a₁z＋a₂z²＋・・としたとき、（整次式）×ω（z）もまた、正則関数であることが分かる。ここで、a₀、a₁等は、実係数とする。では、ω/zは、どうじゃな？」

「ω/z＝xu(x, y)/(x^2 + y^2) + yv(x, y)/(x^2 + y^2) + π(xv(x, y) － yu(x, y))/(x^2 + y^2) として、同様に計算すると、少し、ゴチャゴチャするけど、原点をのぞいて、ラプラスの方程式をそれぞれが満たす、すなわち、正則関数であることが分かったわ」

「と、ここまでをまとめると、
（１）αω（z）は正則関数。ここで、αは、ゼロでない任意の複素数。
（２）ω×（（z）の整次式）は、正則関数。
（３）ω（z）/z は、正則関数。
（４）他の正則関数をη（z）とすると、ω（z）±η（z）
（５）ω（z－α） は、正則関数」

「そうね、あとは、正則関数同士の積は、正則関数であるかどうか、だわね」

「これは、Yesだの。これについては、後日、触れようかの」

「あの、実数の初等関数は、そのまま、複素関数に拡張できるのかしら？」

「基本的な関数は、そうじゃな。
指数関数 exp（z）＝exp（x＋#i y）＝exp（x）（cos（y）＋#i sin（y））
三角関数 sin（z）＝（exp（#i z）－exp（－#i z））/2#i、cos（z）＝（exp（#i z）＋exp（－#i z））/2 など
対数関数 ln（z）＝ln｜z｜＋#i （θ＋2nπ）、n＝0、±1、±2・・
　ここで、対数関数について、注意すべきは、zの主偏角θ（0～2π）により、無限の異なった値があり得ることじゃ。
これは、ln（z）をexp（z）の逆関数として導入しているからじゃな。
　ln（－3）＝ln（3）＋#i（π＋2nπ）、主値は、ln（3）＋#i となって、負数の対数は、複素数となる。もし、ln（z）が実数となるようにするには、zが実数である（x＞0）である必要がある。zが複素数の場合は、ln（3＋#i）＝1/2 ln（10）＋#i（θ＋2nπ）、tan（θ）＝1/3、となる」

「無理関数は、どうなるのかな」

「たとえば、√zなどじゃな。ω＝√zとして、z＝r exp（#i θ）、θ＝0～2π、r>0、から
ω＝√r exp（#i θ/2）、ω平面で考えると、zの偏角θが0～2πで、ωの偏角は、0～πの範囲となる。
これについても、後日、触れることにしよう」

２．零点、特異点、極、分岐点など

「複素関数、ω（z）において、dω/dzが一意に定義できない点が特異点じゃった。いろいろなタイプの特異点がある。
「科学技術者のための数学ハンドブック」（Tai I. Chow 著：鈴木増雄・香取眞理・羽田野直道・野々村禎彦訳：朝倉書店：2002年8月初版）（以下「ハンドブック」という。）に従って分類すると、
「零点」－－特異点じゃないが、ここに挙げておこう。ω（z0）＝0となるz0を零点というのじゃ」

「れいてん！」

「れいてん、ではなくて、ゼロテンと呼んで欲しいのう。
たとえば、ω＝1＋z² は、zが実数の範囲では、零点はないが、複素数の範囲では、すでに、よく知っているようにz＝±#i が零点になる。
さて、特異点じゃが、
「孤立特異点」－－たとえば、ω＝1/z のように、z＝0は、特異点じゃが、z＝0の近くのどこをとっても正則点であるような孤立した特異点をいう。
「極」－－（ ようやく、出てきたのう）　特異点を、z0としたとき、lim（ z－z0）ⁿ ω（z－z0）＝ゼロをのぞく有限な値となるとき、z0をn位の極と呼ぶ。特にn＝1であれば、「単極」という。上の1/zのz＝0は、単極でもある。
「真性特異点」－－ln（z－z0）のz＝z0のように、（z－z0）^nでnをどれほど大きくとっても、lim（z－z0）^n ln（z－z0）＝有限でない、となるような特異点のことじゃ」

「えーと、ω＝1/（1＋z²）のz＝±#i は、極だけど、第何位の極というのかな？」

「うん。そのような分母、分子がzの整次式である、有理関数は、分母の整次式＝0とおいた方程式の根により、分母を（z－z₀）（z－z₁）・・（z－z_n）のように因数分解できることは、明らかじゃな。このように因数分解し、部分分数式の和に分解する。このとき、正則関数の和もまた、正則関数であることを思いだそう。
たとえば、ω＝1/（1＋z²）＝1/（2（1－#i z））＋1/（2（1＋#i z）、このように分解すると、第1項は、lim（z－（－#i））×1/（2（1－#i z））＝#i/2、すなわち、z＝－#iは、第1位の極と言うことになる。2重根の場合は、分解した分母が（z－z_k）² の形になることもある。この場合、z＝z_kは、第2位の極となる。3重根以上の場合も同様じゃ。
このほか、「ハンドブック」では、「除去可能特異点」として、ω＝sin（z）/z の例を挙げている。除去可能特異点とは、lim （z→z0）ω（z）＝有限の値を持つ特異点を言うそうじゃ。この例では、z＝0は、特異点じゃが、lim （z→0）sin（z）/z＝1 となるので、除去可能である。
「無限遠点における特異点」とは、z→∞で、ω→∞となる関数は、z＝∞に特異点があるという。たとえば、ω＝z²では、z→∞で2位の極を持つ。
なぜならば、ω（1/z）＝1/z² となるので明らかに、z＝0は、第2位の特異点となるからじゃな」

３．コーシーの積分公式

「数式処理ソフト DERIVE（デライブ）の第46回に出てきた、「コーシーの積分定理」は、特異点を含まない正則領域を囲む任意の閉曲線C上の線積分、∫ωdzは、その値がゼロとなることを主張している。
これを利用すると、次の公式を証明できる。
領域内にある任意の点をz0と書いたとき、ω（z0）＝1/（2π#i）∫ω（z）/（z－z0） dz、これを「コーシーの積分公式」という。
積分は、C上を反時計回りに一回回る。
z0は、領域内の任意の点であるので、これをzと書いて公式を、ω（z）＝1/（2π#i）∫ω（s）/（s－z） ds、と書き換えることもできる。
　さて、その証明じゃが、「ハンドブック」に従うと、だいたい、こんな風に進めるということじゃな。
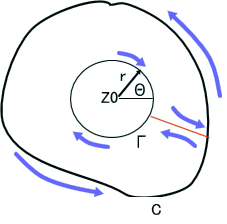左図上で、ωは、領域内で、正則関数としたとき、∫（Cに沿っての積分）ω/（z－z0）dzを考える。第１節の正則関数の積は、また、正則関数という性質を使うと、ω/（z－z0）は、z0を除いた領域で正則であるが、z0を含めた領域での積分値は、一般にゼロとはならない。
この値を計算するため、Cの内部にz0を中心とする小円（半径r）を考えて、それをΓで表す。
C上の任意の始点から出発しCを反時計回りに回り、CとΓを結ぶ直線でΓに移り、Γの回りは、時計回りに回り、Cの始点に戻る積分路に沿って積分値を計算すると、この値は、コーシーの積分定理からゼロとなる。
すなわち、∫（Cに沿って反時計回り）ω/（z－z0）dz＋∫（Γに沿って時計回り）ω/（z－z0）dz＝0、
これから、∫（Cに沿って反時計回り）ω/（z－z0）dz＝∫（Γに沿って反時計回り）ω/（z－z0）dz。
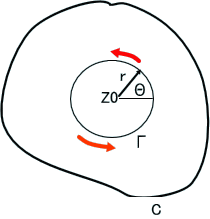次に、左図下のように、∫（Γに沿って）ω/（z－z0）dzの積分を計算するために、z＝z0＋r exp（#i θ）と変数を変換すると、
dz＝#i r exp（#i θ）dθ、
∫（Γに沿っての積分）ω（z）/（z－z0）dz
＝∫（θ＝0～2π）（ω（z0＋r exp（#i θ））#i r exp（#i θ）/（r exp（#i θ）dθ
＝#i ∫（θ＝0～2π）ω（z0＋r exp（#i θ））dθ→ #i ω（z0）×2π、ここで、r→0の極限をとった。
これにより、ω（z0）＝（1/（2π#i））∫（Γに沿っての積分）ω（z）/（z－z0）dz
これはまた、前述のように、ω（z0）＝（1/（2π#i））∫（Cに沿っての積分）ω（z）/（z－z0）dz、となるというわけじゃ」

「なーるほど。でも、なんで、ω/（z－z0）を考えたんだろう？」

「これは、ωは、領域内で正則じゃが、ω/（z－z0）は、z＝z0で正則ではない。z0は、ω/（z－z0）の（孤立）特異点（単極）じゃな。
このように、領域内に特異点を含んだ積分路における積分値を計算するという動機はあるじゃろうな」

３．コーシーの積分公式の応用例

「そこで、早速、いくつかの例をやってみよう。まず、ω＝α（複素数の定数）の場合で、z0＝1＋#iではどうかの」

「ω（z0）＝（1/（2π#i））∫（Cに沿っての積分）ω（z）/（z－（1＋#i））dz、
Cを原点を中心とした、半径Rの円とする。R>2とすると、z0は、領域内に含まれる。z＝1＋#i＋R exp（#i θ）と変換すると、
与式の右辺は、（1/（2π#i））α∫（θ＝0～2π）#i R exp（#i θ）/（R exp（#i θ）dθ＝（1/（2π#i））α×#i 2π＝α、
一方、左辺は、ω＝αであるので、確かに、計算できている」

「exp（z）/（z²＋1）で、z0＝#i ではどうじゃな」

「与式を、exp（z）/（z＋#i）×1/（z－#i）と変形すると、公式で、ω＝exp（z）/（z＋#i）とした場合と考えればいいから、
ω（#i）＝exp（#i）/2#i＝（sin（1）－#i cos（1））/2≒0.4207354924 － 0.2701511529 #i
一方、（1/（2π#i））∫（z＝#iを中心の半径1の円）ω（z）/（z－#i）dz＝（1/（2π#i））×下図の積分≒0.4207354923 － 0.2701511529 #i


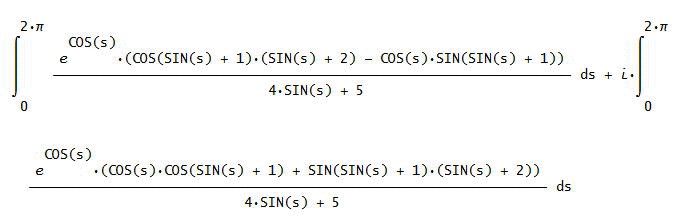
　確かに、合っているみたいね。でも、こんな複雑な定積分が簡単な値（（sin（1）－#i cos（1））/2になるのは不思議だわ」

「そうじゃのう。こう考えれば、どうかな。（1/（2π#i））∫（z＝#i を中心の半径 r の円）ω（z）/（z－#i）dz、z＝#i＋r exp（#i s）、
積分の項は、下図のようになる。


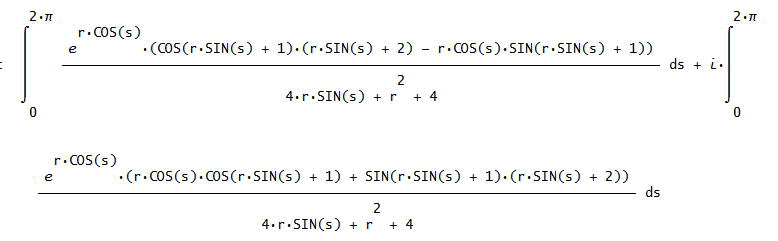
ここで、r→0 と考える。積分内は、exp（#i）/2 と簡単になるので、
与式の積分＝exp（#i）/2×2π となる。これから、（1/（2π#i））×πexp（#i）＝（sin（1）－#i cos（1））/2 となる」

「う～ん。まあ、そうなんだけど、上の積分がrを含んでいるのに、実は、r （<=1）に無関係であることが証明できないのかしらね」

４．n階微分に対するコーシーの積分公式

「コーシーの積分公式により、ω（z）＝1/（2π#i）∫ω（s）/（s－z） ds と表現したとき、ωのn階微分をω^（n）とすれば、
ω^（n）（z）＝n！/（2π#i）∫ω（s）/（s－z）ⁿ⁺¹ ds となるのじゃ。
証明は、nに関する帰納法によるが、ちょと、やっかいなので、簡単な例を挙げておきたいと思う。
まずは、ω＝z²じゃ。ωの2回微分で、ω^（2）（z）＝2となってしまうが、上式の右辺は、2！/（2π#i）∫s²/（s－z）³ ds である。
z²は、無限遠点を除き、全域で正則じゃ。z＝zとして、2！/（2π#i）∫s²/（s－z）³ds おいて、s＝z＋r exp（#i θ）と変換して、
＝1/（π#i）∫（θ＝0～2π）#i（z²exp（－2#iθ）/r²＋2zexp（－#iθ）/r＋1）dθ＝（1/π#i）×2π#i＝2 となり、確かにそのとおりだと分かる、とまあ、こんな感じじゃな」

「えーと。ω＝exp（z）だと、何回微分しても、ω^（n）＝exp（z）だけど、n！/（2π#i）∫exp（s）/（s－z）ⁿ⁺¹ ds 、s＝z＋r exp（#i θ）とすると、ds＝r #i exp（#i θ）dθ、
与式＝exp（z）n!∫(exp(rCOS(θ))COS(rSIN(θ))dθ/(2π)、ここで、たとえば、r＝1とすると、方程式が成り立つためには、
∫(exp（COS(θ)）COS(SIN(θ))dθ＝2πであることが必要だけど、この定積分をDERIVEで概算すると、(6.283185307)≒2πになっているのね」

最終更新日　2008/9/29