数式処理ソフト　DERIVE（デライブ） de ドライブ

４９．複素関数（４）（ガンマ関数、ローラン展開）

０．タイトル名変更のお断り

2008/10/24より、ページのタイトルを第46回に遡って、「積分」からより実際に即した、「複素関数」に変更しました。
また、これに伴い、「複素関数」に続く、かっこ内にそのページの概要が分かる項目を抜粋し、記載するように変更しました。タイトル以外の内容は、変わっておりません。

１．ガンマ関数とラプラス変換

「数式処理ソフト DERIVE（デライブ）の今回は、ここのところ、ラプラス変換について、まったく触れてこなかったな。
　ガンマ関数とラプラス変換について、補足しよう」

「そうね。近藤先生の本（「演算子法」：近藤次郎 著：培風館：昭和４５年初版第13刷）では、変数をtで表したとき、
t ^α → Γ（α+1）/s^（α+1） 、ただし、α＞－1、とラプラス変換されることが「常用ラプラス対函数表（１）」に載っているわ」

「そうじゃな。それと、ラプラス変換の基本性質に挙げてある、exp（－λt）×f(t) → F(s+λ）、ただし、Re（λ）＞0 とを併せて考えると、
exp（－t）t^x+1 → Γ（x+2）/（s+1）^x+2 と変換されるのが分かる。
そして、基本性質 ∫（t＝0～∞）f(t)/t dt＝∫（s＝0～∞）F(s) ds から、
Γ（x+1）＝∫（t＝0～∞）exp（－t）t^x+1／t dt＝∫（s＝0～∞）Γ（x+2）/（s+1）^x+2 ds＝Γ（x+2）/（x+1） となるが、これは、ガンマ関数の関係式そのものじゃ」

「なるほど。合点です」

「ただ、上での変換は、ガンマ関数のラプラス変換ではないので、注意するように。
ガンマ関数は、変数域を正の部分に限定しても、exp（t）より急速に大きくなるので、ラプラス変換はできない。
なお、ガウスにより、Γ（x+1）＝lim （n→∞）（n! n^x）/（（x+1）（x+2）・・（x+n））が示されている。（岩波数学辞典第4版：P215）」

「その数学辞典には、ガンマ関数の元々の定義として、Γ（x）＝（1/x）lim（m→∞）Π（n＝1～m）（1＋1/n）^x／（1＋x/n） が載っているわね」

「そうじゃな。当該式をDERIVEで計算すると、lim（m→∞）(m + 1)^x×m!(x － 1)!/(x + m)!＝（x－1）！、これは、確かにΓ（x）であるの。
ガウスの導いた表現からは、Γ（x+1）＝xΓ（x）であることが、直ちに分かる。
ついでに言うと、ガンマ関数の自然対数を微分した、ψ（x+1）＝d/dx （LN（Γ（x+1））をディガンマ関数またはプサイ関数と呼ぶそうじゃ。
そうそう、前回（第48回）で、「√t＝uと置くと、Γ（x+1）＝2∫（u＝0～∞）exp（－u²）u^（2x+1）du 」という変換は、計算には役に立たないなどと書いてしまったが、x＝－1/2のとき、Γ（1/2）＝2∫（u＝0～∞）exp（－u²）du＝√π の算出に役立つのじゃった。また、「2」という因子も抜けていた。ここで併せて訂正しよう」

「しっかりしてくださいよ！」

「いや、すまんのう」

２．ローラン展開

「さて、複素関数は、正則点でテイラー展開できるというのが、前回、取り上げたテイラーの定理じゃった。
ところが、特異点では、テイラー級数に展開できない。特異点では、ローラン級数という級数に展開できるというのが、ここで取り上げるローラン展開じゃ」

「ローランというのも、人の名前なの？」

「そうじゃ。H. Laurent フランス人。1841－1908。（Tai I. Chow 著：鈴木増雄・香取眞理・羽田野直道・野々村禎彦訳：朝倉書店）による」

「で、どういう級数になるのかしら」

「特異点をz0とすると、ω（z）＝Σ（n＝－∞～∞）a_n×（z－z0）ⁿ 、ここで、a_n＝（1/2π#i）∫ω（s）/（s－z0）ⁿ⁺¹ ds というものじゃ」

「へー。テイラー展開とそっくりじゃん」

「確かに、よく似ているが、下図のような積分路は、C1とC2の間の任意の閉曲線とする。2つの同心円の間では、関数は、正則、かつ、「１価関数」であるとする。

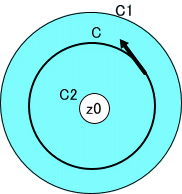
この証明は、上述の本などを参照して欲しい。ここでは、実際の例で確認してみよう。
まずは、ω＝1/（z+1） をz0＝－1でローラン展開する」

「これは、もう最初から、なってるじゃない。ω＝1/（z－（－1））＝1×（z－（－1））^－1 」

「まったく、そのとおりなんじゃが、a_－1＝1であることを上の積分から計算してご覧」

「となると、まずは、Cを、z0＝－1を中心とする円として、s＝z0＋r×exp（#i θ）とおくと、
a_n＝（1/2π#i）∫ω（s）/（s－z0）ⁿ⁺¹ ds で、n＝－1 の場合は、（1/2π#i）∫（θ＝0～2π）#i dθ＝1 である。
そして、n≠－1でないときは、被積分関数に、exp（0以外の整数×#i θ）が表れるので、ゼロになる」

「そうじゃのう。この関数については、特異点がz0＝－1にしか無く、級数も1項だけで、その収束性が問題になることもない。よって、C1は、無限大の大きさにとることができるので、このローラン展開は、z≠－1以外の点で成立する」

「では、次。上述のハンドブックに出てくる例じゃが、ω＝（7z－2）/（z（z²－ z －2））を、1＜｜z+1｜＜3 でローラン展開する」

「えーと、まず、分母を因数分解すれば、特異点は、z＝0、－1、2 の3つで、いずれも1位の極であることが分かる。
しかし、z＝2は、1＜｜z+1｜＜3 の範囲外なので、積分路Cは、z0を中心とする半径 r（1＜ r ＜2） の円とする。
DERIVEでは、∫ω（z）/（z－z0）ⁿ⁺¹ dz で、z＝－1＋r exp（#i s）、dz＝r #i exp（#i s）ds、として、被積分関数は、次のようになる。
((－1 + rEXP(#i s)) + 1)^(－n － 2)(7(－1 + rEXP(#i s)) － 2)/((－1 + rEXP(#i s))((－1 + rEXP(#i s)) － 2))（r#iEXP(#i s))
メニューの解析から「数列の作成」で、n＝－5～5まで、計算する。
この際、あらかじめ、nは、全整数、rは、1＜ r ＜2、sは、正の実数と定義しておく。
そして、ベクトルのままでよいので、s＝0～2πで定積分する。
積分した後に、解析メニューから、極限操作を選択して、r → 1＋（右極限）をとり、（2π#i）で割れば、下記のようなベクトルを得る。
[1, 1, 1, 1, －2, － 2/3, － 2/9, － 2/27, － 2/81, － 2/243, － 2/729]
これは、ω（z）が、z＝－1で、次のように（z+1）のべきに展開できることを示している。
ω（z）≒（z+1）^－5＋（z+1）^－4＋（z+1）^－3＋（z+1）^－2＋（－2）（z+1）^－1＋（－ 2/3）（z+1）⁰
＋（－ 2/9）（z+1）¹＋（－ 2/27）（z+1）²＋（－ 2/81）（z+1）³＋（－ 2/243）（z+1）⁴＋（－ 2/729）（z+1）⁵
なお、ハンドブックの結果とも一致している」

「DERIVE流で、大変結構じゃ。なお、r は、別に極限を取らなくても、r＝1.5などと置換してもよい。
ついでにハンドブックでの解答の骨子を紹介しておこう。
手計算的には、部分分数に展開する。ω＝1/z－3/（z+1）＋2/（z－2）、これは、DERIVEでも代数メニューから「展開」を選択すれば、よい。
ここで、ω＝1/（（z+1）－1）－3/（z+1）＋2/（－3＋（z+1））、ところで、第3項では、分母に工夫がある。
一般に、等比級数 1+a+a²＋・・は、｜a｜＜1 ならば、1/（1－a） に収束する。ところが、第3項では、分母を、（z+1）－3 として、展開すると、｜z+1｜＞3でないと収束しない。ところが、問題では、｜z+1｜＜3 としている。そこで、順序を逆にしているのじゃな。
さて、見やすいように、（z+1）＝u と書くと、第1項は、1/（u－1）＝（1/u）（1/（1－1/u））＝（1/u）（1＋1/u＋（1/u）²＋・・）＝1/u＋（1/u）²＋（1/u）³＋・・
第2項は、そのまま、－3/u、
第3項は、2/（－3＋u）＝（－2/3）（1/（1－u/3））＝（－2/3）（１＋（u/3）＋（u/3）²＋・・）
まとめると、ω＝（1－3）（1/u）＋（1/u）²＋（1/u）³＋・・＋（－2/3）（１＋（u/3）＋（u/3）²＋・・）
ともちゃんの計算した場合とくらべるために、uの －5次から5次までで打ち切ると、
ω≒（1/u）⁵＋（1/u）⁴＋（1/u）³＋（1/u）²＋（－2）（1/u）＋（－2/3）（１＋（u/3）＋（u/3）²＋（u/3）³＋（u/3）⁴＋（u/3）⁵） となって、同一結果となる」

「ガッテン、ガッテン」

３．ローラン展開（続き）

「これも、ハンドブックに載っている例で気が引けるが、正しいかどうかを確認するために正解と照らし合わせることが必要じゃからな。やむを得んじゃろう。
さて、ω＝exp（3z）/（z+1）³ じゃ」

「これは、簡単ね。z＝－1が3位の極で、z+1＝uとすれば、u＝0でテイラー展開できるので、たとえば、5次まで取れば、
exp（3z）＝e^(－3)(81u^5 + 135u^4 + 180u^3 + 180u^2 + 120u + 40)/40
ω＝exp（－3）（81u^2/40 + 27u/8 + 9/(2u) + 3/u^2 + 1/u^3 + 9/2) 」

「では、わしが、DERIVEで、さっき、ともちゃんがやったように積分から計算してみよう。
ところが、残念、厳密な式のままでは、計算が出来ない。
そこで、exp（3z）をz＝－1の回りで5次まで展開し、1/（z+1）^{（－n－4）} を掛けた後に、z＝－1＋r exp（#i s）と変換して、計算を行う。
まず、最初に r＝1と置換しておくと計算が速い。n＝－5～5 までを、解析メニューの数列の作成から実行してベクトルを作り、s＝0～2πで積分する。
最後に計算結果を2π#i で割ると、次のようになる。
exp（－3）×[0, 0, 1, 3, 9/2, 9/2, 27/8, 81/40, 0, 0, 0]
結果は、ともちゃんがやったものと、完全に一致したのう」

「次は、どんな問題かしら」

「最後は、ω＝（z+2）×ｓｉｎ（1/（z+2））じゃ」

「ひぇー。難しいそうじゃないの」

「いや、これは、そうでもないのじゃ。z＝－2は、真性特異点というやつで、（z+2）のべきが－∞から0まである。
さきほどと同様にz+2＝uとおけば、ω＝u×sin（1/u）となる。1/u＝0でテイラー展開すれば、sin（x）＝x－x³/3!＋x⁵/5!－＋・・なので、
ω＝1－1/3!（z+2）²＋1/5!（z+2）⁴－＋・・」

「じゃ、わたしは、DERIVEでやってみるよ。
う～ん。やっぱり、sin関数のままでは、難しいので、上のようにサイン関数を1/（z+2）の0の回りで、5次までテイラー展開して計算すると
、n＝－5～0までで、[0, 1/120, 0, － 1/6, 0, 1] となる。（ベクトルの最初がn＝－5、最後が0に対応している）
これから、ω＝1－1/6×（z+2）^－2＋1/120×（z+2）^－4 であることが分かった。こちらも展開した次数までは、完全に一致したね」

最終更新日　2008/10/24