数式処理ソフト　DERIVE（デライブ） de ドライブ

５５．数値積分（4）（Wijngaarden変換(続き)）

Wijngaarden変換に関する一考察

「数式処理ソフト DERIVE（デライブ）の第54回に出てきた、Wijngaarden変換の基礎付けをしようと思ったんじゃが、なかなか難しいものじゃ」

「Webで検索しても？」

「そうなんじゃな。
実は、検索のときに、『Wijngaarden　tranform』などのキーワードを入れると、英語版のWikiのページが出てくる。
それが、こちら（http://en.wikipedia.org/wiki/Van_Wijngaarden_transformation）なんじゃ」
「なるほど。Euler変換の高速化版ね」
「明らかに、『BASICによる高速ラプラス変換』（細野敏夫：共立出版：1984年4月）に出てくる『Wijngaarden変換』とは別物ね」
「これは、一般に『Euler－Knoop変換』として知られている、Euler変換の加速の一例のようじゃ。
このページの次節で実際に計算してみよう」
「それで、肝心の正項級数を交代級数に変換する『Wijngaarden変換』の方は、どうなの？」
「自分で考えてみたんじゃ。
まずは、ずらし演算子 Eは、見た目上、自然対数に紛らわしいので、以下では、変数 xで代用する。
元の正符号の数列をa(k)としたとき、k=1～∞として、
級数の和 Sは、S＝Σ（k=1～∞）a(k)＝（1＋x＋x²＋・・）a(1)と書ける。
一方、『Wijngaarden変換』では、a(k)を以下のように、v(k)に変換する。
v(k)＝2⁰a(2⁰k)＋2¹a(2¹k)＋2²a(2²k)＋2³a(2³k)＋・・、k=1～。
そして、S'＝Σ（k=1～∞）(－1)^k×v(k)と定義されている。S'→Sとなることを証明したいのじゃな。
さて、v(k)をm項まで取ったものは、v(k)≒Σ（j=1～m）（2^(k－1)a(2^(k－1)×j）であるが、ここで、a(k)＝x^k－1×a(1)であることを思い出して、演算子としてv(k)をとらえると、
v(k)≒Σ（j=1～m）(－ 2^(k － 1)x^(－1)x^(2^(k － 1)j)(－1)^j)
＝2^(k － 1)x^2^(k － 1)x^(－1)/(x^2^(k － 1) + 1) － 2^(k － 1)x^(－1)x^(2^(k － 1)(m + 1))(－1)^m/(x^2^(k － 1) + 1) となる。
そこで、S'(n,m)＝Σ（k=1～n）（2^(k － 1)x^2^(k － 1)x^(－1)/(x^2^(k － 1) + 1) － 2^(k － 1)x^(－1)x^(2^(k － 1)(m + 1))(－1)^m/(x^2^(k － 1) + 1)）×a(1)と書ける」
「具体的に、書いてみると、m=2のときは、a(1)を省略して書けば、
S'(n,2)＝Σ（k=1～n）(2^(k － 1)x^2^(k － 1)x^(－1) － 2^(k － 1)x^2^kx^(－1)) となって、
S'(4,2)＝－ 8x^15 + 4x^7 + 2x^3 + x + 1 となる」
「要は、S'(n,m)が、n、m→∞のときに、1＋x＋x²＋・・となることが言えれば、よい。
実際、m=10として、計算すると、
S(10,10)＝－ 512x^5119 + 512x^4607 － 512x^4095 + 512x^3583 － 512x^3071 + 256x^2559 + 256x^2303 － 768x^2047 + 256x^1791 + 256x^1535 + 128x^1279 + 128x^1151 － 896x^1023 + 128x^895 + 128x^767 + 64x^639 + 64x^575 + 64x^511 + 64x^447 + 64x^383 + 32x^319 + 32x^287 + 32x^255 + 32x^223 + 32x^191 + 16x^159 + 16x^143 + 16x^127 + 16x^111 + 16x^95 + 8x^79 + 8x^71 + 8x^63 + 8x^55 + 8x^47 + 4x^39 + 4x^35 + 4x^31 + 4x^27 + 4x^23 + 2x^19 + 2x^17 + 2x^15 + 2x^13 + 2x^11 + x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1、なる」
「なるほど。これを見ると、太字のx^0～x^9の項までは、係数がすべて1だから、少なくとも部分的には成り立っているわね」
「そうなんじゃ。
mを大きくして、やってみると、xのべき乗のべき数がm未満までは、xのべき乗の項の係数は、上記のように、「1」となっている。
このことから、S'(n,m)が、n、m→∞のときに、1＋x＋x²＋・・＋（残差）となることが期待できるのじゃ」
「期待って？、予想でしょうが。証明ではないのね」
「すまんのう。
証明ではないのは、確かじゃ。
グラフを描いてみると、S'→1/(1－x)＝1＋x＋x^2＋x^3＋・・となりそうなのは、分かるんだけどな。
下図で、p＝20として、n=4のとき、n=10のとき、及び参考として、1/(1－x)の3つのグラフを描いている。

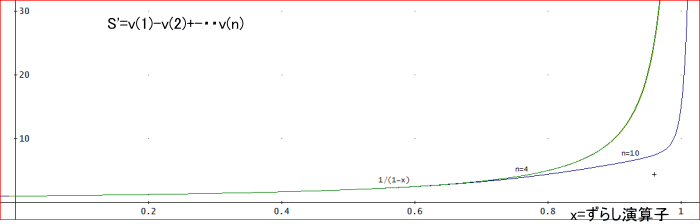
じゃが、特別なa(k)については、確かにそうだという事が分かる。
たとえば、ζ(x)の場合じゃ。x>1とする。
S'(n,m)＝－ 2^(x － 1)∑(2^(k(1 － x)), k, 1, n)∑(j^(－x)COS(πj), j, 1, m)
lim（m→∞）S'(n,m)＝2^x∑(j^(－x)COS(πj), j, 1, ∞)/(2 － 2^x) とまとめられる。
ここで、x=2と置けば、π＾2／6と正しい値が求められる」
「一応、x＝2～10までを表にしてみたわ。
2： π^2/6
3： ζ(3)
4： π^4/90
5： ζ(5)
6： π^6/945
7： ζ(7)
8： π^8/9450
9： ζ(9)
10：π^10/93555
面白いわね。ζ(n）のnが偶数だと、ζ(n）＝π^n/Nの形になるのね」
「うん。n=2、4、6、8、10では、それぞれ、分母のNは、N＝6、90、945、9450、93555となる。
岩波数学辞典等の公式集では、ζ(2n)＝(2π)²ⁿ/(2(2n!））×｜B(2n)｜となるそうじゃ。
ここで、B(2n)は、2n次のベルヌイ数（n>=1）とし、｜｜は、絶対値をとる記号とする。
2n=2： π^2/6
4： π^4/90
6： π^6/945
8： π^8/9450
10：π^10/93555
12：691π^12/638512875
14： 2π^14/18243225
16：3617π^16/325641566250
18：43867π^18/38979295480125
20：174611π^20/1531329465290625」
「なんとなく、予感がしたけど、ベルヌイさんにまた、お目にかかったわね」

交代級数のEuler変換の加速

「前節で、英文のページに紹介されている方法じゃ。
Wijngaarden変換（Van Wijngaarden transformation）と呼ばれている。
そのまま、紹介すると、s(0,n)＝Σ（k=0～n）（－1)^k×a(k)、k=0、1、2、・・として、a(k)は、正とする。
s(0,n)は、(－1)があるように、交代級数じゃが、Euler変換を使わない場合の0項からn項までの和じゃな。
ただし、変数等の記号は、HPとは変えている。
そして、加速具合を、j（＞0）で表し、s(j,0)＝（s(j－1,n)＋s(j－1,n+1)）/2、と再帰的に定義する。
たとえば、s(1,n)＝（s(0,n）＋s(0,n+1)）／2」

「ふ～ん。
じゃ、早速、a(k)＝1/(k+1)として、1－1/2＋1/3－1/4・・＝LN(2)≒0.69314718055994530941 を計算してみよう。
まずは、s(0,n)の値。正直に交代級数を足したものよ。
いちいち、正直に計算って、いうのも面倒くさい。今後、『正直計算』と呼ぶことにするといいわね～。
10： 0.73654401154401154401
20： 0.71639045079447556227
30： 0.70901620220752687376
40： 0.70519362569513309942
50： 0.70285500371317309038
60： 0.70127672465429756635
70： 0.70013984566346397929
80： 0.69928191902148621766
90： 0.69861149828620440112
100：0.69807316940920510423
となって、80項程度で、ようやく小数点以下2桁まで合うようになる。
次、1段加速、s(1,n)よ。
10： 0.69487734487734487734
20： 0.69366317806720283500
30： 0.69339120220752687376
40： 0.69328886379037119466
50： 0.69323961909778847500
60： 0.69321220852526530829
70： 0.69319540121901953484
80： 0.69318435804587646156
90： 0.69317671567750874895
100：0.69317120862489137874
こんどは、小数点以下、3桁目まで求まる。
えい、面倒な。
s(m,100)とnの方を100に固定して、加速度合いmを2から10まで変化させてみましょう。
s(2,100)＝0.69314741269875393347
s(3,100)＝0.69314718389177184265
s(4,100)＝0.69314718062310066992
s(5,100)＝0.69314718056142762893
s(6,100)＝0.69314718055998667003
s(7,100)＝0.69314718055994664339
s(8,100)＝0.69314718055994535813
s(9,100)＝0.69314718055994531140
s(10,100)＝0.69314718055994530950
と、1段ずつ加速する毎に、面白いように1桁ずつ精度が高まるのね」

正項級数に対するWijngaarden変換を利用した和の計算

「前節のように交代級数の場合は、オリジナルのEuler変換あるいは、その加速版が効率的に使える。
しかし、正項級数（正確には、定符号の級数）の場合は、交代級数でないので、そのままでは、Euler変換及び類似の方法を使えないというわけじゃな」

「そこで、v(k)＝2⁰a(2⁰k)＋2¹a(2¹k)＋2²a(2²k)＋2³a(2³k)＋・・＋2^pa(2^p)、k=1～n。
S'(n)＝v(1)－v(2)＋v(3)－＋・・として、S'を交代級数に変換してから、和を求める方法が前回の記事で紹介した『Wijngaarden変換』だったのね」

「前節で紹介したEuler変換の加速法が有効であるかどうかを調べて見よう。
以下では、k＝1から始めたので、vとSの定義式の変数の範囲を前節と変えている。
v(j, p)＝∑(2^(k － 1)a(2^(k － 1)j), k, 1, p + 1) と定義する。
なお、a(k)からv(k)を計算する際の最大項数をp+1としてある。
前節にならって、
s(j, k, p)＝ IF(j = 1, ∑((－1)^(n － 1)v(n, p), n, 1, k), (s(j － 1, k, p) + s(j － 1, k + 1, p))/2) と定める。
ζ(2)＝π^2/6≒1.6449340668482264364・・を例にしてみよう」
「じゃ、計算してみるよ。
なお、計算桁数は、DERIVEの標準では、10桁だけど、オプションメニューのモード設定で、精度の桁を20桁としているよ。
まず、a(k):=1/k^2とDERIVEで定義し直します。
s(1,n,20)として、交代級数の加速を使わない方法で、n=10～100に変えて調べて見る。
10： 1.6359235711524515976
20： 1.6425579734264562357
30： 1.6438591679047002517
40： 1.6443238980257389237
50： 1.6445412794732935866
60： 1.6446601331797019807
70： 1.6447321158030800216
80： 1.6447789853760823413
90： 1.6448111973234561638
100：1.6448342824297774784
100項までで小数点以下3桁までというところね。
次は、Euler変換を使った方法ね。s(m,100,20)として、m=2から10まで、加速した場合を含めて計算よ。
2： 1.6449323119879740122
3： 1.6449332683509264294
4： 1.6449332822108214381
5： 1.6449332824760722675
6： 1.6449332824823575430
7： 1.6449332824825345836
8： 1.6449332824825403474
9： 1.6449332824825405599
10：1.6449332824825405686
前節の交代級数の場合ほど、鮮やかな加速具合ではないわね」
「それじゃ。s(m,100,40)として、pの項数を場合に増やしてみよう。
1： 1.6448350667481084489
2： 1.6449330963530490964
3： 1.6449340527164575428
4： 1.6449340665763591604
5： 1.6449340668416101163
6： 1.6449340668478953948
7： 1.6449340668480724355
8： 1.6449340668480781993
9： 1.6449340668480784117
10：1.6449340668480784205
どうじゃな。
10段加速度で、小数点以下12桁までは正しい。
2＾40×a(2^40）≒9.0949470177292823791×10^(－13) ≒10^(－12)なので、v(k)に含まれる数は小数点以下12桁じゃな」
「というと、小数点以下15桁まで求めるためには、p>=60程度は必要なのね。
s(m,100,60)として、m=1～10として計算したわ。
1： 1.6448350667482564194
2： 1.6449330963531971115
3： 1.6449340527166055583
4： 1.6449340665765071759
5： 1.6449340668417581319
6： 1.6449340668480434103
7： 1.6449340668482204510
8： 1.6449340668482262148
9： 1.6449340668482264273
10：1.6449340668482264360
う～ん。すごいわね。
s(10,100,60)では、小数点以下17桁まで、正しいみたいな」
「結局、v(k)を作る際の、2^p×a(2^p)によっても、精度を抑えられる。これは、a(k)の形によって、違ってくる。
ζ(2)の場合は、a(k)＝1/k²のため、p≒60以上でないと15桁までは求められなかった訳じゃな。
しかし、ζ(4)では、a(k)＝1/k⁴となっているので、p≒40程度で、小数点以下15桁程度は出ると考えられる。
実際、s(10,100,40)＝1.0823232337111381915、真の値は、π4/90≒1.0823232337111381915・・」
「ところが、s(10,100,20)＝1.0823232337111381915 となって、正しい値と計算桁数まで、一致しちゃっているんだな～。
さらに、ビックリしたのは、s(10,n,20)で、n=10～100まで計算させたもの。
合計する項数を10桁ずつ増やす度に精度がどんどんよくなるの。
10： 1.0823232336546117204
20： 1.0823232337110738120
30： 1.0823232337111374094
40： 1.0823232337111381621
50： 1.0823232337111381893
60： 1.0823232337111381912
70： 1.0823232337111381914
80： 1.0823232337111381915
90： 1.0823232337111381915
100：1.0823232337111381915
となって、すでに、70桁程度で小数点以下19桁以上、一致している。
まさに「加速」しているカンジね」

最終更新日　2011/8/2