数式処理ソフト DERIVE(デライブ) de ドライブ
56.数値積分(5)(ニュートン-コーツの公式、IMT公式、DE公式)
ニュートン-コーツの公式
 「数式処理ソフト DERIVE(デライブ)の第54回 数値積分(3)(Euler-Maclaurin展開とラプラス変換、Wijngaarden変換)と第55回の数値積分(4)(Wijngaarden変換(続き))では、『数値積分』と銘打っているものの、ちょっと寄り道しちゃったわね」
「数式処理ソフト DERIVE(デライブ)の第54回 数値積分(3)(Euler-Maclaurin展開とラプラス変換、Wijngaarden変換)と第55回の数値積分(4)(Wijngaarden変換(続き))では、『数値積分』と銘打っているものの、ちょっと寄り道しちゃったわね」
「まあ、それは、わしらのような素人が書いているホームページならではのこと。
そこが短所でもあり、また、長所でもあるじゃろう。『寄り道もまた楽しからず也』という境地こそ、めざしたいところじゃな」
「了解っす。で、今回は、変数変換ですか」
「そう。そもそも、余弦積分 Ci(x)=-∫(t=x~∞)(cos(t)/t)dt、でも、半無限領域での積分を含んでおる。
そして、始末が悪いことには、tが比較的大きいところでも、被積分関数全体としては、なかなかゼロに近づかないばかりか、正負の項が交代に現れることで、桁落ちが大きくなってしまうのじゃ」
「そこで、公式集では、 Ci(x)=γ+Ln(x)-∫(t=0~x)(1-cos(t))/t dt、と積分区間を有限区間に変えているのね。
ここで、γは、前回出てきている、オイラー定数≒0.5772156649・・」
「この公式は、第43回でラプラス変換を通じて、間接的に証明しているが、正面から扱ってはいないのじゃな。直接的な導出については、複素関数のところに戻ったときに扱うと言うことで、宿題にしておこう」
「あの~。これまでのところ、台形公式、シンプソン公式以外のメジャーな名前が挙がっていないよね。
ほら、前に引用した『計算機による 数値計算法』(一松信・戸川隼人:新曜社:昭和50年2月)や『数値計算法基礎』(田中敏幸:コロナ社:2006年4月)では、高次のニュートン-コーツ(Newton-Cotes)の公式やガウス-ルジャンドルの公式が挙げられているし、『計算数学夜話』(森口繁一:日本評論社:昭和53年4月)には、その他にチェビシェフ(Chebyshev)公式やガウス(Gauss)公式などにも触れられているんだけど~」
「そうじゃな。そのような公式にも、ちょっと、触れておくかな。
しかし、また、脇道になるんじゃが、一松・戸川先生の本では、わざわざ『計算機による』と断ってある。ほぼ、同じ内容を扱っている田中先生の本では、もはや、計算機による、などとうたっておらん。30年の時の流れを感じるのう」
「年寄りの話は、長くなるからなあ。
早く本題に戻ってよ」
「ま、言いたかったことは、手計算の時代とは異なり、高次の公式を使って分点数を少なくして、関数の値の計算量を減らすことは、それほど重要ではなくなったとも言えるのかも知れないな。
それはそうと、Newton-Cotesの(高次の)公式じゃ。
ちなみに、コーツという人は、Wikiによると、Roger Cotes(1682年7月10日~1716年6月5日)というイギリスの数学者で、ニュートンと同時代の人じゃな。前回、出てきた、Maclaurinも46才という若さで亡くなっているが、コーツは、33才で亡くなっている。当時は、結核やペストなどの感染症が猛威をふるっていた頃じゃから、仕方がなかったかもしれんが。イギリスの数学界にとっては、惜しまれた死であったようじゃ。
さて、第53回 数値積分(2)(Euler-Maclaurin展開とその応用)で出てきた、積分公式のうち、
積分区間を、c~d、被積分関数は、g(x)とすると、分割数をn、積分の近似値 f(c,d,n,m)は、m=0~3、次のようになった。
f(c,d,n,0)=(d - c)∑(g(k(d - c)/n + c), k, 0, n - 1)/n + (c - d)(g(c) - g(d))/(2n) :台形公式
f(c,d,n,1)=f(c,d,n,0)+(c - d)^2g'(c)/(12n^2) - (c - d)^2g'(d)/(12n^2) :端補正の台形公式
f(c,d,n,2)=f(c,d,n,1) - (c - d)^4g'''(c)/(720n^4) + (c - d)^4g'''(d)/(720n^4) :ほぼシンプソン公式
f(c,d,n,3)=f(c,d,n,2) +(c - d)^6g'''''(c)/(30240n^6) - (c - d)^6g'''''(d)/(30240n^6)
ところで、これらのオイラー-マクローリンの式をそのまま、数値積分の計算に使えるのは、関数が、ここでは、g(x)であるが、式の形で与えられている場合じゃ。
なぜならば、f(c,d,n,1)以降は、g(x)の導関数を含んでいるのでな。
しかし、関数が表のような形で与えらている場合、これでは困ることも多いのじゃ」
「なるほど」
「その点を復習してみよう。
オイラー-マクローリンの式でm=0、1、2の場合の具体的な形は、次のとおりじゃ。
T(c,d,n)≡((d - c)∑(g(k(d - c)/n + c), k, 0, n - 1)/n + (c - d)(g(c) - g(d))/(2n)、
W(c,d,n)≡(c - d)((c - d)g'(c) + (d - c)g'(d) - 12n∑(g(k(d - c)/n + c), k, 0, n
- 1) + 6n(g(c) - g(d)))/(12n^2)、
P(c,d,n)≡ (d - c)((c - d)^3g'''(c) + 60n^2(d - c)g'(c) + (d - c)^3g'''(d) + 60n^2((c
- d)g'(d) + 6n(2∑(g(k(d - c)/n + c), k, 0, n - 1) - g(c) + g(d))))/(720n^4))、と置く。
まずは、(4W(c, d, 2n) - W(c, d, n))/(4-1)=(4W(c, d, 2n) - W(c, d, n))/3 を作ってみると、
(d - c)(4∑(g(k(d - c)/(2n) + c), k, 0, 2n - 1) - 2∑(g(k(d - c)/n + c),
k, 0, n - 1) - g(c) + g(d))/(6n)、
であり、導関数の項を消去できる。
ここで、h=(d-c)/nとして、書き換えると、あるいは、第52回と合わせてΣの中を分解して、
(h/6)(g(c)+g(d)+4Σ(k=1~n)g(h(k-1/2)+c)+2Σ(k=1~n-1)g(hk+c))、とすると、シンプソンの公式ということが分かる。
これと同じようなことをP(c,d,n)でやってごらん」
「合点です。
16P(c, d, 2n) - P(c, d, 2n))/15
=((c - d)((c - d)g'(c) + (d - c)g'(d) - 2n(16∑(g(k(d - c)/(2n) + c), k,
0, 2n - 1) - 2∑(g(k(d - c)/n + c), k, 0, n - 1) - 7g(c) + 7g(d)))/(60n^2))、
うへー、まだ、g(x)の導関数が残っているよ」
「では、P(c,d,4n)も使ってみたらどうじゃな」
「(16P(c, d, 4n) - P(c, d, 2n))/15)
=((c - d)((c - d)g'(c) + (d - c)g'(d) - 4n(16∑(g(k(d - c)/(4n) + c), k,
0, 4n - 1) - 2∑(g(k(d - c)/(2n) + c), k, 0, 2n - 1) - 7g(c) + 7g(d)))/(240n^2))
{4×(16P(c, d, 2n) - P(c, d, n))/15)-(16P(c, d, 2n) - P(c, d, 2n))/15)}/3を作ると、
((d - c)(32∑(g(k(d - c)/(4n) + c), k, 0, 4n - 1) - 20∑(g(k(d - c)/(2n)
+ c), k, 0, 2n - 1) + 2∑(g(k(d - c)/n + c), k, 0, n - 1) - 7(g(c) - g(d)))/(90n))、となって、g(x)の導関数の項がなくなったわ」
「シンプソンの場合と同様に整理すると、h=(d-c)/nとして、書き換えると、Σの仲を分解して、
NC(n)
=(h/90)(7g(c)+7g(d)+32Σ(k=1~n)g(h(k-1/4)+c)+32Σ(k=1~n)g(h(k-3/4)+c)+12Σ(k=1~n)g(h(k-1/2)+c)+14Σ(k=1~n-1)g(kh+c))
となる。これが、ニュートン-コーツの公式と言われるものじゃ。(台形公式やシンプソン公式も含めて言うこともある)
シンプソンの場合も同様じゃが、実用上は、Σの中身を書き換えることは必要ない。ここでは、第52回と合わせてみただけじゃ」
「では、早速、計算してみるよ。
g(x)は、前回と同様に1/(x+1)として、c=0~d=1までの積分、理論値は、LN(2)≒0.69314718055994530941・・。
よーい。スタート。
比較の意味で、T(c,d,n)も計算してみたよ」
| n |
T(n) |
S(n) |
NC(n) |
| 1 |
0.75 |
0.69444444444444444444 |
0.69317460317460317460 |
| 2 |
0.70833333333333333333 |
0.69325396825396825396 |
0.69314790148123481456 |
| 3 |
0.69702380952380952380 |
0.69316979316979316979 |
0.69314725347838822061 |
| 4 |
0.7 |
0.69315453065453065453 |
0.69314719429707826684 |
| 5 |
0.69563492063492063492 |
0.69315023068893037933 |
0.69314718426352850160 |
| 6 |
0.69487734487734487734 |
0.69314866220910102993 |
0.69314718181999875401 |
| 7 |
0.69441946941946941946 |
0.69314798387508936258 |
0.69314718106452348169 |
| 8 |
0.69412185037185037185 |
0.69314765281941904107 |
0.69314718078784986632 |
| 9 |
0.69391760200583729995 |
0.69314747598100690853 |
0.69314718067286216449 |
| 10 |
0.69377140317542794322 |
0.69314737466511611896 |
0.69314718062014535369 |
「台形公式では、10項までで、小数点以下3桁、シンプソンでは、6桁、ニュートン-コーツでは、9桁となって、やっぱり、高次の公式は、有利ね」
「誤差を考えてみよう。
一般に、
T(n)-f(c,d,n,1)=(c - d)^2(g'(d) - g'(c))/(12n^2)・・
ここで、n=10、g(x)=1/(x+1)の場合じゃと、誤差の主要項は、0.000625となって、小数点以下3桁目までは、ゼロとなっている。
同様に、
S(n)-(4f(c,d,2n,2)-f(c,d,n,2))/3=(c - d)^4(g'''(d) - g'''(c))/(2880n^4)・・
ここで、n=10、g(x)=1/(x+1)の場合じゃと、誤差の主要項は、1.953125×10^(-7)となって、小数点以下6桁目までは、ゼロとなっている。
さらに、
NC(n)-((4((16f(c, d, 4n, 3) - f(c, d, 2n, 3))/15) - (16f(c, d, 2n, 3) -
f(c, d, n, 3))/15)/3)
=(c - d)^6(g'''''(d) - g'''''(c))/(1935360n^6)・・
となるので、n=10、g(x)=1/(x+1)の場合じゃと、誤差の主要項は、6.103515625×10^(-11)となって、小数点以下10桁目までは、ゼロとなっている。
上表で、NC(10)が小数点以下、9桁目までしかあっておらんが、さらに高次の誤差項の影響じゃろう」
「同じように、更に高次の公式を考えることもできるのね」
「そう。そういうものは、みんな、ニュートン-コーツの公式と称されている。
なお、チェビシェフの公式やガウス公式は、分点間隔が一定という考えを止めて、(関数に依存しない)特定の点々での関数値を採用したものじゃ。それらについては、ここでは触れられないが、上記書籍等で確認して欲しい。
次節では、第54回で、ともちゃんが目を付けた、端点の値やその導関数値がゼロ又は急速にゼロに近づくときは、『台形公式』でも誤差が極めて小さくなるという結果を踏まえて、変数変換による数値積分を扱ってみよう」
IMT公式(オリジナル版)
「伊理・森口・高澤の頭文字を取って、IMT公式と言われているものじゃ。
元々は、積分区間をx=0~1としたとき、∫f(x)dx=∫f(φ(t))φ'(t)dt≒h×Σ(k=1からn-1)f(φ(kh))φ'(kh)、ここで、h=1/n。
更に、φ(t)=1/Q∫(0~t)(exp(-1/s-1/(1-s))ds、Q=∫(0~1)(exp(-1/s-1/(1-s))ds という要旨で発表(※)されたものだそうじゃ。
(※伊理正夫、森口繁一、高澤嘉光、『ある数値積分公式について』(1970)。記法等は、当時のものとは少し異なる)
この誤差は、exp(-c√n)に比例して減少する。ここで、cは、正の定数」
 「なんか、大変なものね。
「なんか、大変なものね。
じゃ、まずは、一般式をDERIVEで書いてしまおう。
φ(t) :=∫(exp(- 1/s - 1/(1 - s)), s, 0, t)/∫(e^(1/(s(s - 1))), s, 0, 1)
と関数φを定義する。
また、φ'(t)=e^(1/(t(t - 1)))/∫(e^(1/(s(s - 1))), s, 0, 1) である。
これらを使うと、元の被積分関数を一般に g(x) としたとき、x=φ(t)と、変数変換した後の被積分関数全体は、
(e^(1/(t(t - 1)))g(∫(e^(1/(s(s - 1))), s, 0, t)/Q)/Q となる。
上式では、わかりにくいと思うんで、下図を見てね。
さっき、おじさんが書いていた、Qは、∫(e^(1/(s(s - 1))), s, 0, 1)≒0.007029858406・・ となる。
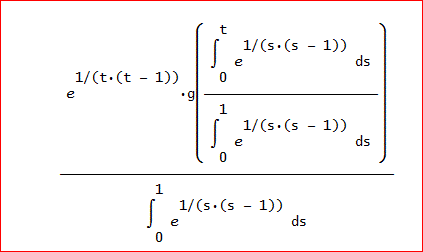
ところで、積分は、上記で、t=0~1で行うということ。
x=φ(t)=∫(exp(- 1/s - 1/(1 - s)), s, 0, t)/∫(e^(1/(s(s - 1))), s, 0, 1)
と変換したのだから、x=0は、t=0に対応し、また、x=1は、t=1に対応しているのよ。
φ(t)とφ(t)×φ'(t)のグラフは、下図を見て欲しいんだな。
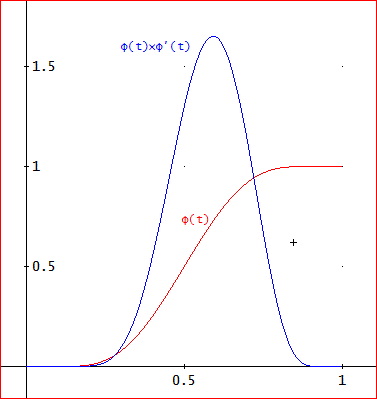
二つとも、きれいな曲線でしょう。φ(t)が変換関数。
図で分かるように、(g(x)がないときは)、φ(t)×φ'(t)は、滑らかで、特に、両端でゼロとなり、また、急速に減少する関数であることが分かるわ。
また、φ'(t)=e^(1/(t(t - 1)))/∫(e^(1/(s(s - 1))), s, 0, 1) から分かるように、端では、任意の次数の導関数値もゼロとなるのよ。
そしてと、このまま積分するんじゃ意味がないけど、というか、変形しようもないけどさ、台形公式を使うのよね。
e^(1/(t(t - 1)))g(∫(e^(1/(s(s - 1))), s, 0, t)/Q)/Q で、t=k×h、h=1/nとして、k=1~n-1まで合計して、hを掛けると、積分の近似値が出てくるという訳。
すなわち、下図のように計算を行う。
端点では、(ほとんど)ゼロとなるから、両端は、計算していなくていいのよ。
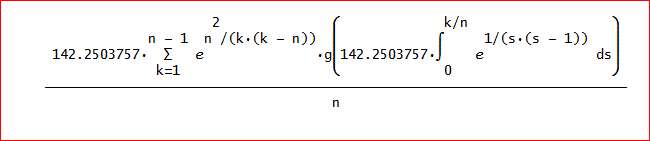
上では、Qの値(概算値)を代入して、簡単化してあるの。g[・・]は、本来の被積分関数。
試しに、g(x):=xと置いてみると、n=1~10で、次のようになるの。
1, 0
2, 0.6513516279
3, 0.5267529767
4, 0.4973702389
5, 0.4960073648
6, 0.4981940496
7, 0.4995375412
8, 0.5000317195
9, 0.5001294407
10, 0.5001008544
真値は、0.5となので、n=8でほぼ、小数点以下、3桁まで求められているでしょ」
「では、前回も、計算している、g(x):=1/(x+1)の場合は、どうじゃな」
「は~い。
n=1~100まで、2つずつ計算してみたよ。
そうすると、n=41あたりで、真値=LN(2)≒0.6931471805・・の小数点以下8桁まで、求まったようね。
DERIVEの表をそのまま、貼り付けると、こんな具合で、とても見にくいと思うけどがまんしてね。
ちなみに、『41,』というのは、nの値が41ということ。
そして、そのときの計算値が『0.6931471804』で、『,』や『;』は区切り文字ということでカンベンカメキチ。
([1, 0; 3, 0.7489720843; 5, 0.6865430552; 7, 0.6924935029; 9, 0.6933404341;
11, 0.6932290769; 13, 0.6931543924; 15, 0.6931411622; 17, 0.6931436113;
19, 0.6931462409; 21, 0.6931472277; 23, 0.6931473765; 25, 0.6931473006;
27, 0.6931472239; 29, 0.6931471859; 31, 0.6931471743; 33, 0.6931471741;
35, 0.6931471766; 37, 0.6931471787; 39, 0.6931471799; 41, 0.6931471804; 43, 0.6931471805; 45, 0.6931471804; 47, 0.6931471803; 49, 0.6931471803;
51, 0.6931471802; 53, 0.6931471802; 55, 0.6931471802; 57, 0.6931471802;
59, 0.6931471802; 61, 0.6931471802; 63, 0.6931471802; 65, 0.6931471802;
67, 0.6931471802; 69, 0.6931471802; 71, 0.6931471802; 73, 0.6931471802;
75, 0.6931471802; 77, 0.6931471802; 79, 0.6931471802; 81, 0.6931471802;
83, 0.6931471802; 85, 0.6931471802; 87, 0.6931471802; 89, 0.6931471802;
91, 0.6931471802; 93, 0.6931471802; 95, 0.6931471802; 97, 0.6931471802;
99, 0.6931471802])
さっきの g(x):=xの場合と一緒に、下図にその様子をグラフで描いてみたわ」
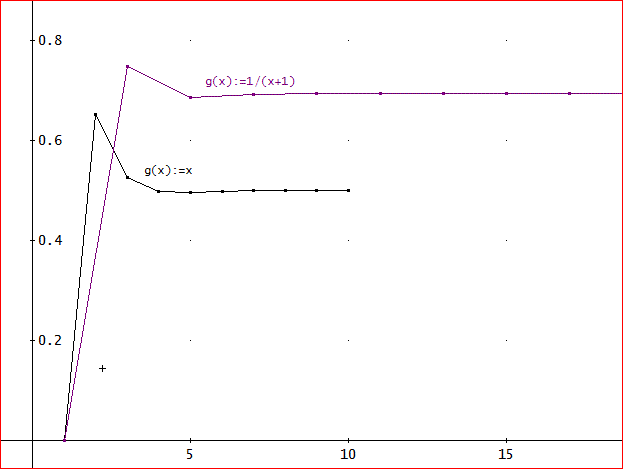
「Qの値やΣの中に含まれている積分、『∫(e^(1/(s(s - 1))), s, 0, k/n)』の計算が、10桁までじゃから、小数点以下8桁目まで求められれば、問題はなかろう」
「でも、あれね。g(x):=xは、ともかく、シンプソン公式を使っても、大きな違いがないみたい」
「確かにな。
1/(x+1)のような『おとなしい』関数では、シンプソン公式などと大して変わらないかもしれん。
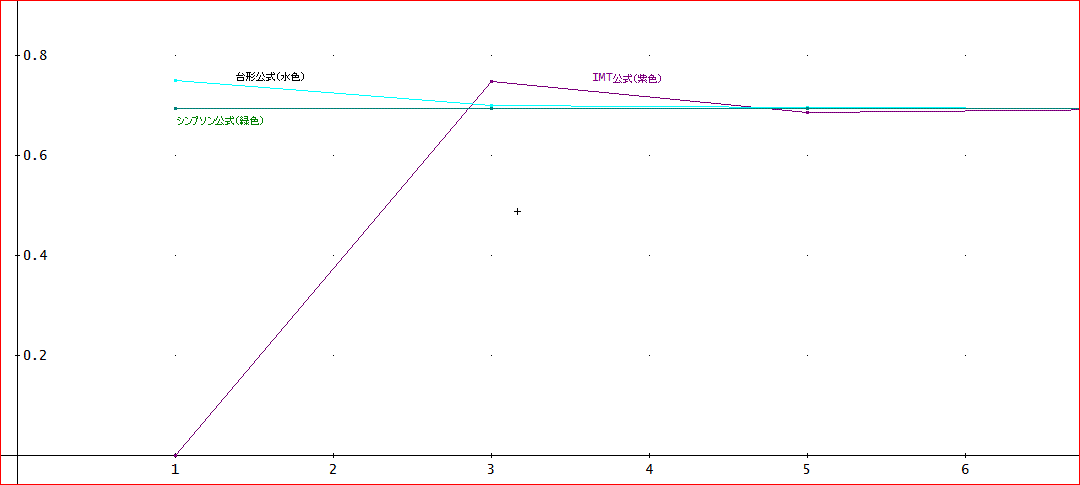
上のグラフでも、IMT公式の方がシンプソン公式と同程度じゃ。
シンプソン公式では、横軸の nで、実は、こっそりと、2nの項も計算しているので、そのままでは比較しにくいがの。
ただ、IMT公式は、積分区間内で正負で激しく振動するなどの、『やっかいな』関数に効き目があるということじゃ」
「そうか。たとえば、
∫(SIN(100x^2)/(x + 1), x, 0, 1) みたいな、積分ね。
これは、こんなに振動して、しかも減衰する関数よ。
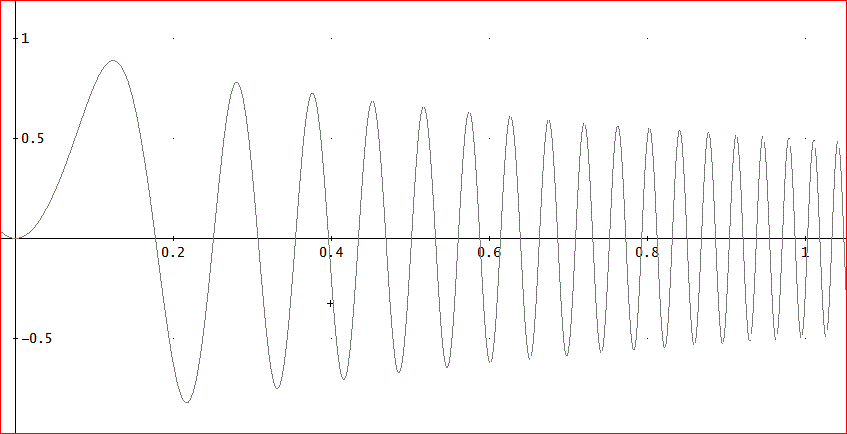
IMT公式の効果や、如何に?」
「ちょっと見では、思ったほどではないように思うが・・。
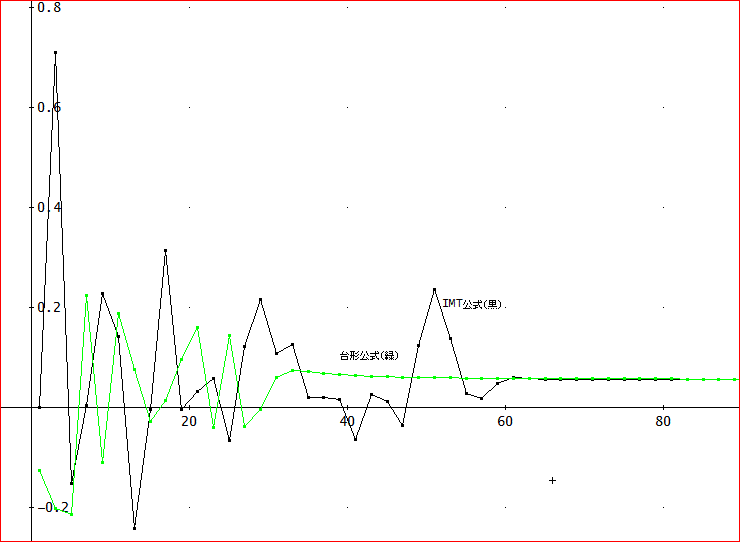
台形公式では、n=30程度で、ほぼ、収束したように見える。IMT公式では、n=60を過ぎないと、安定しないのじゃな。
しかしじゃ。
n=100での計算値を見てみると、
台形公式が、20桁計算で0.056601463971665361156、
IMT公式が、10桁計算で、0.05582918442 。
DERIVEの20桁計算では、0.055829183312919721424 。となって、圧倒的にIMT公式の勝利じゃ」
「て言うか、『えらいぞ、DERIVE!』じゃないの。
試しに、IMT公式で、20桁で計算してみた。だけど、すごい時間がかかる。なんとかしたい」
「確かにな。
初等関数でない、∫(e^(1/(s(s - 1))), s, 0, k/n) を、Σの中で、そのままだと、2n回も計算する必要があるからじゃな。
20桁計算の、n=100のときに、約640秒≒10分は、いかにも、かかりすぎの感がある。
結果は、0.055829183312920364627、となって、小数点以下、13桁まで正しいのは、素晴らしいが」
「でも、DERIVEの数値は、当てになるのかしら?」
「ふ~ん。では、これは、どうじゃ。
g(x):=sin(100x^2) 。
これは、フレネルの積分の変数を少し変えているもので、DERIVEでは、FRESNEL_SIN(x)≡∫(SIN(πt_^2/2), t_, 0, x) で定義されている関数を使えば、計算できる。下図は、sin(100x^2)のグラフじゃ」
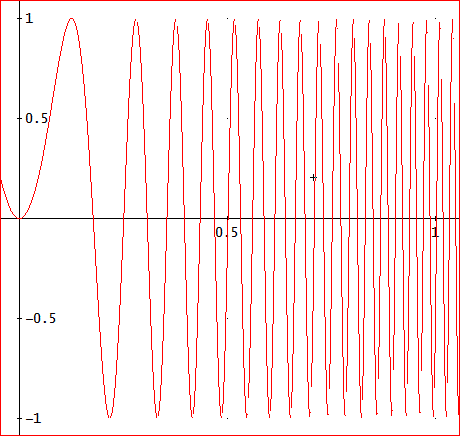
「ほー。ユーティリティファイル『FresnelIntegrals.mth』を読み込むと、その定義が出てくる!
ということは、問題の積分値は、FRESNEL_SIN(10√2/π)×(√π/2)/10≒0.05836708993・・となるわ」
「では、IMT公式、台形公式、シンプソン公式による計算結果をnを横軸にしたグラフにしてみよう。
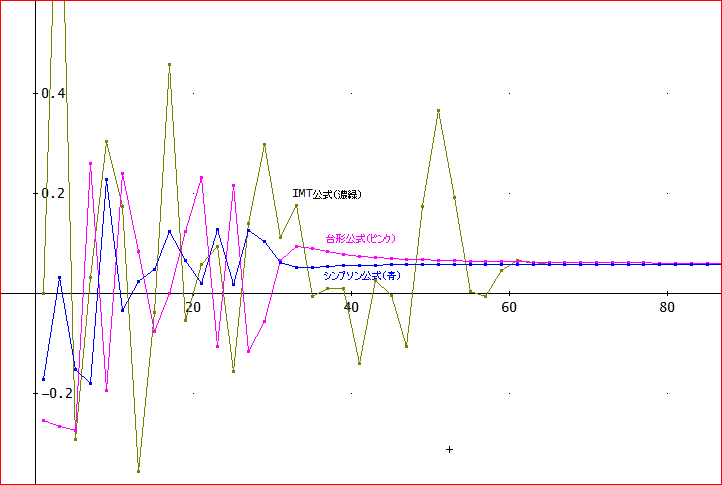
いずれも、n=60前後で安定してくるな。
数値的には、n=100で、
台形公式 :0.05994276300
シンプソン公式:0.05836709009 (実は、こっそりと200点計算している)
IMT公式 :0.05833909827
この場合は、シンプソン公式が小数点以下、7桁まで正しいので、4桁までしか合わないIMT公式より、よいな。
IMT公式でも、n=200で、0.05836709030 となんとか、挽回するが」
積分区間の変更
「積分区間の変更について、実例を交えて、まとめておこう。
まずは、元の変数、xの区間が、いずれも有限範囲、[a,b]である場合を、[c,d]に変更する方法じゃ」
 「この場合は、t= (d-c)x/(b-a)+(bc-ad)/(b-a) と tに写せば、tは、[c,d]に変化するよ」
「この場合は、t= (d-c)x/(b-a)+(bc-ad)/(b-a) と tに写せば、tは、[c,d]に変化するよ」
「では、半無限区間の場合じゃ。
[a,+∞)、あるいは、(-∞,b]のような場合は、どうするかな?」
「この場合は、いろいろとあり得るわね。
たとえば、第1の場合、a>0で、b=∞のときは、t=(d-c)×(x-a)/x+c のようにするとか。
第2の場合は、逆に、a=-∞で、b<0のときは、t=-(d-c)×(x-b)/x+d というように分数関数を使うのが普通かな」
「xが有限区間の場合は、逆変換は、x=((b-a)t+(ad-bc))/(d-c) じゃな。
半無限区間では、第1の場合、すなわち、x:[a,∞)→t:[c,d]であり、x=a(d-c)/(d-t)、
第2の場合、すなわち、x:(-∞,b]、→t:[c,d]であり、x=b(d-c)/(t-c)、となる。
最後に、xの変域が(-∞,+∞)の場合じゃな。
分数関数では、うまくいかないようじゃ。
指数関数を使って、たとえば、t=((d-c)/2)×tanh(x)+(d+c)/2=(d×e2x+c)/(e2x+1) とすれば、よいかもしれん。
逆変換は、x=(1/2)(LN(c-t)-LN(t-d)) となる。この逆変換では、tの変域は、(c,d)となる。
なお、半無限区間でも、t=αtanh(x)+β、ここで、α=(e^(2a)(d - c)/2 - (c - d)/2)、β=(e^(2a)(c
- d)/2 + (c + d)/2)
すなわち、t=((de^(2x) + e^(2a)(c - d) + c)/(e^(2x) + 1)、逆に、x=LN((e^(2a)(c -
d) + c - t)/(t - d))/2 とすることもできる。
では、簡単な例として、1/(x+1)の積分区間が、[2,3]である場合に、[0,1]に変換して計算してみて欲しい」
「x=((3-2)t+(2*1-3*0))/(1-0)=t+2 となる。dx=dtであるので、
∫(x=2~3)(1/(1+x))dx=∫(t=0~1)(1/(t+3))dt と変換できる。
左辺は、LN(4/3)≒0.2876820724 、また、左辺も、当然、同じになる。
右辺をIMT公式で計算すると、nが約50で、小数点以下、末尾まで正しく計算できる」
「では、半無限区間の例として、余弦積分 Ci(x))=-∫(t=x~∞)(cos(t)/t)dtで、Ci(1)≒0.3374039228は、どうかな」
「Ci(1)=-∫(x=1~∞)(cos(x)/x)dx ね。半無限区間の第1の場合、a=1、b=+∞なので、
x=1(1-0)/(1-t)=1/(1-t)、dx=1/(1-t)^2 dt から、
Ci(1)=-∫(x=1~∞)(cos(x)/x)dx=-∫(t=0~1)(cos(1/(1-t)))/(1/(1-t))×(1/(1-t)^2)
dt=-∫(t=0~1)(cos(1/(1-t)))/(1-t) dt
となるが、DERIVEで計算させると、なぜか、1.744325775 となる。
与式を、-∫(t=0~1-r)(cos(1/(1-t)))/(1-t) dt、r>0 として、lim r →+0の極限を取ると、0.3373419302 が求められる。
正解と比較すると、小数点以下、なんとか、3桁目までは求められたみたい」
「同じ式をIMT公式で扱ってみよう。n=1~200まで計算してみた。
こちらは、どうも、うまくいかない。試しに、n=600までとってみても、だめじゃな。
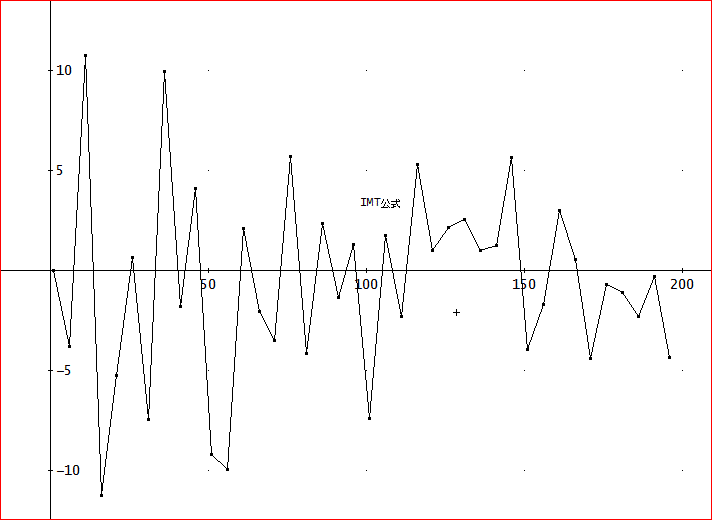
この理由じゃが、変換後の被積分関数のグラフを下図に示した。
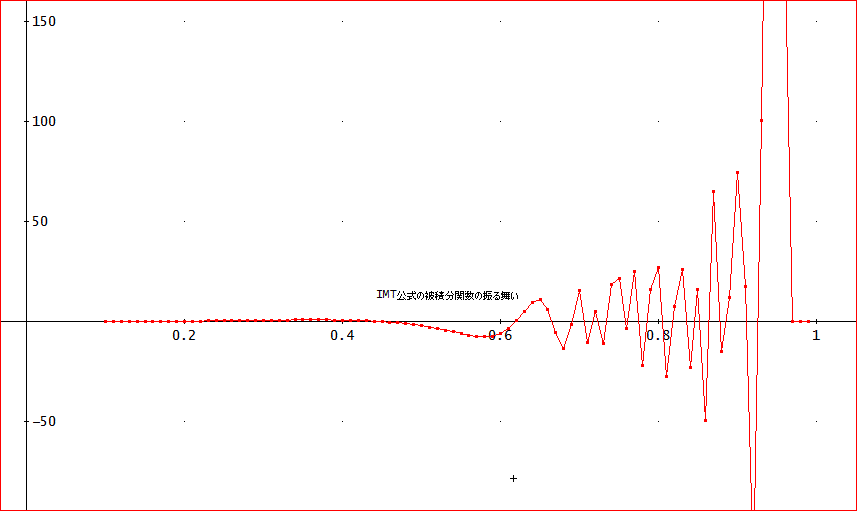
端点の1に近づくあたりから急速に大きくなり、しかも、正負に振動している。これでは、正しい結果が得られないのも無理はないかもしれん」
積分変数変換のご利益を探る(その1)
「前節の問題の解決策を探る意味で実験をしていこう。
まずは、無限区間の変数変換について、あらためて、考えてみよう。
たとえば、g(x)=1/(1+x^2)じゃ。0~∞で、π/2≒1.5707963267948966192・・となる。
1/(1+x^2)の様子は、赤い線のグラフじゃ。左右対称なので、左半面はほぼ省略している。
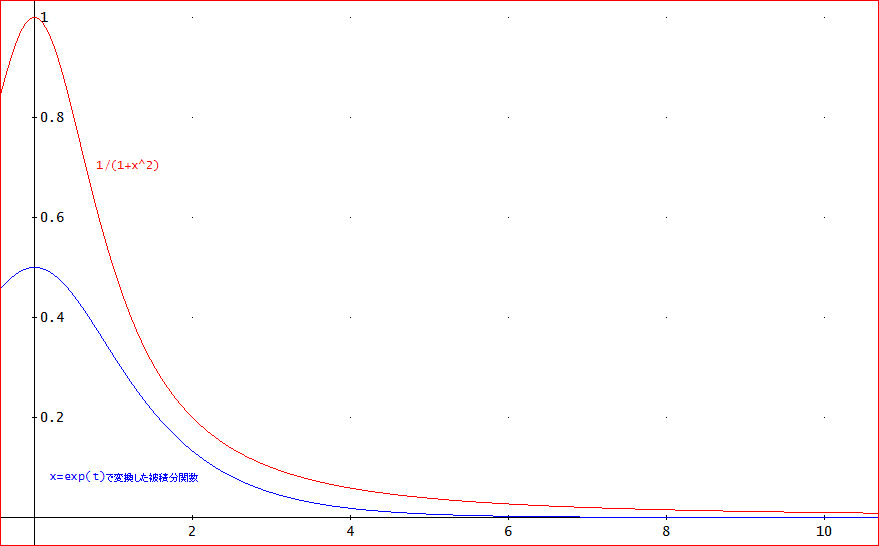
ここで、xが無限区間で、比較的にゆっくりと減衰しているのを、なるべく、速く減衰するように変えたいとする。
すなわち、xを変数 tの関数、x=φ(t)としたとき、φを、少なくとも、1/(元の関数)~x^nであれば、そのnよりも、大きく増加する関数にすれば、よいのではないかと思いつくじゃろう」
 「なるほど。たとえば、φ(t)=exp(t)のようにね」
「なるほど。たとえば、φ(t)=exp(t)のようにね」
「そうじゃ。このように変換したときに、変換した全体の被積分関数は、e^t/(e^(2t) + 1)、となり、これは、図の青い線のグラフのように原関数よりも速く減衰する。
ただし、求めたい積分は、I=∫(x=0~∞)(1/(1+x^2)) dx であるのだが、
φ(t)=exp(t)としたときは、積分下端は、0から-∞に変化することにと注意する必要がある。上端は、同じ+∞じゃ」
「s(h, n)= h∑(e^(hk)/(e^(2hk) + 1)h, k, -n, n) と台形公式で積分を計算するけど、nは、どの程度、取ればよいのかな」
「そこじゃ。
今、小数点以下、6桁程度は、正しく求めたいとする。このとき、(e^(hn)/(e^(2hn) + 1)≒10^(-7)程度まで、とる必要があるじゃろう。
w≡exp(hn)とおいて、w/(1+w^2)=10^(-7)という2次方程式を解くと、w≒10^(-7), 10^7 という2根が得られる」
「不思議!
DERIVEで代数解を出すと、2根が出るのに、数値解だと、10^(-7)の方しか出ないわね。それと、桁数を10桁ではなくて、20桁としておかないと、w=0みたいな、とんちんかんな答えが出る」
「ま、いずれにしても、exp(hn)が10(^±7)程度を目安にするためには、hnは、±16程度以上必要じゃ」
「ということは、hを0.01とすると、n≒1600ぐらいは、必要という事ね。
台形公式で計算すると、I=1.5707961028480233450 となるね。小数点以下、6桁まで合っている!」
「0.1刻みでも、160点計算すると、1.5707961127905372807 と同じように合うのう」
「でも、元の積分ではどうなのかな?」
「hn≒3162ぐらいとなるので、h=0.01では、n=30万点以上とる必要はある。
しかし、1.5754629940294638406、となって、小数点以下、2桁までしか合わない。
h=0.001として、n=300万点とって、1.5709629935294645073。
もっとも、この積分の場合は、シンプソン公式等の高次の公式を使えば、こんなに分点を取らなくてよいのはあらためて言う必要は無い。しかし、無限区間を無限区間に変換する『ご利益」の一例として、挙げてよいのではないかと思う」
「久々に出たわね『ゴリヤク』が~♪
そうすると、もっと、速く、大きくなる関数に変換することも考えられるわね。たとえば、φ=exp(t^2)のような」
「単純には、そうはいかんじゃろう。
台形公式の精度が高くなる条件を忘れてはいないかな?」
「あ、そうか。変換後の被積分関数及び導関数の値が両端で、ゼロ又はゼロに近づくことね。
φ=exp(t^2)のような変換では、全体が奇関数になってしまうので、t=-∞~+∞とすると、積分値が当然、ゼロになってしまう。
t=0~∞とすれば、その点はいいのだけど、t=0では、被積分関数はゼロだけど、導関数がゼロにならないわ。
じゃ、φ=exp(t^3)のようにしないといけない訳ね。
うへ~。今度は、偶関数だけど、ふたこぶラクダみたいになってしまう」
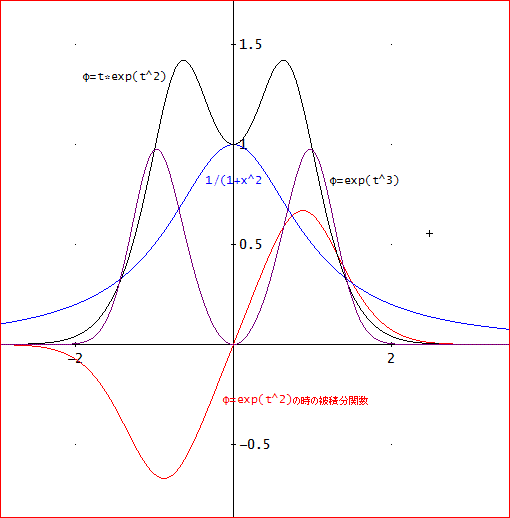
「それでも、問題はない。10^(-7)以下に抑えるためには、hn≒220以上必要じゃ。
ただし、k=0~として、計算する場合は、計算結果を2倍にするのを忘れてはいけないよ。
h=0.01ととれば、n≒260程度、I=1.5707962848164468145。
h=0.001として、n=3000とすれば、I=1.5707963267911880861 となって、小数点以下、11桁まで合ってしまう」
積分変数変換のご利益を探る(その2)からDE公式へ
 「じゃ、いっそのこと、φ=exp(exp(t))のようにしたらいいじゃないの」
「じゃ、いっそのこと、φ=exp(exp(t))のようにしたらいいじゃないの」
「一見いいようにも思うが、その変換では、元の積分区間の下端がゼロという条件を満たすtがないことになる。それでは、具合が悪い。
φ=exp(exp(t))-exp(exp(-t))とすれば、xの0~∞は、t=0~+∞であるのじゃが、今度は、変換後の被積分関数がt=0では、ゼロにならない」
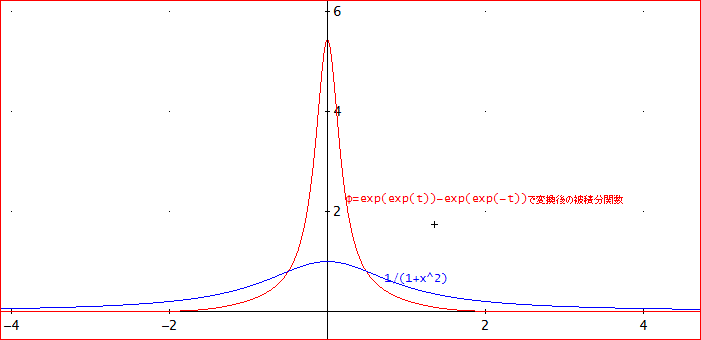
「う~ん。
じゃ、φ=(EXP(EXP(t)) - 1)/(1 + EXP(EXP(-t)) とすれば、いいじゃない」
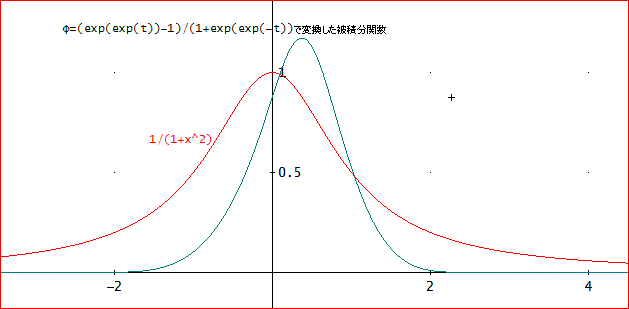
「そのようじゃな。
こうすると、被積分関数=(e^e^t(e^e^(-t)(e^t + e^(-t)) + e^t) - e^(e^(-t) - t))/(e^(2e^t)
- 2e^e^t + e^(2e^(-t)) + 2e^e^(-t) + 2)、となる。
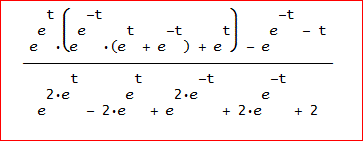
DERIVEの式では、イメージがわかんかもしれんので、DERIVEの画面コピーを見て欲しい。
この式で、tを±3の範囲で、台形公式で計算すると、
h=0.01で、1.5707963232050353981、h=0.001で、1.5707963228572748741
t=±5で計算すると、
h=0.01で、1.5707963267948966192 と計算範囲内で真値と一致してしまう。
このような変換方法は、『二重指数関数型数値積分公式(double exponential formula, 略してDE 公式) 』として知られているものじゃ」
「IMT公式の改良となる訳ね」
「まあ、そうも言えるじゃろう。IMT公式に触発されて、開発されたということじゃから。
詳しい研究によると、このようなDE変換と台形公式の組合せが一定の範囲の関数について最適であることが証明されているとのことじゃ。
次回は、このDE公式について、あらためて、取り上げてみよう」
最終更新日 2011/8/10



 「数式処理ソフト DERIVE(デライブ)の第54回 数値積分(3)(Euler-Maclaurin展開とラプラス変換、Wijngaarden変換)と第55回の数値積分(4)(Wijngaarden変換(続き))では、『数値積分』と銘打っているものの、ちょっと寄り道しちゃったわね」
「数式処理ソフト DERIVE(デライブ)の第54回 数値積分(3)(Euler-Maclaurin展開とラプラス変換、Wijngaarden変換)と第55回の数値積分(4)(Wijngaarden変換(続き))では、『数値積分』と銘打っているものの、ちょっと寄り道しちゃったわね」