数式処理ソフト DERIVE(デライブ) de ドライブ
57.数値積分(6)(DE公式)
DE公式の概要
「数式処理ソフト DERIVE(デライブ)の第56回で、IMT公式を説明した後に、『DE公式』について、少しだけ触れたんじゃが、今回、あらためて、取り上げてみよう。
まずは、記法を説明しよう。
原積分の積分区間を、x=a~x=bとして、定積分 I=∫(x=a~b)f(x)dx を考える。
このとき、a及びbは、有限でも無限でもよい。また、関数f(x)は、端点を除いて、解析的でないといけないが、端点では、特異性を持ってよいものとする。
原積分の変数xを急激に大きくななる関数で置き換える。そのために、x=φ(t)とおく。
a=φ(-∞)、かつ、b=φ(∞)であり、端点に近づく際に、被積分関数が「二重指数型」でゼロに近づくφ(t)を選ぶ必要がある。
すなわち、lim t→±∞ |f(φ(t))×φ'(t)|≒exp(-定数×exp(|t|))。
このような変換後に、Iの数値積分を行う場合は、台形公式によるのが、もっとも、精度が高くなる。
刻み幅をh、打ち切り項数を、それぞれ、M、Nとしたとき、
I≒h×Σ(k=-M~+N)f(φ(kh))×φ'(kh) と近似できる。
以上が、京都大学数理解析研究所(1998年)の森正武先生(1937年~)による『二重指数関数型変換のすすめ』(1998年)に基づく説明じゃ」
 「これによると、DE公式は、1974年に高橋秀俊先生(1915年~1985年)と森先生により『Double exponential formulas for numerical integration, Publ.RIMS Kyoto Univ. 9 (1974) 』として発表されたのが最初なんだ。
「これによると、DE公式は、1974年に高橋秀俊先生(1915年~1985年)と森先生により『Double exponential formulas for numerical integration, Publ.RIMS Kyoto Univ. 9 (1974) 』として発表されたのが最初なんだ。
高橋先生は、工学、コンピュータ、電気、数学まで、本当にいろんな分野で活躍された、スケールの大きい学者さんだったわね」
「まったく、惜しい方であった。
『ロギルギスト』の一員として、「物理の散歩道」(岩波書店)などの啓蒙書でも才筆をふるわれたのじゃったな。
蛇足かもしれんが、二重指数型の関数を使うと、べき乗のべき乗の項が含まれるので、被積分関数の計算中に、オーバーフローする可能性があることには、注意が必要じゃ」
DE公式の例題1(無限区間)
「では、まずは、簡単な例題でDE公式に慣れてみよう。
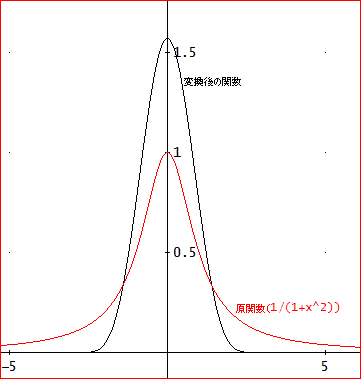
原積分は、∫(x=-∞~∞)1/(1+x^2)dx=π≒3.141592653・・じゃ。
ちなみに、この関数の場合は、不定積分も、ATAN(x)と求められるがの」
 「え~と、f(x)は、実軸上は、至るところ、解析的で問題はなし。
「え~と、f(x)は、実軸上は、至るところ、解析的で問題はなし。
両端が無限区間なので、前節の紹介記事の処方箋に従うと、φ(t)=sinh((π/2)sinh(t))、と変換するのがDE変換ね。
だけど、双曲線関数を使う必要があるのかしら?」
「φ(t)=exp(exp(t))-exp(exp(-t))、としても、同様に計算は可能じゃ」
「じゃ、まずは、お勧めの変換関数を使って、計算してみるよ。
元の関数と変換後の関数は、次のグラフに示しているとおりだよ
まず、n(L, h):= IF(h > 0, FLOOR(L/h) + 1, 0) と項数 nをtの(半)区間の長さLと刻み幅hの関数として定義するの。
ここで、FLOOR()という関数が出てくるけど、これは、()内の引数の値を超えない整数を表す『組み込み関数』なのよ。
引数がマイナスの場合は、たとえば、FLOOR(-1.5)は、-2となるので、注意してね。
次に台形公式の計算結果 S(L, h)を、下記のように定義します。
S(L, h) := h∑(πe^(πe^(hk)/4 + πe^(- hk)/4 - hk)(e^(2hk) + 1)/(2(e^(πe^(hk)/2)
+ e^(πe^(- hk)/2))), k, - n(L, h), n(L, h))
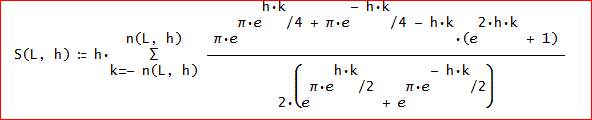
上図が、SのDERIVEの画面表示ね。
最後に、S(L,h)とS(L,h/2)との絶対値の差が10^(-10)より小さくなるまで、刻み幅を半分にしながら計算することを考えたの。
J(L, h):= IF(ABS(ABS(S(L, h)) - ABS(S(L, h/2))) < 10^(-10), S(L, h),
J(L, h/2))、
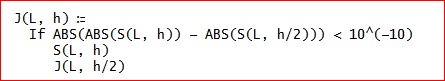
区間のLの値だけど、被積分関数のグラフから、あたりをつけて、t=3で、4.634497644×10^(-6)、t=4で、2.072929865×10^(-17)となるので、
Lを4と置けば、十分。
そこで、J(4,1)とすると、≒3.141592653 と最終桁まで、正しく求められたわ」
「DE公式の定式化としては、問題はないのじゃが、改良したいところが3つあるのう。
(1)近似値が求まったときの刻み幅 hの値を明確にしたい
(2)J(L,h)の中で、前に計算したS(L,h)を再計算しない工夫をしたい
(3)収束しない場合の計算回数の制限を入れたい
そのためには、Jの関数を次のように拡張すれば、よいのじゃな。
J(L, h, p, q, m):=IF(m > 100, exit, IF(ABS(ABS(p) - ABS(q)) < 10^(-10), [q, h, m], J(L, h/2, q, S(L, h/2), m + 1))) 。
下の画面コピーの方が見やすいじゃろう。
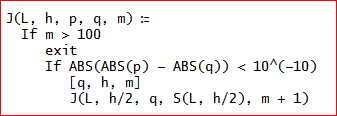
上の新しい定義では、ダミー変数として、pとqを使っている。pとqは、前々回と前回に計算したSの値を保持している。
また、計算回数の制限として、mを使用している。ここでは、mが100回を超えると、『true』と表示して終了する。
J(L,h,1,0,0)のように、p=1、q=0、m=0として、使用する。
実は、pとqの値は何でもよいのじゃが、10^(-10)より、差が大きい組合せでないといけないのは当然じゃ」
「すこし、わかりにくいわね。
[q,h,m]の部分は、ベクトルとして、表示しろ、ということね」
「そうじゃ。
どうやって、J以外の、hやmの値を表示させればよいのか、さんざん迷ったのじゃ。
単にベクトルとして表示させれば、よかったということじゃ。
また、pとqの使用方法は、これは、DERIVEのDOS版のテキストを見て、分かったという次第じゃがな。
q→p、S(L,h/2)→qが次々と置き換えられていくことで、Sの計算は、一回で済ましている。
Basicなどのプログラミング言語流に関数の定義の中で、複数個の命令を書こうとするとエラーになってしまうのじゃな。引数を増やしてダミー変数として使用することは、まず、ないのじゃから、戸惑うのは当然じゃ」
「なるほどね。
だんだんに慣れていきましょう。上記の方法で計算すると、
J(4,1,1,0,0)、すなわち、半区間 L=4、初期刻み h=1として、
[3.1415926535897932384, 0.125, 3]と20桁計算で、刻み幅h=0.125=1/2^3で、真値に十分に近い値が求まったわ」
DE公式の例題2(半無限区間)(exp(-x)を含む場合)
「半無限区間の例として、f(x)=exp(-√x)で、区間、0~+∞じゃ。これは、不定積分が求められるので、厳密解は、2となる」
 「この場合は、さっきの変換関数じゃ、変換後の被積分関数の形が釣り鐘型にならないわ。
「この場合は、さっきの変換関数じゃ、変換後の被積分関数の形が釣り鐘型にならないわ。
無理に計算させようとすると、区間 L=2.5、初期刻み=0.5として、計算が終了せずに、100回を超えてしまう」
「このような場合は、φ=exp(t-exp(-t))とすればよいとある。
実際、原関数と被積分関数、e^(- e^(t/2 - e^(-t)/2) - e^(-t))(e^t + 1) となり、グラフは下図のようになる」
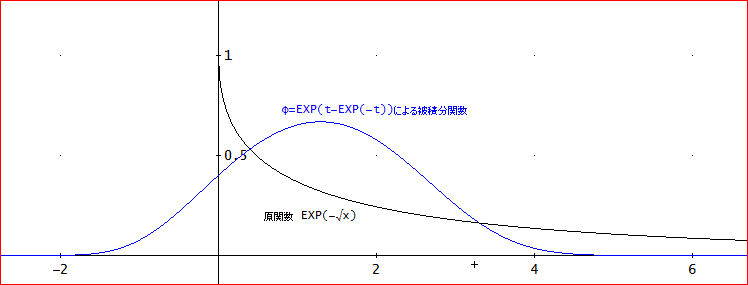
「すごいわ。J(8,1,1,0,0)として、[2, 0.125, 3]が計算できた。
なだらかな被積分関数になると、とたんに精度が異常に高くなるよ。
でも関数f(x)を変える度に、Sの定義式を直すのは、面倒くさいわ」
「Sの定義式を、S(L, h) := h∑(φ'(kh)f(φ(kh)), k, - n(L, h), n(L, h))、すなわち、
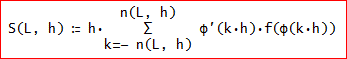
のように、しておけば、f(x)、φ(t)によって、いちいち、Sの定義式を変えなくてもよい」
「なるほど。
では、f(x)=√x×exp(-x)では、どうかな?
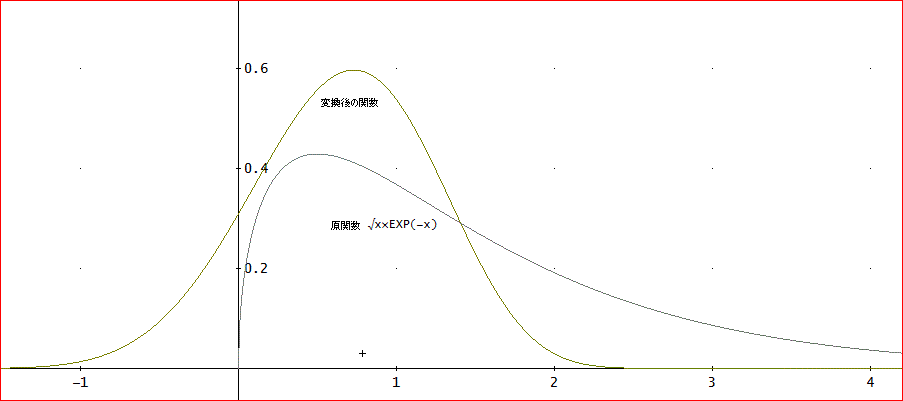
この場合は、
J(4, 1, 1, 0, 0)として、[0.88622692545275801364, 0.125, 3]となって、厳密解 π/2とほぼぴったりね」
「他の例としては、f(x)=sin(x)×exp(-x)で0~∞までの値、厳密解は、0.5にたいしても、J(3, 1, 1, 0, 0)≒[0.50000000001598465727,
0.0625, 4]。
真値に十分に近い値を計算できるているのう」
DE公式の例題3(有限区間)(事前に-1~1に区間を変換が有効)
「有限区間の例として、f(x)=√xをx=0~3まで積分してみよう。
まずは、積分区間の変更により、原積分を、f(x)=√(3(x+1)/2、x=-1~1に変更しておくとよい。
こうすると、積分は、-1~1の積分に変更される。この-1~1の積分については、変換関数、φ=tanh((π/2)sinh(t))を使う。
ただし、事前の変数変換による因子として、3/2倍がかかるので、計算する積分は、
(3/2)×∫(x=-1~1)(√(3(x+1)/2 dx=2√3≒3.4641016151377545870・・となるはずじゃ」
 「J(3,1,1,0,0)として、([2.3094010767585030001, 0.125, 3])が得られるので、3/2倍すると、原積分の値として、3.4641016151377545001となって、十分に高い精度で計算できているね」
「J(3,1,1,0,0)として、([2.3094010767585030001, 0.125, 3])が得られるので、3/2倍すると、原積分の値として、3.4641016151377545001となって、十分に高い精度で計算できているね」
「ちなみに、以前書いたように、u=(2x)/(b-a)-(a+b)/(b-a)、すなわち、x=(b-a)u/2+(a+b)/2として、[-1~1]への変換が可能じゃ。
ここで、元の区間は、x=a~bじゃ」
「じゃ、f(x)=1/√xで、区間が1~2はと、厳密解は、2√2 - 2≒0.82842712474619009760・・。
一方、u=(2x)/(b-a)-(a+b)/(b-a)=2x-3で、積分は、(1/2)∫(u=-1~1)(√2/√(u + 3)du となる。
J(3, 1, 1, 0, 0)≒[1.6568542494923801480, 0.125, 3]となるので、2で割って、0.82842712474619007399 を得る。
なるほど、そのまま、積分するのとは、ずいぶん違うわ。
下図が、f(x)=1/√x の方のグラフよ。
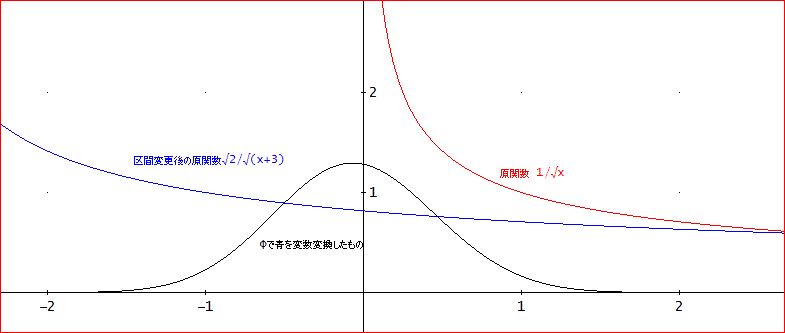
「次回は、振動部分を含む例を取り上げよう」
最終更新日 2011/8/16



 「これによると、DE公式は、1974年に高橋秀俊先生(1915年~1985年)と森先生により『Double exponential formulas for numerical integration, Publ.RIMS Kyoto Univ. 9 (1974) 』として発表されたのが最初なんだ。
「これによると、DE公式は、1974年に高橋秀俊先生(1915年~1985年)と森先生により『Double exponential formulas for numerical integration, Publ.RIMS Kyoto Univ. 9 (1974) 』として発表されたのが最初なんだ。