数式処理ソフト DERIVE(デライブ) de ドライブ
58.数値積分(7)(DE公式 続き)
DE公式の変換関数のまとめ
「数式処理ソフト DERIVE(デライブ)の第57回でDE公式の変換関数が2つ出てきた。これらを含めて、ここでまとめておこう。
以下の表のaとbは、原関数の積分区間じゃ。cとdは、変換後の積分区間とする。ただし、『事前変換』を行った場合は、c,dは、変換後の区間を意味する」
| 原関数 |
a |
b |
事前変換 |
変換関数 |
c |
d |
例 |
備考 |
| f(x) |
-1 |
1 |
不要 |
tanh((π/2)sinh(t)) |
-∞ |
+∞ |
f(x)=tan^2(x)を-1~1で積分 |
本節の第1例 |
| f(x) |
有限 |
有限 |
x=(b-a)u/2+(a+b)/2
で、-1~1に変換 |
tanh((π/2)sinh(t)) |
-∞ |
+∞ |
f(x)=√xをx=0~3まで積分 |
57.数値積分(6)(DE公式)例3 |
| f(x)=1/√xで、区間が1~2 |
57.数値積分(6)(DE公式)例3 |
| f(x) |
-∞ |
+∞ |
不要 |
sinh((π/2)sinh(t)) |
-∞ |
+∞ |
∫(x=-∞~∞)1/(1+x^2)dx |
57.数値積分(6)(DE公式)例1 |
| f(x) |
0 |
+∞ |
不要 |
exp((π/2)sinh(t)) |
-∞ |
+∞ |
f(x)=1/(x^2+√x)で、0~∞ |
本節の第2例 |
| f(x)exp(-x) |
0 |
+∞ |
不要 |
exp(t-exp(-t)) |
-∞ |
+∞ |
f(x)=exp(-√x)で、区間、0~+∞ |
57.数値積分(6)(DE公式)例2 |
 「これまでに例が挙がっていないものがあるのね。何か例を挙げて下さいな」
「これまでに例が挙がっていないものがあるのね。何か例を挙げて下さいな」
「そうじゃな。一番最初のものとしては、f(x)=(tan(x))^2、x=-1~1などでは、どうかな?」
「そうね、この関数は、定義域内で解析的で、両端点でのみ、+無限大に発散するのね。
試しに、DERIVEでは、∫(x=-1~1)(tan^2(x) dx=2×tan(1)-2≒1.1148154493098044610・・と厳密解と近似値が求められる。
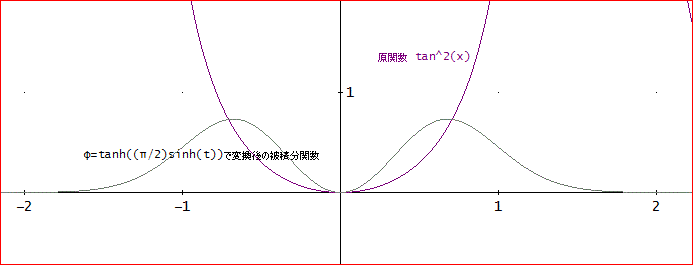
グラフでは、こんな感じで、二つに分かれちゃっているね。φ=tanh((π/2)sinh(t))としているよ。
半区間の長さ L=3とすると、t=3のときの(変換後の)被積分関数値は、10^(-12)以下となるので、L=3で十分。
なので、J(3,1,1,0,0)を(数値)計算すると、([1.1148154493097967341, 0.0625, 4])を得る。小数点以下、11桁まで合っているわ。
J(4,1,1,0,0)=([1.1148154493098044610, 0.0625, 4])」となって、最終桁まで、求められている。
なお、計算桁数は、20桁としています」
「読者に代わって、説明すると、このJ()は、
J(L, h, p, q, m):= IF(m>100, exit, IF(ABS(ABS(p) - ABS(q)) < 10^(-10),
[q, h, m], J(L, h/2, q, S(L, h/2), m + 1)))
と定義した、DERIVEのユーザ定義関数じゃな。
前回の第57回で説明しているが、上式中のS(L,h)は、S(L, h) := h∑(φ'(kh)f(φ(kh)), k, - n(L, h),
n(L, h)) で定義した被積分関数の積分の値を台形公式で計算する関数じゃ。
わかりにくいと思うんじゃが、補助的な変数 p、qは、前々回と前回のそれぞれのSの値を保持するためのものじゃ。
Jの中で、Sの計算をダブって行わないために使われている。計算回数が増えなければ、負担にならんので、p、qを使わない方が分かりやすいかもしれん。
また、n(L, h):= IF(h > 0, FLOOR(L/h) + 1, 0) と定義されている計算項数を決める関数じゃな。簡単のために、正負とも同数の項数を計算しているがな。
最後に出力結果じゃ。ベクトルとして、[積分値、刻み幅、回数]を出力している。
n()、S()、J()のDERIVEの画面は、再掲すると下図のようになる。
ただし、途中の黒い横線は、見やすいように入れたもので、実際の画面では、横線はない」

「そう。第57回の森先生の文では、Sの定義で、計算する項数を、正と負で違えて入れられるように定義しているわね」
「うん。そうじゃな。
われわれの場合は、グラフによって目視で確認しているが、コンピュータで自動計算させる場合は、区間の長さも自動判定させる必要があろう。
その場合は、項数を正負別々にした方がよいじゃろう。そのように上の定義を変更することは、難しくはない」
「抜けている2番目の例は、f(x)で、ゼロから+∞までの積分か。
たとえば、こんなのは、どうかしら。
f(x)=1/(x^2+√x)、x=0~∞、厳密解は、4√3π/9≒2.4183991523122904674・・となるわ」
「この場合は、φ(t)=exp((π/2)sinh(t))で変換する。グラフは下図のようになる。
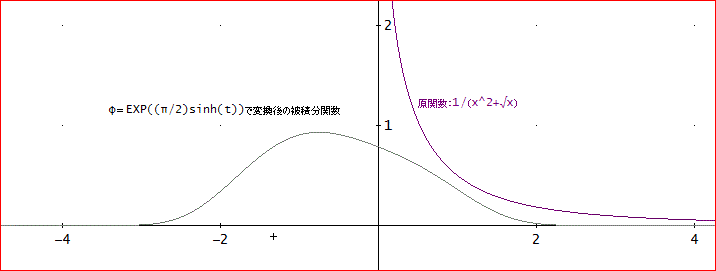
L=5とすれば、十分過ぎるぐらいなので、J(5,1,1,0,0)≒[2.4183991523122904674, 0.125, 3]となって、全桁合っておるわい」
「f(x)=1/(x^2+2√x)、x=0~∞、と係数を変えると、DERIVEで厳密解が求まらないわ」
「√x=u、と置いて、∫(u=0~∞)(2/(x^3+2)) duと、手伝ってあげれば、2√3×2^(1/3)π/9≒1.5234959995230861422・・。
とはいうものの、元の積分でも、DE公式ならば、J(5,1,1,0,0)≒[1.5234959995230861422, 0.125, 3]。
事前に変換した後では、J(4,1,1,0,0)≒([1.5234959995230861524, 0.0625, 4])。
この場合は、Jの定義式の中の、<10^(-10)を<10^(-18)程度に小さくしないと、限度一杯の値は得られない。事前に変換しない方が真値により近い値が得られるという例じゃな」
「そう言ったって、事前に変換した方が被積分関数が尖っているものね」
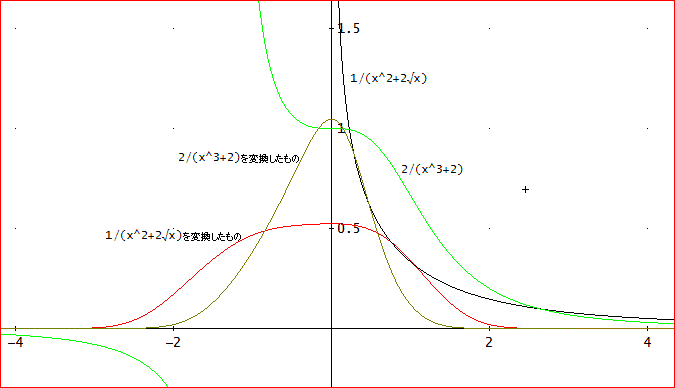
「まあ、そうかもしれんな。
なお、上図で、2/(x^3+2)は、左半面にもグラフがあるように見えるが、実際は、右半面だけが実体じゃからな。注意して欲しい」
DE公式の弱点?
 「弱点ですか?」
「弱点ですか?」
「どんなものにも、弱点があるぞ。
DE公式の弱点は、振動関数に有り、じゃな」
「ははぁ。たとえば、∫(x=-∞~∞)(sin^2(x)/x^2)dx=π、のような積分ですか?」
「この積分は、下のグラフのように、そのまま、変換すると細かく振動する部分が生じてしまう。
一般にじゃな、DE公式では、元のxを変数変換により、exp(exp(t))のように増加させている。ところが、sin(x)やcos(x)などの振動する関数が含まれていると、当然ながら、これらの三角関数なども原関数より、極めて振動数が高く、すなわち、波長が短くなり、しかも、振動数も少しずつ変化してしまうのじゃな。上記の関数は、全体が正であるから、まだしもじゃが、正負の項が現れると特に困ったことになる」
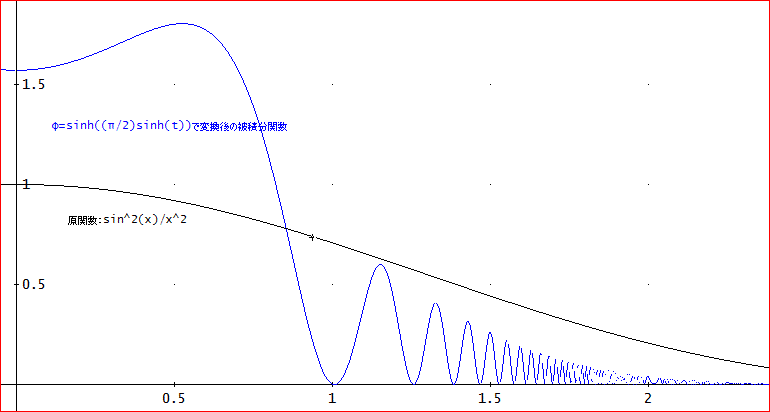
「ほんとだ~。
Jの打ち切り誤差を10^(-10)から、10^(-2)にして、やっと、J(4, 1, 1, 0, 0)=[3.1364011126415462761, 0.00390625, 8]、と収束したわ。
でも、当然だけど、小数点以下1桁までしか合わないとはね」
「いろいと考えるべき点が多い。
ひとまず、上記の定積分より、シンプルな、∫(x=-∞~∞)(sin(x)/x)dx=πを検討してみよう。
そういえば、ともちゃんは、すでに、第51回『複素関数(6)(留数定理の応用)』に出てきたから、この定積分には、見覚えがあろう」
「そうね。そのときは、複素関数の留数の応用例として、解いたんだったわね。
これは、f(x)=sin^2(x)/x^2 と、同じ値となるんだね。こいつは不思議!」
「これは、簡単じゃ。
まずは、(sin^2(x)/x)'=2sin(x)cos(x)/x-sin^2(x)/x^2 であるので、部分積分により、∫sin^2(x)/x^2
dx=∫(sin(2x)/x)dx ということになる。
この変数を、t=2xとおいて、変換すれば、∫(sin(2x)/x)dx=∫(t=-∞~∞)(sin(t)/t) dtとなることがわかるじゃろう」
「なるほど。sin^2(x)から(1-cos(2x))/2の方に変形するのかと思ったけど、それだと、行き詰まっちゃうわね」
正弦積分について
「∫(t=-∞~∞)(sin(t)/t) dtのような定積分はいろいろとある。
この正弦定積分(以下「正弦積分」という)は、正弦積分関数 SI(x)=∫(t=0~x)(sin(t)/t) dt で、x→∞とした極限値(の2倍)となるのじゃ。
また、非負の実数 ωに対して、∫(t=-∞~∞)(sin(ωt)/t) dt=∫(t=-∞~∞)(sin(t)/t) dt となって、左辺の積分内には、ωが含まれているが、その値にかかわらず、右辺と等しいことが知られている。
証明は、左辺をωで微分してみるとよい」
 「え~と。まずは、左辺をg(ω)=∫(t=-∞~∞)(sin(ωt)/t) dt と置くよ。
「え~と。まずは、左辺をg(ω)=∫(t=-∞~∞)(sin(ωt)/t) dt と置くよ。
g'(ω)=∫(cos(ωt)/t dt となるけど、この右辺の積分内は、奇関数なので、g'(ω)=0。よって、g(ω)はωに無関係な定数となる。
具体的には、g(1)=πから、g(ω)=π」
「そのとおり。
この左辺の定積分は、関数 1/tの『フーリエ変換』と考えられるので、ω>0では、F(ω)=πが、そのフーリエ変換された角振動数(角周波数)の関数であることを示しているのじゃな。角振動数にかかわらず、一定の大きさじゃ。
なお、フーリエ変換の定義により積分の前の係数が異なるものがあるので若干の注意が必要じゃが、ここでは、これ以上立ち入らんがの。
また、次のような『ラプラス変換』を使っても、正弦積分の値は、計算できる。
まず、∫(t=0~∞)(exp(-st)sin(t)) dt=1/(s^2+1) であることに注意する。
『ラプラス変換』の形式にそろえるために、tの右半面に限定している。また、ラプラス変換のパラメータを s と書いた。
このようにすると、∫(t=0~∞)(sin(t)/t) dt⇔∫(s=0~∞)(1/s^2+1)ds=π/2 となって、左辺の極限値が分かる。
元の積分には、負の部分もあるんじゃが、偶関数なので、正弦積分自体の値は、2倍のπということがわかる」
「あー。ここで、ようやく出てきたね。
第43回の『積分(3)(演算子法の応用)』の冒頭で提示していたんだけど。
一般に、∫(t=0~∞)f(t)/t dt⇔∫(s=0~∞)F(s)ds なのね。
ここで、f(t)のラプラス変換、すなわち~、∫(t=0~∞)(exp(-st)f(t))dtをF(s)と書いているのよ。
f(t)/tではなくて、f(t)のラプラス変換というところに注意してね」
「早速の応用例じゃが、正の実数を aとしたとき、∫(t=0~∞)(exp(-at)sin(t)/t) dtは、どうなるかな?」
「えーと。これは、exp(-at)sin(t)⊃1/(a^2 + 2as + s^2 + 1)となるので、∫(s=0~∞)1/(a^2 + 2as
+ s^2 + 1)ds=ACOT(a)となるわ」
「試しに、a=2とすると、π/4 - ATAN(1/3)≒0.4636476089 が得られるが、直接、∫(t=0~∞)(exp(-2t)sin(t)/t)
dtを積分してみても、正しいことが分かるじゃろう。
正弦積分、∫(t=0~∞)(sin(t)/t) dt=π/2、からは、変数変換で、見た目の違う定積分がいろいろと導ける。
たとえば、t=u^2とおくと、tの正の側で、∫(u=0~∞)(sin(u^2)/u)du=π/4。
あるいは、やや一般化すると、∫(u=0~∞)(sin(u^y)/u)du=π/(2y)、ここで、y>=1の実数などじゃな」
「∫(t=-∞~∞)(sin(t^2))dt=∫(t=-∞~∞)(cos(t^2))dt=√(π/2)などの『フレネルの積分』は、どうかしら?」
「ラプラス変換の応用でも可能のようじゃが、ここでは、複素関数の続きでやることにして、先へ進もう」
DE公式による正弦積分の数値計算(1)
「さて、懸案となっている、∫(t=-∞~∞)(sin(t)/t) dt などの振動部分を持つ場合に対するDE公式を検討をしようかの」
 「まずは、素直に、このまま、やってみましょうか。
「まずは、素直に、このまま、やってみましょうか。
tの右平面のみを考えて、∫(t=0~∞)(sin(t)/t) dt を扱うものとすると、
φ(t)=exp((π/2)sinh(t))で変換する。変換前と変換後の関数のグラフは次のようになる。
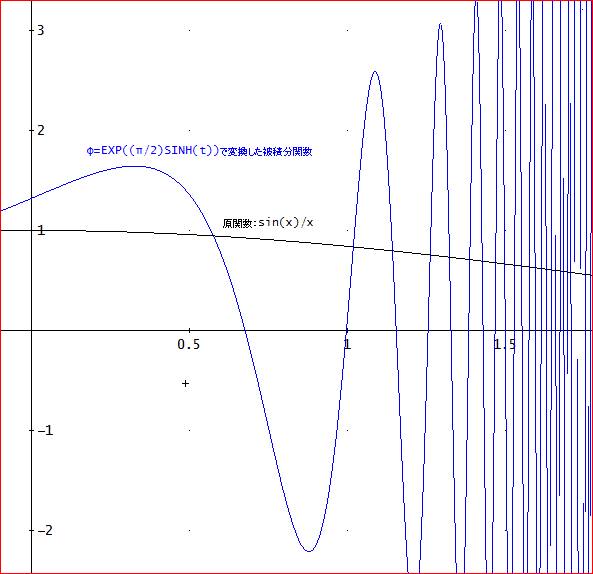
案の定、というか、やっぱりというか、すごいことになるわ」
「まあ、このまま計算しても時間の無駄という感じじゃな。
DE公式を使わない場合は、正負の周期がπ毎に規則正しく正負が変化するので、周期毎に積分してからEuler変換を使うのが常道だろう。
しかし、ここでは、DE公式の使用例じゃからな。何か、工夫が必要じゃ」
「変換関数φを変えてみるとか、かしらね」
「その方向が一つ、あるいは、元の関数の範囲を限定するというか、圧縮してしまう方向じゃろう。
元の関数の変数xは、0~∞なのじゃが、x=2mπでカットして、この間を、u=-1~1に収めるために、u=(x-(mπ))/(mπ)と予備的に変換する。
ただし、得られた値を(mπ)倍する必要がある。(2mπ倍でないのは、区間0~2mπを-1~1の長さ2の部分に写しているから、2で割る)
また、変換関数は、u=-1~1なので、φ=tanh((π/2)sinh(t)) とする」
「じゃ、m=10で、x=0~20πの間の関数を変換してみると、下図のようになったわよ」
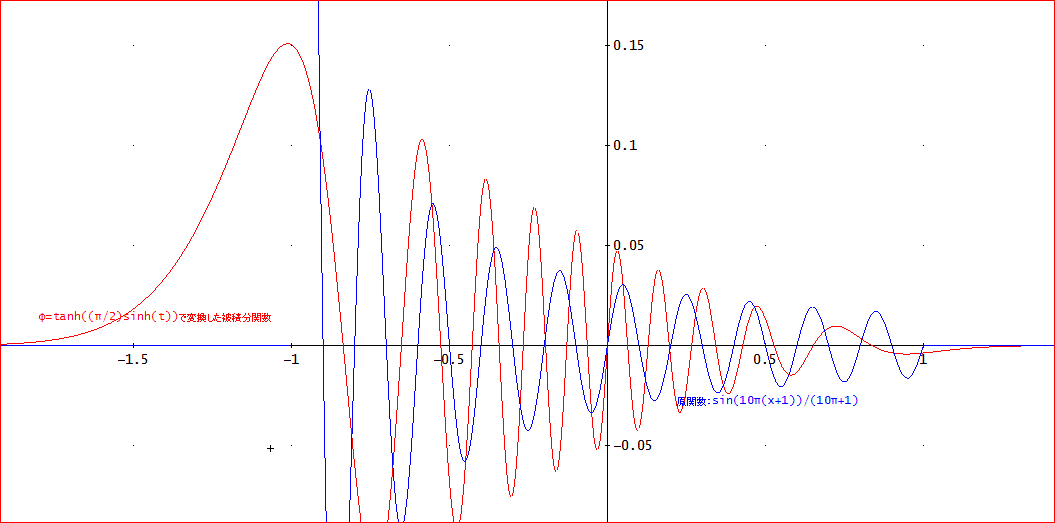
「これで、赤い方が変換後の被積分関数じゃ。
試しに、刻み幅h=0.001として、左右3/0.001≒300点(計600点)を取って計算した値を10π倍すると、1.5548888710434583023、となる。
これで、2桁程度は、π/2≒1.5707963267948966192に近づいてくる」
「ていうか、この場合、正弦積分関数 SI(20π)=1.5548888710447447500・・なので、積分計算自体は、小数点以下、11桁は正しいよ!」
「まずは、初戦突破ということかの。
ただし、相手は無限区間なので、どこでカットするかが大切ではあるの」
「ちょっと、おまけして、m=1000としてみよう。これで、元のxにして、0~2000×π≒6000まで取ったことになるんで、そのときの、sin(x)/xの値は、最大で、0.001より小さいのだから、小数点以下3桁目までは、出て欲しいわ。
次は、刻み幅ね。波の数は、1000個で、1つの波に12個の分点を取るとして、また、区間の長さを3とすると、h=3/(12*1000)=0.00025となるわ。
結果は、ジャーン。1.5706371717265537122。やはり、小数点以下、3桁までということね。
もう一丁。m=2000では、h=0.000125となって、1.5707167490561441722までで、なんとか、ギリギリ小数点以下4桁までね」
「まあ、それでも、最初から、無限区間を扱うよりは、ずいぶんと改善はされたとはおもうがの。
とは言え、振動部分を含まない例と比較すると、かなり結果としては、見劣りがすることは否定できん。
ここは、ともちゃんが言ったように、変換関数、φ(t)の工夫が必要ということじゃろう」
DE公式による正弦積分の数値計算(2)
「1990年に、大浦拓哉先生と森正武先生の論文(※)で、φ(t)の第1階微分φ'(t)が、t→∞で、二重指数型でtに漸近、t→-∞で同様にゼロとなるような関数が変換に有効であるとされ、そこで取り上げられたのは、φ(t)=αt/(ω(1-6exp(sinh(t))))じゃ。
ここで、ωは、一般に振動部分がsin(ωt)の場合を想定しているので、その角振動数。また、αは、αh=πとなるように決める。hは、刻み幅とする。
なお、振動部分が、cos(ωt)の場合は、φ=M(t-(2M/π))/(ω(1-6EXP(sinh(t-2M/π))))、とする。
※T. Ooura and M. Mori, The double exponential formula for oscillatory functions
over the half infinite interval, J. Comput. Appl. Math. 38 (1991) 353-360.
上記では、フーリエ正弦変換:∫(t=0~∞)(f(t)sin(ωt)))dt、あるいは、フーリエ余弦変換:∫(t=0~∞)(f(t)cos(ωt)))dt、へのDE公式の適用を念頭に置いている」
 「この変換では、sin(x)/xのゼロから∞までを変換の対象としている訳ね。
「この変換では、sin(x)/xのゼロから∞までを変換の対象としている訳ね。
じゃ、早速、試してみよう。
まずは、h=0.001、hΣ(k=-g~-1)被積分関数(kh)+hΣ(k=1~r)被積分関数(kh)、として計算するの。
k=0は除いているのね。入れると、分母がゼロとなって計算ができなくなってしまうので。
また、gとrは、負と正の最大項数を表しているんだけど、今回は、g=[2.2/h]+1、r=[5.3/h]+1、としています。
計算結果は、1.5681982344469686448。
同様に、h=0.0001と、更に10分の一に小さくした場合は、1.5705363518184940708、となって、小数点以下、3桁まで計算されている。
ま、計算自体は、項数が少ない分速いわね」
「グラフを描いてみると、下図のようじゃな。
線がかすれているように見えるが、高い振動数で振動しているため、線が密集しているのでこの縮尺では、正しく表せないのじゃな。
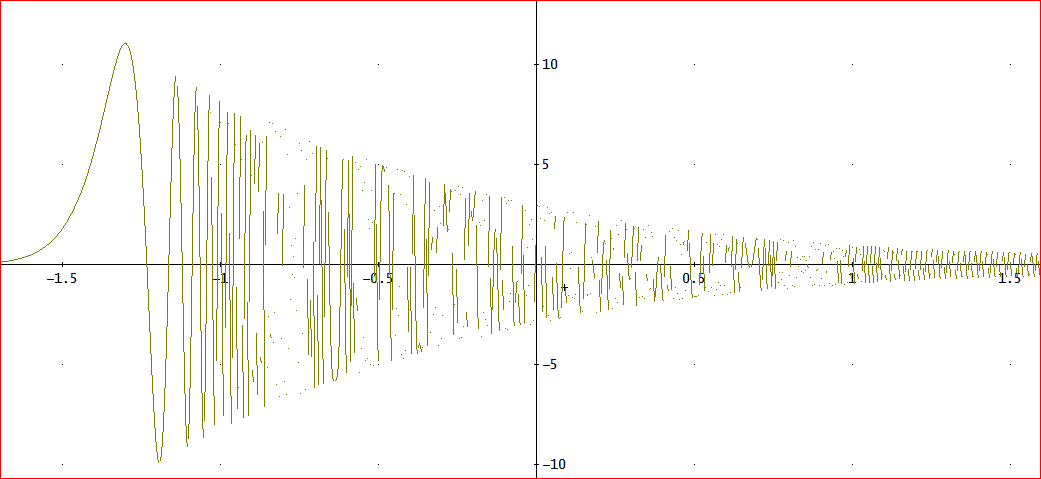
そこで、tの正の側の一部を拡大してみると、下図じゃ。
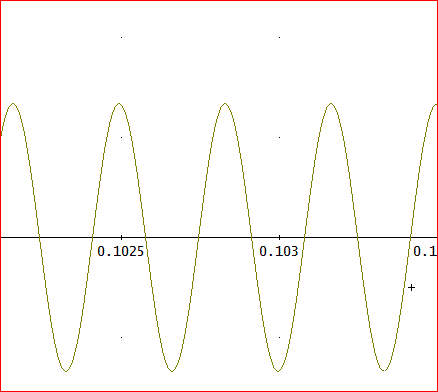
正弦波的に振動しているのが分かる」
「h=0.0001で、分点数は、約75000。絶対精度が10^(-4)というのは、前節よりも改善されているけど、まだ、少し、残念な結果ね。
それと、刻み幅をこれ以上小さくすると、計算時間が急に大きくなっちゃうというのは困るわ」
DE公式による正弦積分の数値計算(3)
「実は、前節の変換関数は、森正武先生による『二重指数関数型変換のすすめ』(1998年)に出てくるのじゃが、その中では、前節の変換関数に続けて、次の変換関数がお勧めであると記載されているので、次にそれを紹介してみよう。(記号は一部変えてあります)
φ= t/(1 - EXP(- 2t - a(1 - EXP(-t)) - b(EXP(t) - 1)))、ここで、b=1/4、a=b/√(1
+ αLN(1 + α)/(4π))である。
また、α=π/h、ここで、hは、台形公式の場合の刻み幅とする」
 「前節の変換関数、φ(t)=αt/(ω(1-6exp(sinh(t))))にくらべると、かなり、複雑ね。
「前節の変換関数、φ(t)=αt/(ω(1-6exp(sinh(t))))にくらべると、かなり、複雑ね。
でも、∫(x=0~∞)sin(x)/x dxの被積分関数、sin(x)/xを変換したグラフを描いてみると、下図のようになって、前節のような大きい振動数の振動がなくなって、きれい」
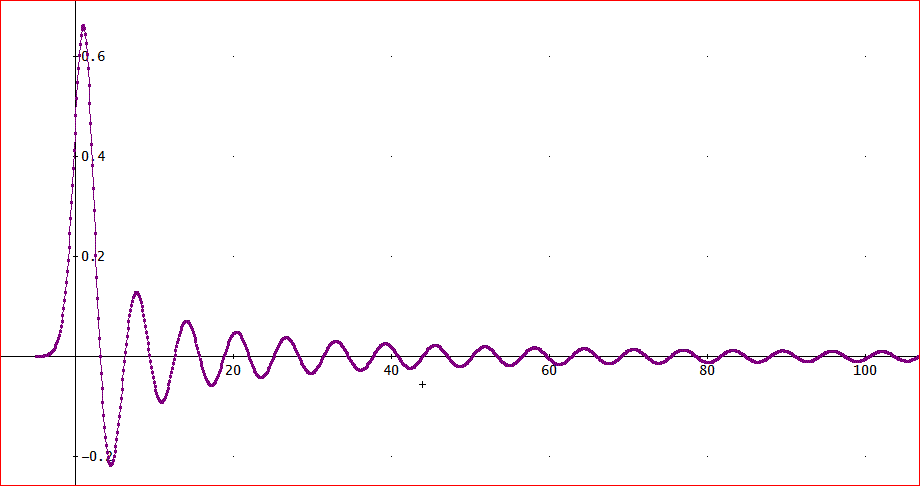
「確かに、その点は、大きく改善されている。素晴らしいんじゃがな。
別の問題が発生したのじゃよ。上図の範囲では、分からないが、下図のような数値的な不安定現象が発生するのじゃ。
DERIVEでの有効桁数(通常は10桁)の取り方により、不安定現象が発生する t の最初の値は、変わるのじゃがな。
下図の場合は、有効桁数を100桁としている場合なので、かなり大きい、t≒350前後で発生していることが分かる。

もっと有効桁数が小さい場合は、tのずっと小さいところで不安定現象が発生する。
たとえば、下図は、有効桁数10桁で、tの初期値を0.01~100まで、0.11刻みで数列の作成メニューから実行した場合じゃ。
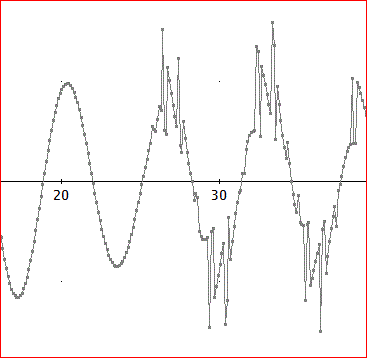
tの25前後で不安定現象が発生しているのが分かるじゃろう」
「それはそうと、今回の被積分関数のグラフは、そのままでは描けないのね?」
「う~ん。
ちょと、不思議なんじゃがな。
普通に『2Dグラフウインドウ』からグラフの作成を指示しても、t=10前の中途半端なところで、停まってしまう。
被積分関数を指定して、『数列の作成』からtの初期値とステップを具体的に指示すると、数列がベクトルで作成されるので、それを描画すると上述のようなグラフが描けるのじゃ。
ま、おそらくは、被積分関数の内部の値が非常に大きくなるので、そのためかと思われるがの」
「上図の場合で、厳密に計算したものを近似しても、同じ様な現象が再現されるわ。
下図は、20~30の間で厳密(DERIVEのEXACTモード)で計算した式をベクトル形式で計算してから数値的に近似してみたの。
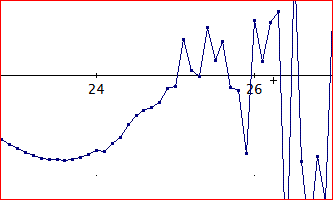 これでみると、t=24あたりまでは、正常なんだけど、その次からおかしくなってくるのね。
これでみると、t=24あたりまでは、正常なんだけど、その次からおかしくなってくるのね。
0.1刻みでグラフを描いているので、t=24.1あたりからね」
「なるほど。
では、DERIVEの有効桁数を4倍の40桁として、同様に、20から30の間を厳密に計算したものから近似値を求めてみよう。
それが、次の図となるんじゃが、これで見ると、先ほどの不安定点のあたりでは、何事も起きていない。
とすると、被積分関数の計算の際、有効桁数が短いと、どこかの項が桁落ちを起こすのではないじゃろうか。
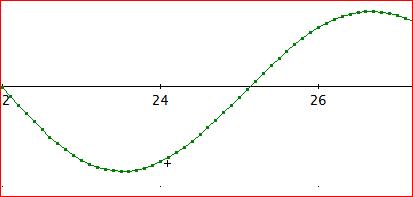
式を良く点検して、桁落ち防止措置ができれば、いいんじゃがな。
式がかなり複雑で、その個所が容易に分からないのは、困った。
だいぶ、長くなってきたので、今回は、ここまでということにして、この問題の解決は、次回に回すことにしよう。
いや、ともちゃんもお疲れさんじゃった」
最終更新日 2011/8/27



 「これまでに例が挙がっていないものがあるのね。何か例を挙げて下さいな」
「これまでに例が挙がっていないものがあるのね。何か例を挙げて下さいな」
