数式処理ソフト DERIVE(デライブ) de ドライブ
59.数値積分(外伝:√t×sin(t)のラプラス変換とベッセル関数)
DERIVE(Ver6.0)のバグなのか? (それは正弦積分がきっかけだった)
 「おじさん、大変!
「おじさん、大変!
DERIVEで、√t×sin(t)のラプラス変換を計算させると、おかしな結果になるよ」
「なんだぇ。朝から騒々しいね。
え、正弦定積分 ∫(0~∞)sin(t)/t dt、を計算させると、π/2にならない?」
「違うよ。その定積分は、DERIVEでは、直ちに、π/2となるの。
そうじゃなくて、数式処理ソフト DERIVE(デライブ)の第58回の『数値積分(7)(DE公式 続き)』の中の「正弦積分について」の節で、ラプラス変換により、定積分を求める方法を紹介しているでしょ。
定積分値が有限で一定の場合は、一般に、∫(t=0~∞)f(t)/t dt⇔∫(s=0~∞)F(s)ds の対応関係があると、説明しているわね。
それにならって、『フレネルの積分』を計算してみようと思ったのよ」
「フレネルの積分というのは、∫(t=0~∞)sin(t^2)dtなどじゃな」
「そう。
J=∫(0~∞)sin(t)/√t dtを考えると、√t=u とおくことにより、2∫(0~∞)sin(u^2)du と変形できるので、Jが求まれば、∫(0~∞)sin(t^2)dt=J/2と計算できるわけでしょ。
そこで、Jなんだけど、分母、分子に√tを掛けることにより、J=∫(0~∞)√t sin(t)/t dtと変形できる。
こう、変形すると、f(t)=√t sin(t)のラプラス変換が求められれば、J=∫(0~∞)f(t)/tdt=∫(s=0~∞)F(s) dsで、Jの値を計算可能ということ。
ここで、F(s)は、f(t)のラプラス変換とする。
具体的には、F(s)=∫(t=0~∞)exp(-st) f(t) dt=∫(t=0~∞)exp(-st) √t sin(t) となるでしょ。これをDERIVEに計算させるとおかしいのよ」
「どんなふうに、おかしいのじゃな」
「それが、F(s)=s/(s^2+1)^2となるのよ?。
このまま、sで0~∞まで積分すると、1/2になっちゃうでしょ。本当は、√(π/2)≒1.253314137・・とならないと。
だって、フレネルの積分、∫(0~∞)sin(t^2)dt=√(2π)/4 と合わないのよ。
だけど、もっと、困っているのは、F(s)=s/(s^2+1)^2 を逆変換表からたどると、(t/2)×sin(t)(=g(t))になることなの。こんなことって、あり?
あー。頭、痛くなっちゃう」
「そう、カッカせんことじゃよ。
一般に、ラプラス変換でf(t) 原関数と F(s) 変換関数とは、『零関数』(∫(t=0~T) n(t) dt=0となる関数 n(t)を零関数という)を使って、f(t)+n(t)⇔F(s) と表される。
n(t)が連続関数であれば、n(t)=0しかないので、通常は、一対一に対応すると考えてよいのじゃ。
今回のように、明らかに、連続、かつ、微分可能で、異なる f(t)とg(t)が、同一のラプラス変換F(s)=G(s)を与えることは、ない。
g(t)⊃G(s)=s/(s^2+1)^2が、正しいことは、直接計算しても、また、近藤次郎先生の『演算子法』(近藤次郎著:培風館:昭和45年6月30日初版13刷)巻末の『常用ラプラス対函数表(1)』の303番によって、t×sin(at)⊃2as/(s^2+a^2)^2
から、分かる。ここで、⊃記号で原関数とラプラス変換した関数との関係を表している。
ところで、ともちゃんは、DERIVEにどのように指示したんじゃな?」
「う~ん。
sqrt(t)sin(t)exp(-st)を入力して、解析メニューから、t=0~∞まで、定積分を指示したの」
「すぐに答が出たんかいな?」
「違うわ。
sが一般では、当然ながら、計算できないので、便宜的に、sを正の実数と宣言したの。そうすると、直ちに答えが出るのよ」
「なるほど。
DERIVEでは、∫(0~∞)exp(-t)t^(x-1)sin(t)dt、としても、xが整数の場合しか、このままでは出ぬようじゃな」
「そうなんだけど、不思議なことに、∫(0~∞)exp(-t)sqrt(t)sin(t)dt、ならば、1/4と出てしまうのよ。
そこで、不定積分を求めると、- e^(-t)((√t/2 + 1/4)COS(t) + √tSIN(t)/2) なる。
こいつをtで微分すると、e^(-t)((4t + √t - 1)SIN(t)/(4√t) - (1/(4√t) - 1/4)COS(t)) となるんだけど、いずれにしても、√tsin(t)exp(-t)ではないのよ。
残差があるの、それは、t→∞でゼロにはなるんだけどね」
「では、まずは、√t×sin(t)のラプラス変換を自分で計算して、確かめてみるこっちゃな。
そう、第53回で『複素関数(3)(テイラー展開、ガンマ関数)』の中で、ガンマ関数の定義を述べておるんじゃが、それを使ってみるとよいじゃろう」
√t×sin(t)のラプラス変換(方法その1)
 「ガンマ関数 Γ(x)=∫(t=0~∞)t^(x-1)exp(-t)dt か。
「ガンマ関数 Γ(x)=∫(t=0~∞)t^(x-1)exp(-t)dt か。
こいつは、似ている。
え~と。計算したいのは、F(s)=∫(0~∞))t^(1/2)exp(-st)×sin(t) dt、なので、上のガンマ関数のx=3/2の場合と形が似ているということなんだけど。
違うところは、三角関数が入っていることで、これは、大きな違いだけど、
そうはいっても、サイン関数は、sin(t)=(exp(#i t)-exp(-#i t))/(2#i)と指数関数で書けるからさ、
J1=∫(0~∞)t^(x-1)exp(-(s-#i)t)dt、J2=∫(0~∞)t^(x-1)exp(-(s+#i)t)dt、と2つに分けてから、
J=(J1-J2)/(2#i)とすれば、求められる。今更なんだけど、#iは、DERIVEの記法による、虚数単位のことね。
x=3/2のとき、結果だけ示すと、J1=1/(s-#i)^(3/2)∫(0~∞)u^(1/2)exp(-u)du=Γ(3/2)/(s-#i)^(3/2)
また、J2=Γ(3/2)/(s+#i)^(3/2)となるので、
J=F(s)=(√2√π(s√(√(s^2 + 1) - s) + √(√(s^2 + 1) + s))/(4(s^2 + 1)^(3/2))
となる。
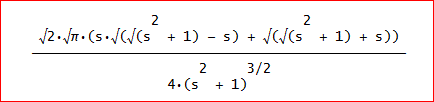
あー。
だけど、肝心の定積分値は、∫(s=0~∞)F(s)ds≒1.253314137・・と数値的にしか求められないよ」
「そうでもないぞ。
F(s)=(√2√π(s√(√(s^2 + 1) - s) + √(√(s^2 + 1) + s))/(4(s^2 + 1)^(3/2))
=√2√π(s√(s^2 + 1) - s^2 + 1)/(4(s^2 + 1)^(3/2)√(√(s^2 + 1) - s)) と書き直すと、
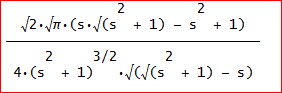
∫(s=0~∞)F(s)ds=√2√π/2 ≒1.253314137・・とDERIVEでも厳密に求められるのじゃな。
もちろん、前の積分を2つに分けて、適切な変数変換(√(s^2 + 1) - s などを変換変数 wの2乗とする)により、少し面倒じゃが、個別に計算して求めることも可能じゃ」
「そうなれば、フレネル積分の値は、その1/2だから、√(2π)/4 となって、合っている!。
でも、なんで、√t×sin(t)が近藤先生の『常用ラプラス対函数表』に載っていないのかな?」
「実は、そのものずばりではないものの、導出に必要なものは載っているのじゃ。
わしも、最初は、載っていないのかな、と思ったんじゃがの。
ともちゃんの解いたF(s)の形を見て、気がついたんじゃ。さすが名著じゃ」
√t×sin(t)、√t×cos(t)のラプラス変換(方法その2)
「今、y(t)≡t^(x-1)sin(t)と置いてみる。
このy(t)が満たす微分方程式を求めてご覧」
 「えーと。y'=t^(x-2)(t cos(t)+(x-1)sin(t))
「えーと。y'=t^(x-2)(t cos(t)+(x-1)sin(t))
y''=t^(x-3)(2t(x-1)cos(t)+(x^2-3x-t^2+2)sin(t))
となるので、y''×t/2-(x-1)y'を作ると、-(t^(x-2)(x^2-x+t^2)sin(t)/2となる。
ところが、t^(x-1)sin(t)=y(t)なので、-(t^(x-2)(x^2-x+t^2)sin(t)/2=-(x^2-x+t^2)y(t)/(2t)とy(t)で置き換えられる。
従って、y''×t/2-(x-1)y'+(x^2-x+t^2)y(t)/(2t)=0 となる」
「そうじゃな。
整理すると、y''(t)+2(1-x)y'(t)/t+(1-(x-x^2)/t^2)y(t)=0 となるじゃろう。
ここで、y'(t)の係数、2(1-x)/t が1/t という特別な場合、すなわち、x=1/2のとき、微分方程式は、y''+y'/t+(1-(1/4)/t^2)y=0
となることが分かる。
ところが、この微分方程式は、『ベッセルの微分方程式』、y''+y'/t+(1-ν^2/t^2)y=0 で、ν^2=1/4の場合にあたる。
すなわち、ν=±1/2のどちらかと同一なんじゃ。
一方、(第1種)ベッセル関数の定義式、
J(t,ν)=(t/2)^ν Σ(k=0~∞)((-1)^k(t/2)^2k/(k!Γ(ν+k+1))、ここで、ν<>-n。
また、J(t,-n)=(-1)^n J(t,n)なので、
この定義に従って、
J(t,1/2)=√(t/2)×Σ(-1)^k(t/2)^2k/(k!Γ(k+3/2))=√(t/2)×Σ(-1)^k(t/2)^2k/(k!(k+1/2)!)
なので、
Σの中の分母に2^(2k)を掛けたものは、(k!(k+1/2)!)×2^(2k)=√π×(2k+1)!/2であるので、分子の(t/2)^(2k)の(1/2)^(2k)が落ちて、
J(t,1/2)=√(t/2)×2/√πΣ(-1)^k×t^(2k)/(2k+1)!=√(2t/π)×(1/t)Σ(-1)^k×t^(2k+1)/(2k+1)!=√(2/πt)×sin(t)
となる。
以上、青字部分は、『物理学への数学的序説』(荒木源太郎著:みすず書房:昭和42年)に書かれていることじゃ。
従って、sin(t)/√t=J(t,ν=1/2)×√(π/2) ということじゃな」
「へー。こんなところにベッセル関数が。名前だけは、知っているけど。
でも、おじさん、目下のところ知りたいのは、sin(t)/√tではなくて、√t sin(t)の方なんだけど」
「ま、もうちょっと、辛抱しておいで。
同じように、y(t)≡t^(x-1)cos(t)とおいて、計算してみると、
y''(t)+2(1-x)y'(t)/t+(1-(x-x^2)/t^2)y(t)=0 となる。x=1/2とすると、y''+y'/t+(1-(1/4)/t^2)y=0
と同型になる。
しかし、ν=1/2のときは、すでにサイン関数の方なので、ν=-1/2の方かなと思うじゃろう。
これも少し計算すると、cos(t)/√t=J(t,ν=-1/2)×√(π/2)ということが分かるのじゃ」
「ははあ、そうすると、fs(t)=√t sin(t)、fc=√t cos(t)、Sr(t)=sin(t)/√t、Cr(t)=cos(t)/t などと略記して、
tで微分すると、
fs'(t)=sin(t)/(2√t)+cos(t)√t=(Sr(t)/2)+fc(t)、fs''(t)=(Sr'(t)/2)+fc'(t)
同様に、fc'(t)=cos(t)/2√t-sin(t)√t=(Cr(t)/2)-fs(t) 、
よって、
fs''(t)=(Sr'(t)/2)+fc'(t)=(Sr'(t)/2)+(Cr(t)/2)-fs(t)、
ここで、ラプラス変換を使って、fs(t)=√t×sin(t)⊃F(s)、fc(t)=√t×cos(t)⊃G(s)、Sr(t)⊃SR(s)、Cr(t)⊃CR(s)と書くと、
s^2 F(s)-sfs'(0)-fs(0)=(sSR(s)-Sr(0))/2+CR(s)/2-F(s)、
fs(0)=0、fs'(0)=0、fc(0)=0、Sr(0)=0 より、s^2 F(s)=s(SR(s)/2)+CR(s)-F(s)
よって、F(s)=(1/2)(sSR(s)+CR(s))/(s^2+1)
一方、Sr(t)=K×J(t,ν=1/2)、Cr(t)=K×J(t,ν=-1/2)、K=√(π/2)と置いている。
これから、J(t,ν)のラプラス変換が分かれば、それをJ(s,ν)と書くと、
F(s)=(K/2)(s J(s,1/2)+J(s,-1/2))/(s^2+1) となる」
「そうなんじゃな。
近藤先生の『演算子法』巻末の常用ラプラス対函数表(1)(長い。『対函数表』と言おう)の402番にベッセル関数のラプラス変換がある。
ここでは、その表の402番のa=1の場合じゃから、
J(t,ν)⊃J(s,ν)=(sqrt(s^2+1)-s)^ν/sqrt(s^2+1) が利用可能じゃ。(ν>-1)。
ただし、以下では、平方根号がわかりにくくなるので、しばらく、√をsqrt()で表したりする。
J(t,ν=1/2)⊃J(s,1/2)=(sqrt(sqrt(s^2+1)-s)/sqrt(s^2+1)から、
SR(s)=K×(sqrt(sqrt(s^2+1)-s)/sqrt(s^2+1)
J(t,ν=-1/2)⊃J(s,-1/2)=1/(sqrt(sqrt(s^2+1)-s) sqrt(s^2+1)) となるので、
CR(s)=K×1/(sqrt(sqrt(s^2+1)-s) sqrt(s^2+1))
よって、F(s)=(1/2)(sSR(s)+CR(s))/(s^2+1)=(1/2)K/(s^2+1)×{(s×sqrt(sqrt(s^2+1)-s)/(sqrt(s^2+1))+(1/(sqrt(sqrt(s^2+1)-s)
sqrt(s^2+1))}
整理すると、F(s)=(√2√π(s√(s^2 + 1) - s^2 + 1)/(4(s^2 + 1)^(3/2)√(√(s^2 + 1) -
s)) となるのじゃ
あーしんど」
「は~い、お疲れ様でした。
前節の式との一致、バッチリです。
当然ながら、∫(0~∞)F(s)ds=√2(√π)/2≒1.253314137・・で合ってます。
ついでに書くと、fc(t)=√t×cos(t)のラプラス変換G(s)は、
fc'(t)=cos(t)/2√t-sin(t)√t=(Cr(t)/2)-fs(t)なので、s G(s)-fc(0)=CR(s)/2-F(s)より、s
G(s)=CR(s)/2-F(s)となり、
G(s)=(1/s){(K/2)(J(s,-1/2))-F(s)}=(√2√π(2s - √(s^2 + 1))/(4(s^2 + 1)^(3/2)√(√(s^2 + 1) -
s)) となります」
「うん。
∫(0~∞)fc(t)/t dt=∫(0~∞)cos(t)/√t) dt=√2(√π)/2、
と、これもまた、同一の値になる。
なお、上式のままでは、定積分の値がDERIVEのExact(厳密)モードでうまく出ないかもしれん。
その際は、s=(1-w^4)/(2w^2)なる、新変数で、w=1~0まで積分すると、√2(√π)/2と正しく答えが出る」
惑星の運動(ともちゃんの誤解)
「対函数表にベッセル関数が載っていたので、前節のようにも、解けるということを示したんじゃがな。
ま、分量から、明らかのように、√t×sin(t)などのようにtのべき乗×三角関数のラプラス変換であれば、ガンマ関数の定義から、変形して計算する方が簡単ではあるな」
 「でしょ。
「でしょ。
でも、これで、ベッセル関数が、ちょっと、身近になってきた感があるわね」
「ベッセル、Friedrich Wilhelm Bessel(1784/7/22-1846/3/17)氏は、ドイツの天文学者・数学者じゃ。
ベッセル関数以外では、ベッセルの補間多項式などでも知られているんじゃよ。
時代的に言えば、かの、オイラーが亡くなった翌年に生まれている。
それはそうと、ベッセル関数は、天文学から生まれたんじゃよ」
「へー。
ベッセルさんには、これまでは、太鼓の振動の方程式なんかで、何回か、お目にかかっただけだもの。
知らなかったよ」
「たとえば、太陽の周りを回っている惑星の(相対)運動は、楕円になることは、知っているじゃろう。
大学初年級の力学で、ニュートンの運動方程式を元に惑星の運動を導くところは、力学前半のクライマックスであって、みんな、感動したもんじゃな。
しかし、天文学専攻者や天文が趣味の人以外は、軌道を時間と共に追跡することは少なかったじゃろう。わしも、特に関心がなかったな。
実は、軌道の形が求まっても、惑星の時間的な運動を追跡しようとすると、手計算では大変じゃ。
また、仮に、時間的変化を追跡しようとしても、コンピュータも自由には使えなかったし、当然、パソコンもなかったしな。
まったく、隔世の感がある。真円であれば、まこと簡単なことなのだがな」
「え! そうなの。
だって、楕円の軌道上の点Pの座標は、x=a×cos(ωt)、y=b×sin(ωt)と書けるんじゃないの?」
「ともちゃん、大きな錯覚をしておるぞ。(下図を参照。a>=bとしている)
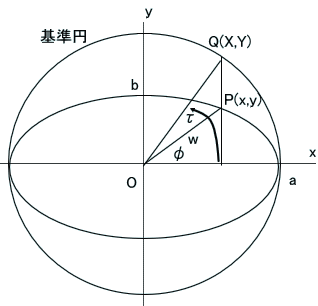 まず、そのωtという角度じゃが、楕円上の点Pと中心Oとを結ぶ線OPがx軸となす角度φではなくて、基準円上の点Qと中心Oとを結ぶ線がx軸となす角度τじゃ。
まず、そのωtという角度じゃが、楕円上の点Pと中心Oとを結ぶ線OPがx軸となす角度φではなくて、基準円上の点Qと中心Oとを結ぶ線がx軸となす角度τじゃ。
Qからx軸におろした垂線が楕円と交わった「楕円上の点」P(x,y)をτで表すと、x=a cos(τ)、y=b sin(τ)と「簡単に」書けるということなんじゃよ。
すなわち、x=a cos(τ)、y=b sin(τ)とは、一般に書けるけど、真円でないときはτ<>φなので、
x<>w cos(τ)、y<>w sin(τ)であって、中心からの距離wを使うときは、x=w cos(φ)、y=w sin(φ)とすべきなのだ」
「ひぇー! 今まで、完全に間違ってたじゃん」
「ははは。
間違っていても気がつかなかったのは、Pの座標値を、x=a cos(τ)、y=b sin(τ)と書いたときに、τを0~2π間で動く単なるパラメータとみれば、τとPの座標は、一対一に対応しているという「描像」は、正しかったからじゃ。
しかし、τがどこの角度なのか?、を問うと、その違いに気がつく。
たとえば、OPの距離、w をφを使って表してご覧」
「楕円の標準形、(x/a)^2+(y/b)^2=1から出発します。(これは間違ってないよね?)
離心率εを使うと、b=a√(1-ε^2)の関係がある。(a>=bとしている)
y^2=(1-ε^2)(a^2-x^2)である。よって、w^2=x^2+y^2=(1-ε^2)a^2+ε^2x^2 となる。
一方、x=a cos(τ)=w より、w=a√(1-ε^2)/√(1-(εcos(φ))^2)となる。
当然だけど、このwを使うと、x=w cos(φ)、y=w sin(φ)は、楕円の方程式、(x/a)^2+(y/b)^2=1を満足する」
「よっしゃ。
ちなみに、x=w sin(φ),y=w cos(φ)、上図のQの位置(X,Y)は、X=a cos(τ)、Y=a sin(τ)から、
Tan(φ)=(b/a)Tan(τ)=√(1-ε^2)Tan(τ)である。
後述のように原点が焦点の場合とは異なり、原点が楕円の中心ととる場合は、wなどはこうなるということじゃ。
(後節で、a√(1-ε^2)は、楕円の半直弦(λ)とよばれることを紹介している。λを使うと、w=λ/√(1-(εcos(φ))^2) とも書ける。)
では、次なる「ともちゃんの誤解」に行くでぇ。
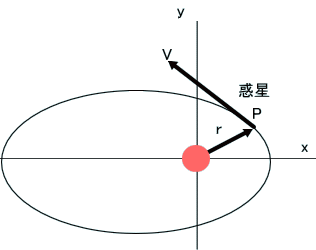 それは、惑星が軌道上を一定の速さで運動すると思っているところじゃ。
それは、惑星が軌道上を一定の速さで運動すると思っているところじゃ。
真円であれば、その通りなんじゃが、一般の楕円では異なる。近日点では速く、遠日点では遅い。
ともちゃんも知っているように、惑星の運動には、面積速度一定の法則(角運動量保存則)があるじゃろう。
速度ベクトルVと位置ベクトルrとを使うと、(r×V)/2=一定。ここで、×はベクトル積じゃ。
運動は、一定の平面上に限られるので、この向きは、面に垂直ではある。Vとrのなす角度は、直角とは一般に異なる。
しかし、真円の場合は、rとVは、常に直角で交わり、Vの大きさも一定なので、r×Vの大きさは、πa^2/T(公転周期)となり、『面積速度』という意味が誰にでも、よく分かるじゃろう。
また、簡単のために、軌道が真円であるとすれば、遠心力=mrv^2/2と太陽の引力GMm/r^2とが釣り合うので、r^3×v^2=2GMmとなる。
T=2πr/vなので、T^2∝r^3という、『ケプラーの第3法則』が得られることになる」
「ありゃ。そうだよね。
さっきの方程式、x=w cos(φ)、y=w sin(φ)にしても、x=a cos(τ)、y=b sin(τ)にしても、楕円を描くときには使えるけど。
真円でない限り、φやτは時間 tに単純に比例する訳がないのか~。
なるほど、納得です。
て言うか。最初のショックで口がきけないよ」
「ま、ずーと思い込んでいたんじゃからな。次からは間違わないから。安心しなさい。
(注:楕円中心と楕円上の点との距離とx軸との角度φとの関係 w=w(φ)は、楕円関数で表されることがわかったので、『続外伝』として追加した)
では、次にいこう。
なお、下記に参考までに、地球などの惑星の長半径、離心率、公転年を掲げよう。(出典:丸善理科年表:2011年版:『惑星表』より抜粋)
長半径(a)の単位は、天文単位。1天文単位は、地球の平均軌道半径で、約1.496×10^8m。
また、公転年の単位は、太陽年。最後の列のT^2/a^3は、ケプラーの第3法則を確認するためのもの。一致は、素晴らしい。
これを発見したときのケプラー(1571年~1630年)の感動が偲ばれる。
※ケプラーの時代には、天王星(発見:1781年)や海王星(同:1846年)は知られていなかった。また、冥王星(同:1930年)は、「惑星」からは除かれた」
| 名称 |
長半径(a) |
離心率 |
公転年(T) |
赤道半径(km) |
T^2/a^3 |
| 太陽 |
- |
- |
- |
696,000 |
- |
| 水星 |
0.3871 |
0.2056 |
0.24085 |
2,440 |
1.00005 |
| 金星 |
0.7233 |
0.0068 |
0.61521 |
6,052 |
0.99992 |
| 地球 |
1.0000 |
0.0167 |
1.00004 |
6,378 |
1.00008 |
| 火星 |
1.5237 |
0.0934 |
1.88089 |
3,396 |
1.00006 |
| 木星 |
5.2026 |
0.0485 |
11.8622 |
71,492 |
0.99923 |
| 土星 |
9.5549 |
0.0555 |
29.4578 |
60,268 |
0.99476 |
| 天王星 |
19.2184 |
0.0463 |
84.0223 |
25,559 |
0.99457 |
| 海王星 |
30.1104 |
0.0090 |
164.774 |
24,764 |
0.99455 |
惑星の運動とベッセル関数(ケプラー方程式)
「運動方程式から、惑星の軌道変化を求める過程を逐一たどるのは、さすがに大変じゃ。
ここでは、『力学』(原島鮮:裳華房:昭和45年3月増補第21版)を元にして、必要な部分のみを補って説明することにしよう。
ただ、上記『力学』では、いわゆる『ケプラー方程式』は書かれているが、ベッセル関数との関係には触れられていないので、『力学の解ける問題と解けない問題』(吉田春夫著:岩波書店:2005年12月)を参考にした。
とは言え、少し、記号を変えていたりするので、説明する必要がある。
さて、太陽と惑星の2体問題じゃが、両者の合成系の重心は、他から力が働かない仮定の下では、等速度運動することが分かる。(質点系の運動量保存)
そこで、通常は、系の重心の位置と速度を共にゼロとおいた慣性座標系で両者の相対運動を考える。すなわち、系全体は、空間に静止していると考える。
相対運動なので、太陽を中心とした座標系をとる。
その上で、運動方程式を立ててそれを解いて得た惑星の軌道は、周期運動するものに限れば、それは、楕円(離心率0=<ε<1)であり、
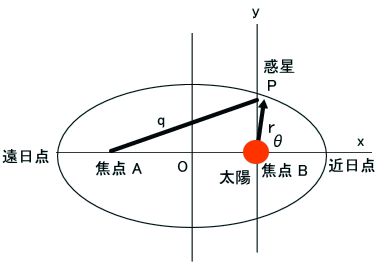
角度θ(焦点Bから近日点(近心点)方向から反時計回りに測った角度)(=真近点(離)角と言う)と、
焦点Bから惑星への距離 rを使って、r=a(1-ε^2)/(1+εcos(θ)) と「極座標」で表される。
しかし、強調すべき点は、太陽を中心とした座標系で運動方程式を立てているが、得た惑星の軌道は、太陽中心の楕円ではなくて、太陽は、軌道の一つの焦点にある事実である。※
(※r=a(1-ε^2)/(1+εcos(θ)) より、θ=0のrの値がr=a(1-ε)=a-aεとなることから、楕円中心Oの回りの極座標表示ではなく、焦点Bからの表示であることが分かる)
なお、楕円の性質から、焦点A、Bの中心との距離は、離心率εを使うと、OA=OB=aεと書くことができる。
更に、焦点Aと惑星Pとの距離を、qとしたとき、やはり、楕円の性質(定義と考えても良い)から、q+r=2aの関係がある。
そこで、楕円の性質を使って、rとθとの関係、r=a(1-ε^2)/(1+εcos(θ))を求めてごらん」
 「なるほど。
「なるほど。
原島先生の本でも、ちゃんと(失礼。当たり前だけど)、r とθは、焦点Bから計ると書かれているけど、見落としてしまうわね。
だって、座標軸は、太陽を中心なので、当然、求まった楕円もその中心が太陽だと思うじゃん。
まして、直角座標では、普通、楕円の中心を原点にして考えるものな~。ハァー。
さてと、r=a(1-ε^2)/(1+εcos(θ)) 。
これは、rとθのみだから、q+r=2aを使うのが便利。両辺を二乗して、
q^2+2qr+r^2=4a^2から、2qr=4a^2-r^2-q^2を経て、16a^4 - 8a^2(q^2 + r^2) + q^4 -
2q^2r^2 + r^4 = 0となる。
ここで、三角形の余弦定理から、q^2=(2aε)^2 + r^2 + 4aεrCOS(θ)を使うと、すこし、計算がややこしいけど、
r^2ε^2COS(θ)^2 + 2arε(ε^2 - 1)COS(θ) + a^2(ε^4 - 2ε^2 + 1) - r^2 = 0 にこぎ着けて、rの2根のうち、正の方を選べば、
r = a(1 - ε^2)/(εCOS(θ) + 1)が求められる」
「そのとおり。
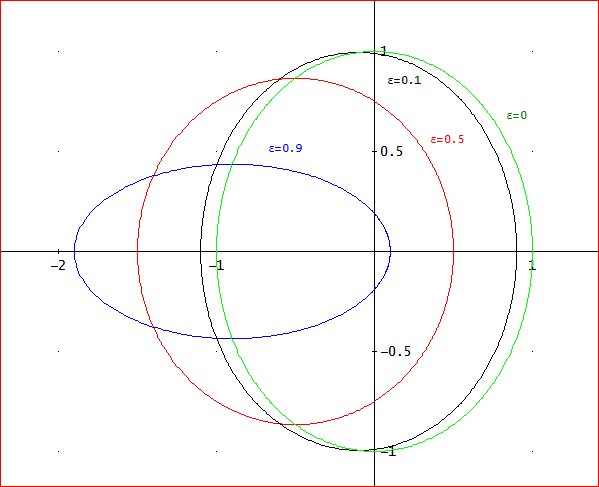
DERIVEの2Dグラフウインドウの「座標」メニューから「極座標」を指示しておくと、フォーカスがあたっている数式が極座標のrを与えているものとして、描画が行われる。
この際、パラメータ(変数)の範囲を聞いてくる。通常は、-πからπとなっているので、必要に応じて、変更、入力すれば、よい。
下図は、こうして描いた、ε=0、0.1、0.5、0.9のグラフじゃ。なお、a=1としている。
画面の縦横比が1でないため、ε=0でも真円に見えないが、勘弁して欲しい。」
「えーと。xとyとをさっきのように、セットで与える場合は、どうすれば、いいのかしら?」
「それは、ベクトルとして、[a cos(θ),b sin(θ)]のように与えればよい。
試しに、x=cos(τ)、y=a√(1-ε^2)sin(τ)、あるいは、x=-aε+cos(τ)、y=a√(1-ε^2)sin(τ)として直交座標で描画して比較して欲しい。
また、r=a(1-ε^2)/(1+εcos(θ))のとき、x=r cos(θ)、y=r sin(θ)から得られる(x,y)が方程式、(x+aε)^2/a^2+y^2/b^2=1を満たしているかどうかもチェックしてご覧」
「ベクトルとして入力して、同じグラフが描けたよ。
また、r=a(1-ε^2)/(1+εcos(θ))、x=r cos(θ)、y=r sin(θ)が、(x+aε)^2/a^2+y^2/b^2=1を満たしている。
すなわち、焦点Bを原点とした場合、図形の方程式は、マイナス方向にaεだけ移動した楕円の標準形と一致することが確認できました」
「前節の末尾で掲げたように実際の惑星に限れば、その離心率は、小さい。
たとえば、地球では、ε=0.0167なので、軌道を描くとほとんど真円のようになってしまう。中心と焦点との距離 aεの2倍、2aεも実距離で、約5,000km程度じゃ。
これは、太陽の赤道半径、696,000kmの約0.8%に過ぎない。すなわち、楕円の中心から左右にある2つの焦点も太陽内に含まれている。
一番大きな、火星でも、離心率が0.0934だから、ε=0.1までいかない。だから、図を円のように描いても、あまり変わらないということはある。
しかし、彗星や人工衛星、人工惑星では、離心率が大きい場合もあるので、原点位置や離心率、焦点のことをまったく忘れていてはいけない。
まとめると、正しい図と間違っている図は、下図のとおりじゃな。赤い丸は、太陽、青い丸は、惑星などじゃ。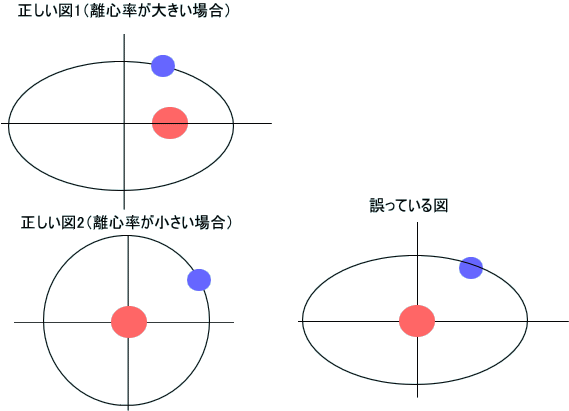 誤っている例は、結構、こういう図を書き勝ちであるという例。
誤っている例は、結構、こういう図を書き勝ちであるという例。
さてと、a √(1-ε^2)を、原島先生の本では、l(エル)と書き、楕円の「半直弦」と書かれている。
何故、半直弦と呼ぶかなども書かれているが、ここでは、省略しよう。
しかし、l 「エル」は、1 「イチ」と非常に見間違いやすいので、ここでは、λと書いておこう。
すなわち、r = λ/(εCOS(θ) + 1)、また、ε^2=1-(b/a)^2なので、b=aλとも書ける。
また、(x,y)は、x=r cos(θ)、y=r sin(θ)である。(しつこいようじゃが、焦点Bが原点としてのことだ)
このあと、運動方程式を積分して、時間変化を導くのであるが、それは、さすがに大変なのでは、前出の書籍等をご覧いただくとして、ごく一部を書こう。
rの時間変化を求めるため、所要の積分を、変数を、r=a(1-εcos(u))なる、u(「離心近点角」と言うそうな)に変えて、
u-εsin(u)=√(GM/a^3)(t-t0)と解くことができる。
ここで、Mは太陽質量、Gは万有引力定数となる。また、t0は、近日点を通る時刻(の一つ)とする。
更に、天文学では、平均運動 nをn=√(GM/a^3)、平均近点角 β=n(t-t0)と書く。(吉田先生の本では、βは、l(エル)と書かれているが、やはり見にくいので、βと書く)
なお、ケプラーの第3法則により、n=2π/Tで、平均の角速度である。(nは特に「整数」という意味ではない)
これらによって、u-εsin(u)=n(t-t0)またはu-εsin(u)=βと簡潔に書くことができる。この式を『ケプラー(Kepler)方程式』と呼ぶ。
この式のuをβ(=n(t-t0))の関数として、表すことができれば、r=a(1-εcos(u))により、rの時間変化が分かることになる」
「ははー。恐れオイラー、じゃなかった、ケプラー方程式!
原島先生の本でも、ケプラー方程式にも触れているよ。
だけど、具体的には、解いていなのね」
「ケプラー方程式は、超越関数である、Sin関数が含まれているので、『超越方程式』とも呼ばれている方程式の一つじゃ。
現在では、通常、数値的にコンピュータで解を求めるそうだ。
しかし、解析的には、εsin(u)=u-βの解、u(β)をβの周期関数と考えて、フーリエ級数に展開する。
u=β+2Σ(m=1~∞)(1/m)(J(mε,m)×sin(mβ))と書くことができることが証明できる。
ここに、至って、(ようやっとじゃったな)、J(mε,m)という整数次のベッセル関数がフーリエ級数の係数(ベッセル係数とも呼ぶ)として登場する」
「吉田先生の本では、J(z,m)=(z/2)^mΣ(k=0~∞)((-1)^k(z/2)^(2k))/(k! (m+k)!) の定義が紹介されている。
前出のベッセル関数の定義式で、νを整数mとしている場合ね。
DERIVEでは、ベッセル関数が定義されているのかしら?」
「ファイルメニューから開く又は読込で、DERIVE6のフォルダ内の「Math」フォルダ内の「BesselFunction.mth」を呼び出せば、使える」
「なるほど。
いろいろあるわね。
DERIVEの改訂2.5版の時代のテキストも参照すると、主なものは、以下のとおり。
1. BESSEL_J(n, z):第1種ベッセル関数、nは、整数又は半整数
グラフでは、下図のようになります。
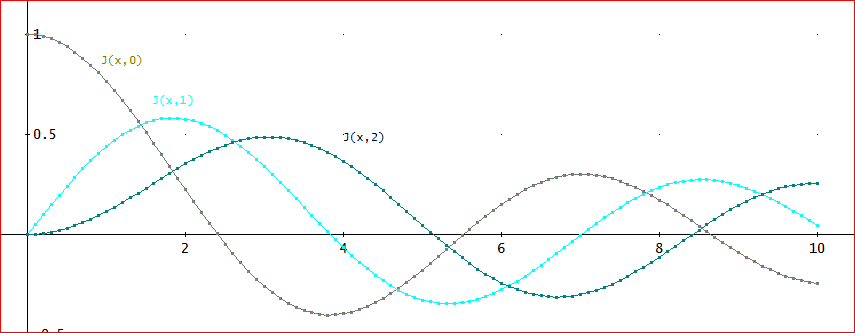
このグラフは、BESSEL_J(n, z)を使って、解析メニューの「表の作成」から、n=0,1,2の場合について、それぞれ、z=0~10まで、0.1刻みで計算して、グラフに描かせたものを表示。
2. BESSEL_J_SERIES(n, z, m):n次の第1種ベッセル関数のm+1項までの展開を与える。
たとえば、吉田先生の本で紹介されているように、
J(z,0)=BESSEL_J_SERIES(0, z, 5)=- z^10/14745600 + z^8/147456 - z^6/2304
+ z^4/64 - z^2/4 + 1 などが得られる。
3. BESSEL_J_ASYMP(n, z):大きいzに対する第1種ベッセル関数の漸近展開第1項を求める。
たとえば、BESSEL_J_ASYMP(0, x)≒(sin(x)+cos(x))/√(πx)
あるいは、BESSEL_J_ASYMP(1/2, x)≒(√2SIN(x))/(√π√x)、
これは、このページの中でも登場しているν=1/2の場合なので、√t×sin(t)になるのは、納得!
4. BESSEL_Y(n, z):第2種ベッセル関数(変形ベッセル関数)
これは、y''+y'/t-(1+(ν/t)^2)y=0を満たす。
5. BESSEL_Y_SERIES(n, z, m):n次の第2種ベッセル関数のm+1項までの展開を与える。
6.BESSEL_Y_ASYMP(n, z):大きいzに対する第2種ベッセル関数の漸近展開第1項を求める。
このほかにも、第1種球ベッセル関数、第2種球ベッセル関数(球ノイマン関数)、エアリー関数なども含まれています」
「ご苦労様。
ということで、惑星の運動の解析のため、歴史上は、ベッセル関数が登場した訳じゃ。
これらから、a/r=1+2Σ(m=1~∞)(J(εm,m)cos(mβ))
また、(x,y)座標値は、βを使って、有限のNで級数を打ち切ると、
x=-3ε/2+2Σ(m=1-N)(1/m)(J'(mε,m)cos(mβ)
y=2√(1-ε^2)/εΣ(m=1-N)(1/m)(J(mε,m)sin(mβ)
などと表される。
上記の、u=β+2Σ(m=1~∞)(1/m)(J(mε,m)×sin(mβ)) の導出などについては、前出の『力学の解ける問題と解けない問題』などを見て欲しい。
また、最後の2つの式のグラフなどは、DERIVEでもできそうじゃが、後日に回そう。
いや、ともちゃんも、お疲れさんじゃった」
最終更新日 2011/9/4



 「おじさん、大変!
「おじさん、大変! まず、そのωtという角度じゃが、楕円上の点Pと中心Oとを結ぶ線OPがx軸となす角度φではなくて、基準円上の点Qと中心Oとを結ぶ線がx軸となす角度τじゃ。
まず、そのωtという角度じゃが、楕円上の点Pと中心Oとを結ぶ線OPがx軸となす角度φではなくて、基準円上の点Qと中心Oとを結ぶ線がx軸となす角度τじゃ。 それは、惑星が軌道上を一定の速さで運動すると思っているところじゃ。
それは、惑星が軌道上を一定の速さで運動すると思っているところじゃ。
 誤っている例は、結構、こういう図を書き勝ちであるという例。
誤っている例は、結構、こういう図を書き勝ちであるという例。