「そうね。そもそも、第４１回の「積分（１）」で扱った、余弦積分などが、そういう、定積分だったものね」「で、まず、最初は、∫（0～∞）（sin（x）/x） dx＝π/2 じゃ。これは、ハンドブックにも登場しているので、わかりやすいじゃろう。
被積分関数は、偶関数なので、積分範囲を－∞～＋無限大に拡大して考える。そして、やや、天下り式じゃが、複素関数、ω＝exp（#i z）/z の定積分、∫ωdzを計算する。
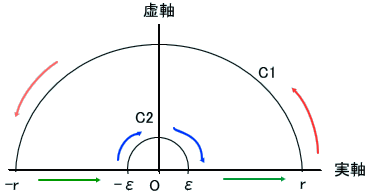
積分路は、左図のようじゃな。
大きな半円 C1に沿った部分は、∫赤、実軸上の緑部分を∫緑、そして、小さな半円 C2に沿った部分は、∫青じゃ。この領域内では、ω（z）は、正則なので、∫ωdz＝0となる。
具体的に、∫赤と∫青を計算してご覧」
「う～ん。じゃ、まず、∫赤ね。半径をr、sは、角度として、z＝r exp（#i s）と書くと、
∫赤＝#i∫（0～π）(exp(－ r SIN(s))COS(rCOS(s)) ds、となる。
r＝10k と置換して、数値計算してみると、k＝1～10（r＝10～1010）で、この積分値は、次のようになる。
([－ 0.1751025348#i, 0.01714172058#i, 0.001126400842#i, － 0.0001904330853#i, － 1.998722000×10^(－5)#i, 1.873509658×10^(－6)#i, － 1.821878076×10^(－7)#i, － 2.269182229×10^(－8)#i, 5.229910638×10^(－8)#i, 5.449823920×10^(－8)#i])
これから、r → ∞で、ゼロになるのではないかと予想できる。事実、ハンドブックにならうと
｜∫（0～π）(exp(－ r SIN(s))COS(rCOS(s)) ds｜≦｜∫（0～π）exp(－ r SIN(s)） ds｜＝2｜∫（0～π/2）exp(－ r SIN(s)） ds｜
＝2｜（∫（0～δ）exp(－ r SIN(s)） ds＋（∫（δ～π/2）exp(－ r SIN(s)） ds｜、δ＞0のπ/2より小さな実数。
ここで、第1項は、被積分関数 exp(－ r SIN(s)）がこの区間で、単調減少なので、最大でも、1であり、積分値は、δより小さい。
第2項は、被積分関数の最大値 exp（－r sin（δ））なので、積分値は、exp（－r sin（δ））×（π/2－δ）より小さい。
従って、｜∫赤｜＜2δ＋exp（－r sin（δ））×（π－2δ）、ここで、δを固定した上で、r→∞にすると、第2項→0、そして、δを0に近づければ、右辺は、いくらでも小さくできるので、｜∫赤｜→0 となる。
次に、∫青＝－#i∫（0～π）(exp(－ εSIN(s))COS(εCOS(s)) ds、となる。ここで、ε＝10－k として、k＝1～10（ε＝0.1～10－10）で、計算してみると、
([－ 2.941703731#i, － 3.121592765#i, － 3.139592666#i, － 3.141392661#i, － 3.141572653#i, － 3.141590653#i, － 3.141592512#i, － 3.141592653#i, － 3.141592653#i, － 3.141592653#i]）
となるので、∫青→（－π #i） と予想できる。事実、被積分関数は、ε→0で、1にいくらでも近づくので、積分値は、－π#i 。
最後に、∫緑＝∫（－r ～－ε）exp（#i x）/x dx＋∫（ε～r）exp（#i x）/x dx、ここで、第1項の変数を、u＝－xと変換すると、
∫緑＝－∫（ε～r）exp（－#i u）du ＋∫（ε～r）exp（#i x）dx となるので、被積分関数をまとめると、
∫緑＝∫（ε～r）（－exp（－#i x）＋exp（#i x））dx＝2#i∫（ε～r）sin（x）/x dx 。
そして、結局、∫ωdz＝0＝∫赤＋∫青＋∫緑なので、－π#i＋2#i∫（ε～r）sin（x）/x dx＝0、この第2項で、εをゼロに近づけると、
∫（0～∞）sin（x）/x＝π#i/（2#i）＝π/2 となる」
「そうじゃな。∫赤、∫青での極限の考え方など、必ずしも、厳密じゃないかもしれんが、ま、よしとしよう。
ところで、∫青＝－π#i じゃったが、これは、ω＝exp（#i z）/z のz＝0における留数＝1から、1×2π#i×（－1）×（1/2）＝－π#i とも計算できる。
ここで、負号を付けているのは、時計回りに回るため、また、2で割っているのは、半周だけするためじゃな」
