数式処理ソフト　DERIVE（デライブ） de ドライブ

５２．数値積分（1）（台形公式とベルヌイ数）

長さと面積

「また、だいぶ、更新が遅くなってしまったのう」

「ホント。数式処理ソフト DERIVE（デライブ）の前回（2009/1）から、約2年半ぶりですよー」

「いや、申し訳ない。「複素関数（6）（留数定理の応用）」の続きは、少し、休ませてもらって、今回から、しばらくの間、数値積分について、扱ってみようかと思うのじゃ」

「なるほど。そもそも、複素関数に入り込んじゃったのも、余弦積分の計算からだったものね」

「そういうことじゃな。まずは、基本的な台形公式じゃ」

「台形公式は、いつ頃から使われていたのかしら？」

「数値積分の公式という意味なら、積分という概念ができてからじゃろうが、面積の計算手段ということであれば、古代から使われてきたものじゃろう」

「たとえば、円の面積の計算ね。
岩波数学辞典では、ピタゴラス（詳しい生没年が不詳。「数学史」（矢野健太郎：科学新興社1967年）によると、紀元前582年頃～493年頃のギリシャ人）が、円に外接及び内接する正96角形の周の長さから円周率の値を、3＋10/71 <π<3＋1/7として求めたとあるわ」

「3.140845・・＜π＜3.142857・・ということになる。真の値は、π＝3.141593・・じゃから、3桁まで、正しいということになるのう」

「96角形というから、もっと、精度がいいのかと思ったわ」

「半径1の円に内接する正n角形の周長は、2n×sin（π/n）、外接する正n角形の周長は、2n×tan（π/n）じゃから、n＝96の場合は、これらを2で割った値から、
3.141031950・・＜π＜3.142714599・・となる。確かに、有効数字3桁までは、合っている。
外接多角形の周長の1/2－内接多角形の周長の1/2は、n×sin(π/n）（sec（π/n）－1）じゃから、nが大きいときは、約、π³／2n²だ。
nが96では、この値は、0.001682198170だから、3桁程度までしか合わないことが分かる」

「じゃ、6桁の精度を出そうとすると、少なくとも、n＞√（π³／（2×9×10^－7））≒4150角形ぐらいを使わないといけないことになるわね」

「そういうことじゃ。
円の面積よりも、円周の長さがまず、問題になったのは、面積よりも長さに対する人々の関心が高かったためじゃろう」

「長さは、比べたい2つを並べれば、比較できるけど、面積は、そうはいかないものね」

「とは言うても、必ずしも並べられるとは限らんじゃろう。
結局は、何か「単位」となる長さ、棒でも縄でもよいが、でもって、対象の長さがそれの何倍あるかということを調べたと思われるのう」

「だけど、離れている場合や大きい場合など、棒や縄で直接測るのは、無理だということで、比例の考えが生まれてきたのね。
ターレスがピラミッドの高さを測ったというのも、比例に基づく方法だもの」

「前述の「数学史」に出てくる話じゃな。
地面に棒を立てて、ピラミッドの高さ H、太陽の光によるピラミッドの影の長さ L、棒の高さ h、棒の影の長さ lとしたとき、比例式、
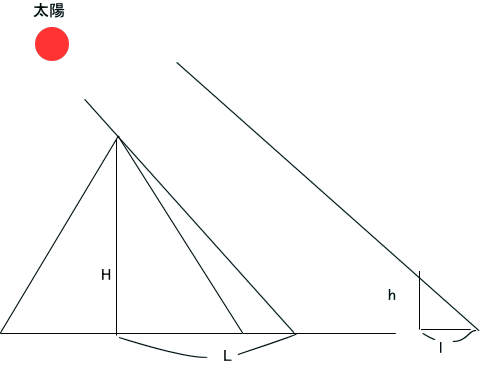H：h＝L：l から、高さ Hが求められる。
ターレスは、ギリシャの数学の父とたたえられている」

「相似三角形などの考えがターレスに始まると書かれているものね」

「長さに比べて、面積も、年貢などのために耕地面積などを測定する必要があったと思われるので、早くから、その重要性は、知られていたと思われる」

「ターレスの孫弟子の「ナクサゴラス」は、円の面積が半径の2乗に比例することを論証したと言われている。（「数学史」による）」

「なるほど。長方形の面積は、単位正方形の何倍かという考えでいけるけど、円の面積の場合は、無限の操作を考える必要があるので、困難になるわね」

「そういうことだな。単位円に内接及び外接する正n角形の面積により、πを見積もると、次式になる。
n×sin（π/n）cos（π/n）＜π＜n×tan（π/n）なので、上限値と下限値の差は、概略、π³/n² となり、減少の様子は、円周の場合と同様じゃ。ただ、円周の近似差は、分母に2があったので、やや、分がある。すなわち、正n角形の面積から、πを有効数字 6桁まで出そうとすると、4150×√2≒5869角形を使う必要がある」

「なるほど。でも、正n角形の近似で円の面積を出そうと努力する中で、円の面積＝πr² という公式が得られたのね」

「そうじゃな。正n角形のnが大になると、1つの小三角形の底面の長さは、円周の長さ／n と考えてよいので、小三角形の面積は、高さ r×円周の長さ／n×1/2となる。
n個の小三角形の面積は、円周の長さを2r×πを使って、πr² となるので、円の面積として、おなじみの公式が得られるという訳じゃ」

「確かに、曲線を多角形で近似して長さや面積を求めるという方法は、このあたりから始まっていると思ってもいいのね」

台形公式

「単積分を考えよう。積分上端をb、下端をaとして、被積分関数をf(x)と書く。定積分は、一般に次のように表せる。
∫_a^bf(x)dx＝(∫(f(x), x, a, b))、ここで、右側は、DERIVEによる表現じゃ。今後は、左側のように書くべきところを右側のように書いていこう」

「台形公式は、定積分を、h＝（b－a）/nと書いて、h×（1/2×（f(a)＋f(b)）＋Σ（k＝1～n－1）f(a＋h×k））と書いてと。
区間［a，b］をn等分（n＞0）してあるのね」

「原理は、あらためて言うまでもないじゃろう。
台形公式の誤差を考えよう。
真値－台形公式≒c₂×h²×（f'(b)－f'(a)）＋c₄×h⁴×（f'''(b)－f'''(a)）＋c₆×h⁶×（f⁽⁵⁾(b)－f⁽⁵⁾(b))＋・・と表される。
ここで、c₂などは、f(x)やhに依存しない定数である。（岩波数学辞典「数値積分法」：p578）
さて、台形公式の値をT（n）と書けば、真値 I として、上記から、概略、I－T(n)≒c₂×h² である。分点を2倍にした結果をT(2n)と書けば、
I－T(2n)≒c₂×h²/4 でもある。
この2式から、c₂×h²を消去すると、I≒（4×T(2n)－T(n)）/3 という結果が得られる。この式は、hの4次に比例する誤差を持つことになる。
この式を具体的に書き下すと、S(n)＝h/6×［（f(a)＋f(b)＋4Σ（k=1～n）f(a+(k－1/2)h）＋2Σ（k=1～n－1）f(a+kh）］、青字部分を2011/8/5訂正
ここで、h＝（b－a）/n である。（この個所は、「計算機による数値計算法」（一松信・戸川隼人著：新曜社：1975年2月）による）
この式、S(n)は、後で書くところの「シンプソン公式」となっているのじゃな」

「ふ～ん。実際に検算して確かみてみるわ。テスト関数は、1/(1+x²)を積分範囲 a=1～b=2とする。
正確な値は、ATAN(1/3)≒0.3217505543・・
まずは、台形公式では、n＝1～100まで、次のとおり。
[0.35, 0.3288461538, 0.3249019607, 0.3235225140, 0.3228843672, 0.3225378274, 0.3223289146, 0.3221933389, 0.3221003964, 0.3220339192, 0.3219847357, 0.3219473289, 0.3219182183, 0.3218951204, 0.3218764865, 0.3218612363, 0.3218485974, 0.3218380059, 0.3218290425, 0.3218213897, 0.3218148039, 0.3218090957, 0.3218041157, 0.3217997451, 0.3217958885, 0.3217924683, 0.3217894210, 0.3217866943, 0.3217842448, 0.3217820362, 0.3217800379, 0.3217782239, 0.3217765724, 0.3217750644, 0.3217736838, 0.3217724167, 0.3217712509, 0.3217701759, 0.3217691826, 0.3217682628, 0.3217674095, 0.3217666164, 0.3217658780, 0.3217651894, 0.3217645462, 0.3217639445, 0.3217633807, 0.3217628519, 0.3217623550, 0.3217618877, 0.3217614476, 0.3217610327, 0.3217606410, 0.3217602709, 0.3217599208, 0.3217595892, 0.3217592750, 0.3217589769, 0.3217586938, 0.3217584247, 0.3217581688, 0.3217579252, 0.3217576930, 0.3217574717, 0.3217572605, 0.3217570588, 0.3217568661, 0.3217566818, 0.3217565055, 0.3217563367, 0.3217561749, 0.3217560199, 0.3217558712, 0.3217557285, 0.3217555914, 0.3217554597, 0.3217553331, 0.3217552114, 0.3217550942, 0.3217549814, 0.3217548728, 0.3217547681, 0.3217546672, 0.3217545698, 0.3217544759, 0.3217543853, 0.3217542977, 0.3217542131, 0.3217541313, 0.3217540523, 0.3217539758, 0.3217539019, 0.3217538303, 0.3217537609, 0.3217536938, 0.3217536287, 0.3217535657, 0.3217535045, 0.3217534452, 0.3217533877]
100分割して、なんとか、小数点以下5桁までね。
次に、（4T(2n)－T(n))/3＝S(n)はというと、
[0.3217948717, 0.3217479674, 0.3217497830, 0.3217502805, 0.3217504365, 0.3217504960, 0.3217505224, 0.3217505354, 0.3217505425, 0.3217505465, 0.3217505490, 0.3217505505, 0.3217505516, 0.3217505523, 0.3217505528, 0.3217505531, 0.3217505534, 0.3217505536, 0.3217505537, 0.3217505538, 0.3217505539, 0.3217505540, 0.3217505541, 0.3217505541, 0.3217505541, 0.3217505542, 0.3217505542, 0.3217505542, 0.3217505542, 0.3217505542, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543, 0.3217505543]
となって、約30分割で、小数点以下10桁の精度が出ている！」

「グラフで書くと一目瞭然じゃ。

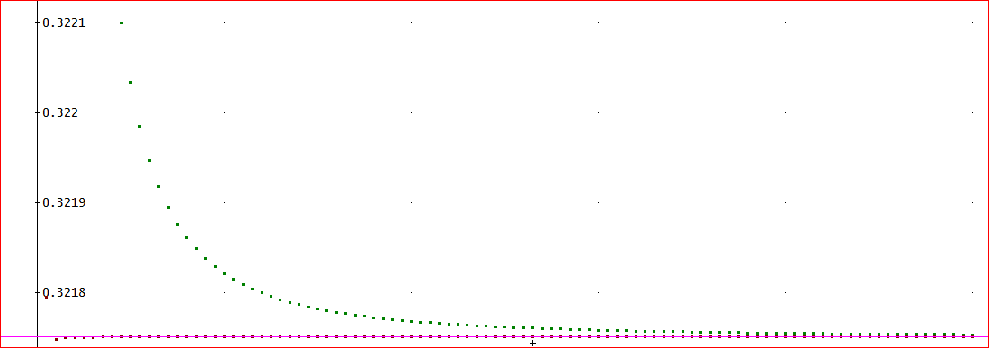
上図で、ピンク色の直線がATAN（1/3）≒0.3217505543・・、なだらかに減少している緑色のドットがT(n)、ほとんどグラフ上では、ピンク色の直線に重なっているドットがS(n)じゃ」

「ほんと。T(n)は、n=1では、小数点以下1桁しか正しくないのに、S(n)の方は、小数点以下4桁まで正しいのは、オドロキよ」

「この例では、単調減少型のたちのよい関数と積分範囲じゃったので、誤差が、台形公式は、hの2乗、シンプソン公式は、hの4乗に比例することがかなり明確に分かるのう。
別の例として、f(x)＝sin(x)/（1+x²）を積分範囲、1～10までで積分してみよう。
下が計算結果じゃ。グラフだけを掲げておこう。

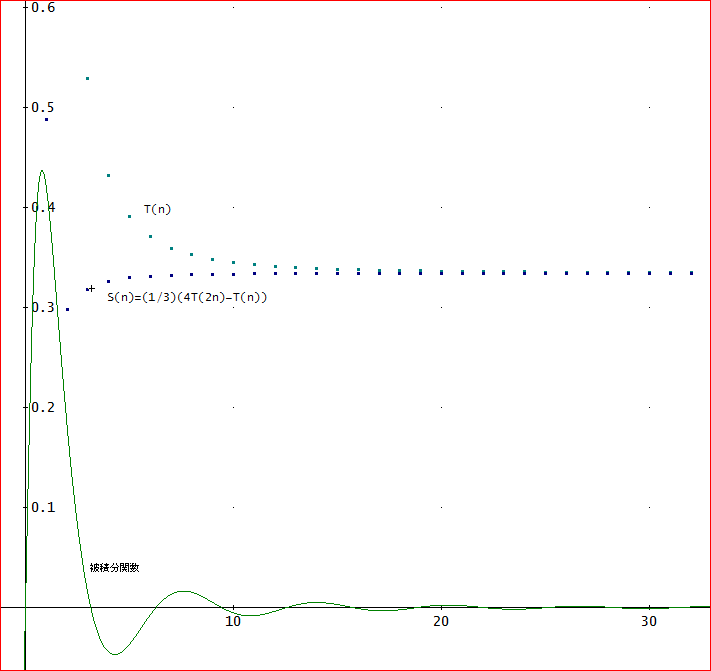
ちょっと、見づらいかもしれんが、S(n)も最初のうちは、そんなに精度が高くない。
被積分関数が正負で振動しているからな」

ドットのグラフの書き方

「読者に代わって質問なんだけど、グラフの書き方について、再確認して下さいな」

「そうじゃな。
まずは、f(x)のような場合は、DERIVEで、その行を指定して、2次元グラフを描けばよいので、簡単じゃ。
ところが、T(n)の様な場合、nを整数と指定しても、そのまま描くと、次のようになってしまう。

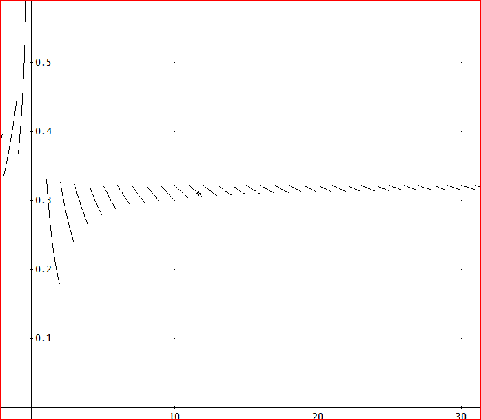
このようなときは、T(n)を選択して、解析メニューから「表の作成」を指示する。
すると、nの範囲を聞いてくるので、たとえば、1～10とすると、左図のような行列が作成される。
これをグラフに描くとドットのグラフが描けるという次第じゃな」

「ふ～ん。前に出てきたときよりも、「表の作成」を使うと、自分でベクトルを定義しなくてもよいので簡単ね」

「そういうことだな。今回、表の作成を使って見て分かった。ははは」

「しっかりしてくださいよ」

「うん。そうじゃ。
ついでじゃから、「表の作成」を使用しない方法も書いておこう。
まずは、解析メニューから、T(n)を任意の、たとえば、n=1～10の範囲で「数列の作成」を行う。
すると、
[0.35, 0.3288461538, 0.3249019607, 0.3235225140, 0.3228843672, 0.3225378274, 0.3223289146, 0.3221933389, 0.3221003964, 0.3220339192]のようにベクトルが作られる。
この行が、仮に14行目であるとすると、
新規にベクトルVをV:=[k，#14↓k］の様に定義する。
そして、あらためて、vと入力後に、数列の作成から、kを1～10で計算する。
すると、先に出した表と同様のものが計算されるので、それを元にグラフを描けばよい」

「えーと。ドットを線で結んで表示したいときは、どうするのかしら？」

「グラフ画面のオプションから表示をクリックすると、下図のようなダイアログボックスが表示される。

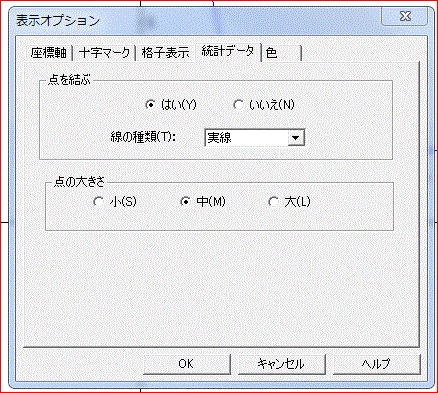
ここで、「統計データ」タブの「点を結ぶ」を「はい」にしてから、再度、描画させればよい。
すると、次の図のように点を結んでくれる」

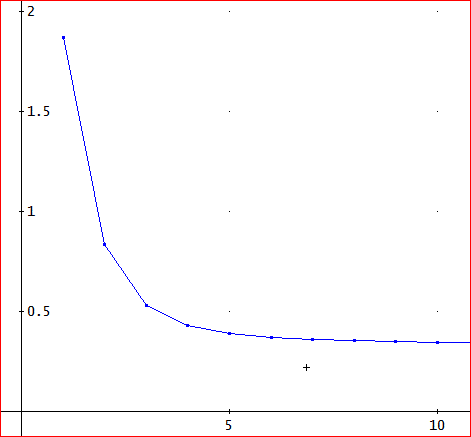
「なるほど、なるほど。これは、便利ね」

ベルヌイ数

「以前に出てきた「計算数学夜話」（森口繁一著：日本評論社：1978年4月）に、このような積分公式とその誤差についての記事が載っている。
それには、まず、ベルヌイ（Bernoulli）数について、知っておく必要があるのう」

「ベルヌイさんって、何人もいるよね」

「そう、ベルヌイ家は、数学者を輩出しているので有名じゃな。岩波数学辞典でも「ベルヌーイ家」という項目を立てているほどじゃ。
少なくとも、8人の著名な数学・物理学者を出している。
『なかでも、ヤコブ（1654/12/27～1705/8/16）とヨハン（1667/7/27～1748/1/1）の兄弟と、ヨハンの次子ダニエル（1700/2/8～1782/3/17）が優れていた』（同書より抜粋）」

「ベルヌーイとも書くのね」

「そう、ベルヌイあるいはベルヌーイ家は、元々、新教徒で、宗教的な軋轢を逃れるために、オランダからスイスに移り住んだということじゃな。
『新教徒』などと書くと、まあ、ずいぶん、昔の話ではあるの」

「キリスト教の旧教に対しての新教徒よね」

「そう、プロテスタントとも書くが、旧教であるカトリック教会のような統一された組織を持つものではないそうだ。このあたり、わしらのような「異教徒」は、何度聞いても、その違いが分からんが」

「ま、それは、日本の仏教の宗派、たとえば、「南都六宗」（『奈良時代における仏教の宗派。すなわち三論・法相（ほっそう）・華厳（けごん）・律・成実（じょうじつ）・倶舎（くしゃ）の六宗』：広辞苑による）に「真言宗」、「天台宗」を加えた「八宗」の違いを外人さんに説明せよ、といわれても、サッパリ分からんというようなもんでしょう。
だいたい、私たちが「仏教徒」というのは、ホントなんでしょうか？！」

「ともちゃん。すごく、脱線しかかっているよ」

「ま、そうですが。もとい、ベルヌイ数を発見したのは、どの人なんですか？」

「その前に、ベルヌイ数とはなんぞや、でしょうが・・。
n次のベルヌイ数をB(n)と書くと、x／（exp(x)－1）＝Σ（n=0～∞）B（n）xⁿ／n! の係数と定義されるものじゃ。
これは、母関数による定義じゃな」

※岩波数学辞典のベルヌーイ多項式とベルヌーイ数の項を参考にした。ただし、本稿では、『ベルヌイ』に表記を統一している。
「へー。
じゃ、x／（exp(x)－1）をxの10次まで微分してx→0の極限を計算すると、あれれ、B(1)～B(9)までは、簡単に求められるけど、10番目が求められずに極限の式が出るだけだよ」

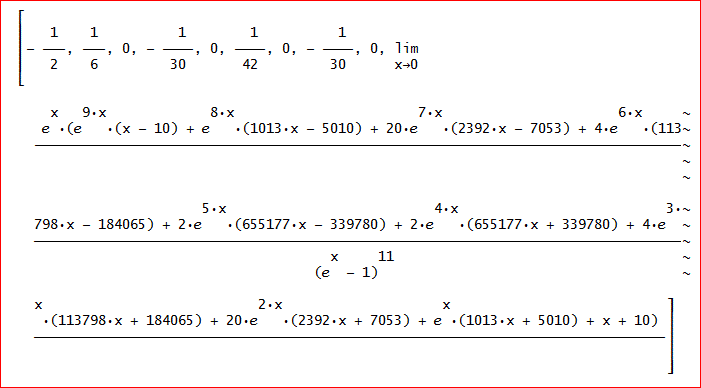
「10番目は、『ロピタルの定理』で分母、分子をそれぞれxで微分してから、極限を取ると、B(10)＝5/66のように求められる。
そういえば、ともちゃんは、どのように上の式を計算したのじゃな」

「えーと。まずは、関数 f(x)をf(x):=x／(exp(x)－1）のように定義します。
次に、関数 B(n)を B(n):= IF(n = 0, 1, ∂(f(x), x, n)) のように定義する。
そしてと、B(n)と書いてから、解析メニューで、nを1～10まで変化させて、計算する。
これは、ゴチャゴチャしたxの分数式になるけど、解析メニューで、極限を選択して、xをゼロに近づけると、上の図のように数値がベクトルで計算されるという方法ね」

「そうじゃな。もう少し、簡単化するために、n階微分を取ってから、極限を取る操作を一つにまとめてみよう。
B(n):= IF(n = 0, 1, LIM(∂(f(x), x, n), x, 0)) 同じ事が、
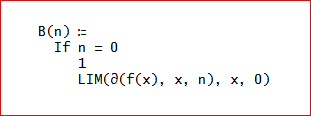実際は、左図のように画面上では、表示されるのじゃがな。
この、LIM（式，変数，極限値）というのが、極限をとる関数じゃな」

「なるほど。
でも、B(10)が、すでに、ロピタルの定理を使って、手動でしか求められないというのは、つらいわね」

「確かにな。漸化式を使う方法をすぐ下で紹介するが、なぜ、求めにくいかを考えることも必要じゃな」

「そうね、このf(x)とそれを微分した式が、ことごとく、xのゼロ極限で、分母、分子ともゼロになっちまうという、まったくケシカラン関数だからでしょう」

「はは、まったくじゃな。
では、漸化式を導いてみよう。
分母と分子をひっくり返して、
1/f(x)＝exp（x）－1／x＝1＋x/2!＋x²/3!＋・・であることは、確かじゃが、これと、元のf(x)を掛け合わせたものが、常に1となることに注意する。
元の式は、定義により、B(0)＋B(1)x/1!＋B(2)x²/2!＋・・であるので、xの同次数の項をまとめると、
B(0)＝1は、すぐに分かる。
n>0では、
B(0)／0!(n+1)!＋B(1)／1!(n)!＋B(2)／2!(n－1)!＋・・＋B(n－1)／(n－1)!1!＋B(n)／n!0!＝0 が成り立つ。
すると、B(n)＝－n!Σ（k=0～n－1）B(k)／(n－k+1)!k! ということは、すぐに分かるじゃろう」

「な～る。
そこで、(n+1－k）!と合わせるために、n!／(n+1－k)!k!＝(1/(n+1))×(n+1)!／(n+1－k)!k!＝(1/(n+1))×comb(n+1，k）と一工夫すれば、
公式集などに出てくる式に一致するのね」

「そう。B(n)＝－1/(n+1)Σ（k=0～n－1）comb(n+1，k)×B(k) と表せるというわけじゃな」

「これを使うと、n＝1～10までは、
[－ 1/2, 1/6, 0, － 1/30, 0, 1/42, 0, － 1/30, 0, 5/66] と簡単に求められるのじゃ」

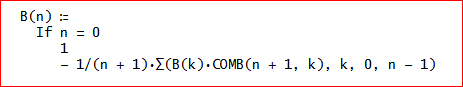
「じゃ、n＝1～20に挑戦してみよう。
うへー。28秒程度かかったわ。大変。
[－ 1/2, 1/6, 0, － 1/30, 0, 1/42, 0, － 1/30, 0, 5/66, 0, － 691/2730, 0, 7/6, 0, － 3617/510, 0, 43867/798, 0, － 174611/330]、
答えは、合っているけど。10番目と20番目は、赤字よ」

「再帰的帰納関数による定義になっているため、同じ値を何回も行ってしまうからじゃな」

「記憶させておけばいいのね。配列を使うとかして」

「そう、具体的には、次のようにするのが簡単じゃ。
まずは、求めたい次数よりも1つだけ大きい、ベクトルを宣言する。
一つ大きくするのは、DERIVEでは、ベクトルの引数にゼロを使えないためじゃな。
ここでは、50番目までを求めるために、51次元とする。初期の要素は、すべて、ゼロとなっている。
このベクトルをvと定義する。v:=[0,0,0,0・・・]となる。
次に、1番目を1、2番目を－1/2と置き換える。初期値を入れておこうという訳じゃ。
このためには、v↓1:=1、v↓2:=－1/2として「計算」させる。
この:=は、代入演算子じゃ。下のパレットから選択して使ってもよい。
そして、B(n)の定義式の中を下のように工夫する。
vの要素をv↓iではなくて、i+1としているのは、前述のようにゼロから始められないためじゃ。

最後に3番目の式のようにv↓kにB(n－1)を代入する命令を書いてから、解析メニューの数列の作成から、たとえば、nを1～20まで指示すると、
結果がベクトルで並ぶが、再度、vのみを入力して、表示させると先ほどと同一の結果が直ちに得られる」

「代入演算子というところが、ポイント高いわね。単にイコールでは、だめだったんだ。
じゃ、n＝0～50番までを表にしてみよう。
[1, － 1/2, 1/6, 0, － 1/30, 0, 1/42, 0, － 1/30, 0, 5/66, 0, － 691/2730, 0, 7/6, 0, － 3617/510, 0, 43867/798, 0, － 174611/330,
0, 854513/138, 0, － 236364091/2730, 0, 8553103/6, 0, － 23749461029/870, 0, 8615841276005/14322, 0, － 7709321041217/510,
0, 2577687858367/6, 0, － 26315271553053477373/1919190, 0, 2929993913841559/6, 0, － 261082718496449122051/13530, 0,
1520097643918070802691/1806, 0, － 27833269579301024235023/690, 0, 596451111593912163277961/282, 0,
－ 5609403368997817686249127547/46410, 0, 495057205241079648212477525/66]、ただし、赤字は、10番目毎を表す。
今度は、コンマ何秒というか、あっという間。だけど、ホント合っているのかしら。」

「Webの、たとえば、Sugimoto氏の「数学研究ノート」（http://homepage3.nifty.com/y_sugi/index.htm）を参照させてもらうと、
n＝40の値までは、一致していたので、正しいと思うのう。
また、『岩波数学辞典』第4版の付録の数表5にも、30番目までのベルヌイ数が掲載されていたので、照合してみたが正しいようだな。
ちなみに、DERIVEでは、98番までは、計算できた。
DERIVEでは、100次元までしかベクトルを定義できなかったので、99番目以上のベルヌイ数は、この方法では、求められない。
今回は、ベルヌイ数の計算で時間を使ってしまって、肝心の数値積分との関係に触れられなかったのが残念じゃが、次回に回すことにしよう。
いや、ともちゃんも、久々の登場で、お疲れさんじゃった」