数式処理ソフト DERIVE(デライブ) de ドライブ
53.数値積分(2)(Euler-Maclaurin展開とその応用)
ベルヌイ数の母関数のテイラー級数と収束半径
「数式処理ソフト DERIVE(デライブ)の第52回の最後の節では、ベルヌイ数 B(n)を、B(n)=lim(x→+0)f(n)(x) という定義を基に計算した。
ここで、f(x)=x/(exp(x)-1)、また、f(n)(x) は、n階微分を表すものとする」
 「だけど、定義式から直接、ベルヌイ数を計算するのは、nが8ぐらいまでは、簡単だけど、それ以上になると難しかったのね」
「だけど、定義式から直接、ベルヌイ数を計算するのは、nが8ぐらいまでは、簡単だけど、それ以上になると難しかったのね」
「そこで、漸化式、B(n)=-1/(n+1)Σ(k=0~n-1)comb(n+1,k)B(k) を導いて使ったのじゃったな。
ここで、B(0)=1、comb(n+1,k)は、組合せの数 n+1CkをDERIVE流に標記したものじゃ」
「しかし、このままの手順だと、一度計算したB(k)を何度も呼び出して計算するため、B(n)の20番目までで、20数秒もかかっちゃう。
そこで、配列(ベクトル)を使って、一度計算したB(k)を記録しておき、計算の手間を省いたんだったわね。
それで、98番目までは、あっという間に求められるようになったわ」
「そうじゃったな。
もっとも、98番目というのは、DERIVEでのベクトルの次元が100次元を上限としているという制約によるもので、解法の限界ではない。
とはいえ、我々は、ベルヌイ数の計算そのものに大きな関心がある訳ではなくて、関心は、むしろ、その応用なんじゃがな」
「とはいうけど、母関数のテイラー展開式を、g(x,n)=Σ(k=0~n)B(k)×xk/k! と表すとき、これらが母関数をどの程度近似しているかを調べて見たの。
下の図は、母関数 f(x)=x/(exp(x)-1)とg(x,n)のn=2、4、6、8 としたときの原点付近の様子よ。
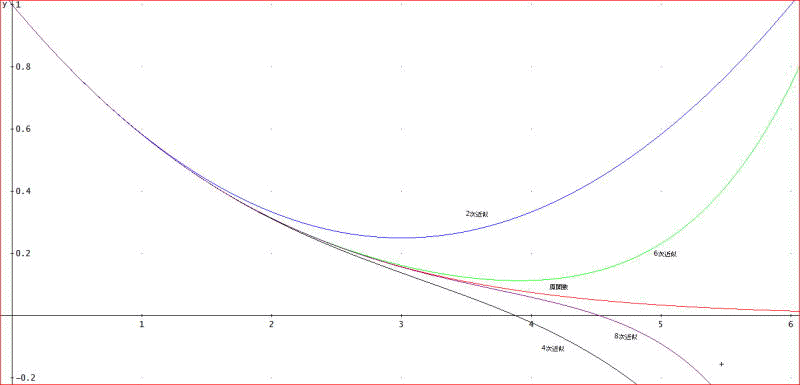
xが1ぐらいまでは、いずれも、よく近似しているけど」
「原関数が赤線じゃな。
母関数というのは、数列の定義のためじゃから、特にその数列を使った級数の収束性を問題にしているわけではない。
ま、今回の場合は、xを複素数に拡張して考えると、極が、±2πi にあるので、収束半径は、2πじゃ。
よって、テイラー級数も、|x|<2πで収束すると考えるのが正しいじゃろう」
「でも、どうみても、xが3程度で、すでに、原関数とずいぶん差が開いてしまうみたい」
「そうじゃな。もっと、次数を上げてみたらどうじゃな」
「そうね。g(x, n):= ∑(v↓(k + 1)x^k/k!, k, 0, n) と再定義してみよう。ここで、v↓(k+1)=B(k)とする。
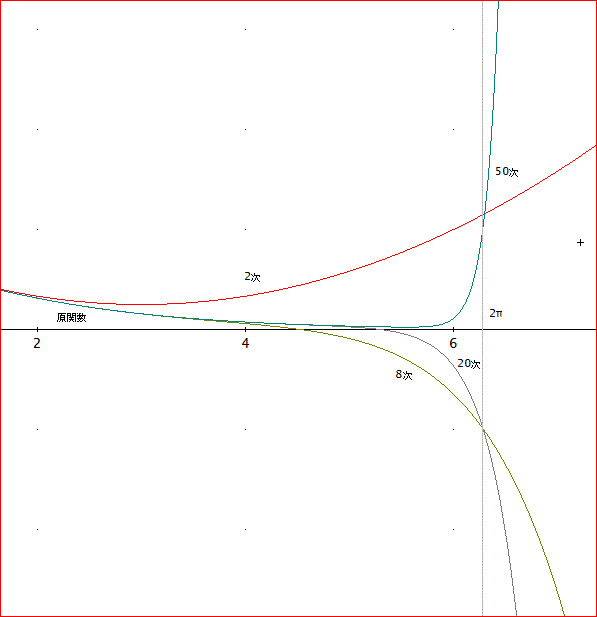
なるほど。20次とか50次まで取れば、ずいぶんと原関数と接近してくるわね!」
「そういうことじゃ。
しかし、x=2πで、テイラー展開は、破れるのじゃな。それはそうと、そろそろ、本題に戻らねばならん」
オイラー・マクローリン(Euler-Maclaurin)展開
「まずは、交代級数で非常な成功を収めた「オイラー変換」について、復習してみよう」
 「えーと。交代級数の各項をa(k)のように表したとき、S=Σ(k=0~∞)(-1)k×a(k) と書くことにする。
「えーと。交代級数の各項をa(k)のように表したとき、S=Σ(k=0~∞)(-1)k×a(k) と書くことにする。
このとき、記法上で特に注意する点は、a(k)自身は、正ということで、(-1)k を使っているという事ね。
具体的には、S=a(0)-a(1)+a(2)-+・・なのね。この級数は、収束すると仮定している。
ここで、差分演算子 ΔをΔa(k)=a(k+1)-a(k) のように定義する。これは、通常の差分ね。
だから、Δ2a(k)=a(k+2)-2a(k+1)+a(k) などとなる。
また、『ずらし演算子』 Eをa(k+1)=E a(k) で、定義する。これも、E2 a(k)→a(k+2) のように考えようということ。
さ~て、お立ち会い。
ここからが、オイラー変換の見せ所よ!
Sは、交代級数なので、
S=a(0)-E a(0)+E2 a(0)-E3 a(0)+-=(1-E+E2-E3+-)a(0) と表せる。
この(1-E+E2-E3+-)を等比、-Eの等比級数と考えると、無限和を、1/(1+E)と表記できる。
よって、S=(1/(1+E))a(0) となる。
一方、Eと差分演算子 Δとの関係を調べると、Δa(k)=a(k+1)-a(k)=E a(k)-a(k)=(E-1)a(k) より、E=1+Δと考えられるのではないか。
そこで、S=(1/(1+E))a(0)=(1/(2+Δ))a(0)=(1/2)(1/(1+(Δ/2)))a(0) 。
従って、S=(1/2)a(0)-(1/4)Δa(0)+(1/8)Δ2a(0)-(1/16)Δ3a(0)+-・・
とまあ、こんなところだったかしら」
「うん。これは、「第41回の積分(1)(単積分、数値積分とEuler変換)」で掲げた内容であるな。
そこでも注意してあるが、オイラー変換を行うのは、初項からでなくても、適切な任意の項からでもよい」
「出典は、『計算数学夜話』(森口繁一著:日本評論社刊:昭和53年4月10日初版)」の森口先生の記事ね」
「積分の計算でも、これと似たアイデアが使えないかという点を調べることにする。
以下、上記の森口先生の本にならって、考えてご覧」
「そうね。まずはと、f(x)のa~bまでのを定積分を∫(a~b)f(x)dxとすると、
この区間をn等分して、h=(b-a)/n と微小幅 hで区切る。b=a+nhである。
ここで、差分演算子にならって、微分演算子をDとして、Dk f(x)=f(k)(x)を定義する。
また、(1/D)f(x)=∫f(x)dx、(f(x)の不定積分)でもある。
一方、ずらし演算子 Eを、E f(x)→f(x+h)としたとき、関数のn個の和 Sを、S=Σ(k=0~n-1)f(a+kh) を計算してみる。
これは、S=f(a)+f(a+h)+f(a+2h)+・・+f(a+(n-1)h) であって、項数は、n個の和なんだけど、
S=f(a)+Ef(a)+E2f(a)+・・En-1f(a)=(1-En)/(1-E)f(a) とも表せる。
さて、微分演算子とずらし演算子の関係を考える。
f(x+h)=f(x)+f(x)(1)h/1!+f(x)(2)h2/2!+・・、これから、f(x+h)=E f(x)を、f(x+h)=exp(hD)f(x)とも表せ、すなわち、E=exp(hD) と推定される。
この式は、前述のE=1+Δと似ていることに注意する。
事実、Δf(x)=f(x+h)-f(x)、lim(h→0)Δf(x)/h=D f(x)からも、
Δ≒hDとなって、E=exp(hD)≒exp(Δ)=1+Δ+・・と第2項まで展開したものと同一となる。
さて、S=(1-En)/(1-exp(hD))f(a)=(En-1)/(exp(hD)-1)f(a) 書くことができる。
問題は、この後ね」
「そうじゃ。上の最後の式で、分子の(En-1)をexpn(hD)-1 と書いてしまわないことがポイントじゃな。
分母のexp(hD)-1を前回出てきた、x/(exp(x)-1)を利用して変形するために、x/(exp(x)-1)のテイラー展開式 Σ(k=0~∞)B(k)xk/k! から、
1/(exp(x)-1)=(1/x)Σ(k=0~∞)B(k)xk/k! として、
ここで、xをhDに置き換えれば、
S=((En-1)(B(0)/hD+B(1)/1!+B(2)(hD)/2!+B(3)(hD)2/3!+B(4)(hD)3/4!+・・))f(a) となる」
「B(k)は、k=0から書くと、
[1,- 1/2, 1/6, 0, - 1/30, 0, 1/42, 0, - 1/30, 0, 5/66, 0, - 691/2730, 0, 7/6, 0, - 3617/510, 0, 43867/798, 0, - 174611/330]と10番目まで。
まずは、上式の第1項目は、((En-1)/hD)f(a) となるわ。
ここで、f(x)の不定積分をF(x)と書くと、
1/D f(x)=F(x)であるから、この項は、(1/h)(En F(a)-F(a))=(1/h)(F(a+nh)-F(a))=(1/h)∫(x=a~b)f(x)dxと書ける。
よって、S=f(a)+f(a+h)+f(a+2h)+・・+f(a+(n-1)h)は、
S=(1/h)∫(x=a~b)f(x)dx+B(1)(En f(a)-f(a))+hB(2)/2!(En f'(a)-f'(a))+(h3B(4)/4!)(En f(3)(a)-f(3)(a))+・・。となる。
定積分を移項すると、
∫(x=a~b)f(x)dx=hS-hB(1)(f(b)-f(a))-h2B(2)/2!(f'(b)-f'(a))-(h4B(4)/4!)(f(3)(b)-f(3)(a))-・・が得られるということね」
「結局、
∫(x=a~b)f(x)dx=h×Σ(k=0~n-1)f(a+kh)+h/2×(f(b)-f(a))-Σ(j=1~)h(2j)B(2j)/(2j)!(f(2j-1)(b)-f(2j-1)(a)) とまとめられる。
この形式を、Euler-Maclaurin(オイラー-マクローリン)展開と呼んでいる。
なお、定積分の真の値を I、台形公式の値をT(n)とすれば、
I=T(n)-Σ(j=1~)h(2j)B(2j)/(2j)!(f(2j-1)(b)-f(2j-1)(a))とも書くことができる」
「具体的に書き下してみると、
I=T(n)-h2/12(f'(b)-f'(a))+h4/720(f(3)(b)-f(3)(a))-h6/30240(f(5)(b)-f(5)(a))+h8/1209600(f(7)(b)-f(7)(a))-・・となって、
森口先生の「計算数学夜話」のP44の式と一致したわ!」
Euler-Maclaurin展開を使った数値積分(1)
「早速、前回計算した一番目の例、1/(1+x2)のx=1~2までの定積分の計算を行ってみよう。
まずは、一般的に、被積分関数 g(x)の計算をできるようにしておこう。計算結果をf(a,b,n,m)の関数として、返すようにする。
また、便宜的にh(a,b,n)=(b-a)/nとして定義しておく。
f(a, b, n, m):= h(a, b, n)∑(g(a + kh(a, b, n)), k, 0, n - 1) + h(a, b,
n)/2(g(b) - g(a)) - IF(m = 0, 0, ∑(h(a, b, n)^(2j)B(2j)/(2j)!(LIM(∂(g(x),
x, 2j - 1), x, b) - LIM(∂(g(x), x, 2j - 1), x, a)), j, 1, m)) じゃな。
DERIVEの画面表示は、下図を参照して欲しい」
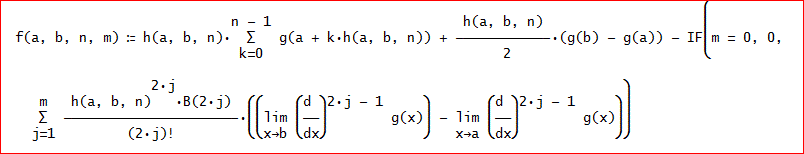
 「この、m=0の場合が、台形公式と一致するわけね」
「この、m=0の場合が、台形公式と一致するわけね」
「そういうことじゃ。
実際、g(x)=1/(1+x^2)として、f(1,2,n,0)を計算してみる。以下のようになる。
正確な値は、ATAN(1/3)=0.3217505543966421934・・(有効数字20桁で計算)
[0.35, 0.3288461538, 0.3249019607, 0.3235225140, 0.3228843672, 0.3225378274,
0.3223289146, 0.3221933389, 0.3221003964, 0.3220339192, 0.3219847357, 0.3219473289,
0.3219182183, 0.3218951204, 0.3218764865, 0.3218612363, 0.3218485974, 0.3218380059,
0.3218290425, 0.3218213897, 0.3218148039, 0.3218090957, 0.3218041157, 0.3217997451,
0.3217958885, 0.3217924683, 0.3217894210, 0.3217866943, 0.3217842448, 0.3217820362,
0.3217800379, 0.3217782239, 0.3217765724, 0.3217750644, 0.3217736838, 0.3217724167,
0.3217712509, 0.3217701759, 0.3217691826, 0.3217682628, 0.3217674095, 0.3217666164,
0.3217658780, 0.3217651894, 0.3217645462, 0.3217639445, 0.3217633807, 0.3217628519,
0.3217623550, 0.3217618877, 0.3217614476, 0.3217610327, 0.3217606410, 0.3217602709,
0.3217599208, 0.3217595892, 0.3217592750, 0.3217589769, 0.3217586938, 0.3217584247,
0.3217581688, 0.3217579252, 0.3217576930, 0.3217574717, 0.3217572605, 0.3217570588,
0.3217568661, 0.3217566818, 0.3217565055, 0.3217563367, 0.3217561749, 0.3217560199,
0.3217558712, 0.3217557285, 0.3217555914, 0.3217554597, 0.3217553331, 0.3217552114,
0.3217550942, 0.3217549814, 0.3217548728, 0.3217547681, 0.3217546672, 0.3217545698,
0.3217544759, 0.3217543853, 0.3217542977, 0.3217542131, 0.3217541313, 0.3217540523,
0.3217539758, 0.3217539019, 0.3217538303, 0.3217537609, 0.3217536938, 0.3217536287,
0.3217535657, 0.3217535045, 0.3217534452, 0.3217533877]
これは、前回の記事の台形公式の計算結果と当然ながら、一致しておる」
「なるほど。じゃ、m=1の場合をn=1~100まで計算してみるよ。
ジャーン。
[0.3216666666, 0.3217628205, 0.3217538126, 0.3217516807, 0.3217510339, 0.3217507904, 0.3217506833, 0.3217506305,
0.3217506022, 0.3217505858, 0.3217505759, 0.3217505696, 0.3217505654, 0.3217505626,
0.3217505606, 0.3217505592, 0.3217505582, 0.3217505574, 0.3217505568, 0.3217505563, 0.3217505560,
0.3217505557, 0.3217505555, 0.3217505553, 0.3217505552, 0.3217505550, 0.3217505549, 0.3217505549, 0.3217505548, 0.3217505547, 0.3217505547, 0.3217505547,
0.3217505546, 0.3217505546, 0.3217505546, 0.3217505545, 0.3217505545, 0.3217505545,
0.3217505545, 0.3217505545, 0.3217505545, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544,
0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505544, 0.3217505543, 0.3217505543]
シンプソン公式と、ほぼ、等しい。細かいところで、やや見劣りがする。
m=2の場合、有効数字20桁で計算してみたよ。
[0.32134666666666666666, 0.32174282051282051282, 0.32174986201888162672, 0.32175043073796122576, 0.32175052195064192598, 0.32175054352726264803, 0.32175055008568329191, 0.32175055246181247105, 0.32175055344222926479, 0.32175055388942391276,
0.32175055411032993113, 0.32175055422677534000, 0.32175055429155844477,
0.32175055432927835983, 0.32175055435211280591, 0.32175055436640972216, 0.32175055437562864861, 0.32175055438172946282, 0.32175055438586092134, 0.32175055438871697754, 0.32175055439072828193, 0.32175055439216862519, 0.32175055439321591432, 0.32175055439398806492, 0.32175055439456465521, 0.32175055439500028590, 0.32175055439533299363, 0.32175055439558964985, 0.32175055439578948595, 0.32175055439594643203, 0.32175055439607069174, 0.32175055439616981763, 0.32175055439624945471, 0.32175055439631386104, 0.32175055439636627619, 0.32175055439640918481, 0.32175055439644450714, 0.32175055439647373792, 0.32175055439649804860, 0.32175055439651836320, 0.32175055439653541502, 0.32175055439654978943, 0.32175055439656195624, 0.32175055439657229453, 0.32175055439658111170, 0.32175055439658865824, 0.32175055439659513914, 0.32175055439660072297, 0.32175055439660554884, 0.32175055439660973210, 0.32175055439661336870, 0.32175055439661653877, 0.32175055439661930947, 0.32175055439662173728, 0.32175055439662386985, 0.32175055439662574750, 0.32175055439662740448, 0.32175055439662886992, 0.32175055439663016872, 0.32175055439663132218, 0.32175055439663234861, 0.32175055439663326373, 0.32175055439663408113, 0.32175055439663481256, 0.32175055439663546820, 0.32175055439663605688, 0.32175055439663658632, 0.32175055439663706323, 0.32175055439663749347, 0.32175055439663788221, 0.32175055439663823394, 0.32175055439663855265, 0.32175055439663884183, 0.32175055439663910456, 0.32175055439663934358, 0.32175055439663956129, 0.32175055439663975984, 0.32175055439663994114, 0.32175055439664010688, 0.32175055439664025856, 0.32175055439664039753, 0.32175055439664052499, 0.32175055439664064202, 0.32175055439664074959, 0.32175055439664084855, 0.32175055439664093969, 0.32175055439664102371, 0.32175055439664110123, 0.32175055439664117282, 0.32175055439664123900, 0.32175055439664130022, 0.32175055439664135691, 0.32175055439664140945, 0.32175055439664145818, 0.32175055439664150341, 0.32175055439664154542, 0.32175055439664158448, 0.32175055439664162083, 0.32175055439664165466, 0.32175055439664168619]
となって、第14分割で有効数字10桁が求まっている。
更に、m=3としてみると、
[0.32134666666666666666, 0.32174282051282051282, 0.32174986201888162672,
0.32175043073796122576, 0.32175052195064192598, 0.32175054352726264803,
0.32175055008568329191, 0.32175055246181247105, 0.32175055344222926479,
0.32175055388942391276, 0.32175055411032993113, 0.32175055422677534000,
0.32175055429155844477, 0.32175055432927835983, 0.32175055435211280591, 0.32175055436640972216, 0.32175055437562864861,
0.32175055438172946282, 0.32175055438586092134, 0.32175055438871697754,
0.32175055439072828193, 0.32175055439216862519, 0.32175055439321591432,
0.32175055439398806492, 0.32175055439456465521, 0.32175055439500028590,
0.32175055439533299363, 0.32175055439558964985, 0.32175055439578948595,
0.32175055439594643203, 0.32175055439607069174, 0.32175055439616981763,
0.32175055439624945471, 0.32175055439631386104, 0.32175055439636627619,
0.32175055439640918481, 0.32175055439644450714, 0.32175055439647373792,
0.32175055439649804860, 0.32175055439651836320, 0.32175055439653541502,
0.32175055439654978943, 0.32175055439656195624, 0.32175055439657229453,
0.32175055439658111170, 0.32175055439658865824, 0.32175055439659513914,
0.32175055439660072297, 0.32175055439660554884, 0.32175055439660973210,
0.32175055439661336870, 0.32175055439661653877, 0.32175055439661930947,
0.32175055439662173728, 0.32175055439662386985, 0.32175055439662574750,
0.32175055439662740448, 0.32175055439662886992, 0.32175055439663016872,
0.32175055439663132218, 0.32175055439663234861, 0.32175055439663326373,
0.32175055439663408113, 0.32175055439663481256, 0.32175055439663546820,
0.32175055439663605688, 0.32175055439663658632, 0.32175055439663706323,
0.32175055439663749347, 0.32175055439663788221, 0.32175055439663823394,
0.32175055439663855265, 0.32175055439663884183, 0.32175055439663910456,
0.32175055439663934358, 0.32175055439663956129, 0.32175055439663975984,
0.32175055439663994114, 0.32175055439664010688, 0.32175055439664025856,
0.32175055439664039753, 0.32175055439664052499, 0.32175055439664064202,
0.32175055439664074959, 0.32175055439664084855, 0.32175055439664093969,
0.32175055439664102371, 0.32175055439664110123, 0.32175055439664117282,
0.32175055439664123900, 0.32175055439664130022, 0.32175055439664135691,
0.32175055439664140945, 0.32175055439664145818, 0.32175055439664150341,
0.32175055439664154542, 0.32175055439664158448, 0.32175055439664162083,
0.32175055439664165466, 0.32175055439664168619]
う~ん。mを増やしても、頭打ちの感があるわね~」
「そうでもないぞ。m=4の場合じゃ。
[0.32185745701587301587, 0.32175075961202686202, 0.32175055832144874410, 0.32175055462232382497, 0.32175055442102331518, 0.32175055440058879604,
0.32175055439748782968, 0.32175055439686476752, 0.32175055439671075215, 0.32175055439666610197, 0.32175055439665141204,
0.32175055439664605535, 0.32175055439664392801, 0.32175055439664302014,
0.32175055439664260811, 0.32175055439664241090, 0.32175055439664231202, 0.32175055439664226038, 0.32175055439664223240, 0.32175055439664221675, 0.32175055439664220773, 0.32175055439664220240, 0.32175055439664219917, 0.32175055439664219717, 0.32175055439664219590, 0.32175055439664219509, 0.32175055439664219456, 0.32175055439664219420, 0.32175055439664219396, 0.32175055439664219380, 0.32175055439664219369, 0.32175055439664219361, 0.32175055439664219355, 0.32175055439664219351, 0.32175055439664219348, 0.32175055439664219346, 0.32175055439664219345, 0.32175055439664219343,
0.32175055439664219343, 0.32175055439664219342, 0.32175055439664219341,
0.32175055439664219341, 0.32175055439664219341, 0.32175055439664219341,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340, 0.32175055439664219340,
0.32175055439664219340, 0.32175055439664219340]
となって、約35分割で、有効数字20桁でも真値と見分けがつかないようになっておる」
Euler-Maclaurin展開を使った数値積分(2)
「前回の記事のsin(x)/(1+x2)について、確認してみよう」
 「m=0、1、2、4の各場合について計算結果をグラフに表示したよ。
「m=0、1、2、4の各場合について計算結果をグラフに表示したよ。
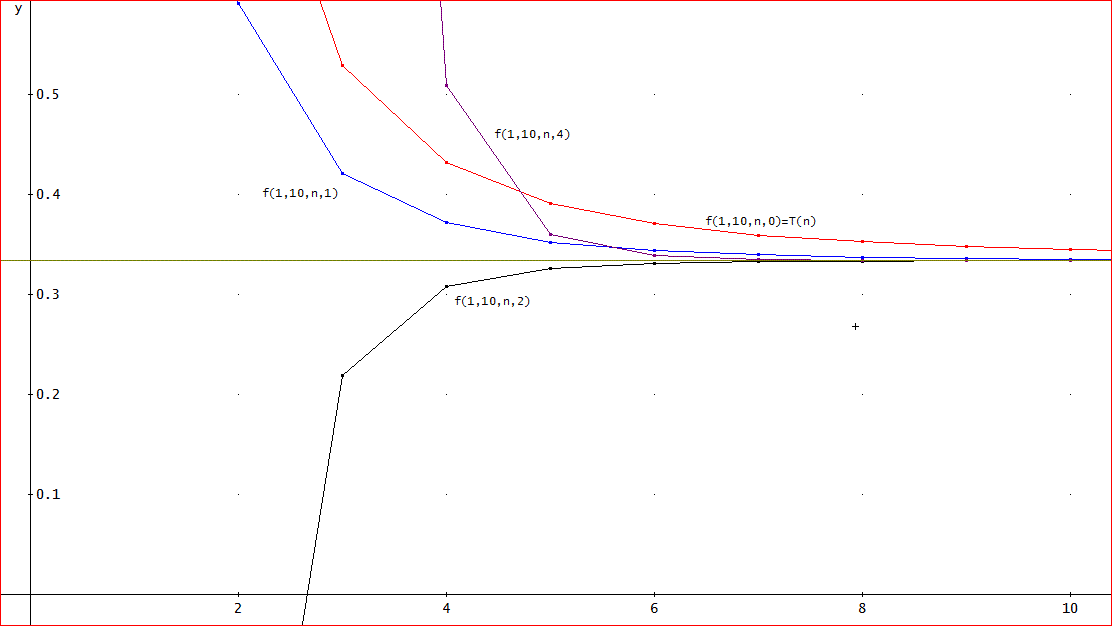
横軸がnの値。縦軸が積分計算値よ。
上図で、赤線がf(1,10,n,0)=T(n):台形公式の場合。
青線がf(1,10,n,1):端補正の台形公式の場合。
y軸の負方向から上がってきている黒線がf(1,10,n,2)の場合。
y軸の正方向から下がってきている黒線がf(1,10,n,4)の場合。
そして、水平線(y=0.3338252429・・)がDERIVEで計算させた値ね」
「なるほどな。このグラフで見る限り、f(1,10,n,2)とf(1,10,n,4)との差異は、それほどないな。
分点間隔を狭くして、f(1,10,n,2)でも十分な程度じゃな」
Euler-Maclaurin展開式を使った積分公式のまとめ
「ここで、m=0~4の具体的な形をまとめておこう。積分区間は、c~d、被積分関数は、g(x)とする。
f(c,d,n,0)=(d - c)∑(g(k(d - c)/n + c), k, 0, n - 1)/n + (c - d)(g(c) - g(d))/(2n) :台形公式
f(c,d,n,1)=f(c,d,n,0)+(c - d)^2g'(c)/(12n^2) - (c - d)^2g'(d)/(12n^2) :端補正の台形公式
f(c,d,n,2)=f(c,d,n,1) - (c - d)^4g'''(c)/(720n^4) + (c - d)^4g'''(d)/(720n^4) :ほぼシンプソン公式
f(c,d,n,3)=f(c,d,n,2) +(c - d)^6g'''''(c)/(30240n^6) - (c - d)^6g'''''(d)/(30240n^6)
f(c,d,n,4)=f(c,d,n,3)+(c - d)^8g'''''''(d)/(1209600n^8)- (c - d)^8g'''''''(c)/(1209600n^8)
ま、実用上は、m=2~4程度で、刻み幅を細かくする方が安全だとは思うのう」
 「これをみると、被積分関数のx=a、b、すなわち、端点の微分係数がゼロ又はゼロと見なせると、精度が上がるわね」
「これをみると、被積分関数のx=a、b、すなわち、端点の微分係数がゼロ又はゼロと見なせると、精度が上がるわね」
「よ!。ともちゃん、よいところに目を付けましたな」
「おじさん、あんたは、『水戸黄門』ですかい」
「あはは。
今回は、触れられなかったが、次回、積分変数の変換による数値積分法を勉強するとしよう」
n! の評価
「以前、扱ったことがある『階乗』の評価をオイラー-マクローリン展開の応用として行ってみよう」
 「『第10回 n!に対するスターリングの公式』だったわね。
「『第10回 n!に対するスターリングの公式』だったわね。
なつかしい・・・♪
そのときは、LN(n!)≒(n+1/2)LN(n)-n+1 で終わったんだ。
さて、LN(n!)=Σ(1~n)LN(k) なんだけど、オイラー-マクローリン展開では、次式が成り立つでしょ。
∫(x=a~b)f(x)dx=h×Σ(k=0~n-1)f(a+kh)+h/2×(f(b)-f(a))-Σ(j=1~)h(2j)B(2j)/(2j)!(f(2j-1)(b)-f(2j-1)(a))
和の部分と定積分を入れ替えると、
h×Σ(k=0~n-1)f(a+kh)=∫(x=a~b)f(x)dx-h/2×(f(b)-f(a))+Σ(j=1~)h(2j)B(2j)/(2j)!(f(2j-1)(b)-f(2j-1)(a))
ここで、f(x)=LN(x)として、a=1、b=n+1、h=1とすれば、
1×Σ(k=0~n)LN(1+k)=∫(x=1~n+1)LN(x)dx-1/2×(LN(n+1)-LN(1))+Σ(j=1~)B(2j)/(2j)!(f(2j-1)(n+1)-f(2j-1)(1))
左辺=LN(n!)、
右辺=(n+1)LN(n+1)-(n+1)+1-(1/2)LN(n+1)+B(2)/2!×((1/(n+1)-1)+B(4)/4!×((2/(n+1)^3-2)+・・
よって、LN(n!)=(n+1)LN(n+1)-n-(1/2)LN(n+1)+(1/12)(1/(n+1)-1))-(1/720)(2/(n+1)^3+1))+・・」
「そうじゃな。ここで、n=100としてみると、
正確な値 LN(n!)=363.73937555556349014・・
前回の近似 (n+1/2)LN(n)-n+1=363.81960369180318248 :3桁まで一致
今回の近似 nLN(n + 1) + LN(n + 1)/2 - n- 29/360- 1/(360(n + 1)^3) + 1/(12(n
+ 1)) =363.7398814 :6桁まで一致
となって、B(2)の項までで、有効数字6桁まで一致するのう」
「え~と。森口先生の本にあるように最初の10項まで、普通に計算して、その後は、近似してみたの。
100!の場合よ。
Σ(k=0~n)LN(1+k)=Σ(k=0~9)LN(1+k)+∫(x=a~b)f(x)dx-h/2×(f(b)-f(a))+Σ(j=1~)h(2j)B(2j)/(2j)!(f(2j-1)(b)-f(2j-1)(a))
ここで、右辺第2項以下は、a=11、b=101、h=1、n=90として、B(2)までを計算に含めて、
右辺第一項の和は、15.10441257 と合計して、LN(100!)≒363.7393754 と計算できたわ。
すごい、これで、9桁まで、正しい!」
オイラー定数の計算
「オイラー定数というのは、以前にも出てきたんじゃが、γ=0.57721566490153286060・・という数値じゃな。
これは、1+1/2+1/3+・・1/n-LN(n) で、n→∞の時の値と定義されているのじゃ。
超越数と想像されているものの、未だに、無理数かどうかでさえ、証明はされていないということじゃな。
ここでは、調和級数(1+1/2+・・)の第n項までの値をS(n)として、S(n)-LN(n)の極限値からγを計算してみよう」
 「となると、まずは、Σ(k=0~10)(1/k)=2.9289682539682539682 と求めておく。
「となると、まずは、Σ(k=0~10)(1/k)=2.9289682539682539682 と求めておく。
次に、Σ(k=11~11+n)(1/k)=∫(x=a~b)f(x)dx-h/2×(f(b)-f(a))+Σ(j=1~)h(2j)B(2j)/(2j)!(f(2j-1)(b)-f(2j-1)(a))と近似する。
具体的には、右辺で、f(x)=1/x、a=11、b=11+n、h=1、B(4)の項まで取ると、
S(n)≒2.9289682539682539682+LN((n + 11)/11) + 1/(120(n + 11)^4) - 1/(12(n
+ 11)^2) - 1/(2(n + 11)) + 27023/585640となり、
S(n)-LN(n)で、n→∞の極限を取れば、オイラー定数 γの近似値として、
γ≒0.57721566268070918746 が求められる。ちなみに、有効数字8桁まで、求まったようね」
最終更新日 2011/7/26、LN(n!)の計算式の青字個所の誤りを修正しました(2014/9/17)



 「だけど、定義式から直接、ベルヌイ数を計算するのは、nが8ぐらいまでは、簡単だけど、それ以上になると難しかったのね」
「だけど、定義式から直接、ベルヌイ数を計算するのは、nが8ぐらいまでは、簡単だけど、それ以上になると難しかったのね」
