数式処理ソフト　DERIVE（デライブ） de ドライブ

８１．連立常微分方程式の数値解法（2重振り子）

（1）2重振り子の運動（数値計算）

「数式処理ソフト DERIVE（デライブ）の第80回では、単振り子の運動を数値計算と解析的計算の両方で調べて見た。
　今回は、2重振り子の運動を考えてみよう」

「わかりやした。
　単振り子の場合の図に似せて描くとこんな感じになる。

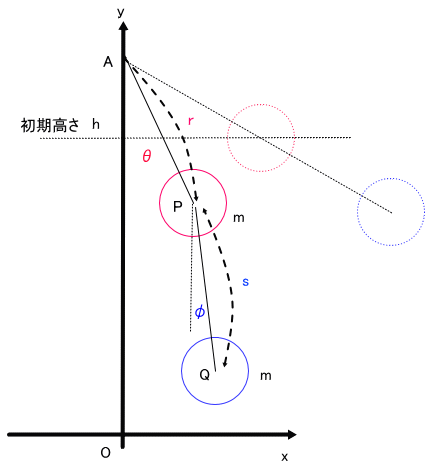
　支持点 A（原点Oからの高さ= r＋s）から垂直につり下げられた2重振り子の振動を考えます。
　振り子の重り自体は、その大きさを無視できるものとして、ま、要するに質点と考えるわけですね。
　また、糸は、質量を無視できる細い糸とします。
　糸の長さは、図のように、r とs、重りの質量は、2つとも同じとし、m とします。
　位置エネルギー U は、O点の位置でのエネルギーを、ゼロ とすると、
　U=mg（r＋s－r cosθ）＋mg（r＋s－r cosθ－s cosφ）、
　Pの運動エネルギーは、（m/2）r^2θ'^2、
　Qの位置は、直交座標による表現は、（r sinθ＋s sinφ，r＋s－r cosθ－s cosφ）、
　この位置座標のx成分とy成分をそれぞれ時間で微分して、2乗和を作ると、
　r^2θ’^2＋s^2φ’^2＋2 r sθ’φ’cos（θ－φ）、となる。
　よって、運動エネルギー T は、
　T=（m/2）r^2 θ'^2＋（m/2）（r^2θ’^2＋s^2φ’^2＋2 r sθ’φ’cos（θ－φ））、
　ラグラジアンをLとすると、L=T－U、　オイラーの方程式は、
　d/dt（∂（L，θ'））－∂（L，θ）=0、
　d/dt（∂（L，φ'））－∂（L，φ）=0、となるので、
　まとめると、
　kφ''(t)·COS(θ(t) －φ(t)) ＋ kφ'(t)^2·SIN(θ(t) －φ(t)) ＋ 2ω^2·SIN(θ(t)) ＋ 2θ''(t) = 0、
　θ''(t)·COS(θ(t) －φ(t)) －θ'(t)^2·SIN(θ(t) －φ(t)) ＋ω^2·SIN(φ(t)) ＋ kφ''(t) = 0、
　となります。
　ここで、k≡s/r、ω^2≡g / r、と書いている」

「ご苦労さんじゃった。
　具体例で、数値計算を行ってみよう。
　ともちゃんが導いてくれた2つの式から、θ' ' とφ' '、を解くと、
　p=dθ/dt、q=dφ/dt、と書くことにすれば、
　dp/dt=((COS(2·θ － 2·φ)·(k·q^2·SIN(θ － φ) － 2·ω^2·SIN(θ)) － SIN(2·θ － 2·φ)·(k·q^2·COS(θ － φ) + 2·p^2) + 4·ω^2·SIN(φ)·COS(θ － φ) － 4·ω^2·SIN(θ)·SIN(θ － φ)^2 － 3·k·q^2·SIN(θ － φ) － 6·ω^2·SIN(θ))/(4·(SIN(θ － φ)^2 + 1)))、
　dq/dt=((k·q^2·SIN(2·θ － 2·φ) + 4·ω^2·SIN(θ)·COS(θ － φ) + 4·p^2·SIN(θ － φ) － 4·ω^2·SIN(φ))/(2·k·(SIN(θ － φ)^2 + 1)))、
　じゃ。
　m次までのオイラー展開法を適用するためには、
　k=1（上下の糸の長さが等しい）、ω^2=98、（r=0.1 m、重力加速度g=9.8 m/sec^2）、として、
　初期位置は、t=0の時に、θ=φ=π/6、初期速度はゼロ、p=0、q=0 、刻み幅をh=0.01として、
　Eulerm_user_R（［1，p，q，pの右辺，qの右辺］，［t，θ，φ，p，q］，［0，π/6，π/6，0，0］，0.01，4，1000）、とすればよい。
　しかし、p ' 及びq ' の表式に三角関数が含まれる複雑な式であるため、テイラー展開項も複雑になるようで、このままでは、計算が終わらないようじゃ。
　そこで、ルンゲ・クッタ法に頼るとしよう。
　DERIVEのルンゲ・クッタ法関数は、組み込み関数、RK（ ）であるが、特別なユーティリティ関数を呼び出す必要は無く、
　RK（［p，q，pの右辺，qの右辺］，［t，θ，φ，p，q］，［0，π/6，π/6，0，0］，0.01，1000）のように引数を与えればよい。
　なお、わしらが作った、Eulerm_user_R（）と異なり、第1引数と第2、3引数の次元が1つ異なるので注意するようにな。
　k=1、ω^2=98、、初期角度 θ=φ=π/6、初期速度はゼロのグラフは下図の通りじゃ。


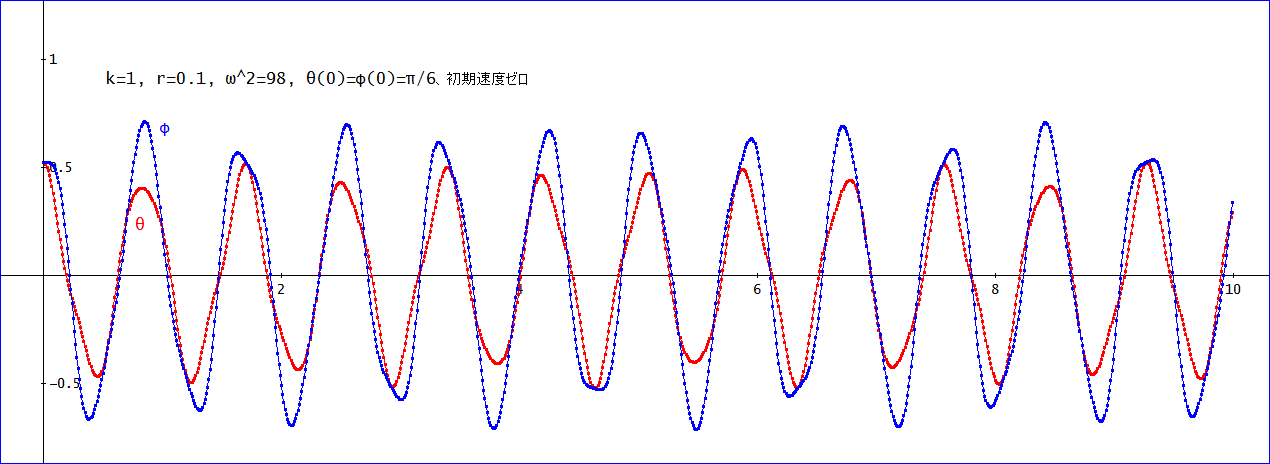
　これを見ると、上の振り子の波形（θ=赤）と下の振り子（φ=青）の周期は、同じであるが、波形は、純粋のコサインカーブから少し崩れている。
　また、振幅は、下の振り子の方が上の振り子に比べて、変動が大きいようじゃ」

「じゃ、わたしは、下の振り子の糸の長さが長い、k=2、（r=0.1、s=0.2）の場合を計算してみるよ。
　その他のパラメーターは、同じとします。


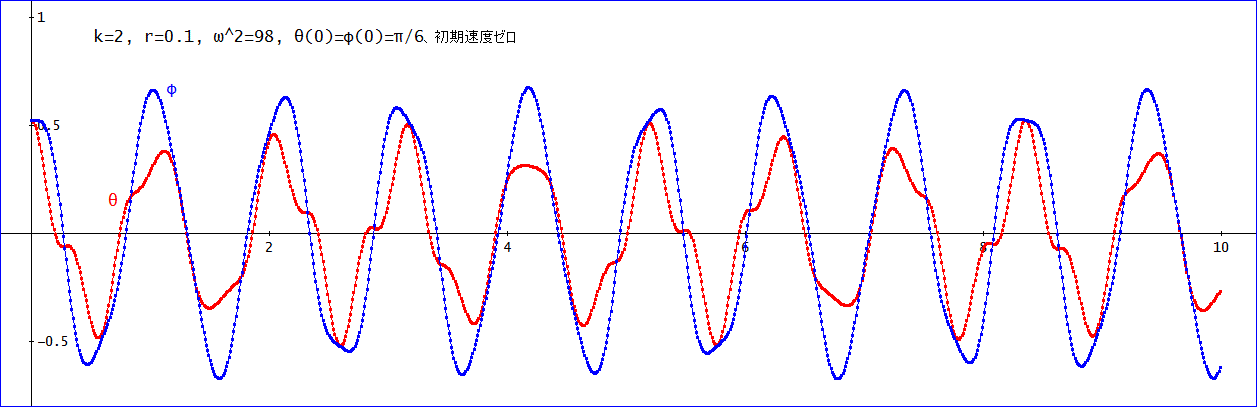
　この場合は、上の振り子の波形（赤）は、k=1の場合より、崩れている感じね。
　一方、下の振り子（青）は、多少の崩れはあるもののコサインカーブに近づいてきた。

　では、k=3の場合がこれ。
　
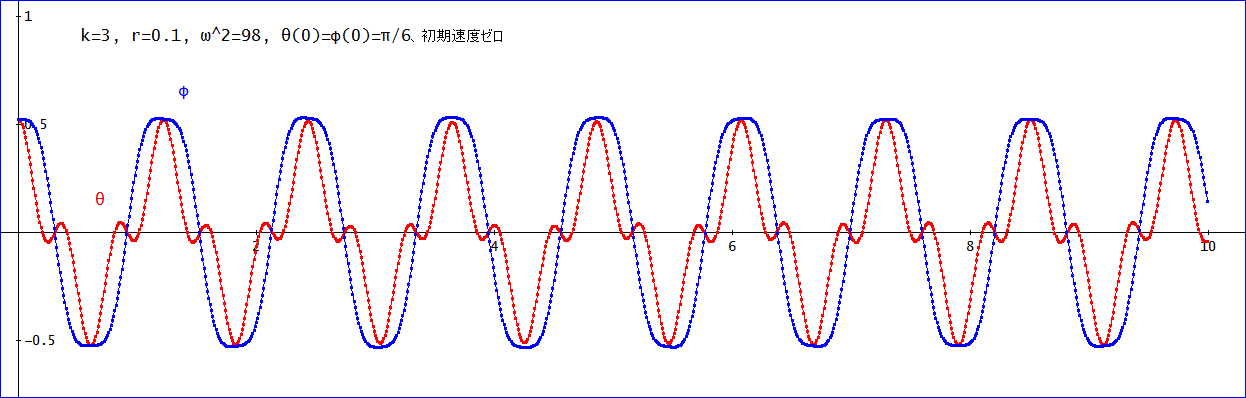
　下の振り子は、ほぼ、コサインカカーブ。
　上の振り子の波形は、崩れているなりに、左右対称になっている。

　最後は、下の振り子の糸が短い場合、k=0.5、（r=0.1、s=0.05）その他の諸元は、同じ。
　

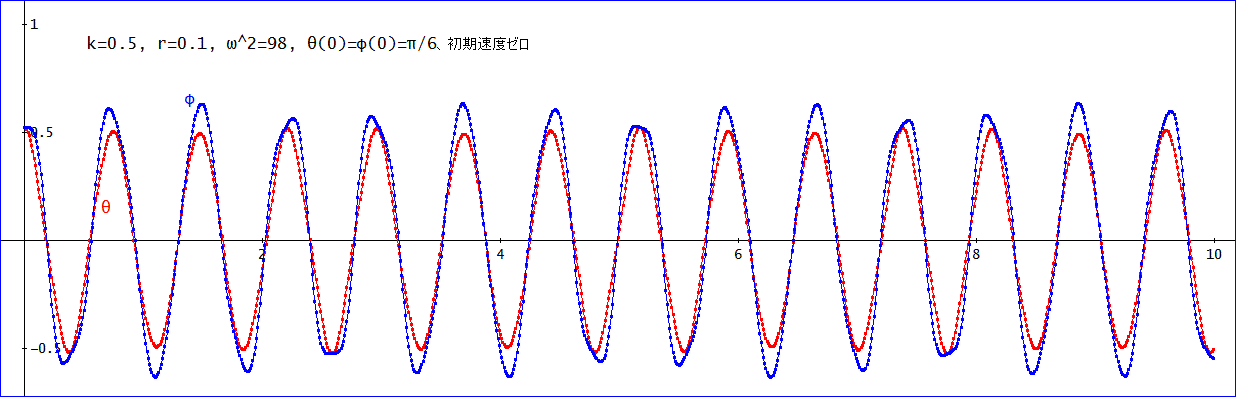
　今度は、上、下とも振り子の波形は、整ってきている感じだわ」

「では、わしは、下の振り子の糸を、k=0.1、（r=0.1、s=0.01）と、さらに短くしてみよう。
　

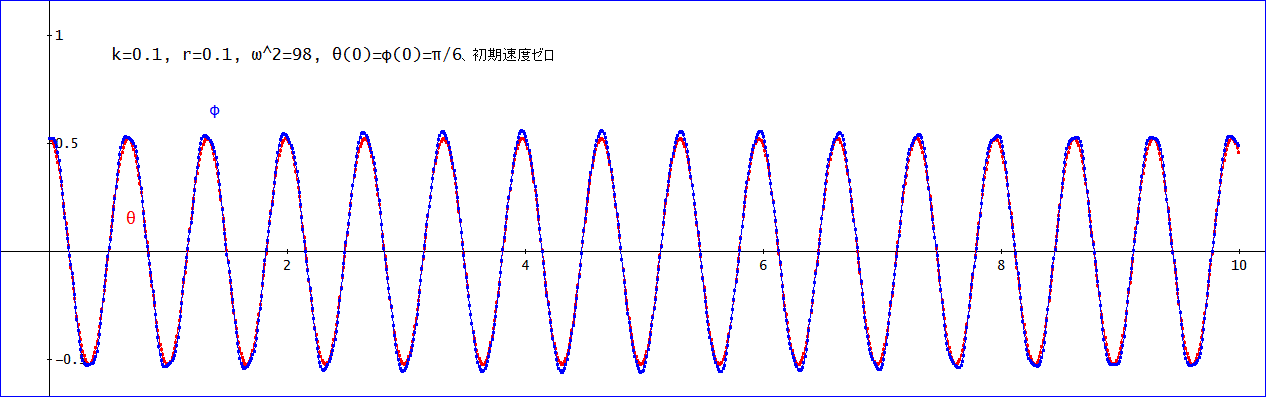
　上、下の振り子の振幅、周期ともほぼ等しいものとなった。波形は、きれいじゃ。
　次節で、解析的な扱いを行って、みよう」

（2）2重振り子の運動（線形近似）

「2重振り子の運動方程式は、p=θ'、q=φ'、と書いたとき、
　dp/dt=((COS(2·θ － 2·φ)·(k·q^2·SIN(θ － φ) － 2·ω^2·SIN(θ)) － SIN(2·θ － 2·φ)·(k·q^2·COS(θ － φ) + 2·p^2) + 4·ω^2·SIN(φ)·COS(θ － φ) － 4·ω^2·SIN(θ)·SIN(θ － φ)^2 － 3·k·q^2·SIN(θ － φ) － 6·ω^2·SIN(θ))/(4·(SIN(θ － φ)^2 + 1)))、
　dq/dt=((k·q^2·SIN(2·θ － 2·φ) + 4·ω^2·SIN(θ)·COS(θ － φ) + 4·p^2·SIN(θ － φ) － 4·ω^2·SIN(φ))/(2·k·(SIN(θ － φ)^2 + 1)))、じゃった。
　（１）節の数値計算では、上の振り子の糸の長さ r を0.1 m、重力加速度gを9.8m/sec^2、として、ω^2=g/r、から、ω^2=98と置いて計算した。
　初期角度は、θ=φ=π/6≒0.5235・・、であるので、θ、φの一次までとることにする。
　同様に、p、q の2乗等の項もゼロと見なす。
　このような線形近似で、前節の結果をどの程度、説明できるかを調べて見よう。
　上掲の複雑な2つの式は、近似的に、
　2·θ''(t) + k·φ''(t) + 2·ω^2·θ(t) = 0、
　θ''(t) + k·φ''(t) + ω^2·φ(t) = 0、となることが分かる。
　初期条件は、θ(0)=φ(0)=a、θ' (0)=φ' (0)=0、じゃな。
　ともちゃん、ラプラス変換法により、この2つの方程式の初期条件を満たす解（特解）を求めてご覧」

「待ってました。
　θ(t)のラプラス変換をf(s)、φ(t)のそれを、g(s)としますね。
　ここで、sは、ラプラス変換の変数とする。（2つめの振り子の糸の長さではないので注意してね）
　初期条件を勘案して、（ωの代わりにwを使っている）
　s^2·f － s·a + w^2·f + k/2·(s^2·g － s·a) = 0、
　s^2·f － s·a + w^2·g + k·(s^2·g － s·a) = 0、
　整理すると、
　（s^2＋w^2）f＋(k/2)s^2 g=s*a(1＋(k/2)）、
　s^2 f＋k s^2 g=s*a（1＋k）、
　となる。
　この連立方程式から、f、g、を解くと、
　f = a·s·(k·(s^2 + w^2) + 2·w^2)/(k·s^2·(s^2 + 2·w^2) + 2·w^2·(s^2 + w^2))、
　g = a·s·(k·(s^2 + 2·w^2) + 2·w^2)/(k·s^2·(s^2 + 2·w^2) + 2·w^2·(s^2 + w^2))、
　この逆変換を求めれば、特解が得られる。
　一見すると、分母は、sの4次式なんだけど、s^2の2次式に過ぎないので因数分解が可能。
　その上で、部分部数展開を行う、というのが定番ね。
　と、まあ、原理は簡単なんだけど、係数がややこしいので、DERIVEの「代数」メニューの「展開」で、変数をs、「分母を実数の範囲で因数分解」を指示すると、
　f=a·k·s·(√(k^2 + 1) + 1)/(2·√(k^2 + 1)·(k·s^2 － w^2·(√(k^2 + 1) － k － 1)))＋a·k·s·(√(k^2 + 1) － 1)/(2·√(k^2 + 1)·(k·s^2 + w^2·(√(k^2 + 1) + k + 1)))、
　が得られる。
　ここで、一般に、cos(αt)のラプラス変換が、s/（s^2－α^2)、であることを使うと、
　θ(t)=a·k·(√(k^2 + 1) + 1)/(2·k·√(k^2 + 1))·COS(w·t·√(k + 1 － √(k^2 + 1))/√k) + a·k·(√(k^2 + 1) － 1)/(2·k·√(k^2 + 1))·COS(w·t·√(√(k^2 + 1) + k + 1)/√k)、
　が得られる。
　同様に、φについても、
　φ(t)=a·k·(√(k^2 + 1) + k + 1)/(2·k·√(k^2 + 1))·COS(w·t·√(k + 1 － √(k^2 + 1))/√k) + a·k·(√(k^2 + 1) － k － 1)/(2·k·√(k^2 + 1))·COS(w·t·√(√(k^2 + 1) + k + 1)/√k)、
　と求まったわ」

「どれどれ、検算してみるかの。
　θとφを、線形近似式に代入して計算させると、2つの式のどちらも、満足していることが分かった。
　ついでに言うと、DERIVEでのラプラス逆変換は、ユーザー定義ファイルが下記に置かれている。
　C:\Program Files (x86)\TI Education\Derive 6\Users\Transforms、内にある「LaplaceTransforms.dfw」を使うこともできる。
　逆変換表を目で引くのが面倒なときに使ってよいじゃろう。
　たとえば、InvLaplace(f(s))、と計算させれば、f(s)の逆変換 θ(t)が求められる。
　近藤先生の本（「演算子法」（近藤次郎 著：培風館：1970年6月30日第13刷）の逆変換表ほどの結果は、得られないかもしれんがの。
　さてと、こうして、線形近似解が求まったので、（１）節の数値計算結果をどの程度、再現できているかを検証してみよう。
　初期角度 a=π/6、w=√(98)、は、共通なので、最初に置いてしまう。
　残されたパラメーターは、k （第2の振り子の糸の長さ／第1の振り子の糸の長さ）のみになる。
　k=1の結果は、次のようになる。
　θ=·(√2/24 + 1/12)·COS(7·t·√(4 － 2·√2)) + ·(1/12 － √2/24)·COS(7·t·√(2·√2 + 4))、
　φ=·(√2/12 + 1/12)·COS(7·t·√(4 － 2·√2)) + ·(1/12 － √2/12)·COS(7·t·√(2·√2 + 4))、
　θを赤、φを青の線で表すと、グラフは下図の通り。
　
　
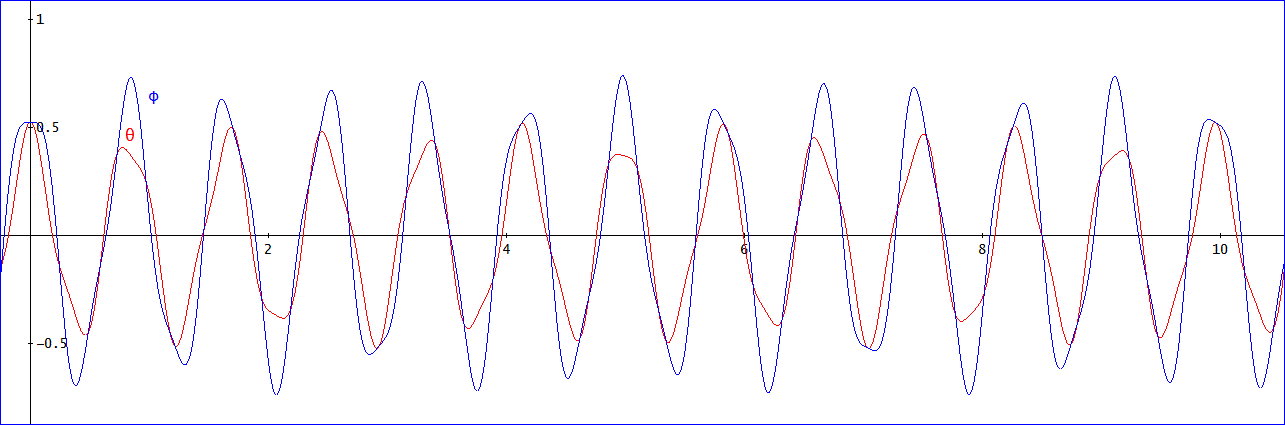
　一方、、k=1のRK法による計算結果を再掲したものが下図じゃ。
　

　よく似ているようじゃが、時間 t が大きくなると、線形近似は、（１）節の計算結果とずれてくる傾向がある。
　その点を検証するために、下図では、線形近似値と前節のRK法による計算値との比較じゃ。
　k=1、ω^2=98、初期角度π/6、初期速度ゼロ、線形近似値－RK計算値と時間との関係を示している。
　
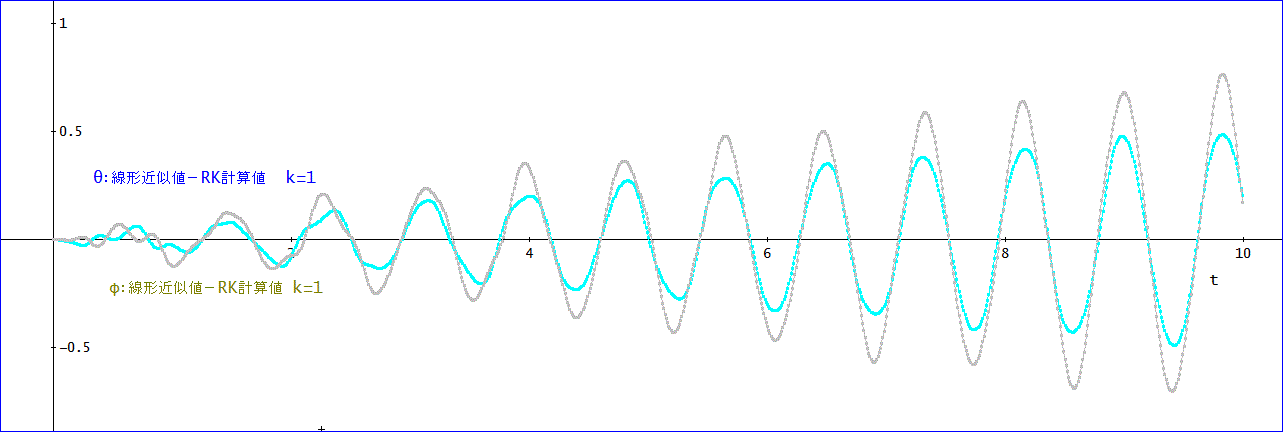
　θ－RK計算値を水色、φーRK計算値をグレーで示す。
　どちらも、t が大きくなるにつれて、線形近似値は、RK法による計算値から外れ、その差が徐々に拡大している。

　ついでに言うておくと、
　線形近似解は、θ=A cos(λt)＋B cos(μt)、φ=C cos(λt)＋D cos(μt)、の形をしている。
　すなわち、
　A=a·k·(√(k^2 + 1) + 1)/(2·k·√(k^2 + 1))、B=a·k·(√(k^2 + 1) － 1)/(2·k·√(k^2 + 1))、
　C=a·k·(√(k^2 + 1) + k + 1)/(2·k·√(k^2 + 1))、D=a·k·(√(k^2 + 1) － k － 1)/(2·k·√(k^2 + 1))、
　λ=w√(k + 1 － √(k^2 + 1))/√k、
　μ=w√(√(k^2 + 1) + k + 1)/√k、
　λとμの振動は、「基準振動」と呼ばれる。
　これから、A/B=(√(k^2 + 1) + 1)^2/k^2、
　また、C/D=－ (√(k^2 + 1) + k + 1)^2/(2·k)、
　グラフで示すと下図の通り。
　
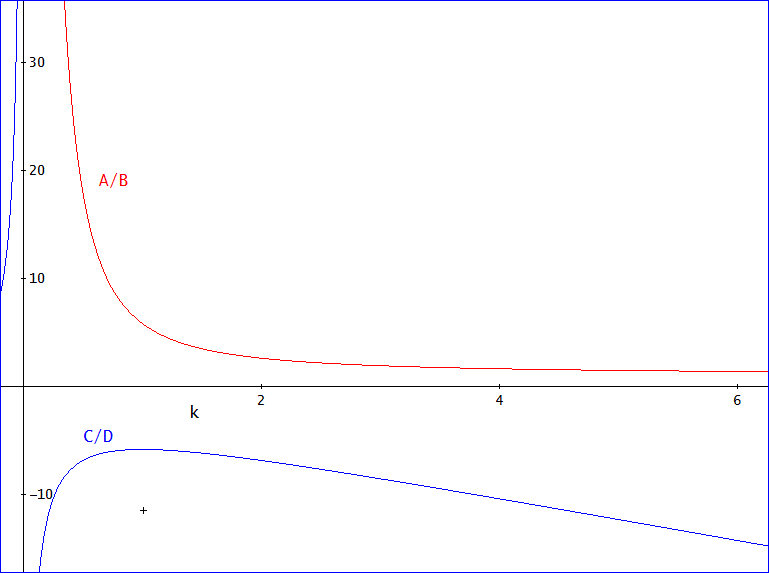
　kが小さいときは、θ、φとも、λの角周波数の振幅が支配的になる。
　k=0.1の場合がそれじゃな。
　逆にkが大きくなると、θでは、λとμの寄与がほぼ等しくなる。k=3の場合が、そのようなケースじゃ。
　φについては、kの全域でλの振動が支配的じゃ。（k=1のとき、C/Dの絶対値が最小となるが、その値は、約5.82）」

「θとφの図形を描いてみたよ。［θ，φ］ね。
　
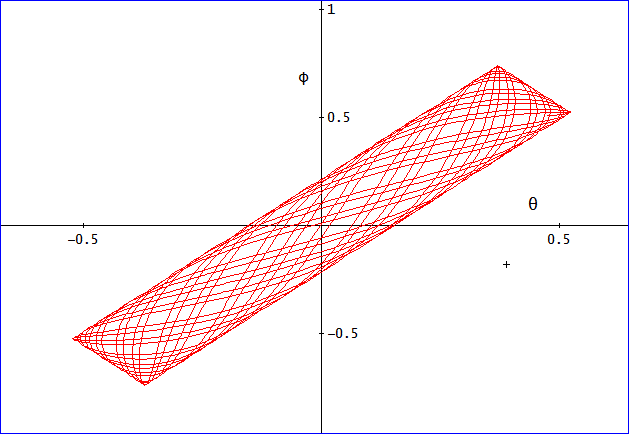
　横軸がθ、縦軸がφ、t=0～10まで。
　λとμの比率は、無理数なので、厳密には、θとφの値が同じ組み合わせは、起きないのよね。
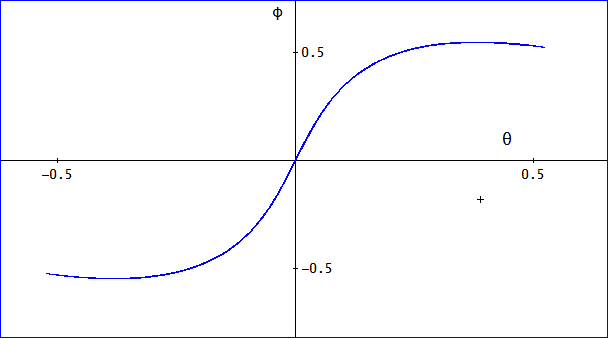
　もし、λ=1、μ=3、とすれば、下図のようになる。（t=0～100）
　この場合は、tをいくら増やしても、このカーブ以外にずれることがない。
　
　
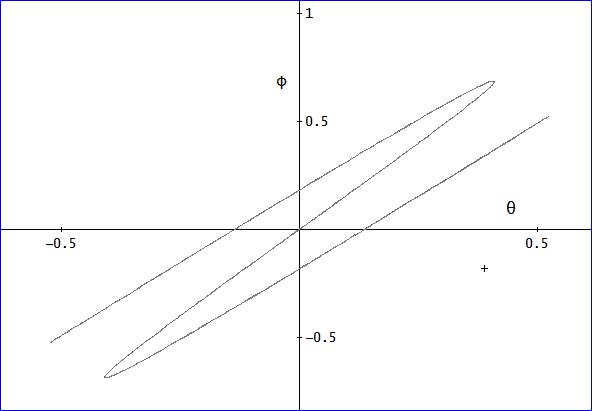
　λ=1、μ=1/3、の場合は、下図のよう。（t=0～100）
　この場合も、これ以上、tを増やしても変わらない。
　
　
　とはいえ、有理数の比の場合も、λ=5/13、μ=3/11、などでは、下図のよう。（t=0～100）。
　やや複雑になってくる。
　
　
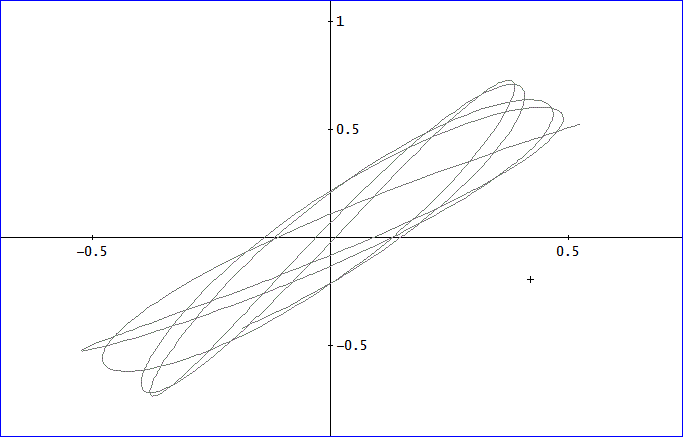
　この場合は、tを1000までとると、下のように密になる。
　
　しかし、tをこれ以上増やしても、四角形の領域内が、これ以上、塗りつぶされることはない。

　一方、λ=1、μ=√2 では、t=100までで、下図のように、上の有理数比の場合と変わらないように見える。
　
　
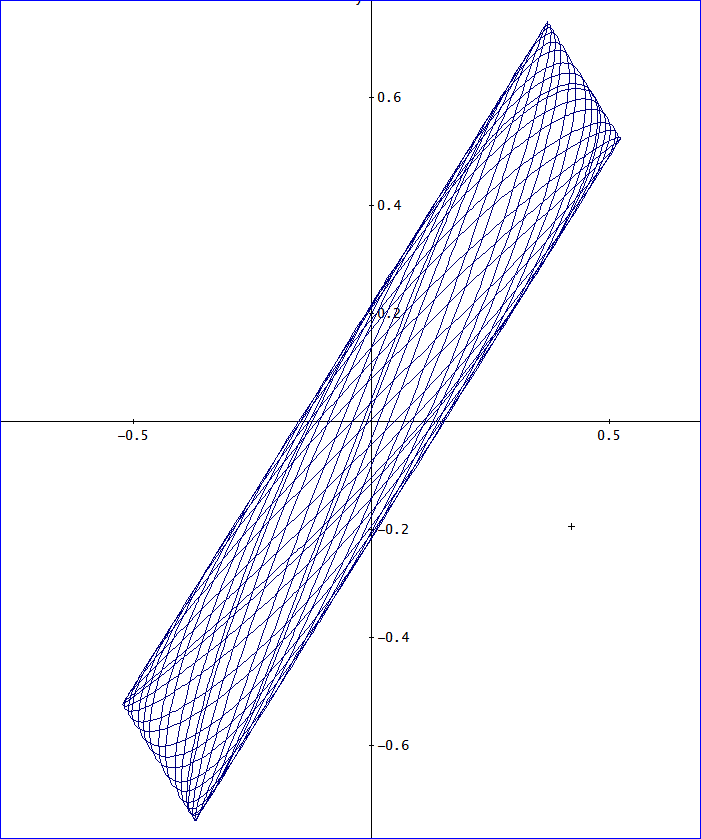
　けれども、t=1000まで増やしてみると、下図のようになる。
　
　t=10000まで経過するとこの解像度では、白い部分がなくなってしまう」

「角周波数の比率が有理数か、無理数かにより、同じ軌道を通るか、否かが決まっていることがよく分かるのう。
　比率が無理数の場合は、許される範囲内をまんべんなく、通り過ぎるので、t を増やしていくと、べた塗りになってしまうのじゃな。
　線形近似解についての検討は、不十分かもしれんが、これくらいにしておこう。
　（１）節の数値計算では、（初めて）わしらのオイラー展開法では、うまいかなかったな。
　何故うまくなかったかを調べて見ると、テイラー展開項を求める「Difm_user_R」関数で、2次までは、求められるんじゃが、3次以上では、途方もなく時間がかかってしまう。
　ルンゲ・クッタ法（4次）は、DERIVEに組み込み関数としてあるので、次回は、多段階法の「（陽的）アダムス公式」を取り上げてみよう」　

最終更新日　2016/4/25