数式処理ソフト DERIVE(デライブ) de ドライブ
80.連立常微分方程式の数値解法(単振り子)
(1)単振り子の運動(数値計算)
「数式処理ソフト DERIVE(デライブ)で、前回は、連立1階常微分方程式について調べて見た。
しかし、振り返ると、そもそもは、2階以上の高階微分方程式の数値解法のために連立1階常微分方程式を説明したんじゃが、肝心の2階の方程式の例を出さなかったな。
ともちゃん、単振り子の振動の例を挙げて、説明してくれんかな」
 「わかりやした。
「わかりやした。
えーと。単振り子というのは、みなさん、よーくご存じのあれです。
こんな感じ。
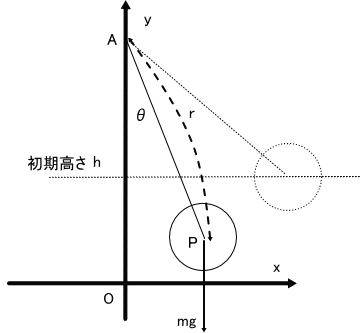
支持点 Aから垂直につり下げられた振り子の振動を考えます。
振り子自体は、その大きさは無視できるものとし、質点と考えます。
また、糸は、質量を無視できる細い糸としますね。
位置エネルギー Uは、O点の位置でのエネルギーを、ゼロ とすると、U=mgr(1-cosθ)、
また、運動エネルギー T は、T=(m/2)r^2 θ'^2、
ラグラジアンをLとすると、L=T-U、
オイラーの方程式は、d/dt(∂(L,θ'))-∂(L,θ)=0、から、
r θ''=-g sin(θ)、と運動方程式が求められるということだったでしょ。
ここで、θが小さい場合は、右辺がsin(θ)≒θと近似できるので、θ≒A sin(ωt)+B cos(ω t)、とθの時間変化が分かる。
ただし、ω=√(g/r)、振り子の周期 τは、τ=2π√(r/g)、と重力加速度と糸の長さのみに依存してθによらない。
これが等時性ということだった」
「そうじゃな。
運動方程式を立てる方法で別解を出しておこう。
振り子が糸から受ける張力をFとすると、
mx ' '=-F sin(θ)、
my ' '=-mg+Fcos(θ)、
一方、x=r sin(θ)、y=r-r cos(θ)、なので、(※yの式に青字の r の項が抜けていました。2016/2/22訂正)
x '=r cos(θ)×θ'、x''=-rsin(θ)×θ' ^2+r cos(θ)θ''、
y '=r sin(θ)×θ'、y''=r cos(θ)×θ' ^2+r sin(θ)θ''、
よって、
m(-r sin(θ)×θ' ^2+r cos(θ)θ'')=-F sin(θ)、
m(r cos(θ)×θ' ^2+r sin(θ)θ'')=-mg+F cos(θ)、
第1式にcos(θ)、第2式にsin(θ)を掛けて、両式を足すと、
mrθ' '=-mg sin(θ)、となるので、これから、r θ''=-g sin(θ)が求められるという訳じゃな。
ところで、r θ''=-g sin(θ)に、mrθ' を掛けて、積分すれば、(m/2)(rθ')^2=mgr cos(θ)+定数、これは、エネルギー保存を表す」
「そこで、振り子の初期位置がO点からhだけ上の位置とすれば、その点では、速度はゼロである。
また、その点では、cos(θ0)=(r-h)/r、から、定数=-mgr+mgh、となり、
(m/2)(rθ')^2+mgr(1- cos(θ))=mgh、となる。
ここから、(θ')^2=2ω^2(cos(θ)-cos(θ0))、ω=√(g/r)、となるんだけど、厳密に解くためには、楕円積分を使うので、少し難しなっちゃう。
そこんところは、次節に回します。
ここでは、数値解法ということで、連立方程式の形にします。
これは、簡単で、
dθ/dt=w、
dw/dt=-ωsin(θ)
という連立1階常微分方程式を、初期条件、θ(0)=θ0、θ'(0)=0、の下で解けばよいという訳。
例1 として、ω=1、かつ、θ0=π/2(=90度)、すなわち、h=r の位置から、振り子を静かに離した場合を計算してみますよ。
計算は、ユーザー定義のm次までのオイラー展開法関数、
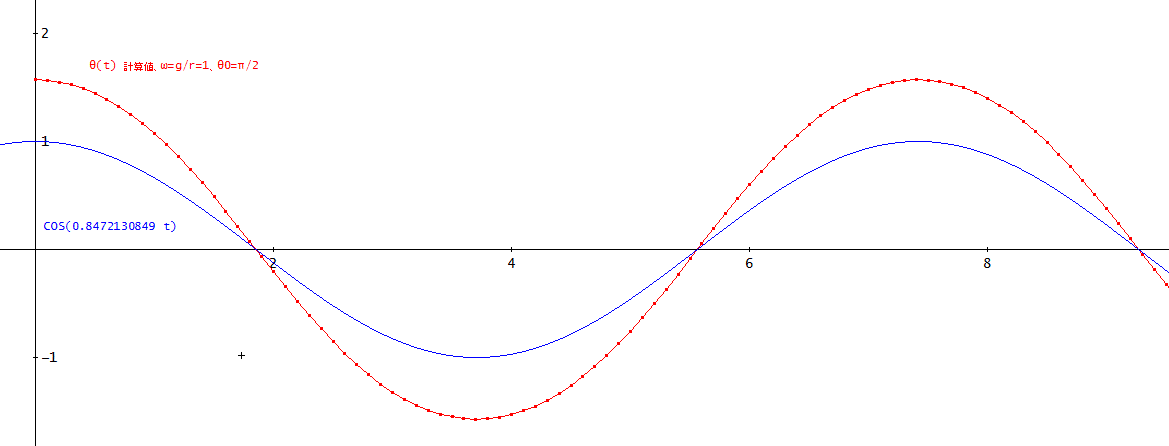
Eulerm_user_R([1, w, -SIN(θ)], [t, θ, w], [0, /2, 0], 0.01, 4, 1000)、により、4次のオイラー展開法により、時間 t=0~10までを計算した。
計算したθ(t)を赤い曲線で表示した。
なお、参考に示した青い曲線は、COS(0.8472130849 t)を表す。
ここで、0.84・・は、2π/T、T=4×K(1/√2)≒7.416298708・・、K(k)は、「第1種完全楕円積分」の値を示す。
ここんところは、次節で解説しますけど、Tは、周期で、計算したθの周期がこれと等しいことを示すために描いてみたものなの」
「上の例1では、θ0=π/2なので、sin(θ)は、とても、sin(θ)≒θとは近似できないじゃろう。
試しに、元々の方程式は、ω=1、なので、θ''=-sin(θ)。
ここで、もし、sin(θ)≒θと近似すると、θ=Asin(t)+Bcos(t)、から、θ(0)=π/2、θ'(0)=0、なので、A=0、B=π/2、となり、
θ≒π/2×cos(t)、じゃ。
しかし、振幅は合っているが、周期は、2π≒6.283185307・・じゃから、例1の7.416298708・・とは、かなり違うことが分かる。
では、例2として、初期位置がθ0=π/6 (=15度)、とかなり小さい場合を調べて見よう。
Eulerm_user_R([1, w, -SIN(θ)], [t, θ, w], [0, /6, 0], 0.01, 4, 1000)、により、4次のオイラー展開法により、時間 t=0~10までを計算した。
sin(θ)≒θの近似では、θ=Asin(t)+Bcos(t)、から、θ(0)=π/6、θ'(0)=0、なので、A=0、B=π/6、となり、
θ≒π/6 cos(t)、が下図のピンクの曲線じゃ。(ドットをつなげている曲線が計算値)。
理論値は、4*K(k)≒4*K(sin^2(π/12))≒6.392568008・・、で、これは、sin(θ)≒θと近似した場合の周期、2π≒6.283185307・・、にかなり近いじゃろう。
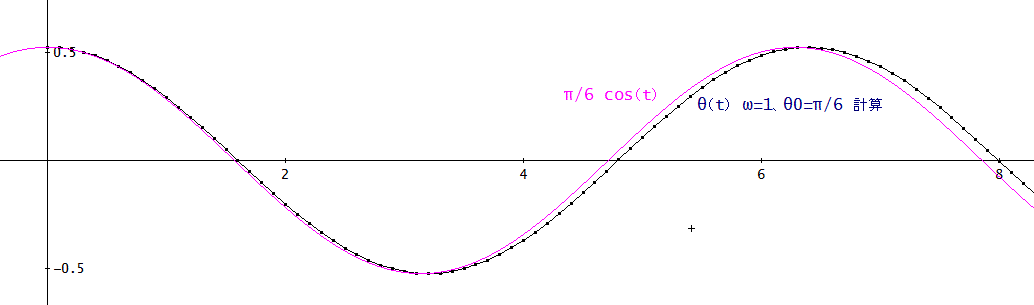
すなわち、この場合は、sin(θ)≒θの近似でも、かなり計算結果に近づくことがわかる。
最後に、例1の場合の、θ、θ' と運動及び位置エネルギーの和を示す。
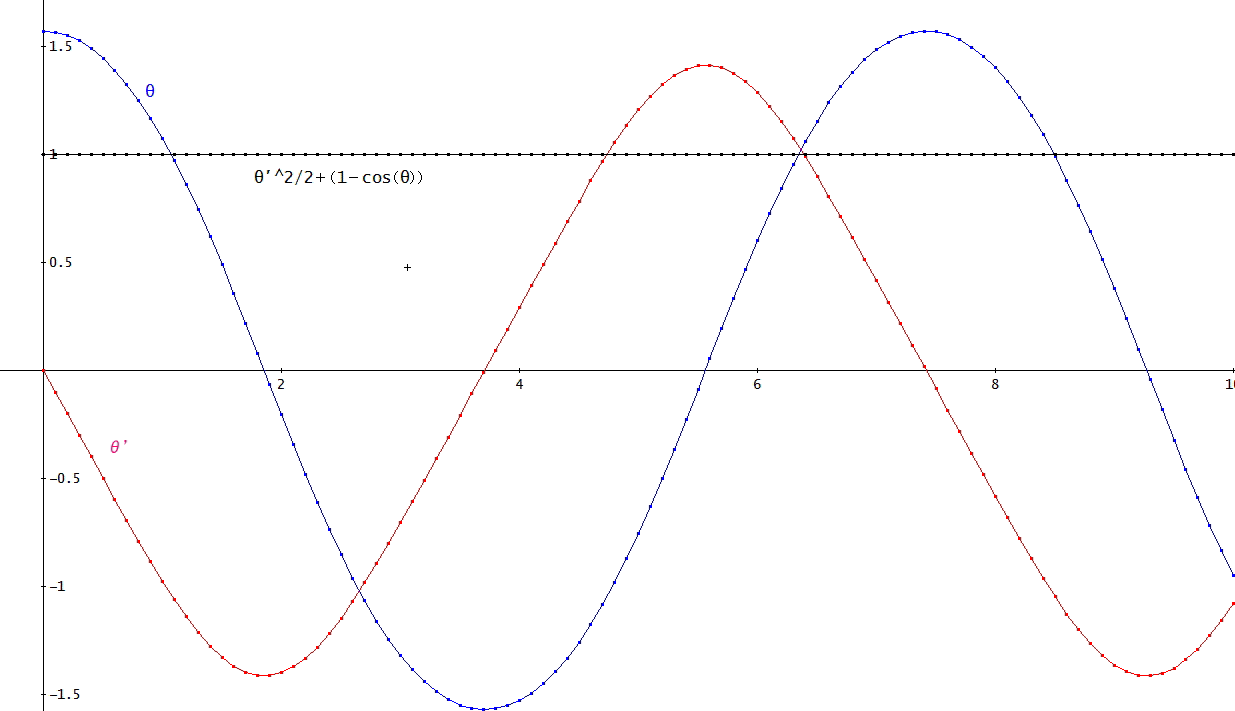
青い曲線がθ、赤い曲線がθ' 、また、黒い水平線は、(θ')^2/2+(1-cos(θ))の計算値。
(θ')^2/2+(1-cos(θ))は、運動エネルギーと位置エネルギーの和で、その値は、h/r×ω^2=1、(ω=1、かつ、h=r)、と一定値であることが見て取れるのう」
※上図のθとθ’の説明が逆でした。お詫びして訂正いたします。2016/2/4
(2)単振り子の運動(楕円積分と楕円関数)
「楕円積分と楕円関数については、第60回の「楕円積分と楕円関数(1)」で簡単に紹介したんじゃったな」

「定義を書くだけで手一杯だった感じね」
「確かにな。
そこで今回は、(1)節で計算した単振り子について、楕円積分との関係をあらためて記述してみよう。
記号等は、(1)節のものを流用する。
まずは、(θ')^2=2ω^2(cos(θ)-cos(θ0))、ω=√(g/r)、から出発する。
ここで、θ0は、0~π/2の間の角度で、θ(0)=θ0、θ'(0)=0、が初期条件じゃ」
「コサイン関数は、-π/2~π/2の間で、単調減少関数なので、|θ|<=θ0、であれば、cos(θ)<=cos(θ0)となるので、
(θ')^2=2ω^2(cos(θ)-cos(θ0))、の右辺は、常に正となる。
さてと、第1種楕円積分を使うことを考えると、コサイン関数ではなくて、サイン関数に変換した方が都合が良さそうなのがなんとなく分かるでしょ。
ちなみに、第1種楕円積分の標準形は、F(φ,k)=∫(0~φ)1/√(1-k^2 sin^2(φ))dφ。
そこで、cos(θ)=cos(θ/2×2)=1-2sin^2(θ/2)と変形して、θ=θ0~0の間では、
θ'=-2ω√(sin^2(θ0/2)-sin^2(θ/2))、
よって、
θ'=-2ωsin(θ0)√(1-(sin^2(θ/2)/sin^2(θ0/2))、
ここで、sin(θ0/2)=k、と置く。
|sin(θ/2)|<=kに注意して、(1/k)sin(θ/2)=sinφ、と置く。(青字部分を2016/2/3に訂正)
なぜって思うけど、こうするのが一番手っ取り早い「術」なのよ。
つまり、こう置くと、θ(0)=θ0のときに、sinφ=1、これは、φ=π/2、また、θ=0のときは、φ=0、となるので、
θ=θ0~0と変化するにつれて、φ=π/2~0と変化することになるわけ。
ここは、「楕円関数入門」(戸田盛和 著:日本評論社:2001年9月)を参考にしたの。
θ'=-2ωk√(1-(sin^2(θ/2)/k^2)=-2ωk√(1-sin^2(φ))=-2ωk cos(φ)、と変形出来る。
一方、(1/k)sin(θ/2)=sinφ、の両辺をtで微分すると、
(1/2k)cos(θ/2)θ'=cos(φ)×φ'、となるので、左辺のθ' を-2ωk cos(φ)に置き換えると、
φ'=-ωcos(θ/2)=-ω√(1-k^2 sin^2(φ))、とようやっと、目的地が見えてきたわね。
∫(π/2~φ)(1/√(1-k^2 sin^2(φ))dφ=-ωt+const、
t=0では、φ=π/2なので、const=0、
第1種楕円積分を F(φ,k)=∫(0~φ)1/√(1-k^2 sin^2(φ))dφ、
また、第1種完全楕円積分をK(k)=F(π/2,k)、で表すと、
K(k)=∫0~π/2=∫0~φ+∫φ~π/2、なので、
∫φ~π/2=K(k)-∫0~φ、の関係から、
∫(π/2~φ)(1/√(1-k^2 sin^2(φ))dφ=-ωt、は、
F(φ,k)-K(k)=-ωt、
すなわち、F(φ,k)=-ωt+K(k)、とやっと、tとφとの関係が求められる。
これから、t=K(k)/ω、でφ=0(θ=0)であることから、周期Tは、T=4K(k)/ω=4√r/g×K(k)、
例1では、ω=1、k=sin(θ0/2)=sin(π/4)=1/√2、から、T=4K(1/√2)となる」
「DERIVEで楕円積分を計算するためには、「EllipticIntegrals.mth」を開くか読み込む。
すると、第1種楕円積分は、ELLIPTIC_F(φ,m)と定義されている。
ここで、m=k^2、とDERIVEでは、定義されていることに注意する必要があるがの。
K(1/√2)=ELLIPTIC_F(π/2,1/2)≒1.854074677・・、から、周期 T≒7.416298708・・と求められるのじゃな。
Fの逆関数を、am(F)と書いて、ヤコビの振幅関数と呼ぶことは、第60回で書いてある。
従って、φ=am(-ωt+K(k))、両辺のサイン関数を作ると、
sin(am(○))=sn(○,k)であるので、
sin(φ)=sn(-ωt+K(k))、
左辺は、(1/k)sin(θ/2)、であるので、
sin(θ/2)=k*sn(-ωt+K(k))、
この関係を例1の場合に確認してみよう」
「そのためには、sn関数を計算しないいけないわね。
sn(u,k)=sin(am(u,k))、の関係がある。
右辺の振幅関数 am(u,k)は、「岩波数学辞典」(岩波書店:第4版の付録の公式16、または、「楕円関数入門」によれば、
am(u,k)=πu/2K+Σ(n=1~∞)(2q^n/(n(1+q^2n))sin(nπu/2K))、とフーリエ展開されることが分かっている。
ここで、K=K(k)、q=exp(-πK/K')、K'=K(√(1-k^2))、
例1では、k=sin(θ0/2)=1/√2、これから、K(1/√2)=(Γ(1/4))^2/(4√π)、
K'=K(1/√2)、よって、q=exp(-π)、となる。
しかし、ここでは、DERIVEのユーティリティファイル「EllipticIntegrals.mth」を開くか読み込むことで使用できる振幅関数を利用します。
それは、JACOBI_AM(u,m,n)、ここで、m=k^2、nは、項数を表し、大きいほど精度が高い。
ついでに、今回、発見したけど、第1種完全楕円積分は、KI(m,n)で定義済みだった。
たとえば、今回のk=1/√2、では、KI(1/2,10)≒1.854074677、と計算できる。
一方、第1種楕円積分を使って、Elliptic_F(π/2,1/2)として計算させても同一の値となる。
試してみると、今回のk=1/√2、に対しては、KI(1/2,3)として、n=3で、10桁の精度が出ている。
なお、DERIVEのユーティリティでは、m=k^2、であることに注意してね。
さてと、問題のsin(θ/2)=k*sn(-ωt+K(k))、よね。
左辺は、オイラー展開法で直接、微分方程式を計算して、そのθを利用して、グラフを描くことができる。
一方、右辺は、ω=1、k=1/√2、K(k)=K(1/√2)≒1.854074677・・、を利用して、√2 sn(-t+1.854074677)=sin(am(-t+1.854074677))、
よって、sin(θ/2)のグラフと、(1/√2) sin(JACOBI_AM(-t+1.854074677,1/2,10))、のグラフを描いてみれば、いいと言うことになるのね。
実際、重ねると一致してしまうので、下図は、2つに分けた。
上の図が、微分方程式を数値計算により計算したθから求めた、sin(θ/2)のグラフ。(刻み幅0.01、t=0~10まで、4次)
下の図が、(1/√2) sn(-t+1.854074677,1/2)≒(1/√2) sin(JACOBI_AM(-t+1.854074677,1/2,10))、として計算したもの。
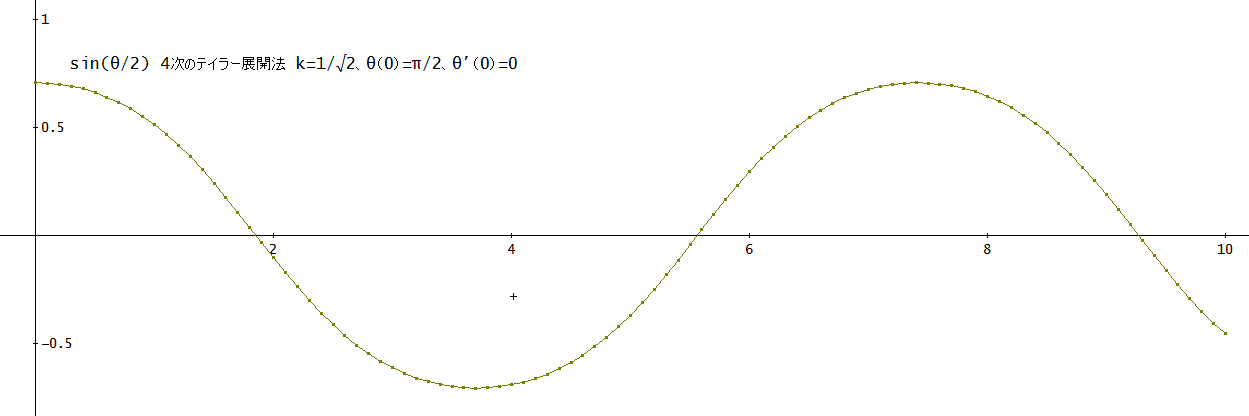
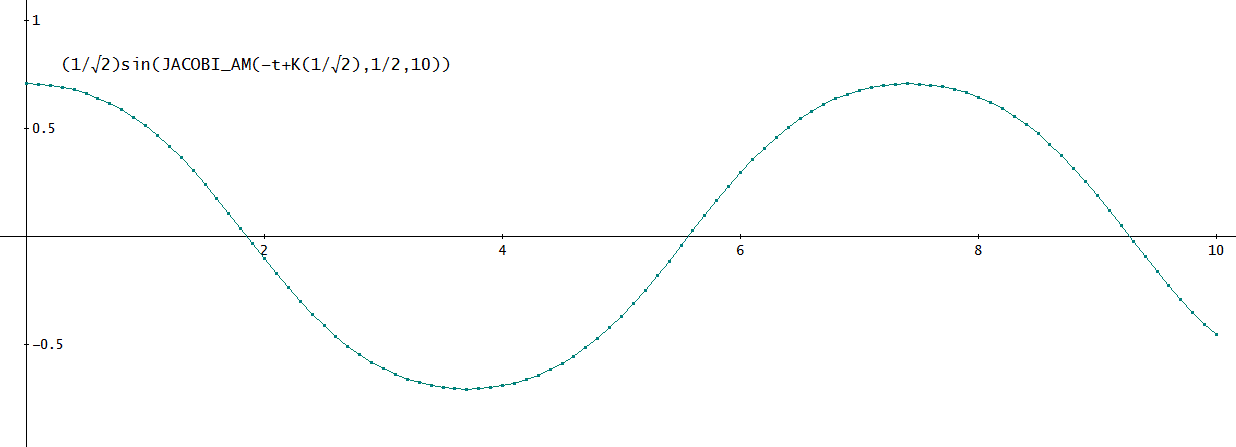
ね、ほぼ、ぴったりと言ってもいいでしょ」
「なるほど。
これは、ちょと、感動した。
数値的一致程度はというと、t=10、の時点の双方の値を比較すると、
sin(θ(10)/2)≒-0.4559427865、一方、sn関数から計算した値は、-0.4559427863、と小数点10桁目が異なる程度じゃ」
「DERIVEの振幅関数は、フーリエ展開を使って計算していないようね」
「うん。
そのようじゃな。
これは、逐次近似法を使っている気がするな。
F=Elliptic_F(φ,k)、において、振幅関数の値を求めると言うことは、Fを与えて、φを求めることじゃ。
これは、am(u,k)=Newton(u-Elliptic_F(x,k),x,第1近似値,回数)と、ニュートン法で求められるはずじゃ。※末尾補足参照。
xの第1近似値としては、u と等置でよいと思う。
たとえば、JACOBI_AM(u,1/2,10)として計算させると、u=1~10まで、
1, 0.9323150798;
2, 1.674163922;
3, 2.460002101;
4, 3.431410753;
5, 4.304620857;
6, 5.026814633;
7, 5.872672281;
8, 6.851503073;
9, 7.661640563;
10, 8.391830823、
が得られるが、
一方、NEWTON(u - ELLIPTIC_F(x, 1/2), x, u, 5)、として、u=1~10までを5回ずつ計算したものがこれじゃ。
1, 0.9323150798;
2, 1.674163922;
3, 2.460002099;
4, 3.431410754;
5, 4.304620857;
6, 5.026814633;
7, 5.872672218;
8, 6.851503282;
9, 7.661640563;
10, 8.391830820、
ニュートン法で計算した値がJACOB_AMで計算させた値と一致している部分を青色で示した。
最低7桁まで一致していることが分かる。
10桁目まで一致していないもの、u=3、8 は、丸め誤差と考えられる。
ちなみに、JACOBI_AMを使った方が計算時間は、10倍ぐらい速い。(u=8の振幅関数の値を、JACOBI_AMは、0.015秒、Newton法で10回計算させると1.01秒) 」
「これで、将来、「楕円積分と楕円関数(2)」を書く際の基本ができたね」
「確かにな。
振幅関数をフーリエ級数で展開して計算するのが少し面倒だったのでな。
しかし、第60回の時は、気がつかんかったのう。
さて、次回は、2重振り子の運動を調べて見よう」
※振幅関数の値を求めるニュートン法について(2016/1/26 補足)-------------------------------
第1種楕円積分を、g(x)、と置けば、g(x)=∫(0~x)(1/√(1-k^2 sin^2(θ))dθ、
今、u=g(x)、として、u を与えて、x を求めることを考える。
y(x)=u-g(x)、とy(x)を定義すると、xを求めることは、y(x)=0の解を求めることと同じである。
xの第n+1近似値を、x(n+1)と書くと、ニュートン法の原理から、x(n+1)=x(n)-y(x(n))/y '(x(n))、と逐次近似できる。
ここで、y '(x(n))=-g '(x)=-√(1-k^2 sin^2(x(n))、
なお、x(1)は、第1種楕円積分では、|k^2 sin^2(x)|<1となるので、根号内を1に置き換えて計算すれば、g(x)≒x、となる。
よって、y(x)=u-x(1)≒0、として、第1近似値 x(1)=u、とした。
この計算は、Iterates関数、または、Iterate関数でも可能だが、組み込み済みの関数、Newton()があるため、この関数を利用するのが簡単である。
Newton(u-g(x),x,u,計算回数)、とすればよい。
ただし、今回、u が大きいときは、0~π/2の範囲に引き戻して、計算させれば、効率的である。
実際、g(x)をそのまま、Elliptic_F(x,k^2)、とおき、NEWTON(u-Elliptic_F(x,1/2),x,u,5)、と計算させた場合、
次のように、u が大きくなると、非常に時間がかかる。その原因は、Elliptic_F関数の計算に時間がかかるためである。
| u |
NewtonでElliptic_Fを使う |
Iterates関数でElliptic_user_Fを使う |
JACOBI_AM(u,1/2,5) |
| 1 |
0.218 |
0.25 |
0.031 |
| 10 |
0.516 |
0.34 |
0.015 |
| 100 |
4.72 |
0.438 |
0.031 |
| 1000 |
68.9 |
0.297 |
0.016 |
上の表は、k=1/√2、u=1~1000までを、2つの方法で計算し時間(単位:秒)を比較したものである。
このように、そのまま、Elliptic_F(x,m)を使うと、uが大きくなると加速度的に計算時間が大きくなってしまう。
そこで、Elliptic_user_F(x,m)を次のように定義し代わりに利用すると計算時間は、短縮される。
ただし、Newton関数を使えない(微分係数が機械的に求められない)ため、Iterates関数を使う必要がある。
Elliptic_user_F(x,m):=
PROG(x_ ≔ ABS(x),
n_ ≔ FLOOR(x_/π),
IF(n_ < 1, SIGN(x)*ELLIPTIC_F(x_, m),
SIGN(x)(2n_* KI(m, 5) + ELLIPTIC_F(x_ - n_*π, m))))、
ここでは、xが負の場合に備えて絶対値をとってから処理している。
最後に、x の符号に応じて、符号を付けている。KI(m,5)は、m=k^2の第1種完全楕円積分である。
振幅関数の値は、ITERATES(x + (u - Elliptic_user_F(x, m))√(1 - m·SIN(x)^2), x, u,
5)、とすれば求められる。
なお、この補足は、原理的なことで、振幅関数を使うだけであれば、JACOBI_AM関数を使うのが便利であることは言うまでもないが、定義済みのElliptic_F関数には、このような問題が含まれていることは、知っておきたい。
最終更新日 2016/2/22



 「わかりやした。
「わかりやした。

