数式処理ソフト DERIVE(デライブ) de ドライブ
79.連立常微分方程式の数値解法(ランチェスターの法則、ロトカ・ヴォルテラ型)
(1)はじめに
 「単独の高階常微分方程式は、たとえば、2階のy ' '=r(x, y, y ' )であれば、第78回で y '=p、とおいて、p '=r(x,
y, p)との2つの1階常微分方程式の連立として扱ったわけね。
「単独の高階常微分方程式は、たとえば、2階のy ' '=r(x, y, y ' )であれば、第78回で y '=p、とおいて、p '=r(x,
y, p)との2つの1階常微分方程式の連立として扱ったわけね。
今回は、複数の常微分方程式の系を考える訳ね」
「ともちゃん。毎回、ご苦労様じゃな。
さて、数式処理ソフト DERIVE(デライブ)の第78回の「高階常微分方程式の数値解法」では、y '=p とおいたが、もう少し、一般化して、y '=F(x, y, p)、p '=G(x, y, p)のようなものを解くことを考える。
なお、’ は、独立変数 x による微分を表すものとする。
ここで、もし、F=p 、かつ、G=r(x, y, p)であれば、前回の2階の常微分方程式、すなわち、y ' '=r(x, y, y ' )、と同等じゃろう」
「なるほど。
今回は、前回を含むことになるのね。
同様に、y ' '=F(x, y, y ', z, z ')、z ' '=G(x, y, y ', z, z ')のようの場合も視野に入れていくということね」
「そうじゃ。
前回に定義した関数が使える。
実用上も、2つ以上の常微分方程式で表される系の解析が必要となることが多いしな。
まず、今回は、1階の場合を調べて見よう」
(2)2元連立1階常微分方程式
「テイラー展開を与える関数を、DIFm_user_R(f,v,h,m)として、第78回では、次のように定義したんじゃった。
PROG(n_ := DIMENSION(v),
IF(m = 1, h·f,
h/m∑(f↓k_·∂(DIFm_user_R(f, v, h, m - 1), v↓k_), k_, 1, n_)))、
ここで、2階の場合は、f=[1,p,r]、v=[x,y,p]、である。
3階以上では、それぞれの要素を増やせば良かった。
この関数は、そのまま使えると思うのう」
 「そうね。
「そうね。
しかし、記号を整理しないと混乱してしまうわね」
「そこでじゃ。
当面、y及びzをxの関数と考えて、y '=r(x, y, z )、z '=s(x, y, z )のように2元連立1階常微分方程式として表されている場合を考えてみよう。
f=[1,r,s]、v=[x,y,z]、として、DIFm_user_R(f,v,h,m)を計算すると、
m=1に対しては、h[1,r,s]、
m=2に対しては、(h^2/2)[0,∂(r, x)+r∂(r, y)+s∂(s, z),∂(s, x)+r∂(s, y)+s∂(x, z)]が返ってくる。
あとは、以下同様じゃな」
「すると、模式的には、
v(k+1)=v(k)+Σ(DIFm_user_R(f,v,h,j))、ここで、和は、j=1~m、とする。
のように、vの変化が計算できることになるわね」
「そうじゃな。
この場合、当然じゃが、前回のm次までのオイラー法関数がそのまま使えることになる。
再掲すれば、Eulerm_user_R(f, v, v0, h, m, n)、として、
PROG(f_:=∑(DIFm_user_R(f, v, h, k_), k_, 1, m),
ITERATES(u_ + LIM(f_, v, u_), u_, v0, n))、
となる」
「何か具体的な例を出して欲しいよね」
「次節で、ランチェスターの二次法則について、触れることにしよう」
(3)2元連立1階常微分方程式の例(ランチェスターの二次法則)
「2元連立常微分方程式のシステムについては、「自然の数理と社会の数理」(佐藤總夫 著:日本評論社:1988年1月第1版第1刷)が詳しい。
第1巻では、ランチェスターの法則、特に、二次法則が紹介されている。
2つの勢力、ここでは、y とz とすると、それらの競合を考える。
なお、変数、x は、時間である。
また、x、y、zは、本来は、とびとびの量であるが、なめらかな連続量のように扱う。
さて、近代の戦争で2つの勢力が戦う場合、両軍の勢力がどのように減少するかをモデル化する。
y軍の勢力(人数と考えて良い)をy(x)、z軍の勢力をz(x)で表すと、それらは、次の微分方程式に従って、減少すると考える。
すなわち、自軍の損害は、敵戦力に比例すると考える。
y '=-αz、
z'=-βy、
ここで、α、βは、比例係数で、正の定数とする。
また、戦闘終了時まで、互いに戦力の補充はないものとする」

「初期値を、x=0、で、y(0)=a、z(0)=b、であるとすれば、
ラプラス変換により、
sY(s)-a=-αZ(s)、
sZ(s)-b=-βY(s)、
ここで、y(x)の像関数をY(s)などと書くことにする。
この解は、
Y(s)= (as -bα)/(s^2 -αβ)
Z(s)= (bs - aβ)/(s^2 -αβ)、
となる。
y(x)=^(√α√β·x)(a√β - b√α)/(2√β) + ^(- √α√β·x)(a√β + b√α)/(2√β)、
z(x)=^(√α√β·x)(b√α - a√β)/(2√α) + ^(- √α√β·x)(a√β + b√α)/(2√α)、
たとえば、α=β、(両方が同等の兵器や互角の技量で戦うとした場合)は、
y(x)=(1/2)((a-b)exp(αx)+(a+b)exp(-αx))
z(x)=(1/2)(-(a-b)exp(αx)+(a+b)exp(-αx))、
となり、a>bならば、xが大きくなると、いずれ、必ず、z(x)=0となってしまう。
それまでの時間は、x=(LN(a+b)-LN(a-b))/(2π)、であり、そのときのyの残存数は、y=√(a^2-b^2)である。
また、もし、a>bのときに、z軍がy軍と同格に戦うためには、(a/b)^2>=(α/β)が必要である。
たとえば、a=2b の場合(y軍がz軍の2倍の兵力)は、α>=4βである。
これは、z軍がy軍より4倍以上の能力を持たねば同格には戦えないことを示しているということね」
「そのとおりじゃな。
戦闘開始時に両軍の兵力に差があると、戦闘能力が同一であれば、戦闘終了時の勝者の残存兵力は、開始時の兵力の2乗の差の平方根になる。
これがランチェスターの2次法則と言われる例じゃな。
古代の源平合戦のような時代では、1対1の戦いが主流だったので、兵力の大きい方が勝つ。
「衆寡敵せず」ということわざもあるが、戦闘終了時の兵力 のyの残存数は、初期兵力の差に比例する。
すなわち、y=a-b。
一方、近代以降では、2乗の差(の平方根)に比例するので、その差は、著しく、大きくなる。
現代では、コンビニの出店数、店舗面積などでも、ランチェスターの2次法則は、応用されているということじゃ」
「たとえば、前節の方法で、具体的に数値計算をしてみるよ。
α=β=1、a=2000、b=1000、という場合。
Eulerm_user_R([1, -z, -y], [x, y, z], [0, 2000, 1000], 0.01, 4, 60)、のように刻み幅 h=0.01、m=4の4次のオイラー法で計算してみた。
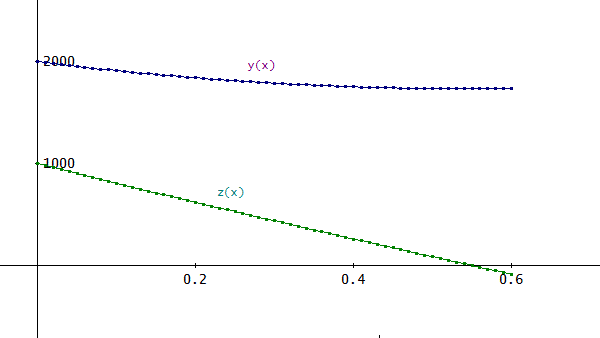
結果は、一目瞭然。
戦闘終了時のy軍の残存数は、約1730と86%以上が生存しているのに対して、z軍は、1000人が全滅してしまっている。
恐ろしい結果」
「上のモデルでは、(b/a)^2=(α/β)でない限り、どちらかが減少して、ついには、ゼロとなってしまう。
また、等しいときは、両者とも全滅してしまう。
なので、循環的な変動は、起こらない」
「でも、結局は、数が多い方が勝つというのは、なんか、当たり前の結果だわね」
「確かにな。
じゃが、y軍とz軍、ここで、戦闘能力は、互角で、初期戦力が、y(0)=2000、z(0)=1500とした場合を考えよう。
図で示すと、下図のようになる。
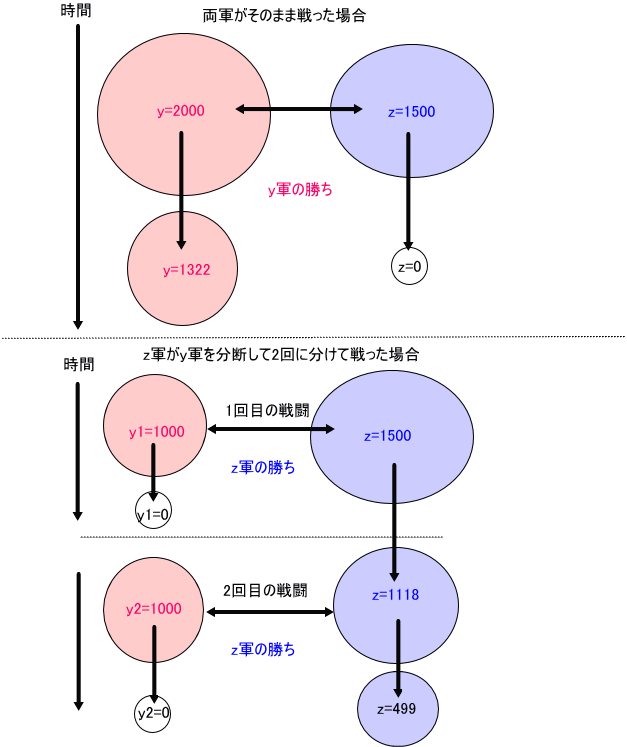
このまま戦うと上に述べたように、戦闘終了時 t=t1で、y(t1)=√(2000^2-1500-2)≒1322、z(t1)=0、となって、明らかに、z軍が負ける。
しかし、何らかの方法で、y軍の戦力を分断できたとすると、結果は、異なってくる可能性がある。
もっとも効果的なのは、数で劣るz軍が、y軍の初期戦力 2000を半分ずつに分断して2回に分けて戦闘を行った場合じゃ。
yの1つの集団をy1軍、他をy2軍とし、y1(0)=1000、y2(0)=1000、とする。
このとき、第1回目の戦闘時に、y1軍とz軍が交戦できたと、第1回目の戦闘終了時 t=t1で、y1(t1)=0、z(t1)=√(1500^2-1000^2)≒1118、となり、z軍の残存数が1118である。
次にy2軍とz軍の交戦が行われると仮定すると、この第2回目の戦闘終了時 t=t2で、y2(t2)=0、z(t2)=√(1118^2-1000^2)≒499、となる。
これは、z軍(1500)がy軍(2000)に勝ち、なお、かつ、z軍の残存数が約500というとになる。数で劣っていたz軍の勝利じゃな。
佐藤先生の本では、「トラファルガーの海戦」(1805年にスペイン海軍とイギリス海軍がトラファルガー沖で戦いイギリス軍が大勝利した)を例に、この一見不思議な現象を説明されている。
わしの考えでは、「日本海海戦」(1905年5月)の連合艦隊の大勝利も原理は、同じような気がするのう。
さて、次節では、動物の数の増減をモデル化した方程式を見てみよう」
(4)2元連立1階常微分方程式の例(ロトカ・ヴォルテラ型の方程式)
「いわゆる、自然界における動物の数の変動を説明するために、ロトカ(Lotka:アメリカ:1925年)、ヴォルテラ(Voltella:イタリア:1926年)などにより独立に提出された方程式じゃ。
「動物の数は何で決まるか」(伊藤嘉昭・桐谷圭治 著:NHKブックス:1972年12月第4刷)や「計算数学夜話」(森口繁一 著:日本評論社:1978年4月初版)の第18回「食う魚と食われる魚」にその例が掲載されている。
前者は、実際の動物の数の変動は、このような簡単なモデルでは、説明できないと述べている。(理由は後述)
後者では、一つの例として平易に説明されているが、紙数の関係であまり詳細には、説明されていない。
さて、食う魚を Y(X)、食われる魚をZ(X)で表す。
ここで、Y、Zは、個体数を示す。時間は、X。
Y '=-a Y+bYZ、第1項は、単位時間当たりの死亡数。第2項は、Zを捕食することで、Yが増える数。
Z '=+cZ-dYZ、第1項は、単位時間当たりの増殖数。第2項は、Yに捕食されることによりZが減る数。
ここで、a、b、c、dは、正の定数とする。
「動物の数は何で決まるか」では、この方程式の問題点として、次の点を挙げている。
・捕食される Z には、種内競争による減少が見込まれていない。
・Z の減少は、捕食者 Y のみに依存する(のはおかしい)。
・捕食者 Yは、いくらでも捕食する。すなわち、満腹しない。
・捕食者 Yには、種内競争による減少が見込まれていない。
従って、実際のフィールドにおける現象を解析するには、不十分であるとしている。
以下では、このような問題点は、理解した上で、一つのモデルとして、計算してみよう。
まずは、ともちゃん、パラメータが4つもあって、面倒なので、「計算数学夜話」にならって、簡単化してくれんかの」
 「えーと。計算数学夜話に従って、X=β×x、Y=γ×y、Z=δ×z、と変換する。
「えーと。計算数学夜話に従って、X=β×x、Y=γ×y、Z=δ×z、と変換する。
dy/dx=(β/γ)(-aγy+bγδyz)=-aβy+bβδyz、
ここで、aβ=1、bβδ=1、とおくことにすると、β=1/a、δ=a/b、となるので、
dy/dx=y '=-y+yz、と簡単化される。
いっぽう、
dz/dx=(β/δ)(cδz-dγδyz)=cβz-dβγyz、となるけど、
β=1/a、δ=a/b、なので、
dz/dx=(c/a)z-(d/a)γyz、となる。
さらに、(d/a)γ=(c/a)となるように、γ=c/d、と置いてから、(c/a)=αと書けば、
dz/dx=z '=αz-αyz、と整理できる。
結局、
α=c/a、β=1/a、γ=c/d、δ=a/b、とおいたことになるわね」
「なるほど。
だいぶん、すっきりした、
y '=-(1-z)y、
z '=α(1-y)z、
のような方程式系が得られる。
ここで、α>0のパラメータとする。
y(0)=1.5、z(0)=1.5、α=2、の場合を刻み幅 h=0.01、4次のオイラー法、
Eulerm_user_R([1, -y + yz, 2z - 2yz], [x, y, z], [0, 1.5, 1.5], 0.01, 4,
1000)、として、0~10までを計算してプロットしたものが下のグラフじゃ」
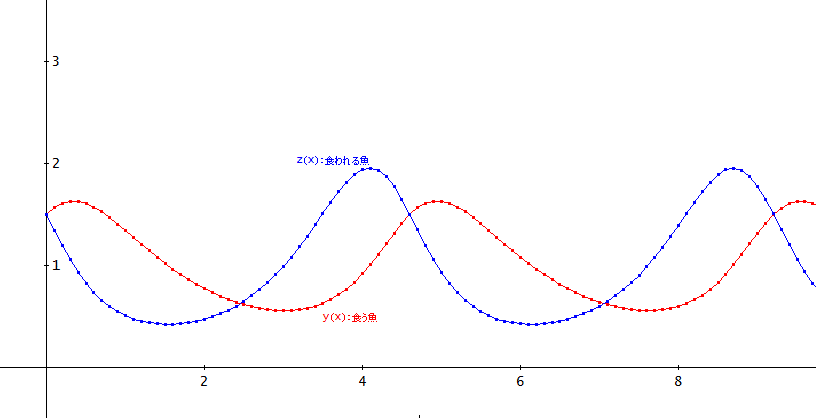
「この場合は、周期的に変化しているね。
[y(x),z(x)]のグラフは、下図のようになったわ。
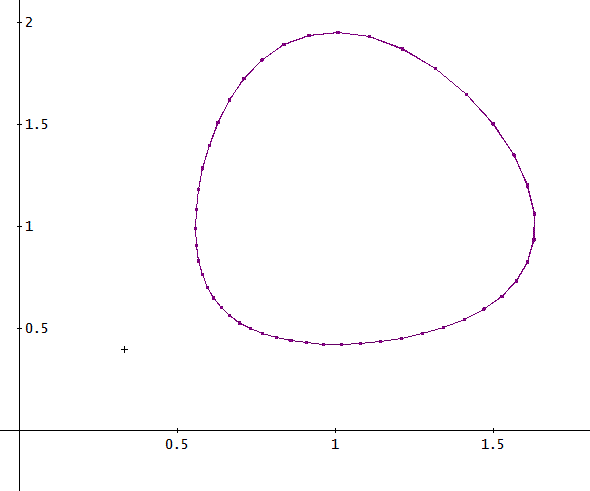
横軸がy(x)、縦軸がz(x)。
おむすび、みたいな図形ね」
「それは、こういうことじゃ。
「計算数学夜話」にならって、記述すると、
y '=-(1-z)y、
z '=α(1-y)z、
y'/z'=dy/dx dx/dz=dy/dz=-(1-z)y/α(1-y)z、とyをzの関数と考えて、
整理して、α(1-y)z dy+(1-z)y dz=0、
両辺を、yz で割れば、(1/(yz)が積分因子)
α(1/y-1) dy+(1/z-1) dz=0、となる。これは、完全微分方程式であるので、直ちに積分できて、
zy^α=c×exp(αy+z)、ただし、c= z(0)exp(-y(0)α - z(0))y(0)^α。
たとえば、y(0)=z(0)=1.5、α=2の場合は、下図のようになる。
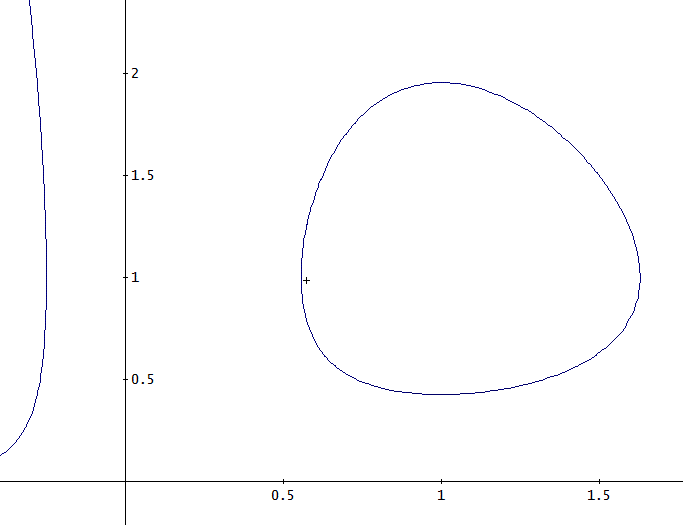
図の横軸は、y、縦軸は、z、であり、第2象限の部分は、無縁解じゃな」
「完全微分方程式と積分因子については、第70回の「1階常微分方程式の解法(2)」に掲載しているので、必要な方は、チェックしてくださいな。
さてと、のαを0.1から5まで、0.5きざみで、変化させて、上のグラフを描いてみたよ。
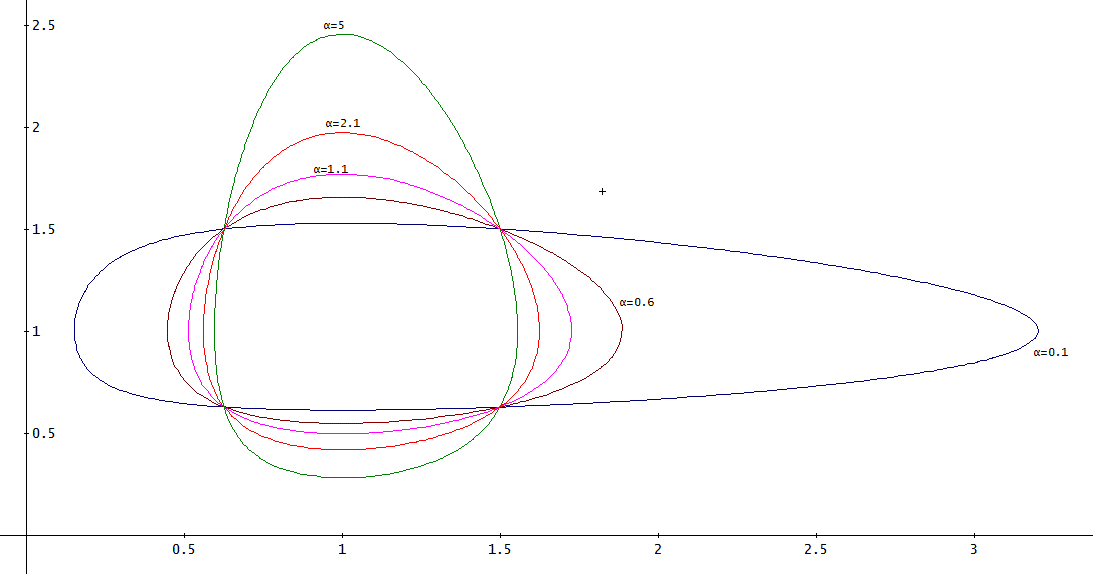
αが0.1のときは、[y(x),z(x)]の形は、横長、αが大きくなるにつれて、縦長になる。
次に、α=2、y(0)=1.5、と固定して、z(0)を0.1から3まで、0.2ずつ変化させてみた。
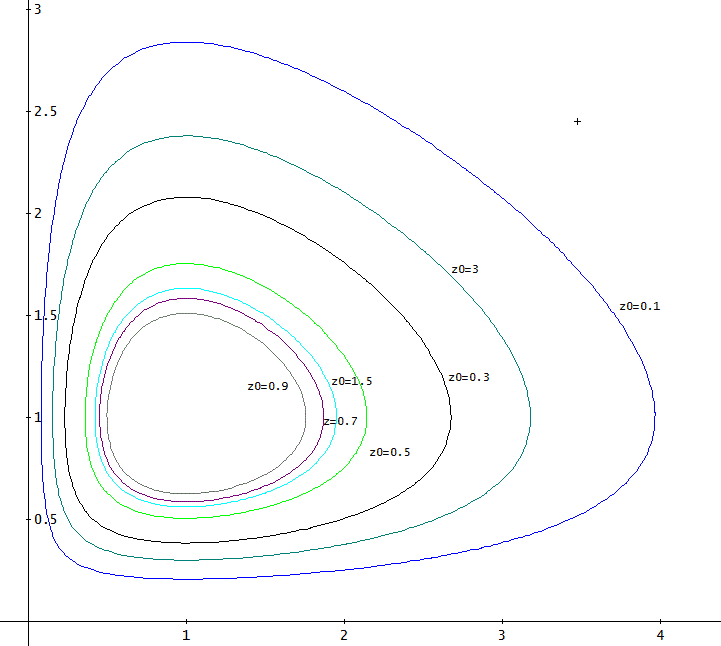
こちらは、z0=0.1から大きくするたびに小さくなると言い切ることはできないけど、とにかく閉じた図形ね」
「では、時間変化を調べて見よう。
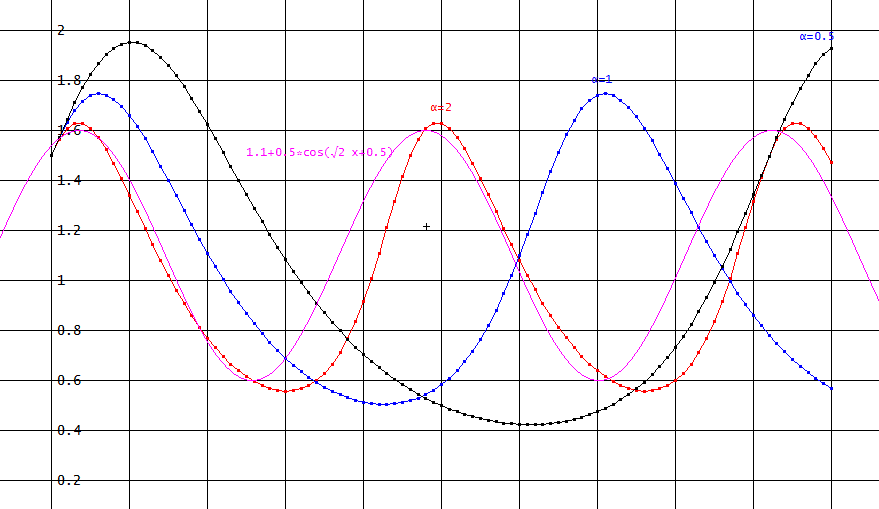
α=2の場合は、おおざっぱに言うと、角周波数ω=√2、波長=2π/√α の正弦波で近似でるようじゃな」
「計算数学夜話の演習問題に、y=z=1.1=1+ε、ε=0.1、の場合、
y=1+ε(cos(√α x)+1/√α sin(√α x))
z=1+ε(-(√α)sin(√α x)+cos(√α x))、と近似できることを証明しなさい、というものがあるわ。
これは、y '=0、z '=0の近くで展開すると求められそうね。
y=1+εu(x)、z=1+εv(x)と置いてから、方程式に代入すると、
εu'=εv+ε^2×uv、すなわち、u ' ≒v、
同様に、
εv'=-αεu-αε^2×uv、すなわち、v ' ≒-αu、
これらから、u ''≒-v'=-αu、
よって、u≒A*sin(√α x)+B*cos(√α x)、と求められる。
なお、A、Bは、u(0)=y0-ε=1.1-0.1=1から、B=1、なので、
u≒A*sin(√α x)+cos(√α x)、
v'≒-αu=-α(A*sin(√α x)+cos(√α x))、から、
v≒(√α)A*cos(√α x)-(√α)sin(√α x)、
v(0)=z0-ε=1.1-0.1=1より、A=1/√α、
結局、
u≒cos(√α x)+(1/√α)sin(√α x)、
v≒cos(√α x)-√αsin(√α x)、となるので、
y≒1+ε(cos(√α x)+(1/√α)sin(√α x))
z≒1+ε(cos(√α x)-√αsin(√α x))、と求められる。
この式で、α=2の場合を下図に示してみた。
計算値というのが、微分方程式を刻み幅 h=0.01、4次のオイラー法で、x=0~10まで計算したもの。
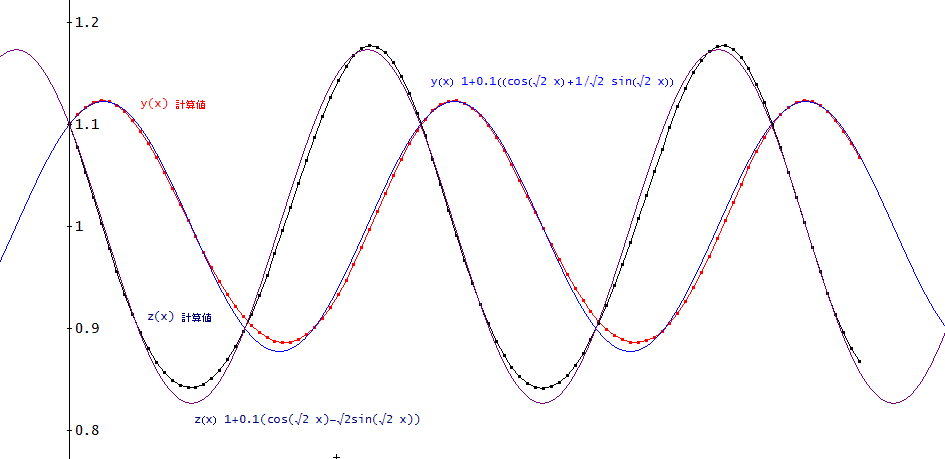
ほぼ、一致しているようね」
「そうじゃな。
y=z=1は、元の方程式の「不動点」というものじゃ。
不動点では、y'=z'=0となっているので、その付近では、線形化が可能なことが多い。
初期値がこの点から外れると、すなわち、ε が大きくなると、ともちゃんが計算してくれた第1近似式から外れが大きくなるはずじゃ。
たとえば、ε=0.5で計算してみよう。(y0=1.5、z0=1.5、α=2の場合)
図が見にくくなるので、y(x)の計算値と第1近似式のみを示す。
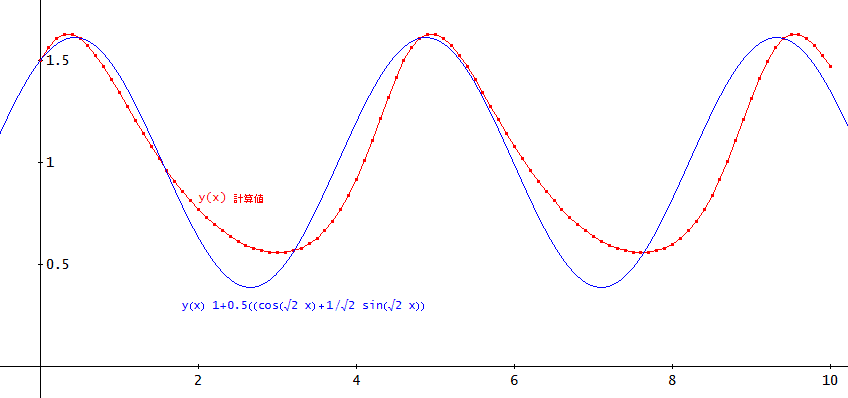
上の図では、大きくは外れてはいないがε=0.1の場合よりは、一致度合いは、減っていることが分かる」
「εの2次までとって計算すれば、良い訳ね。
でも、εが1より大きい場合は、かえって近似が悪くなるような気がするね」
「εが1より大きい場合は、1/εを使って、y=1+(1/ε)u(x)+・・、と展開すれば良いじゃろう。
しかし、このような近似計算を手計算で行うのは、大変じゃな。
次節で、解析的な近似解の求め方を考えてみよう」
(5)2元連立1階常微分方程式の例(ロトカ・ヴォルテラ型の方程式)の近似解
「(4)節で、出てきた方程式系、
y '=-(1-z)y、
z '=α(1-y)z、
これの第1近似解として、
y1(x)=1+ε(cos(√α x)+(1/√α)sin(√α x))、
z1(x)=1+ε(cos(√α x)-√αsin(√α x))、をともちゃんに求めてもらった。
ただし、y(0)=z(0)=1+ε、とする。
この第2近似を求めるために、DERIVEの関数を使用する。
ともちゃん。ユーティリティファイル「ODEApproximation.mth」を開くか読み込んでから、PICARD関数を使って見てご覧」
 「PICARD関数か。
「PICARD関数か。
これは、一度もお目にかかっていないわね。
DERIVEの日本語版のテキストに少し例が載っているけど。
たとえば、y '=x+y、y(0)=0、を解く場合、
PICARD(x + y, x^2/2, x, y, 0, 0)、に次のように引数を与える。
第1引数は、方程式の右辺、x+y、
第2引数は、第1近似解、ここでは、x^2/2、としている。
第3引数は、x、これは変数名、
第4引数は、y、これは、関数名、
第5引数は、xの初期値、ここでは、ゼロ
第6引数は、yの初期値、ここでは、ゼロ、
この計算で、第2近似として、(x^3/6 + x^2/2)が得られる。
厳密解は、exp(x)-x-1≒・・x^5/120 + x^4/24 + x^3/6 + x^2/2、なので、テイラー展開の第2項までが得られたことになる」
「PICARD関数は、フランスの数学者、ピカールの名前をもとに名付けられているようじゃ。
日本語では、逐次代入法とも呼ばれる。
この関数は、テキストに書かれているように、今回のような2元連立方程式に対しても有効じゃ。
PICARD([-y + yz, αz - αzy], [y1(x), z1(x)], x, [y, z], 0, [1 + ε, 1 + ε])、
ここで、
第1引数は、[-y+yz,αz-αyz]のように方程式の右辺を2次元のベクトルとしたもの、
第2引数は、[y1(x),z1(x)]、これは、第1近似解のベクトル。
第3引数は、x、これは変数名、(ベクトルではないので注意)
第4引数は、[y,z]、これは、関数名のベクトル、
第5引数は、xの初期値、ここでは、ゼロ、ベクトルでは無いので注意。
第6引数は、[1+ε,1+ε]、関数の初期値のベクトル。
のように、引数にスカラーとベクトルが混じっているので、気をつけないといけない。
今回は、第2近似解として、次の式がベクトルとして得られる。
y2(x)=COS(√α·x)(ε^2·SIN(√α·x)/√α + ε) + ε^2(1 - α)SIN(√α·x)^2/(2α) + εSIN(√α·x)/√α
+ 1、
z2(x)=COS(√α·x)(ε - √α·ε^2SIN(√α·x)) + ε^2(α - 1)SIN(√α·x)^2/2 - √α·εSIN(√α·x)
+ 1、
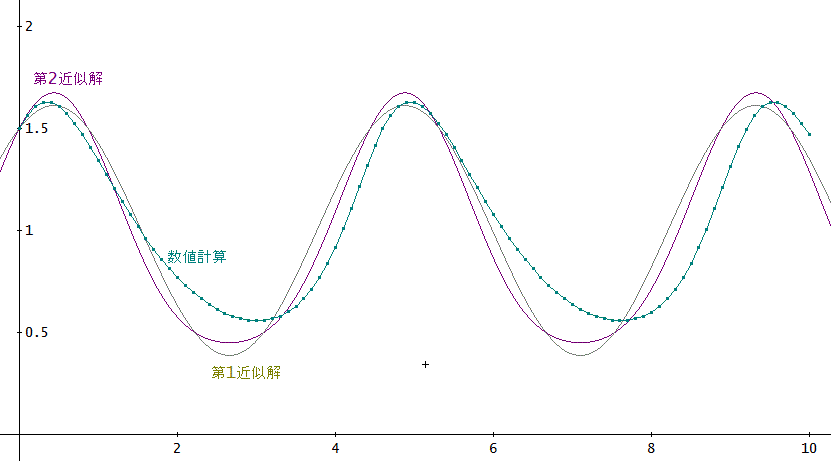
上のグラフは、y(x)の数値計算(刻み幅h=0.01、4次のオイラー法、y(0)=z(0)=1.5、α=2、x=0~10)の結果と第1近似解、第2近似解の様子を表したものじゃ。
また、下のグラフは、z(x)の数値計算結果と第1近似解、第2近似解の様子じゃ。
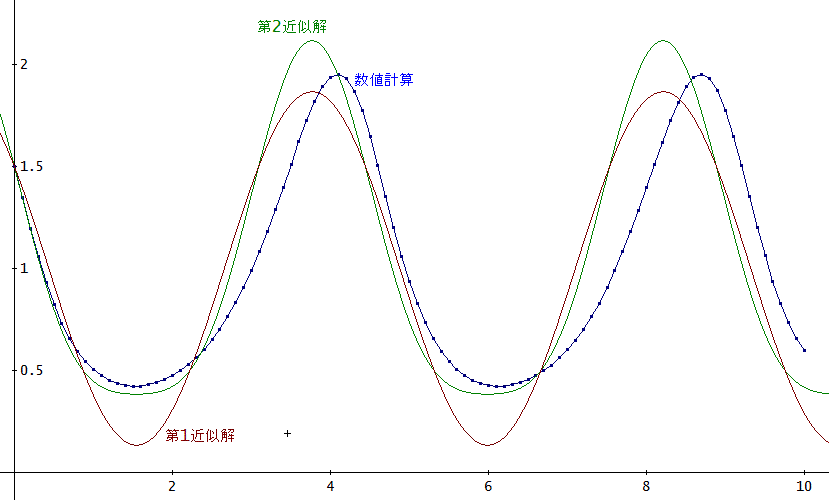
第1近似解よりも第2近似解の方が、数値計算にやや近づいていると思うのう」
「おむすび形のグラフを描かせてみたよ。
横軸がy(x)、縦軸がz(x)。
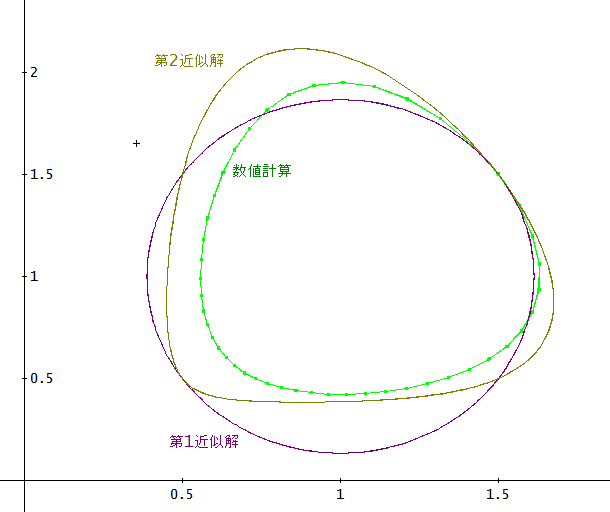
たしかに、これを見ると、第1近似解は、楕円だけど、第2近似解は、数値解に近いおむすび形でいびつな特徴を表している。
けど、数値解とは少し差があるわね。
第3近似を求めてみたよ。
Exactモードでは、解が出てこないので、数値的に求めたけど、第3近似解にxの項があるので、解が斜めにずれてしまう」
「ピカールの方法では、1回目は、ほぼ、正しい結果に近づくが2回目以降の近似で、ずれてしまうことが多いようだ。
今回の場合、定数と三角関数以外は含まれないので、xの項は、単純に削除してしまう。(式の置換を使ってゼロにすると便利)
すると、下図のように、第3近似解は、第2近似解よりも、数値解に近づいてはいる。
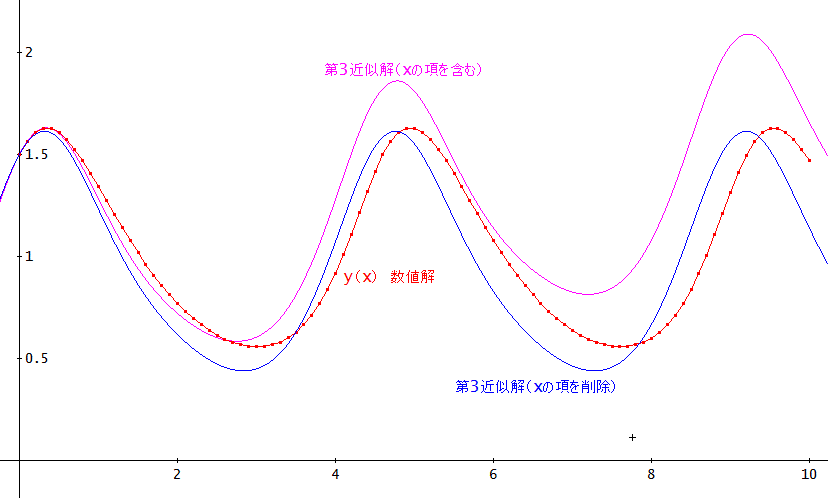
例のおむすび形のグラフを見ると、よりはっきりする。
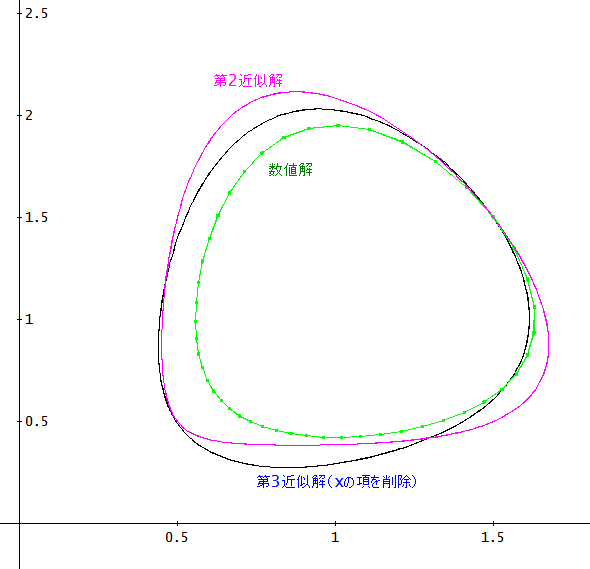
ただ、パラメーターを数値でしか含まない解では、あまり近似解の意味がないかもしれん。
これ以外の方法としては、今回のような方程式に特化しておるが、
y '/ y=-1+z、
z '/z=αz-αyz、
と書き直して、両辺を積分することにより、
y=exp(∫z(x)dx-x+LN(1+ε))、などとして、
z(x)=z1(x)とおけば、
y≒exp(εCOS(√α·x) + ε·SIN(√α·x)/√α -ε)(ε + 1)、
これから、εの2次までテイラー展開して、
y≒COS(√α·x)·(ε^2·SIN(√α·x)/√α + ε) + ε^2·(1 - α)·SIN(√α·x)^2/(2·α) + ε·SIN(√α·x)/√α
+ 1、
などとすることができる。
これは、すでに求めた第2近似解と等しい。この方法は、本質的には、ピカールの方法と同じじゃな。
あと考えられる有力な方法は、フーリエ級数に展開して、方程式に代入して各係数を決める未定係数法的な解法じゃ。
このとき、変数を√αx=t、と変更してから、
y=a0/2+(a1εcos(x)+a2 ε^2 cos(2x)+・・)+(b1 ε sin(x)+b2 ε^2 sin(2x)+・・)、のように展開するとやや式が見やすい。
zも同様。
そして、これらを下記の方程式に代入して、sin(x)などの項を比較する。
√αdy/dt+y-yz=0、
dz/dt-√αz+√αyz=0、
実際に実行すると分かるんじゃが、方程式が非線形なので、途中、εの適宜な項までテイラー展開を指示しないとなかなか計算を進めることができない。
また。各項を比べるよりも、sin(x)、cos(2x)などをかけて、-2πと2π間で定積分を実行して係数間の方程式を求めるのが容易じゃ。
このように原理は易しいが、計算の見通しが悪いのでそう簡単ではないように思う。(第1近似まではなんとか求めてみたんじゃがな)
プログラム的にこれらの係数を求められると良いんじゃがな。
ま、今回も、奥の深道に足を取られたようじゃ。
次回は、2階の連立常微分方程式の系を調べて見よう。
いや、ともちゃんもお正月からご苦労さんじゃった」
(6)ロトカ・ヴォルテラの方程式の周期解と同一周期の初期値 2016/2/15追記 2016/2/20加筆・訂正
(4)節で取り上げた「ロトカ・ボルテラ」の方程式については、初期条件及びパラメーターαの値に関わらず、常に周期解がある。
ただし、実際は、y(x)やz(x)が限りなくゼロに近づくことはあり得ないため、あくまでも理論的なことではある。
y(0)=a、z(0)=b、とするとき、α=2と固定しておくと、√α≒1.414214・・、であるが、
4次までのオイラー展開法により、初期値を変えて、連立微分方程式を解くことにより、下記の表を得た。
青字部分は、2016/2/20に加筆・訂正。
| y(0)=a |
z(0)=b |
yの波長(λ) |
yの角周波数ω=2π/λ |
yの最大振幅(y(0)からずれ) |
備考 |
| 1 |
1 |
2π/√2≒4.44288・・ |
√2 |
0 |
ω=√2であるが、その振幅がゼロなので、
y=z=1の時間によらない定常解となる |
| 1.1 |
1.1 |
4.45070 |
1.4117 |
0.122 |
ωは√αに相当近い |
| 1.5 |
1.5 |
4.60175 |
1.3654 |
0.1309 |
|
| 2 |
2 |
4.967214 |
1.2649 |
0.2879 |
|
| 3 |
3 |
6.030838 |
1.0418 |
0.6453 |
|
| 4 |
4 |
7.326653 |
0.8576 |
1.0372 |
図を参照 |
| 5 |
5 |
8.722607 |
0.7203 |
1.4498 |
図を参照 |
下図は、y(0)=z(0)=4、α=2の場合のy(x)の数値計算結果。
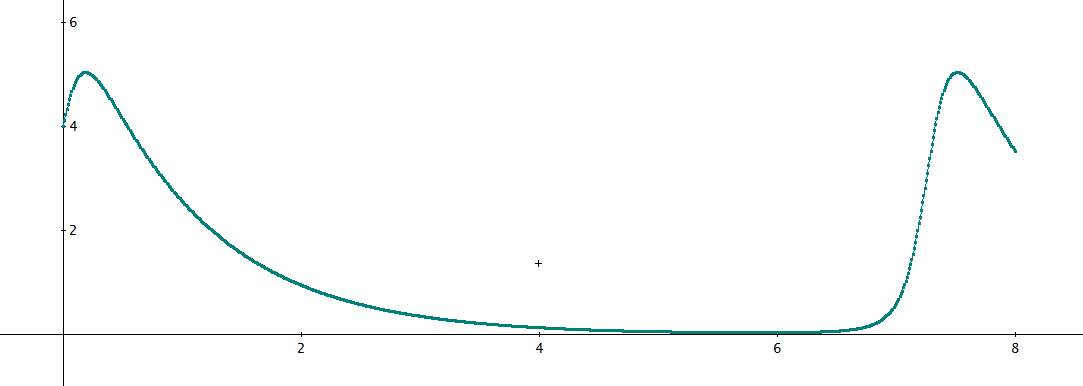
同様に、y(0)=z(0)=5の場合の、y(x)は、次の通り。
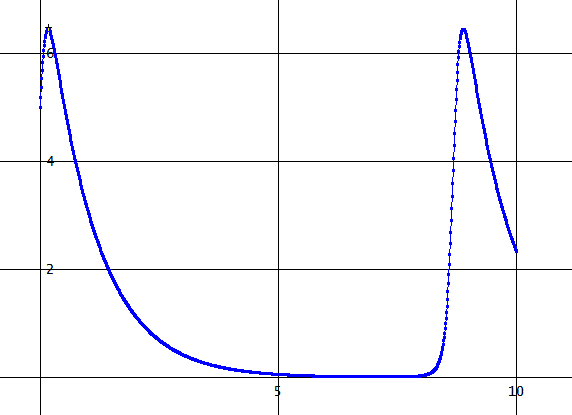
ちなみに、y(0)=z(0)=5の際の[y(x),z(x)]のグラフも次のように閉じる。
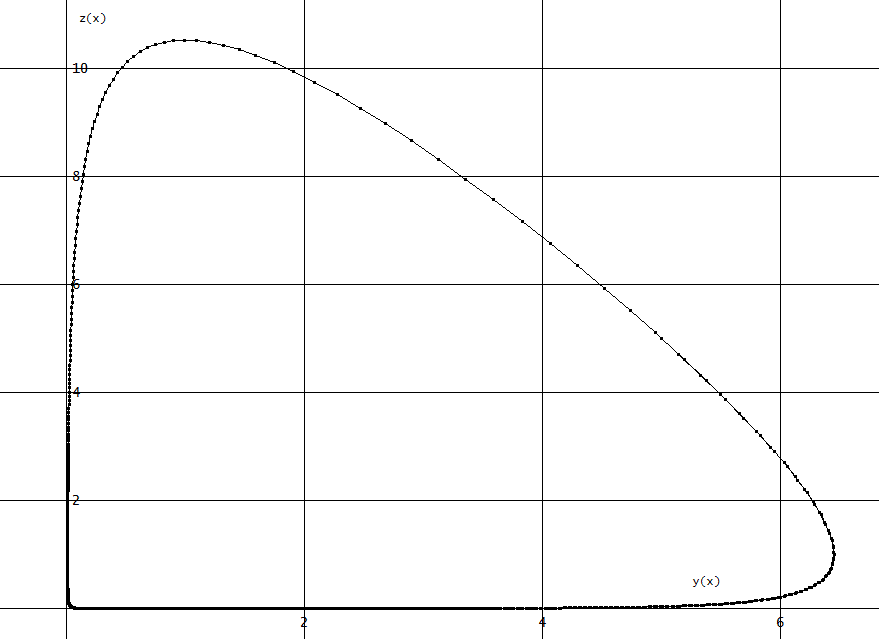
上では、y(x)とz(x)の初期値を等しくした場合を調べてきた。
一方、y(0)=z(0)=a と同一の周期解を与えるbを考えてみた。
[y(x),z(x)]のグラフの周上の2点の関係から分かる。
すなわち、
zy^α= z(0)exp(-y(0)α - z(0))y(0)^α×exp(αy+z)、
ここで、y(0)=a、z(0)=b、として、これと同一周期となる[c,d]は、
d c^α=b exp(-a α-b)a^α×exp(αc+d)、
たとえば、[a,b]=[3,3]と同一周期となる、[c,d]は、上の式から、
d c^α = 3^(α + 1)·^(c·α + d - 3·α - 3)、ここで、α=2、c=3、とすると、d = 0.1785606278、と数値的に求められる。
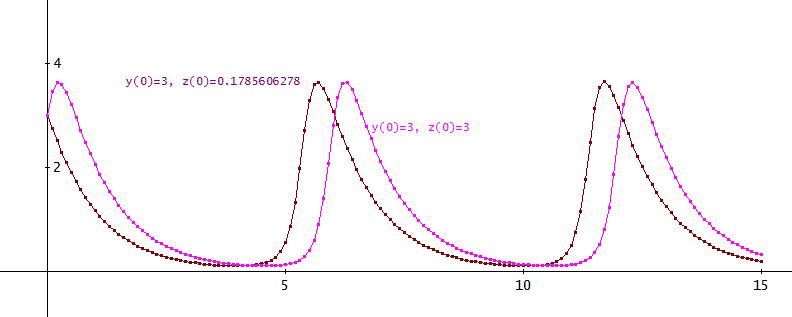
α=2、y(0)=z(0)=3の場合の[y(x),z(x)]のグラフを示す。
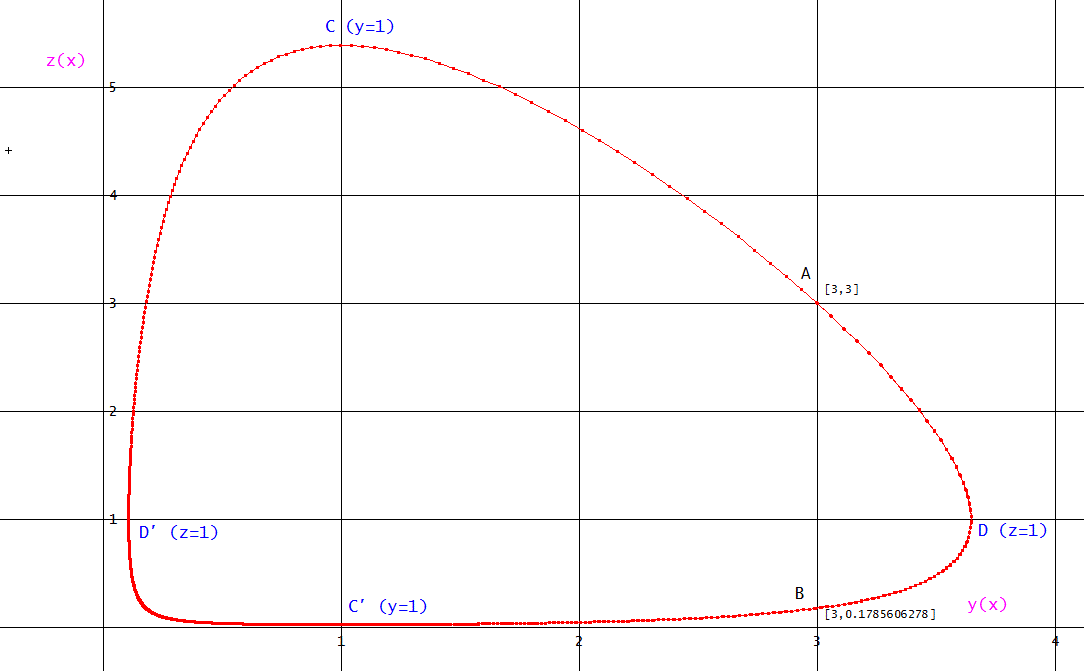
この赤い曲線上の点、たとえば、A[3,3]、B[3,0.1785606278]などは、すべて同一角周波数、ω≒1.0418、を持つ。
また、C、C '、D、D ' は、特徴的な点を示す。
最終更新日 2016/2/20



 「単独の高階常微分方程式は、たとえば、2階のy ' '=r(x, y, y ' )であれば、第78回で y '=p、とおいて、p '=r(x,
y, p)との2つの1階常微分方程式の連立として扱ったわけね。
「単独の高階常微分方程式は、たとえば、2階のy ' '=r(x, y, y ' )であれば、第78回で y '=p、とおいて、p '=r(x,
y, p)との2つの1階常微分方程式の連立として扱ったわけね。

