数式処理ソフト DERIVE（デライブ） de ドライブ
７０．1階常微分方程式の解法（2）
目次
１．はじめに
２．一般解、特殊解、特異解、変数分離型
３．線形微分方程式
４．同次形（y '=r（y/x））
５．求積法
６．ラプラス変換法
７．ベルヌイ（ベルヌーイ）の微分方程式 y ' + p(x)y = q(x)y^k、ここで、kは、0、1でない
８．完全微分方程式（1）
９．完全微分方程式（2）
10．完全微分方程式（3） 積分因数（積分因子）
11．特殊な半線形微分方程式 r(x, y)y ' + p(x)b(y) = q(x)、ただし、（db/dy）／rは、yを含まない
12．y ' がxとyの1次式の関数 y '＝r（u）、ただし、u = px + qy + k、p、q、kは定数
13．y ' がxとyの1次式の分数式の関数 y '=r（（ax＋by＋d）/（px+qy+k））、a,b,d,p,q,kは、すべて定数
14．ダランベール（ラグランジュ）の微分方程式 非正規形 y=x*f（p'）＋g（p'）、p=y '
15．クレローの微分方程式 非正規形 p（x*v－y）=q（v）、v=y '、
はじめに
「1階常微分方程式の解法は、第32回で「1階常微分方程式の解法」として、取り上げているわね」
「ともちゃんは、よく覚えておるのう。
そこでは、DERIVEで、あらかじめ定義されているユーティリティーファイル「FirstOrderODE.mth」の説明をしている。
しかし、第32回は、定義済み関数の簡単な説明だけで、分量も少なく、ちょっと、愛想が足りなかったと思う。
次回以降、2階の常微分方程式を取り上げたいと思っているので、今回は、もう少し、丁寧に紹介しよう」
「ホント、第32回は、木で鼻をくくったような記述だったものね。
で、具体的には、どう進めるの」
「手元にある「常微分方程式の解法」（木村俊房 著：培風館：昭和45年3月10日第13刷）を元にして、常微分方程式の解とは何か、というようなあたりから、ゆるゆると進めていこう」
「じゃ、まずは、記法のお約束ね。
以下では、y=y（x）として、変数 xに関する関数y（x）の1階常微分方程式を考えるわよ。
dy/dx=y'（x）=y' と略記し、また、いちいち、1階常微分方程式と書かずに、簡単に、方程式と書く場合もあるわよ。
初期値は、DERIVEの記法に従い、任意定数は、c、初期値を取り上げる際は、x=x0のとき、y=y0などと書きましょう」
「念のためじゃが、以下では、実数値をとる実関数を考えていく。
変数も変形過程で複素数を使う場合は、あり得るものの、基本的には、実数じゃ。
さて、そもそも、1階常微分方程式の「1階」は、何のことじゃろう？」
「こいつは、考えている方程式に、yとy' 以外のy''、y'''などの高階微分係数が含まれないことを言っているのね」
「そうじゃな。
一般に、f（x,y,y'）=0、のように書けるものじゃな。
このうち、y'（x）=g（x,y）のように表されたものを「正規形」、そうでないものを「非正規形」と呼ぶ。
正規形は、数値解法をはじめとして、扱いやすい形式じゃ。
なお、特に、正規形において、g（x,y）にyの1次の項しか現れないものを、1階の「線形微分方程式」という」
目次に戻る
一般解、特殊解、特異解、変数分離型
「前節では、習慣上、y=y（x）と記述して、xを独立変数、yを従属変数のように考えているが、木村先生の本でも解説されているように、常微分方程式の解としては、x,yの関係式が得られれば、これを方程式の解と言ってもよい」
「つまり、y=y（x）として、yをxの陽の形に表せなくても、解ということにするのね」
「そうじゃ。
関係式には、既知関数の積分などが含まれていてもよい」
「何か、例はないのかな」
「（1－x^2）y'^2－1=0、などはどうじゃな」
「与式は、変数分離型なので、第32回の記事によると、
y'＝p(x)q(y)の場合－－－－－SEPARABLE(p, q, x, y, x0, y0) または SEPARABLE_GEN(p, q, x, y, c)なので、
p（x）=1/sqrt（1－x^2）、q（y）=±1、として、一般解を求める場合は、 SEPARABLE_GEN(p, q, x, y, c)を使うと、
y=Asin（x）＋c、または、y=－Asin（x）＋c、が得られる。
ここで、Asin（x）は、逆正弦関数、cは、任意定数よ」
「実際問題としては、初期値が数値ならば、正負の符号のいずれかの解を選択すればよいので、場合を分けても差し支えはない。
一方、より簡潔に表すために、xをyの関数とみて、x=sin（y+d）、dは、任意定数、と書き表しても、よいこともわかるじゃろう。
証明は、両辺をyで微分して、dx/dy=cos（y+d） より、dy/dx=1/cos（y+d） となるので、
方程式の左辺は、（1－x^2）y'^2－1=（1－sin2（y+d））/cos2（y+d）－1=0となって満たされていることが分かる。
すなわち、x=sin（y+d）も方程式を満足する解の表現じゃ」
「なるほど。
y=Asin（x）＋c から、y－c=Asin（x）なので、sin（y－c）=x
一方、y=－Asin（x）＋c からは、x=－sin（y－c）となるけど、c=c'+πとすれば、x=sin（y－c'）、となるので、
どちらも、一つの式、x=sin（y+d）、で表せるってことか」
「上のように、解に任意定数が含まれているものを「一般解」と呼んでおる。
また、一般解の任意定数が特定の値をとった解を「特殊解」または「特解」と呼ぶことは、知っておるじゃろう」
「そうだったわね。
方程式によっては、一般解に含まれない解があるんじゃなかった？」
「いつもあるわけではないが、特異解といって、一般解に含まれない解があることがある。
ああ、それから、任意定数じゃが、「任意」とはいうものの、本当にどんな値でも許されるかというと、そうではない。
解が成り立つ上での制限がある場合があるからの」
「y×y'＋x=0 のような場合ね。
SEPARABLE(x, －1/y, x, y, c)と解くと、y^2=－x^2－2c、移項して、
すなわち、x^2+y^2=－2c、という一般解が得られるんだけど、右辺の「任意」定数cは、ここでは負でないと、右辺全体が正とならないものね」
「そういうことじゃ。
なお、ちょうどよい例なので、一言注意しておくが、 y×y'＋x=0 は、y=0、では、意味がない。
しかし、だからといって、一般解の条件として、y<>0、を付けるかというと、通常は、そうせずに、解の意味を拡張して、x^2+y^2=定数、を一般解と言っている。
これは、木村先生の本で、説明されていることじゃ」
目次に戻る
線形微分方程式
「y'＋p（x）y=q（x）のように、yとy'について、線形の常微分方程式のための関数がDERIVEには、用意されておる。
線形常微分方程式は、正規形じゃ」
「第32回から引用すると、LINEAR1(p, q, x, y, x0, y0) または LINEAR1_GEN(p, q, x, y, c)を使えばいいことになるわね。
前節の例で確かめてみると、y'－1/√（1－x^2）=0、から、p（x）=0、q（x）=1/√（1－x^2）、なので、
LINEAR1_GEN(0,1/sqrt(1－x^2),x,y,c)＝ASIN（x）+c、同一の解が求められた」
「上の線形微分方程式で、特に、q（x）=0、すなわち、y'＋p（x）y=0、を元の方程式に属する（=随伴）同次線形微分方程式と呼んでいる。
この同次線形微分方程式は、変数分離型であるので、解を得ることができる。
その特解を、φ（x）と書くと、定数×φ（x）も、また、同次線形微分方程式の解となる。このとき、y'＋p（x）y=q（x）の一つの解をψ（x）とすると、
y'＋p（x）y=q（x）の一般解は、定数×φ（x）＋ψ（x）であることが知られている」
「逆に、ψ（x）が不明なときに、（たいていはこっちなんだけど）、定数をz（x）と置いて、y（x）=z（x）φ（x）を、同次でない方程式の解の候補として計算する方法を「定数変化法」というのだったわね」
「よう覚えておるな。
この定数係数法は、高階の線形微分方程式にも使える方法じゃ。
もっとも、2階以上の高階の場合は、同次方程式の解を求める段階で、すでに困難があるがの。
木村先生の本から、一つの例題を解いてみよう。
y'＋y×cos（x）=exp（－sin（x））、じゃ」
「DERIVEのユーティリティーファイルの利用については、前に書いたことがあるので、ダブルけど、ここで、ちょっと説明しておくよ。
ファイルメニューから「開く」あるいは、「読み込み」で、C:\program Files （x86）\TI Education\DERIVE
6\Mathフォルダ内の
「FirstOrderODE.mth」を利用すると、画面上で各関数の名前と引数がズラーっと表示されるので結構煩わしい場合もあるの。
なので、関数の名称等が分かっている場合は、ファイルから「読み込み」でユーティリティフォルダから読み込めば、画面上には、現れないのね。（メモリーには読み込まれているけどね）
さて、問題の方程式の左辺を 0とする、同次方程式の解は、y'=－cos（x）y、から、
y'＝p(x)q(y)の場合の SEPARABLE_GEN(p, q, x, y, c)を使って、p（x）=－cos（x）、q（y）=y、として、計算させると、
y=const×exp（－sin（x））となる。
非同次方程式の解は、y=z（x）×exp（－sin（x））を代入・整理すると、z'－1=0が得られるので、これから、z（x）=x、
よって、一般解は、y（x）=（x+c）×exp（－sin（x））と求められる」
「そのとおりじゃな。
DERIVEのy'＋p（x）y=q（x）の場合の LINEAR1_GEN(p, q, x, y, c)を使って確認してみよう。
この関数を使う場合は、p（x）=cos（x）、q（x）=exp（－sin（x））なので、
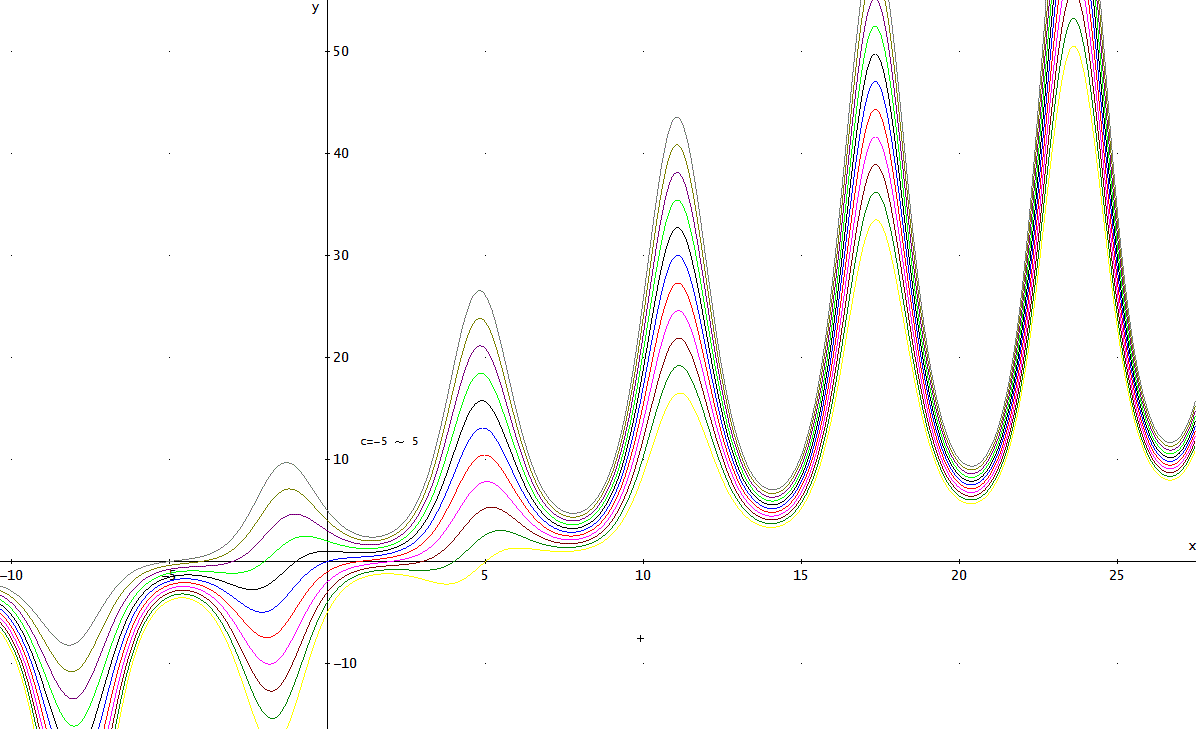
これより直ちに、y=exp（－sin（x））×（x+c）を得ることができる。
グラフは、c=－5～5まで、１ずつ変化させて描いてみると下図のようになる」
目次に戻る
同次形（y'=r（y/x））
「この節で出てくる「同次」というのは、y'=r（x,y）のときに、r（x,y）が（y/x）のみの関数である場合じゃ。
前節の線形微分方程式で出てきた「同次」とは、少し意味が違うので、注意してほしい。この場合も、正規形となる」
「木村先生の本の問題の中に、（3x^2+y^2）y'－2xy=0、という例が出ているわね。
y/x=uと置いてみると、y=xu から、両辺をxで微分して、y'=u＋x×du/dx。
一方、方程式の両辺をx^2で除して、uとxを使って変形すると、（3+u^2）（u+xu'）－2u=0 となり、整理して、
u'=du/dx=－（1/x）×（u（u^2+1）/（u^2+3））、となるので、SEPARABLE_GEN(p, q, x, y, c)を使うと、
LN（u^2+1）－3LN（u）=LN（x）－c、が得られる。
u=y/xを代入して、LN((x^2 + y^2)/x^2) － 3LN(y/x) = LN(x) － c、となるが、
DERIVEでは、これから先がキレイに変形出来ないけど、手作業では、LN（（x^2+y^2）/y^3）=－c と変形できるので、
結局、一般解は、x^2+y^2=c×y^3」
「DERIVEの同次形の1階常微分方程式に対する定義済み関数は、
y'＝r（x，y）の場合－－－－－HOMOGENEOUS(r, x, y, x0, y0) または HOMOGENEOUS_GEN(r, x, y, c)となるので、
HOMOGENEOUS_GEN(2xy/(3x^2 + y^2), x, y, c)を使うと、
LN((x^2 + y^2)/x^2) － 3LN(y/x) = LN(x) + c、となって、ともちゃんが計算してくれたものと同様の結果となることが分かる」
「三角関数の場合もそうなんだけど、対数関数も、DERIVEでは、キレイに変形してくれないわね」
「オプションメニューのモード設定で、式変形タブの対数関数の項目の「Auto」を「Collect」に一時的に変えることで、効果がある場合もあるがの。
今回も、 LN(x^3/(x^2 + y^2)) ＋ LN(y^3/x^3) = －c、までは、変形出来るがな。ここから先は、自動的にはならんの」
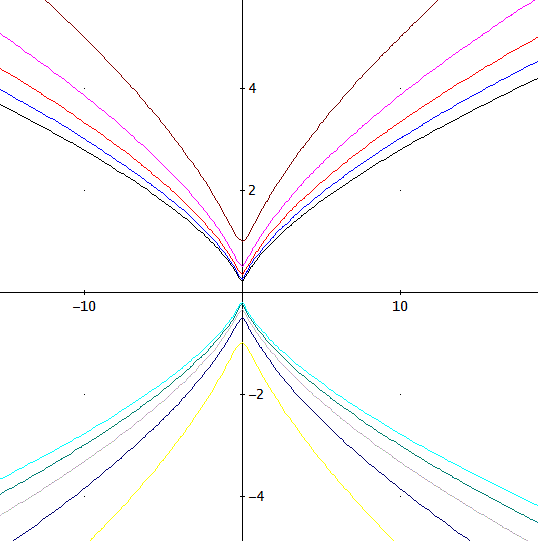
「ザンネン。
グラフは、こんな感じ。c=－5～5まで」
目次に戻る
求積法
「1階常微分方程式の解法をここまで進めてきたが、これまでの方法で求められる解は、みな、厳密解じゃ。
実際のところ、微分方程式でなくても、何らかの方程式で、その厳密解が求められる場合は、少ない。1階常微分方程式も例外ではない。
常微分方程式の厳密解は、通常、積分を1回以上使う必要がある。このため、このような解法を伝統的に、「求積法」と呼んでおる」
「求積法って、なんか、ギリシャ時代っぽい名前！」
「ギリシャ時代の数学では、図形の面積や体積を求めること、すなわち、「求積」は、大きなテーマじゃった。
今から見返せば、それらは、区分求積法～定積分の系譜につながっているのじゃがな。
当時、当然ながら、求積は、微分の逆演算とはとらえられていない時代じゃったから、ともちゃんの言う「求積法って、むかし！」、みたいな気分も分からなくはない。
純粋の「求積法」以外の解法としては、すでに出てきた「演算子法」（代表例は「ラプラス変換法」、「フーリエ変換法」など）、がある。
また、べき級数に展開する方法、「変分法」により、解の近似関数を構成する方法や数値解法もある。
高階の場合でも、1階の連立常微分方程式に帰着できるので、1階の常微分方程式の数値解法は、大切じゃ。
数値解法では、方程式内のパラメーターを数値で与えないといかんが、今や、数値解法なくして、現代の生活が成り立たないことは、自明じゃろう。
しかし、（電子式）コンピューターが発明される以前は、アナログ型計算機、手回し計算機などを使うしかなかったから、実用的な規模、安価なコストで、かつ、素早く、行うことは、難しかった。「電子式」コンピューターは、「合理的と云うこと（2013年7月のご挨拶）」の射撃表の節に書いたように第2次大戦前後に、発明されたがな」
「えーと、話が脱線しそうなので、軌道修正、軌道修正と。
ラプラス変換では、y、y'について、線形で、かつ、その係数が定数である必要があるんじゃない？」
「基本的には、その通りじゃ。
ただ、yやy'の係数が変数の場合でも特別なケースは、像空間における常微分方程式になるので、そちらが解ける場合もある」
目次に戻る
ラプラス変換法
「ラプラス変換法の話が出てので、それによる解法も掲げておこう。
1階の線形、かつ、定数係数の場合じゃ。あらためて、記載するほどでもないがの。
ここでは、変数をtで、像空間の変数をsで表す。（t>=0）
y'（t）＋a*y（t）=f（t）、ここで、aは定数。このとき、y（t）→Y（s）、f（t）→F（s）で、ラプラス変換後の関数を表すと、
（s＋a）Y（s）=y（0）＋F（s）、から、Y（s）=y（0）/（s+a）＋F（s）/（s+a）、となる。
ここで、原空間に移すと、第1項は、y（0）exp（－at）となるが、問題は第2項じゃ。
ラプラス変換では、f（t）とg（t）のたたみ込み積分=∫f（ξ）g（t－ξ）dξは、像空間で、通常の積 F（s）×G（s）で表されるので、
F（s）→f（t）、G（s）=1/（s+a）→exp（－at）と考えれば、第2項の、F（s）/（s+a）→∫（f（ξ）exp（－a（t－ξ））dξ、
整理すると、第2項 F（s）/（s+a）→exp（－at）×∫f（ξ）exp（aξ）dξ、以上をまとめて、ξをtに変えておくと、
y（t）=y（0）exp（－at）＋exp（－at）×∫f（t）exp（at）dt、となる。（※）」
「なるほど。
右辺第1項は、同次方程式の一般解、第2項は、非同次方程式の特解なのね」
「そういうことじゃ。
y（0）は、t=0のときのy（t）の値じゃが、一般解を求めたい場合やt=0以外の値で決めたい場合は、任意定数 c とおいてもよい。
たとえば、y'+y=t^2、では、ただちに、
y（t）=c*exp（－t）＋t^2－2t＋2、と求められる」
「だけど、定数係数の線形方程式に限るわけね」
「方程式がyとy'についての一次式の積に分解される場合にも利用できる。
y'^2＋yy'－2y^2＋y'－y=0 は、（y'－y）（y'＋2y＋1）=0と分解が可能じゃ。
このとき、y'－y=0、または、y'+2y+1=0 の解を一般解とすることができる。なお、任意定数は、複数必要はなく、1つとなる。
この例では、1番目の方程式から、y=c*exp（x）、2番目の方程式から、y=c*exp（－2x）－1/2、が得られる。cは任意定数。
線形方程式で変数係数の場合の例は、2階常微分方程式の際に取り上げよう」
※ラプラス変換については、以前にもご紹介した（「演算子法」：近藤次郎著：培風館：1970年）をご参照ください。
なお、新しい本としては、「ラプラス変換（数学のかんどころ13）」：國分雅敏著：共立出版：2012年7月、が分かりやすいでしょう。
ただ、後者は、初学者向けに易しく書かれていますが、ラプラス変換・逆変換表の分量は、前者に比して、かなり少なめです。
目次に戻る
ベルヌイ（ベルヌーイ）の微分方程式
「また、ベルヌイさんにお目にかかりましたね。
第52回の「数値積分（1）（台形公式とベルヌイ数）」などで、何度も現れているもの」
「まったくじゃな。
ベルヌイ（ベルヌーイ）の微分方程式と呼ばれているのは、
y' + p(x)y = q(x)y^k、ここで、kは、0、1でない、という形式じゃから、やはり正規形となる」
「k=0のときは、線形微分方程式だから問題なし。
また、k=1のときは、移項すると、y'＋（p（x）－q（x））y=0、となって、同次線形微分方程式であるので、こちらもOKね」
「そこで、以下では、kが0、1でないものとして、両辺をy^kで除すと、y'×y^（－k）＋p（x）y^（1－k）=q（x）、
ここで、z（x）=y^（1－k）とおくと、dz/dx=（1－k）y^（－k）×y'であることから、
z'（x）＋（1－k）p（x）z（x）=（1－k）q（x）、と変形することができる。
これは、z（x）に対する線形微分方程式となるため、これまでの方法で解ける」
「なるほど。
木村先生の本のそこんところの例題では、y'＋2xy=2x^3×y^3、が載っている。
これは、k=3の例で、p（x）=2x、q（x）=2x^3、なので、z（x）に対する方程式は、z'（x）－2×2x×z（x）=－2×2x^3、
整理すると、z'－4xz=－4x^3、となる。
y'＋P（x）y=Q（x）の場合の LINEAR1_GEN(P, Q, x, y, c)を使うと、
z = ce^(2x^2) + (2x^2 + 1)/2、と求められるので、z=1/y^2、から、えい、符号が面倒な！」
「無理にyを陽にあらわさんと。
1/y^2=c*exp(2x^2) + (2x^2 + 1)/2 を一般解とすればええんやで」
「おじさん、急に大阪弁にならないでくださいね。（こうも暑いとおかしくなってくるのとちゃうやろな？）
c=0、c=1、の場合のグラフを描いてみたよ。
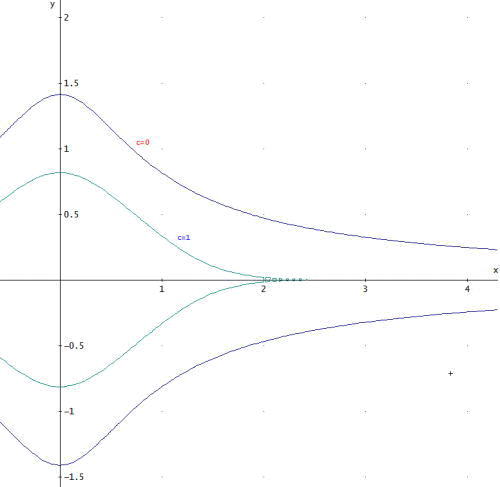
c=－1は、右辺がマイナスになってしまうので、yが実数でなくなる。
c>=0ならば、xのすべての値でyが実数解を持つけど、－1/2＜c＜0 の値をとる場合は、
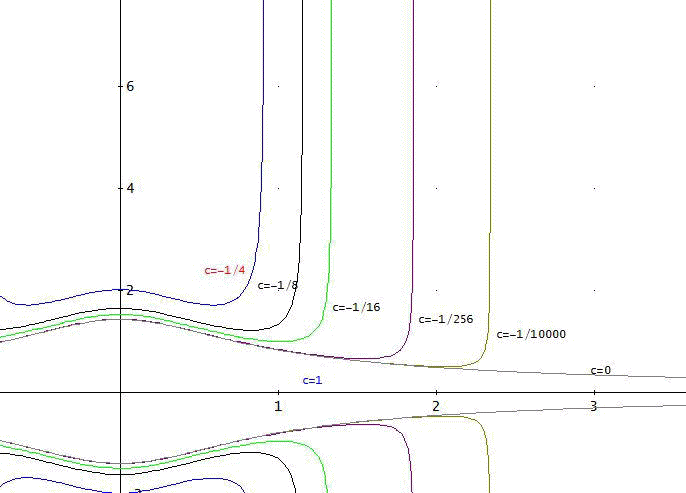
のように、c=－1/4、－1/8、－1/16、－1/256、－1/10000、と描いてみたけど、
cが負数の場合は、c>=0とは、劇的に様子が違うのには、ビックリ」
「なるほど。
これを見ても、任意定数は、任意ではない、ことが分かるのう。
さて、DERIVEの、ベルヌイの微分方程式 y' + p(x)y = q(x)y^k のための専用関数が、こちらじゃな。
BERNOULLI_ODE(p, q, k, x, y, x0, y0) またはBERNOULLI_ODE_GEN(p, q, k, x, y, c) 。
一般解を得る場合は、BERNOULLI_ODE_GEN(2x, 2x^3, 3, x, y, c)、の方から、
1/y^2 = ce^(2x^2) + (2x^2 + 1)/2、をただちに得ることができる」
目次に戻る
完全微分方程式（1）
「はじめに述べたように、y'=r（x,y）のように書くことができるものを正規形と呼んでいる。
正規形は、これまで、いくつかの解法を記載してきた。変数分離型のように直ちに解が求められるものもあったが、アイデアが必要なものもある。
この節では、ある意味で、万能の方法について調べて見よう」
「方程式を解くためのアイデアって、幾何の場合の補助線のようね。
確かに、言われれば、それって、ポイント高いって思うけど、いったいどこから、それを思いついたの？、と考えちゃう」
「その点は、同感じゃのう。いわば、天下り式じゃからな。
その芽は、すでに2次方程式の解法で現れておる。
ax^2＋bx＋c=0、において、x=z－b/2a と変換すると、1次の項が消去されて、平方完成ができる」
「ホント。
もっとも、そのアイデアも4次方程式止まりかと思っていたけど、第68回の「方程式の数値解法（3）（解の重心と範囲、DKA法）」で、5次以上のn次方程式の場合も、n－1次の項が消去されるだけでなく、まさか、それが、すべての根（解）の重心位置を与えていると知って驚いたよ」
「ま、こういったものは、多分に歴史的なものがあるじゃろう。
過去に、だれかが、うまいアイデアを思いついた場合、時間の早い、遅いはあっても、いずれ全体で共有されることになる。
最初は、それが天啓的な思いつきで、孤立したものでも、次第に体系化（一般化）されていくのが常じゃ。
幾何の補助線が、デカルトの解析幾何学にその主役の地位を譲ったようにな。
さて、1階の正規形の常微分方程式は、必ず、p（x,y）dx＋q（x,y）dy=0、の形に書き直すことができる。
なぜなら、もし、その方程式の解が r（x,y）=0、であることが分かれば、r（x,y）=0の両辺をxで微分することにより、
∂（r,x）＋∂（r,y）×dy/dx=0となるので、∂（r,x）dx＋∂（r,y）dy=0と書き直せるのでな。
これは、p（x,y）=∂（r,x）、q（x,y）=∂（r,y）とおけば、p（x,y）dx＋q（x,y）dy=0となる」
「えーと、早速の質問だけど、それって、1階の常微分方程式には、必ず、解があることを前提としているよね？」
「そうじゃ。
難しく言うと、「解の存在定理」の一つじゃな。
木村先生の本の最後の方に記載されているがの。ここでは、略していこう。
まあ、変数、関数として許される範囲内で、1階の常微分方程式には、解があるものとして話を進めよう」
「一応、よしとしましょうか。
じゃ、もう一つ、質問なんだけど、y'=r（x,y）をわざわざ、p（x,y）dx＋q（x,y）dy=0、と書き直すご利益は、なんなのでしょう？」
「久々に「ゴリヤク」登場やな。
目下、それを説明しようとしているがな。p（x,y）dx＋q（x,y）dy=0、
この表現には、不定性が含まれていることに注意する必要がある。
当たり前なんじゃが、y'=r（x,y）=－∂（r,x）/∂（r,y）=－p/q、であるため、p（x,y）、q（x,y）は、互いに独立ではないのじゃ。
普通、y'=r（x,y）と表現されている場合、λ（x,y）を任意関数として、両辺に掛けて、わざわざ、λ（x,y）y'=λ（x,y）r（x,y）、というような変形はしない。
それこそ、ご利益が薄い。
しかし、p（x,y）dx＋q（x,y）dy=0、という表現の場合、両辺に、関数、λ（x,y）を掛けた式、
λ（x,y）×p（x,y）dx＋λ（x,y）×q（x,y）dy=0、は、元の方程式と等価でも、解法としては異る場合があり得る。
この意味は、後に説明しよう。
さて、そもそも、p（x,y）dx＋q（x,y）dy=0、と書き直しただけでは、「完全微分方程式」とは限らない。
p（x,y）、q（x,y）がある条件を満たす場合のみ、「完全微分方程式」と呼ばれるのじゃ。
一方、条件を満たさないものも、微分方程式であることに違いはない（不完全微分方程式とは呼ばんようじゃな）。
今、その条件を求めるために、φ=φ（x,y）を考えると、その全微分dφは、dφ=∂（φ,x）dx＋∂（φ,y）dy、となるが、
これが上記の方程式と等しいとき、すなわち、p（x,y）=∂（φ,x）、q（x,y）=∂（φ,y）の場合のみを完全微分方程式という。
もし、そのようなφ（x,y）があれば、完全微分方程式の一般解は、φ（x,y）=c、ここで、cは、任意定数と書ける」
「つまり、p（x,y）dx＋q（x,y）dy=0の表現は、全微分が存在しているという意味とは限らない、ってことね。
そこは、なるほど、ガッテンですが、そもそも、そのφ（x,y）があるかどうかをどうやって見つけるのかしら？」
「完全微分方程式の条件を求めよう。
定義から、p（x,y）=∂（φ,x）が成り立つので、両辺をyで偏微分すると、∂（p（x,y）,y）=∂（∂（φ,x）,y）、
同様に、q（x,y）=∂（φ,y）から、両辺をxで偏微分すると、∂（q（x,y）,x）=∂（∂（φ,y）,x）、
偏微分の順序を入れ替えることが可能と仮定すると、2つの式の右辺が等しいので、
∂（p（x,y）,y）=∂（q（x,y）,x） が得られる。これが完全微分方程式の必要条件じゃ。
逆に、∂（p（x,y）,y）=∂（q（x,y）,x） が成り立つ場合は、p（x,y）=∂（φ,x）、q（x,y）=∂（φ,y）なる関数φ（x,y）が存在することが証明できる」
「例として、変数分離型の線形方程式、g（y）y'=f（x）は、f（x）dx－g（y）dy=0、と書き換えられるので、
∂（f（x）,y）=0、∂（－g（y）,x）=0、であり、両者が等しいので、これは、完全微分方程式ね」
「このとき、第1項から、φ=∫f（x）dx＋ψ（y）、これをyで微分したもの∂（ψ,x）が －g（y）と等しいので、
ψ'（y）=－g（y）、よって、ψ=－∫g（y）dy、
ゆえに、φ=∫f（x）dx－∫g（y）dy、そして、これをcと置けば、∫f（x）dx－∫g（y）dy=c、と一般解を書くことができる。
ともちゃんが挙げてくれた例で、少し、注意しておくと、具体的にf（x）=x^2＋1、g（y）=1であれば、
（x^2+1）dx－dy=0、一般解は、（x^3/3+x）－y=c、となる。
ところが、（x^2+1）dx－dy=0の両辺に、たとえば、exp（x）を掛けたもの、（x^2+1）exp（x）dx－exp（x）dy=0、を考えると、
この方程式は、もはや、完全微分方程式ではない。
なぜならば、∂（x^2+1）exp（x）,y）=0、∂（－exp（x）,x）=－exp（x）、となり、この右辺は、等しくないからじゃ」
「そうか、完全微分方程式、∂（φ,x）dx＋∂（φ,y）dy=0、では、ただちに、∫（φ,x）dx＋∫（φ,y）dy=c、と書けるということね。
このとき、∫（φ,x）dxでは、yは、定数のように考えて、xのみで積分する。∫（φ,y）dyも同様」
「そうとは限らないのじゃ！
木村先生の本の例で説明しよう。
（2xy+6x）dx＋（x^2－1）dy=0、これは、p=2xy+6x、q=x^2－1、として、
∂（p,y）=2x、∂（q,x）=2x、であるから、これは完全微分方程式じゃ。
∂（φ,x）=p=2xy+6x、∂（φ,y）=q=x^2－1、から、ともちゃん流に計算すると、
∫（2xy+6x）dx＋∫（x^2－1）dy=c、となるので、x^2y＋3x^2＋x^2y－y=c、から、一般解は、（2x^2－1）y＋3x^2=c、となる。
ところが、正解は、LINEAR1_GEN(2x/(x^2 － 1), － 6x/(x^2 － 1), x, y, c)、から、y = （3x^2 － c)/(1 － x^2)、
よって、（x^2－1）y＋3x^2=c。つまり、ともちゃん流の計算は、間違っているのじゃ」
「えぇ！。なんで、なんで。
まあ、確かに、正解は、φ=x^2y＋3x^2－y、の方だけども」
「φ（x,y）=∫（2xy+6x）dx=x^2y＋3x^2＋ψ（y）としなければ、ならないのじゃよ。
これから、∂（φ,y）=q=x^2－1から、x^2＋ψ'（y）=x^2－1、となり、ψ（y）=－y がわかるので、
φ（x,y）=x^2y＋3x^2－y、とすべきなのじゃな」
「う～ん。
じゃ、φ（x,y）=∫（x^2－1）dy=x^2y－y＋ψ（x）と計算して、
∂（φ,x）=p から、2xy＋ψ'（x）=2xy+6x、から、ψ（x）=3x^2、として、
φ（x,y）=x^2y－y＋3x^2、と計算してもよいわけね。
なるほど。こうしても正しい結果になる。でも、なんとなく納得がいかないなあ」
「では、もう少し、説明しよう。
完全微分方程式では、φ（x,y）=∫p（x,y）dx＋ψ（y）、であるので、q=∂（φ,y）=∂（∫p（x,y）dx,y）＋ψ'（y）、じゃな。
従って、ψ（y）=∫（q（x,y）－∂（∫p（x,y）dx,y））dy、となるので、
φ（x,y）=∫p（x,y）dx＋∫（q（x,y）－∂（∫p（x,y）dx,y））dy、
すなわち、φ（x,y）=∫p（x,y）dx＋∫q（x,y）dy－∫（∂（∫p（x,y）dx,y））dy、となり、
ともちゃん流の計算とは、第3項があるのが、異なる点じゃ。
従って、方程式によっては、∫（∂（∫p（x,y）dx,y））dy=0となることもあり、その場合に限り、どちらも同じ結果となる。
第3項 ∫（∂（∫p（x,y）dx,y））dy、は、たとえば、∂（p（x,y）,y）=0ならば、ゼロとなる。あるいは、∂（q（x,y）,x）=0、も同様。
従って、（2xy+6x）dx＋（x^2－1）dy=0、p=2xy+6x、q=x^2－1、の例では、
∂（2xy+6x,y）=2x、となり、ゼロではないため、ともちゃん流の計算は違っていた。
一方、最初の例題、（x^2+1）dx－dy=0、このときは、p=x^2+1、q=－1、なので、∂（p,y）=0となる例で、
第3項の寄与がなく、φ（x,y）=∫p（x,y）dx＋∫q（x,y）dyと計算しても、結果は、正しかったということじゃ」
「つまり、p（x,Y）が、xのみの関数、または、q（x,y）が、yのみの関数というケースね。
ここで、遅くなっちゃったけど、DERIVEの完全微分方程式の関数を紹介するわよ。
p(x, y) + q(x, y)y' = 0、－－－ EXACT(p, q, x, y, x0, y0) または EXACT_GEN(p, q, x, y, c)
上に掲げている、 （2xy+6x）dx＋（x^2－1）dy=0、では、EXACT_GEN(2xy + 6x, x^2 － 1, x, y, c)、として、
直ちに、y(x^2 － 1) + 3x^2 = c、と正解を得ることができるわよ」
目次に戻る
完全微分方程式（2）
「必ずしも完全微分方程式ではない、1階の常微分方程式、p（x,y）dx＋q（x,y）dy=0 を取り上げる。
z=0のxy平面上に、この方程式の解が、解曲線として存在するものとする。
なお、xy平面上で解曲線は、複数個が存在してもよいが、考えている始点Aから終点Bまでの曲線は、1本とする。
すなわち、途中で枝分かれする場合は、始点から終点までに分枝点等を含まないものとする。
さて、今、xy平面上のベクトル FをF≡［p（x,y）,q（x,y）,0］と定義する。
こう定義すると、rot（F）=［0,0,∂（q,x）－∂（p,y）］となることが分かる」
「みなさん、DERIVEでは、ベクトルの回転は、rot（F）ではなくて、CURL（F）なの。
カールよ。思い出してくれたかな？
なるほど、rot（F）=0が、完全微分方程式の条件と同一となる訳ね」
「そうじゃ。
さて、解曲線を、u（x,y）=0、とすれば、∂（u,x）dx＋∂（u,y）dy=0、なので、
方程式 p（x,y）dx＋q（x,y）dy=0、のp（x,y）、q（x,y）とは、
λ（x,y）p（x,y）=∂（u,x）、λ（x,y）q（x,y）=∂（u,y）、の関係がある。
ここで、λ（x,y）は、ゼロでない関数。
ところで、解曲線の接線の傾きは、dy/dx=－∂（u,x）/∂（u,y）=－p/q、
また、F［p（x,y）,q（x,y）,0］の解曲線上における傾きは、xy面内では、q/pである。
これらから、解曲線とFとは、直交していることが分かる」
「えーと。
それは、完全微分方程式でない場合もそうなのかな？」
「そうじゃ。正規形では、y'=－p/q、なので、解曲線の接線は、F=［p,q,0］と直交することが、これからも容易に分かる」
「でも、完全微分方程式であれば、解曲線に沿って移動するときに、力Fが解曲線に垂直（F・dt=0）で、仕事をしないから、ポテンシャルを持つことは、分かるけど、完全でない方程式でも、解曲線にFが垂直というところが分からないわ」
「F・dt=0でも、Fが仕事をしないとは、即断できないぞ。解曲線との間に摩擦がないとしなければな。
つまり、完全微分方程式では、解曲線と質点との摩擦はなく、従って、Fは仕事をしない、完全でない方程式では、摩擦力が働くと考えればどうじゃろうかな。
もし、摩擦力が、摩擦係数（x,y）×Fに比例する大きさで、向きは接線方向に運動と逆向きに働くとすれば、スカラーポテンシャルで力を表すことはできない。
まあ、これは、一つのたとえだがの。
だから、方程式を摩擦係数（x,y）で割れば、完全微分方程式に変わるのではないかと考えられる。これについては、次節の「積分因数」で説明しよう。
さて、具体例で見てみよう。
例1 完全微分方程式 （2xy+6x）dx＋（x^2－1）dy=0の場合
一般解は、x^2y＋3x^2－y=c、となる。
下図は、c=1とした場合で、始点A（√3/3,0）、終点B（4/5,23/9）とする。
点AとBは、同一の解曲線上にある。
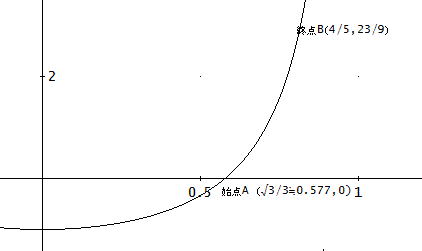
この方程式は、完全微分方程式なので、積分範囲を、AからBとすれば、どんな経路をたどっても、定積分∫F・dt=0となるはずである。
たとえば、Aから垂直にD（√3/3,23/9）まで行き、DからB（4/5,23/9）に行ったとすると、
∫F・dt=∫（A→D）（2xy+6x）dx＋（x^2－1）dy＋∫（D→B）（2xy+6x）dx＋（x^2－1）dy、
ここで、右辺第1項=∫（0～23/9）（（√3/3）^2－1）dy=－46/27、
同様に、右辺第2項=∫（√3/3～4/5）（2x×23/9+6x）dx=46/27、
よって、∫F・dt=－46/27＋46/27=0、
あるいは、AからBに直線で行った場合は、y = x(25√3/9 + 20/3) － 20√3/9 － 25/9、
∫F・dt=∫（√3/3～4/5）（2xy+6x）dx＋∫（√3/3～4/5）（x^2－1）y'dx、
右辺第1項=3496/2025 － 92√3/405、
右辺第2項=92√3/405 － 3496/2025、
よって、∫F・dt=3496/2025 － 92√3/405＋92√3/405 － 3496/2025=0、
例2 完全微分方程式でない方程式 （x－y）dx＋xdy=0の場合
この解は、y=c*x－x*ln（x）。解であることは、直接、代入して確認できる。
※本例は、y'=1－y/x、なので、同次方程式である。HOMOGENEOUS_GEN(－1＋y/x, x, y, c)として、
y = －xLN(x) － c*x、と解が求められる。この任意定数cを、－cと置き換えると、先の解と同一であることが分かる。
さて、c=1として、始点A（1/e,2/e）、終点B（e,0）とする。
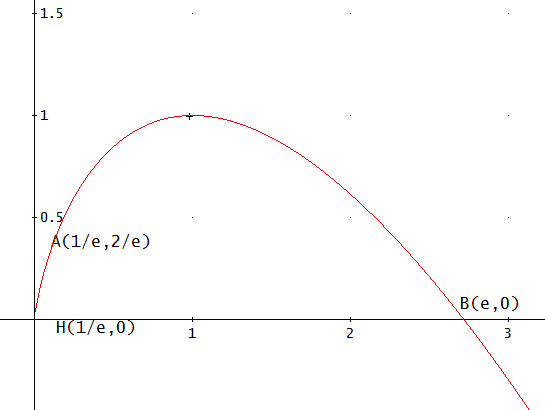
p（x）=x－y、q（x,y）=1、として、p（x,y）dx＋q（x,y）dy=（x－y）dx＋x×y'dx、
ここで、y=x－x*ln（x）、y'=－ln（x）、を使うと、
p（x,y）dx＋q（x,y）dy=（x－x＋x*ln（x））dx－x*ln（x）dx=0、となる。
すなわち、解曲線上では、p（x,y）dx＋q（x,y）dy=0、であることが確認できる。
従って、解曲線に沿った 線積分∫F・dt=0となる。
しかし、A（1/e,2/e）から垂線の足のH（（1/e,0）を通って、B（e,0）に行く経路では、
∫F・dt=∫（A～H）p（x,y）dx＋q（x,y）dy＋∫（H～B）p（x,y）dx＋q（x,y）dy、
右辺第1項=∫（2/e～0）（1/e）dy=2/（e^2）、
右辺第2項=∫（1/e～e）（x－0）dx=（1－e^4）/（2e^2）
よって、∫F・dt=5/（2e^2）－e^2/2≒－3.356189841・・、となり、ゼロとはならない。
また、AからBまで、直線、y=2x/(1 － e^2) + 2e/(e^2 － 1)、を通って行く場合は、
∫F・dt=∫（1/e～e）（x－y）dx＋xdy=∫（1/e～e）（x－y）dx＋xy'dx、
ここで、y=2x/(1 － e^2) + 2e/(e^2 － 1)、y'=2/(1 － e^2)、を使うと、
∫F・dt=∫（1/e～e）(x － 2e/(e^2 － 1)dx=e^2/2 － e^(－2)/2 － 2≒1.626860407、とこれもゼロとはならない。
このように、完全微分方程式でない場合に、解曲線以外を通ると、線積分∫F・dtは、ゼロとはならないことが分かる」
目次に戻る
完全微分方程式（3） 積分因数（積分因子）
「ふぅ。疲れたのう。
簡潔に書くと、p（x,y）dx＋q（x,y）dy=0が完全微分方程式でないとき、すなわち、∂（q,x）－∂（p,y）<>0のとき、
共通の関数λ（x,y）を掛けた方程式、λ（x,y）p（x,y）dx＋λ（x,y）q（x,y）dy=0、を考える。
※前節の摩擦係数のたとえでは、摩擦係数（x,y）f（x,y）dx＋摩擦係数（x,y）g（x,y）dy=0、でf（x,y）dx＋g（x,y）dy=0が完全微分方程式であるとすれば、見えている方程式のp,qとは、p=摩擦係数（x,y）f（x,y）、q=摩擦係数（x,y）g（x,y）となっていると考え、λ=1/摩擦係数（x,y）と見なすと同じ結果じゃ。
さて、閑話休題。
今は、この新しい、λ（x,y）p（x,y）dx＋λ（x,y）q（x,y）dy=0、に対して、
完全微分方程式となる条件は、∂（λq,x）=∂（λp,y）なので、整理すれば、
q∂（λ,x）－p∂（λ,y）＋λ（∂（q,x）－∂（p,y））=0、である。
このようなλが見つかれば、λ（x,y）p（x,y）dx＋λ（x,y）q（x,y）dy=0は、完全微分方程式となる。
関数λを「積分因数」（あるいは「積分因子」）と呼ぶのじゃ。
しかし、上記のλに関する方程式は、偏微分方程式なので、一般に、容易に解が見つからないがの」
「なるほど。摩擦係数のアナロジーならば、λの定数倍も、また、積分因数であるわね」
「それ以外には、λがxのみの関数である条件を求めると、qλ'（x）=λ（∂（p,y）－∂（q,x））なので、
λ'/λ=（∂（p,y）－∂（q,x））/q、となるが、左辺は、xのみの関数なので、
もし、右辺の（∂（p,y）－∂（q,x））/qがxのみの関数であれば、λ=exp（∫（（∂（p,y）－∂（q,x））/q）dx）は、積分因数となるのじゃ。
これは、木村先生の本にも書かれていることじゃ」
「そうすると、pとqを入れ替えて、（∂（q,x）－∂（p,y））/pがyだけの関数であれば、λ=exp（∫（（∂（q,x）－∂（p,y））/p）dy）が積分因数となるのね。
まあ、こんな風に考えると、任意の完全でない方程式 pdx＋qdy=0、から、積分因数を見いだすことは、一般には困難だけど、
逆に、λに様々な関数を仮定したときに、それを満たすp,qの関係を見いだすことはできるわ」
「確かにな。
木村先生の本でも、上記の2つ以外として、
・ （∂（q,x）－∂（p,y））/（xp－yq）が、xyのみの関数、ψ（xy）であれば、exp（∫ψ（xy）d（xy））は、積分因数である。
・ x^2（∂（q,x）－∂（p,y））/（xp＋yq）が、y/xのみの関数、ψ（y/x）であれば、exp（∫ψ（y/x）d（y/x））は、積分因数である。
・ x^j（Aydx＋Bxdy）＋y^k（Cydx＋Dxdy）=0、ただし、AD－BC<>0であれば、x^m×y^nは、積分因数である。
上の3番目を説明してごらん」
「え～と。
整理すると、p=（x^m×y^n）（Ayx^j＋Cy^（k+1））、q=（x^m×y^n）（Bx^（j+1）＋Dxy^k）、
これから、∂（q,x）－∂（p,y）を作り、ゼロと置けば、
x^(j + m)y^n(b(j + m + 1) － a(n + 1)) + x^my^(k + n)(d·(m + 1) － c(k +
n + 1)) = 0、を得る。
両辺をx^my^nで割ると、
x^j(b(j + m + 1) － a(n + 1)) + y^k(d(m + 1) － c(k + n + 1)) = 0、となる。
ここで、xとyの係数をゼロとするように、m,nを選択すると、
m = (A(Ck － D) + BC(j + 1))/(AD － BC)、
n = (AD － B(C(k + 1) + Dj))/(BC － AD)、
とすれば、可能。
なるほど、ここで、AD－BC<>0がものを言うのね」
「DERIVEでは、p(x, y) + q(x, y)y'＝0で、積分因数がx^m*y^nの形であるかどうかを調べる関数がある。
MONOMIAL_TEST(p, q, x, y)じゃ。x^m*y^nの形が存在する場合は、その積分因数を返す。
試しに、y^2（3ydx－6xdy）=x（ydx＋2xdy）の場合はと言うと、
（3y^3－xy）dx－（6xy^2+2x^2）dy=0、これは、DERIVEの記法では、p=3y^3－xy、q=－（6xy^2+2x^2）なので、
MONOMIAL_TEST(3y^3 － xy, － 6xy^2 － 2x^2, x, y)とすれば、1/(x^2y)を得ることができる。
この1/(x^2y)が積分因数となる。この積分因数を使って、
EXACT_GEN(p(x, y), q(x, y), x, y, c)から、LN(x) + 2LN(y) + 3y^2/x = －c、が解として求められる」
「木村先生の本の末尾の模範解答と違っているわ。
LN(x) + 2LN(y) + 3y^2/x = －cを変形しても、LN（xy^2）＋3y^2/x=－c、となって、
解答の 3y＋x^2×LN（xy^2）=cx^2、と少し違うもの」
「確かにな。
だが、LN(x) + 2LN(y) + 3y^2/x = －cは、（3y^3－xy）dx－（6xy^2+2x^2）dy=0を満たしている。
もし、その模範解答が正しいとすれば、逆に、問題が、（x^2y－6y^2）dx＋（2x^3＋3xy）dy=0、でないといけない。
変形すれば、x^2(ydx+2xdy)=3y(2ydx－xdy)の場合じゃのう。このときの積分因数は、1/（x^3y）となる」
目次に戻る
特殊な半線形微分方程式
「y'について、線形で、yについては、非線形のものを半線形（準線形）の方程式という。
これは、正規形の方程式となるが、特殊な係数を持つものには、DERIVEの関数が用意されておる」
「第32回の（7）で説明しているものだね」
「そうじゃ。今回見直ししたところ、第32回の（7）と（13）とが実は、同じ内容じゃったことに気がついた。
r(x, y)y' + p(x)b(y) = q(x)、ただし、（db/dy）／rは、yを含まないこととする。
ALMOST_LIN(r, b, p, q, x, y, x0, y0) または ALMOST_LIN_GEN (r, b, p, q, x, y, c)
（7）の例では、（2y+1）y'＋x^2（y^2+y）=x^2、を挙げている。
r（x,y）=2y+1、p（x）=x^2、b（y）=（y^2+y）、q（x）=x^2、なので、
db/dy=2y+1、より、（db/dy）/r（x,y）=1、となり、yを含まないので、一般解は、
ALMOST_LIN_GEN(r(x, y), b(y), p(x), q(x), x, y, c)、として、
y^2 + y = c×exp(－ x^3/3) + 1、ここで、cは、任意定数じゃ」
「一応、検算してみるね。
y^2 + y = c×exp(－ x^3/3) + 1、から、両辺をxで微分すると、
（2y+1）y'=－cx^2×exp（－x^3/3）、
これから、問題の方程式の左辺を計算すると、（2y+1）y'＋x^2（y^2+y）=－cx^2×exp（－x^3/3）＋x^2（y^2+y）、
ここで、（y^2+y）=c×exp(－ x^3/3) + 1を使うと、左辺=－cx^2×exp（－x^3/3）＋x^2（c×exp(－ x^3/3)
+ 1）=x^2、である。
これは、方程式の右辺のx^2と等しいので、正解！」
「方程式は、（2y+1）y'＋x^2（y^2+y）=x^2、であるが、w'（y）y'＋x^2w（y）=x^2、ここで、w（y）=y^2+y－1、と置いている。
変形すると、x^2wdx＋w'dy=0、すなわち、x^2dx＋（w'/w）dy=0、
最後の式を見ると、（w'/w）は、yのみの関数なので、変数分離形で、直ちに、x^3/3＋LN（w）=LN（c）、よって、w=c×exp（－x^3/3）、
これと、w（y）=y^2+y－1から、y^2+y－1=c×exp（－x^3/3）、の解が得られる」
「あとさ、今回の方程式は、正規形なので、x^2（y^2+y－1）dx＋（2y+1）dy=0、と書き直せる。
p（x,y）=x^2（y^2+y－1）、q（x,y）=（2y+1）、として、∂（q,x）=0、∂（p,y）=x^2（2y+1）、両者は等しくない。
従って、これは、完全でない方程式となるけど、完全微分方程式とするための積分因数はどうなってるのかな」
「これは、簡単じゃ。
x^2dx＋（w'/w）dy=0が変数分離型で、完全微分方程式なので、
x^2dx＋（（2y+1）/（y^2+y－1））dy=0、これと、元の方程式を比較すると、
積分因数λ=1/（y^2+y－1）となる。
実際に、∂（λp（x,y）,y）=0、∂（λq（x,y）,x）=0、なのでな」
目次に戻る
y'がxとyの1次式の関数
「 y'＝r（u）、ただし、u = px + qy + k、ここで、p、q、kは定数。
これは、正規形の方程式じゃ」
「第32回の（11）に出てくるものだね。
ここでは、y'=px+qy+k、として、DERIVEの関数では、
FUN_LIN_CCF(r, p, q, k, x, y, x0, y0) または FUN_LIN_CCF_GEN(r, p, q, k, x, y, c)
となるの。
FUN_LIN_CCF_GEN(px + qy + k, p, q, k, x, y, c)、から解は、
LN(pqx + q^2y + kq + p)/q = x + c、と得られる。yについて、整理すると、
y = exp(qx + cq)/q^2 － (pqx + kq + p)/q^2、 となる」
目次に戻る
y'がxとyの1次式の分数式の関数
「y'=r（（ax＋by＋d）/（px+qy+k））の形で、これも正規形の方程式じゃ。
ここでは、DERIVEの関数にならった記法を掲げているが、a,b,d,p,q,kは、すべて定数じゃ」
「第32回の（12）で説明しているものだね。
LIN_FRAC(r, a, b, d, p, q, k, x, y, x0, y0) または
LIN_FRAC_GEN(r, a, b, d, p, q, k, x, y, c) で解を求めることができる。
木村先生の本の例題の中から、一つ試してみると、
y'=2（（y+2）/（x+y+1））^2、は、
LIN_FRAC_GEN(2((y + 2)/(x + y + 1))^2, 0, 1, 2, 1, 1, 1, x, y, c)、として
2ATAN((y + 2)/(x － 1)) + LN((y + 2)/(x － 1) = － LN(x － 1) － c、が得られる。
整理すると、LN（y+2）＋2ATAN((y + 2)/(x － 1))=c、となって、これは、模範解答と一致している。
それと、前節で取り上げた、第32回の（11）のy'＝r（u）、ただし、u = px + qy + k、p、q、kは定数、に対する関数、
FUN_LIN_CCF(r, p, q, k, x, y, x0, y0) または FUN_LIN_CCF_GEN(r, p, q, k, x, y, c)が、
第32回での説明では、本節の関数に含まれているとしていたけど、今回のように、分母がない場合には、適用できないみたい」
「全く、その通りじゃった。
この場を借りて、お詫びして訂正いたします」
目次に戻る
ダランベール（ラグランジュ）の微分方程式
「正規形でない場合じゃ。
y=xf（y'）＋g（y'）のような形となる」
「木村先生の本にならって、ここでは、p=y'と書くと、y=xf（p）＋g（p）、
両辺をpで微分すると、左辺は、dy/dp=dy/dx×dx/dp=p×dx/dp、
一方、右辺は、dx/dp×f（p）＋xf'（p）＋g'（p）、
よって、p×dx/dp=dx/dp×f＋xf'＋g'、
これから、（f－p）dx/dp＋xf'＋g'=0、となる。
もし、f（p）－p<>0であれば、（dx/dp）＋（xf'＋g'）/（f－p）=0、
dx/dp＋xf'/（f－p）＋g'/（f－p）=0、
あるいは、dx/dp＋（f'/（f－p））x=－g'/（f－p）、と変形してみると、
関数xと変数pに関する線形微分方程式と見なすことができるので、これは、解ける。
yの方は、y=xf（y'）＋g（y'）の関係式に、xを代入すれば、OKね」
「そう、yをxの陽に表せなくても、pをパラメーターとして、xとyとの関係が得られれば、解とすることでもよい。
また、f（p）－p=0の場合は、pの根をp0とすれば、y=f（p0）x＋g（p0）が解となる。
ひとつ、簡単な例を出しておこう。
y=2xy'＋（y'）^2、じゃ」
「DERIVEの記法にならって、ここでは、v=y'と書くわよ。
例題は、y=2xv＋v^2、両辺をvで微分すると、v（dx/dv）=2x＋2v（dx/dv）＋2v、
vdx＋（2x＋2v）dv=0、これは、完全微分方程式ではないんだけど、積分因数として、vを掛けるの。
どうして分かったかというと、MONOMIAL_TEST関数を使うのよ。
v^2dx＋（2xv＋2v^2）dv=0、は、完全微分方程式である。
この解は、v^2×x＋2v^3/3=c、すなわち、x=c/v^2－2v/3、
従って、y=2xv＋v^2=2c/v－v^2/3、となる」
「検算をしておこう。
y'=dy/dx=（dy/dv）/（dx/dv）、の関係を使って、検算すると、確かに、合っているな。
一般解以外に、v=dy/dx=0の場合の、y=0も一応、解にはなる」
「DERIVEで、グラフを描かせたので、参考にしてくださいな。
c=0のときは、［x,y］=［－2t/3,－t^2/3］として、ただし、便宜的に、vをtで表している。
このときは、tを簡単に消去できて、y=－3x^2/4、という放物線となる。
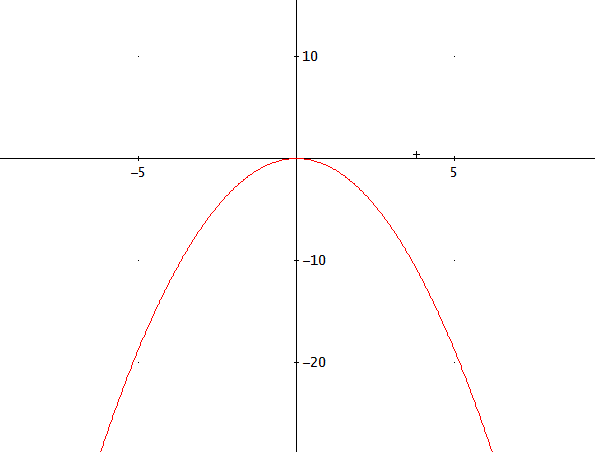
c=1のときは、［x,y］=［1/t^2 － 2t/3, 2/t － t^2/3]、ただし、便宜的に、vをtで表している。
簡単には、tを消去できないので、t=－10～10まで変化させて描画すると、下図のようになる。
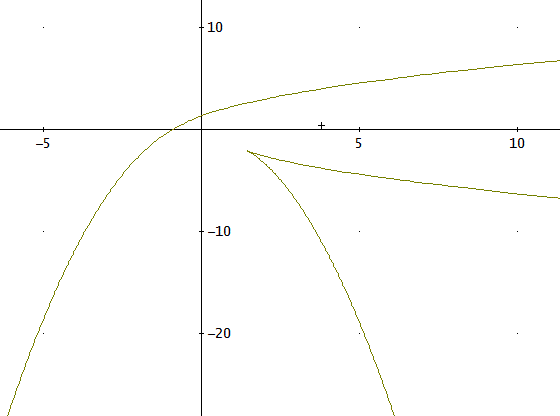
実は、tをxで表すと、3根があり、それに応じて、3つの分枝がyの側に現れる。
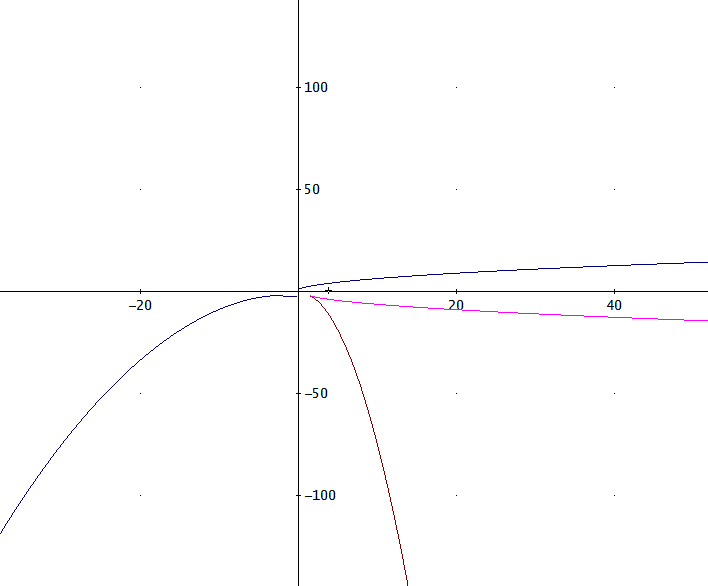
上図の色が異なる曲線がそれに対応している」
「任意定数cの値によっても、グラフは変化する。
ま、調べれば、おもしろいが、本題から外れてしまうので、この程度にしておこうかの」
目次に戻る
クレローの微分方程式
「アレクシス・クロード・ド・クレロー（Alexis Claude de Clairault）は、フランスの数学者（1713年－1765年）。（クレーローとも書くようである）
彼の名前で呼ばれている方程式は、p(x*v － y) = q(v)、ただし、v=y'（x）である。
クレローの微分方程式は、y'=v=g（x,y）のように一般には、表せないため、「非正規形」となる。
ただし、p、qが簡単な関数のときは、正規形となることもある。
クレローの微分方程式に対するDERIVEの関数は、CLAIRAUT(p, q, x, y, v, c)となる」
「木村先生の本では、y'をpと書いているので、混乱してしまいそうだけど、DERIVEでは、y'をvで書き記しているのね。
早速の例題だけど、y=xy'＋y'^2、は、DERIVE流の記法では、xv－y=－v^2、となるので、
CLAIRAUT(xv － y, － v^2, x, y, v, c)と入力すると、
結果は、ベクトルとして、[cx － y + c^2 = 0, x + 2v = 0]で返ってくる。
第1項は、yについて、y=cx＋c^2、第2項からは、v=y'=－x/2 が得られるので、さらに、y=－x^2/4 が出てくるけど、これが、「特異解」なんだな」
「クレローの微分方程式では、p(x*v － y) = q(v)の両辺をxで微分すると、
（v＋xv'－v）×p'（xv－y）=v'×q' から、（xp'（xv－y）－q'）v'=0 が得られる。
v'=0は、この方程式を満足するので、v=c（定数）を元の方程式に代入すると、p（cx－y）=q（c）となる。
この方程式は、xとyと任意定数cのみの関係式となっており、一般解である。
一方、v'がゼロでないときは、xp'（xv－y）－q'=0とp(x*v － y) = q(v)からvを消去して、xとyの関係式が得られる。
この後者が特異解となるんじゃな。
もっとも、vを消去しないでも、vをパラメーターと考えてもよい。
本題の場合は、p（cx－y）=q（c）からは、cx－y=－c^2なので、y=cx＋c^2 が出てくる。
また、xp'（xv－y）－q'=0 からは、p（α）=α、q（v）=－v^2、であることから、
x－（－2v）=0 となるため、v=－x/2 、これを p(x*v － y) = q(v)に代入すると、－x^2/2－y=－x^2/4、となるので、
y=－x^2/4が得られる。これが特異解となるわけじゃ」
「ベルヌイの微分方程式の場合と比較すると、技巧的ね。
一般解と特異解をグラフにしてみたよ。
下の図では、c=－5～5まで１つずつ変化させている」
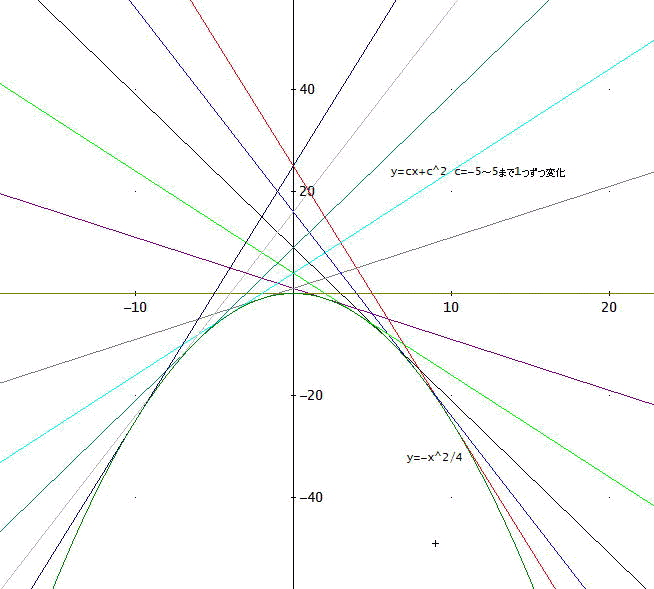
「特異解 y=－x^2/4が、一般解 y=cx＋c^2 の包絡線になっているのが分かるじゃろう。
次回は、数値解法を取り上げることにしよう。
いや、ともちゃんも、お疲れさんじゃった」
目次に戻る
最終更新日 2014/8/19 ：目次追加 2016/1/16
