数式処理ソフト DERIVE(デライブ) de ドライブ
71.1階常微分方程式の解法(3)(リッカチの微分方程式)
リッカチの微分方程式(1)
 「おじさん。今回は、微分方程式の数値解法の巻じゃなかったの?」
「おじさん。今回は、微分方程式の数値解法の巻じゃなかったの?」
「お、ともちゃんか。暑いところを、ご苦労さんじゃな。
数式処理ソフト DERIVE(デライブ)で、だんだんと、数値解法に移っていきたいが、その前に、「リッカチの微分方程式」を取り上げておくのを忘れていたからな。
y'+ay^2=b×x^m、ただし、a、b,mは、定数とする。
木村先生の「常微分方程式の解法」(木村俊房 著:培風館:昭和45年3月10日第13刷)によれば、リッカチの微分方程式(狭義)では、定数間にある関係が成立する際に限り、求積法で解ける、とある」
「ところで、リッカチさん、というのは、どこの国の人なんだろうね」
「J.F. Riccati氏は、イタリアの人じゃそうだ。
Wikipediaによると、1676年~1754年というから、活躍したのは、18世紀中頃ということになるのう。
手元の「数学・物理 100の方程式」(日本評論社:1989年)にも、「いろいろな初等微分方程式」の章に「リッカチの微分方程式」が紹介されている。
ただ、残念ながら、リッカチ氏本人については、どんな人なのかは、紹介されていない」
「木村先生の本では、y'+ay^2=b×x^m、は、狭い意味でのリッカチ型としているね」
「うん。その本でも紹介されておるが、今は、より一般化した、y'+P(x)y^2+Q(x)y+R(x)=0、を(一般)リッカチ型常微分方程式と呼んでおるそうじゃ。
しかし、ここでは、狭義のリッカチ型方程式を取り上げよう。
y^2の項があるため、「非線形方程式」じゃ。非線形ゆえに線形方程式のように解の重ね合わせができないなどの難点がある。
y'+ay^2=b×x^m、には、パラメーターが、a,b,m、と3つも入っているので、もう少し、すっきりとさせたい。
そこで、変数を、x=αt、と置いて、1/α×dy/dt+ay^2=b×(αt)^m、から、dy/dt+αay^2=α^(m+1)bt^m、
ここで、αa=1、として、α=1/a、dy/dt+y^2=a^(-(m+1))bt^m、
a^(-(m+1))b、を改めて、B=b/a^(m+1)、とおけば、
dy/dt+y^2=Bt^m、といくぶんかすっきりする」
「なるほど。
しかし、a<0のときに、a^(m+1)が虚数になる場合があるのじゃないの?」
「おっと、そうじゃったのう。
y'-a'y^2=bx^m、ここで、a'>0の場合じゃな。
そのときは、両辺に-1を掛けると、-y'+a'y^2=-bx^m、となるので、
あらためて、-yをYと書けば、Y'+a'Y^2=-bx^m、から、B=-b/a'^(m+1)、と考えれば、
dy/dt+y^2=Bt^m、でBを負に、yを-yに変えた場合と見なせばよいじゃろう」
「そうね。じゃ、mの正負はどういう影響があるのかしら、何か仮定しているの」
「う~ん。それは、根本的な点じゃな。
次節以降、m=ゼロ、正、負の場合を順次検討してみよう」
リッカチの微分方程式(2) m=0の場合
「m=0の場合は、dy/dt+y^2=B、じゃな。変数分離型であるので、
この解は、B>0では、SEPARABLE_GEN(1, B - y^2, t, y, c)、として、y=√B×(c+t+1)/(c+t-1)、と求められる。
y(0)>0から出発すると、t=0~∞で有界で常に正、かつ、単調に減少する解となる。
下図は、B=1でy(0)=3、(c=2)の場合のy(t)=(t+3)/(t+1)。
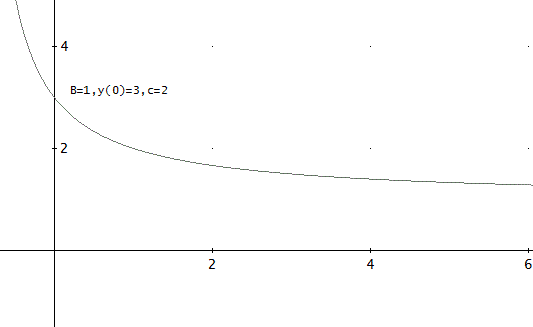
しかし、y(0)<0から出発すると、単調減少ではあるが、t=0から連続した変域は、1-cまで。
t=1-cで、y=-∞に発散してしまう。
下図は、B=1、y(0)=-1、(c=0)の場合のy(t)=(t+1)/(t-1)、
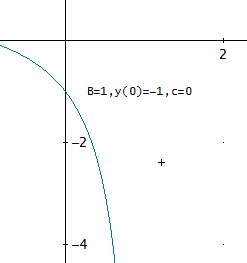
一方、B<0では、y = IF(- π/2 < √-B(c + t) < π/2, - √-B*TAN(√-B(c + t)))、
y(0)>0から出発しても、t=-cでゼロから負へと変化し、t=π/2-cで、y=-∞に発散する。
下図は、B=1、y(0)=1、(c=-π/4)、
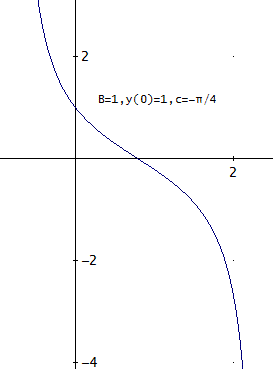
また、y(0)<0から出発したときは、常に負で、t=π/2-cで、y=-∞に発散するというのは同じじゃ。
ただし、解全体は、周期πをもつ、無数の分枝に分かれているので、yの値を指定するtによって、どの分枝に乗るかが決まるという状況であるな」
 「なるほど。
「なるほど。
m=0の場合に限れば、B>0、かつ、y(0)>0が自然な条件かもね」
リッカチの微分方程式(3) m>0の場合
 「じゃ、今度は、m>0の場合を考えてみるよ。dy/dt+y^2=Bt^m、ね。
「じゃ、今度は、m>0の場合を考えてみるよ。dy/dt+y^2=Bt^m、ね。
B>0のときは、y'(0)=-y(0)^2、なので、y(0)の正負にかかわらず、y'(0)<0となる。
一方、y'=Bt^m-y^2、で、B>0から、tの有限の値で、y'>0と逆転する可能性はある。
逆転した場合は、Bt^m-y^2=0、となるtは、1実根のみなので、y'が正となった後は、yは、そのまま単調に増大する。
この際、y^2=Bt^m-y'、であるから、y'>0となった後は、左辺は負になれないため、tの有限な値で発散する可能性もあると思うの。
しかし、y'=Bt^m-y^2、を見ると、右辺第1項のBt^mよりy^2の方が大きい状態のまま、y'<0を維持する可能性もあり得る。
ここは、Bとmによって、異なる可能性があるかもしれないわ。
B<0の場合はというと、y'=Bt^m-y^2、から、常にy'<0が維持され、いずれ、-∞に発散すると思う。
この際、y^2=Bt^m-y'、から、tが有限の値で発散するかt=∞の時になるのかは、断定できない」
「m>0の場合は、厳密解が簡単に求まらないからな。
後述の数値解法を使うと、ともちゃんが言ったように、y(0)>0から出発して、減少後に、上昇するケースがあることが分かった。
下図は、m=1、B=1、y(0)=3、の場合じゃ。
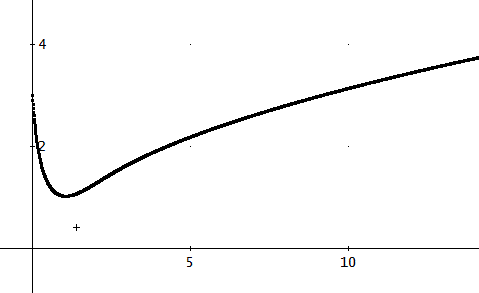
これは、数値解法の内で最も簡単なオイラー法を使ったものじゃ。(4次のルンゲ・クッタ法でも同様の結果になることを確認した)
数値解法は、DERIVEのユーティリティーファイル「ODEApproximation.mth」を開くか、読み込めば利用できる。
EULER_ODE(- y^2 + t, t, y, 0, 3, 0.01, 2000)、
初期値は、t=0でy=3、刻み幅 h=0.01、2000点を計算して、t=0~20までを追跡した」
「やったー!。すごい。
しかし、こんな簡単な方程式の厳密解が簡単に計算できないなんて、不思議!
y(0)<0から出発すると、どうなるかを試してみるよ。
m=1、B=1、初期値は、t=0でy=-3、刻み幅 h=0.01、としてt=0~20までを追跡してみた。
うへ-。やはり、yが急速に負の∞に発散しそう。計算が終わらないよ」
「4次のルンゲ・クッタ法で試してみた。
RK([- y^2 + t], [t, y], [0, -3], 0.01, 35)、
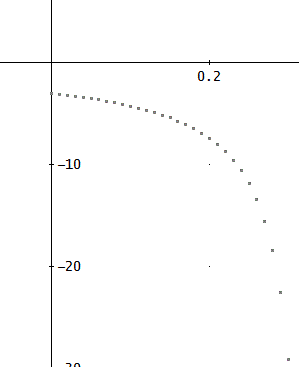
刻み幅を0.01として、t=0.35程度までは計算可能。
しかし、t=0.33で、y≒-214、が、t=0.34でy≒-3.6×10^5と急速に増大。
その後は、計算ができなくなっていたのじゃな」
「あらためて、m=1で、B=1、10、50、100と変化させて、数値計算をしてみたよ。
ルンゲ・クッタ法で、刻み幅は、0.01、DERIVEでは、RK([100t - y^2], [t, y], [0, -3], 0.01, 100)、と指定する。

「なるほど。
この図を見ると、Bが大きい(例:B=100)ときは、ともちゃんが言ったように、y(0)=-3から出発して、いったん、減少し、再び増加する解もあることが分かるのう」
リッカチの微分方程式(4) m<0の場合(1)
「m<0の場合。
(求積法で)解析的に解くという目的では、このm<0が本命というべきか。
実は、木村先生の本で説明されているように、リッカチの微分方程式では、m=-4k/(2k-1)、k=1,2,3・・の場合にのみ、求積法で厳密解が求められる。
m=-2でも求められるが、これは、上式で、k=+∞の場合と考えればよいということじゃな」
 「なんだー。すべて、mがマイナスの場合だけじゃないの。
「なんだー。すべて、mがマイナスの場合だけじゃないの。
m=0やm>0は、問題外だったのか」
「微分方程式として意味があるかどうかと、厳密解が得られるかどうかには、深い関係はないと思うのう。
m=0やm>0でも解は、ある。それは、大切な点じゃろう。
「岩波数学辞典」(第4版)によれば、1階の代数的微分方程式で、動く分岐点を持たないものは、初等関数で表されるもの以外は、リッカチの方程式か楕円関数の方程式に帰着できるそうじゃ。
また、2階の有理的微分方程式の場合は、19世紀末~に、ピカード、パンルヴェらにより研究されたそうじゃが、パンルヴェ氏は、これらは、6種類の方程式に分類できることを証明し、現在、「パンルヴェ方程式」と呼ばれているという」
「その有理的微分方程式って、代数的微分方程式とは、違うものなの?」
「1階の代数的微分方程式とは、F(x,y,y')=0、と書けるもので、係数がxの解析関数であるy、y'の多項式の場合を言うとのこと。
当然ながら、変数 x、関数 y とも、複素数まで拡張して考えているのじゃがな。
これが、有理的であれば、y'=P(x,y)/Q(x,y)と書ける。PとQは、係数が複素数のxとyの多項式じゃ。
なお、ここで、y'をyの代数関数と見たときの「種数」が0ならば、リッカチの方程式、1ならば、楕円関数を使って積分でき、1より大きければ、代数的に積分可能となるそうじゃ。
おっと、「種数」とは何か、などと、わしに聞かんで欲しいのう」
「聞きゃしませんよ。どうせ、分からないんでしょ。
そういえば、最初に出てきた、「数学・物理 100の方程式」にも「パンルヴェ方程式」の章があるわね。
P1からP6まで6個載っている。P6は、すっごい複雑な式だけど、P1は、y''=6y^2+x、とずいぶん簡単な形」
「たいていの関数は、1階または2階の常微分方程式を用いれば、定義できる。
そこで、19世紀末にパンルヴェ氏は、この6個の方程式で定義される関数が新しい超越関数であると「主張」したそうじゃ。
しかし、それを証明することはできなかった。1988年にP1について、それが肯定的に解決されるまで、すなわち、未解決じゃったそうだ」
「その「超越関数」というのは、方程式の解が超越数になるという意味なの?」
「超越関数とは、変数と関数とが複素係数の有限の項数の多項式で結びつけられているもの(=代数関数)ではない関数とのことじゃ。
だから、超越関数といえども、一般には、その方程式の解(根)がすべて「超越数」というわけではない。
これは、Sin(x)で、x=0を考えれば、分かる」
「どんな関数も、微分方程式で定義できるのかしら。
たしか、ガンマ関数は、できないって、聞いた気がしたけども」
「うん、そうじゃな。
Γ(x+1)=x×Γ(x)、と差分方程式で定義されるが、どのような代数的微分方程式の解にもならない、という変わり者じゃ。
ガンマ関数の定義などは、第59回の「数値積分(外伝:√t×sin(t)のラプラス変換とベッセル関数」の章で出てきている。
しかし、肝心のm<0の求積法で厳密解を求める方法を説明できておらん。
長くなってきたので、次節に回そう」
リッカチの微分方程式(5) m<0の場合(2)
「y'+y^2=Bt^m、ここで、m<0じゃ。
ところで、リッカチの方程式の1つの解が求められたとき、たとえば、それをφ(t)とすれば、
y=φ(t)+ψ(t)を作ると、φ'+ψ'+φ^2+2φψ+ψ^2=Bt^m、
ところが、φ'+φ^2=Bt^m、なので、ψ'+2φψ+ψ^2=0、から、
ψの満たす式は、ψ'+2φψ=-ψ^2、となる。
このψに関する方程式は、第70回で出てきた「ベルヌイ(ベルヌーイ)の微分方程式」なので、ψが(原理的に)求められる。
すなわち、ψ' + p(t)ψ = q(t)ψ^k、ここで、kは、0、1でないものをベルヌイの微分方程式と呼び、
DERIVEでは、BERNOULLI_ODE_GEN(p, q, k, t, ψ, c)、で一般解が求められる。
今回の場合は、p(t)=2φ、q(t)=-1、k=2、なので、BERNOULLI_ODE_GEN(2φ, -1, 2, t, ψ, c)、となるがの。
このψには、任意定数が入っているので、y=φ(t)+ψ(t)は、一般解となる。
そこで、dφ/dt+φ^2=Bt^m、ただし、m<0、の特別解φ(t)が求められばよいことになる」
 「木村先生の本にならい、φ=u(t)z(t)+v(t)、と置いてみるよ。
「木村先生の本にならい、φ=u(t)z(t)+v(t)、と置いてみるよ。
方程式の左辺は、
z(t)u'(t) + v'(t) + u(t)z'(t) + z(t)^2u(t)^2 + 2z(t)v(t)u(t) + v(t)^2、
整理して、
u(t)z'(t)+z(t)^2u(t)^2+z(t)(u'(t)+2v(t)u(t))+(v'(t) + v(t)^2)、
となるけど、
v'(t) + v(t)^2=0、かつ、 u'(t)+2v(t)u(t)=0となる、u、vを選択すれば、
与式の左辺は、u(t)z'(t)+z(t)^2u(t)^2、となる。
ここで、v'(t) + v(t)^2=0、から、v=1/(t+c)、
u'(t)+2v(t)u(t)=0、から、u=c'/(t+c)^2、ただし、c'は2つめの任意定数。
よって、u(t)z'(t)+z(t)^2u(t)^2=c'/(t+c)^2×z'+z^2×(c'/(t+c)^2)^2、
とはいっても、1つの解が求められれば、よいので、c=0、c'=1と置いてしまうと、
z'+z^2/t^2=Bt^(m+2)、となるわ」
「そうじゃな。
zの方程式の解が求められれば、φ=z(t)/t^2+1/t、としてφが求められる。
そうすれば、ψ'+2φψ=-ψ^2、として、ψが求まり、結果として、yの一般解が得られるという訳じゃな」
「でも、なんか、すごいめんどいわね。
リッカチさんは」
「ははは、そう、セッカチになっても仕方がないじゃろうが。
まあ、そうはいっても、面倒であることには違いはないのう。
手始めに、m=-2の場合を調べて見よう」
リッカチの微分方程式(6) m=-2の場合
「さて、m=-2の場合は、z'+z^2/t^2=Bt^(m+2)は、
z'=-z^2/t^2+B、となる。ここで、B=b/a^(m+1)=ab。
ここで、B>0と、当面は、考えている。
この方程式は、(z/t)の関数なので、いわゆる同次形となり、第70回でやったものじゃ。
といっても、目の子でも、z=t×(-1±sqrt(1+4B))/2、が解であることは分かるな。
H=-1+sqrt(1+4B)とおけば、
z>0の方の解は、前節のφ(t)=z(t)/t^2+1/t=t×H/(2t^2)+1/t、
よって、φ=H/(2t)+1/t、ここで、H=-1+sqrt(1+4B)、じゃ。
ここから、y=φ+ψ(t)、が求められるので、ψ' + 2φψ = -ψ^2の一般解は、
BERNOULLI_ODE_GEN(2φ, -1, 2, t, ψ, c)として、
1/ψ = t^(H + 2)(c(H + 1) + 1)/(H + 1) - t/(H + 1)、cは、任意定数。
これより、y(t)=(t^(H + 1)(H + 2)(c(H + 1) + 1) + H)/(2t(t^(H + 1)(c(H + 1)
+ 1) - 1))、と求められる」
 「複雑な式だけど、
「複雑な式だけど、
y'+y^2=Bt^(-2)、が直接、検算できたわ」
「グラフを描くために、t=1の値、すなわち、y(1)=3、としてみよう。
このとき、任意定数、cは、c = 2/(5 - √(4B + 1))、となる。
先に出た、B=1、10、50、100、に対応する、cは、
c = √5/10 + 1/2、
c = - √41/8 - 5/8、
c = - √201/88 - 5/88、
c = - √401/188 - 5/188、となる。
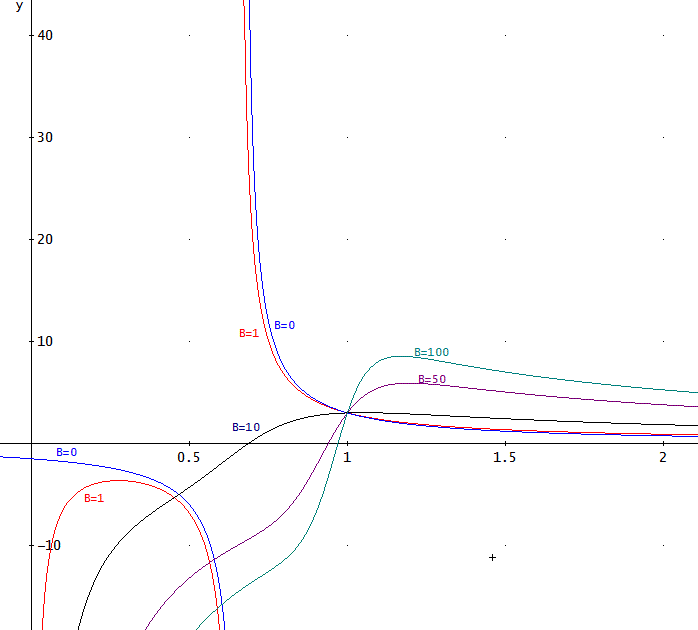
B=0の場合も参考で描いてある。
これを見ると、B=1では、t=1/2のあたりで、不連続となる。
一方、B=10、50、100では、t>0で不連続とならずに連続関数のようじゃ」
「方程式、y'+y^2=Bt^(-2)は、t=0で連続でないので、t=0で関数が不連続なのは当然だけど、
yの分母は、(2t(t^√(4B + 1)(c√(4B + 1) + 1) - 1)))、なので、
B=1、c=√5/2 + 3/2、では、(t^(√5 + 1)(√5 + 3) - 2t)=0は、t=0以外に、
t = (3/2 - √5/2)^(√5/5)≒0.6502431292・・、という根を持つため、
yがt=0.65・・で不連続になるのね」
「B=10、50,100では、分母は、実根を持たないので、t>0で連続な曲線になったということかの。
ここで、気になる、B<0の場合じゃが、sqrt(1+4B)があるため、B>=-1/4であれば、y(t)の表式には、変わりがない。
そこで、B=-1/8の場合を調べて見たが、ほとんど、B=1と変わらない。
B=0とすれば、y'+y^2=0、なので、y(1)=3となる解は、y=3/(3t-2)、これは、t=0の近くを除くと、ふるまいは、B=1と非常によく似ている」
「なるほどね。
じゃ、今度は、B<-1/4の場合を調べて見るよ。
y'+y~2=Bt^-2、で、とりあえず、B=-1、y(1)=3として、数値的に解いてみる。
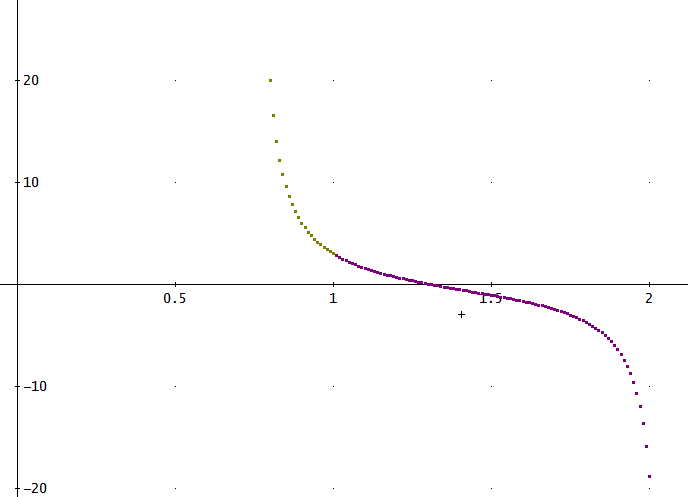
やはり、zの解である、ATANの影響で、正負の無限大に発散する様子は、分かるわね」
「そうじゃのう。
不連続点がくりかえし現れるのでな。初期値からたどれるのは、その一つの分枝内だけじゃ。
しかし、m=0のときのB<0の場合のように、ゼロ点や極の周期は、単一ではない。
次節で、そのあたりを含めて、mが-2のときの別解を説明しよう」
リッカチの微分方程式(7) m=-2の別解
「ここでは、mが一般の場合の方法について触れよう。
それは、前出の岩波数学辞典の付録の公式集の注釈(「一般には、ay=u'/uとおけば、uに関するベッセルの微分方程式に帰着する」)にならって、
y'+y^2=Bt^m、において、y(t)=u'(t)/u(t)と未知関数、u(t)の2階の微分方程式に変換する方法じゃ」
 「へー。
「へー。
u''-Bt^m×u=0、なんと、線形になる!」
「まー、そうなんじゃな。
そこは、非常にうれしいのじゃが、mが一般の場合は、解は、ものすごく複雑になる(ベッセル関数が現れる)というので、ここでは、m=-2の場合を説明しよう。
y'+y^2=B/t^2、は、変換、y(t)=u'(t)/u(t)で、u''-Bu/t^2=0、へと変換される。
特解を求めるために、u=t^ρ、とおいてみると、t^(p - 2)(p(p - 1) - b) = 0、となり、
tの如何に関わらず成立するためには、ρ=(1+√(4B + 1))/2 、ρ= (1-√(4B + 1))/2、が必要じゃ。
B>-1/4の場合は、ρは、相異なる2実根となるため、u(t)の方程式の一般解は、任意定数をC、Dとして、、
u(t) = C*t^((√(4B + 1) + 1)/2)+D*t^((1 - √(4B + 1))/2)、と線形結合で表される。
従って、y(t)=u'(t)/u(t)=((Ct^√(4B + 1)(√(4B + 1) + 1) - D(√(4B + 1) - 1))/(2t(Ct^√(4B
+ 1) + D))、
任意定数が2つ含まれているが、たとえば、y(t1)=y1のように、一つの点のtとyの値を決めれば、元の方程式から、
y'(t1)=B*t1^(-2)-y(t1)^2、も条件として得られるため、2つの任意定数、C、Dを決められるのじゃな」
「グラフを描いてみたよ。
B=0、1、10、100の場合。
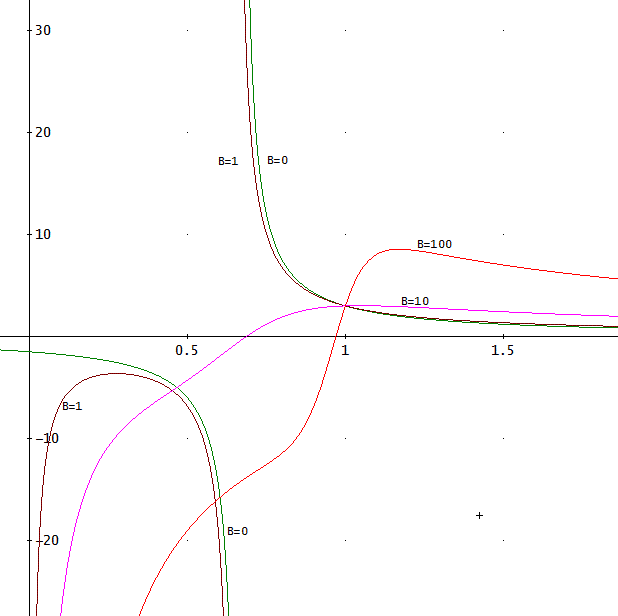
う~ん。
前の節でやったのと同じみたいね。
検算しても、方程式を満足しているわ」
「上記では、B>-1/4としていた。
では、もし、B=-1/4では、どうなるじゃろう」
「ρを決める方程式でρ=1/2が2重根、となるので、uの一般解が、u(t)=C*t^(1/2)+D*(なんとか)、となるんだけど、なんとかは何でしょう?」
「u''+u/(4t^2)=0、の場合じゃな。(元の方程式では、y'+y^2=-1/(4t^2)の場合)、
ρ=1/2が2重根なので、なんとかは、LN(t)*t^(1/2)じゃな。(※参照)
従って、u(t)の一般解は、u(t)=C*t^(1/2)+D*LN(t)*t^(1/2)、から、
y=u'/u=(D*LN(t) + C + 2D)/(2t(D*LN(t) + C))、となるのじゃ」
「t=1でy=3の場合はというと、y=(5LN(t) + 12)/(2t(5LN(t) + 2))、となるので、
グラフは下図のようになる。t=exp(-2/5)≒0.6703・・、では、発散する」
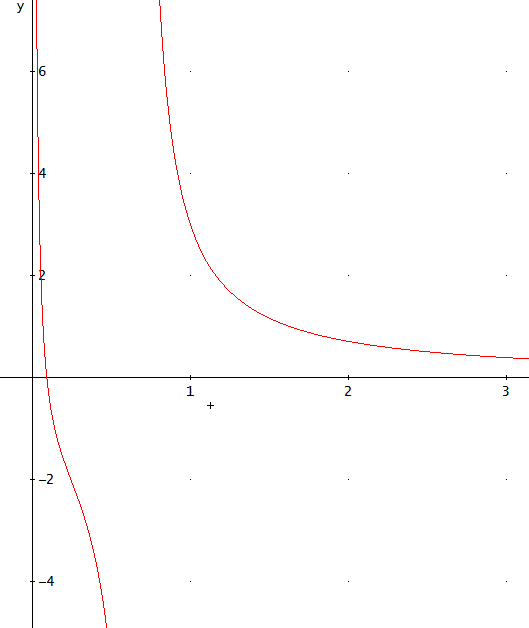
※2重根の場合の他の特解の求め方。
u''+u/4t^2=0、において、t^(1/2)以外の特別解を求めるためには、u(t)=t^(1/2)×v(t)とおくと、v''+v'/t=0、となるので、
これから、v(t)=LN(t)、従って、u(t)=t^(1/2)×LN(t)が求められる。
t^(1/2)×LN(t)が、t^(1/2)と互いに独立な解であることは、いわゆる、ロンスキー行列式、W、
w=DET([t^(1/2), t^(1/2)LN(t); ∂(t^(1/2), t), ∂(t^(1/2)LN(t), t)])=1、であり、恒等的にゼロでないことから分かる。
「次は、ρが複素数となる場合じゃ。
B<-1/4の時じゃな。
このときは、ρ1=(1+√(4B + 1))/2 、ρ2= (1-√(4B + 1))/2、の根号内が、負となり、ρが複素数となる。
uの一般解は、u=C*t^(ρ1)+D*t^(ρ2)、としたのでは、今は、yを実関数であると考えているのに複素数が現れてしまう。
そこで、u=C*RE(t^ρ)+D*IM(t^ρ)とすれば、よい。(ρは、実部が同一で虚部が符号のみ違うだけなのでどちらの根を採用しても同様)
ここで、REは、実部を、また、IMは、虚部を取り出す関数じゃ」
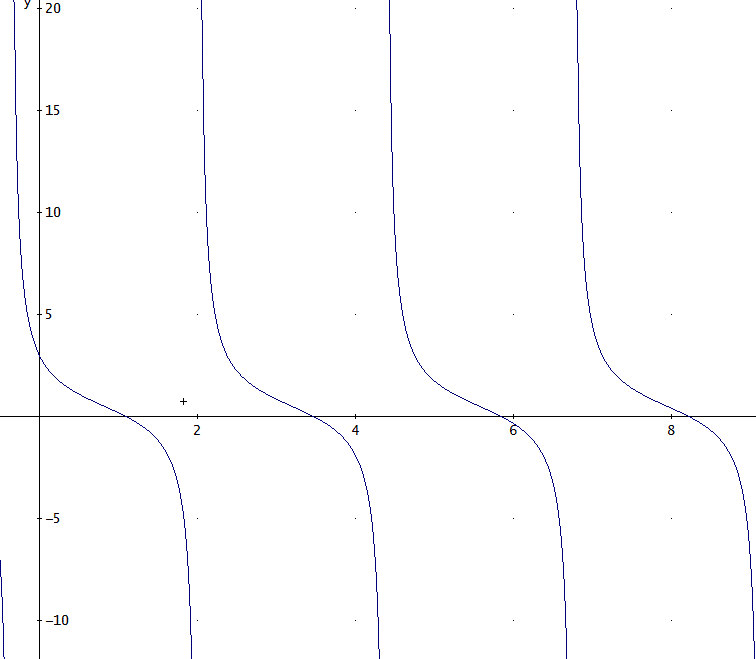
「たとえば、B=-2、のような場合ね。(元の方程式では、y'+y^2=-2/(t^2)の場合)、
u''+2u/(t^2)=0、では、ρ=1/2±#i×(√7)/2、ここで、#iは、虚数単位。
t>=0で、u=C√tCOS(√7LN(t)/2) + D√tSIN(√7LN(t)/2)、
また、t<0では、u=exp(- √7π/2)(D√(-t)COS(√7LN(-t)/2) - C√(-t)SIN(√7LN(-t)/2))、
従って、t=1でy=3の場合は、
t>=0で、y=(3√7COS(√7LN(t)/2) - SIN(√7LN(t)/2))/(t(√7COS(√7LN(t)/2) +
5SIN(√7LN(t)/2)))、
また、t<0では、y=(COS(√7LN(-t)/2) + 3√7SIN(√7LN(-t)/2))/(t(√7SIN(√7LN(-t)/2)
- 5COS(√7LN(-t)/2)))、
ただし、t<0の場合のC、Dは、t>0の場合と同一とした」
「分母分子に現れる三角関数内にLNの項があるため、yには、無限個のゼロ点と極がある。
ゼロ点は、(3√7COS(√7LN(t)/2) - SIN(√7LN(t)/2))=0の解なので、TAN(√7/2×LN(t)+nπ)=ATAN(3√7)、から、
t=exp(8√7ATAN(√7/7)/7 - 2√7πn/7)、n=0、±1、±2、・・。
n=0~±5までで、近似値は、次の通り。m>0の場合と異なり、ゼロ点の周期は、同一ではない。(ゼロ点は、おそらく超越数)
([4.279559691×10^5, 3.981323883×10^4, 3703.871662, 344.5754650, 32.05625409,
2.982230398, 0.2774403435, 0.02581059608, 0.002401189609, 0.0002233854468,
2.078180651×10^(-5)])、
一方、極は、t(√7COS(√7LN(t)/2) + 5SIN(√7LN(t)/2)) = 0、から、t=0以外に、TAN(√7LN(t)/2
+ nπ) = - √7/5、から、
t = exp(- 2√7ATAN(√7/5)/7 - 2√7πn/7)、n=0、1、2、・・。
n=0~±5までで、近似値は、次の通り。
([9.932944311·10^4, 9240.732988, 859.6760789, 79.97666002, 7.440321192,
0.6921816869, 0.06439446299, 0.005990691379, 0.0005573209485, 5.184821251·10^(-5),
4.823499183·10^(-6)])、
グラフも描いてみたが、グラフをちょっと見るだけだと、それは、わかりにくいじゃろう」
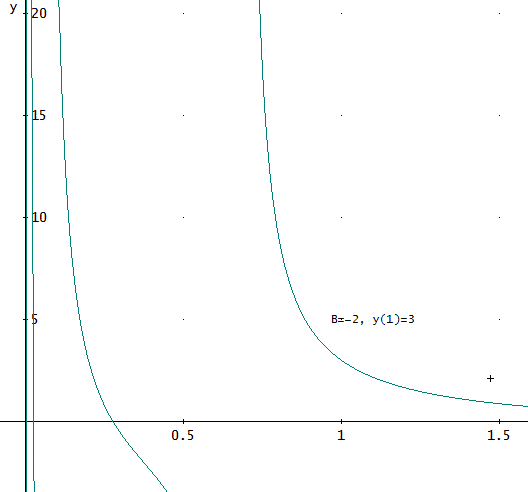
「確かに。
そこで、下図では、t>=0の場合の、y(t)のLN(t)をxに変えて、1/tの係数を除いて、グラフにしてみたよ。
横軸は、x=LN(t)、縦軸は、y(t)×t、となるけど」
「今回は、「リッカチの微分方程式」で終始してしまい、数値解法については、実例を挙げただけで、内容を説明できんかった。
次回こそは、常微分方程式の数値解法を取り上げることにしよう」
「まったくよ。
どっぷりと、「リッカチ沼」に、はまってしまったマーニーは夏の思い出、という感じです~」
リッカチの微分方程式(8) m<>-2の実数mの場合 2014/9/3追記
y'+y^2=Bt^m=0、ここで、m<>-2としておく。
さて、mが一般の場合に、ベッセルの微分方程式(とその仲間)との関係を備忘録的に記載しておく。ただし、以下は、検算していないのでご注意ください、
詳しい検算は、2階の常微分方程式の「ベッセル関数」の巻で取り上げる予定です。
前節までで、m=-2の場合は、済んでいるので、ここでは、mは、m<>-2の実数とする。
y=u'/u、において、u''-Bt^m×u=0、と変換する。ここで、t=αr^x、u(r)=g(r)×r^y、とさらに変数と関数を変換すると、
g''(r) - (x - 2y - 1)g'(r)/r - Bx^2r^(2x + mx - 2)α^(m + 2)g(r) - y(x
- y)g(r)/r^2=0、
ここで、m<>-2なので、x=2/(m+2)、と置けば、
g''(r)+(g'(r)/r)((2y(m + 2) + m)/(m + 2))-(g(r)/r^2)(y(2 - y(m + 2))/((m
+ 2)))-4Bα^(m + 2)g(r)/(m + 2)^2=0、
さらに、(2y(m + 2) + m)/(m + 2)=1となるように、y=1/(m+2)、と置けば、
g''(r)+g'(r)/r +g(r)(-4Bα^(m + 2)/((m + 2)^2)-1/(r^2(m + 2)^2))=0、
このとき、m<>-2であれば、α=(-(m+2)^2/(4B))^(1/(m+2))、により、
従って、g''+g'/r+g(±1-1/((r^2)(m+2)^2)=0、となる。
g(r)の係数の定数項がプラスの場合は、z''+z'/x+(1-ν^2/x^2)z=0、という「ベッセルの微分方程式」に帰着する。
たとえば、m=-1の場合は、α=1/4B、として、g''+g'/r+(1-1/r^2)g=0、
この場合のg(r)は、νが整数なので、第1種ベッセル関数である、J(ν=1,r)は、一つの解であるが、ν=-1のものとは、一次従属関係となるため、もう一つの独立な解は、第2種ベッセル関数(ノイマン関数)となる。
もし、νが整数でなければ、J(ν,r)とJ(-ν,r)は、一次独立な解となる。g(r)は、それら二つの解の一次結合となる。
また、m=1の場合は、g''+g'/r-(1+1/9r^2)g=0、となり、係数の符号が一部異なる。
これは、変形ベッセル関数、I(ν=±1/3,r)の方程式である。I(ν,r)=#i^(-ν)J(ν,#ir)、の関係がある(という)。
変形ベッセル関数の場合も、ベッセル関数と同様に、νが整数の場合、νと-νの解が一次独立とならないため、第2種変形ベッセル関数が他の解となる。
m=0は、g''+g'/r-(1+1/r^2)g=0、α=1/sqrt(B)、この解は、変形ベッセル関数で表され、しかも、νが整数となる例である。
いずれの場合も、u(r)=(r^y)×g(r)、t=αr^(x)、
ここで、α=((4B/(m + 2)^2)^(- 1/(m + 2))、x=2/(m+2)、y=1/(m+2)、として、u(t)が求まり、
y(t)=u'(t)/u(t)により、y(t)が求められることになる。
※m=1、B=1の場合について、ルンゲクッタ法(以下「RK法」)による数値計算と上記の変形ベッセル関数の近似値との比較を行った。
DERIVEでは、Bessel_I_Series(ν,変数,項数)の形で、変形ベッセル関数の近似値を計算できる。
x=2/(m+2)=2/3、y=1/(m+2)=1/3、α=((m+2)^2/4B)^(1/(m+2))=(9/4)^(1/3)、
t=α×r^x=(9/4)^(1/3)×r^(2/3)、
従って、u(t)=C×(2/3)^(1/3)×√t×Bessel_I_Series(1/3,(2/3)t^(3/2),項数)
+D×(2/3)^(1/3)×√t×Bessel_I_Series(-1/3,(2/3)t^(3/2),項数)、と置き、
y(t)=∂(u(t),t)/u(t)、とすれば、解析解の近似値は、計算できる。
ここでは、項数として、10項、及び20項を取り、いずれも、t=0でy(0)=3の条件を課して、グラフを描いてみた。
RK法による数値解法では、初期値をt=0でy=3として、tの刻み幅0.01、t=0~10までとして計算した。
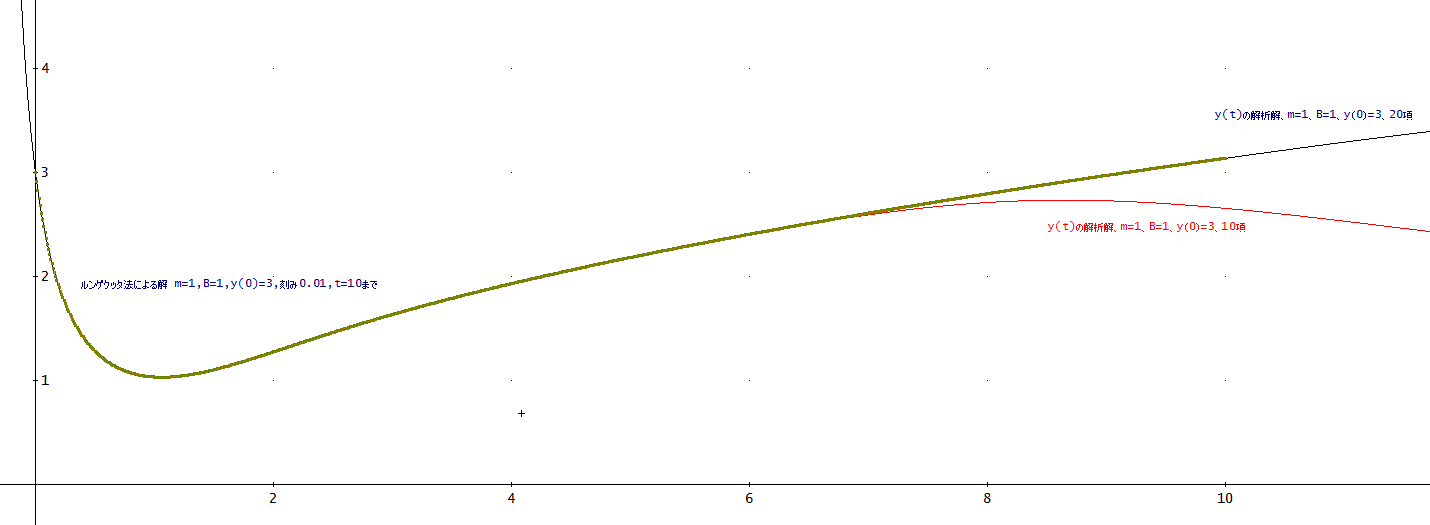
これを見ると、項数を20項とった場合は、t=0~10まで、両者は、ほぼ一致していると言ってよい。
一方、10項の場合は、t=6ぐらいまでは、両者は、ほぼ一致するが、その後、10項までの解は、RK法の値から乖離するようになる。
最終更新日 2014/9/3



 「おじさん。今回は、微分方程式の数値解法の巻じゃなかったの?」
「おじさん。今回は、微分方程式の数値解法の巻じゃなかったの?」