数式処理ソフト DERIVE(デライブ) de ドライブ
72.常微分方程式の数値解法(初期値問題)(1)
はじめに
 「やっと、数値解法にたどり着いたわね」
「やっと、数値解法にたどり着いたわね」
「ともちゃんか。しのぎやすい気候になったのう。
今年は、9月にならないうちに、涼しくなってしまったので、わしも、驚いたぞ。
ところで、数式処理ソフト DERIVE(デライブ)の第71回の「1階常微分方程式の解法(3)(リッカチの微分方程式)」で、すでに数値解法の実例を、少々、挙げてしまったのじゃが、今回、あらためて、常微分方程式の数値解法を説明しよう。
「ENIAC」というコンピューターをアメリカが開発した大きな目的の一つに、大砲の弾道計算が必要じゃったという話は、聞いておろう」
「第2次大戦の時代ね。
コンピューターも、戦争の申し子だったということね。いつもながら矛盾を感じるわ」
「まことに、不幸なことだがな。
戦時というのは、平時では思いもよらぬほど、経済的な採算を度外視し、兵器の開発が進められるものじゃからな。
原子爆弾の開発計画なども、そういった背景がなければ、とうてい、行われなかったろう」
「だけど、ENIACの完成時には、すでに戦争が終結しつつあったので、弾道計算には、間に合わなかったそうね」
「そのようじゃ。
しかし、水爆の開発やその後の原水爆の小型化について、電子計算機の果たした(今も果たしている)役割は、大きいと思われるのう。
機械や計算手法には、本来、善悪の別はないが、それは、まさに人間次第じゃということは、理解はしていても、むなしい気持ちは残るな。
さてと、気を取り直して、話を進めていこうかの。
標題で「初期値問題」と書いたのは、常微分方程式には、「固有値問題」、「境界値問題」などの大きなテーマがあるのでな。それと区別するためのものじゃ。
常微分方程式の初期値問題の数値解法として、代表的なものには、原理的な「オイラー法」とその修正、及びそれらを発展させた古典「ルンゲ・クッタ法」などがある。
この回では、2つを中心に説明していこう。
一松信先生の「計算機による数値計算法」(一松信・戸川隼人 著:新曜社:昭和50年(1975年)2月初版)の常微分方程式の章の冒頭にこんな趣旨がある。
すなわち、「解くべき方程式の関数を差分で近似するのが一般的である。数学一般の関数であれば、どんなに細かい分点をとっても分点以外の関数値を規定できないはずであるが、対象とする関数は、少なくとも、微分可能で、そしてずっとなめらかに変化するものが多いため分点以外の関数値を推定することは多くの場合に可能である。また、実用上は、関数全体の形より、具体的などこそこの点での関数の値はいくつかということを知れば十分なことが多い」とな」
「ガッテンです。
その、一松先生の本と以前にも紹介した「数値計算法基礎」(田中敏幸 著:コロナ社:2006年4月初版)を参考に進めていきますので、よろしくね」
「そして、DERIVEも使っていきますぞ」
オイラー法(1)(オイラー法)(1次)
 「じゃ、まずは、記法ね。
「じゃ、まずは、記法ね。
とりあえず、1階の常微分方程式の数値解法なんだけど。
といっても、2階以上の常微分方程式は、連立の1階常微分方程式として扱えるので、こ安心を。
以下、y'=r(x,y)、という正規形の方程式の数値解法を考えます。
変数xについては、等間隔に分点を取り、x(nh)=x(0)+nh、n=0、1、2、・・とする。ここで、hは、刻み幅ね。
また、x(nh)に対応する関数値、y(x)あるいはy(nh)などと書きます」
「y(nh+h)の値を直前のx(nh)とy(nh)のみから計算する方法を1段階法(single step method)という。
これに対して、x(nh)、y(x)以外に、それ以前のy(x-h)・・も利用する方法を多段階法というそうじゃ。ここでは、もっぱら、1段解法を取り上げる。
また、一松先生の本では、y(x+h)の値を計算するために、関数r(x,y)の値をm回計算する方法 m段(stage)法と説明されている。
このとき、関数のテイラー展開とp乗の項まで一致する解法をp位の(一般の)ルンゲクッタ型の公式と呼ぶ。
p=4までは、すなわち、テイラー展開とp次までの項が一致する公式は、m=p、すなわち、関数値をp回計算させて済ますことができる。
しかし、p>=5とするには、m>pとしなければ、ならないそうじゃ。つまり、5以上の次数まで、一致する公式では、4次までより相対的に計算回数が増えてしまう。
とはいえ、1次は、当然としても、2次や3次でも精度が不足する場合があり、実用上は、4次のルンゲ・クッタ法が多く使われているそうじゃ」
「y'=r(x,y)で、y(x+h)=y(x)+h×r(x,y(x))、とするのが、元々のオイラー法ね」
「極めて、分かりやすい方法であるな。
微分係数の根本的な応用とも言える。解の曲線を折れ線で表していこうという趣旨じゃからな」
「DERIVEでは、ファイルを開くか、または、読み込みで、ユーティリティの「ODEApproximation.mth」を利用する。
EULER_ODE(r, x, y, x0, y0, h, n)、
第1引数: y'=r(x,y)、のときの、右辺の関数r(x,y)
第2引数: 変数名(xなど)
第3引数: 関数名(yなど)
第4引数: 変数の初期値
第5引数: 関数の初期値
第6引数: 刻み幅
第7引数: 計算点数
例として、y'=x+y、の場合、線形微分方程式なので、厳密解は、y=c*exp(x)-x-1、
ここでは、c=1、すなわち、x=0で、y=0、を初期値とする。
EULER_ODE(x + y, x, y, 0, 0, 0.1, 100)、刻み幅を0.1と粗めにして、x=0~10まで、100点を取ってみた。
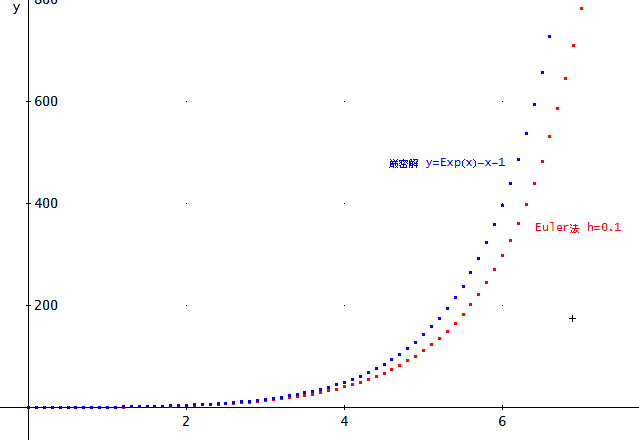
赤い点列がEuler法の場合、青い点列が厳密解(y=Exp(x)-x-1)。
xの増大とともに徐々に正確な値と離れてしまうことが見て取れる。
しかし、刻み幅を、0.01として、1000点とってみると、下図のように、グラフでは、x=10までほぼ一致しているように見える」
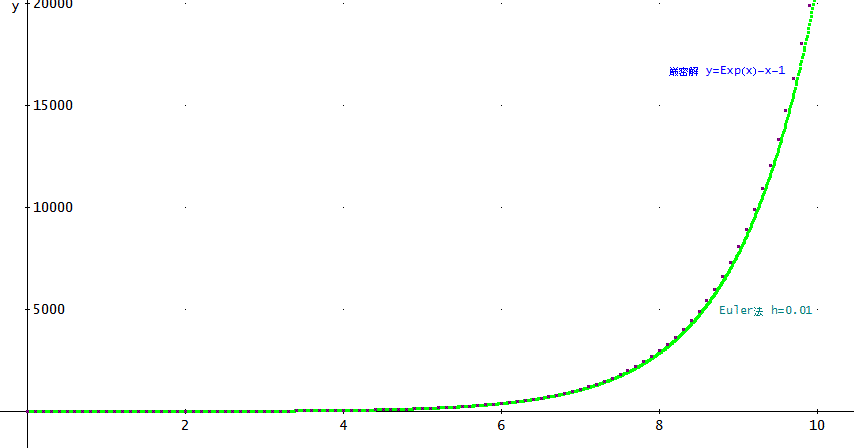
「これは、分かりやすいのう。
緑色の実線のように見えるものがEuler法の結果で、黒い点列が厳密解じゃな。
テストした関数は、Exp(x)を含んでいるので、急速に大きくなる関数じゃから、刻み幅、h=0.01程度で、x=10までをほぼ、正確に計算できるのは、たいしたものじゃ」
「実際の数字でチェックしてみると、そうでもなかったのよ。
厳密解のy(10)≒2.201546579×10^4、に対して、
h=0.01の場合、y(10)≒10, 2.094815563×10^4、相対誤差は、4.84%、
厳密解 y(5)≒142.4131591、に対して、y(5)≒138.7727724、相対誤差は、-2.55%程度」
「xが0~10まで変化する間に、yは、0~約2万と、xより約2000倍も大きく変化するのでな。
まあ、u(x)=LN(1+y(x))、と置いて、du/dx=1+(x-1)exp(-u)を同じ、h=0.01で解いてみると、
u(10)≒9.996031572、y(10)=exp(u(10))-1≒2.193822856×10^4、となって、絶対誤差で77程度、相対誤差で0.35%と、直接解いた場合の4.84%と比較して、13倍ほど精度が上昇するがの」
「なるほど。
とは言っても、いちいち、変換を考えるというのも、うっとうしいわね」
「方程式の変換については、後日、取り上げるとして、次節で、オイラー法の改良を考えてみよう」
オイラー法(2)(オイラー法)(2次)
「前節の(元祖)オイラー法は、はなはだ、簡明ではあるが、精度を上げるには、刻み幅をかなり小さくしないといけなかった。
改良方法は、いろいろとあるが、2次導関数までを考慮したとき、どの程度、精度が向上するかを検証してみよう」
 「ということは、y'=r(x,y)としたときに、y(x+h)≒y(x)+h×y'(x))+(h^2/2)×y''(x)、と近似するということね」
「ということは、y'=r(x,y)としたときに、y(x+h)≒y(x)+h×y'(x))+(h^2/2)×y''(x)、と近似するということね」
「DERIVEのEuler_ODE関数を参考にして、拡張してみるのがよいじゃろう。
その場合は、2次導関数 y''=g(x,y)の右辺のg(x,y)を新しく引数リストに追加するとよい」
「例のITERATES関数を使うのね。
繰り返し処理に使う、ITERATE関数、ITERATES関数は、ちょっと使わないと、すぐ、使い方を忘れてしまうのよね。
第62回の「再帰関数(1)(等差・等比数列、フィボナッチ数列、繰り返し処理)」の繰り返し処理の節で出てきているので、皆さんも、読み返してみてくださいな。
ITERATES(引数1,引数2,引数3,引数4)としたとき、
引数4で指定した回数の処理が実行される。擬似的には、次のような感じ。
引数3(初期値)→引数1
for k=1 to 引数4
引数1を計算して引数2に代入
next k」
「うん、そうじゃな。
たとえば、前節の1次のオイラー法をユーザー定義で作るとすれば、y'=r(x,y)、初期値、x0、y0、刻み幅h、点数n、として、
ベクトルv=[x(k),y(k)]を変数として考えて、r(x,y)が外部で定義されている状態では、
ITERATES([v↓1+h,v↓2+h*r(v↓1,v↓2)],v,[x0,y0],n)
とすればよい」
「念のためだけど、「v↓1」などの「↓」は、ベクトルの要素を取り出す添え字を表すDERIVEの記号よ。
v↓1は、ベクトルvの第1成分を表します。
ITERATES([h + v↓1, v↓2 + h×r(v↓1, v↓2)], v, [0, 0], 10)とすれば、
Iterates関数の外で、r(x,y):=y+x、h:=0.1、と規定しておけば、 (:=は、定義を表すDERIVEの記号。=とは異なる。)
上式は、EULER_ODE(y + x, x, y, 0, 0, 0.1, 10)で計算したのと全く同一の結果となる。
ここで、問題となるのは、ユーザー定義関数として作る場合、rとhなどを引数リストで与えたいことね」
「ユーザー定義のオイラー法関数として、Euler_User(r, x, y, x0, y0, h, n)を次のように定義すればよい。
ITERATES([h + v_↓1, v_↓2 + h*LIM(r, [x, y], v_)], v_, [x0, y0], n)とな」
「ここがポイント。
h*LIM(r, [x, y], v_)、という極限値を計算する関数を使っている訳なの。
DERIVEの関数の定義では、定義する関数の「引数リスト」に、rに()を付け、r(x,y)とは書けないという制約があるためなの。
Euler_User(r(x,y), x, y, x0, y0, h, n)では、エラーとなるのよ。
それだけじゃなくて、定義式内で、r(x,y)のように、引数リストにある関数名には引数を付けて使えないの。
ここは、すごく、不便だとは思うけど、引数リストにない(外部で定義されている)関数は、定義式内で()を付けて書くことは、許されているんだけどね。
そこで、仕方がないので、極限値をとる関数、LIM(関数,変数名,極限値)を使って、rに[x,y]を入れてベクトルのv_の値に置き換えているの。
分かってもらえたかしら。
これで、2次のオイラー法関数、Euler2_User(r, g, x, y, x0, y0, h, n)を次のよう作ることができた。
ITERATES([h + v_↓1, v_↓2 + h×(LIM(r, [x, y], v_) + (h/2)LIM(g, [x, y],
v_))], v_, [x0, y0], n)、
まずは、テストする方程式、y'=y+x、初期値[0,0]で、刻み幅、0.1の場合、
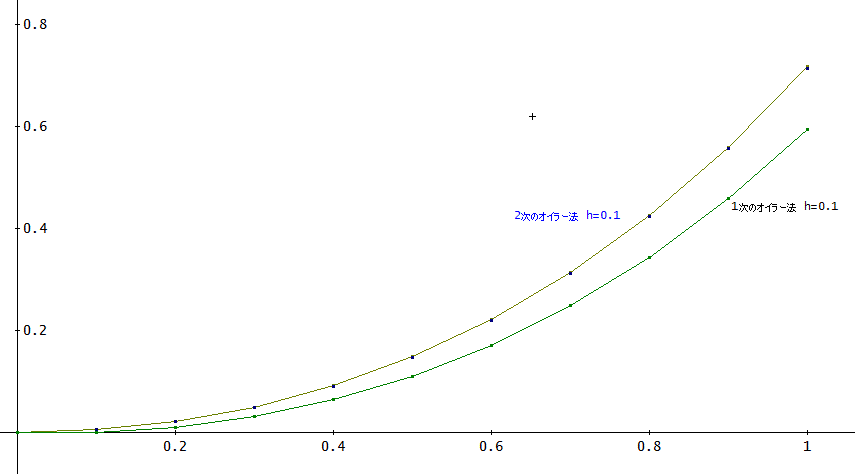
1次のオイラー法は、当然ながら、EULER_ODE(y + x, x, y, 0, 0, 0.1, 10)と同一の数値を与える。
前節で見たように、厳密解(y=EXP(x)-x-1)とはかなり見劣りがするのね。
そこで、2次のオイラー法である、Euler2_User(y + x, y + x + 1, x, y, 0, 0, 0.1, 10)は、x=0~1の範囲では、グラフ上は、厳密解と区別が付きにくいほど一致する。これは、すごいわ。
今度は、前節と同様に、刻み幅を0.01として、x=0~10までを計算して、数値的一致の度合いを比べてみると、下表のようになる。
| x |
厳密解 |
1次のオイラー法 |
相対誤差 |
絶対誤差 |
2次のオイラー法 |
相対誤差 |
絶対誤差 |
| 1 |
0.7182818284 |
0.7048138294 |
-1.87% |
-0.01346799905 |
0.7182368625 |
-0.0062% |
- 4.496595831×10^(-5) |
| 5 |
142.4131591 |
138.7727724 |
-2.55% |
-3.640386702 |
142.4008842 |
-0.0086% |
-0.01227490259 |
| 10 |
2.201546579×10^4 |
2.094815563×10^4 |
-4.84% |
-1067.310164 |
2.201182244×10^4 |
-0.016% |
-3.643354861 |
2次のオイラー法の方が、x=10でも、相対誤差0.02%未満、絶対誤差ても、約-3.64とものすごく精度が上がっているわ」
「これは、歴然とした結果じゃのう。
2次までとることにより、相当の改善をはかれたということじゃな。
方程式の解が直線でない限り、折れ線近似による解が厳密解と離れていくのは、やむを得ないことであった。
刻み幅hの2次項までとることにより、解曲線の丸みにある程度対応できるようになり、大きく精度が向上したというわけじゃ。
しかし、実用上からは、y'=r(x,y)のr(x,y)以外に、y''=g(x,y)のg(x,y)を新しく、引数として関数に与えないといけないという不便さは、ある。
これは、次数が3次、4次と上がるごとに、より面倒となる点じゃ。
もちろん、DERIVEであれば、3次や4次導関数を自動的に計算させたり、n次までのテイラー展開式をrの代わり指定する方法もあり得る。
しかし、次節では、一般的な方法である、g(x,y)などの2次導関数を与えない工夫を調べて見よう」
オイラー法(3)(修正オイラー法)(2次)
 「厳密解、y(x+h)=y(x)+h*y'(x)/1!+h^2y''(x)/2!+・・、とテイラー展開した式と、近似式がh^2まで一致するようにを考えるんだけど、前節のように、y''=g(x,y)を与えずに行おうという訳ね」
「厳密解、y(x+h)=y(x)+h*y'(x)/1!+h^2y''(x)/2!+・・、とテイラー展開した式と、近似式がh^2まで一致するようにを考えるんだけど、前節のように、y''=g(x,y)を与えずに行おうという訳ね」
「そのために、以前に出てきた、定積分の計算方法を元にして考えよう。
第56回の「数値積分(5)(ニュートン-コーツの公式、IMT公式、DE公式)」のなかに、いろいろな数値積分公式が出てきている。
なかでも基本的なものは、台形公式じゃ。
積分する関数をg(x)としたとき、x=a~bまでをn個の区間に分割すると、h=(b-a)/nとして、
台形公式:∫(x=a~b)g(x)dx≒h∑(k=0~n-1)(g(a+kh)) + (h/2)(g(b) - g(a))、となる。
これをベースに考えていくのじゃ。
まずは、解くべき方程式、y'=r(x,y)、において、両辺をxで積分する。
積分範囲は、x=x~x+h、左辺は、∫(x=x~x+h)y'dx、これは、定義から直ちに、 y(x+h)-y(x)、となる。
一方、右辺は、∫(x=x~x+h)r(x,y)dx、であるが、y(x)が明らかであれば、単に両辺が等しいという関係(恒等式)を確認するだけじゃ。
じゃが、当然、y(x)は、不明であり、積分を和に置き換えて近似的に計算するしか手立てがない。そこで、
積分にn=1の台形公式を適用すると、∫(x=x~x+h)r(x,y)dx≒(h/2)×r(x,y(x)+r(x+h,y(x+h)))、
となるが、問題は、r(x+h,y(x+h))である。
y(x)の値(y(0)を除き、近似値ではあるが)からは、y(x+h)の正確な値を知ることはできない。
そこで、y(x+h)≒y(x)+h×r(x,y(x))、と1次のオイラー法で近似することにすれば、
∫(x=x~x+h)r(x,y)dx≒(h/2)(r(x,y(x))+r(x+h,y(x)+h×r(x,y(x)))、となる。
こうすると、実は、前節同様、hの2次の項まで、テイラー展開した方法とh^2の項までは同等となるのじゃ」
「つまり、y(x+h)≒y(x)+(h/2)r(x,y)+(h/2)r(x+h,y+h×r(x,y))、と計算を行うのね。
なお、x(nh)をx、y(nh)を単にyと書いている。
本当にhの2次まで近似できているかどうかは、
右辺=y(x)+(h/2)(r(x,y)+r(x,y)+h∂(r,x)+h×r(x,y)∂(r,y))
=y(x)+h×r(x,y)+(h^2/2)(∂(r,x)+r(x,y)∂(r,y))、となるけど、
右辺の第3項の()内は、y''(x)=∂(r,x)+∂(r,y)×y'=∂(r,x)+r(x,y)×∂(r,y)、と全く同じになることから証明できたよ」
「そこでじゃ、新しいユーザー定義関数、Euler2R_User(r, x, y, x0, y0, h, n)を次のように定義してみた。
ITERATES([v↓1 + h, v↓2 + (h/2)LIM(r, [x, y], [v↓1, v↓2])+(h/2)LIM(r, [x, y], [v↓1 + h, v↓2 + h×LIM(r, [x, y], [v↓1, v↓2])])], v, [x0, y0], n)、
テスト方程式、y'=y+x、初期値[0,0]としてn=100まで、Euler2R_User(y + x, x, y, 0, 0, 0.01, 100)、として計算させると、前節の、Euler2_User関数を使った場合と全く同一の数値が得られることを確認できたぞ。
やれやれや、よかった」
「でも、苦心していたんじゃない」
「いや、確かにな。
ITERATES関数に限らないが、引数が多くて、定義式が複雑になってくると、カンマ、( )、[ ]などの位置や数が合わないなど、エラーが出て、なかなか、正しい結果に至るまでの時間がかかったのが本当のところじゃった。
主な原因は、LIM関数が入ることにより式が複雑になることじゃな。
いや、もうこれ以上、定義式が複雑になるのは、カンベンして欲しいのう」
「だから、「困難を分割せよ、しかる後に総合せよ!」を使うのは。今でしょうが!
たとえば、代入関数、Fd(g,x,y,x0,y0):= LIM(g, [x, y], [x0, y0])、と外部でユーザー定義で作成しておくと、
さっきの複雑な式も、下のようにかなり分かりやすくなる。
Euler2R_User(r, x, y, x0, y0, h, n):=
ITERATES([v↓1 + h, v↓2 + (h/2)fd(r, x, y, v↓1, v↓2) + (h/2)fd(r, x, y,
v↓1 + h, v↓2 + h×fd(r, x, y, v↓1, v↓2))], v, [x0, y0], n))とね」
「おっ、ともちゃん、これは、一本参りましたな。
なお、PROG関数を使って、関数内部で、fd関数を定義しようとすると失敗する。これは、fd()のように関数に引数をつけて定義できないためじゃ。
まあ、4次のルンゲ・クッタ法に話を進めていくと、定義関数をいくつかの関数に分割することは、避けられないとは思っていたがの」
「DERIVEのルンゲ・クッタ法の「RK」関数の定義を見ると、複数の関数に分割されているわね」
「分割することにより、簡単化や汎用化が図れるが、同じグループの関数群をまとめて、読み込んでおく必要があることには注意が必要じゃ」
ルンゲ氏、クッタ氏と四方山話
 「ルンゲ・クッタというのは、2人の名前なのかしら?」
「ルンゲ・クッタというのは、2人の名前なのかしら?」
「おー、そのこと、そのこと。気になっておったのじゃが、今回、調べましたぞ。
Runge-Kutta methodのルンゲ・クッタは、やはり、2人のお名前じゃった。
一人目の、ルンゲ氏は、Carl David Tolme Runge(1856/8/30~1927/1/3)であり、ドイツの物理学者・数学者じゃった。
岩波数学辞典の人名索引では、「Runge, C.D.T.」 とあり、C.D.T.とは、何の略かなと思っておったが、ウィキペディアのルンゲ氏の項を見て、C.D.T.とは、カール・ダーフィト・トルメの略ということが分かった。19世紀から20世紀にかけて活躍した人じゃった」
「前に天体運動を調べていたときに「ルンゲ・レンツ ベクトル」というのがあったんじゃない。
そのルンゲ氏かしら?」
「そうかもしれないな。分光学でも著名な学者じゃったそうだ。
ちなみに、「ルンゲ・レンツ ベクトル」とは、中心力場で質点が運動する際、力が重力や点電荷のように距離の2乗に逆比例する場合、全エネルギー及び角運動量と並んで、もう一つの保存量(時間により変わらない量)がある。これが、ルンゲ-レンツベクトルe じゃ。
e=定数×P×L-r/r、と表される。ここで、Pは系の運動量、Lは角運動量、rは位置ベクトルじゃ。
天体力学では、ラプラスの本にすでに現れているというので、その頃には知られていたことのようだが、量子力学の草創期に、水素原子等のシュレディンガー方程式に関連して、あらためて、注目されたことで、現在では、(ラプラス-)ルンゲ-レンツベクトルの名称が定着している。
一方、クッタ氏は、Kutta W.M.、1867/11/3~1944/12/25、ドイツの方じゃそうだ。ルンゲ氏より10歳ほど若い。
1901年にルンゲ氏とともに、ルンゲ・クッタ法を開発したとのこと。流体力学の「クッタ・ジューコフスキーの定理」(Kutta-Joukowski's
theorem)などでも知られている。※Wikipedia等を参照しました」
「こうみると、○○の定理や□□の方程式など、○○や□□は、歴史上の誰なのか、特定しづらい場合があるわね」
「そうじゃのう。「ベルヌーイ家の人々」には、少なくとも、3人の有名なベルヌイ(ベルヌーイ)氏が登場するが、単に、ベルヌーイの定理などと書かれていると、どのベルヌーイ氏の創案によるものか?、とはなるな」
「意外に書かれていない場合があるわね。そこんところが」
「その理由の一つは、非常に有名な人で、名前にも紛れがなく、書くまでもない。オイラーやガウスなどじゃな。
二つ目には、本筋から外れてしまうので、あえて、余分な情報は書かない。専門書などでは、こうなりがちじゃ。
そして、三番目は、著者や編集者も、詳しくは知らない」
「ちょっと、三つ目の、著者らも知らないというのは、問題発言でしょうが~」
「いや、案外、そういうこともあり得ると思うのじゃな。
有名な学者の方が書かれた本でも、特に、歴史上の人物像や逸話は、一々原典にあたらず、既存の本を参考にされることが多いと思う。
すると、最近の「コピー&ペースト」というわけではないが、同じような内容になるのは、致し方がない面はある。
以前の書物に偶々、詳しく書かれていないとその後も詳しく書かれないことが多いじゃろうし、何か事実を間違えて書かれていると同じ間違いが伝播しがちじゃ。
話がそれるが、「ブラウン運動」(水中の微粒子が水分子の衝突により細かく揺れ動く運動)は、1827年に、植物学者 R.Brown氏が花粉から出てくる「微粒子」が細かく揺れ動く様を観察したことにより、その名称が付いた。後年、それが「分子」の存在を証拠立てたことで有名になった。
しかし、「思い違いの科学史」(青木国夫・板倉聖宣・市場泰男・鈴木善次・立川昭二・中山茂 著:朝日新聞社:1978年1月第1刷)によれば、1978年当時の日本の多くの書籍等のブラウン運動に関する紹介では、「水中で花粉が動く」と書かれていたそうじゃ。
実際は、水中に入れた花粉(粒径:30~50ミクロン)から出てくる微粒子(数ミクロン程度)が水分子の衝突により揺れ動くのであって、花粉そのものは、大きくて重いので動かない。ブラウンの原論文には、花粉と微粒子とは、はっきりと区別されて記述されているそうじゃが、日本では、花粉と花粉から出てくる微粒子とが混同されて、単に花粉と記載されているものが実に多かったということじゃ。
もっとも、最近の書籍では、「水中に浮かぶ花粉から出てくる小さな粒子が・・」と書かれているものもある。(物理学大事典:鈴木增雄・荒船次郎・和達三樹
編:朝倉書店:2006年2月第2刷)。
ただ、あらためて、上の文章をみると、水中に「浮かぶ」、というのは、どうかな。水中に浸した花粉の膜が破れて中から微粒子が漏れ出すのだからのう」
「その漏れ出すっていう微粒子は、いったい何者なのよ?」
「デンプンなどの大きな分子じゃそうだ。
デンプンとは、炭水化物に属し、分子式は、(C6H10O6)nという多糖類だ」
「うへー。
デンプン、こんなに種類があるの!
グリコのホームページ(http://nu.glico.jp/tabemono/material/02/)では、キャッサバ(タピオカ)、サゴヤシ、馬鈴薯(じゃがいも)、甘藷(サツマイモ)、トウモロコシ(コーンスターチ)、小麦、米、クズなどから作られるデンプンが挙げられているわ」
「わしも驚いたぞ。でんぷんの由来の植物により、形状、粒径、性状などが様々じゃ。
このなかで、サゴヤシというのが分からなかったので、調べたがな。
 しかし、今ひとつ、ぴんとこないのじゃが、普通のヤシとは、だいぶん違うようじゃ。
しかし、今ひとつ、ぴんとこないのじゃが、普通のヤシとは、だいぶん違うようじゃ。
わしにとって、普通のヤシとは、「ココヤシ」(この実がココナツ)というものらしい。
左のように海外のリゾートの写真などでよく目にする植物じゃな。
このほか、熱帯植物園の温室などで、「トックリヤシ」という幹の下の方が徳利のように丸く膨らんだものも見た記憶がある。
そのほか、「ナツメヤシ」、「アブラヤシ」(パーム油の原料)、「アサイー」(実を食用)、「サラクヤシ」(果実を利用、本体や実にとげがある)、「ビンロウ」(実をガムのような嗜好品に加工)、ノコギリヤシ(薬用)、トウ(つるを利用)などなど、ヤシ科に属する植物は、およそ3000種は、あるという(主として、Wikipediaによる)が、その多くが熱帯・亜熱帯なので、わしらになじみが薄いのも無理はないかな」
「さ、この辺で、お仕事、お仕事、次節に移りましょう」
任意次数までのオイラー法
「今まで、1次と2次のオイラー法について、調べてきた。
この節では、任意の次数までのオイラー法を実行するユーザー定義関数を作成してみよう。
いろいろな考え方はあろうが、Eulerm_User(r,x,y,h,m,n)と引数にm(最大次数>=1)を追加して、計算させよう。
そのために、外部に1~m次までのテイラー展開式を返す関数を定義するとよいじゃろう。
DIFm_User(f,x,y,h,m)は、関数f=f(x,y(x))をm次まで展開して返す関数じゃが、(h^k/k!)の因子(k=1~m)を含めて返すことにしたい」
 「何度も計算させるわけではないので、再帰的に定義すればいいわね。
「何度も計算させるわけではないので、再帰的に定義すればいいわね。
m次の項を、DIFm_user(f, x, y, h, m)として、
IF(m = 1, h×LIM(f, [u_, v_], [x, y]), h×(∂(DIFm_user(f, x, y, h, m - 1),
x) + LIM(f, [u_, v_], [x, y])∂(DIFm_user(f, x, y, h, m - 1), y))/m)、
でよし。
そして、Eulerm_User(r,x,y,h,m,n)は、
Eulerm_user(r, x, y, x0, y0, h, m, n):=
PROG(f_:=∑(DIFm_user(r, x, y, h, k), k, 1, m), ITERATES([v↓1 + h, v↓2 +
LIM(f_, [x, y], v)], v, [x0, y0], n))、
で、OKみたいね」
「読者のみなさんのために説明すると、PROGという関数は、PROG(命令1,命令2,・・)という形で、()内の命令1から順次実行する。
よって、f_:=∑(DIFm_user(r, x, y, h, k), k, 1, m)は、最初に1回だけ実行される。
命令1では、ともちゃんが定義してくれた、DIFm_user(r, x, y, h, k)をk=1~mまでの加算し和を仮の関数、f_に代入している。
なお、仮の関数f_には、()を付けて、引数を指定することはできない(エラーとなる)。
命令2のITERATES関数は、そのf_に対して、m次までのオイラー法を適用しているのじゃな。
しかし、1次や2次までのオイラー法と比較して、yの増分の表示は、v↓2 + LIM(f_, [x, y], v)と非常に簡素な形になった。
これは、f_の中に1~m次までのテイラー級数がhのべき乗の項を含めて入っているからじゃ」
「m=1、2、について、実行してみると、前節までの結果と数値的にぴたりと一致したわ」
「以下に、m=1~10までの計算結果をグラフで示してみた。
ただし、テスト関数は、これまでと同一の、y'=y+x、初期値は、[0,0]、刻み幅は、h=0.01に固定しておる。
また、DERIVEの精度を20桁としている。(オプションメニューのモード設定)
縦軸をLN(|計算値-厳密値|)、横軸を次数 m(1~10)とする。

具体的には、TABLE(LN(ABS(Eulerm_user(y + x, x, y, 0, 0, 0.01, m, 1000)`↓2 -
(EXP(10) - 10 - 1))), m, 1, 10, 1)、
のように、解析メニューの表の作成を使った。(上式は、x=10の場合)
ここで、'は、転置を意味する。
なお、この計算にあたっては、Eulerm_user(r, x, y, x0, y0, h, m, n)を一時的に、
PROG(f_ :=∑(difm_user(r, x, y, h, k), k, 1, m), ITERATE([v↓1 + h, v↓2
+ LIM(f_, [x, y], v)], v, [x0, y0], n))、
とITERATESをITERATEに変更している。これにより、0.01×回数の時の値のみを[x,y]として返すことになっている」
「う~ん。
これを見ると、x=10という計算結果の中では、いちばん厳しいy(10)は、
m=2では、絶対誤差は、3.63、m=3では、0.01弱、m=4で約2×10^-5まで減っている。
だけど、グラフの傾きは、x=1、5、10では、みな同じぐらいなのは、何か秘密があるのかな」
「これまで、誤差と言ってきたものは、正確には、打ち切り誤差(「離散化誤差」ともいう)というべきものじゃ。
その他の誤差には、丸めや桁落ちなどによる誤差もあるが、ここでは、打ち切り誤差を考えよう。
これは、大切な事柄なので、次節であらためて扱うことにしよう」
オイラー法の打ち切り誤差(1)
「さて、y'=r(x,y)の厳密解をy(x)、1次のオイラー法で得た結果を、y(x)+E(x)と書くことにしよう。
この関数 E(x)は、打ち切り誤差をで表し、また、x,yは、離散値ではあるが、以下では、場合によって、連続量のように扱う。
このとき、x=x+hの誤差は、E(x+h)=E(x)+h×r(x,y+E(x))-y(x+h)、と差分式で表される。
y(x+h)=y(x)+hy'(x)+h^2/2×y''(x)+・・とテイラー展開可能であれば、
E(x+h)≒E(x)+h×r(x,y+E(x))-hy'(x)-h^2/2×y''(x)、
ただし、y'''以上の高次項を無視している。
また、r(x,y+E(x))≒r(x,y)+∂(r,y)E(x)、とE(x)についても、2次以上を無視して展開すると、r(x,y)=y'(x)を考慮して、
E(x+h)≒E(x)+h×∂(E(x),x)と近似できて、E(x)に関する次の微分方程式を得る。
∂(E,x)≒∂(r,y)E(x)-h/2×y''(x)、
なお、誤差関数の意味から、E(0)=0、が初期値である。
今、例題1として、前節までのテスト関数である、y=exp(x)-x-1、r(x,y)=y+x、の場合を取り上げると、
∂(E,x)=E(x)-h/2×exp(x)、ここで、E(0)=0、であることに注意すると、方程式の解は、
E(x)=-hx/2×exp(x)、となる。具体的には、h=0.01、x=1、5、10の場合に、計算すると、下表のようになる。
| x |
厳密解 |
1次のオイラー法 |
絶対誤差 |
E(x) |
| 1 |
0.7182818284 |
0.7048138294 |
-0.013467999 |
-0.013591409 |
| 5 |
142.4131591 |
138.7727724 |
-3.640386670 |
-3.710328977 |
| 10 |
2.201546579×10^4 |
2.094815563×10^4 |
-1067.310156 |
-1101.32328 |
この誤差評価方法は、「計算機による常微分方程式の解法Ⅰ」(P.ヘンリチ著:清水留三郎・小林光夫 訳:サイエンス社:昭和48年5月初版)の記述にならったものじゃ。数学的に厳密な記述は、上記の本などを参照して欲しい」
 「ということは、1次のオイラー法を使う場合は、x=10で、絶対誤差を1程度にするためには、
「ということは、1次のオイラー法を使う場合は、x=10で、絶対誤差を1程度にするためには、
|E(10)|=h×10/2×exp(10)≒1から、刻み幅、hは、h≒1×10^(-5)以下に小さくしないといけないのね。
実際、h=10^-5で、オイラー法の値は、2.2014364506391332784×10^4、となり、絶対誤差は、約-1.1・・、となる。
しかし、h=10^-5とすると、x=10で、n=10^6=100万回計算しないといけないので、計算時間が約90秒かかり、実用には、向かないわね」
「確かにのう。
やはり、1次のオイラー法では、hを小さくすると計算時間が増し、まして、100万個もの値を合計すれば、丸め誤差も顕在化しやすくなるじゃろうな。
しかし、E(x)=-hx/2×exp(x)を見ると大切なことが分かるので、ここで、ちょっと解説しておこう。
・xを固定して、hをゼロに近づけると、E(x)→ 0、である。
・hを固定して、xを∞にすると、E(x)→∞、となる。増加は、指数関数的。
・相対誤差は、E(x)/(exp(x)-x-1)である。x→∞で、やはり無限大となるが、増加は、xに線形に比例する。
テスト関数は、y'=x+yであり、y'=r(x,y)のrが、特に、yについて、線形じゃ。
そのため、上の解析では、E(x)の微分方程式を作成したが、E(x)の差分方程式として解析してもほぼ同様の結果となろう。
けれども、r(x,y)がyについて、線形でない場合は、E(x)の一次までとる近似では不十分な場合もあり得るので、無理に微分方程式にせずに、差分のまま、扱った方が、より実際に近いじゃろう。
ここで、例題2として、第71回で登場した、「リッカチの微分方程式」を取り上げる。
y'+y^2=10/(x^2)、初期値は、第71回と少し変えて、[1/8,-20]とする。
この方程式の厳密解は、y(x)=(x^(F + 1)(F + 2)(c(F + 1) + 1) + F)/(2x(x^(F + 1)(c(F
+ 1) + 1) - 1))、
ここで、F=-1+sqrt(1+4×10)、c = 2^(3√41)(12/5 - 77√41/205) - √41/41、
r(x,y)=-y^2+10/x^2、1次のオイラー法の誤差関数は、
E(x+h)=E(x)+h×r(x,y+E(x))-(h×y'(x)+h^2/2×y''(x))、で与えられるというのが、例題1の結果じゃった」
「例題1のように、E(x)の微分方程式として、扱ってみたわ。
h×r(x,y+E(x))≒h×r(x,y)+h×∂(r,y)E(x)=h×y'(x)+h×∂(r,y)E(x)、と近似し、
∂(E,x)+2yE=-h/2×y''、x=1/8~、h=0.01、
LINEAR1(2v(x), u(x), x, y, 1/8, 0)、ここで、v(x)=y(x)、u(x)=-(h^2/2)y''(x)、
なお、便宜的に、E(x)を上のLinear1では、yと記載しているけど、これはy(x)(厳密解)ではないので、ご注意を。
E(x)は、数値的に積分するしかないけど、いわゆる求積法で厳密解が求められた。
グラフで表してみると、下図のようになったわ。厳密解 y(x)も同時に表示している。
E(x)は、小さすぎるので、絶対値の自然対数を取り、LN(|E(x)|)を縦軸として図示した。
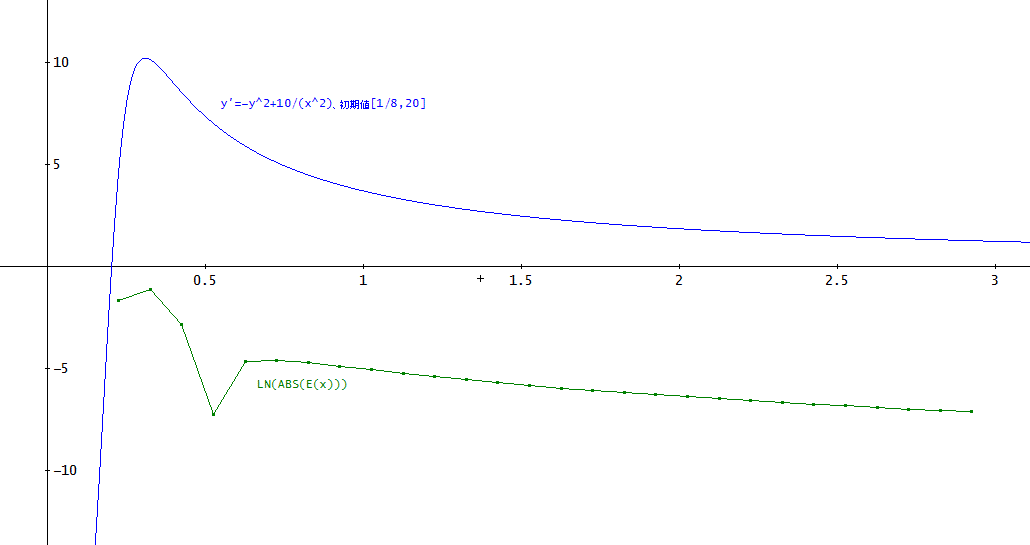
これを見ると、誤差評価関数E(x)の変化は、不思議だわ」
「では、E(x)やy(x)について近似せずに、E(x+h)=E(x)+h×r(x,y+E(x))+y(x)-y(x+h)として扱ってみるとどうか、というところじゃな。
x=nh、x=1/8が初期位置じゃから、h=1/128≒0.0078125、としよう。こうすると、16h=1/8が初期位置ということになる。
E(nh+h)=E(nh)+h×(-(v(nh)+E(nh))^2+10/(nh)^2)+(v(nh)-v(nh+h))、n=16~、E(16h)=0、とする。
ここで、v(x)は、厳密解じゃ。
ITERATES([p_↓1 + h, p_↓2 + h(- (v(p_↓1) + p_↓2)^2 + 10/p_↓1^2) + v(p_↓1)
- v(p_↓1 + h)], p_, [16h, 0], 3000)、
により、E(nh)が求められる」
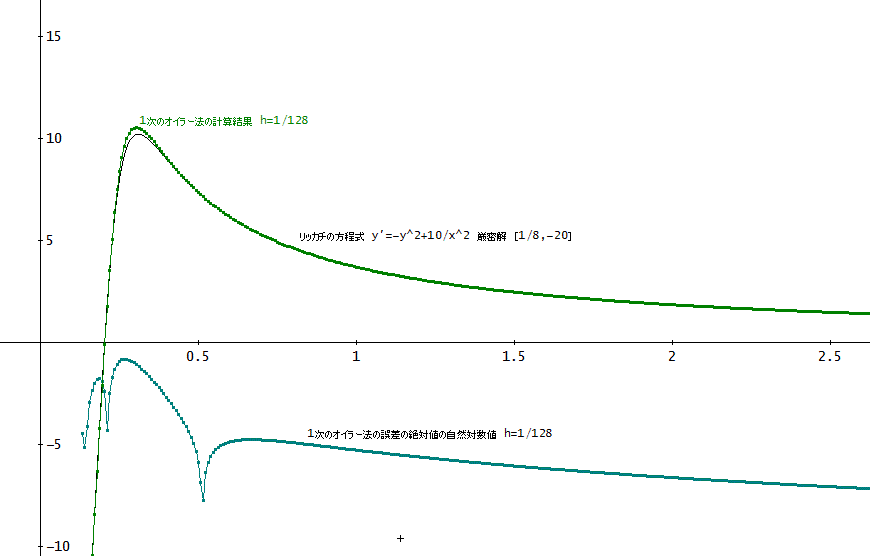
「これを見ると、全体の傾向としては、あたしがやった微分方程式による解析と変わらないようね」
「そこなんじゃな。そこと言っても井戸の底ではないぞ。(これは、何度も言うてる気がする。年のせいかのう)
となると、絶対誤差は、打ち消しあって、増減することもあることを認めんといけないようじゃな。
ちなみに、上のグラフの黒色の線が厳密解、緑色が1次のオイラー法による計算結果を表示している。
y(x)が極大値をとるあたりを除くと、グラフ上では、1次のオイラー法の結果と厳密解には、大きな違いは認められない。
xが大きくなると(計算回数が増えると)、E(x)が単調に増大するというのは、思い込みじゃったかな」
「刻み幅が、もっと、大きい場合をやったみたわ。
h=1/16の場合、
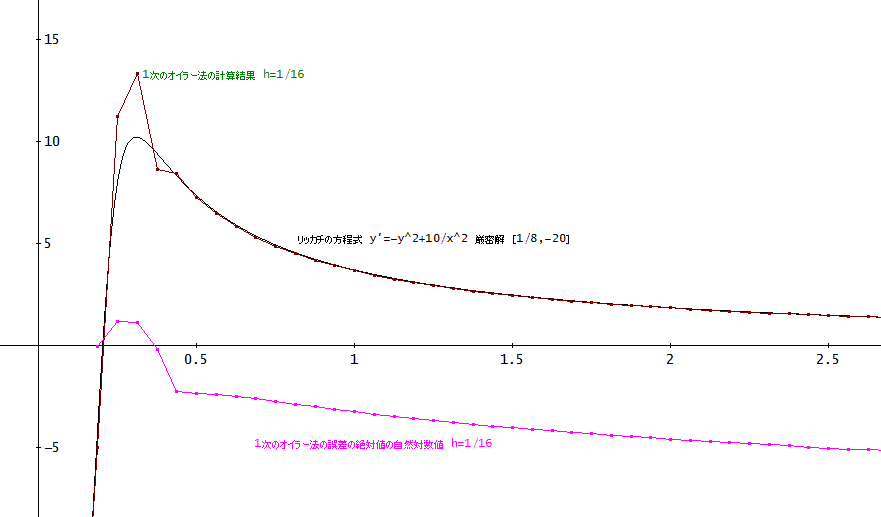
この場合は、明らかに、極大値付近で、絶対誤差が大きくなっているけど、xが大きくなると、厳密解とかなり一致してくる。
また、誤差関数の変化もそれに対応しているようね。ここの誤差関数は、厳密な差分式から計算している」
「なるほどな。
では、厳密解が不明として、やってみることにしよう。
E(x+h)=E(x)+h×r(x,y+E(x))+y(x)-y(x+h)、において、y(x)の関数形が不明とする。
ここで、y(x)-y(x+h)≒-h×r(x,y)-h^2/2×(∂(r,x)+r(x,y)∂(r,y))と近似して、
x=nhと置き、E(nh+h)=E(nh)+h×r(nh,nh+E(nh))-(h×r(x,y)+h^2/2×(∂(r,x)+r(x,y)∂(r,y)))、
ただし、右辺のxは、x=nh、yは、1次のオイラー法による計算値とする。
例題1については、r(x,y)=x+y、初期値[0,0]、h=0.01、とすると、
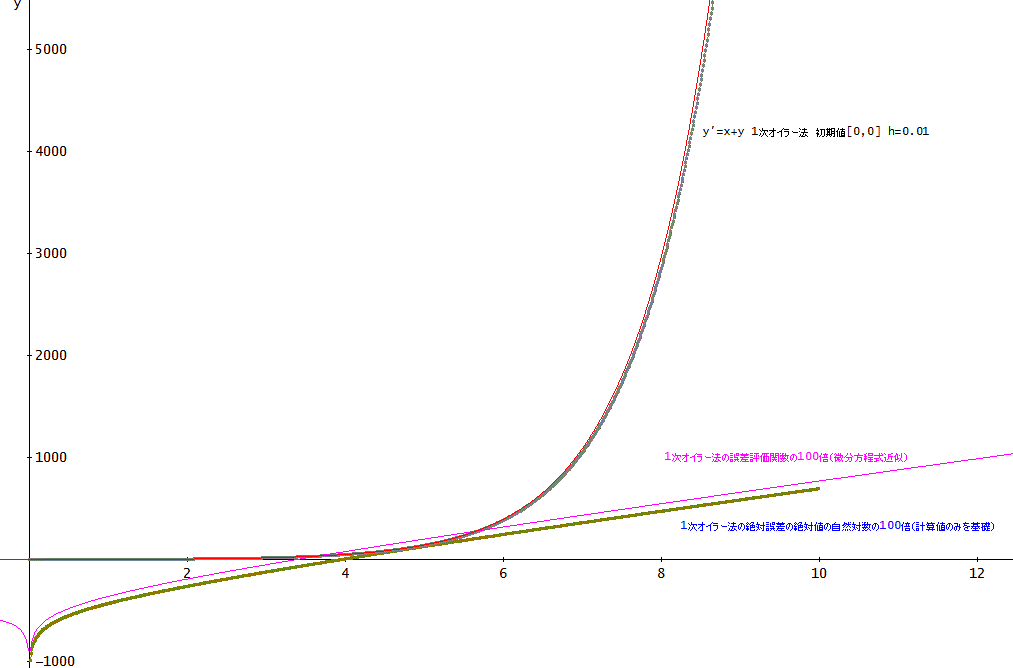
上のグラフでは、厳密解、1次のオイラー法の計算結果及び、
厳密解を基にした微分近似に基づくE(x)の絶対値の自然対数の100倍及び、
計算値のみに基づくE(x)の絶対値の自然対数の100倍を表示している」
「誤差評価については、傾向としては、厳密解に基づくものと方程式の計算結果のみに依存するものとは、同じね。
細かく見ると、厳密解から微分近似で求めたE(x)の方が方程式の計算結果のみに依存するものより大きい(誤差を大きく評価)けれど実際は、どうなのかな?」
「そうじゃな。
x=1、5、10について、下表にまとめた。絶対誤差=(計算結果-厳密解(exp(x)-x-1))じゃ。
| x |
厳密解 |
1次のオイラー法 |
絶対誤差 |
厳密解を基にした微分近似のE(x) |
1次のオイラー法計算値のみに依存するE(x) |
| 1 |
0.7182818284 |
0.7048138294 |
-0.01346799905 |
-0.01359140914 |
-0.01339016747 |
| 5 |
142.4131591 |
138.7727724 |
-3.640386702 |
-3.710328977 |
-3.583484465 |
| 10 |
2.201546579×10^4 |
2.094815563×10^4 |
-1067.310164 |
-1101.323289 |
-1037.581961 |
やはり、厳密解を基にした微分近似式による評価の方が上からの評価であり、厳しいことが分かる。
1次のオイラー法の計算値のみに依存するE(x)は、この場合は、絶対誤差より、やや小さめとなる。
これは、E(nh+h)=E(nh)+h×r(nh,nh+E(nh))-(h×r(x,y)+h^2/2×(∂(r,x)+r(x,y)∂(r,y)))
の右辺第2項のr(x,y)及びその微分内に現れている y を1次のオイラー法によって得た yに等しくしているためじゃろう。
これを避けるためには、E(x)の評価に使用するyの値を、より精度の高いものとする必要がある」
「理屈は、そうなんだけど、誤差評価のためだけに高次まで計算して保持しないといけない訳よね?
それだと、結局は、高次の公式で計算したらどうなの?、という話になってしまうわ」
「ある意味で、矛盾じゃのう。
そもそも、絶対誤差が正しく評価できれば、それを計算結果に反映した数値は、ほぼ厳密解に等しいものじゃからな。
誤差評価は、不要となってしまう。
ここまでのところでは、だいたいの評価で満足しておこう。
さて、例題2の場合も、同様に計算してみた。
y'=-y^2+10/x^2、h=1/128、初期値は、[1/8,-20]、n=3000、
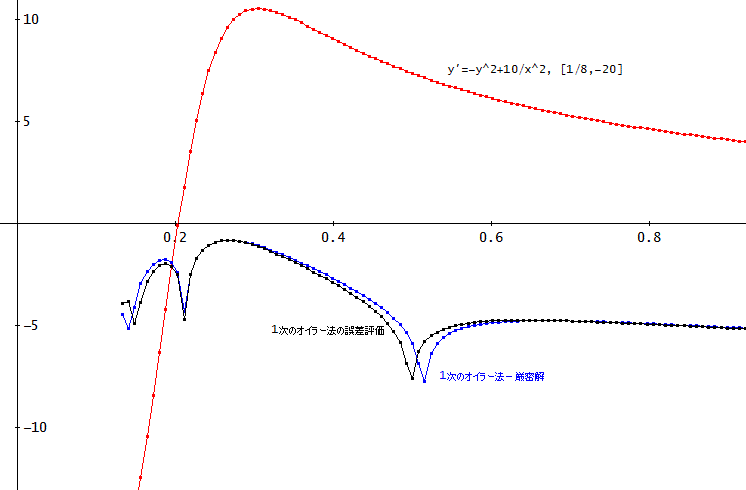
少し分かりにくいかもしれんが、青字の方が1次のオイラー法の計算値から厳密解を引いた値の絶対値の自然対数値じゃ。
黒い曲線の方は、1次のオイラー法の計算ルーチン内で計算した誤差評価関数の絶対値の自然対数値じゃな。
まあ、ほぼ、同様の変化と大きさであると思う。
なお、赤い曲線は、y'=-y^2+10/x^2の厳密解である」
「もっとも、絶対誤差の大きい位置は、x=0.265625
このとき、yの計算値=9.6057207542636890657、誤差評価=0.43953271362963125619、だわ」
オイラー法の打ち切り誤差(2)
「m>=2である m次のオイラー法の計算値を、y(x)+E(x,m)とする。
ここで、E(x,m)は、m次のオイラー法の誤差関数じゃ。
y(x+h)+E(x+h,m)=y(x)+E(x,m)+LIM(Σ(k=1~m)((h^k/k!)×(d/dx)^(k-1)(r(x,y))),y,y+E(x,m))、
y(x+h)=y(x)+Σ(k=1~∞)(h^k/k!×y(k)(x))、とテイラー展開すれば、
E(x+h,m)=E(x,m)+LIM(Σ(k=1~m)((h^k/k!)×(d/dx)^k(r(x,y))),y,y+E(x,m))-Σ(k=1~∞)((h^k/k!×y(k)(x)))、
前節の例題1では、r(x,y)=y+xであれば、d/dx(r)=∂(r,x)+r×∂(r,y)=x+y+1、(d/dx)2(r)=x+y+1、以下すべて同一なので、
∂(E(x,m),x)=E(x,m)×{1+h/2!+h^2/3!+・・+h^(m-1)/m!}-h^m/(m+1)!×y(m+1)(x)、
ただし、E(x,m)の2次以上を無視した。
ここで、S(m)=1+h/2!+h^2/3!+・・+h^(m-1)/m!と置けば、
∂(E(x,m),x)=E(x,m)×S(m)-h^m/(m+1)!×exp(x)、である。(m>=2)
この方程式の解は、E(x,m)=h^m(exp(S(m)x) - exp(x))/((1 - S(m))(m + 1)!)、となる」
| x |
厳密解 |
2次のオイラー法 |
絶対誤差 |
E(x,2) |
4次のオイラー法 |
絶対誤差 |
E(x,4) |
| 1 |
0.7182818284 |
0.7182368625 |
- 4.496589908×10^(-5) |
- 4.541814787×10^(-5) |
0.7182818282 |
- 2.246438565×10^(-10) |
- 2.270926382×10^(-10) |
| 5 |
142.4131591 |
142.4008842 |
-0.01227486841 |
-0.01252365670 |
142.41315904 |
- 6.132569492×10^(-8) |
- 6.262091008×10^(-8) |
| 10 |
2.201546579×10^4 |
2.20118244×10^4 |
-3.643353325 |
-3.764403502 |
2.201546577×10^4 |
- 1.820308022×10^(-5) |
- 1.882360312×10^(-5) |
 「E(x,m)の誤差評価の数値的な一致には、驚いたわ。y=exp(x)-x-1、の場合、
「E(x,m)の誤差評価の数値的な一致には、驚いたわ。y=exp(x)-x-1、の場合、
グラフは、下図の通り。ただし、横軸は、次数 m(2~10)、縦軸は、LN(|E(x,m)|)、x=1、5、10の3通りについて、計算した。

でも、この例では、厳密解が得られているので、E(x,m)が計算できたので、厳密解が得られない場合は、できないわね」
「それは、もっともな疑問じゃ。
とはいえ、y(x)が未知の場合、まあ、未知だから、微分方程式を解くんじゃがの。
E(nh+h,m)≒E(nh,m)+LIM(Σ(k=1~m)((h^k/k!)×(d/dx)^k(r(x,y))),y,y+E(nh,m))-Σ(k=1~m+1)((h^k/k!×y(k)(x)))
を、E(x,m)に関する差分方程式と見なせる。ただし、y(x)のm+2階微分以上を無視した。
Σ内及びy(x)のm+1階微分、y(m+1)(x)は、(d/dx)^(m)(r(x,y))であるので、x=nh、yの値には、近似的に、元の微分方程式の関数計算値を使うことで、Eの評価は、ある程度まで可能と考えられる」
「誤差評価付きのm次までのオイラー法関数を作ってみたよ。
EulermE_user(r, x, y, x0, y0, h, m, n):=
PROG(f_:=∑(difm_user(r, x, y, h, k), k, 1, m),
g_:=∑(difm_user(r, x, y, h, k), k, 1, m + 1),
ITERATES([v↓1 + h, v↓2 + LIM(f_, [x, y], [v↓1, v↓2]), v↓3 + LIM(f_,
[x, y], [v↓1, v↓2 + v↓3]) - LIM(g_, [x, y], [v↓1, v↓2])], v, [x0, y0, 0],
n))、
ここで、Difm_User(f,x,y,h,m)は、既出だけど、再掲すると、
IF(m = 1, h×LIM(f, [u_, v_], [x, y]), h(∂(difm_user(f, x, y, h, m - 1),
x) + LIM(f, [u_, v_], [x, y])∂(difm_user(f, x, y, h, m - 1), y))/m)、となる。
テスト関数、y(x)=exp(x)-x-1、r(x,y)=x+y、h=0.01、m=4の場合は、
EulermE_user(x + y, x, y, 0, 0, 0.01, 4, 1000)、にて計算。
x=10のベクトル要素は、[10, 2.2015465776603636288×10^4, - 1.8172748983520652881×10^(-5)]、
ここで、1番目は、xの値、2番目は、yの計算値、3番目は、新規に追加した E(x,m)=E(10,4)の誤差評価値を示す。
絶対誤差は、「- 1.820308022×10^(-5)」であり、誤差評価は、「 - 1.8172748983520652881×10^(-5)」であるけど、ほぼ、同程度となっていることが分かる」
「m=1、2、4の場合のグラフを描いてみたよ。
y'=x+y、初期値[0,0]、h=0.01、n=2000とした。
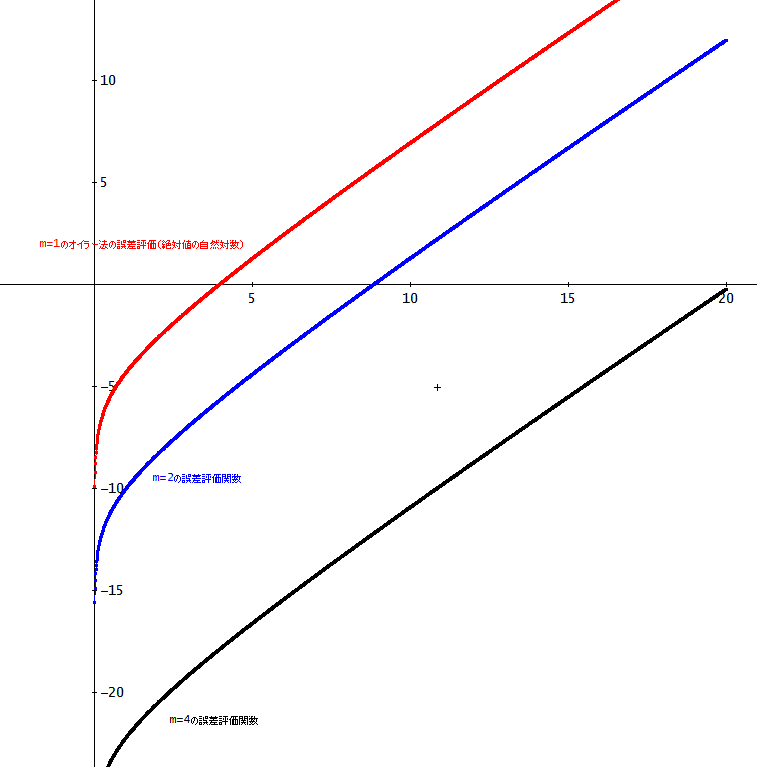
mが増加すると、誤差の評価関数は、大きく減少する。
また、その場合でも、今回のテスト関数(y=exp(x)-x-1)では、hを一定したとき、xが増大すれば、誤差評価関数値は、増加する傾向が反映されている」
4次のルンゲ・クッタ法
「ようやく、ルンゲ・クッタ法に入ってきたな。
今や、計算数学としては、古典となったが、この方面では、先駆的存在であるし、実用面でも、よく使われている(らしい)」
 「でもさ、すでに、私たちは、m次のオイラー法を作っているので、ルンゲ・クッタ法を使わなくても困らないのじゃない?」
「でもさ、すでに、私たちは、m次のオイラー法を作っているので、ルンゲ・クッタ法を使わなくても困らないのじゃない?」
「簡単な方程式については、そうも言えるのう。
コンピューターのリソース(CPU、メモリーなど)が少なかった時代は、たとえば、ヘンリチ先生の本では、「Talor展開法の算法としての欠点は明らかである。この方法では、1個の関数を使うかわりに、m個の関数を同時に扱わねばならない。計算機では、プログラムを記憶するために要する空間が増大する。さらに、(大部分は閉じた形で積分可能である)最も簡単な方程式を除いて、m次導関数を解析的に表現することは、mが増大するのに伴い、ますます複雑になる(y'=x^2+y^2のような簡単に見える微分方程式についてこれを確かめてみられたい)。したがって、この方法を実際に用いることは、一般にすすめられない」と書かれておるがの。
この本の出版は、1973年(昭和48年)じゃからな。時代の流れを感じるのう」
「このTalor展開法というのが、m次のオイラー法のことね。
導関数といっても、m=4でも、4つだからな。一回計算しておけばいいし、長い式にはなるけどね。
例に挙げてある、r(x,y)=x^2+y^2は、1次から4次導関数までの展開で、次式のようになる。
h^4(4x^4y + 3x^3 + 10x^2y^3 + 5xy^2 + 6y^5 + y)/6
+ h^3(x^4 + 4x^2y^2 + 2xy + 3y^4 + 1)/3
+ h^2(x^2y + x + y^3)
+ h(x^2 + y^2)」
「メモリーは、もはや、それほど大きな影響はなかろう。
テイラー展開の面倒や間違いも、わしらのような数式処理ソフトでは、苦にはならない。
問題は、演算速度じゃな。
比較してみよう。精度は、20桁とする」
| 問題[初期値] |
刻み幅h |
点数n |
1次オイラー法 |
2次オイラー法 |
修正オイラー法(2次) |
4次オイラー法 |
6次オイラー法 |
ルンゲ・クッタ法(4次) |
| y'=x+y、[0,0] |
0.0001 |
10000 |
1.44秒 |
1.75秒 |
2.16秒 |
2.03秒 |
2.00秒 |
3.89秒 |
| y'=-y^2+10/x^2、[1/8,-20] |
1/1024 |
10000 |
1.81秒 |
3.95秒 |
5.22秒 |
8.11秒 |
17.9秒 |
8.78秒 |
| y'=cos(x)、[0,0] |
1/128 |
10000 |
2.31秒 |
3.78秒 |
12.1秒 |
3.88秒 |
3.72秒 |
8.03秒 |
「ルンゲ・クッタ(RK)法は、4次のオイラー法と比べて、多少、遅いか、ほぼ同じのようね」
「DERIVEのRK関数は、連立の1階常微分方程式を解くためにも、使えるようになっているため、そういうオーバーヘッドがあるのかもしれんな。
それと、DERIVE側なのか、パソコン側の問題なのかは、不明じゃが、結構、計算時間には、ばらつきが出るのう。
上の表は、ひとつのサンプルに過ぎない」
「4次のルンゲ・クッタ法の精度は、4次のオイラー法と変わらないので、アルゴリズムに工夫があるのね。
修正オイラー法では、台形公式から導いたけど」
「修正オイラー法では、y'=r(x,y)について、y(x+h)≒y(x)+(h/2)×(r(x,y(x))+ r(x+h,y(x+h))と近似した。
ここで、右辺に現れている、y(x+h)≒y(x)+h×r(x,y(x))と置いたのじゃった。
修正オイラー法を分解して書いてみよう。
k1=h×r(x,y(x))
k2=h×r(x+h,y(x)+k1)
y(x+h)=y(x)+(1/2)(k1+k1)
この3つの式を逐次計算することと修正オイラー法とは同等なものとなっている。
4次のルンゲ・クッタ法は、これと横並びの形式となる」
「ルンゲ氏は、数値積分のシンプソン公式の拡張を意識して、ルンゲ・クッタ法を開発したとのことね」
「ヘンリチ先生の本でも、そのような記述があるのう。
さて、オイラー・マクローリンの展開を利用して、f(x)、x=a~bの間をn等分した場合、h=(b-a)/nとすると、
数値積分Iに対する台形公式は、T(n)=h×Σ(k=0~n-1)(f(a+kh))+(h/2)(f(b)-f(a))、と書ける。
I=∫(x=a~b)f(x)dx=T(n)-(h^2)/12(f'(b)-f'(a))+(h^4/720)(f'''(b)-f'''(a))-(h^6/30240)(f'''''(b)-f'''''(a))+・・
ここで、4×T(2n)-T(n)を作ると、∫(x=a~b)f(x)dx≒(1/3)(4×T(2n)-T(n))、の誤差は、hの4次以上となる。
これがシンプソンの公式じゃな。
なお、端点における導関数がゼロまたはゼロに非常に近い場合は、精度が高まる。これは、第53回の「数値積分(2)(Euler-Maclaurin展開とその応用)」で触れた点じゃな。
ところで、本題に戻って、修正オイラー法では、n=1として、f(x)=y'(x)=r(x,y)、a=x、b=x+h、と置き、
∫(x=x~x+h)y'(x)dx=y(x+h)-y(x)≒T(1)=(h/2)(r(x,y)+r(x+h,y(x+h))、と近似したのじゃった。
今回は、∫(x=x~x+h)y'(x)dx=y(x+h)-y(x)≒(1/3)(4×T(2)-T(1))、とシンプソンの公式を元にする。
ここで、T(1)=(h/2)(r(x,y)+r(x+h,y(x+h))
T(2)は、hをh/2として、T(2)=h/2×((r(x,y(x))+r(x+h/2,y(x+h/2)))+(h/4)(r(x+h,y(x+h))-r(x,y(x)))、から、
T(2)=(h/4)(r(x,y(x))+2r(x+h/2,y(x+h/2))+r(x+h,y(x+h)))、となる。
したがって、y(x+h)-y(x)≒(1/3)(4×T(2)-T(1))
=(1/6)(h×r(x,y(x))+4h×r(x+h/2,y(x+h/2))+h×r(x+h,y(x+h)))、が得られる。
ところで、修正オイラー法を分解した例にならうと、
k1=h×r(x,y(x))、
k2=h×r(x+h/2,y+k1/2)、
k3=h×r(x+h/2,y+k2/2)、
k4=h×r(x+h,y+k3)、
と置くことが考えられる。
| |
h |
h^2 |
h^3 |
h^4 |
| k1 |
r(x, y) |
|
|
|
| k2 |
r(x, y) |
Rx(x, y)/2
+ r(x, y)Ry(x, y)/2 |
Rxx(x, y)/8
+ r(x, y)Rxy(x, y)/4
+ Ryy(x, y)r(x, y)^2/8 |
Rxxx(x, y)/48
+ r(x, y)Rxxy(x, y)/16
+ Rxyy(x, y)r(x, y)^2/16
+ Ryyy(x, y)r(x, y)^3)/48 |
| k3 |
r(x, y) |
Rx(x, y)/2
+ r(x, y)Ry(x, y)/2 |
Rxx(x, y)/8
+ r(x, y)Rxy(x, y)/4
+ Ryy(x, y)r(x, y)^2/8
+ Ry(x, y)Rx(x, y)/4
+ r(x, y)Ry(x, y)^2/4 |
Rxxx(x, y)/48
+ r(x, y)Rxxy(x, y)/16
+ Rxyy(x, y)r(x, y)^2/16
+ Ryyy(x, y)r(x, y)^3/48
+ Ry(x, y)Rxx(x, y)/16
+ Rxy(x, y)Rx(x, y)/8
+ r(x, y)Ryy(x, y)Rx(x, y)/8
+ r(x, y)Ry(x, y)Rxy(x, y)/4
+ 3Ryy(x, y)Ry(x, y)r(x, y)^2/16 |
| k4 |
r(x,y) |
Rx(x, y)
+ r(x, y)Ry(x, y) |
Rxx(x, y)/2
+ r(x, y)Rxy(x, y)
+ Ryy(x, y)r(x, y)^2/2
+ Ry(x, y)Rx(x, y)/2
+ r(x, y)Ry(x, y)^2/2 |
Rxxx(x, y)/6
+ r(x, y)Rxxy(x, y)/2
+ Rxyy(x, y)r(x, y)^2/2
+ Ryyy(x, y)r(x, y)^3/6
+ Ry(x, y)Rxx(x, y)/8
+ Rxy(x, y)Rx(x, y)/2)
+ r(x, y)Ryy(x, y)Rx(x, y)/2
+ 3r(x, y)Ry(x, y)Rxy(x, y)/4
+ 5Ryy(x, y)Ry(x, y)r(x, y)^2/8
+ Rx(x, y)Ry(x, y)^2/4
+ r(x, y)Ry(x, y)^3/4 |
| (k1+2k2+2k3+k4)/6 |
r(x, y) |
Rx(x, y)/2
+ r(x, y)Ry(x, y)/2 |
Rxx(x, y)/6
+ r(x, y)Rxy(x, y)/3
+ Ryy(x, y)r(x, y)^2/6
+ Ry(x, y)Rx(x, y)/6
+ r(x, y)Ry(x, y)^2/6 |
Rxxx(x, y)/24
+ r(x, y)Rxxy(x, y)/8
+ Rxyy(x, y)r(x, y)^2/8
+ Ryyy(x, y)r(x, y)^3/24
+ Ry(x, y)Rxx(x, y)/24
+ Rxy(x, y)Rx(x, y)/8
+ r(x, y)Ryy(x, y)Rx(x, y)/8
+ 5r(x, y)Ry(x, y)Rxy(x, y)/24
+ Ryy(x, y)Ry(x, y)r(x, y)^2/6
+ Rx(x, y)Ry(x, y)^2/24
+ r(x, y)Ry(x, y)^3/24 |
y(x+h)-y(x)のTaylor展開
ここで、y'=r(x,y) |
r(x, y) |
Rx(x, y)/2
+ r(x, y)Ry(x, y)/2 |
Rxx(x, y)/6
+ r(x, y)Rxy(x, y)/3
+ Ryy(x, y)r(x, y)^2/6
+ Ry(x, y)Rx(x, y)/6
+ r(x, y)Ry(x, y)^2/6 |
Rxxx(x, y)/24
+ r(x, y)Rxxy(x, y)/8
+ Rxyy(x, y)r(x, y)^2/8
+ Ryyy(x, y)r(x, y)^3/24
+ Ry(x, y)Rxx(x, y)/24
+ Rxy(x, y)Rx(x, y)/8
+ r(x, y)Ryy(x, y)Rx(x, y)/8
+ 5r(x, y)Ry(x, y)Rxy(x, y)/24
+ Ryy(x, y)Ry(x, y)r(x, y)^2/6
+ Rx(x, y)Ry(x, y)^2/24
+ r(x, y)Ry(x, y)^3/24 |
上の表で、k1~k4までは、それぞれ、順にhの1次から4次項までを展開したものじゃ。
ただし、hのべき乗は、1行目に表示しているので、セル内には、記載していない。
そして、6行目に(k1+2k2+2k3+k4)/6を計算している。
なお、ここで、Rxxy(x,y)などは、∂(∂(r(x,y),x,2),y,1)などを記号で分かりやすく表示するためのものじゃ。
y'=r(x,y)から、y(x+h)-y(x)をhの4次まで展開して、上の記号で表記し直したものを7行目に表示している。
6行目の(k1+2k2+2k3+k4)/6 と一致していることを確認して欲しい」
「k1については、そのままだけど、k2=h*r(x+h/2,y+k1/2)をhの4次まで展開しようとするとしっちゃかめっちゃかになってしまう。
どうしたらいいの!」
「わしもそこで悩んだんじゃよ。
正解の表式は、一松先生の本の末尾に掲載されているんじゃが、hのべき乗でまとめられていないところがあるんじゃ。
そこで、確実性を期すため、2通りの方法で計算してみた。
まず、r(x,y):=、として、rを関数として宣言しておく。
このとき、ワークシートの最初に、オプションメニューのモード設定で入力タブの変数の個所で「連続した文字列を1変数と見なす」にチェックしておく。
InputMode:= Word、と表示される。(※通常は、「1文字は1変数と見なす」にチェックが付いている。InputMode := Character)
こうすると、k2は、k×2ではなく、k2という変数とみなされる。これは、あとで、Rxxy(x,y)などの関数名を使う必要があるので、必須じゃ。
変数同士の乗算は、間に必ず*を使用する。k1×2は、k1*2のようにな。
うっかり、k1*2をk12と書いてしまうと、k12という変数になってしまうので、「連続した文字列を1変数と見なす」場合は、特別に注意が必要じゃ。
さて、今回、hで展開したいので、y(x):=の宣言は不要というより、むしろ、有害じゃな。
一度、代入文でy(x):=と宣言してしまうと、当該行を削除しても、y(x)の定義を削除できなくなり、新しいワークシートにする必要が出てきて面倒じゃ。
一方、Rx(x,y):=などは、宣言しておく。(Rxなどの宣言は必須ではないが、見やすくするために行ったことじゃな)
(1) DERIVEのテイラー展開を生かす方法(1変数ずつ展開)
1. k2の計算を行うため、h*r(x+h/2,y)をhの4次まで展開する。
2. 1.で展開した式中の∂(r(x, y), x)などをRx(x,y)などと、代数メニューの「式の置換」で置き換える。
3. 代数メニューの「変数の置換」により、2.の展開式のyをy+h*r(x,y)/2と置き換える。
4. 3.をTaylor(式,h,0,4)として、hの4次までとする。
5. 4.の中のLIM(∂(Rx(x, @), @, 2), @, y)などをRxyy(x,y)など、式の置換で置き換える。
6. 5.でk2が得られる。
7. k3の計算では、2.までは同様に行う。
8. 代数メニューの変数の置換により、2.の展開式のyをy+p/2と置き換える。
ここで、pは適当な変数名。
9. 8.の式をpで4次まで展開する。
10. 9.の式のpをk2で置き換える。
11. hの5次以上の項目も含まれているので、Taylor(式,h,0,4)として、hの4次までにする。
12. 再び、∂(Rx(x, y), y, 2)などをRxyy(x,y)などと式の置換で置き換える。
13. 12.で置き換えたものが、k3となる。
14. k3と同様に、k4:=h*r(x+h,y+k3)の計算を行う。
15. 結果をまとめる。
(2)再帰関数を定義して使う方法
(1)の計算結果と一松先生の本の回答が、k3で合わないと思い込んだので、実は、こちらの方法を最初にやってみたのじゃ。
k2を求めるためには、まず、k2m(x, y, m):=
IF(m = 1, hr(x, y), h/2(1/(m - 1))(∂(k2m(x, y, m - 1), x) + k∂(k2m(x,
y, m - 1), y)))
のように、再帰的に定義する。
上式の中の、kは、仮の変数で、後で、k=r(x,y)と置き換える。
最初から、kをr(x,y)とおいてしまうと、r(x,y)を含めて、xで偏微分することになってしまうのでな。
そして、k2:=TAYLOR(LIM(∑(k2m(x, y, j), j, 1, m), k, r(x, y)), h, 0, m))と、する。
Σは、1次からm次までの和を取り、LIM関数で、hのm次までに整理する。
以下同様に、k3、k4もできる。
ただ、この方法を試みているうちに、結局は、(1)と同一と分かり、再度、一松先生の本を見ると正解であることが分かったという次第じゃ」
「k2とk3のところは、シンプソン公式(のかっこ内)は、4×r(x+h/2,y(x+h/2))なんだけど、なぜ、4×k3ではなくて、2×k2+2×k3としているんだろう」
「いや、そこが不思議じゃったので、細かく計算してしまったのじゃな。
k2=h×r(x+h/2,y+k1/2)=h×r(x+h/2,y+h*r(x,y)/2)は、r(x+h/2,y(x+h/2))の第1近似値じゃ。
それを使って、k3=h×r(x+h/2,y+k2/2)とk3を計算すると、当然ながら、r(x+h/2,y(x+h/2))の第2近似値となると思う。
じゃによって、2×k2+2×k3ではなくて、4×k3となるのではとな」
「でも、それじゃ、合わなかったのね」
「ま、強いて言えば、4×(k2+k3)/2=2×k2+2×k3、という考えからかとも思うがの。
打ち切り誤差を指定しても、ルンゲ・クッタの公式の分点の取り方や係数には、任意性があるので、多数の候補が考えられる。
しかし、一松先生の本をはじめとして、一般には、ここで紹介したものが、最も簡単な係数とのことじゃ。
今回は、だいぶん長くなったので、この辺でおしまいにしよう。
次回は、今回の補足と物理などで多く現れる2階以上の微分方程式を1階の連立微分方程式として解く方法について説明しよう」
4次のルンゲ・クッタ法(追記:2014/10/3)
前節の(1)の方法は、やや、つたなかったので、少し一般的な改良を追記する。
h*r(x+p,y+q)の2変数関数のテイラー展開の定理により、
h*r(x+p,y+q)=h*Σ(k=0~∞)(1/k!)(p*d/dx+q*d/dy)^k×r(x,y)、
なお、(p*d/dx+q*d/dy)^kは、演算子的に右側のr(x,y)に働くものとする。
この演算子的な部分を具体的に展開すると、
Σ(k=0~∞)(1/k!)Σ(j=0~k)Comb(k,j)(p^j∂(r,x,j)+q^(k-j)∂(r,y,j))
=Σ(k=0~∞)Σ(j=0~k)(p^j/j!×∂(r,x,j)+q^(k-j)/(k-j)!×∂(r,y,j))、
従って、h*r(x+p,y+q)をm-1項まで、計算したものは、
h*Σ(k=0~m-1)Σ(j=0~k)(p^j/j!×∂(r,x,j)+q^(k-j)/(k-j)!×∂(r,y,j))
上の展開式で、m=4、p=h/2、q=h*r(x,y)/2、と置けば、
(h^4r(x, y)∂(∂(r(x, y), x, 2), y)/16 + h^4r(x, y)^2∂(∂(r(x, y), x), y,
2)/16 + h^3r(x, y)∂(∂(r(x, y), x), y)/4 + h^4∂(r(x, y), x, 3)/48 + h^3∂(r(x,
y), x, 2)/8 + h^2∂(r(x, y), x)/2 + h^4r(x, y)^3∂(r(x, y), y, 3)/48 + h^3r(x,
y)^2∂(r(x, y), y, 2)/8 + h^2r(x, y)∂(r(x, y), y)/2 + hr(x, y))、が得られる。
これは、前節で求めたk2である。
k3を求める場合は、m=4、p=h/2、また、qに含まれるhの最大次数をαとすると、α=m-k、程度で十分であるので、
q=Taylor(k2,h,0,m-k)/2、とする。(実際は、もっと、少なくともよいがここでは、このようにしておく)
そして、k3=Taylor(展開式,h,0,4)とするのが簡便である。
k3=h^4r(x, y)∂(∂(r(x, y), x, 2), y)/16 + h^4r(x, y)^2∂(∂(r(x, y), x),
y, 2)/16 + h^4∂(r(x, y), x)∂(∂(r(x, y), x), y)/8 + h^4r(x, y)∂(r(x, y),
y)∂(∂(r(x, y), x), y)/4 + h^3r(x, y)∂(∂(r(x, y), x), y)/4 + h^4∂(r(x, y),
x, 3)/48 + h^4∂(r(x, y), x, 2)∂(r(x, y), y)/16 + h^3∂(r(x, y), x, 2)/8
+ h^4r(x, y)∂(r(x, y), x)∂(r(x, y), y, 2)/8 + h^3∂(r(x, y), x)∂(r(x, y),
y)/4 + h^2∂(r(x, y), x)/2 + h^4r(x, y)^3∂(r(x, y), y, 3)/48 + 3h^4r(x,
y)^2∂(r(x, y), y)∂(r(x, y), y, 2)/16 + h^3r(x, y)^2∂(r(x, y), y, 2)/8 +
h^3r(x, y)∂(r(x, y), y)^2/4 + h^2r(x, y)∂(r(x, y), y)/2 + hr(x, y)、
k4も、m=4、p=h、q=Taylor(k3,h,0,m-k)として、k4=Taylor(展開式,h,0,4)とする。
k4=h^4r(x, y)∂(∂(r(x, y), x, 2), y)/2 + h^4r(x, y)^2∂(∂(r(x, y), x), y,
2)/2 + h^4∂(r(x, y), x)∂(∂(r(x, y), x), y)/2 + 3h^4r(x, y)∂(r(x, y), y)∂(∂(r(x,
y), x), y)/4 + h^3r(x, y)∂(∂(r(x, y), x), y) + h^4∂(r(x, y), x, 3)/6 +
h^4∂(r(x, y), x, 2)∂(r(x, y), y)/8 + h^3∂(r(x, y), x, 2)/2 + h^4r(x, y)∂(r(x,
y), x)∂(r(x, y), y, 2)/2 + h^4∂(r(x, y), x)∂(r(x, y), y)^2/4 + h^3∂(r(x,
y), x)∂(r(x, y), y)/2 + h^2∂(r(x, y), x) + h^4r(x, y)^3∂(r(x, y), y, 3)/6
+ 5h^4r(x, y)^2∂(r(x, y), y)∂(r(x, y), y, 2)/8 + h^3r(x, y)^2∂(r(x, y),
y, 2)/2 + h^4r(x, y)∂(r(x, y), y)^3/4 + h^3r(x, y)∂(r(x, y), y)^2/2 + h^2r(x,
y)∂(r(x, y), y) + hr(x, y)、
これらと、k1=h*r(x,y)から、(k1+2*k2+2*k3+k4)/6を作ると、
(h^4r(x, y)∂(∂(r(x, y), x, 2), y)/8 + h^4r(x, y)^2∂(∂(r(x, y), x), y, 2)/8
+ h^4∂(r(x, y), x)∂(∂(r(x, y), x), y)/8 + 5h^4r(x, y)∂(r(x, y), y)∂(∂(r(x,
y), x), y)/24 + h^3r(x, y)∂(∂(r(x, y), x), y)/3 + h^4∂(r(x, y), x, 3)/24
+ h^4∂(r(x, y), x, 2)∂(r(x, y), y)/24 + h^3∂(r(x, y), x, 2)/6 + h^4r(x,
y)∂(r(x, y), x)∂(r(x, y), y, 2)/8 + h^4∂(r(x, y), x)∂(r(x, y), y)^2/24
+ h^3∂(r(x, y), x)∂(r(x, y), y)/6 + h^2∂(r(x, y), x)/2 + h^4r(x, y)^3∂(r(x,
y), y, 3)/24 + h^4r(x, y)^2∂(r(x, y), y)∂(r(x, y), y, 2)/6 + h^3r(x, y)^2∂(r(x,
y), y, 2)/6 + h^4r(x, y)∂(r(x, y), y)^3/24 + h^3r(x, y)∂(r(x, y), y)^2/6
+ h^2r(x, y)∂(r(x, y), y)/2 + hr(x, y))、となる。
一方、前回の記事で定義した、Difm_user(f,x,y,h,n)から、Σ(n=1~4)(Difm_user(r(x,y),x,y,h,n)を計算し、上で計算した、(k1+2*k2+2*k3+k4)/6、から減ずると、ゼロになり、両者がh^4の項まで等しいことが確認できる。
最終更新日 2014/10/3



 「やっと、数値解法にたどり着いたわね」
「やっと、数値解法にたどり着いたわね」 しかし、今ひとつ、ぴんとこないのじゃが、普通のヤシとは、だいぶん違うようじゃ。
しかし、今ひとつ、ぴんとこないのじゃが、普通のヤシとは、だいぶん違うようじゃ。