「数式処理ソフト DERIVE（デライブ）では、１８．関数の定義で、『帰納的（再帰的）定義関数』がでてきているわね」
「お、ともちゃんか。
さすが、『DERIVE de ドライブ』の担当者じゃな。
2013年の今月のご挨拶で『干支拳』を取り上げたな。
与えられた関係行列を基にして、ある頂点からすべての頂点をたどることが出来るかどうか、あるいは、その経路を求めたいということがあったのは、覚えているじゃろう」
「そうだったわね。
結構、大変だったという話よね」
「そうなのじゃ。
出来てみると、たいしたことがないものじゃが、二、三日かかってしまった。
それは、ExcelのVBAで書いたプログラムじゃったが、『再帰関数』なり『再帰手続き』を使う場面では、どうしても、試行錯誤に陥りがちなところがあるのう。
今回、DERIVEで、そのあたりを、ゆっくりと、再確認しておこうと、こういうことなのじゃ」
「なるほど。
再帰関数、ぶらり旅、ということね」
「なお、再帰的帰納関数とも、言われるが、以下では、簡単に『再帰関数』という呼び方にしておこう」
「もっとも、基本的なところから、ということで、等差数列・等差級数から始めてみよう」
「いまは、中学校で習うのかしらね。
x,yなどの代数記号を知ってからでないと、説明が難しいものね（できないわけじゃないけど、鶴亀算のときみたいにかえって分かりづらそう）」
「初項をa、公差をd、一般項の番号をnで表そう。
等差数列は、a+ndとなる。ここで、n=0～の整数とする」
「等差級数の方は、ガウスの小さい頃のエピソードで有名よね。
第61回の『多面体の体積公式』で取り上げられてます。
等差数列の第m項までの和 S(m) は、DERIVEでは、『解析』メニューの『総和』から行うと、
S(m)=(m + 1)(2a + d*m)/2 と求められる。
ガウスのお話しに出てくる例は、ここで、a=0、d=1、m=100のとき（または、a=1、d=1、n=99）なので、答えは、5050となる」
「等差数列の方は、やはり、『解析』メニューから、『数列の作成』を指示して、nの範囲を指定、たとえば、n=0～10とすると、
[a, a + d, a + 2d, a + 3d, a + 4d, a + 5d, a + 6d, a + 7d, a + 8d, a +
9d, a + 10d]
のように、ベクトルとして、答えが与えられる。
以上のように、利用者が定義するまでもなく、DERIVEの標準の機能から、容易に計算できる」
「だけど、それらの機能を使わないときはどうするか、ということね」
「そうじゃな。
自分にとって、わかりにくい機能を練習するときは、よく知っている事柄を題材として、取り上げるのが良いと思う。
まずは、再帰関数で、等差数列の一般項を得る方法じゃ。
一般項をf(n,a,d)で表そう。
これは、解説するまでもないが、IF関数を使って、
f(n,a,d):=IF(n = 0, a, f(n － 1,a,d) + d)
と、再帰的に定義できる。
ここで、たとえば、f(10,a,d)とすれば、a+10dのように11項目が得られる。
なお、初項をn=1で表して、その値を aとしたい場合は、
f(n, a, d):= IF(n = 1, a, d + f(n － 1, a, d))とする。
ただし、f(n,a,d)=a+nd、と一般項が得られるわけではない点に注意じゃ」
「関数の定義は、さっきのように、直接、入力してもいいけど、普通は、『入力』から、『関数の定義』でよかったのよ。
一方、和の方はというと、n=0～mまでの和として、S(m,a,d)と書くことにすれば、
S(m,a,d):= IF(m = 0, a, S(m － 1, a, d) + m*d)
と再帰的に定義できる。ここで、m=100、a=0,d=1 とすれば、5050なる答が得られる。
実際は、∑(f(n, a, d), n, 0, m)とすれば、簡単だけど」
「一般項の方をベクトルで得るには、通常は、『解析』メニューから『数列の作成』とすれば、よい。
しかし、すぐに計算せずに『命令式』のボタンを押すか、同じことじゃが、直接、Vector関数を使えば、ベクトルとして数列が得られる。
VECTOR(f(n), n, 0, 10, 1)のようにな」
「は～い。読者のみなさま。
第23回の『ベクトルと行列（マトリックス）』で、ちょっとだけ、登場した関数よ。
覚えていてくれたかしら？
Vector（数式，変化させたい変数，その変数の初期値，変数の終了値，変数の増分値）という記法になるのよ。
この『数式』は、計算可能な式ならば、再帰関数であってもなくても任意なのね。ま、当然よね。
このベクトルの第k項を取り出すときは、ベクトルをvで表したとき、v↓k（これは、式番号↓kでもよい）とするんだったの。
ただし、ベクトルの要素番号は、1番から始まるので、v↓k=f(k－1)が得られることに注意してね」
「まとめると、再帰関数 f(n)、ここで、n=n0から計算可能であれば、
f(n):=IF（n=n0，f(n0)，f(n－1)を含んだ式）のように定義すればよい、ということじゃ」
「nがn0より小さい値を入れないように利用者が注意するのね」
「まあ、プログラムで書く場合には、そのような範囲外の入力データの値チェックは、必要じゃ。
ただ、ここでは、エラーチェックについては、触れないようにしよう。
なお、あとで、フィボナッチ数列の漸化式による定義を述べるので、等差数列についても、一応、漸化式を書いておこう。
これは、f(n)=f(n－1)＋d、f(0)=a である」
「初項a、公比rの等比数列は、
f(n, a, r):=IF(n = 0, a, r*f(n － 1, a, r))、のごとく、定義できる」
「VECTOR(f(n, a, r), n, 0, 10, 1)とすれば、
[a, ar, ar^2, ar^3, ar^4, ar^5, ar^6, ar^7, ar^8, ar^9, ar^10]
のように、第11項までの値が表示できる」
「一方、和の方は、s(m, a, r):= IF(m = 0, a, s(m － 1, a, r) + ar^m)
のようになるわ。
Σ関数を使って、書いた方が分かりやすい。
慣れているせいもあるけども」
「ここで、DERIVEでの繰り返し処理を取り上げよう。
再帰関数について、良く言われるのが、再帰関数として定義するよりも、ループ処理（VBAなどの、For k=1 to n ～ next k）で書ける場合は、その方が速いということじゃ」
「DERIVEで、ループ処理は、どう書いたらいいのかしら」
「29回の方程式の数値解法の章で、ITERATE関数及びITERATES関数について、少し触れてはいるがの」
「そうだったわね。
等差数列を例にすると、簡単なために、a=0、d=1として、第n+1項は、
h(n):=ITERATE(k+1, k, 1, n)
のように、ITERATE関数を使って定義すれば、ループ処理でも書けるのね」
「Iterate関数で、ITERATE(k + 1, k, 1, n)の第1引数の関数、k+1全体の初期値が、第3引数の1となっているのじゃ。
k+1が1とされて（ここは重要じゃ）、次に、その値が、変数kに代入されて、それが、第1引数のk+1に反映されて、・・という流れになる。
この、k+1→kの回数が、第4引数（ここでは、n）回繰り返される。
すなわち、初期値の代入を含めると、第4引数+1回実行する」
「他の例で挙げるとどんな使い方があるかな？」
「ITERATE(√x, x, 2, 10)とすれば、1.000677130 がとなり、どんどんと、1に近い値になる。
2に対して、平方根を繰り返しとった場合の推移じゃ。11項目は、2の1024乗根（2^10=1024）じゃ。
これを利用すると、Ln(x)≒－ x^2/2 + 2x － 3/2 程度の展開でも、x=2^(1/1024)として、
Ln(2)≒1024*（x^2/2 + 2x － 3/2）≒0.6931470718となり、
Ln(2)≒(0.6931471805)と比較して、8桁の精度が出ている。
もし、2をそのまま使うと、0.5が得られるだけじゃから、驚く」
「Iterates関数との違いは、何でしたっけ？」
「Iterates関数は、結果をベクトルとして、返す関数じゃな。
ITERATES(√x, x, 2, 5)とすると、[2, √2, 2^(1/4), 2^(1/8), 2^(1/16), 2^(1/32)]を得る」
「等差数列の和の方は、どうすればいいのかな？
和を保存しておく変数をIterate関数なりで、どう定義していいか分からない」
「そこなんじゃ。
そこと言っても、井戸の底ではないぞ！
DERIVEでは、Iterate関数の中で、ベクトルを変数として利用できるので、それを使う。
今、模式的に示すと、一般項は、a+nd、であり、和は、n=0～mまで取るものとする。
ここで、ベクトル v:=［v1,v2］を考える。
n回目の繰り返しの際に、［Σ（n=0～m）（a+nd），a+（m+1）d］のように、vを変化させることを考える。
そのためには、v1の初期値は、aであり、v2の初期値は、a+d である。
そして、v1＋v2→v1、v2＋a+d→v2とする必要がある。
ITERATES([v↓1 + v↓2, v↓2 + d], v, [a, a+d], 5)
のように、第6項までの和がv1に求められている」
「なるほど。
ベクトルの次元は、2次元までしか、許されないのかしらね？」
「いや、これは、3次元でもよい。
上の例で言えば、v↓3に、項の番号nを入れることも出来る。
ITERATES([v↓1 + v↓2, v↓2 + d, v↓3 + 1], v, [a, a + d, 1], 5)
とすればよい。
このようにすれば、v↓3に、項の番号nを入れておくことも出来る。
言い換えれば、VBAなどでの、Forループの制御変数と同一の値を入れておくことが出来る」
「f(0)=0、f(1)=1、f(n)=f(n－1)+f(n－2)で定義される数列を『フィボナッチ数列』というのは、ともちゃんも知っておるじゃろう。
イタリアの数学者、フィボナッチ（Fibonacchi：1180－1250）による。
後述の『数学100の問題』によると、ウサギが次々と子供を作った場合の増え方から、彼が思いついたとのこと。
さて、再帰的定義で書くと、
f(n):= IF(n < 2, n, f(n － 1) + f(n － 2))
となる。上式では、f(0)=0、f(1)=1であり、たまたま、f(n)のnと同じ値であるため、If文を簡素化できている。
もし、違う条件であれば、
g(n):= IF(n = 0, 1, IF(n = 1, 3, g(n － 1) + g(n － 2)))
のように、多重IF文を利用する必要があるのう。
いずれにしても、nが20程度までは、1秒以下で計算できるが、nが30程度まで大きくなると、極度に時間がかかる。
最初のf(n)の31項までは、次のとおりじゃ。
これは、解析メニューの数列の作成又はVector関数を使って得られたものじゃ。
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,
2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811,
514229, 832040]」
「ホント。
f(20)は、0.17秒なのに、f(30)では、なんと、16.9秒もかかるの」
「このフィボナッチ数列じゃが、前節のIterate関数を使うと、素早く計算できると想像できるじゃろう」
「Iterate([v↓1+v↓2,v↓1],v,[0,1],n)のようにすれば、いいのね。
すごいわね。
瞬時に、832040と求められるわ」
「正確には、2次元ベクトルとして、([832040, 514229])が得られて、第1項が、f(30)となる訳じゃ。
（第2項は、f(29)）
もし、第1項だけとりだしておきたい場合は、Iterate関数の式番号↓1とすれば、よい。
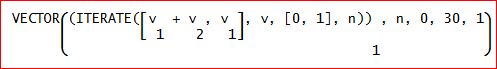
上図のようにな」
「日本評論社の『数学100の問題』（1984年）によると、フィボナッチ数列の隣接する2項の比の極限値があるのね。
実際、
[1, 2, 1.5, 1.666666666, 1.6, 1.625, 1.615384615, 1.619047619, 1.617647058, 1.618181818, 1.617977528, 1.618055555, 1.618025751, 1.618037135, 1.618032786, 1.618034447, 1.618033813, 1.618034055, 1.618033963, 1.618033998]
のように、ほぼ、1.618033・・になる。
で、f(n)=f(n－1)＋f(n－2)から、f(n)/f(n－1)→α、ただし、n→∞と考えると、
αは、α=1+1/αを満たす。
この解は、α = 1/2 － √5/2 または β = √5/2 + 1/2となるけど、n→+∞の場合の極限値は、正の値の、√5/2 + 1/2≒1.618033988・・の方となる」
「そうじゃな。
フィボナッチ数列の話題は、多いので、また、『奥のわき道』かもしれんが、次節で、少しだけ触れてみよう」
「まずは、一般項を閉じたかたちで書けることについて、解説しなければならんじゃろう。
以下では、f(0)=1、f(1)=1、f(2)=1、・・・のような数列を考える。
さて、f(n)=f(n－1)+f(n－2)は、（同次線形）定差方程式なので、標準的には、f(n)=ρ^nと、まずは、置いてみる。
すると、ρの満たす方程式は、ρ^2－ρ－1=0となり、2根は、ρ1 = 1/2 ＋ √5/2、ρ2 = 1/2－√5/2 となる。
なお、この2根は、前節の極限値でもある。
ところで、どちらのρを使っても、方程式を満足する。この2根を使った、ρ^nは、方程式の特殊解となっているという訳じゃな。
一方、この方程式は、『線形』なので、特殊解の線形結合の式、
A(ρ1)^n＋B（ρ2）^n、ここで、A、Bは、nによらない定数、もまた、方程式を満足する。
この定数 A、Bは、初期条件、f(0)=0、f(1)=1を満足するように決めれば、よい。
すると、A=√5/5、B=－√5/5と求められる。
これで、一般項は、f(n)=（1/√5）((√5/2 + 1/2)^n － (√5/2 － 1/2)^n(－1)^n)、となる。
ここで、DERIVEでは、今ひとつきれいな形にならないので、少し、手伝ってあげると、公式集に載っている形、
f(n)=（1/√5）((1/2＋√5/2)^n － (1/2－√5/2)^n)と変形することができる。
数列を作ってみると、n=0～20で、
([0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765])
のように正しく、フィボナッチ数列を再現できていることが分かる。
この公式を『ビネの公式』（P.M.Binet：1786－1856）と呼ぶ」
「なるほど。
無理数が入っていて、n乗しているのに、整数しか出てこないところは、まったくオドロキです。
上の方法は、一般の線形の定差方程式に適用できるということね」
「線形の微分方程式と、似た解き方になっている。
なお、f(n)=f(n－1)+f(n－2)なので、f(n)/f(n－1)=1+f(n－2)/f(n－1)=1+1/（f(n－1)/f(n－2)）
右辺は、1+1/（f(n－1)/f(n－2)）=1+1/（1+1/（f(n－2)/f(n－3)）・・と連分数の形で書けることに気がつくかも知れない。（いや、気がついて欲しい）
すると、左辺の極限値がρ1=√5/2 + 1/2であることを使うと、
結局、√5=2（1+1/(1+1/(1+・・）－1、これでは、はなはだ、見にくいので、整理すると、
√5は、再帰関数g(n)を使って、g(n):= IF(n =1, 1, 1 + 1/g(n － 1))としたとき、n→∞で、√5=2g(n)－1
となることがわかる。
実際、n=20までの変化を見ると、
([1, 3, 2, 2.333333333, 2.2, 2.25, 2.230769230, 2.238095238, 2.235294117,
2.236363636, 2.235955056, 2.236111111, 2.236051502, 2.236074270, 2.236065573,
2.236068895, 2.236067626, 2.236068111, 2.236067926, 2.236067997])となっていて、
真値は、√5≒2.236067977と比較して、近づくことが分かる。nが30程度で、10桁の精度では、一致する。
これは、√5≒930249/416020であり、無理数を有理数で近似する場合に連分数展開が有効なことを示している例であると言われる」
「とは言っても、Newton法で、x^2－5=0を解くとして、初期値を2として、容易に、
ITERATE(x/2 + 5/(2x), x, 2, 5)とすれば、(5374978561/2403763488)≒2.236067977が求められるもの。
これは、もちろん、NEWTON(x^2 － 5, x, 2)とするのが、DERIVE流だけど」
「最後に、天下り式で申し訳ないが、フィボナッチ数列の母関数は、1/(1－x－x^2)じゃ。
母関数とは、1/(1－x－x^2)=Σ（f(n+1)x^n）、n=0、1、・・・。
※f(n+1)=Lim（x→0）（∂(1/(1 － x － x^2), x, n)/n!となっている。青字部分を2013/1/25に訂正、追加。
なお、今回は、f(0)=0、f(1)=1、ｆ（2）＝1、・・という、フィボナッチ数列を使っているため、係数に少し手を加えている。
さて、n=0の場合も補って、g(n)を次のように定義すると、
g(n):=IF(n = 0, 0, 1/(n － 1)!×LIM(∂(1/(1 － x － x^2), x, n － 1), x, 0, 0))
たとえば、g(0)以降、g(20)までで、
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,
2584, 4181, 6765, 10946]のように、フィボナッチ数列が求められる。
なお、上のg(n)の定義では、DERIVEの第n階微分を使っている。
これを避けるには、やや煩雑になるが、3次元ベクトル変数を利用し、Iterate関数又はIterates関数を使って記述する方法もある。
ITERATE([LIM(v↓2, x, 0), (1/v↓3)×∂(v↓2, x), 1 + v↓3], v, [0, 1/(1 － x － x^2), 1], n)、
この場合、n=0～とすると、vの第1項にフィボナッチ数列の値が入ることになる。
何で、1/(1－x－x^2)を思いついたのだという内心の声もあるが、再帰関数については、まだ、いろいろと、題材があるので、次回のお楽しみとしておこう。
いや、ともちゃんも、お疲れさんじゃった」
最終更新日 2013/1/25、2014/9/11（ITERATE（s）関数の第5引数を第4引数に名称を修正）
