数式処理ソフト DERIVE(デライブ) de ドライブ
63.再帰関数(2)(数列の母関数、固有値のべき乗法)
フィボナッチ数列の母関数
「数式処理ソフト DERIVE(デライブ)の第62回の『再帰関数(1)』で、宿題になっていた、フィボナッチ数列の母関数の件じゃがな。
g(x)=1/(1-x-x^2)として、g(x)=1 + 1x + 2x^2 + 3x^3 + 5x^4 + 8x^5 + 13x^6 + 21x^7 + 34x^8 + 55x^9 + 89x^10・・
とx=0でテイラー展開できる。x^nの係数を見てみると、フィボナッチ数列のf(n+1)であることが分かる。
念のため、n=0~11までを、再掲すると、([0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89])
なお、前回、説明しているように、ここでのフィボナッチ数列は、f(0)=0、f(1)=1を初期値とし、f(n)=f(n-1)+f(n-2)のように漸化式で定義されているものとする」
 「なるほど、確かに、f(1)以降と、g(x)のテイラー展開の係数が一致しているわね」
「なるほど、確かに、f(1)以降と、g(x)のテイラー展開の係数が一致しているわね」
「まずは、g(x)が母関数であるとして、そのx^nの展開係数がf(n+1)になることを説明してみよう。
母関数の分母は、1-x-x^2=(x-ρ1)(x-ρ2)、ここで、ρは、前回出てきている、ρ1=(√5-1)/2、ρ2=-(√5+1)/2とする」
「あー、分かった。
部分分数に展開するのね。
g(x)=1/(1-x-x^2)={1/(ρ1-ρ2)}{(1/ρ1)(1/(1-(x/ρ1))-(1/ρ1)(1/(1-(x/ρ2))}、
ここで、1/(1-r)=1+r+r^2+・・を使うと、
g(x)={1/(ρ1-ρ2)}{(1/ρ1-1/ρ2)+(1/ρ1^2-1/ρ2^2)x+(1/ρ1^3-1/ρ2^3)x^2+・・・}、
なので、
g(x)=Σ(n=0~∞)(√5(√5/2 - 1/2)^(n + 1)(-1)^n/5 + √5(√5/2 + 1/2)^(n + 1)/5)x^n
=Σ(n=0~∞)(1/√5)(1/2+√5/2)^(n+1)-(1/2-√5/2)^(n+1))x^n、
一方、第62回のビネの公式によると、
f(n)=(1/√5)(1/2+√5/2)^n - (1/2-√5/2)^n)なので、
f(n+1)=(1/√5)(1/2+√5/2)^(n+1) - (1/2-√5/2)^(n+1)となるので、g(x)のx^nの係数とf(n+1)が等しいことが分かるってことか。
でも、母関数の右辺の無限級数は、収束するの?」
「母関数を数列の一般項や漸化式の導出等に利用しているときは、xとは書いてはいるものの、それは、□でも○でもよい(『不定元』と呼ばれるらしい)ので、級数も形式的なものであるから、その収束は、無視して取り扱ってよい。収束範囲の吟味が必要なときは、母関数を使って、級数の和を評価したいときなどじゃな。
収束範囲外では、母関数自体の計算はできても、両辺は、等しくなくなり、級数は、振動するか、発散してしまうかであろうから」
数列の母関数の例
「母関数の例は、多い。
すでに、ベルヌーイ(ベルヌイ)数の母関数が登場している。(第52回『数値積分公式(1)(台形公式とベルヌイ数)』)
母関数は、x/((exp(x)-1)じゃった。
ベルヌーイ数 B(n)は、ΣB(n)x^n/n!、で定義される。ここで、n=0~∞、とする。
0から50番目までの部分は、再掲すると、
[1, - 1/2, 1/6, 0, - 1/30, 0, 1/42, 0, - 1/30, 0,
5/66,
0, - 691/2730, 0, 7/6, 0, - 3617/510, 0, 43867/798, 0, - 174611/330,
0, 854513/138, 0, - 236364091/2730, 0, 8553103/6, 0, - 23749461029/870,
0, 8615841276005/14322,
0, - 7709321041217/510, 0, 2577687858367/6, 0, - 26315271553053477373/1919190,
0, 2929993913841559/6, 0,
- 261082718496449122051/13530, 0,1520097643918070802691/1806, 0, - 27833269579301024235023/690, 0, 596451111593912163277961/282,
0,- 5609403368997817686249127547/46410, 0, 495057205241079648212477525/66]、となる。
ただし、赤字は、10番目毎を表す」
 「あれれ。
「あれれ。
今、気がついたんだけど、母関数による定義の方法が、フィボナッチ数(列)の場合と違うのね。
だって、フィボナッチ数の場合は、母関数=1/(1-x-x^2)=Σf(n+1)x^n、ただし、n=0~∞、であって、1/n!がない!」
「そうなんじゃな。
一般に、数列をa(n)で表すとき、
F(x)=Σa(n)x^n、のように、x^nの係数、a(n)が数列となる場合に、F(x)をその数列の『母関数』と言うことが多いようだ。
F(x)のn階微分をF(n)(x)で表すと、F(n)(0)/n!=a(n)の関係があるんじゃな。
ところが、ベルヌーイ数の場合は、n!で割っている。すなわち、ΣB(n)x^n/n!。
こういう定義には、多分に歴史的なものがあると思われるが、第62回の記事で、フィボナッチ数列の母関数の定義をうっかりと間違えてしまった。
2013/1/25に訂正させてもろうたがな」
「ウィキペディアの『母関数』の項を見ると、
Σa(n)x^n、を通常型母関数、ベルヌーイ数のような母関数を『指数型母関数』と呼んでいるわ」
「そのようじゃな。
普通、母関数を形式的に展開した際に無限級数が出てきて欲しいので、母関数は、分数関数、指数関数、三角関数、逆三角関数などが候補となる。
簡単な母関数の例が、フィボナッチ数の一般項を導く際にも利用している、
1/(1-x)=1+x+x^2+・・・=Σa(n)x^n、じゃ。
右辺の級数は、x^nの係数が、a(0)=1、a(1)=1、a(2)=1、・・・とすべて、1となる。
また、もし、xで微分して、更に、xをかけた式、x/(1-x)^2=x+2x^2+3x^3+・・・=Σn*x^n、となり、a(n)=nの母関数になる。
これらを組み合わせると、初項a、公差dの等差数列、a+nd、の母関数は、
{(a*x/(1-x)+d*x/(1-x)^2)+a}、であることが分かるじゃろう」
「なるほど。
n=0から5までで、
(x^5(a + 5d) + x^4(a + 4d) + x^3(a + 3d) + x^2(a + 2d) + x(a + d) + a)となって、等差数列を再現できるわね。
それと、初項a、公比rの等比数列、a+ar+ar^2+・・・の場合は、むしろ、簡単で、a/(1-r*x)であることが分かるわ。
一番簡単だと思った等差数列の方が母関数が複雑になるというのは、ちょっと、不思議だけど」
「等差数列の場合は、一般項が、nの1次式となっているので、nの2次式の場合は、どうすればよいかを考えてみよう。
このとき、Σn^2x^n、ただし、n=0~の場合が求められれば、良いわけじゃ。
簡便には、x/(1-x)=x+2x^2+3x^3+・・・なので、微分して、(x+1)/(1-x)^3=36x^5 + 25x^4 + 16x^3
+ 9x^2 + 4x + 1・・となることから、
x(x+1)/(1-x)^3を母関数とすれば、25x^5 + 16x^4 + 9x^3 + 4x^2 + x・・のように、Σn^2x^nの母関数が求められる」
「n^3も同様に求めて、次の表になるのね」
| 数列 |
母関数 |
例 |
備考 |
| 1 |
1/(1-x) |
1,1,1,・・・ |
|
| a |
a/(1-x) |
a,a,a,・・ |
aは定数 |
| n |
x/(1-x)^2 |
1,2,3・・ |
^2を追加
2020/5/18修正 |
| a+nd |
ax/(1-x)+dx/(1-x)^2+a |
a,a+d,a+2d・・ |
a,dは定数 |
| n^2 |
x(1+x)/(1-x)^3 |
1,4,9,16・・ |
|
| n^3 |
x(x^2+4x+1)/(1-x)^4 |
1,8,27,64・・ |
2013/1/30修正 |
調和数列
「前節では、数列が、nの整次式の場合について、母関数を調べてみた。
nが4次式以上でも、n^3と同様に、母関数を求めることができる。
さて、今度は、数列の一般項が1/n、ただし、n=1~、という『調和数列』を考えよう」
 「1,1/2,1/3,・・・という数列ね。
「1,1/2,1/3,・・・という数列ね。
この母関数は、-Ln(1-x)ね。
-LN(1-x)=x^10/10 + x^9/9 + x^8/8 + x^7/7 + x^6/6 + x^5/5 + x^4/4 + x^3/3
+ x^2/2 + x・・、と展開できる」
「ま、そうじゃ。
ただ、調和数列の和は、発散するので、上の母関数を、たとえば、調和級数の第1~m項までの和の近似計算に、このままでは、利用できない。
なお、本題の再帰関数に戻って、第m項までの級数の和を再帰関数と書く場合は、
Σ(n=1~m)1/n=S(m)、これは、特に、難しくなく、
S(m)=IF(m = 1, 1, s(m - 1) + 1/m)、となる。
そして、フィボナッチ数列の時のように、計算に時間がかかることはない。
もちろん、ITERATE([v↓1 + 1/v↓2, 1 + v↓2], v, [0, 1], m )↓1、としてもよいが、初期ベクトルの値など、うっかりとミスをおかしやすいので、Iterate関数を使う際は、注意して、検算する必要があるのう」
行列の固有値と固有ベクトル
「行列の固有値と固有ベクトルについて、少しだけ、触れておこう。
これは、大きなテーマなので、詳細は、別の機会に取り上げるとして、ここでは、2,3の例をやってみよう」
 「えーと。たとえばと、
「えーと。たとえばと、
A=[[4,3],[-2,-1]]として、Au=λu、なるλ(固有値)と固有ベクトルを求めてみるわ。
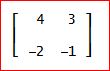
ここで、uは、2行1列のベクトル。u=[u,v]とする。
なお、DERIVEでのベクトルは、1行2列の横ベクトルとなるので、A*[u,v]は、計算不能であるはずなのに、A*[u,v]'と転置したとして計算してしまいます。
すなわち、A*[u,v]=[4u+3v,-2u-v]のようにね。
逆に、左から、uをかけると、u*A=[4u-2v,3u-v]となります。
以下では、転置を付けるのは、面倒なので、u*Aと、DERIVE上では、計算する。(ただし、式の上では、習慣に従い、A*uのように書く)
そもそも、Au=λu、は、左辺は、行列×ベクトルなのに、右辺は、スカラー×ベクトルとなっている。
いつでもこうなるはずがない。特別な場合だけということ。
そのような場合は、A*u-λu=ゼロベクトルなので、Iを単位行列(対角要素のみ1、以外はゼロの行列)とすれば、
(A-λI)u=ゼロ、すなわち、[[4 - λ, 3],[2, 1 - λ]]u=ゼロベクトルなので、
u(4 - λ) + 3v=0
-2u - v(1 + λ)=0
となる必要がある。
u、vが両方ともゼロというトリビアルな場合でなければ、行列(A-λI)の行列式=0、つまり、λ^2-3λ+2=0が必要十分な条件となる。
なぜならば、第1の式から、v=u(λ-4)/3 であるから、第2の式に代入すると、(- u(λ^2 - 3λ + 2)/3)=0を要求される。
しかし、uがゼロでないとしているので、λ^2 - 3λ + 2=0が必要十分な条件となり、ここから、固有値として、λ=2、または、λ=1となる。
λ=2のとき、2u+3v=0、なので、u=定数×[-3/2,1]が固有ベクトル。
また、λ=1のときは、u+v=0から、u=定数×[-1,1]が固有ベクトルとなる」
「蛇足だとは思うが、(A-λI)u=ゼロベクトル、から、DET(A-λI)=0の部分は、uの任意性を利用している。
すなわち、DET(A-λI)がゼロでない場合は、連立方程式の解として、ベクトルuの要素が決定される。しかし、uは、任意なので、それは、不可となる。
そこで、固有方程式、DET(A-λI)=0から、固有値λを算出して、その場合は、連立方程式の解が不定となるが、まったく任意なのではなく、各要素の比率は、決定される。
おやおや、uは、任意じゃないのか、と思ってしまうが、決定されるのは、比率だけで、定数×ベクトルで、その定数分の任意性は残る」
「固有ベクトル同士は、直交するんじゃなかったかしら?」
「固有ベクトル同士が直交するのは、対称行列の場合じゃ。いつでも直交するわけではない。
それと、固有値が重根の場合は、どうなるかというと、たとえば、A=[[1,1],[-1,3]]のようなもの。
この場合は、固有方程式が、λ^2-4λ+4=0、となり、λ=2は、2重根となる。
固有ベクトルは、定数×[-1,1]、一つしかない。一般には、行列のランクと同数の固有値がある」
「ところで、DERIVEでは、どうやって、求めるのかな?」
「固有方程式は、CHARPOLY([4, 3; -2, -1], z)を使い、第1引数に行列を、第2引数に変数名を入れると、固有方程式の左辺が、z^2-3z+2のように求められる。
しかし、固有値を得るには、別途、上式=0として、方程式を解く必要がある。
一方、EIGENVALUES(行列, z)関数は、固有値を、([z = 1, z = 2])のように返す関数じゃ。(zは、変数名なので、zでなくてもかまわない)
たとえば、([1, 0, -1; 0, -1, 0; -1, 0, 1])、

については、([z = 0, z = -1, z = 2])を与える。
DERIVEでは、だいぶ以前に出てきたように、4次方程式までは、厳密解を得ることができるので、EIGENVALUES関数を使えば、4次行列までは、固有値を直ちに求めることができる。
しかし、5次以上の行列については、一般には、厳密解を得ることができないため、そのままでは、固有ベクトルを求めることもできなくなってしまう。
さて、今、固有方程式が4次以下か、あるいは、5次以上でも、因数分解により、幸運にも、『厳密な』固有値が求められたとしよう。
このときは、EXACT_EIGENVECTOR(行列, 厳密な固有値)関数を使って、行列の固有値(ここでは、2)の固有ベクトルが、定数倍を除いて、([1; 0; -1])と求められる。
これは、下図のような、縦ベクトルである。

ところが、前述のように、固有値は、厳密に求められないことが多く、誤差を含んだ値となることが多い。
この場合、Exact_EigenVector関数を使うと、ゼロベクトルが返ってしまう。
従って、固有値、固有ベクトルを近似的に扱う必要が出てくる。
以下では、簡便な方法である、『べき乗法』について、説明しておこう。
これは、行列Aが実対称行列(対称行列でなくてもよいが収束が遅い場合がある)であれば、
u(n+1)=Au(n)として反復する方法で、1つの固有値が求められる。
VECTOR(u(n)/MAX(VECTOR(ABS((u(n))↓k), k, 1, ベクトルの次元数(本例は3), 1)), n, 2, 繰り返し数(本例では100), 間隔(本例では1)))
とすれば、手軽に試せるじゃろう。
ちなみに、Maxは、ベクトルの中の最大値を求める関数じゃが、要素の絶対値の最大値を求めるために、少し工夫をしている。
あるいは、再帰関数を使わずに、ITERATES(U*a/ABS(U), U, u, n)のようにIteratesまたはIterate関数を使うと計算が速い。
ここで、Uは、ベクトルと考えている。ABS(U)で割っているのは、値の急激な増加を抑える意味じゃな。収束の状況を見るには、Iterates関数の方が良いじゃろう。
初期ベクトルを[1,1,1]とすると、反復後に、u=[0,1,0]となる。(振動しても、[0,1,0]→[0,-1,0]を繰り返すような場合は、定数倍を除き等しい)
固有ベクトルが求められれば、固有値は、元の行列×近似固有ベクトルであり、これは、求めたい固有値×近似固有ベクトルに近いので、『残差平方和』を最小にするようにして固有値の近似値を得る。本例では、[0,1,0]から、-1となる。(固有ベクトルが[0,-1,0]となることもあるが定数倍の違いは無視する)
今度は、A-λIに対して、再度、べき乗法を適用した後に求められた固有値に先のλを加えると、別の固有値が求められる。
本例では、A-λIの固有ベクトルが、([1, 0, 1])となり、対応する固有値は、1となるが、先の-1を加えると、ゼロを得る。
対応する固有ベクトルは、[1, 0, 1]である。([0.7071067811, 0, 0.7071067811]のようになっても、定数倍を除いて同一)
なお、べき乗法をAの逆行列に適用すると、1/λが求められる。これを応用して、近似度を高める『逆反復法』と呼ばれる方法がある。
ただし、本例では、DET(A)=0となるため、逆行列が求められない」
「上とは違った行列、A:=[1, 1, 1; 1, 2, 2; 1, 2, 3]に対して、やってみたよ。
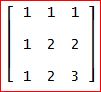
これだと、初期ベクトル[1,1,1]から、([0.4450418679, 0.8019377358, 1])が求められて、固有値は、λ≒ 5.048917338、
EigenValues(A)では、([λ = 5.048917339, λ = 0.3079785283, λ = 0.6431041321])となるので、
ほぼ、べき乗法で求めた値λ≒ 5.048917338、は正しい。
また、Aの逆行列について、べき乗法を実行すると、固有ベクトルが、([0.8019407054, -1, 0.4450405462])となる。
このとき、対応する固有値は、(3.246979603)となるが、この逆数をとると、(0.3079785284)となり、最小の固有値にほぼ、一致することが分かる」
「2番目の行列は、正則行列なので、逆行列が存在する。
1/λがべき乗法で計算できる例となっている。
これは、A-λI=0に対して、Aの逆行列を左からかけると、I-A-1λI=0なので、
整理すると、A-1-(1/λ)I=0となることから、1/λが、Aの逆行列の固有値となることが分かる。
また、固有ベクトルはというと、
Au=λu
A-1w=(1/λ)w
であるので、第2式に左から、Aをかけると、w=(1/λ)Awなので、Aw=λwとすれば、恒等的に等しい。
すなわち、Aとその逆行列A-1の固有ベクトルは、同じことが分かる」
「2番目の行列に対して、A-λIをあらためて、Aとおいて、固有ベクトルを求めると、
([-0.8019438373, 1, -0.4450391524])となり、対応する固有値は、-4.740935163となるけど、
これに最初の固有値を加えると、(0.3079785299)となる。
なお、DERIVEでは、単位行列Iは、IDENTITY_MATRIX(次数)で求められるって。
それと、Approx_EigenVector関数があって、たとえば、固有値を粗く、0.308として、この場合に使って見ると、
APPROX_EIGENVECTOR(行列, 固有値の概算値(0.308))≒([0.5909920507, -0.7369843180, 0.3279977299])、
と、固有ベクトルとして求められ、これから、固有値が、0.3079785283と精密に求まったわ」
「なるほど。
DERIVEの(内部の)アルゴリズムは、『逆反復法』と呼ばれるそうじゃ。Approx_EigenVector関数は、なかなか実用的じゃ。
とは言え、行列の次元が大きいときは、すべての固有値と固有ベクトルを求める場合は、DERIVEの定義済み関数だけでは難しく、プログラムを作る必要があると思われる」
最終更新日 2013/1/30
一個所修正 2020/5/18



 「なるほど、確かに、f(1)以降と、g(x)のテイラー展開の係数が一致しているわね」
「なるほど、確かに、f(1)以降と、g(x)のテイラー展開の係数が一致しているわね」