数式処理ソフト DERIVE（デライブ） de ドライブ
６４．再帰関数（3）（漸化式による積分計算）
部分積分
「数式処理ソフト DERIVE（デライブ）の今回は、積分の計算によく登場する『漸化式』について、考えてみよう。
たとえば、実数xに対する、ガンマ関数は、Γ(x+1)=∫（t=0～∞）txexp(－t)dt、と定義される。
これは、第48回の複素関数（3）に登場しているがの。
一般の f(t)、g(t)の関数の積に関する、よく知られた公式、（f*g）'=f'*g＋f*g'から、∫（f'*g）dt=［f*g］－∫（f*g'）dt、と変形する。
この部分積分による変形は、初等的ではあるが、とても、強力な方法じゃ。
実際、ガンマ関数の積分内の、tx=f、（－exp(－t)）'=g'、と置いてみると、
Γ(x+1)=[f*g]－∫f'*g dt=[tx×（－exp(－t)）]－∫x（tx－1（exp(－t))dt、と変形できる。
第1項は、積分両端、0と∞で、ともにゼロとなるので、右辺は、x×∫（tx－1exp(－t)dtとなる。
結局、この式は、Γ(x+1)=xΓ(x)、というよく知られた形に変形できた。
Γ(1)=∫（t=0～∞）exp(－t)dt=－[exp(－t)]=1なので、x=nという正整数であると、
Γ(n+1)=nΓ(n)、Γ(1)=1、から、Γ(n)が、nの階乗を表すことが分かる」
「Γ(x+1)=xΓ(x)は、差分方程式とも見ることができるのね。
でも、部分積分のとき、どっちをどっちに置いたら良いかで、混乱してしまう」
「わしは、次のような図を描いて考えるがの。
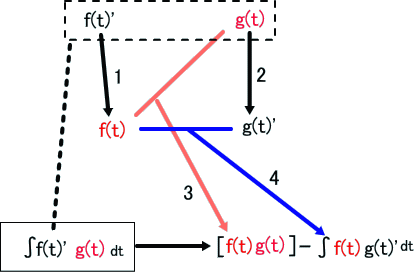
上の図で、長方形の点線で囲んだ部分が、問題の積分内の関数じゃ。
ここで、関数を、f'×gと分解することを考える。
この1の手順が肝心な個所だが、f(t)は、微分したときにf'となるものじゃ。
ガンマ関数では、f'=exp(－t)、なので、f=－exp(－t)、すなわち、不定積分が容易に求まらないと始まらない。
1の手順ができれば、2のgからg'、例では、tx、の微分じゃ。これは、通常は、1の不定積分よりも簡単じゃろう。
そうすると、3と4のように、積分が、2つの項に分解できる。
第1項は、定積分では、f(上端）g(上端）－f(下端）g(下端）となり、不定積分では、単に関数の積じゃがな。
問題は、第2項の積分が、最初の積分よりも簡単になるか、あるいは、ガンマ関数のように、パラメータの階差の形になるか、いずれにして、積分計算に役立つ形に変形出来ないと意味がない」
「そう言えば、部分積分は、ちょっと、割り算に似ているわね。
暗算か、手計算とかは別として、最初の商、部分積分では、f'(t)は、カンで決めないとできないもの。
ガンマ関数の例では、fとgを逆に考えても、うまくいくけど」
「DERIVEのガンマ関数は、Γ(x)であり、負の整数を除き、実数域で連続な関数として呼び出すことが出来る。
あと、『部分積分』は、DERIVEでは、INT_PARTS(g,f',t)で、計算可能じゃ。
たとえば、
INT_PARTS(t^x, EXP(－t), t)=x∫(e^(－t)t^(x － 1), t) － e^(－t)t^x、となる。
手で行った時と項の順序は、逆じゃがな。上式で、赤色の部分は、定積分なので、ゼロとなり、第1項の積分のみが残ることになる。
さて、部分積分のケースをいくつかに分けて、検討してみよう」
多項式×指数関数(exp(t))
「∫（tの多項式）×exp(at)dt、のような積分じゃな。
例では、t^m*exp(t)、ここで、mは、整数とすると、どうかな」
「I(m)=∫t^m*exp(t)dtとおくと、I(m)=t^m*exp(t)－m∫t^(m－1)exp(t)dt=t^m*exp(t)－I(m－1)という漸化式が得られる。
これで、m>=0については、計算可能。具体的なmについては、I(0)=exp(t)は、簡単。
だけど、m<0の場合のスタート地点で、I(－1)=∫exp(t)/t dtは、『この先行き止まり』という感じね。
調べると、こいつは、『指数積分』というもので、Ei(t)=∫（t=－∞～t）exp(t)/tdt、という特殊関数になってしまう。
これは、岩波書店の数学辞典第4版の公式集に掲載されているものだけど。
その注では、積分上端が、正の場合は、主値をとるようにするとあるわ」
「DERIVEでは、ユーティリティファイルとして、『ExponentialIntegrails.mth』を読み込むと、EI(t,n)として、定義されている。
ただし、DERIVEのEI(t,n)の n は、定義されている級数の上限のことで、nが大きいほど精度が高いと考えられる。
また、DERIVEのEI関数は、t>=0の場合で定義されているため、t<0では、正しい値が求まらない。
※Ei(t)は、奇関数ではないので、Ei(－t)は、－Ei(t)ではない！」
「ユーティリティファイルというのは、『TI Education\Derive 6/Math/』フォルダ内の拡張子が『mth』のファイルのことよ。
ファイルメニューから、『読み込み』または『開く』で、使えるようになります。
読み込みの場合は、その内容がDeriveの画面に表示されないので、内容を見たい場合は、『開く』がオススメ！」
「再帰関数の説明としては、
もし、m>=0でよければ、I(m):=IF(m = 0, EXP(t), t^m×EXP(t) － I(m － 1))と再帰的に定義すればよい。
m=0～4までで、下のように求められる。
e^t, e^t(t － 1), e^t(t^2 － t + 1), e^t(t^3 － t^2 + t － 1), e^t(t^4 － t^3
+ t^2 － t + 1),・・」
「m<0も含める場合、ユーティリティファイルを読み込んでいれば、
J(m):=IF(m = 0, EXP(t), IF(m > 0, t^m×EXP(t) － J(m － 1), IF(m = －1,
EI(t, 5), IF(m < －1, J(m + 1) － t^m×EXP(t)))))、
と、少し複雑になるけども、再帰関数J(m)、mは、（正負の）整数、と定義できる。（ただし、EI関数の精度は、n=5としている）
ちなみに、m=－3～3で、求めてみると、VECTOR(J(m), m, －3, 3, 1)により、
m=－3のとき、－ e^t(1/t^2 + 1/t^3) + LN(t) + γ + t^5/600 + t^4/96 + t^3/18 +
t^2/4 + t、
m=－2のとき、－ e^t/t^2 + LN(t) + γ + t^5/600 + t^4/96 + t^3/18 + t^2/4 + t、
m=－1のとき LN(t) + γ + t^5/600 + t^4/96 + t^3/18 + t^2/4 + t、
m=0のとき、 e^t、
m=1のとき、 e^t(t － 1)、
m=2のとき、 e^t(t^2 － t + 1)、
m=3のとき、 e^t(t^3 － t^2 + t － 1)、
と正しく求めることができる」
「上の指数積分の級数じゃが、DERIVEのユーティリティでは、
EI(t, n) := γ（オイラーの定数） + LN(t) + ∑(t^k/(k*k!), k, 1, n)と級数で定義されている。
定義から分かるように、このままでは、t<0 では、正しい結果が得られない。
上のDERIVEの変数名は、本節の記載に合わせて、少し、変更しているが内容は同一じゃ」
「さっきの数学辞典の公式集では、（やはり、多少の記法をかえるけど）
Ei(t)=γ（オイラーの定数）＋LN(|t|)＋Σ(t^k/(k*k!), k, 1, ∞)と定義されているわね。
この定義ならば、t<0 でも、計算可能なように思うけども」
「h(t, n):= IF(t > 0, EI(t, n), IF(t < 0, γ + LN(－t) + ∑(t^k/(k*k!),
k, 1, n)))、と定義してみたんじゃ。
t=－5～5まで、1.0刻みで、数値計算してみた。t=0は、未定義なので、?と表示されている。（n=20）。
[－0.001147930877, －0.003779348914, －0.01304838108, －0.04890051070, －0.2193839343,
?, 1.895117816, 4.954234356, 9.933832570, 19.63087446, 40.18527478]
確認のため、「数表」（吉田洋一・吉田正夫編：培風館：昭和47年4月20日初版第19刷）の表27にある『積分指数』を参照すると、
t=－5は、－0.001148、であり、上記の計算値は、－0.001147930877、
t=－4は、－0.003779、であり、計算値は、－0.003779348914
t=－3は、－0.01304、であり、計算値は、 －0.01304838108
t=－2は、－0.04890、であり、計算値は、－0.04890051070
t=－1は、－0.2194であり、計算値は、－0.2193839343
t=1では、1.8951、であり、計算値は、1.895117816
t=2では、4.9542、であり、計算値は、4.954234356
t=3では、9.9338、であり、計算値は、9.933832570
t=4では、19.6309、であり、計算値は、19.63087446
t=5では、40.1853、であり、計算値は、40.18527478
t=15では、234956、であり、計算値は、222863.5781、かなり異なってしまったが、n=100として、計算すると、(2.349558524×10^5)を得ることができた。
しかし、
t=－15、n=20では、－0.00000001918、であり、計算値として、(2797.093070)と途方もない数値が出てしまった。
これは、tが負では、級数が交代級数となるため、精度が保ちづらくなったものと思われる。
そこで、n=100までとって、(－ 9.423420815×10^(－8))
更に、n=1000までとって、(－ 9.414460278×10^(－8))
とどうもうまくないのう」
「t=－5程度までは、かなり精度よく、計算できているから、2つに分割したら、精度の高い数値が得られたよ。
h(t, n):=IF(t > 0, EI(t, n), IF(t > －5, γ + LN(－t) + ∑(t^k/(k×k!),
k, 1, n), γ + LN(5) + ∑((－5)^k/(k×k!), k, 1, n) + ∫(EXP(t)/t, t, －5, t)))
これで、h(－15,100)≒(－ 1.9186278921478020880×10^(－8))、ただし、DERIVEのオプションの『モード設定』で、桁数を標準の10桁から、20桁に変更した結果。
前出の数表では、有効桁数の大きい値が得られないので、カシオがWEB上で公開している、『keisan（生活や実務に役立つ計算サイト）』（http://keisan.casio.jp/）を参照して、サイトの特殊関数の指数積分の計算をすると、
t=－15に対して、－1.918627892147866977104×E－8、が得られた。
結果を比較すると、有効数字14桁程度まで一致している。
ただ、『keisan』の方が、計算が速いのは、残念！（さすが、元祖計算機メーカー、カシオ！）」
「なるほど。
では、少し、ずるいが、上記サイトで、t=－5の時の値を－0.00114829559127532579733、と得てから、
h(t, n)の定義式の中に直接、値を書き込めば、
IF(t > 0, EI(t, n), IF(t > －5, γ + LN(－t) + ∑(t^k/(k×k!), k, 1, n),
－0.0011482955912753257973 + ∫(EXP(t)/t, t, －5, t)))
(－ 1.9186278921478669736×10^(－8))、と有効数字が18桁程度まで、一致するのう。
この結果から、｜t｜の大きいところは、普通の定積分として計算し、｜t｜の小さいところは、級数展開の式を使えば良いことに気がつく。
IF(t > 5, 8037055071160635491/200000000000000000 + ∫(e^x/x, x, 5, t),
IF(t > 0, EI(t, n), IF(t > －5, γ + LN(－t) + ∑(t^k/(k×k!), k, 1, n),
∫(e^x/x, x, －5, t) － 11482955912753257971/10000000000000000000000)))
この新しい定義では、tの値により、4つに分割して計算している。
t>5、では、Ei(5)の高精度計算値＋普通の定積分（t=5～t）
0<t=<5 では、DERIVEの定義関数で、EI(t,n)、
－5<t<0、では、γ＋LN(－t)＋Σ(t^k/(k×k!), k, 1, n)
t<－5、では、Ei(－5)の高精度計算値＋普通の定積分（t=－5～t）
このようにすると、tの0を除き、広い範囲で、精度の高い数値が得られることが分かる」
「tが負の場合は、例のオイラー変換も有効でしょうね」
「そうじゃな。
ただ、今回の『指数積分』の被積分関数は、｜t｜の大きいところで、急速に減少するので、よほど、高精度の数値を要求されなければ、大丈夫じゃろう」
「確かに。
t=100で、DERIVEの10桁の計算桁数でも、(2.715552744×10^41)が得られて、高精度計算サイトの数値と末尾まで一致する」
多項式×三角関数
「前節と同様に、t^m*sin(t)を考えてみよう。ここで、mは、整数とする。
S(m)=∫t^m*sin(t)dt、
C(m)=∫t^m*cos(t)dt、
とおく。
S(m)=－t^m*cos(t)＋m*C(m－1)
同じく、
C(m)=t^m*sin(t)－m*S(m－1)
と、2組の漸化式が得られる。
S(0)=∫sin(t)dt=－cos(t)、
C(0)=∫cos(t)dt=sin(t)、
なので、m>=1については、
ベクトルvとして、v:=[S(m)，C(m)］とすると、
v(m):=IF(m = 0, [－ COS(t), SIN(t)], [－ t^m×COS(t) + m(v(m － 1))↓2, t^m×SIN(t)
－ m(v(m － 1))↓1])、
再帰的に定義できる。
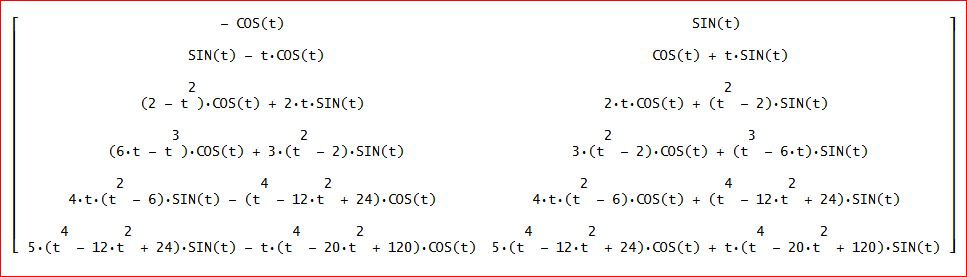
上図は、m=0から5までの、S(m)とC(m)じゃ」
「m=－1のときが、以前出てきた、正弦積分、余弦積分なのね。
正弦積分は、Si(t)=∫（0～t）sin(t)/t dt、
余弦積分は、Ci(t)=－∫（t～∞）cos(t)/t dt、
上は、岩波の数学辞典による定義ね。さっきの培風館の『数表』の『積分指数」と同一のページに正弦積分、余弦積分の定義と数値が載っているわ。
で、正弦積分は、あんまり問題は無いけど、余弦積分は、そのまま、普通に計算すると、不明な精度、で現れてしまう。
※第41回 積分（１）（単積分、数値積分とEuler変換）の記事を参照。
ここは、Ci(t)=γ＋LN(t)－∫（0～t）(1－cos(t))/t dt、という恒等式を利用して計算するということだったわね。
DERIVEでは、SI(t)、CI(t)で計算できます」
「SI(t)は、奇関数で、SI(－t)=－SI(t)となり、DERIVEでも、t<0の場合も、そのまま計算可能じゃ。
CI(t)は、負の場合は、定義からして、計算不能じゃな。無理に計算すると、虚数が含まれてしまう。
なお、m<0の場合も含まれるように、vの定義式を見直せば、mの正負に関わらず、計算できることになる。
また、IterateまたはIterates関数を利用した繰り返し処理も可能じゃ」
多項式×対数関数
「t^m×LN(t)の場合じゃ。
I(m)=∫t^m×LN(t)dt=((t^(m + 1)LN(t)/(m + 1) － t^(m + 1)/(m + 1)^2)、ただし、m<>－1のとき。
また、I(－1)=（LN(t))^2/2、
これは、再帰関数を使うまでもなく、IF関数のみで、
IF(m = －1, LN(t)^2/2, ((t^(m + 1)LN(t)/(m + 1) － t^(m + 1)/(m + 1)^2))、で十分じゃ」
多項式×指数関数（EXP(－t^2)）
「統計の誤差関数で出てくる例ね。
DERIVeでは、ERF(t)=2/√π×∫exp(－t^2)dt、積分範囲は、0からtまで。
また、ERF(t1,t2)は、ERF(t2)－ERF(t2)を返す。
さらに、ERFC(t)=1－ERF(t)も定義されているわ」
「そこで、一般に、t^m×exp(－t^2)のような被積分関数を考えよう。
I(m)=∫（t=0～t）∫（t^m×exp(－t^2)dt、
I(0)=ERF(t)じゃな。
I(m)=（t^(m+1)）/(m+1)）exp(－t^2)＋（2/（m+1）)I(m+2)、と部分積分で導くのはたやすい。
これから、
I(m+2)=（（m+1)/2）I(m)－（t^(m+1)/2)EXP(－t^2)、となる。
I(0)=(√π/2）ERF(t)、I(1)=－(exp(－t^2))/2、を使えば、m>=2の整数で、次の関数で、計算可能じゃ。
I(m):=IF(m = 0, ERF(t), IF(m = 1, － e^t^2/2, － √πI(m － 2)/4 － e^(－ t^2)t^(m
－ 1)/2))、
m=0～5まで、変化させて、I(m)を計算すると、
[ERF(t),
－ e^t^2/2,
－ te^(－ t^2)/2 － √πERF(t)/4,
√πe^t^2/8 － t^2e^(－ t^2)/2,
e^(－ t^2)(√πt/8 － t^3/2) + πERF(t)/16,
e^(－ t^2)(√πt^2/8 － t^4/2) － πe^t^2/32]
のようになる」
多項式×指数関数（EXP(－t^4)）
「古い本じゃが、『パーソナルコンピュータによる 量子力学』（J.P.Killingbeck：有馬朗人・川合敏雄 訳：サイエンス社：1985年5月）が手元にあった。
今から、30年近く前の本じゃによって、著者が言及しているパーソナルコンピュータの機種は、シャープのPC－1211ポケットコンピューター、コモドール社のPET、テキサスインスツルメント社のTI－58など、すでに、コンピュータ博物館に収納されているであろう機種ばかりじゃ。
プログラムとは何か、Basic言語とは何か、などの章もあり、時代を感じさせる。
また、メインメモリーが、8KB（8GBではない。百万分の1のサイズ）程度しかない。従って、多くの記憶容量を使わないようにプログラムを組み立てる必要がある。当然、ハードディスクも無い。
パソコンの性能は、この30年間で、極めて向上しているが、同書には、今も新鮮な印象を受けるな」
「1行、1行が濃いというか、含蓄を感じるわね」
「含蓄とは、ともちゃんも良いことをいう。
まさにそういうことじゃ。
著者は、数学者ではなく、物理学者で、量子計算の専門家のようじゃ。だから、翻訳も、物理学者の有馬先生等がなされている。
桁落ちや情報落ち、2進計算の初歩から説き起こし、学生や社会人に役立つと思う。
とは言え、翻訳本で、200ページあまりの本じゃから、数値解析の全般を網羅したものではもとよりない。
また、今日から見れば、古めかしい記述もあるじゃろう。
なので、読者は、たとえば、『数値計算法基礎』（田中敏幸 著：コロナ社：2006年4月）のような、テキストを併せて参照すると良いと思う。
『パーソナルコンピュータによる 量子力学』をここで、紹介したのは、同書が、上に述べたように、今から見れば、非常に制約されたメモリーの上で動くプログラムを書く必要があったことから、アルゴリズムとして、逐次計算法をもっぱら多用しているためじゃ。
さて、前置きが長くなったが、同書の33～34ページに、I(n)=∫（x=0～∞）（x^n×exp(－λx^4)）dx、という定積分が表れている。
ここで、nは、正の整数、λは、正の実数とする。
キリンベック氏は、I(n)をλで微分することにより、Ｉ(ｎ＋4)=((n+1)/4)I(n)、という漸化式を導いている。その趣旨は、nとλが与えられたときに、I(n)からI(n+3)までの積分を行っておけば、n+4
以上の定積分は、上の漸化式から計算できる。
数値計算は、やみくもに、計算するのではなく、必要な計算のみを行えば済むように解析した上で（可能ならばだが）、計算しなさい、と指摘している。
同書の他の個所では、『天才が作り、馬鹿が走らす』という言葉を引用してこの点を説明している」
「その、ことわざというか、警句なんだけど、Googleで検索しても、ヒットしないのよね。
私は、別の本でも読んだ気がするのに不思議。
もしかすると、アインシュタインの次の文章、
『Any fool can make things bigger, more complex, and more violent. It takes
a touch of genius and a lot of courage to move in the opposite direction.』
から出ているのかなと思うけど。
あるいは、英語圏では、昔から使われているのかと思うんだけど、なぜか、日本語では、検索してもヒットしないわね。
ま、それは、それとして、I(n)は、ガンマ関数で表せるんじゃないのかな」
「そのとおり、実は、同書のこの部分は、ほんの数行で書かれているので、今回、テーマに合わせて、上の漸化式を導いてみようと思ったんじゃが、意外と思うように行かないのじゃ。
∂（I(n),λ)＝－I(n+4)は、すぐ出るのじゃがな。
そこで、基本に立ち返り、変数変換と部分積分を使うことで、I(n)=∫（x=0～∞）（x^n×exp(－λx^4)）dx、は、次のようになることが分かった。
I(n)=λ^((n+1)/4)×(1/4)Γ((n+1)/4))、Γ(x)=∫(t=0～∞)(t^(x－1)exp(－t))dt、
ちなみに、I(0)=∫（x=0～∞）（exp(－λx^4)）dx=((1/4)!/λ^(1/4))、
また、I(4)=((1/4)!/(4λ^(5/4)))、なので、I(4)/I(0)=1/(4λ)、じゃ。
一般に、Ｉ（ｎ＋4)=(n+1)/(4λ)I(n)である。
実際に、I(4)（λ=2）=(2^(3/4)(1/4)!/16)≒(0.09527382421)
また、I(0)（λ=2）=(2^(3/4)(1/4)!/2)≒(0.7621905937)、なので、I(4)/I(0)=1/8となる。
一方、∫（x=0～∞）（x^4×exp(－2x^4)）dx=(2^(3/4)(1,/4)!/16)≒(0.09527382421)
同様に、∫（x=0～∞）（exp(－2x^4)）dx=(2^(3/4)(1/4)!/2)≒(0.7621905937)、なので、比率は、やはり、1/8となる」
「なるほど。
同書のミスプリントっぽい感じね。
λが落っこちちゃったということかしら」
「おそらくはな。
ただ、漸化式を導くために、被積分関数内のパラメーターなどで微分する方法というのは、結構、定番じゃ。
また、今回は、分数関数×指数関数、分数関数×三角関数のような積分を検討できなかった。
次回は、そんな方向の内容を考えてみようかの」
最終更新日 2013/2/3
