数式処理ソフト DERIVE(デライブ) de ドライブ
73.常微分方程式の数値解法(初期値問題)(2)(リチャードソン加速)
リチャードソン加速(1)
「数式処理ソフト DERIVE(デライブ)の第72回では、1階常微分方程式の数値解法として、(1次の元祖)オイラー法、2次のオイラー法、(2次の)修正オイラー法、m次のオイラー法(テイラー展開法)、そして、4次のルンゲ・クッタ法などを挙げて、説明してきた」
 「こうした近似解の打ち切り誤差についても、調べたわね」
「こうした近似解の打ち切り誤差についても、調べたわね」
「そうじゃったな。
今回は、主要な打ち切り誤差を、打ち消す方法として、「リチャードソン加速」を使った加速法(補外法)について、説明しよう」
「リチャードソン加速(Richardson extrapolation)のリチャードソン氏(Lewis Fry Richardson)は、ウィキペディアによれば、イギリスの数学者、気象学者、心理学者。
1881/10/11~1953/9/30。
現在のコンピューターによる気象予報の先駆けとも見なせる数値計算による気象予報に取り組んだが、電子計算機が出現前で手計算のため、6時間先の気象予報に2ヶ月かかったという話が載っているわ。だけど、計算精度や元データ等に問題があったため失敗に終わったという」
「その話は、知らなかったのう。
脇道になるが、少し、余談を続けようかの。
リチャードソン氏は、手計算でも、64000人を集めて一斉に計算させれば、現実の時間と同じ程度の速度で計算できると見積もったということじゃが、この手間は、実際的なものではなかったため、「リチャードソンの夢」と言われたということじゃ」
「すごい先見力というしかないわ。
コンピューターの先祖の一つとも言える「バベッジ機関」を思い出すわ」
「バベッジの解析機関は、19世紀末のことじゃから、リチャードソン氏より1世紀ほど前のことじゃな。
やはり、これもイギリス人のチャールズ・バベッジ(Charles Babbage)(1791/12/26~1871/10/18)が創案したものじゃ。
当時、発達しつつあった蒸気機関とパンチカードを組み合わせて、方程式を機械的に解くという試みじゃった。
このあたりのことは、「計算機の歴史」(ハーマン・H・ゴールドスタイン 著:末包良太・米口肇・犬伏茂之 訳:共立出版:昭和55年10月初版3刷)に詳しい。
パンチカードは、当時、織物の自動織機(ジャカール織機:ジャカールは、フランスの発明家)の制御用に使われていたので、自動織機が蒸気機関の力によりパンチカード制御で織物を織るように、パンチカードにより方程式の解法を与えることを夢見たということだ。
バベッジは、イギリス政府から資金を受けて開発に取り組んだのじゃが、歯車の精度不良など動作制御の難しさから、複雑な機械になるほど、製作は困難になり、ついに完成しなかったという。
これから、実現しない夢を見る夢想家のことを「バベッジ・フール」と言われるようになったということじゃ」
「その解析機関の前身とも言える「階差機関」(階差を利用して多項式を計算する機械)は、一応完成したのね」
「上の本によれば、スウェーデンの「ペール・イオエリ・シュウツ」氏がバベッジのアイデアを具体化して、実際に利用できる階差機関を製作したということじゃ。
この機械は、パリの万国博覧会に出品されて、その後、アメリカのダッドリー天文台(ニューヨーク州:Dudley Observatory)の計算用に買い上げられたとのこと。
こう書いてみると、イギリス-スウェーデン-アメリカ、と世界的な話につながっているのじゃな。
1783年:アメリカ合衆国独立、1815年:ワーテルローの戦い、1851年:フランスのパリでの第1回万国博覧会・・・。
飛行機が発明されたのは、第1次世界大戦(1914年~1918年)の頃じゃから、19世紀は、太平洋、大西洋などを渡り、ヨーロッパと北米、東洋、南米大陸との往来は、汽船によるしかなく、その航海のために、正確な天文計算が必要になっていたのじゃな。イギリス政府が資金を提供した背景にはこういう事情があったのじゃろう。
バベッジ氏は、相当、風変わりな、気むずかしい人じゃったようで、発明家にありがちじゃが、新しいアイデアを得ると、今やっている作業をうち捨てて、次へと移ってしまうので、実用的な域に達する機械を作れなかった。
一方、シュウツ氏は、小さな成果物から着実に歩を進めたため、なんとか動く機械を作れたとのこと。
アイデアを出す人と実際に作る人、この2人があって、初めて、動く機械を作れるという教訓と言えるのう」
「その本には、バベッジの解析機関を、エイダ夫人(イギリスの詩人 バイロンの娘でラブレス伯爵夫人)が深く理解して、紹介したというる話も載っているわね」
「彼女は、世界で最初のプログラマーとも言われている。
プログラミング言語「Ada」(エイダ)は、彼女にちなんで命名されたということじゃ。
さて、閑話休題。
m次のオイラー法で、常微分方程式を解いたとして、その解を、y(x;h)と書こう。ここで、hは、刻み幅じゃ。
このとき、厳密解をy(x)とすれば、一般に、y(x;h)≒y(x)+αh^(m+1)+βh^(m+2)+・・、と表される。
α、β等は、yの高階微分係数に比例し、hには依存しない打ち切り誤差の項目を表す。※
そこで、刻み幅を半分にした場合の解、y(x;h/2)が、
y(x)+(1/2)^(m+1)αh^(m+1)+(1/2)^(m+2)βh^(m+2)+・、であることに注意すれば、
容易に、よりよい近似解は、(2^m×y(x;h/2)-y(x;h))/(2^m-1)、で与えられることが分かる。
この簡単な計算により、打ち切り誤差の中のαh^(m+1)次の項が除かれているのじゃ」
「なるほど。m=2の場合は、(4×y(x;h/2)-y(x;h))/3、となって、台形公式と中点公式とを組み合わせて、シンプソンの公式を得る時と同じね。
とすれば、さらに、βh^(m+2)の項まで除くには、hの1/4の場合を追加で計算し、
(2^(2m + 1)y(x;h/4)- 3×2^m×y(x;h/2)+y(x;h))/(2^(2m + 1)- 3×2^m + 1)、とすればよい訳か。
m=2のときは、(32×y(x;h/4)-12×y(x;h/2)+y(x;h))/21、となる」
「次節では、そのリチャードソン加速の様子を実験してみようかの」
※打ち切り誤差がm+1次から始まるかどうかなどは、解法に依存していて、m次のテイラー展開法の場合は、m+1次からになる。
リチャードソン加速(2) y'=x+yの例
「前回と同様に、y'=x+y、x=0でy=0の例を取り上げよう。
厳密解は、y(x)=exp(x)-x-1、じゃ」
 「じゃ、m次までのオイラー法で、x=0~10までの範囲を計算し、いちばん誤差が大きくなる、x=10のときのy(10)で比べてみよう。
「じゃ、m次までのオイラー法で、x=0~10までの範囲を計算し、いちばん誤差が大きくなる、x=10のときのy(10)で比べてみよう。
以下では、h=0.1としている。
厳密解:y(10)≒2.2015465794806716516×10^4。なお、計算精度は、20桁」
| 次数(m) |
加速なし |
一致桁数 |
一段加速 |
一致桁数 |
二段加速 |
一致桁数 |
| 1 |
1.3769612339822270184×10^4 |
0 |
2.0793549290497701805×10^4 |
1 |
2.1938923856186103136×10^4 |
1 |
| 2 |
2.1677414370399447360×10^4 |
1 |
2.2010513723071864428×10^4 |
4 |
2.2015487370384209689×10^4 |
6 |
| 3 |
2.2006994192471624276×10^4 |
3 |
2.2015416322742080421×10^4 |
6 |
2.2015465700502146736×10^4 |
9 |
| 4 |
2.2015296900876202491×10^4 |
5 |
2.2015465316583207452×10^4 |
8 |
2.2015465794305405358×10^4 |
11 |
| 5 |
2.2015462986655650107×10^4 |
7 |
2.2015465790845542767×10^4 |
10 |
2.2015465794804624880×10^4 |
13 |
| 6 |
2.2015465754762478238×10^4 |
9 |
2.2015465794778321176×10^4 |
11 |
2.2015465794806708957×10^4 |
15 |
「なるほど、これは、明瞭じゃの。青字の数までが厳密解と一致している部分じゃな。
加速なしの場合は、h=0.1の大きさでは、2次のオイラー法で、1桁の精度じゃ。6桁の精度を得るには、4次以上が必要じゃ。
しかし、リチャードソン加速を使うと、2次オイラー法でも、一段加速(誤差の第1項を打ち消し)で、4桁の精度が出ておる。
二段加速(誤差の第2項まで打ち消し)では、6桁とな」
「一段加速で、加速なしの桁数+3、二段加速では、加速なしの桁数+6程度は、得られてるってことね。
恐るべし、リチャードソン加速!」
「今の場合は、h=0.1と、かなり刻み幅を大きくとっている。
これを、前回多く取り上げたように、h=0.01としてみよう。
とはいえ、少し面倒じゃな」
「えへへ。
そこで、お作りしました。リチャードソン加速のためのユーザー定義関数。
すでに作ってある、m次までのオイラー法関数 Eulerm_user(r, x, y, x0, y0, h, m, n)は、
PROG(f_ ≔ ∑(difm_user(r, x, y, h, k), k, 1, m),
ITERATES([v↓1 + h, v↓2 + LIM(f_, [x, y], v)], v, [x0, y0], n))、と既出で定義されている。
ここで、difm_user(f, x, y, h, m)も、既出だけど、関数fのm次までのテイラー展開式を与えるユーザー定義関数。
IF(m = 1, h×LIM(f, [u_, v_], [x, y]),
h×(∂(difm_user(f, x, y, h, m - 1), x) + LIM(f, [u_, v_], [x, y])×∂(difm_user(f,
x, y, h, m - 1), y))/m)、だった。
今回、Richardson(r, x, y, x0, y0, h, m, n)を一段加速用として下記のように定義。
PROG(u_ ≔ Eulerm_user(r, x, y, x0, y0, h, m, n),
v_ ≔ Eulerm_user(r, x, y, x0, y0, h/2, m, 2×n),
VECTOR((2^m×v_↓(2×k + 1) - u_↓(k + 1))/(2^m - 1), k, 0, n, 1))、
同様に、二段加速用として、Richardson2(r, x, y, x0, y0, h, m, n)を定義。
PROG(u_ ≔ Eulerm_user(r, x, y, x0, y0, h, m, n),
v_ ≔ Eulerm_user(r, x, y, x0, y0, h/2, m, 2×n),
w_ ≔ Eulerm_user(r, x, y, x0, y0, h/4, m, 4×n),
VECTOR((2^(2×m + 1)×w_↓(4×k + 1) - 3×2^m×v_↓(2×k + 1) + u_↓(k + 1))/(2^(2×m
+ 1) - 3×2^m + 1), k, 0, n, 1))、
上記で定義した、Richardson(r,x,y,x0,y0,h,m,n)は、関数r(x,y)を初期値[x0,y0]から、刻み幅h、m次、分点数n、として計算する。
計算にあたり、y(x;h)をベクトルu_に格納、同様に、y(x;h/2)をベクトルv_に格納した上で、VECTOR関数で、複数のベクトルを加減算している。
ここで、一つ注意すると、本来は、[x,y]のyのみ加速対象とするんだけど、xを含めて、(2^m×v_↓(2×k + 1) - u_↓(k +
1))と加減算している。
これで、十分で、xの数値は、複数のベクトルの計算の係数等が正しいか、検算用としても使えるわ」
「なるほど、これは、便利じゃな。
以下の表は、h=0.01の場合じゃ。y(10)≒2.2015465794806716516×10^4。計算精度は、20桁」
| 次数(m) |
加速なし |
一致桁数 |
一段加速 |
一致桁数 |
二段加速 |
一致桁数 |
| 1 |
2.0948155637813660064×10^4 |
1 |
2.1998672408761571496×10^4 |
1 |
2.2015359788199870490×10^4 |
5 |
| 2 |
2.2011822441481159821×10^4 |
4 |
2.2015461158343289644×10^4 |
7 |
2.2015465798160467325×10^4 |
10 |
| 3 |
2.2015456690231016812×10^4 |
6 |
2.2015465789594753687×10^4 |
9 |
2.2015465794805641080×10^4 |
13 |
| 4 |
2.2015465776603636288×10^4 |
9 |
2.2015465794801650464×10^4 |
13 |
2.2015465794806715977×10^4 |
16 |
| 5 |
2.2015465794776385283×10^4 |
11 |
2.2015465794806712315×10^4 |
16 |
2.2015465794806716514×10^4 |
19(20) |
| 6 |
2.2015465794806673194×10^4 |
14 |
2.2015465794806716514×10^4 |
18 |
2.2015465794806716517×10^4 |
19(23) |
「h=0.01では、2次のオイラー法でも、二段加速すると、10桁の精度が出てしまう。加速なしだと、4次でも10桁は苦しいのに」
「リチャードソン加速などの加速法を使うと、比較的小さな手間(時間)で高精度の結果が得られる。
その効果は、刻み幅 hが小さいほど、顕著じゃ。m=5以上で、20桁目が合わないのは、丸め誤差の影響じゃろう。
実際、計算精度を30桁とすると、y(10)≒2.20154657948067165169579006452×10^4、
m=5の二段加速で、2.20154657948067165167387608793×10^4、とすでに、20桁まで求められている。
m=6の二段加速で、2.20154657948067165169578214049×10^4、と、なんと、23桁まで求められている。
そこで、二段加速の場合の一致桁数にかっこでその桁数を表示した。
今回のように、hが小さく、従って、分点数が多いとき、そのまま関数を計算させると、DERIVEの画面が見づらくなる。
y(10)のみを比較するのであれば、
(Richardson(x + y, x, y, 0, 0, 0.01, m, 1000))↓1001、と入力して、解析メニューの数列の作成から、次数mを1から6まで変化させて計算すると
y(10)の部分のみを、たった6行で表示してくれるので、わかりやすいじゃろう」
「読者の皆さん、DERIVEのベクトルは、添え字が1から始まるのよ。
だから、1000点目のx=10を取り出すための添え字は、1001であることに注意してね」
「そういうことじゃ。
Richardson関数の定義式内でも、u_↓(k+1)のように、1だけ下駄を履かせてある」
リチャードソン加速(3) y'=-y^2+10/x^2
「前節では、y'=x+y、初期値[0,0]、という例で、リチャードソン加速を施してみた。
この節では、第72回でも取り上げている、リッカチの微分方程式について、適用してみよう」
 「たしか、そこでは、y'=-y^2+10/x^2、ただし、初期値は、[1/8,-20]とするというヤツね。
「たしか、そこでは、y'=-y^2+10/x^2、ただし、初期値は、[1/8,-20]とするというヤツね。
前節の場合は、hを固定すると、絶対誤差は、指数関数的に増大していたのに、リッカチさんでは、絶対誤差が奇妙に増減していたわね」
「そうじゃったな。y'=-y^2+10/x^2、ただし、初期値は、[1/8,-20]。
さて、この方程式の厳密解は、y(x)=(x^(F + 1)(F + 2)(c(F + 1) + 1) + F)/(2x(x^(F + 1)(c(F
+ 1) + 1) - 1))、
ここで、F=-1+sqrt(41)、c = 2^(3√41)(12/5 - 77√41/205) - √41/41、じゃ。
このリッカチの微分方程式の例では、前節のように一個所の点で、観察するのではなく、x=1/8~3の範囲で連続的に観察してみよう。
そのために、LN(|数値解-厳密解|)を上記の範囲でプロットする」
「m=1、2、4の3つの場合について、加速なし、一段加速、二段加速を試してみたよ。
刻み幅は、h=1/128、と固定している。
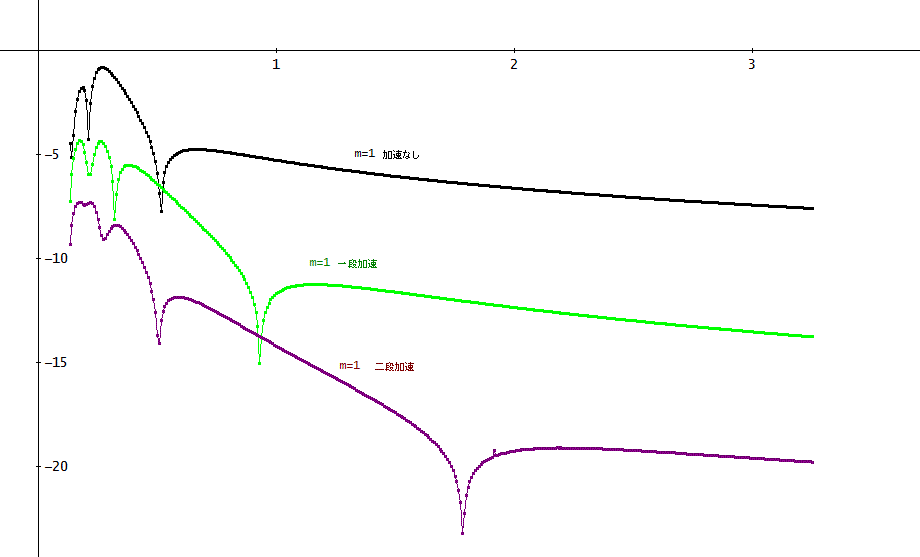
1次のオイラー法に対する、加速なし、一段加速、二段加速の効果は、上図のとおり。
横軸は、xで、縦軸は、LN(|数値解-厳密解|)なので、下に行くほど絶対誤差が小さいことを示している」
「加速効果は、やはり出ておるな」
「ホント。このところどころ、誤差が小さくなる個所が不思議よね。
じゃ、m=2の場合は、ジャン。
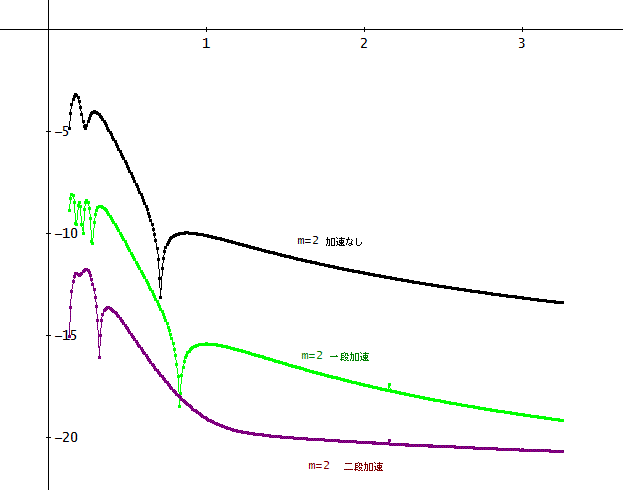
さらに、m=4の場合は、下図の通り。ただし、横軸は、m=1、2の場合より、拡大して表示、また、計算精度を20桁としています」
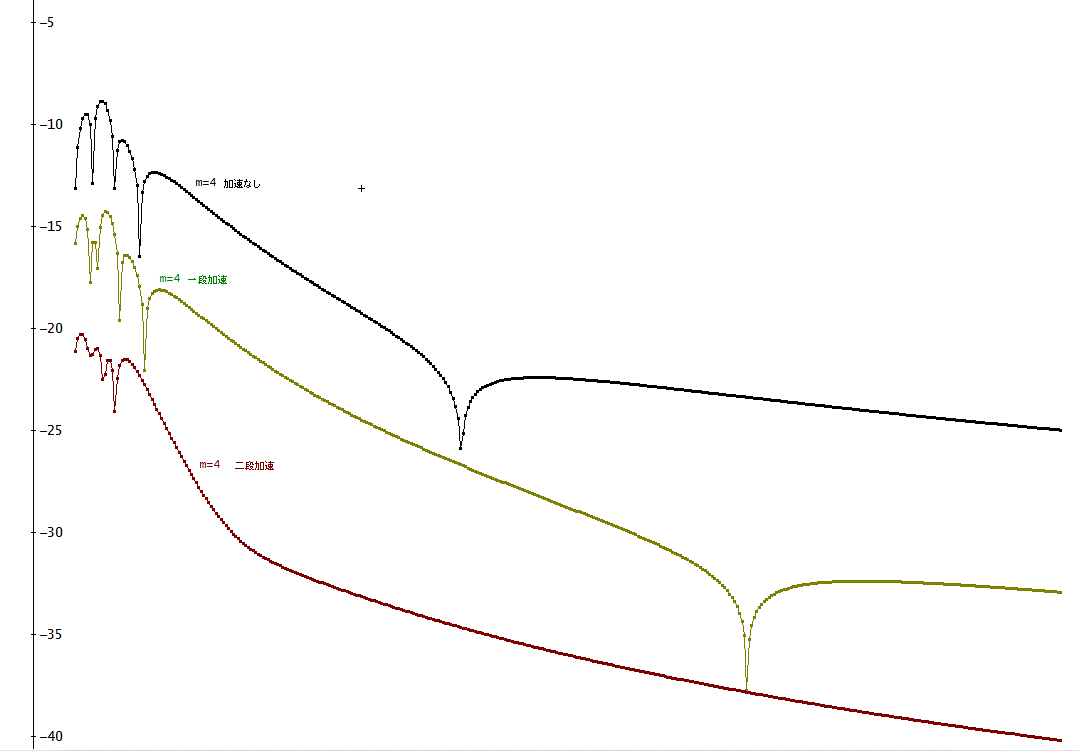
「縦軸は、絶対誤差の大きさの自然対数じゃから、-10というと、約4.5×10^-5、
-40では、4.2×10^-18、という程度の小さな値じゃな」
「その絶対誤差なんだけど、前節の例では、厳密解は、無限大に増大するんだけど、リッカチさんでは、逆にゼロに収束してしまうので、相対誤差はどうなっているのか、調べる必要があるんじゃない?」
「確かにそうじゃのう。
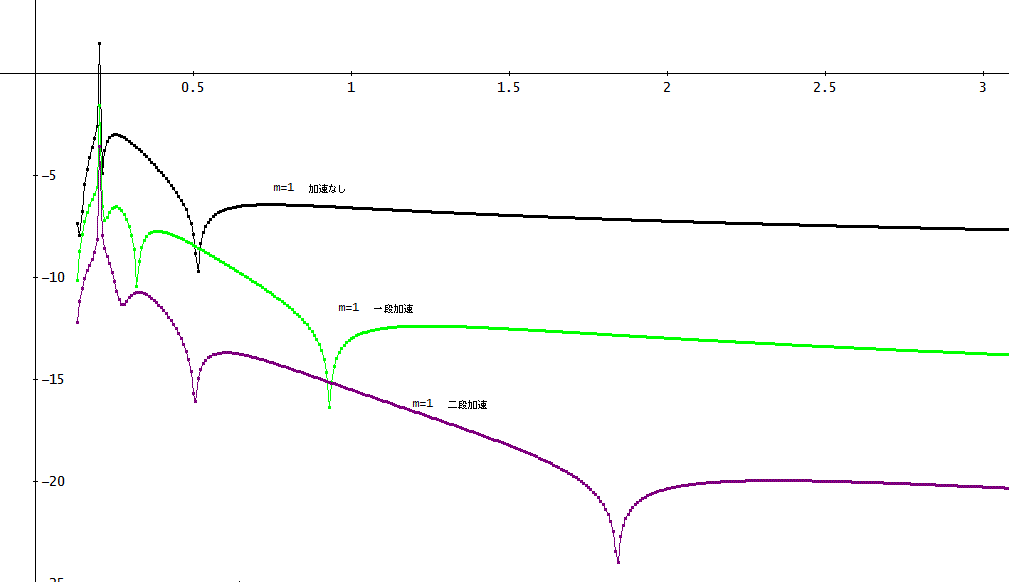
上図が、m=1の場合の、LN(|(数値解-厳密解)/厳密解|)を表したものじゃ。
だいたいの傾向は、絶対誤差と同様じゃが、厳密解が鋭く上昇するあたりの数値解の相対誤差が大きいことが分かる。
そのあたりは、x≒0.2近傍じゃ。
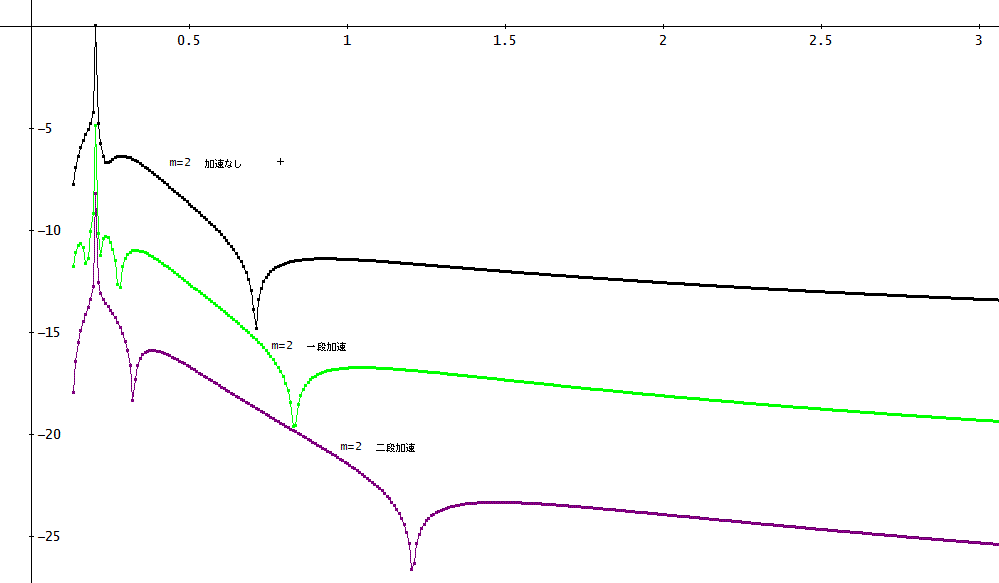
上図は、m=2の様子。二段加速では、x=0.203125で、
厳密解 :-0.021271613529826703065、
数値解 :-0.02126565572234843556、
絶対誤差: 5.9578074782675051622×10^(-6)、
相対誤差: 約0.028%となっている」
「このx=0.203125は、厳密解のゼロ点である、x = 0.20321280417191967671に非常に近い。
これは、この点で厳密解がゼロとなるため、この近傍でも、分母がゼロに非常に近くなり、正確な相対誤差が計算できないことによる見かけ上の上昇じゃな」
「なるほど。
じゃ、xがゼロ点より大きいときに、ところどころ絶対誤差が急に減少するあたりはどうなのかしらね?」
「う~ん。
そのあたりで、数値解-厳密解の符号が逆転しているからじゃないかな。
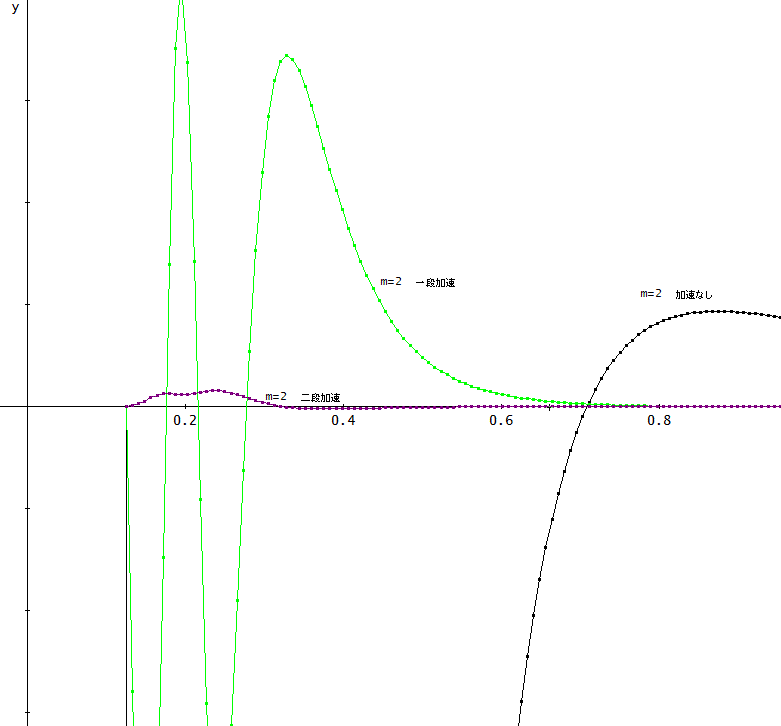
m=2として、(数値解-厳密解)をそのままプロットしたものが上図じゃ。
加速なしについては、符号変化は、1回だけじゃが、一段加速では、細かく変化していることが分かる。
二段加速でも、拡大すると、極めて小さいが、符号が変化している個所がある。そのあたりが、絶対値の自然対数をとったときに反映されているのではなかろうか?」
最終更新日 2014/10/25



 「こうした近似解の打ち切り誤差についても、調べたわね」
「こうした近似解の打ち切り誤差についても、調べたわね」