数式処理ソフト DERIVE(デライブ) de ドライブ
69.方程式の数値解法(4)(ハレー法、DERIVEのPROGとRETURN)
ハレー法(2次のNewton法)
「数式処理ソフト DERIVE(デライブ)の今回は、まずは、Newton法による方程式の解法の改良を考えてみよう」
 「えーと、Newton法の場合は、y=y(x)で、x=x0という初期値から出発して、逐次的に、y(x)=0の解を求める方法だったわね。
「えーと、Newton法の場合は、y=y(x)で、x=x0という初期値から出発して、逐次的に、y(x)=0の解を求める方法だったわね。
こいつを、改良するためには、y(x)をx=xnで、テイラー展開して、
y(x)=y(xn)+y'(xn)(x-xn)+(1/2!)y''(xn)(x-xn)^2+・・、
1次まで考えるのが、元々のNewton法だったのね。
そこで、近似度を上げるために、x=xn+1と置いて、y(xn+1)≒0、と仮定して、2次の項までを考慮する。
ただし、添え字は、煩雑のため、以下では、xnをu、xn+1をvと書くと、
DERIVEでは、y(u) + LIM(∂(y(x), x), x, u)(v - u) + 1/2LIM(∂(y(x), x, 2), x,
u)(u - v)^2=0、
ここで、LIM(関数,変数名,値)は、DERIVEの関数で、「関数」の極限をとる関数ね。
vについて、解くと、
v = u+{±sqrt(y'(u)^2 - 2y(u)y''(u)) - y'(u)}/y''(u)、が得られる。
今、H≡y'(u)^2 - 2y(u)y''(u)と仮に置くと、
v=u+(±sqrt(H)-y'(u))/y''(u)、である。sqrt()は、平方根を求める関数よ。
右辺第2項で、分母分子に、±sqrt(H)+y'(u)を掛けると、
v=u+{H-y'(u)^2}/{y''(u)(±sqrt(H)+y'(u))
=u+{-2y(u)}/(±sqrt(H)+y'(u))、となる。
もし、y''(u)をゼロと見なせる場合は、y'(u)>0ならば、±のプラスを採用して、sqrt(H)≒y'(u)なので、
v=u-y(u)/y'(u)、となって、Newton法の場合に等しくなる。
従って、Newton法の改良としては、
v=u-2y(u)/{±sqrt(y'(u)^2 - 2y(u)y''(u))+y'(u)}、である」
「ようできたな。
上のように、2次まで考慮し、無理式で表したものを、『ハレー(無理)法』(ハリー無理法)というそうじゃ」
「え!
ハリーって、ハリー・ポッターみたい」
「ハハハ。
ハリー・ポッターは、Harrey Potter、(J.K.ローリング作の小説の主人公)、だな。
一方、『ハレー彗星』の研究で有名な、エドモンド・ハレー氏(Edmond Halley :1656~1742)は、イギリスの天文学者じゃ。
ハレー、ハーレー、ハリーなどとカナ表記されるようじゃ。
普通は、『ハレー彗星』という呼び方になじみがあるので『ハレー法』の方がとおりが良い。
ハーレーでは、『ハーレーダビッドソン』(Harley-Davidoson:アメリカの有名なオートバイメーカー)と紛らわしいしな。
しかし、この3つ、みな、少しずつ、スペルが違うのう」
「また、話がそれてしまうわよ。そこまで、そこまで。
v=u-2y(u)/{±sqrt(y'(u)^2 - 2y(u)y''(u))+y'(u)}、で
y(x)=x^2-2、の場合はと言うと、
v=√2、または、-√2、と、初期値に関わらず、2回目の近似値が正解となる。
すごいわね」
「まあ、2次式で近似しているので、2次方程式の解が得られるのは、当然と言えば、当然じゃな。
一般に、y(x)=(x-a)(x-b)としても、
v = (a + b)/2 - ABS(a - b)/2 ∨ v = ABS(a - b)/2 + (a + b)/2、と正解が得られる。
一次のNewton法では、逐次近似値が発散する他に、振動する場合もあったが、無意味な値に収束することは、ほぼない。
しかし、2次のハレー法では、無縁根のように、間違った値に収束することもある。
元の方程式に代入して、確認する必要があるじゃろう。
たとえば、x^3-2=0の様な場合じゃな。
v=±(√3(√(u(8 - u^3)) + √3u^2)/(6u))、であるが、
実根、x=2^(1/3)≒(1.259921049)を得るには、プラス符号の式で、初期値が、2未満であることが必要じゃ。
一方、マイナスの符号の式からは、振動する解が出てくるが、これは、意味が無い」
「平方根号が入っていると面倒だわね」
「そこで、平方根号を入れない工夫もある。
v=u-2y(u)/{±sqrt(y'(u)^2 - 2y(u)y''(u))+y'(u)}、において、
sqrt(y'(u)^2 - 2y(u)y''(u))をy''が小なることを仮定して、近似する。
y'>0と考えると、平方根の第1近似値は、y'である。
平方根の第2近似値を、(第1近似値/2)+(根号内の式)/(2*第1近似値)、とするとよい。
これは、y'/2+(y'(u)^2 - 2y(u)y''(u))/(2y')となるので、結果として、
v=u-2y(u)/{2y'(u)-(y(u)y''(u))/y'(u)}、が得られる。
たとえば、y(x)=x^2-2、に対しては、上の式は、
v=u(u^2 + 6)/(3u^2 + 2)、を与える。
第1近似値を1とすると、第2近似値は、7/5≒1.4、となり、元の無理法の√2には、及ばないものの、相当よい近似となっている」
「なるほど。
y''のテイラー展開だと、1.4より悪い結果になって、うまくないのよね」
「岩波の数学辞典第4版では、『ハレー法』の導出について、概ね次のように説明している。
y(x)=y(u)+y'(u)(x-u)+(1/2)y''(u)(x-u)^2+・・、
第2項までを考えて、x=v、y(v)≒0と仮定すると、
y(u)+y'(u)(v-u)=0、なので、v-u=-y(u)/y'(u)、
そこで、元の式で、第3項の、(1/2)y''(u)(x-u)^2、に上記のv-u=-y(u)/y'(u)を(半分だけ)使うと、
y(u)+y'(u)(v-u)+(1/2)y''(u)(y(u)/y'(u))(v-u)≒0、
これを解いて、
v=u-y(u)/{y'(u)+(y(u)y''(u))/y'(u)}、としている。
先ほどと、同じ結果となる。
ただ、(1/2)y''(u)(x-u)^2=(1/2)y''(u)(x-u)(x-u)≒(1/2)y''(u)(x-u)(-y(u)/y'(u))、と変形するあたり、
ちょっと、技巧的で、気がつかないかも知れんな」
「とはいうものの、平方根の第2近似値を、(第1近似値/2)+(根号内の式)/(2*第1近似値)もなんだか唐突だけど」
「そうじゃな。
y(x)=x^2-a、と置いて、y(x)=0の解、√a をNewton法で求めると、第1近似値をxとして、
([x, x/2 + a/(2x), (x^4 + 6ax^2 + a^2)/(4x(x^2 + a))])のような系列が得られる。
2つ目の近似値を利用している。
なお、数学辞典を見る限りは、単に、『ハレー法』というときは、(無理式を含まない)有理式で表したものを意味するようじゃな」
「3次以上も同様に出来るということね」
「まあ、そうじゃが、高次の式は、高次の導関数やそのべき乗を含んでいる上に、引き算も多く含まれてくるじゃろうから、桁落ちも多くなると思われる。
なので、せいぜい、Newton法は、2次程度まで、考えれば、よいのではないかのう。
いずれにしても、初期値によっては、適切な解に収束しない、局所的収束というそうじゃが、グラフ等で解の範囲を確認しつつ、利用するとよいじゃろう」
高次のハレー法(2013/4/22追記)
「2次を含めて、高次のハレー法の導出について、補足してしておこう。
y(x)をx=uで5次まで、テイラー級数に展開した。
以下では、前節に合わせて、x=vで、y(v)≒0としている。
(v - u)^5y'''''(u)/120 + (u - v)^4y''''(u)/24 + (v - u)^3y'''(u)/6 + (u
- v)^2y''(u)/2 + (v - u)y'(u) + y(u)≒0、
簡潔にするために、v-uをwと置く。
w^5y'''''(u)/120 + (u - v)^4y''''(u)/24 + w^3y'''(u)/6 + w^2y''(u)/2 +
wy'(u) + y(u)=0、
まず、wの一次まで考えて、青字の部分、wy'(u) + y(u)を=0と置き、w≒-y(u)/y'(u)を得る。
今、2次までのハレー法の式を得たい場合は、wの2次までをとって、
w^2y''(u)/2 + wy'(u) + y(u)=0、をwの2次方程式と考えて、Newton法(1次のハレー法)で第2近似値を得る。
そのためには、g(w)=w^2y''(u)/2 + wy'(u) + y(u)、として、初期値、-y(u)/y'(u)に対して、
第2近似値は、w-g(w)/g'(w)=w/2 - (wy'(u) + 2y(u))/(2(wy''(u) + y'(u)))、から、w=-y(u)/y'(u)として、
w=y(u)(y(u)y''(u) - 2y'(u)^2)/(2y'(u)(y'(u)^2 - y(u)y''(u)))、
ここで、w=v-uであるので、
v=u+y(u)(y(u)y''(u) - 2y'(u)^2)/(2y'(u)(y'(u)^2 - y(u)y''(u)))、
これは、2次のハレー法の式じゃ」
 「なるほど、じゃ、3次について計算してみるよ。
「なるほど、じゃ、3次について計算してみるよ。
w=y(u)(2y'''(u)y(u)^2 - 3y'(u)(y(u)y''(u) - 2y'(u)^2))/(3y'(u)(2y'(u)(y(u)y''(u)
- y'(u)^2) - y'''(u)y(u)^2))、
図で表すと、下図のよう。
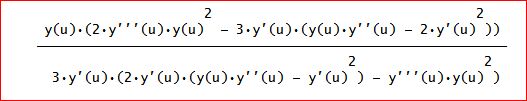
v=u+(y(u)(2y'''(u)y(u)^2 - 3y'(u)(y(u)y''(u) - 2y'(u)^2))/(3y'(u)(2y'(u)(y(u)y''(u)
- y'(u)^2) - y'''(u)y(u)^2)))、
5次までとった場合は、
v=u+(y(u)(4y'''''(u)y(u)^4 - 5y'(u)(3y''''(u)y(u)^3 - 8y'(u)y'''(u)y(u)^2
+ 12y(u)y''(u)y'(u)^2 - 24y'(u)^4))/(5y'(u)(4y'(u)(y''''(u)y(u)^3 - 3y'(u)y'''(u)y(u)^2
+ 6y(u)y''(u)y'(u)^2 - 6y'(u)^4) - y'''''(u)y(u)^4)))、
第2項の複雑な式は、図にすると次のようになる。
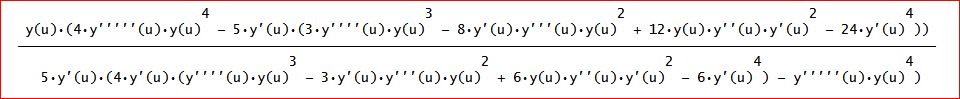
y(x)=exp(-x)-x、初期値=1、に対して、第2近似値以降、精度10桁として計算。
1 次:(0.5378828428)→(0.5669869914)→(0.5671432859)→(0.5671432904)、
無理法:(0.5635034453)→(0.5671432933)→(0.5671432904)、(vのマイナス側の分枝)
2 次:(0.5649192899)→(0.5671432907)→(0.5671432904)、
3 次:(0.5666252720)→(0.5671432904)、
5 次:(0.5669849147)→(0.5671432904)、
正解は、(x ≒ 0.567143290390959・・)、正解のみ精度15桁で計算。
となって、高次の式は、それなりに早く収束するけどもね」
「ハレー無理法は、健闘しとるな」
ProgとReturn
「DERIVEの新しい関数と記法を紹介しよう。
それが、Prog関数とReturnじゃ。
これまで、DERIVEで、続けて2つの処理をするときに、2つの式を別々に書いて、その順に式を演算すれば、よかったので、これまで、この命令に触れることがなかった。
DERIVEは、LISPで書かれているので、+、-、*、/、^、などの少数の算術演算子以外は、関数になっている。
そこで、Basicなどで、当たり前に書いているプログラムの記法が通用しないので、書きにくい場合がある」
 「そうね。
「そうね。
式1、式2、式3を続けて、書くことは出来ても、実行する度に、式1~式3を手作業で実行する必要があるものね」
「たとえば、関数f(x)を変域x=a~b、における定積分を台形公式で数値計算するとする。
このとき、h=(b-a)/n、
S=h(f(a)+f(b))/2+hΣ(k=1~n-1)(f(a+kh))、
という、2つの式を書くとき、やむを得ず、hを使わずに、Sの式の中に含めてしまった。これは、見づらい」
「ちょっと、その前に、基本的なことなんだけど、ユーザ定義関数を作るときに、引数に関数を与えるときは、どのようにしたら良いのかしら?
上の例でも、関数f(x)を意識して、Sの引数に、S(y(x),a,b,n)と書くことは許されないのよね。
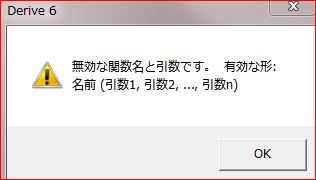
上図のような、エラーが発生するよ」
「そうじゃのう。
わしも、その点を今まで、疑問に思っていたんじゃな。
ユーザ定義関数の外で、別に定義されている関数をユーザ定義関数の定義内で使うのは、差し支えなかったので、深く追求してこんかった。
今回、ごく簡単に、f(x)の微分を行い、変数をx=aとする関数を、Testとして作ってみた。
Test(y_, t_, a_) := LIM(∂(y_, t_), t_, a_)、とな。
Test(x^2+3x-5,x,b)→2b+3、と計算できる。
一方、
Test(x^2+3x-5,y,b)→0、※変数名がxでないと、微分するとゼロになるため。
確かに、関数と変数を受け渡しているのが分かる」
「Test(x^2+3x-5y,y,b)とすると、-5、となる。
なるほど」
「そこで、台形公式をProgを使って、定義してみる。
y_のような、アンダーバー付きの記号を強いて使う必要は無いが、外部で同じ記号を使うといけないので、あえて、このようにしている。
これは、DERIVEのユーティリティ関数などの記法に従った。
S(y_, t_, a_, b_, n_)
:= PROG(h_ ≔ (b_ - a_)/n_,
s_ ≔ (LIM(y_, t_, a_) + LIM(y_, t_, b_))h_/2,
s_ + h_∑(LIM(y_, t_, a_ + k_h_), k_, 1, n_ - 1))、
試しに、f(x):=と、f(x)を外部で関数として指定しているときは、
S(f(x),x,a,b,3)、を計算すると次のようになる。
((b - a)(2f((2a + b)/3) + 2f((a + 2b)/3) + f(a) + f(b))/6)、
確かに、f(x)の台形公式の計算となっていることが分かる」
「Prog(式1,式2,・・)と書くことができるのね、区切りの文字は、半角のカンマ。
途中で、計算を終了したときは、Exit命令のようなものはあるの?」
「Return 式、という形を挿入できる。
例として、Test2(変数,しきい値)として、変数の値が負の時は、-2、しきい値が負の時は、-3、
また、変数の値が正であって、しきい値未満は、-1、しきい値に等しいときは、0、しきい値を超えているときは、1、を返す関数とする。
Test2(x_, y_)
:= PROG(IF(x_ < 0, RETURN -2),
IF(y_ < 0, RETURN -3),
IF(x_ < y_, RETURN -1),
IF(x_ = y_, RETURN 0),
IF(x_ > y_, RETURN 1))、
上の式で、RETURN 数値、というのが、新しい記法じゃ」
「これは、便利ね。
Progは、入れ子式に使えるのかしら?」
「これは、つかえるようじゃな。
さて、ハレー法を次のように、DERIVEで定義してみた。
Halley(y_, t_, a_, n_)
:=PROG(y1_ ≔ ∂(y_, t_),
y2_ := ∂(y_, t_, 2),
y3_ := 2y_y1_/(2y1_^2 - y_y2_),
t2_ := ITERATE(t1_ - LIM(y3_, t_, t1_), t1_, a_, n_),
IF(ABS(LIM(y_, t_, t2_)) < 10^(-8), t2_, false))、
DERIVEの画面表示は、下図のようじゃ。

このHalley関数では、一時変数として、y1_、y2_、y3_、t1_、などを使っている。
このように整理すると、見やすいじゃろう。
なお、a_は、初期値、n_は、繰り返し回数じゃ。
繰り返し回数分の計算が終わったときに、元の方程式に代入して値を計算する。
そして、値の絶対値が10^-8より小さいとき、計算した根の値を、そうでないときは、falseと表示させている。
実際に使うときは、Halley(x^5 - 2, x, 1, 5)、のように利用する」
「定義式内では、y_(t1_)のようには書けないのね?」
「そうなんじゃな。
外部で定義されている関数を使うときは、h(t_)のように利用するのは、差し支えないんじゃがな。
引数の関数や関数の微分などの値を計算したいときは、y_(x)とするところを、Lim(y_,t_,x)などと書かなくては、いけない」
最終更新日 2013/4/23



 「えーと、Newton法の場合は、y=y(x)で、x=x0という初期値から出発して、逐次的に、y(x)=0の解を求める方法だったわね。
「えーと、Newton法の場合は、y=y(x)で、x=x0という初期値から出発して、逐次的に、y(x)=0の解を求める方法だったわね。