数式処理ソフト DERIVE(デライブ) de ドライブ
68.方程式の数値解法(3)(解の重心と範囲、DKA法)
「キリンベック近似法」の導出
「いや、実は、数式処理ソフト DERIVE(デライブ)の前回、第67回の終わりで、DERIVEでの整式の除算は、単純に、『/』でよかったことに気づいたのじゃ」
 「そうでしょう。バレバレだよね。
「そうでしょう。バレバレだよね。
オプションの初期設定では、『Exactモード』になっているので、(x^5+4x+3)/(x+0.7061149157)、みたいな、分母が近似値の場合は、当然ながら、厳密に割り切れるはずもなく、同語反復の様に表示されるもの。
『代数』メニューから『展開』して、≒ボタンで近似値を求めるように指示すれば、ちゃんと、求められるよ。
ま、あたしも知らなかったけど」
「そうじゃろう。
何か、整式の除算用の関数があるんかなと思うてな、ヘルプをあちこち、読んでみた。
確か、整数に関する『ユークリッドの互除法』関係の関数があるのは分かったがな。
いや、すまんかったのう」
「で、今回は、何なの」
「前回、キリンベック氏の著書に挙げてある逐次近似式(以下『キリンベック近似法』と仮に呼ぶ)を使って、aの逆数を計算し、また、適切な初期値の範囲を調べた。
しかし、その導出方法について、触れることができんかった。
まずは、そのことから考えてみることにしよう」
「そうね。
方程式と言っても、ax-1=0、では、あんまり、簡単すぎて、解 x=1/a、を求める方法が、かえって、浮かばない」
「そうじゃのう。
一般に、x(n+1)=x(n)-βf(x(n))、は、、f(x)=0の根を逐次近似的に計算する方法の一つと考えられる。
ここで、βは、フィードバックする効果をコントロールしている。
前回、最初に取り上げた方法では、f(x)=a*x-1、とすると、
初期値、x(1)に対する制限はないが、βは、aと同符号で、かつ、|β|<|2/a|、が収束のために必要じゃった。
以下、上の方法による近似値の導出法を『単純近似法』と呼ぼう。
一方、f(x)=x(a*x-1)とおけば、
x(n+1)=(1+β)x(n)-aβx(n)^2、となり、β=1の場合が、キリンベック近似法と考えられる。
すなわち、キリンベック近似法とは、
x(n+1)=2x(n)-ax(n)^2=x(n)×(2-a*x(n))。
このとき、初期値、x(1)に制限が出てきて、aと同符号で、かつ、|x(1)|<|2/a|、が必要となった。
なお、単純近似法やキリンベック近似法という言い方は、本欄でのみ通用する呼び方なので、注意して欲しい」
「なるほど。
でも、a*x-1=0、を含む関数は、無数に考えられるけど、単純近似法やキリンベック近似法で利用した以外の関数ではどうなのかな?」
「コンピューターの速度が飛躍的に増加しているとは言え、計算量をなるべく少なくしたいので、あまり複雑な関数にしない方が良い。
もちろん、特別な理由、たとえば、収束速度が速いとか、収束条件が緩いとか、理由はいろいろとあり得るので、上記以外はダメというものでもなかろう」
「x(n-1)、x(n-2)などにも依存してよいのね」
「そのとおり。
前回、例として取り上げたのが、逆数を求めることだったので、近似計算中に割り算を使っていなかった。
割り算を使うと、たちまち、正解が出てしまうのでな。
一般には、Newton法のように近似計算中に除算を含める方が、収束が早いじゃろう。
Newton法の場合、関数の微分が必要になるが、x(n)を含めて、x(n-1)などの値を利用すると微分係数を近似できる。次節で、そのあたりを調べて見よう」
微分を差分で近似する
「この節以降、f(x(n))などを、y(n)、などと略記する。
x(n-1)の値を利用すると、y=f(x)における点[x(n),y(n)]での接線の傾きを、次のように近似できる。
接線の傾き=(y(n)-y(n-1))/(x(n)-x(n-1))、
そして、この直線が[x(n),y(n)]を通ることから、直線のx軸との交点の値を導くことができる。交点のx座標を、x(n+1)と書くと、
x(n+1)=((y(n)x(n-1)-x(n)y(n-1))/(y(n)-y(n-1))、である。
これを整理して、
x(n+1)=x(n)-y(n)×(x(n)-x(n-1))/y(n)-y(n-1))、が得られる。
上式は、x(n+1)=x(n)-y(n)×Δx(n-1)/Δy(n-1)=x(n)-f(x(n))/((Δf(x(n-1))/Δx(n-1)))、と書ける。
これは、Newton法の、f(x)のx(n)での微分係数、f'(x(n))≒Δf(x(n-1))/Δx(n-1)と、近似したものと考えられる。
ここで、Δx(n-1)=x(n)-x(n-1)、Δf(x(n-1))=f(x(n))-f(x(n-1))、である」
 「じゃ、早速、試してみるよ。
「じゃ、早速、試してみるよ。
逆数では、割り算を使う近似式では、正解が直ちにでるので、テスト関数は、f(x)=x^5+4x+3、とする。
この実根は、前回、求めているけど、(-0.7061149162・・)となる。
ITERATES([v↓1 - f(v↓1)(v↓1 - v↓2)/(f(v↓1) - f(v↓2)), v↓1], v, [b, 0], 10)、と計算する。
ここで、ベクトル変数、vは、v↓1=x(n)、v↓2=x(n-1)と考える。
また、初期値は、[b,0]としている。([b,b]とすると、分母がゼロとなってしまう)、
b=0.1として、結果は、第10項まで計算させて、x(n)の方だけ表示すると、
([0.1, -0.7499812503, -0.6945498688, -0.7057662261, -0.7061175994, -0.7061149151,
-0.7061149151, ?, ?, ?, ?])
となる。
一方、Newton法によると、同じ初期値である、0.1から出発して、
([0.1, -0.7498962629, -0.7074810960, -0.7061161716, -0.7061149157, -0.7061149157,
-0.7061149157])、となる。
両者は、末尾の桁のみが異なる程度に一致している」
「一致具合は、良好のようじゃな。
なお、ともちゃんの計算で、?となっている部分は、分母がゼロとなり、計算できんかったことを示している。
これを避けるには、
ITERATES([h(v↓1, v↓2), v↓1], v, [b, 0])、
ITERATES関数の第4引数が省略されていることに注意して欲しい。このように回数が略された場合は、h(v↓1, v↓2)≒v↓1まで計算を続行する。
ポイントは、ここで、関数h(x,y)であり、次のように定義される関数じゃ。
h(x, y):=IF(ABS(x - y) < 10^(-8), x, x - f(x)(x - y)/(f(x) - f(y)))、
すなわち、h(x,y)は、xとyとの差の絶対値が10^(-8)より小なるときは、xを返し、
それ以外の時は、前出の、x-f(x)(x - y)/(f(x) - f(y))、を返す。
このため、分母がゼロか、または、極めて小となるときに、xが返るため、ITERATES関数の終了条件が満たされることになる。
([0.1, -0.7499812503, -0.6945498688, -0.7057662261, -0.7061175994, -0.7061149151,
-0.7061149151, -0.7061149151])、
これは、ともちゃんが計算してくれたものと、同一ではあるが、?がないところだけが異なる。
実際は、ITERATESではなく、ITERATE関数にすれば、最後の結果だけが、(-0.7061149151)と表示できる」
「えーと、Newton法を使った場合と末尾の桁が違ったね」
「そうじゃな。
これは、f'(x(n))≒Δf(x(n-1))/Δx(n-1)と微分係数を差分で近似しているが、Newton法では、f'(x)=5x^4+4x、とf'(x)を正しく計算しているからじゃろう。
もっとも、DERIVEのオプションのモード設定で、精度の桁数を10桁から15桁に増やし、h(x,y)の中の10^(-8)を10^(-10)にすれば、
(-0.706114915774181)と求められて、同一条件で、NEWTON法で得られる(-0.706114915774183)とやはり、末尾のみ異なる結果まで正しく求められる」
「ところで、虚根の方は、大丈夫かな。
f(x)=x^5+4x+3、では、残りの4つは、複素数となるんだけどね。
ここでは、精度を10桁に戻している。
ためしに、Newtonでは、初期値(1+#i)と(-1-#i)から、それぞれ、
(1.149701856 + 1.022912937 #i)と(-0.7966443983 - 1.076756664 #i)、が得られる。
残りの2根は、これらの共役複素数と求められる。
一方、今回の方法では、
初期値が、[1+#i,0]からでは、収束しないが、[1+#i,1]から、(1.149701859 + 1.022912938 #i)が得られる。
また、初期値が[-1-#i,-1]では、収束しないが、[-1-#i,1]から、(-0.7966443980 - 1.076756664 #i)が得られた」
「その収束しない場合じゃが、たまたま、f(1+#i)=3、f(0)=3、であるためじゃ。
このとき、上のh(x,y)の定義式で、|x-y|と10^(-8)を比較して、差が小なるときは、xを返す仕様としている。
ところが、x=1+#iとx=0とで、関数の値が一致してしまっていたため、そこで、
h(x, y):IF(ABS(x - y) < 1/10^8 ∨ ABS(f(x) - f(y)) < 10^(-9), x, x - f(x)(x - y)/(f(x) - f(y)))、と
引数又は関数値の差の絶対値が極めて小なるときは、計算を止めるように、xを返す仕様にすれば、よい」
「『または』は、ORと入力しても、DERIVEの画面上では、∨という、集合記号に変わるのね」
「そうじゃな。
『かつ』のANDも、∧に変わる。
これは、今までも、特に注意してこんかったかもしれんが、そういうことじゃ」
「こうやって苦労して改良してみたものの、結果として、Newton法の効果を実感させられたわね」
「まあ、そういうことじゃな。
とは言え、Newton法の改良案も浮かんでこようか、というプラス面もあるぞ。
Newton法は、適切な初期値から出発すると、収束が早いが、1つ(複素数については、共役複素数も結果的には求められるが)ずつしか求まらない。
また、適切な初期値をどうやって決めたらよいのか、という問題がある。
次節で、そのあたりを調べて見よう」
解(根)の平均値(重心)
「以下では、実数を係数とするn次方程式に限定して、
f(x)=a(1)x^n+a(2)x^(n-1)+・・・+a(n+1)=0、を考えると、
f(x)=0の解を、α(k)、k=1~n、として、f(x)=a(1)(x-α(1))(x-α(2))・・・(x-α(n))、とも書ける。
ここで、積の記号を使うと、f(x)=a(1)Π(k=1~n)((x-α(k))、である。
一方、f(x)=Σ(k=1~n+1)(a(k)x^(n-k+1))、から、
f(x)をxでn-1回微分すると、n!×a(1)x+(n-1)!×a(2)=0、すなわち、n×a(1)x+a(2)=0、となる。
f(x)=a(1)Π(k=1~n)((x-α(k))についても、同様に、n-1回微分すると、
a(1)(n!×x+(n-1)!×Σ(-α(k))=0、であり、nx+Σ(-α(k))=0、
よって、先の式から、xを消去すると、Σ(α(k))=-a(2)/a(1)、となる。
この式は、(1/n)Σ(α(k))=-a(2)/(n×a(1))、であり、言い換えれば、
n個の解の平均値(重心といってもよい)が、-a(2)/(n×a(1))となることを示すものじゃ」
 「なるほど。
「なるほど。
じゃ、a(2)=0のときは、原点が重心という訳ね」
「そのとおり。
一般に、変換、x=t-a(2)/(n×a(1))により、x^(n-1)次の項は、消去されるので、
f(x)=a(1)x^n+(n-2次以下の式)=0、のように変換できる。
この場合、解の重心は、常に原点となる」
「たとえば、2x^5 - 3x^4 - 4x^3 - 5x^2 - 10x + 50=0、であれば、
DERIVEの『解く』メニューから、数値解を求めると、以下の5つある。
(x = -0.3981893240 - 1.758484819#i∨ x = -0.3981893240 + 1.758484819#i∨
x = 1.762761853 ∨ x = -1.838865538 ∨ x = 2.372482333)、
これらを加算し、5で割った、重心位置は、1.5/5=0.3、となる。
これは、-a(2)/(n×a(1))=-(-3)/(5*2)=0.3、と一致する。
一方、変換、x=t-(-3)/(5*2)、により、与式は、
g(t)=t^5 - 29t^3/10 - 121t^2/25 - 14323t/2000 + 290141/12500、と変換される。
数値解は、(t = -0.6981893240 - 1.758484819#i∨ t = -0.6981893240 + 1.758484819#i∨
t = -2.138865538 ∨ t = 2.072482333 ∨ t = 1.462761853)、となり、解の重心は、ゼロとなる。
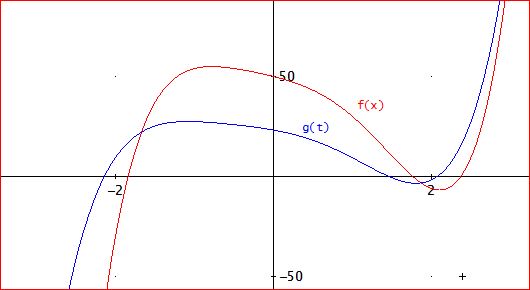
これは、オドロキね。
ax^2+bx+c=0、の2次方程式では、変換、x-b/2a、により完全平方式が出たし、3次や4次方程式でも、この-a(2)/(n×a(1))という変換法は、大活躍したんだけども。
5次方程式以上では、加減乗除と開平操作のみで、一般には厳密解が得られないというアーベルの結果や更に一般のn次方程式について考察したガロア以来、この変換には、『残念な変換』というイメージしかなかったけど、まさか、解の平均値と結びついていたなんて!
しかも、平均値が『こんな』簡単な式、-a(2)/(n×a(1))、で表せるとはね」
「アハハ。『根な』というしゃれかいな。
確かに、変換、x=t-a(2)/(n×a(1))、というのは、n次方程式の原点を、根の平均値の点に移動させる操作じゃったというわけだな。
今、方程式の係数は、すべて、実数としているので、平均値もまた、実数じゃ。
よって、原点を移動すると言っても、x軸上を水平に移動するだけじゃがな。
このように原点を解の平均値に移動しても、しなくても、次の問題は、この平均値を中心とした半径Rの円内に解があるとして、Rの大きさの具体的な見積もりじゃ」
「円内というのは、複素平面上だけど、解の候補は、R×exp(2πk*#i/n)、ここで、i=1~n、のRより小さいということね」
「そうじゃな。
ただし、R×exp(2π#i*(i-3/4)/n)、i=1~n、とするのが、『アバースの初期値』と言われているものじゃ。
これは、次節で、Newton法を変形して、n次方程式のn個の根をいっぺんに求める『DKA法』というものを取り上げる。
そのDKAの最後の頭文字が『Aberth』氏のAじゃったということだな。
なお、上の式で、-3/4という因子が含まれているが、初期値が実軸に対して対称的にならない配慮とのことじゃ。
この初期値(正確には、n次ベクトル)を出発点として、Newton法を変形した逐次計算により、解を求めていく」
「f(x)を変換しない場合は、初期値ベクトルは、-a(2)/(n×a(1))+R×exp(2π#i*(i-3/4)/n)、ということね。
変換された方程式は、g(t)=b(1)t^n+b(3)t^(n-2)+・・+b(n+1)=0、このときは、重心位置は原点なる」
「次節で、Rの見積もりをしてみよう」
解(根)の絶対値の上限
「さて、f(x)=a(1)x^n+a(2)x^(n-1)+・・・+a(n+1)=0、
あるいは、x=t-a(2)/(n*a(1))で変換した、g(t)=b(1)t^n+b(3)t^(n-2)+・・+b(n+1)=0、を考えよう。
以下では、後者のg(t)=0を取り上げる。また、簡単のために、b(1)=1、x<>0としても一般性を失わない。
t^n=-b(3)t^(n-2)-・・-b(n+1)、であるので、両辺の絶対値をとると、
|t^n|=|-b(3)t^(n-2)-・・-b(n+1)|=<|b(3)||t^(n-2)|+・・+|b(n+1)|、
よって、解の絶対値の最大のものをα、と書くと、
|α^n|=α^n=<|b(3)|α^(n-2)+|b(4)|α^(n-3)+・・+|b(n)|α+|b(n+1)|、なので、
解の上限をあらためて、Rと書けば、
R^n=|b(3)|R^(n-2)+|b(4)|R^(n-3)+・・+|b(n+1)|、を解けば、Rが求められることになる」
 「さっきのg(t)=t^5 - 29t^3/10 - 121t^2/25 - 14323t/2000 + 290141/12500、で試してみると、
「さっきのg(t)=t^5 - 29t^3/10 - 121t^2/25 - 14323t/2000 + 290141/12500、で試してみると、
R^5= 29R^3/10 + 121R^2/25 + 14323R/2000 + 290141/12500、
実数解は、R = 2.646449720・・、となる。
元の方程式の解は、(t = -0.6981893240 - 1.758484819#i∨ t = -0.6981893240 + 1.758484819#i∨
t = -2.138865538 ∨ t = 2.072482333 ∨ t = 1.462761853)であるので、確かに、R = 2.646449720・よりも絶対値が小さいことが分かるわ」
ワイエルシュトラス法又はDKA法(デュラン・カーナー・アバースの公式)
「代数方程式の解をまとめて求める方法じゃ。
『数値計算法基礎』(田中敏幸 著:コロナ社:2006年4月)に従って、DKA法と呼ばれるNewton法の拡張版を取り上げてみよう。
ワイエルシュトラスは、ドイツの著名な数学者じゃ。
また、DKAは、Durand(デュラン)氏、Kerner(カーナー)氏、及び、前々節で既出の、Aberth(アバース)氏の頭文字じゃ。
f(x)=a(1)x^n+a(2)x^(n-1)+・・・+a(n+1)=0、とする。
Newton法では、x(k+1)=x(k)-f(x(k))/f'(x(k))、として、逐次近似的に、f(x)=0の解を求めていく。
ここで、x(k)は、k番目の近似値、x(1)が初期値じゃな。
一方、DKA法では、f(x)=a(1)Π(i=1~n)(x-α(i))、解α(i)で展開してみる。
このとき、f'(x)=a(1)Σ(i=1~n)Π(j=1~n、ただし、i<>j)(x-α(i))、となるので、
f'(α(i))=a(1)Π(j=1~n、ただし、i<>j)(α(i)-α(j))、であることが分かる。
これらから、α(i)k+1=α(i)k-f(α(i)k)/(a(1)Π(j=1~n、ただし、i<>j)(α(i)k-α(j)k))、
なお、下付きのk、k+1は、逐次近似の段数を表す」
 「Π(j=1~n、ただし、i<>j)(α(i)-α(j))というのが、ちょっと、面倒ね。
「Π(j=1~n、ただし、i<>j)(α(i)-α(j))というのが、ちょっと、面倒ね。
でも、関数、h(α, i, j)を次のように定義、 ここで、αは、n次元のベクトルとして、
h(α, i, j):=IF(i = j, 1, α↓i - α↓j)、から、
Π(j=1~n、ただし、i<>j)(α(i)-α(j))=∏(h(α, i, j), j, 1, n))、と計算できる。
更に、i=1からnまでの値は、VECTOR(∏(h(α, i, j), j, 1, n), i, 1, n, 1)、でベクトルとして求めることができる。
αの初期値ベクトルは、-a(2)/a(1)+R×exp(2π#i*(i-3/4)/n)、で、i=1~nとする。
この初期値ベクトルが、『アバースの初期値』と呼ばれることは、既出ね。
また、Rの値は、前節のように推定することが出来る」
「そのとおりじゃな。
f(x)=2x^5 - 3x^4 - 4x^3 - 5x^2 - 10x + 50=0、を取り上げてみよう。
x=t-(-3)/(5*2)=t-0.3、と変換して、最高次の係数を1となるように調整すると、
g(t)=t^5 - 29t^3/10 - 121t^2/25 - 14323t/2000 + 290141/12500=0、となる。
α↓i - g(α↓i)/∏(h(α, i, j), j, 1, 5)、がα(i)の逐次近似値となるので、
VECTOR(α↓i - g(α↓i)/∏(h(α, i, j), j, 1, 5), i, 1, 5, 1)、がα(n次元ベクトル)の次の近似ベクトルとなる。
初期値は、α:=Vector(R×EXP(2#i(i - 3/4)/5),i,1,5,1)、
Rは、前節の値、R≒2.65、を使う。
ITERATE(VECTOR(α↓i - g(α↓i)/∏(h(α, i, j), j, 1, 5), i, 1, 5, 1), α, αの初期値ベクトル,
繰り返し数)、
なお、ITERATE関数の代わりに、Iterates関数を使うと、収束の具合を観察できる。
初期値:
([2.520299768 + 0.8188950350#i,
8.107857109·10^(-12) + 2.65#i,
-2.520299768 + 0.8188950350#i,
-1.557630918 - 2.143895035#i,
1.557630918 - 2.143895035#i])
20回目の近似値
([2.072482333 + 3.792260550×10^(-113)#i,
-0.6981893240 + 1.758484819#i,
-2.138865538 + 1.651665240×10^(-23)#i,
-0.6981893240 - 1.758484819#i,
1.462761853 - 1.180705640·10^(-156)#i])
100回目の近似値:
([2.072482333 + 1.289362543×10^(-1004)#i,
-0.6981893240 + 1.758484819#i,
-2.138865538 + 1.756368223×10^(-23)#i,
-0.6981893240 - 1.758484819#i,
1.462761853 - 3.860969310×10^(-1058)#i])
前々節の計算値:
(2.072482333,
-0.6981893240 + 1.758484819#i,
-2.138865538,
-0.6981893240- 1.758484819#i,
1.462761853)」
「なるほど。
20回程度の反復で、ほぼ、十分な解が求められているわね」
「赤い色の部分が誤差の部分を表しているのじゃ。
なお、x=t+0.3、と変換しているので、元の方程式の解は、上の数値に0.3を加えた値となる。
今回は、この辺までにしておこうかの」
DERIVEの代数方程式の数値解法(2015/11/1 追記)
DERIVEでの代数方程式の数値解法について、追記します。
以前に述べたように、代数方程式の根の公式は、4次までしか存在せず、5次以上は、一般には、Newton法などを利用して、数値解を求めるしかないわけです。
本稿でも、方程式の数値解法と題して、第67回~第69回まで、いくつかのアルゴリズムをDERIVEで実行するケースを取り上げてきました。
これは、アルゴリズムの勉強を兼ねてのことです。
しかし、これは、DERIVE自体に解く機能が欠けているという意味ではありません。
たとえば、前節で掲げたような5次方程式、2x^5 - 3x^4 - 4x^3 - 5x^2 - 10x + 50=0、は、
メニューバーの「解く」から「方程式/不等式/関係式」をクリックして、下図のダイアログボックスを開きます。

解法を「数値解」と選択して、「解く」ボタンを押せば、0.07秒足らずで、下記のように解が求まります。
NSOLVE(2·x^5 - 3·x^4 - 4·x^3 - 5·x^2 - 10·x + 50 = 0, x)、(これがDERIVEの数値解を求める関数)
x = -0.3981893240 - 1.758484819·#i、
x = -0.3981893240 + 1.758484819·#i、
x = 1.762761853 、
x = -1.838865538、
x = 2.372482333、
※前節末の注釈のように前節の値は、上の値から0.3を減じてものにあたります。
また、実数解だけで良い場合は、解の領域を「実数」とすれば良いのです。すると、3つの実解だけが表示されます。
解法を「代数解」とすると、5次以上では、一般には、方程式そのものが再表示されるだけですが、簡単な因数で式を分解できる場合は、代数解も求まる場合があります。
最終更新日 2013/3/20 (追記:2015/11/1)



 「そうでしょう。バレバレだよね。
「そうでしょう。バレバレだよね。