数式処理ソフト DERIVE(デライブ) de ドライブ
67.方程式の数値解法(2)(Newton法、逐次近似法)
Newton法の復習
「数式処理ソフト DERIVE(デライブ)の今回は、方程式の数値解法の続きをやってみよう」
 「えーと。
「えーと。
これまで、この『DERIVE de ドライブ』では、方程式の解法を何回に分けて、扱った来たわね。
第11回『1次方程式及び2次方程式』、
第12回『3次方程式』、
第13回『4次方程式』、
第29回『方程式の数値解法』、ね」
「そう。
今回は、内容的には、第29回に続くものじゃな」
「第29回の数値解法では、一変数の方程式に対するニュートン法の説明と、専用関数である、Newton(方程式の左辺,変数名,初期値,回数)が登場してくるの。
この関数の第1引数の方程式の左辺というのは、f(x)=0という方程式があったときの左辺のf(x)の部分を言うのよ。
それと、そこでは、Iterates関数、Iterate関数が初めて、出てきたのよ」
「さすが、DERIVE de ドライブの担当者じゃな。
蛇足じゃが、関数、Newtonの第4引数を省略すると、DERIVEのオプションで指定されている精度(通常は、10桁)以内に2項の差が縮まるまで繰り返すことになる。
たとえば、x^5+4x+3=0、という方程式は、奇数次なので、下図のように、(少なくとも)1つの実根がある。
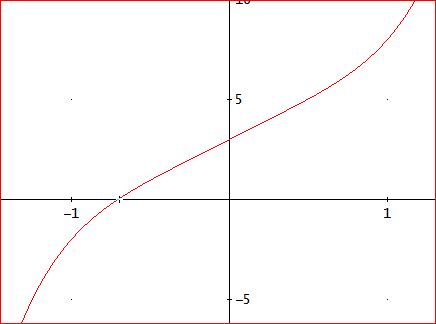
この解を求めるために、NEWTON(x^5 + 4x + 3, x, 1, 10)としてみると、
([1, 0.1111111111, -0.7498402055, -0.7074775055, -0.7061161650, -0.7061149157,
-0.7061149157, -0.7061149157, -0.7061149157, -0.7061149157, -0.7061149157])
であるが、
NEWTON(x^5 + 4x + 3, x, 1)と第4引数を省略すれば、
([1, 0.1111111111, -0.7498402055, -0.7074775055, -0.7061161650, -0.7061149157,
-0.7061149157, -0.7061149157])
が得られる。
すなわち、8回目までの逐次近似計算で、x1≒-0.7061149157、と、求められていることになる」
「すると、方程式の次数を4次にすることができるため、後は簡単という訳ね」
「とは言っても、その4次方程式の係数を求めなくてはならんじゃろう」
「それは、仕方ないじゃん。
といっても、少し、面倒だけど、
x^4 - 0.7061149153x^3 + 0.4985982734x^2 - 0.3520676776x + 4.248600237≒0、と
なることが分かる。この4次方程式の解は、
x2 = -0.7966443983 - 1.076756664 #i
x3 = -0.7966443983 + 1.076756664 #i
x4 = 1.149701856 - 1.022912937 #i
x5 = 1.149701856 + 1.022912937 #i
となる。
2つずつ、互いに共役複素数となっているのよ。
つまり、x2の共役複素数x3は、x2の虚数部の符号を変えたもの。x4とx5もそういう関係。
あと、#iというのは、虚数単位ね」
「では、別法で確認してみよう。
NEWTON(x^5 + 4x + 3, x, 1 + #i)、と置き、近似計算させると、
1.149701856 + 1.022912937 #i、となって、x5が求められる。
これから、共役複素数のx4も求められる。
また、NEWTON(x^5 + 4x + 3, x, -1 - #i)からは、
-0.7966443983 - 1.076756664 #i、が得られて、こちらは、x2であり、共役複素をとると、x3も求められる。
どちらの方法でも、10桁の精度の範囲内では、一致したようじゃな」
「でも、整式の割り算は、係数の桁数が多いと、間違いやすいわ」
「そう思うじゃろう。
ところが、DERIVEでは、整式の除算は、簡単なんじゃ。
単純に、x^5+4x+3/(x+0.7061149157)とすると、『代数』メニューの『展開』を押して、
OKを押してから、≒(近似計算)を指示すると、
(3.889416901/(10^10×x + 7.061149157×10^9) + x^4 - 0.7061149156×x^3 + 0.4985982741×x^2 - 0.3520676783×x + 4.248600239)
と求められる。ここで、最初の項は、余りじゃよって、消してしまうと、
(x^4 - 0.7061149156×x^3 + 0.4985982741×x^2 - 0.3520676783×x + 4.248600239)が残るので、ゼロと置いて解くと、
x = 1.149701856 - 1.022912937×#i
x = 1.149701856 + 1.022912937×#i
x = -0.7966443983 - 1.076756664×#i
x = -0.7966443983 + 1.076756664×#i
とたちまち、求められたな」
「なんだー。
がっかりじゃん」
「まあ、可愛い子には、旅をさせろとも言うからな。
せっかくじゃから、次節以降で、割り算をしないで商を求める方法を調べて見よう」
除算をせずに商を求める
 「割り算をしないで商を求める、というのは、どういう意味なの?」
「割り算をしないで商を求める、というのは、どういう意味なの?」
「第64回で、『パーソナルコンピュータによる 量子力学』(J.P.Killingbeck:有馬朗人・川合敏雄 訳:サイエンス社:1985年5月)を引用したのを覚えておるじゃろう。
この本の中に、著者のキリンベック氏が、逐次近似法の例として、割り算をせずに商を求める方法を紹介している個所がある。
ここでは、少し、記号を変えて、説明してみようかの。
変数をx として、a*x-1=0、という方程式を考える。
解は、aがゼロでなければ、x=1/a、じゃ。これは、aの逆数であるのは、当然じゃが。
それを、次の式で逐次近似的にもとめる。
以下の→は、左側で計算した値を新しいxとして、ふたたび、左辺に代入するという意味じゃ。
x(2-a*x)→ x、
なお、xの初期値は、あとで述べるが、とりあえず、小さい値(ただし、ゼロではない)にしておく」
「へー。
じゃ、ちょっと、やってみるよ。
xの第n個目の近似値を関数、x(n)、で表して、0.001=x(1)は、xの初期値とする。
x(n):= IF(n = 1, 0.001, (2 - a*x(n - 1))x(n - 1))、
たとえば、a:=2とすると、
VECTOR(x(n), n, 1, 20, 1)
([0.001, 0.001998, 0.003988015992, 0.007944223440, 0.01576222550, 0.03102755551,
0.06012969262, 0.1130282253, 0.2005056912, 0.3206063181, 0.4356358137,
0.4917145030, 0.4998627010, 0.4999999622, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5])
となって、確かに、1/aの0.5にはなるわね。
では、すこし、意地悪して、a:=-10ではというと、
発散してしまったよ」
「aが負の場合は、初期値も、負としておくのが肝心じゃな。
ともちゃんの再帰関数の初期値を、下のようにaの符号と同じものにしておく。
x(n):= IF(n = 1, 0.001×SIGN(a), (2 - a×x(n - 1))x(n - 1))、のようにな」
「なるほど。
だけど、どうして、1/aが求まるのかな?」
負帰還回路
「キリンベック氏の本には、このような面白いポイントが随所に出てくるが、教科書的な解説が簡略化されていたり、省かれていたりする。
そこは、読者自らが、いろいろと試して、考えてご覧、というような姿勢が見える。
こういう点は、学ぶべき点があると思うのう。
ところで、ともちゃんは、『負帰還増幅器』というのを知っているかな?」
 「フキカンゾウフクキ?」
「フキカンゾウフクキ?」
「フィードバックというのは、聞いたことがあろう。
出力の一部を(逆位相で)入力側に戻すと、結果として、出力が極めて安定する、という電気回路のことじゃ。
この原理や回路の発明の背景などは、いずれ、別の記事で、触れるとして、逐次近似法の有力な背景の一つとして、フィードバックの考え方があると思う。
前節の式を、差分方程式の形に書くと、x(1)を初期値として、
x(n+1)=x(n)×(2-a*x(n))、n=1、2、・・。
この右辺は、x(n)×(1-(a*x(n)-1)、と分解できる。
そして、さらに、一般化すると、解くべき方程式を、f(x)=0であるとして、
x(n+1)=x(n)-x(n)×f(x(n))、とも書けるのではないかと気がつく」
「ははー。
その、-x(n)f(x(n))が、負帰還の部分ね。
x(n)が十分、解に近ければ、負帰還部分は、小さくなり、逆に解から遠ければ、大きくなる。
でも、それであれば、f(x(n))×定数のようなものでも役に立ちそうじゃない?」
「確かにな。
x(n):= IF(n = 1, 0.001, x(n - 1) - 0.1×f(x(n - 1)))、
のような式を再帰関数として、定義すれば、a=2の場合には、正解の、x=0.5に近づいていく。
しかし、a=20では、振動し、a=21では、発散してしまう」
「なるほど。
それにしても、nが大きくなると、計算時間がかかって大変。
そこで、
ITERATES(x - β(ax-1), x, 初期値,回数)のように、Iterates関数又はIterate関数を使うのがお勧め!」
「さて、x(n+1)=x(n)-βf(x(n))、と逐次近似法的にf(x)の解を求めようとしたとき、
f(x)=a*x-1では、a=2のときは、収束したが、a=20では振動、21以上では、発散した。
なお、上の例では、β=0.1としている。
その原因を探ってみよう。
x(n+1)-γx(n)=β、γ=1-aβである。
この差分方程式は、線形であるので、厳密解が、容易に、、
x(n+1)=(γ^n)×x(1)+β×(1-(γ^n))/(1-γ)、であることは、分かる。
ここで、a=2、β=0.1のときは、γ=1-aβ=0.8となり、nが十分に大きくなると、
右辺の第1項は、初期値の如何に関わらず、ゼロに近づく。
一方、右辺の第2項でも、γ^n がゼロに近づく。
残るのは、β×1/(1-γ)=0.1/0.2=1/2 であるので、nが大きくなると正解に至ることが分かるじゃろう」
「a=20のときは、γ=1-aβ=-1となるため、γ^nの項が振動し、a>20では、γ>1のため発散してしまうのね」
「そういうことじゃ。
収束するためには、|γ|<1であることが必要十分じゃ。
すなわち、-1<(1-aβ)<1、
これから、0<aβ<2、という条件が導かれる。
これは、aとβが同符号で、|β|は、|2/a|より小とする必要があることを示している」
「では、キリンベックさんの式はというと、
x(n+1)=x(n)-x(n)(a*x(n)-1)、から、
x(n+1)=2x(n)-x(n)^2、となる。
だけど、このときは、差分方程式が、線形でなくなってしまうので、さっきのようには、解析できない」
不動点
「まずは、前節で、調べた、単純な差分方程式についてじゃ。
x(n+1)-γx(n)=β、γ=1-aβ、であった。
ここで、βは、x(n+1)=x(n)-β(a*x(n)-1)、のフィードバック部分の大きさを決めるパラメータじゃ。
このとき、x=h(x)、ここで、h(x)=x-β(ax-1)、とすると、この解は、βがゼロでない限り、x=1/aとなる。
このように、x=h(x)となる点のことを関数h(x)の『不動点』という。
さて、y=x(n+1)、x=x(n)と仮に置き、グラフを描いてみると、
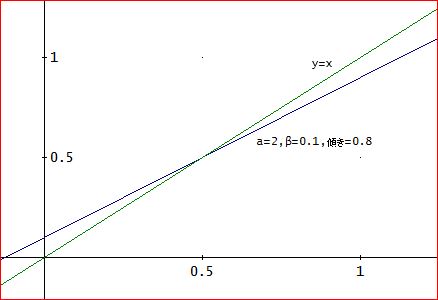
上図のようになる。
黒い直線が、y=(1-aβ)x+β=0.8x+0.1、じゃ。
緑色の方は、比較のために描いたもので、こちらは、y=xとなっている。
黒の方の傾きは、0.8と1より小なため、拡大率(1-aβ)の絶対値が常に1を下回る状態となり、発散をしないことが分かる。
一方、下図のように、a=20、β=0.1のときは、y=-x+0.1、
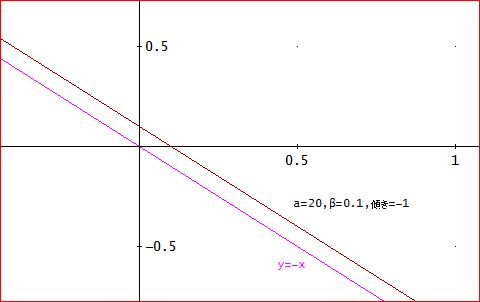
であり、比較のために描いた、y=-xと同じ傾きとなっている。
このときは、([0.3, -0.2, 0.3, -0.2, 0.3, -0.2, 0.3, -0.2, 0.3])のように、振動を繰り返す。
(初期値=0.3)
さらに、a=20、β=0.2、では、y=-3x+0.2、となり、発散する。
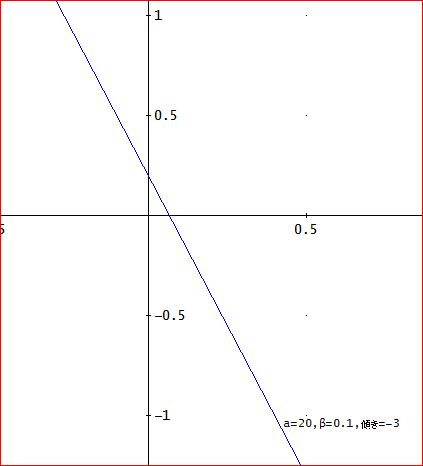
このように、拡大率(上では、傾き)が1未満であれば、どのような初期値から出発しても、収束するであろうことが分かる。
これは、前節で、示した、|1-aβ|<1、と同じことじゃな」
 「う~ん。
「う~ん。
なんとなくは、分かるんだけどね。
a<0の場合は、どうなるのかな?」
「a<0、かつ、β<0の場合は、傾きが変わらず、y軸の切片が、正から、負になるだけで結論は同じやな。
一方、a<0、かつ、β>0の場合は、a=-2、β=0.1で、傾きが、1.2となり、
([2, 2.5, 3.1, 3.82, 4.684, 5.7208, 6.96496, 8.457952, 10.2495424, 12.39945087,
14.97934105, 18.07520926, 21.79025112, 26.24830134, 31.59796161, 38.01755393,
45.72106472, 54.96527766, 66.05833320, 79.36999984, 95.34399981])のように増大を止められない。
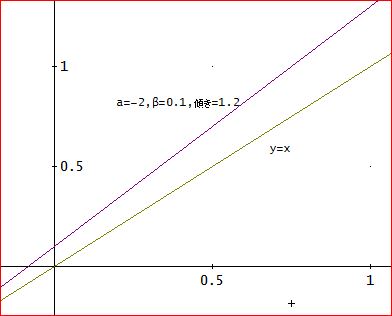
a>0、かつ、β<0の場合も、同様じゃ。
たとえ、わずかでも、傾きの大きさが1を上回ると、発散する」
「初期値に対する依存性を調べるために、こんなことを考えてみたの。
x(n)/x(1)のグラフを描いてみた。
a=2、β=0.1としている。
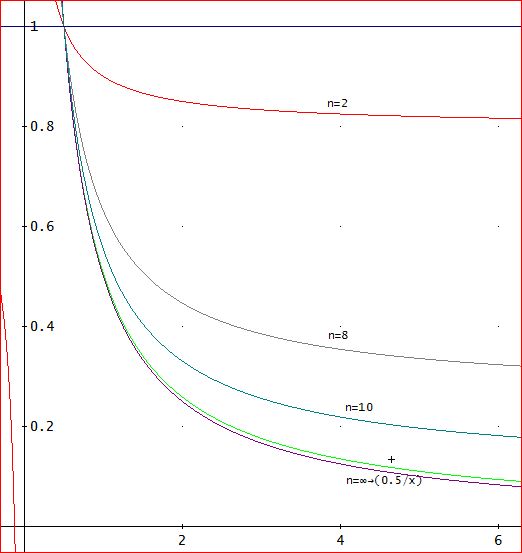
横軸が、初期値(x)を示して、縦軸が初期の何倍(増幅率)になっているかを示している。
繰り返し数が増加すると、理論値の(1/a)/x(1)=0.5/xに近づいている様子が分かる。一番下の線が0.5/x、その上の緑線がn=20のときの値。
増幅率は、初期値が、1/aで、上図の水平線で示した、1となる。(これは、nに関わらない)
初期値が、1/aより小さいときは、増幅率が1より大きく、初期値が拡大され、初期値が1/aより大きいときは、増幅率は(正で)1より小さいことが分かる。
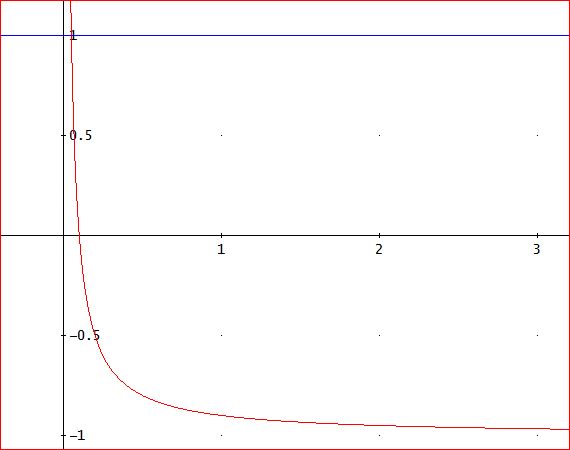
上の図は、a=20、β=0.1のときで、n=10の場合。
このとき、増幅率は、+1と、ほぼ、-1の間を振動する。
最後に、a=21、β=0.1の場合。
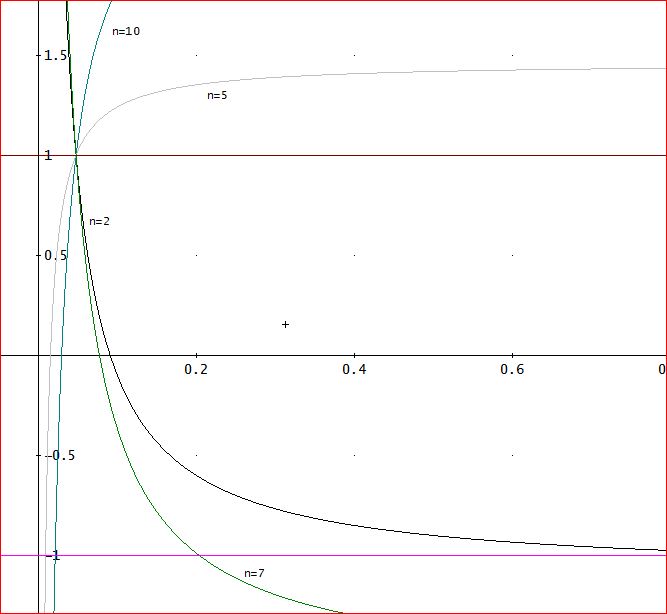
このときは、初期値が、1/aより小さいとき、増幅率は、繰り返し数により、正又は負で、絶対値は、1より大きな値となる。
ここで、負の値が出ることが、安定的な、|β|<2/a、のときと異なる。
この結果、繰り返し数が大きくなると、増幅率の絶対値は、1よりどんどん大きくなり発散してしまう」
「いや、ともちゃん。
これは、分かりやすい図じゃのう。
次節で、キリンベック氏の式を検討する際に使って見よう」
x(n+1)=x(n)(2-a*x(n))の検討
「では、早速じゃが、前節の最後で、ともちゃんが描いてくれたグラフにならって、x(n+1)=x(n)(2-a*x(n))の検討をしてみよう。
この逐次近似式には、前節のβのような、パラメーターが含まれていないので、初期値、すなわち、x(1)に対する依存性を調べて見るとしよう。
以下では、b=x(1)と便宜的に置く。
また、a>0、かつ、b>0の場合だけを調べれば、よいことに注意する。
なぜなら、a<0、かつ、b<0の場合は、xの符号も反転して考えると、x(n+1)=x(n)(2-x(n))の形は、まったく変わらないためじゃ。
さらに、a>0、かつ、b<0、あるいは、a<0、かつ、b>0の場合は、調べるまでもなく、発散してしまうであろうことは、明らかじゃな。
そこで、代表的な、a=2の場合をbを変化させて調べて見よう」
 「ITERATES関数を使って、ITERATES(x(2 - 2x), x, b, n)/b)のようにすると、n+1回目までの増幅率(x(n)/b)の式を求めることができる。
「ITERATES関数を使って、ITERATES(x(2 - 2x), x, b, n)/b)のようにすると、n+1回目までの増幅率(x(n)/b)の式を求めることができる。
たとえば、n=3とすると、
[1, 2(1 - b), 4(1 - b)(2b^2 - 2b + 1), 8(1 - b)(2b^2 - 2b + 1)(8b^4 - 16b^3
+ 12b^2 - 4b + 1)]、
これでは、わかりにくいので、グラフにしてみると、
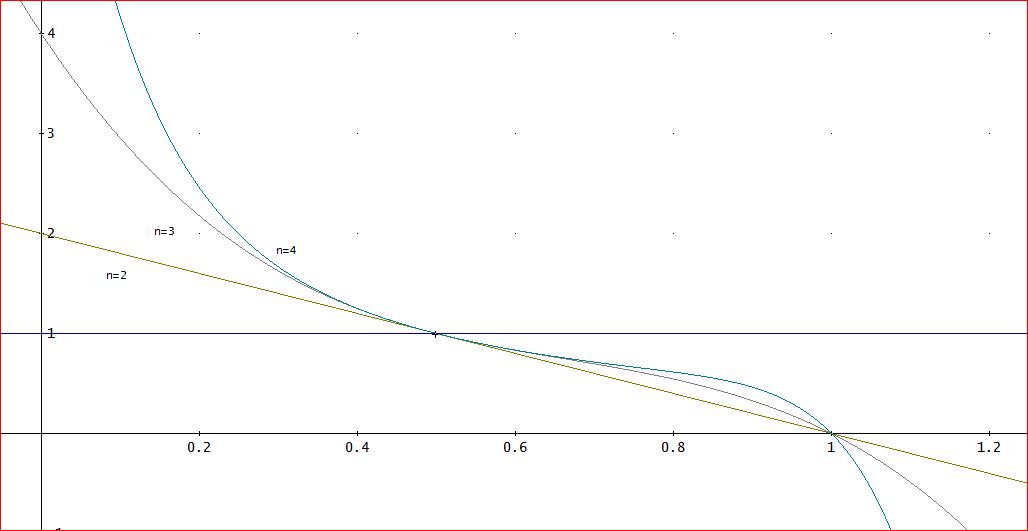
解である、1/a=0.5でちょうど、増幅率が1となるのは、繰り返し数には、依存しない。
この(不動)点の前後では、前節で描いてもらった、a=2、かつ、β=0.1のときと同様に、b<0.5では、1より大、b>0.5では、1より小である。
しかし、b=1の前後では、様子が激変する。
b>1であると、増幅率は、負となり、繰り返し数の増加とともに、限りなく負方向に増大する。
一方、b<1のあたりでは、増幅率は、1より小の正の値を保つ」
「初期値(b)への依存性が、1=2/aの前後で、ものすごく、変わってしまうのね」
「そうじゃな。
b=1では、繰り返し数が大きくなると、bの負の側では、増幅率の微分係数が、-∞に近づく。
試しに、n=10のときで、-512となっている」
「そうなのよね。
繰り返し数が、大きいときのグラフが、『メモリーオーバー』となって描けないよ」
「bが1より小さい方から、1に近づく場合は、緩やかに、0.5に近づくが、b=1では、ゼロになる。
b=0.9で、(0.5555555555)
b=0.99で、(0.5050505050)
b=0.999で、(0.5005005005)、
b=0.9999で、(0.5000500050)
b=0.9999では、(0.5000050000)
b=1では、ゼロ。
一方、bが1より大きい方から1に近づく場合は、極端に大きさが変わる。
b=1.000001で、(-3.571460763)
b=1.00001で、(- 6.407520406×10^8)
b=1.0001で、(- 5.861032198×10^90)
b=1.001で、(- 3.719702902×10^909)
b=1.01では、(- 4.249658667×10^9017)、のように、途方もなく大きくなる。
これは、x(n+1)/x(n)=1/(2-2x(n))、であるから、
x(1)=b=1+hとおいてみると、x(2)=(-1-3h-2h^2)、であるので、
(x(2)-x(1))/h≒-1/h、より、h>0でゼロに近づくときは、この値は、負の∞になる。
また、h<0のときも、hを-hで置き換えることにより、(x(2)-x(1))/(-h)≒1/h、となり、同様に、負の無限大になる。
ただし、b=1では、繰り返すこと無しに、正解の1/aが得られる」
逆行列への応用
「前節までの逆数を求める逐次近似式は、理論的には、面白いが、数値の逆数を求める実用的な方法ではないじゃろう。
そこで、キリンベック氏の本で示唆されているように、正則行列の逆行列を求めてみよう。
簡単な例として、A=[4, 3; 1, 2]をとりあげてみよう」
 「DERIVEでは、A^(-1)で、([2/5, - 3/5; - 1/5, 4/5])が得られるわ。
「DERIVEでは、A^(-1)で、([2/5, - 3/5; - 1/5, 4/5])が得られるわ。
小数で書けば、([0.4, -0.6; -0.2, 0.8])となる。
さっきの式で逆行列X=A^(-1)を求めるとすると、
近似式を、X(2I-A*X)=2X-X*A*X、と書く。Iは、単位行列だけど、掛けた方が簡単かな。
さて、(x ≔ [0.0001, 0.0001; 0.0001, 0.0001])から出発すると、行き詰まるけど、
(ITERATES(x(2I - Ax), x, [0.0001, -0.0001; 0.0001, 0.0001], 20))、のように、負の要素があると、
20回ほど反復で、正解にたどり着く。
x=[0.4, -0.6; -0.2, 0.8]、
しかし、 [-0.0001, 0.0001; 0.0001, 0.0001]、では、発散。
やはり、正解の符号とは、一致していないと難しそう」
「確かにな。
A:=[1, 2, 3; 2, -5, -25; 3, -25, 30]
A^(-1)=[0.6739130434, 0.1173913043, 0.03043478260; 0.1173913043, -0.01826086956,
-0.02695652173; 0.03043478260, -0.02695652173, 0.007826086956]、
このとき、Xを(0.01×[0.01, 0.1, 0.1; 0.1, -0.01, -0.1; 0.1, -0.1, 0.01])のように、正解の符号と一致させると、20回程度の反復で満足のいく値に漸近する。
とは言え、やはり、なんらかのプログラムで、近似行列の|要素|の最大値が発散しそうになったら、初期行列のXを定義し直して、再度、試みるようにしないと、nが大きいときは、実用に耐えないじゃろう」
「そこまでしなくても、こうすると、いくらか、実用的になるわ。
ITERATES(2X - XAX, X, 0.001×RANDOM_MATRIX(3, 3, 1), 20)、とするの。
ここで、Random_matrix(3,3,1)関数は、3行3列の行列の各要素に、-1~+1、の範囲の乱数を入れて作る関数なの。
この計算行を繰り返して、安定するまで、≒ボタンを押して、近似計算させると、
([0.6739130434, 0.1173913043, 0.03043478260; 0.1173913043, -0.01826086956,
-0.02695652173; 0.03043478260, -0.02695652167, 0.007826086956])
となって、元のAとの積が、
[1, 2.074027696×10^(-10), 0; 0, 1, 0; 0, 2.074027696×10^(-9), 1]、程度と、満足できる数値となっている」
「なるほど。
ランダムマトリックス関数というのがあるんじゃな。
とは言え、だいぶ、分量が多くなってしまったので、今回は、このぐらいにしておこうかの」
最終更新日 2013/3/7



 「えーと。
「えーと。