数式処理ソフト DERIVE(デライブ) de ドライブ
66.再帰関数(5)(オイラー変換、差分、和分)
Euler変換(オイラー変換) 再見
 「えー。また、Euler変換なの!」
「えー。また、Euler変換なの!」
「まーまー。
ともちゃん、そう言わんとな。
数式処理ソフト DERIVE(デライブ)では、様々な便利な関数が定義されておる。
たとえば、前回出てきた、フーリエ級数を求める、Forier(関数,変数名,始点,終点,項数)などなどじゃ。
ところが、無限級数に対する、Euler変換法については、どういうわけか、定義済みの関数の中に見つからん。
(※第53回に出てきた『Euler-Maclaurin展開』による級数計算は、Userフォルダ内に利用者が定義したものはあるようじゃが)
そこで、無限級数のオイラー変換による計算式をユーザー定義関数として、すぐに使えるようにしておきたい」
「はー、確かに、その都度、Euler変換の関数を作るのは、面倒ですもの。
第64回の『指数積分』でも、変数が負の場合、Euler変換を使って級数を計算してみたいな、と思って、ちょこっと計算するだけなのに関数を定義しなくてはならないしー」
「でな、調べると、2008/9の第41回『積分(1)(単積分、数値積分とEuler変換)』で、Euler変換が出てきているが、そこでは、オイラー変換を使っているだけじゃ。
導出は、第45回の『積分(5)(高速ラプラス逆変換2)』で簡単に触れているがな。
なお、第45回の記事の文中に、係数が一部正しくなかったので、2013/2/7に訂正しておいた。すまんのう」
「じゃ、まず、記号を整理しますね。
数列をa(n)で表す。
数列の添え字 n の始点をゼロにするか1にするかで、いつも頭を悩ますのよね。
DERIVEのベクトルでは、添え字のゼロが許されないから。
でも、前も、n=0から始めているので、n=0から始めます。
だから、1-1/2+1/3-1/4・・の一般項は、a(n)=(-1)^n/(n+1)、n=0、1、2、・・と書く。
また、差分演算子を、Δで表し、Δa(n)=a(n+1)-a(n)、と定義する。
Δ^mの添え字 m を『階差』と言い、Δ^0 a(n)=a(n)、Δ^2 a(n)=Δ(Δa(n+1)-Δa(n))=a(n+2)-2a(n+1)+a(n)などを意味する。
なお、差分演算子の定義には、以前引用した『BASICによる高速ラプラス変換(細野敏夫著:共立出版:1984年)』のように差分演算子をDで表し、D
v(n)=v(n+1)+v(n)という流儀もあり得るけど、やはり、わかりにくいと思うので、『計算数学夜話(森口繁一著:日本評論社刊:昭和53年4月10日初版)』など、数学や物理で普通、使用している例にならう。
このとき、数列の項に正負が交互に現れる『交代級数』で、かつ、その和が収束する場合、無限級数の和をS、S=Σ(k=1~∞)a(k)は、
第ゼロ項から第n-1項までは、普通に計算し(正直計算よ)、n項目からオイラー変換を使う方法によると、第m階差までで、
S≒Σ(k=0~n-1)a(k)+(a(n)の符号)Σ(k=0~m)(2)^(-k-1)×(-1)^(k)×Δ^(k)|a(n)|、
ここで、無限和は、原理的には、m→∞だけど、実際は、適当なところで打ち切る。
なお、||は絶対値をとる意味で、DERIVEでは、ABS()関数ね。なぜって言えば、オイラー変換法を使う場合、a(n)の値を符号を含めずに、正と考えているた め。
それと、実用上、大事なのは、a(n)の符号を考えていることね。
それは、上の近似計算が、第0項からn-1項まで、正直に計算して、n項目からオイラー変換を使うんだけど、n項目を正として、立てているんだ。
だから、場合によっては、そのn項が負の場合への対処。これがないと、利用者が、nを注意して、入力しないと、誤差が多くなります。
DERIVEでは、符号関数は、SIGN(a(n))と書けます。
SIGN()は、引数が正の場合は、+1、負の場合は、-1、ゼロの場合は、±1となるので注意!」
「そうじゃな。
符号の件は、これまで、無意識に、n項が正となるようにしていたので考えなかった、実用上は、利用者の注意に委ねるのは、危険なことが、分かったのう。
なお、ともちゃんが例に挙げた、無限級数は、既知のように、LN(2)≒0.69314718055994530941・・に収束する。
n=0~1000までとる、正直計算のみでは、S(n=1000)≒(0.69364643155882130866)となり、有効数字で2~3桁が精一杯じゃ。
100万と1項とっても、正直計算のみでは、S(n=1000000)≒(0.69314768055919531041)で、有効数字5~6桁程度。
ただし、ここでは、DERIVEのオプションのモード設定で『精度』を通常の10桁から20桁に変更している」
「ジャン!
そこで、オイラー変換が登場したということね。
Δ^m |a(k)|=f(k,m)と書くと、
f(k,m)は、次の漸化式を満たす再帰関数として定義できる。
f(k,m)=f(k+1,m-1)-f(k,m-1)、
ただし、f(k,0)=|a(k)|とする。
こうすると、S≒Σ(k=0~n-1)a(k)+SIGN(a(n))Σ(k=0~m)((-1)^(k)/2^(k+1))×Δ^(k)|a(n)|
=Σ(k=0~n-1)a(k)+SIGN(a(n))Σ(k=0~m)((-1)^(k)/(2)^(k+1))×f(n,k))、
DERIVEでは、
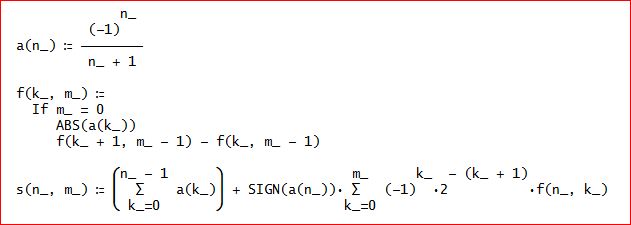
となる。
f(k_, m_):= IF(m_ = 0, ABS(a(k_)), f(k_ + 1, m_ - 1) - f(k_, m_ - 1))、
s(n_, m_):= ∑(a(k_), k_, 0, n_-1) + SIGN(a(n_))∑((-1)^k_2^(- (k_ + 1))f(n_, k_), k_, 0, m_)、
で、試しに、
S(10,5)≒(0.69314710896742146742)、0.00秒、
0~9項を正直計算し、10項目の第5階差まで考えるだけでオドロキの結果ね。正直計算では100万項とらないとこの精度は出ないもの。
S(20,5)≒(0.69314717912049736656)、0.00秒、
S(20,10)≒(0.69314718055983489642)、0.047秒、
までは、計算自体も、ほぼ瞬時にできるけど、
S(20,20)≒(0.69314718055994530938)となると、精度は、素晴らしい(有効数字18桁)けど、時間がかかる。(33.1秒)
なお、所要時間は、DERIVEで自動的にステータスバーの右側に出ます。
環境は、Windows 7 64ビット版、CPUは、インテルCore i5 661(3.33GHz)、8GBメモリー」
「その点は、後で、劇的に改善できるから、安心しなさい」
記号と演算
 「プラスとかマイナスも『演算子』だよね」
「プラスとかマイナスも『演算子』だよね」
「演算子と関数とは、言い方の違いだけじゃな。
もちろん、記法としては、+を使った方が簡便じゃが、数値のaとbを足すという『働き』を関数と見なせば、関数として、たとえば、Add(a,b)とも書ける(Addは仮の関数名)。
さらに、aやbは、数値ではなくて、体系内で定義されている(あるいは無定義用語でもよいが)なんらかのオブジェクトであればよい。
このとき、Addという操作が何を意味しているかが、その体系内で明確(計算可能)になっていることは必要じゃ。
体系を形作る『集合』の要素(要素同士も含む)に対する何らかの『操作』により、集合内の要素への対応付けを『演算』と呼び、操作の指示する記号を『演算子』と呼べば、数学の計算とは、要素に対する演算子を用いた作業と言えるじゃろう。
なお、数学では、『演算』は、『関数』、『写像』、『対応』、『作用』とも呼ばれるが、ニュアンスの違いはあっても、ほぼ、同じ意味で使われているようじゃ」
「微分とか積分とかの記号も演算子の一つだね。
記法は、ライプニッツの方が、ニュートンの'などよりも勝っていたね」
「ライプニッツ(1646~1716)は、ドイツ生まれの数学者じゃが、フランスでも、大いに活躍した。
『解析の秘密はその記号法にある』と言ったと言われている。
岩波の数学辞典の彼の略歴は、比較的短いが、『微分の d や積分の∫などの巧妙な記号法を導入して微分積分学の基礎を築いた』とある。
また、コンピュータの歴史の上でも、17世紀末に現れた、ライプニッツの発明といわれる手回し計算機は、17世紀初めのパスカルの計算機が加減算しかできなかったのに対して、加減乗除の四則と桁上がり機能を備えた計算機じゃった。当時とすれば、まさに知性を持った機械と言うべきものだった思われる。
これは、勝手な推測じゃが、このような経験から、ライプニッツは、普遍(万能)計算というアイデアを持ったのではないじゃろうかな。
こうしたスピリッツ(精神)は、イギリスのバベッジ(1791~1871)の解析機関(製作は未完に終わった)、チューリング(1912~1654)の『チューリングマシン』(仮想万能計算機:数学基礎論)など、プログラム(アルゴリズム=算法)により演算を制御するという現代のコンピュータにまでつながっていると思われるのう。
今や、それこそ、数学や物理等のどのページを開いても、そこには、無数というべき記号や記法が溢れている。
そう、いまだ、ライプニッツの夢は、果てないと思われる」
「ニュートンは、万有引力を発見し、ライプニッツは、万能の記号法を発見したとも言えるわね。
もし、数学から、すべての記号を追放したら、鶴亀算みたいになっちゃうかも」
「まあ、もちろん、17世紀以前も現代の物と形は違うかもしれんが、記号や演算子は、使われていた。
ただ、ライプニッツほど、記法と実際の演算を強く結びつけて考えた人は、彼以前にはいなかったのかもしれん。
操作という概念が、『手を動かして何かを行う』意味であるとすれば、操作と記法は、密接に結びつくはずじゃ。
たかが、記法と侮るなかれじゃ。記法には、思考を助ける精神が宿っている」
「そこまで言えば、言語は、文字集合の要素を組み合わせるという演算を行うのだから、数学とも言えるわね」
「そう、数学は言語である、と言えるのう。
ま、もっとも、自然言語は、数学とは言えない部分も多いがな。
さて、そろそろ、わき道から元に戻ろう」
差分と和分
 「差分は、これまでも、使ってきたけど、『和分』は、初めての登場ね」
「差分は、これまでも、使ってきたけど、『和分』は、初めての登場ね」
「そうじゃな。
数列に限らず、一般の関数をg(x)と書き、(g(x+h)-g(x))/ h=Δg(x)と定義する。
これは、言うまでもないが、h→0での極限値が存在すれば、g(x)の導関数、g'(x)に等しくなる。
しかし、hが有限、特に、h=1としたときは、Δg(x)=g(x+1)-g(x)、
また、x=nと置けば、通常の数列の差分と同等になり、Δg(n)=g(n+1)-g(n)、となって、a(n)=g(n)の場合、同一じゃ。
ところで、不定積分を、∫g'(x)dx=g(x)+積分定数と表せば、それに対応して、『不定和分』を記号、Σで表すことにより
ΣΔg(x)=g(x)+和分定数、と書けることに気がつく。
なお、不定和分をΔ-1で表すことが多いようじゃが、HTMLでは、上付き添え字や下付添え字が見づらいこともあるので、ここでは、Σで表そう」
「すると、定積分、∫(x=a~b)g'(x)dx=g(b)-g(a)に対応して、
和分、Σ(k=p~q)(Δg(x))=g(q)-g(p)、あるいは、Σ(k=p~q)(Δa(n))=a(q)-a(p)、
となることか」
「Δ1=0、一般に、nに無関係な定数に対して、Δ定数=0、
Δn=1、一般に、Δ(定数×n)=定数
ここまでは、微分と同様じゃがな、違いもあるぞ。
それは、積の差分じゃ。
一般に、a(n)、b(n)の積、a(n)b(n)の差分、Δ(a(n)b(n))は、
(Δa(n))b(n)+a(n)(Δb(n))ではない!
丁寧に書くと、Δ(a(n)b(n))=a(n+1)b(n+1)-a(n)b(n)である。
一方、ずらし演算子をEと書くと、E a(n)=a(n+1)などじゃが、Δとの間で、a(n+1)-a(n)=Δa(n)=E a(n)-a(n)=(E-1)a(n)から、
E-1=Δ、あるいは、E=1+Δ の関係が得られる。
すると、Δ(a(n)b(n))=a(n+1)b(n+1)-a(n)b(n)=(Ea(n))(Eb(n))-a(n)b(n)
=(1+Δ)a(n)+(1+Δ)b(n)-a(n)b(n)=(Δa(n))b(n)+a(n)(Δb(n))+(Δa(n))(Δb(n))、となる
すなわち、積の差分は、(Δa(n))b(n)+a(n)(Δb(n))に、(Δa(n))(Δb(n))が余分に加算されるのじゃ」
「ははー。
たとえばと、a(n)=n、b(n)=nとしてみると、積は、n^2で、その差分は、
Δn^2=Δ(a(n)b(n))=(Δa(n))b(n)+a(n)(Δb(n))+(Δa(n))(Δb(n))
=(Δn)(n)+(n)(Δn)+(Δn)(Δn)=1×n+n×1+1=2n+1、
一方、((n+1)^2)-n^2=2n+1となるので、正しいわね。
すると、n×n^2ではと、n^3だけど、
Δn^3=(Δn^2)n+n^2Δn+(Δn^2)(Δn)=(2n+1)n+n^2(1)+(2n+1)(1)
=3n^2+3n+1、
これも、(n+1)^3-n^3=3n^2+3n+1、で正しい。
結局は、
Δn^kは、k>0の正整数とすると、
Δ(n^k)=Σ(j=0~k-1)(Comb(k,j)×n^j)と書ける。
ここで、Comb(k,j)は、k個のうちからj個をとるときの組合せの数を与えるDERIVEの関数よ」
「あらためて、書くまでもないが、
Δ(a(n)+b(n))=Δa(n)+Δb(n)、
Δ(a(n)-b(n))=Δa(n)-Δb(n)
これらは、差分の定義から明らかじゃ。
積の差分が複雑になる原因は、もちろん、差分が微分と異なり、有限の差があるからじゃな。
こうしてみると、積の微分公式((f*g)'=f'*g+f*g')が簡明になっているのは、無限小のお陰というわけだ。
なお、これまでも出てきたが、Δのべき乗による演算は、
Δ^k=Δ(Δ^(k-1))、Δ^0=1と約束すると、
Δ^k(n^k)=k!、ということじゃ」
「Δ^k(n^k)=k!を数学的帰納法で証明してみるよ。
k=0、k=1は、明らかに成立するので、k>=2のkのときに、成立するとして、
Δ^(k+1)(n^(k+1))=Δ^k(Δn^(k+1))=Δ^k(Σ(j=0~k)(Comb(k+1,j)×n^j)
=Comb(k+1,k)×Δ^k(n^k)=(k+1)×k!=(k+1)!で確かに成り立つことが分かる。
なお、上で、j<kのとき、Δ^k(n^j)=0、を使っている」
「この式は、∂(x^n,x,n)=n!と同じ形じゃ。
次は、不定和分じゃ。
不定和分の定数を無視して、
Σ1=n、Σ定数=定数×nは、当然じゃな。
Σn=n(n+1)/2、
Σn^2=n(n+1)(n+2)/6、
Σn^3=n^2(n+1)^2/4、
一般には、Σn^k=ζ(-k,0)-ζ(-k,n+1)、なる。
ここで、ζ関数は、第65回に登場している、DERIVEの定義済み関数じゃ。
ζ(s,n)=ζ(s)-Σ(m=1~n)(1/s^m)、
ここで、ζ(s)=Σ(m=1~∞)(1/s^m)、これから、lim(n→∞)ζ(s,n)→ζ(s)じゃった。
なので、
Σn^4=n(n+1)(2n+1)(3n^2+3n+1)/30、なども分かる」
「部分積分に相当する『部分和分』を使ってみたよ。
Δ(a(n)b(n))=(Δa(n))b(n)+a(n)(Δb(n))+(Δa(n))(Δb(n))なので、
a(n)(Δb(n))=Δ(a(n)b(n))-(Δa(n))b(n)-(Δa(n))(Δb(n))、
これから、
Σ(m=1~n-1)(a(m)Δb(m))=a(n)b(n)-a(1)b(1)-Σ(m=1~n-1)(Δa(m)b(m)+Δa(m)Δb(m))、が一般に成り立つ。
S(k)=Σ(m=1~n-1)m^kを求めるために、a(m)=m^k、Δb(m)=1とすると、b(m)=m、
左辺は、Σ(m=1~n-1)m^k、これをS(k)と置く。しばらくの間は、n-1までの和と考える。
右辺の第1項と第2項は、n^k×n-1=n^(k+1)-1、ただし、ここは、nでいいのね。
右辺の第3項は、-Σ(m=1~n-1)(Δa(m)b(m)+Δa(m)Δb(m))
=-Σ(m=1~n-1)(Σ(j=0~k-1)comb(k,j)(m^j×m+m^j))
=-Σ(m=1~n-1)(Σ(j=0~k-1)comb(k,j)(m^(j+1)+m^j))、
ここで、Σの順序を交換して、j=k-1のときは、m^kの項が現れるので、これを左辺に移項して、次式を得る。
(1+k)S(k)=n^(k+1)-1-kΣ(m=1~n-1)(m^(k-1))-Σ(j=0~k-2)(comb(k,j)Σ(m=1~n-1)(m^(j+1)+m^j))
よって、
S(k)=(1/(1+k))(n^(k+1)-1-k*S(k-1)-Σ(j=0~k-2)comb(k,j)(S(j+1)+S(j))))、
ここで、見やすいように、nをn+1で置き換えて、
あらためて、S(k)=Σ(m=1~n)m^kと再定義すれば、
k=0、1、・・の整数に対して、S(k)=Σ(m=1~n)m^k、は、
s(k):= IF(k = 0, n, 1/(k + 1)((n + 1)^(k + 1) - 1 - k*s(k - 1) - ∑(COMB(k,
j)(s(j + 1) + s(j)), j, 0, k - 2)))、
と、Σ(m=1~n)m^k、を再定義関数を使って、表すことができる。
試しに、S(0)~S(5)を計算してみると、
n,
n(n + 1)/2,
n(2n^2 + 3n + 1)/6,
n^2(n^2 + 2n + 1)/4,
n(6n^4 + 15n^3 + 10n^2 - 1)/30,
n^2(2n^4 + 6n^3 + 5n^2 - 1)/12]
と正しく計算されていることが分かる。
S(10)=n(6n^10 + 33n^9 + 55n^8 - 66n^6 + 66n^4 - 33n^2 + 5)/66、と計算は出来るけど、遅くなる。
これで、約2秒かかっている」
「もう一つ、後で出てくるが、
Δ(定数^n)の場合は、定義から、Δ(定数)^n=(定数-1)(定数)^n、じゃな」
Euler変換法の導出
「第45回の『積分(5)(高速ラプラス逆変換2)』で、森口先生の本(計算数学夜話(森口繁一著:日本評論社刊:昭和53年)の解説に従い、Euler変換の簡単な導出を行った。
ともちゃんは、覚えているじゃろう」
 「はーい。ちょっと、おさらいをしてみます。
「はーい。ちょっと、おさらいをしてみます。
前節の差分演算子Δとずらし演算子Eが活躍します。
ここでも、数列をa(n)のように表示して、n=0から始めるよ。
さーて、お立ち会い。
交代数列、a(n)=|b(n)|(-1)^n、と書き、分かりやすいように、b(n)は、a(n)の絶対値とする。
交代級数の無限和が存在する場合には、その和を、2つの部分に分けて、ゼロ項からn-1項までと、n項からの部分に分割する。
Σ(k=0~∞)a(k)=Σ(k=0~n-1)a(k)+SIGN(a(n))×Σ(k=n~∞)b(k)(-1)^k、
2つ目の和について、ずらし演算子を使うと、E b(n)=b(n+1)となることに注目する。
Σ(k=n~∞)b(k)(-1)^k=b(n)-b(n+1)+b(n+2)-b(n+3)+・・
=b(n)-E b(n)+E^2 b(n)-E^3 b(n)+-・・・
=(1-E^1+E^2-E^3+-・・)b(n)
そして、ここが、びっくり、
=1/(1+E)×b(n)
ところで、前節に出ているように、E b(n)=b(n+1)から、b(n+1)-b(n)=(E-1)b(n)=Δb(n)の関係から、
Δ=E-1に気がつくので、E=1+Δ、と置くと、
これから、1/(1+E)=(1/2)(1/(1+(Δ/2))=(1/2)(1-(Δ/2)^2+(Δ/2)^4-+・・)
第2項の和、Σ(k=n~∞)b(k)(-1)^k
=Σ(j=0~)(Δ^j×b(n)×(-1)^j×(2^(-j-1)))、
従って、第ゼロ項から第n-1項まで、正直に計算して、第n項からEuler変換した場合の近似和をS(n,m)と書くと、
S(n,m)=Σ(k=0~n-1)a(k)+SIGN(a(n))×Σ(j=0~m)(Δ^j×b(n)×(-1)^j×(2^(-j-1)))、
となる」
「よくできましたな。
変換法というよりも、変換術と呼びたい。まさに、Euler先生は、数式の魔術師じゃな。
では、ここからは、わしが、差分と和分を使って、導出を試みようぞ。
ここで、a(n)、b(n)は、一般の数列で、n=0から始めるものとする。
さて、積の差分法則から出発する。
Δ(a(n)b(n))=(Δa(n))b(n)+a(n)(Δb(n))+(Δa(n))(Δb(n))
上の式を変形して、Euler変換法の式を導きたいので、
a(n)(Δb(n))がa(n)×(-α)^nのように書けないかと考える。
なお、αは、正の実数とする。(あとで、1と置くがの)
そのためには、Δb(n)=(-α)^nとなる必要があるので、n=0からn=n-1まで足し合わせると、
Δb(0)=b(1)-b(0)、
Δb(1)=b(2)-b(1)・・
Δb(n-1)=b(n)-b(n-1)、
これから、b(n)=b(0)+(-α)^0+(-α)^1・・(-α)^(n-1)
よって、b(n)=b(0)+(1/(α + 1) - (-α)^n/(α + 1))とb(n)が求められる。
ここで、b(0)=0と選ぶと、b(n)=(1-(-α)^n)/(1+α)でよいことが分かる。
Δ(定数^n)=(定数-1)×定数^n、であることを使うと、Δb(n)=(-α)^nを確かめることができる。
積の差分則に代入して整理すると、
a(n)×(-α)^n=Δ(a(n)×係数)-(Δa(n)×係数)-(Δa(n)×(-α)^n)、となることが分かる。
ここで、係数=(1-(-α)^n)/(1+α)じゃ。
さ~て、お立ち会い、おっと、これは、ともちゃんの真似じゃな。
左辺を見ると、α=1として、a(n)が正項数列ならば、a(n)×(-α)^nは、交代数列にすることが出来る。
そこで、以下では、a(n)が常に正と考えて、α=1と置く。
a(n)×(-1)^n=Δ(a(n)×係数)-(Δa(n)×係数)-(Δa(n)×(-1)^n)、
係数=(1-(-1)^n)/2、じゃ。
両辺をn=0~nまで和をとると、
左辺=Σ(k=0~n)a(n)(-1)^k
右辺第1項は、a(n)/2-(-1)^n×a(n)、
右辺第2項は、-1/2(a(n-1)-a(0))、
右辺第3項は、-1/2Σ(k=0~n-1)(-1)^k×Δa(k)、
整理すると、
Σ(k=0~n)a(n)(-1)^k=a(0)/2-1/2Σ(k=0~n-1)(-1)^k×Δa(k)+残差項、
と書けることが分かるじゃろう。
ここで、残差項=(1/2)((a(n)-a(n-1)-(-1)^n×a(n))、である。
なんだか、変わらないような気がすると思うが、大違いなのじゃな。
級数が収束するときは、残差項がゼロに近づく。そこで、ゼロと置いてしまう。
Σ(k=0~n)a(n)(-1)^k=a(0)/2-1/2Σ(k=0~n-1)(-1)^k×Δa(k)
右辺第1項は、a(0)/2であり、第2項が、a(n)をΔa(n)で置き換えたものになっていることに気づいて欲しい。
すると、右辺第2項のΣ内を更に、
Δa(0)/2-Σ(-1)^k×Δ^2a(k)と置き換えることができる。
右辺は、a(0)/2-1/2(Δa(0)/2-Σ(-1)^k×Δ^2a(k))、となる。
すなわち、
a(0)/2-Δa(0)/4+(1/4)Σ(-1)^k×Δ^2a(k)、
こうして、どんどんと、右辺の末尾の項を差分で置き換えていくと、
Σ(k=0~∞)a(n)(-1)^k=Σ(k=0~∞)((-1)^k×Δ^k×a(0)/2^(k+1))、
これが、オイラー変換の方法じゃ。
なお、上では、n=0から適用した形になっているが、ともちゃんが、やってくれたように、第0項~第n-1項までは、正直に計算して、第n項から適用するとして、上のa(0)の部分をa(n)と考えると同じ形になる。
数値計算としては、途中から、Euler変換を適用する方が精度が高くなることは、森口先生の本でも指摘されているとおりじゃ」
「お疲れ様でした。
なるほど、納得、ガッテンですが、チョー面倒。
さすがに、Euler先生」
「まあ、それは、そうじゃ。
しかし、上の方法で、交代級数でないときなどを考えて欲しいと思うのう」
Euler変換の高速化
「最後は、高速化じゃ」
 「確かに、それは必要ね。一番最初の節で出てきた、a(n)=(-1)^n/(n+1)=1、-1/2、1/3、-1/4、・・・、だと、
「確かに、それは必要ね。一番最初の節で出てきた、a(n)=(-1)^n/(n+1)=1、-1/2、1/3、-1/4、・・・、だと、
正直計算を第0項から、19項までと階差を20として、S(20,20)で、約30秒は長すぎるわ」
「それは、差分の計算に時間がかかっているからじゃ。
Δ^m |a(k)|=f(k,m)としたとき、
f(k, m):= IF(m = 0, ABS(a(k)), f(k + 1, m - 1) - f(k, m - 1))、
と差分を再帰関数、f(k,m)で計算している。
ここに無駄な時間がかかっているのだな。
そこで、コロンブスの卵じゃが、差分を止めてしまう。
といっても、Δ=E-1の関係で、
f(k,m)=Δ^m |a(k)|=(E-1)^k×|a(k)|、
すなわち、f(k,m)=Σ(j=0~m)Comb(m,j)×(-1)^k×|a(k+m-j)|、と2項定理で展開するのじゃ」
「じゃためしてみるよ。
さっきの例と記号を合わせると、交代数列、a(n)=(-1)^n/(n+1)として、

|ABS(a(n)|の差分求める関数、f(n_, m_):=∑(ABS(a(n_ + m_ - j_))COMB(m_, j_)(-1)^j_,
j_, 0, m_, 1)、
と変わっています。
さてと、
S(20,20)=(0.69314718055994530938)、0.015秒、
なんと、30秒から0.015秒に超高速化、
これには、Euler先生も、ビックリでしょう!
更に、
S(20,30)=(0.69314718055994530941)、と、LN(2)≒(0.69314718055994530941)に末尾まで、一致。
計算精度を30桁として、
LN(2) =(0.693147180559945309417232121458)、なので、
S(20,30)=(0.693147180559945309417232038549)でも、0.016秒、
S(20,50)=(0.693147180559945309417232121458)、も、余裕の0.047秒で30桁までぴったりと計算」
「やれやれ、よかったのう。
ま、階差の式を書き下してしまうとよい、というのは、森口先生の本でも、数値解析の本でも、記載されてはいることなのだかな。
ここまで、差が出てしまうとは、わしも驚いたぞ。
さて、Euler変換式は、結局、差分の f をSに組み入れて、次のようになった。

S(n,m):=∑(a(k_), k_, 0, n - 1)
+∑(2^(-k_)COS(k_)∑((-1)^j_COMB(k_, j_)ABS(a(n + k_ - j_)), j_, 0, k_),
k_, 0, m)SIGN(a(n))/2、
ここで、右辺の第1項は、a(k)を第0項からn-1項まで、正直に計算する。
第2項は、長いが、ここが、オイラー変換術による部分だ。
なお、式中に、cos(πk_)が現れているが、(-1)^k、をDERIVEでは、このように置換してしまうのじゃな。
また、これまで、断ったこなかったが、mをm_のように記載している。
これは、DERIVEの同一ウインドウ内で、大域変数(グローバル変数)として、同一の変数記号が使われないようにする便宜的な手段じゃ。
すなわち、アンダーバーの付いた記号は、局所変数(ローカル変数)と扱いたいということなのだ。
DERIVEでの変数や関数の宣言と使用法には、わしも、不明な部分が残っているが、いずれ、何か分かったらば、報告したいと思うのでな。
本当は、打ち切り誤差を与えて、それにより、階差なり、第n項なりを決めるのが本来じゃが、今回は、長くなってしまったので、略すことにしよう。
いや、ともちゃんも、お疲れさんじゃった」
最終更新日 2013/2/12



 「えー。また、Euler変換なの!」
「えー。また、Euler変換なの!」