数式処理ソフト DERIVE(デライブ) de ドライブ
78.高階常微分方程式の数値解法(初期値問題)
(1)はじめに
 「高階常微分方程式は、先に数値解法から入るのね?」
「高階常微分方程式は、先に数値解法から入るのね?」
「おう、ともちゃんかい。
1階の常微分方程式は、数式処理ソフト DERIVE(デライブ)の定義済み関数による解法から入っていったので、少し、趣向を変えようということではあるな」
「いちおう、これまでの1階の常微分方程式関係の主なページへのリンクを記載しておきますよ。
第70回 1階常微分方程式の解法(2)
第71回 1階常微分方程式の解法(3)(リッカチの微分方程式)
第72回 常微分方程式の数値解法(初期値問題)(1)
第73回 常微分方程式の数値解法(初期値問題)(2)(リチャードソン加速)
第72回と73回では、特に「1階・・」とタイトルにないけど、実質的には、1階の常微分方程式の数値解法に終始しているわ」
「ご苦労様。
あらためて、説明するまでもないじゃろうが、物理や工学などでは、高階と言っても、主として2階の常微分方程式が出てくることが多い。
また、いわゆる特殊関数がこれらの典型的な方程式の解として定義されていることも多い。
ま、これは、当然といえば、当然で、それらの方程式の解を求めることが実用上有用であったので、そのような解を特殊関数として扱ってきたという歴史的な理由があるのだな。
しかし、特殊関数の理論的な扱いは、なかなか、やっかいじゃ。
そこで、まずは、数値解法から入って、後に理論的な扱いに進めてみようという心づもりじゃ」
「となると、第72回にならって、一次のオイラー法からということになるわね」
(2)オイラー法(1次)
「これまでと同様に、変数をx、関数をyで表す。
また、n階の常微分方程式が、y(n)(x)=r(x,y,y,・・,y(n-1))と書ける場合を取り上げる。
まずは、n=2の2階の常微分方程式の場合を例にして説明しよう。
2階の場合は、y '=p(x)、とおき、y(x)とp(x)の2つの関数に関する連立1階常微分方程式として扱うのが定法じゃ」
 「つまり、
「つまり、
p'=r(x,y,p)、
y'=p、
ということね。
初期値は、x=x0、で、y(x0)=y0、p(x0)=p0と書くことにする。
ここで、刻み幅をhとして、1次のオイラー法では、
x(nh+h)=x(nh)+h、ここで、n=0、1・・。
また、x(nh)をxと略記すれば、
y(x+h)=y(x)+h*p(x)、
p(x+h)=p(x)+h*r(x,y(x),p(x))、
として計算を進めるのが元祖オイラー法ということよ」
「では、早速、ユーザ定義関数を作ってみる。
関数内では、ベクトル v_ を[x,y,p]として、利用する。
第72回のオイラー法(2)(2次)の節の最初の方に具体的な構成法が出ているので、ここでは繰り返さないがの。
Euler_User_2(r,x,y,p,x0,y0,p0,h,n)を次のように定義する。
ITERATES([v_↓1 + h, v_↓2 + h*v_↓3, v_↓3 + h*LIM(r, [x, y, p], v_)], v_, [x0, y0, p0], n) 」
「読者の方のために説明すると、まずは、ITERATES関数ね。
ITERATES(引数1,引数2,引数3,引数4)としたとき、
引数4で指定した回数の処理が実行される。
擬似的には、こんな感じ。
引数3(初期値)→引数1
for k=1 to
引数4
引数1を計算して引数2に代入
next k
注意すべき点は、最初に、k=0の場合と考えると分かりやすいかしら。
引数3(初期値)→引数1が実行されるので、引数1は、引数3の初期値となる点ね。
その次からn回、計算が開始される。
それと、DERIVEのベクトルの添え字は、1から始まるので、ITERATES関数の実行結果の行列(n+1行,3列)から、xとyのベクトルを求める際は、
[(結果↓j)↓1,(結果↓j)↓2]として、j=1~n+1とするのよ」
「そういうことじゃ。
さて、第72回でも取り上げた問題をやってみよう。
それは、厳密解が、y=exp(x)-x-1、と表される場合で、2階の方程式は、y''=x+y+1、じゃな。
初期値は、x=0、で、y=0、y'=0、となる。
Euler_User_2(x + y + 1, x, y, p, 0, 0, 0, 0.01, 1000)、とすれば、よい。
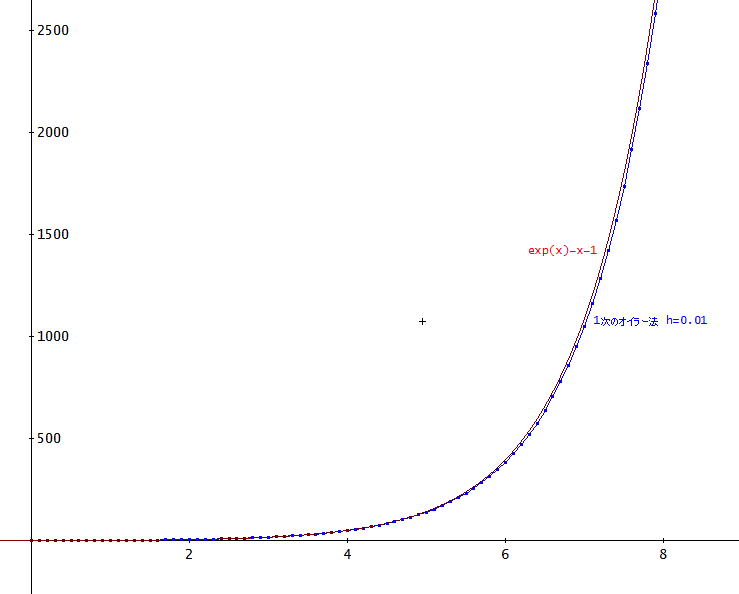
計算結果は、上図の通り」
「まあ、1階の方程式のときも、数値解は、グラフ上、結構合っている感じなんだけど、実際の数値で確認してみるとそうでもないのよね」
「それは、当然じゃな。
厳密解 y(5)≒142.4131591、y(10))≒2.201546579×10^4、に対して、
一方、数値解は、h=0.01の場合、
y(5)≒ 138.7727724、相対誤差は、-2.55%、
y(10)≒2.094815563*10^4、相対誤差 4.84% となっている。
解法が同一なので、1階の場合と、誤差の大きさは、同じじゃ」
「でも、n>3の場合は、関数の定義が難しいわね」
「そうじゃな。
そこで、少し、考えを変える必要がある。
3次元のベクトル f を[1,p,r]と定義する。
これは、x'=1、y'=p、p'=r、のそれぞれの右辺を並べたものじゃ。
なお、変数 v は、[x,y,p]のままとする。
すると、模式的に、v(k+1)=v(k)+h*f、とかけることが分かるじゃろう」
「つまり、独立変数 xも連立させて、3元の連立常微分微分方程式と考える訳ね」
「そうじゃ。
すると、このように修正した一次のオイラー法関数は、
Euler_user_2R(f,v,v0,h,n)として、
ITERATES(u_ + h*LIM(f, v, u_), u_, v0, n) 、
と簡潔に定義できることが分かる」
「このように定義すると、一般の高階の場合も対象になっているということになるわね。
たとえば、y(x)=exp(x)の場合、y'=y でもあるけど、y''=y''=・・・・=y、なので、'
試しに、3階の常微分方程式 y'''=y を解くとすると、初期条件を、x=0で、y(0)=y'(0)=y''(0)=1、として、
Euler_user_2R([1,p,q,y],[x,y,p,q],[0,1,1,1],0.01,100)、で解を求めることができる。
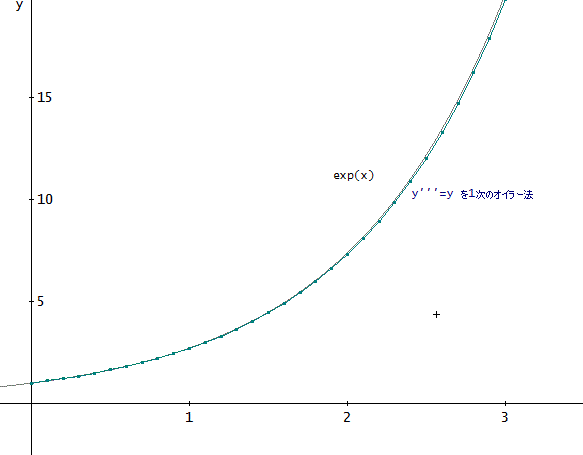
ここで、y'=p、y''=q、と置いている」
「その通りじゃな。
では、次節で、任意の次数までのテイラー展開による解の求め方を調べよう」
(3)オイラー法(m次)
「まずは、m次までのテイラー展開を求める関数は、以前に出てきているが、少し修正を考える」
 「テイラー展開については、第72回の「常微分方程式の数値解法(初期値問題)(1)」に次のように定義されてるのね。
「テイラー展開については、第72回の「常微分方程式の数値解法(初期値問題)(1)」に次のように定義されてるのね。
DIFm_user(f, x, y, h, m)として、
IF(m = 1, h×LIM(f, [u_, v_], [x, y]), h×(∂(DIFm_user(f, x, y, h, m -
1), x) + LIM(f, [u_, v_], [x, y])∂(DIFm_user(f, x, y, h, m - 1), y))/m)、
ただし、上の式の f は、ベクトルではない普通の関数よ」
「修正版の関数を DIFm_user_R(f, v, h, m) と書くことにすると、これは、ベクトルになるが、
PROG(n_:= DIMENSION(v), IF(m = 1, h*f, (h/m)∑(f↓k_*∂(DIFm_user_R(f, v, h, m -1), v↓k_), k_, 1, n_)))、
なお、ベクトル f =[1,p,q,・・,r]、v=[x,y,p,q,・・]とする。
また、DIMENSION(v)は、ベクトルvの次元を求める関数じゃ。
n階の場合は、DIMENSION(v)=n+1となる。1を足すのは、独立変数 x の分じゃな」
「上で出てきた、PROG(命令1,命令2,・・)は、命令1、命令2を順次実行する関数なのよ。
これは、第69回の「方程式の数値解法(4)(ハレー法、DERIVEのPROGとRETURN)」で紹介しているので、詳しく知りたい方は、ご覧になってくださいな。
IF関数の部分が少し分かりにくいと思うので、説明しますね。
再帰的に書いてあるけど、m=1 は、前節で出てきている h*f を返す。
簡単のために、2階の場合を例にして、f=[1,p,r]とします。
すると、f*h は、[h,ph,rh]なので、1次近似では、
x(k+1)=x(k)+h、
y(k+1)=y(k)+h*y'(k)=y(k)+h*p、
p(k+1)=p(k)+h*p'=p(k)+h*r、
オイラー法の中で利用できることになる。
m=2では、(h/2)((1×∂([h,ph,rh],x)+p×∂([h,ph,rh],y)+r×∂([h,ph,rh],p))、
から、(h/2)[0,r*h,h∂(r,x)+p*h∂(r,y)+r*h∂(r,p)]、となり、オイラー法の式で該当部分を青字で示すと、
x(k+1)=x(k)+h+0、
y(k+1)=y(k)+h*y'(k)=y(k)+h*p+(h^2/2)*r、
p(k+1)=p(k)+h*p'=p(k)+h*r+(h^2/2)(∂(r,x)+p∂(r,y)+r∂(r,p))、
と2次近似となっていることが分かる。
ただし、注意する点は、yやpは、実際は、xの関数なんだけど、変数のように扱っている点ね。
あと、n_は、再帰のたびに、n_=DIMENSION(v)として、vの次元数を計算してしまうけど、特に問題は無い。
じゃ、簡単な例を計算してみるね。
2階の常微分方程式 y ''=-y、では、f=[1,p,-y]、v=[x,y,p]として、
DIFm_user_R([1,p,-y],[x,y,p],h,m)、において、m=1~4は、次のようになる。
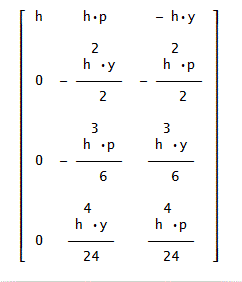
これから、m=1~4までの和は、
[h, y*(h^4/24 - h^2/2) - h^3*p/6 + h*p, y*(h^3/6 - h) + h^4*p/24 - h^2*p/2]、
つまり、
x(k+1)=x(k)+h、
y(k+1)=y(k)+y(k)*(h^4/24 - h^2/2) - h^3*p(k)/6 + hp(k)、
p(k+1)=p(k)+y(k)*(h^3/6 - h) + h^4*p(k)/24 - h^2*p(k)/2、
として計算を進めるということ。※
※x(k)は、x(kh)、y(k)なども、本当は、y(x(kh))なんだけど、こんなふうに略記してみたの、分かるでしょ。
y''=-yの解は、初期値を、x=0、y(0)=0、y'(0)=1とすると、sin(x)なんだけど、sin(x)は、x=0の近くで、y=sin(x)=x-x^3/6、y'=cos(x)=1-x^2+x^4/24、とテイラー展開することができる。
一方、k=0として上の3つの式を計算すると、最初のステップの x=h における、それぞれの値は、
x=0+h、
y=0+h-h^3/6、
p=1-h^2/2+h^4/24、となり、y=sin(x)、y'=p=cos(x)のテイラー展開と4次まで一致することが分かる」
「さてと、m次までのテイラー展開法によるオイラー法の関数は、上に出てきた、DIFm_user_R(f,v,h,m)を利用して、
Eulerm_user_R(f, v, v0, h, m, n) と書くことにすれば、
PROG(f_ :=∑(DIFm_user_R(f, v, h, k_), k_, 1, m), ITERATES(u_ + LIM(f_,
v, u_), u_, v0, n)、
と定義できる」
「早速、y''=x+y+1、初期値は、x=0、y(0)=0、y'(0)=0、とすると、刻み幅を h=0.01、n=1000、として、
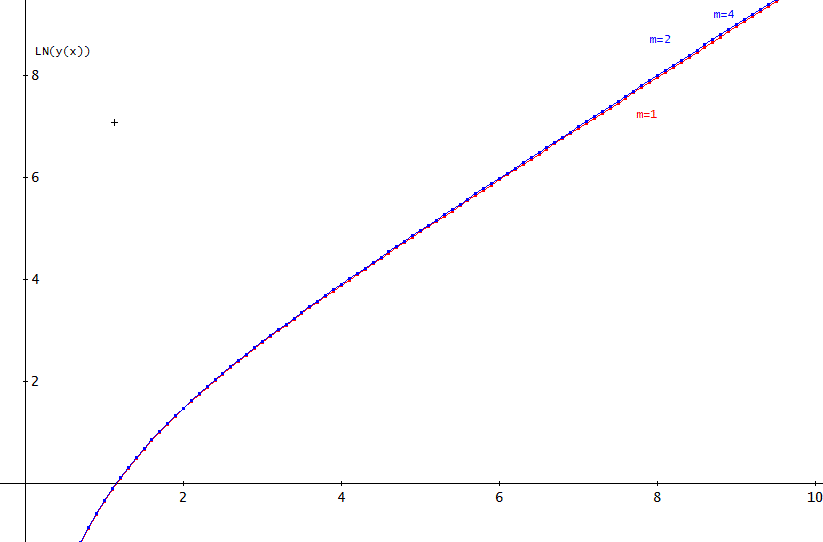
結果は、上の図のようになる。
ただし、縦軸は、LN(y(x))としていることに注意してね。
グラフでは、m=1とm=2の違いは、分かるけど、m=2とm=4との違いは分からない。
そこで、下記の表に数値をまとめた。
ここで、厳密解は、y(x)=exp(x)-x-1、で、これは、第72回の例と同じ」
| x |
厳密解 |
1次のオイラー法 |
絶対誤差 |
2次のオイラー法 |
絶対誤差 |
4次のオイラー法 |
絶対誤差 |
| 1 |
0.7182818284 |
0.7048138294 |
-0.01346799905 |
0.7182368625 |
- 4.496595831*10^(-5) |
0.7182818283 |
- 1.585756595*10^(-10) |
| 5 |
142.4131591 |
138.7727724 |
-3.640386702 |
142.4008842 |
-0.01227490259 |
142.4131590 |
- 1.026542252*10^(-7) |
| 10 |
2.201546579×10^4 |
2.094815563*10^4 |
-1067.310164 |
2.201182244*10^4 |
-3.643354861 |
2.201546577*10^4 |
- 2.486443909*10^(-5) |
「誤差の大きさは、1階の場合と変わりは、ないようじゃ。
上の例では、計算の桁数は、標準の10桁としている。
次節では、DERIVEの定義済み関数である、ルンゲ・クッタ法の関数を使って、高階の微分方程式を解いてみよう」
(4)ルンゲ・クッタ法(4次)
「DERIVEのルンゲ・クッタ法の関数は、第71回で例を、第72回で原理をそれぞれ紹介しているが、第71回の例は、1階の場合であったので、2階以上の場合を補足しておこう。
ルンゲ・クッタ法の関数は、ユーティリティーファイル「ODEApproximation.mth」を開くか、読み込めば利用できる。
ユーティリティーファイルは、通常は、C:\Program Files (x86)\TI Education\Derive 6\Math 内に存在する。
2階の場合は、y''=r(x,y,y'')、初期値は、x=x0 で、y=y0、y'=p0 とすると、
RK([p,r],[x,y,p],[x0,y0,p0],h,n)、のように、おのおのの引数を与えて、刻み幅 h、の場合の解を計算できる」
 「具体的には、前節の例で、y''=x+y+1、x=0で、y(0)=0、y'(0)=0、なので、
「具体的には、前節の例で、y''=x+y+1、x=0で、y(0)=0、y'(0)=0、なので、
刻み幅、h=0.01、100点の計算をさせる場合は、
RK([p, x + y + 1], [x, y, p], [0, 0, 0], 0.01, 100)、のように引数を与えるわけ。
ここで、注意点は、私たちのオイラー法関数は、f として、[1,p,r]を与える必要があるんだけど、DERIVEのRK関数では、[p,r]となっている点ね。
ま、考えてみれば、x'=1 というのは、いつも同一なので、間違いを避ける意味でも、あえて、与える必要は、なかったのかも知れないけど」
「確かにな。
とはいえ、RK関数では、第1引数のベクトルが第2、第3引数のベクトルの次元と一つ食い違っているのが気になる点ではある。
わしらの関数は、当面、このままにしておこう。
次節では、第73回で紹介した「リチャードソン加速」を行う関数を高階の場合に拡張してみよう」
(5)リチャードソン加速
 「1階の場合、一段加速の関数は、Richardson(r, x, y, x0, y0, h, m, n) として、
「1階の場合、一段加速の関数は、Richardson(r, x, y, x0, y0, h, m, n) として、
PROG(u_ ≔ Eulerm_user(r, x, y, x0, y0, h, m, n),
v_ ≔ Eulerm_user(r, x, y, x0, y0, h/2, m, 2*n),
VECTOR((2^m*v_↓(2*k + 1) - u_↓(k + 1))/(2^m - 1), k, 0, n, 1)、と第73回では、定義しているのね。
そこで、今回は、次のように修正して、高階の場合にも利用できるようにしたわ。
Richardson_R(f, v, v0, h, m, n)
PROG(g_ := Eulerm_user_R(f, v, v0, h, m, n),
h_ :=Eulerm_user_R(f, v, v0, h/2, m, 2n),
VECTOR((2^m h_↓(2k_ + 1) - g_↓(k_ + 1))/(2^m - 1), k_, 0, n, 1))、
ただし、ここで、Eulerm_user_Rは、(3)節のm次までのオイラー法関数とする」
「どれどれ。
先ほどの例で、ちょと確認してみよう。
y''=x+y+1、x=0で、y(0)=y'(0)=0、の初期値の場合。
刻み幅を h=0.01、n=1000として、x=10の値を計算精度を20桁として計算。
厳密解の値 y(10)≒2.2015465794806716516*10^4、に対して、次表のようになった」
| 次数 |
加速無し |
一致桁数 |
一段加速 |
一致桁数 |
二段加速 |
一致桁数 |
| 1 |
(2.0948155637813660064*10^4) |
1 |
(2.1998672408761571497*10^4) |
1 |
(2.2015359788199870490*10^4) |
5 |
| 2 |
(2.2011822441481159821*10^4) |
4 |
(2.2015461158343289635*10^4) |
7 |
(2.2015465798160467329*10^4) |
10 |
| 4 |
(2.2015465776603636288*10^4) |
9 |
(2.2015465794801650464*10^4) |
13 |
(2.2015465794806715976*10^4) |
16 |
| 6 |
(2.2015465794806673194*10^4) |
14 |
(2.2015465794806716513*10^4) |
18 |
(2.2015465794806716516*10^4) |
20 |
「第73回のリチャードソン加速でやった場合と一致しているね。
では、2段加速用の関数も手直ししてみた。
Richardson2_R(f, v, v0, h, m, n)
PROG(g_:= Eulerm_user_R(f, v, v0, h, m, n),
h_ ≔ Eulerm_user_R(f, v, v0, h/2, m, 2*n),
i_ ≔ Eulerm_user_R(f, v, v0, h/4, m, 4*n),
VECTOR((2^(2*m + 1)*i_↓(4*k + 1) - 3*2^m*h_↓(2*k + 1) + g_↓(k +
1))/(2^(2*m + 1) - 3*2^m + 1), k, 0, n, 1))、
結果は、上の表に追加しておいたよ」
「お、ご苦労様。
数値的には、ほぼ、第73回と同一となっているので、問題は無かろう。
今回は、短かったが、高階の常微分方程式の数値解法は、この辺で終わることにしよう。
次回は、y '=F(x, y, z)、
z '=G(x, y, z)、
ここで、y,zは、ともにxの関数、で表せるような、 連立の常微分方程式の数値解法を考えてみよう」
最終更新日 2016/1/10



 「高階常微分方程式は、先に数値解法から入るのね?」
「高階常微分方程式は、先に数値解法から入るのね?」