数式処理ソフト　DERIVE（デライブ） de ドライブ

１１．1次方程式～2次方程式

数式処理ソフト DERIVE（デライブ）の今回の記事では、DERIVEのマニュアルなどで触れている1次方程式、連立方程式をはじめとする方程式に関するDERIVEでの扱いについては、多くを取り上げないつもりでした。
しかし、考えてみれば、これらは、やはり重要ですので、以下にまとめてみました。
なお、DERIVEを起動した直後は、「1文字は1変数と見なす」を使用する設定になっていますが、以下では、オプション－モード設定－入力タブの「連続した文字列を1変数と見なす」の方に丸を付けて変更しています。

1次方程式

私の頃は、中学校で代数を習ってから、変数という便利なものがあるのだということを知りました。小学校の頃の鶴亀算など凝った問題は、私の頭が悪いせいか、どうしても、すっきりと理解できなかった印象が残っていますが、代数では、そのような曖昧さが消えて、視界が明瞭になった印象が残っています。
さて、以下では、a*x＋b＝0と数式入力行に入力します。この式を未知数xに関する方程式と考えた場合、xは、1次なのでこれを、1次方程式と呼びます。
DERIVEでの解法です。
まず、この数式が数式シート上で選択されて状態で、「解く」メニューから「方程式／不等式／関係式」を選択します。
ダイアログボックスが開きます。まず、左側のボックスで未知数としてxを選択します。
次に「代数解」か「数値解」かを選択します。今回の場合は、代数解を選択します。解の領域は、「複素数」でよいでしょう。「解の制限」は、数値解を求める場合に必要となります。
「解く」というボタンをクリックすると、おなじみのx＝b／aという解答が数式シートに表示されます。
この1次方程式により、解をゼロを含めた正の整数で考えていたのでは、十分に表現できず、どうしても有理数（±m／nの形で表現できる数）を導入しなくては、ならなくなりました。
幾何学的には、xy平面上の直線（1次関数。y＝a*x＋b）とx軸との交点がその方程式の解を与えるという描像は、直感的でしかも他の方程式の解法にも応用がきくとらえ方です。
なお、数学的には、aがゼロの場合は、どうなるのかという疑問が起きますが、xの解答式で代数メニューから変数の置き換え（ツールバーのSUB）を選択して、aをゼロとしてから、＝（計算）をクリックすると、x＝±∞となります。
一方、a*x＋b＝cの段階でa＝0と置換してから、xを「解く」という方法では、b＝ｃという自明な結果が表示されます。

2次方程式

2次方程式は、古くは、ギリシャのピタゴラスの時代から、一辺が1の正方形の対角線の長さ√２を求める問題として、知られていました。
すなわち、実世界には、±m／nという有理数だけでは表現できない平方根などを含んだ無理数がどうしても現われてきます。有理数と無理数を一括して実数といいます。
なお、無理数には、代数方程式（Σa_kx^k＝0。a_kは複素数でk＝0～nの（有限の）整数）の解にならない超越数（πやeなどが代表）が含まれます。
さて、a*x^2＋b*x＋c＝0というおなじみの2次方程式とその根の公式などを習ったのも中学の頃でしたね。
DERIVEでの扱いは、1次方程式の場合とほとんど、同一です。その解は、次のとおりです。

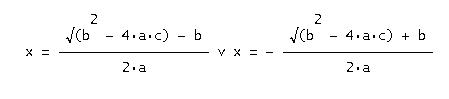
2次方程式の解の図で、v のような記号があります。これは、「OR（または）」を表すためDERIVEで使われているものです。ちなみに ∧は、「AND（かつ）」を表します。
ところで、2次方程式では、解の範囲が実数にとどまらず、複素数を使う必要が出てきました。複素数（とベクトル）は、確か、高校で習いましたな。
判別式D＝b^2－4acにより、2根の状態（正ならば、2実根、ゼロならば、重根、負ならば、2虚根）が判別されます。
また、1次方程式が直線と関係したのに対して、2次方程式の根はは、2次関数、すなわち、y＝a*x^2＋b*x＋cという放物線とx軸との交点として与えられます（2実根。1点で接するときは、重根）。
現実世界でも、放物線は、重力下での質点の運動を記述する際に現われるなど重要な曲線です。放物線と親戚の双曲線、楕円と合わせてこれらは、円錐曲線とも呼ばれます。それは、円錐を様々な角度から平面で切ったときの切り口の形がこれらのいずれかになるからです。
なお、xとyの任意の2次関数は、これらのいずれかを表し、必要に応じて、座標の回転と平行移動を組み合わせれば、標準形式に変換することができます。