数式処理ソフト　DERIVE（デライブ） de ドライブ

１５．連立方程式

連立1次方程式

「鶴亀算は、連立方程式の問題だね？」

「おう、ともちゃんか。そうだな。正確には、連立1次方程式というべきじゃが」

「数式処理ソフト DERIVE（デライブ）では、簡単に解けるのでしょ」

「うん。手順は、1～4次方程式の場合と大きくは変わらないのう。
ま、もっとも、問題をどのように定式化するかが大事な事じゃがな。
ちょうど、ここに「計算機による数値計算法」（新曜社 1975年：一松信、戸川隼人　共著）という本がある。
ここに連立方程式の計算例が載っておる。こんな3元連立1次方程式じゃ。
これは、ヒルベルト行列の係数と言って計算過程で桁落ちしやすい問題として有名なのじゃ。
（1）x＋（1/2）y＋（1/3）z＝11/6
（1/2）x＋（1/3）y＋（1/4）z＝13/12
（1/3）x＋（1/4）y＋（1/5）z＝47/60」

「このまま、DERIVEに入力してみるね」

「そう、入力すると数式シートに#1などの番号がついて現われるの。
そこで、これを解くには、「解く」メニューから「連立方程式」を選択する。ダイアログボックスが出て何元か聞いてくるので、3と入れる。そして、式を入れるダイアログボックスが開くので、それぞれのテキストボックスに#1などと先ほどの式の番号を入れるか、または、それぞれの式を選択しては、ダイアログボックス内のテキストボックス内にF3キーで貼り付けるのじゃな」

「あとは、変数欄をクリックして解きたい変数名を指定するのね。この場合は、x、y、zの3つだわ」

「それで、ダイアログボックス内の「解く」というボタンをクリックするのじゃ」

「[x = 1 ∧ y = 1 ∧ z = 1]となって、3つとも１だったわ」

「それが正解じゃな」

「ちょー。簡単！」

「ま、一松・戸川先生の本には、Fortranでコーディングしたプログラムが載っておる。当時は、パソコンがなかったからの、これを見ると、まったく隔世の感があるな」

「100元でも解けるのかしら？」

「それはどうかな。ま、時間があったらやってみたらよい。一応、「連立方程式」のダイアログボックスの次元には100と入れることはできるの」

2次以上の式を含む連立方程式

「2次関数と1次関数との交点を求める問題の場合は、どうすれば、よいのかしら？」

「1次関数が、y＝ax＋bとすれば、この式を元に2次関数のyに代入して、xのみの方程式にしてから、それを解けばよい。
たとえば、y＝3x^2－2x－3、y＝2x－1とすると、どうじゃな」

「まず、2つの式を入力するね。そして、2番目の式から右辺を1番目の式のyに代入するのね。ここは、どうすれば簡単かしら？」

「まず、1番目の式を選択した状態で、ツールバーの「SUB」をクリックする。置き換えたい変数として、左側の欄のyをクリックしてから2番目の式をクリックする。
そのままでは式全体が選択されているので、右辺をもう一度、クリックする。うまく、2x－1のみが選択されたら、先ほどのダイアログボックスの右欄にカーソルを入れてから、F3キーを押す。これで、後は、「置換」というボタンをクリックするだけじゃ」

「あとは、2次方程式の時と同様にすればいいのね。x = 2/3 － √10/3 ∨ x = √10/3 + 2/3≒x = －0.3874258867 ∨ x = 1.720759220となったわ」

「2つの式を2Dグラフで描かせて見てみると確かにその辺りに解があるのが分かるじゃろう」

「2次関数と2次関数との交点では、どうかしら？」

「これは、今のような放物線同士であれば、特に問題はない。y＝3x^2－2x－3、y＝－x^2＋5x－5では、どうじゃ」

「そうね。これは、両方の右辺同士を等しいと置けば、簡単ね。x = 7/8 － √17/8 ∨ x = √17/8 + 7/8となったわ」

「ところが、両方がx、yの2次式であると少し面倒であるな。
たとえば、楕円、（x－1）^2＋（y－2）^2＝2、（x+3）^2＋（y－1)^2＝20、同士の交点のような」

「1次関数と2次関数の時と同じすると、まず、1番目の式をyで解いて2番目の式に入れるのかしら？
これだと、2番目の式に代入して計算すると、（x = 3√15/34 + 19/17、y = 69/34 － 6√15/17 ∨ y = 6√15/17 + 67/34）、（x = 19/17 － 3√15/34、y = 67/34 － 6√15/17 ∨ y = 6√15/17 + 69/34）と4通り解が出てくるわ」

「楕円同士なので最大4つの点で交わる場合もあるが、このケースでは、2点だな。4つあるのは、ちょと、おかしいのう」



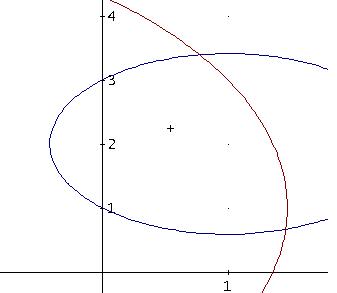
「そうね。グラフで見ると、（x = 3√15/34 + 19/17≒ 1.459380883、y = 69/34 － 6√15/17≒ 0.6624764660）
（x = 19/17 － 3√15/34≒x = 0.7759132341、y = 6√15/17 + 69/34≒y = 3.396347063）の2つが本当の解なのね」

「残りの2つは、無縁根というやつじゃな。このようなときは、連立1次方程式の時と同じにすれば、よいのじゃ。2元連立として、素直にそのまま、2つの式を入れて、解けば、[x = 3√15/34 + 19/17 ∧ y = 69/34 － 6√15/17, x = 19/17 － 3√15/34 ∧ y = 6√15/17 + 69/34]と簡単に解けてしもうた」

「なんだぁ」

「もっとも、1番目の式－2番目の式として、－ 8x － 2y = －13を得てから、yを求めて、1番目の式に入れて、xについて解き、yを求めてもよい。こうすれば、無縁根は、入り込まない。3次以上の変数がある場合は、このように工夫する必要があるときもあるの」

「あんまり、強引にするのも考えものなのね」

「まったくじゃよ」