
 「お早う。あれ、おじさん、頭を抱えているわね」
「お早う。あれ、おじさん、頭を抱えているわね」
「おっと。いや。恥ずかしいことだが、楕円の離心率と扁平率を勘違いしておったのじゃ」
「なに、離心率って」
「ちょうど、いいチャンスだから、数式処理ソフト DERIVE(デライブ)で再確認してみるかの」
「まず、楕円じゃが、その定義は、なんじゃな?」
「平面上で相異なる2点からの距離の和が等しい点の軌跡でしょ」
「うん。よく覚えておったな。
そこで、直交座標での方程式とその定義との関係を確かめてごらん」
「えーと。標準的な方程式は、x^2/a^2+y^2/b^2=1でしょ。
一方、2点をA(-c,0)、B(c,0)とするとき、点P(x,y)との関係は、AP+BP=一定かどうかを確かめるのね?」
「そうじゃ。そのとき(c,0)が一つの焦点となるのじゃ」
「√((x + c)^2 + y^2) + √((x - c)^2 + y^2)が距離の和だけど、方程式の方から、その和の大きさは、y=0のときのxの大きさの2倍なので、2aとなることが分る。
そして、y^2を方程式から距離の和=2aの式に代入して、xの如何に関わらず、この式が成立するためには、c=√(a^2-b^2)であることが分る。
そして、この値を距離の和の式に代入して整理するとその値は、恒等的に2aとなる。
こんなことかしら。でも、DERIVEだと、なかなか、平方根の中の式が因数分解できないのね」
「そうじゃな。こういうときは、ずるいがx=acos(s)、y=bsin(s)として、距離の和の式に代入すれば、標準形の式は、自動的に満足されているので、比較的、簡単じゃな。それでも、ABS(√(a^2
- b^2)COS(s) - a) + ABS(√(a^2 - b^2)COS(s) + a)となって、a>bを使うとなんとか、恒等的に2aとなることが示せるの」
「それで、離心率って?」
「そうじゃったな。離心率e=√(1-(b/a)^2)。さっきのcとの関係は、c=a×eとなるのじゃ。
一方の扁平率は、1-(b/a)じゃった」
「もうひとつ、焦点は?」
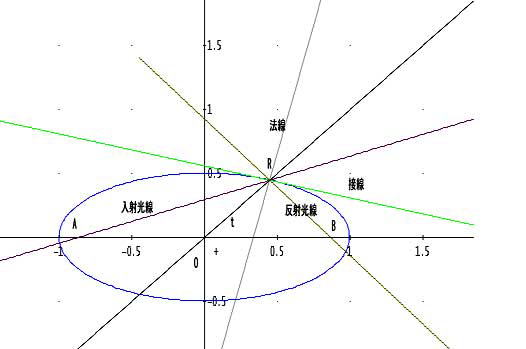
「今、(-c,0)から出た光線が楕円周上で反射されたとする。
このとき、この反射光線は、必ず、もう一つの焦点(c,0)を通るのじゃよ」
「じゃ、その光線の方程式を立てるよ。
この直線と楕円との交点を計算すると、2点があるね。そうか、反対側もあるわけだし、結構ややこしいわね」
「まあ、そうじゃな。そのまま、計算しようとすると面倒になる。ここは、もう少し、一般的に考えてみよう。
曲線の方程式が、[x(t),y(t)]とパラメータ表示されていたとする。楕円の場合は、x=a*cos(t)、y=b*sin(t)じゃ。
点A(-c,0)から発した光線と交わる点をR(x,y)とする。楕円の場合は、Rが第1象限の場合としてみる。
Rにおける接線の方向をθとするとtan(θ) =y'(t)/x'(t)。接線方向の単位ベクトルをvtとするとvt=(cosθ,sinθ)であることは分るな。
Rでの法線(接線に垂直な外向き)の単位ベクトルはどうなるじゃろう」
「接線ベクトルvtを反時計回りに90度回転すればよいわけね」
「そう。ここで、前回出てきた行列を使ってみよう。行列M=[[cos(z),sin(z)],[-sin(z),cos(z)]]が反時計回りにzだけ回転する場合の変換行列じゃ。
法線方向の単位ベクトルをvsとすると、vs=vt×M(z=π/2)= [- SIN(θ), COS(θ)]。
次にRA方向の単位ベクトルをvaとすると、va=-vs×M(z=-φ)。ここで、入射角をφとした。
一方、反射光線の方向の単位ベクトルをvbとすると、
vb=-vs×M(z=φ)である。
まず、vaの具体的な式は、
va= [SIN(θ)COS(φ) - COS(θ)SIN(φ), - COS(θ)COS(φ) - SIN(θ)SIN(φ)]
ここで、単位ベクトルvaの延長線上の点は、すべて原点Oからの位置ベクトル、ra=α×va+[x(t),y(t)]と表せることに注意する。αは、任意の実数じゃ」
「ということは、raは、点A(-c,0)を通るので、[-c,0]=ra=α×va+[x(t),y(t)]とおいて、αと未知の角度φがここから決められるのね」
「うん、そういうことじゃな。楕円では、長径を長さの単位と考えて、1として、短径をw(<1)としよう。x(t)=cos(t)、y(t)=w*sin(t)となるので、具体的な計算は、少し、込み入るが、
α = (COS(t) + c)/(COS(θ)SIN(φ) - SIN(θ)COS(φ)) ∧ α = wSIN(t)/(COS(θ)COS(φ)
+ SIN(θ)SIN(φ))となる。
αの最初の式を使って、raを具体的に表し、このあたりで、tanθ=-w/tan(t)、c=√(1-w^2)を使うと、
tanφ=√(1 - w^2)SIN(t)/w
と簡単化できる」
「一方、vb=-vs×M(z=φ)=[COS(θ)SIN(φ) + SIN(θ)COS(φ), SIN(θ)SIN(φ) - COS(θ)COS(φ)]なので、さっきと同様に単位ベクトルvbの延長線上の位置ベクトルは、rb=βvb+[x,y]とかけるので、反射光線とx軸との交点である、Bの位置をrb=[x2,0]とすると、
βの値は、β=(x2 - COS(t))/(COS(θ)SIN(φ) + SIN(θ)COS(φ))となる。これをrbに入れてBのy座標がゼロであることから、
wCOS(t)^2TAN(φ)/SIN(t) - COS(t)(wx2TAN(φ)/SIN(t) + w^2 - 1) + wSIN(t)TAN(φ)
- x2 = 0。
先に求めていた、tanφ=√(1 - w^2)SIN(t)/wを使うと、- (x2√(1 - w^2) + w^2 - 1)COS(t) +
√(1 - w^2) - x2 = 0。
この式がtの如何に関わらず、恒等的にゼロとなるためには、x2=√(1-w^2)が必要である。これは、Bの位置は、原点についてAの位置と対称的であることで、B(c,0)がもう一つの焦点であるということなのね」
「そうじゃな、ところで、αの2つめの式と先ほど使った1つめのαの式を等しいと置いてもtanφに関する式は、出てくるようじゃ」
「三角関数の計算は、DERIVEでは、苦手のようね」
「特に三角関数を含んだ式の因数分解が苦手じゃな。そういうときは、「代数」メニューの「式の置換」を使って、一時的にcosθなどを一時変数、uやvなどと置いてみるとよいようじゃな」