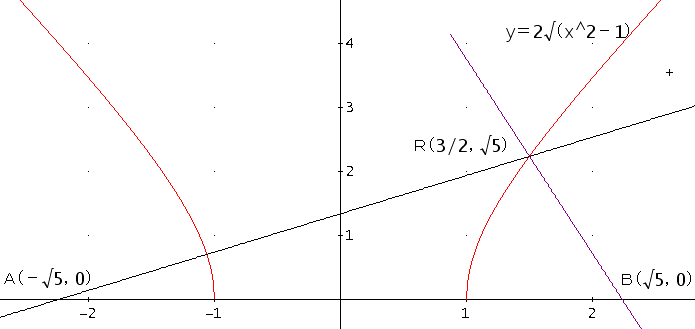
「ともちゃんは、今日は、来ないのかな。では、その間に「双曲線」についても、調べておこう。まず、標準形はと、x^2/a^2-y2/b^2=1じゃったな。
たとえば、a=1、b=0.5として、グラフを描いてみると、ふーん。放物線とよう、似てる。確か、2点からの距離の差が等しい点の軌跡じゃったな。
2点を楕円にならって、A(-c、0)とB(c,0)としてみるか。
数式処理ソフト DERIVE(デライブ)では、
√((-c - x)^2 + y^2) - √((c - x)^2 + y^2) = const。これを変形して、少し、面倒だが、結局は、4x^2/const^2
+ 4y^2/(const^2 - 4c^2) = 1となる。ここで、const^2/4 = a^2、c^2 - const^2/4 = b^2とおいてみると、const=2a、c=√(a^2+b^2)となる。これらにより、与式は、x^2/a^2-y2/b^2=1となる」
 「光の反射との関係は?」
「光の反射との関係は?」
「おっと、ともちゃんか。それは、焦点という名前があるぐらいじゃから、関係はあるじゃろう」
「WEBで調べてみたら、「焦点Bからの光線と双曲線との交点Rとしたとき、Rからの反射光線は、あたかも焦点Aから直接進んだ光線と同一と見なせる」らしいの」
「ほー。ちと、複雑じゃな。グラフの第1象限を考えて、a=1として長さの単位とする。y(x) = w√(x^2 - 1)、c=√(1+w^2)じゃな」
「第1象限の双曲線上のR(x、y)の接線ベクトルvt=[cosθ,sinθ]で、tanθ=wx/√(x^2 - 1)。
Rでの法線ベクトルvs=vt×M(z=π/2)。ここで、Mは、回転行列だったわね。vs=[- SIN(θ), COS(θ)]となるわ」
「そうじゃ。そこで、入射光線方向への単位ベクトルva=-vs×M(-φ)、反射光線方向への単位ベクトルは、vb=-vs×M(φ)だな」
「va=[COS(θ)SIN(φ) + SIN(θ)COS(φ), SIN(θ)SIN(φ) - COS(θ)COS(φ)])となるのね]
「また、vb=[SIN(θ)COS(φ) - COS(θ)SIN(φ), - COS(θ)COS(φ) - SIN(θ)SIN(φ)]じゃな。
ただ、放物線や楕円のケースとは、証明しようとすることが少し、異なる。
つまり、入射光線は、たとえば、本当は、B点(c,0)から出ているのじゃが、逆にX軸の正方向遠方からA点(-c,0)を目指しR点を経由して、直進してくる入射光線がR点で反射し、その反射光線がB点を通るかどうかで真偽を判定してもよい訳じゃ」
「言葉で書くとややこしいわね」
「う~ん。確かにのう。ra=αva+[x,y]というベクトルは、OAと一致するようにαを決められる。一方、rb=βvb+[x,y]というベクトルは、OBと一致するようにβを決められる。反射角φは、この両方を満足させる必要がある、ということかの」
「まずは、最初の方の条件からは、
αCOS(θ)COS(φ) - αSIN(θ)SIN(φ) - w√(x^2 - 1) = 0 --(1)
c = - αCOS(θ)SIN(φ) - αSIN(θ)COS(φ) - x --(2)が出てくるわ。
2つめの条件からは、
βCOS(θ)COS(φ) + βSIN(θ)SIN(φ) - w√(x^2 - 1) = 0 --(3)
c = - βCOS(θ)SIN(φ) + βSIN(θ)COS(φ) + x --(4)がでてくる。
「(1)から、α = w√(x^2 - 1)/(COS(θ)COS(φ) - SIN(θ)SIN(φ))、
(3)から、β = w√(x^2 - 1)/(COS(θ)COS(φ) + SIN(θ)SIN(φ))、
一方、(4)-(2)からは、上の関係とtanθ等を利用して、COS(φ) = w/√(x^2(w^2 + 1) - 1)となる」
「うん。φが出てくるの。それを使うと、α= - x√(w^2 + 1) - 1、β= (x^2(w^2 + 1) - 1)/(x√(w^2 +
1) + 1)と具体的に係数を決められるな」
「そうすると、たとえば、xが1のときは、α=-√(w^2+1)-1なので、ra=αva+[x,y]=[1 - √(w^2 + 1), 0]=[-
√(w^2 + 1), 0]となるわ」
「x=1のときは、φ=0、θ=π/2なのでそうなるの。グラフを描いてみようかの。
w=2、R点を(3/2,√5)として、グラフを描くと上図のようになるな。上図では、縦横比が1:1ではないので、注意して欲しい」