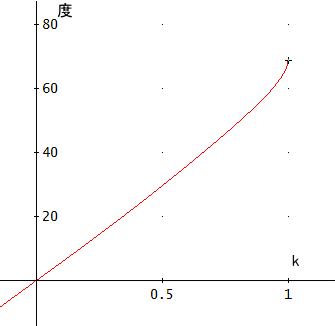「ねえ、テレビで放送してた、「ゴールデンロック」って、びっくりだね。何で、落ちないだろう。おじさんは、行ったことある？」
「わしゃ。ミャンマーには、行ったことがないからの。テレビで見ただけじゃ。ともちゃんと同じじゃな。
それに、高所恐怖症だからな。あそこまで、行けるかどうかなあ、と思ってしまうがな」
「ホント。人が揺すると、ゆらゆら、動くんだから。ヒヤヒヤだね」
「ゴールデンロックは、完全な楕円体でもなく、また、上部に仏塔が付いているので、その安定性は、複雑じゃの。球を水平な面で切断した残りの上の部分を、一般に、「球欠」と呼んでいるようなので、ここでも「球欠」と呼ぼう。とりあえず、この「球欠」の安定性を考えることにしようかな」
「じゃ、まず、「球欠」の重心位置を計算してご覧」
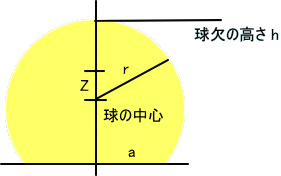
「球の半径をr、切断面を水平な面に置き、球の中心がz軸を通るように考える。切断面の半径をaとする （a=<r） 。重心位置は、対称性から考えて、球の中心を通る。このとき、球の中心を原点に取ると、「球欠」の重心位置を（0,0,Z）、石の密度は、1として考える。
このとき、「球欠」の体積は、半径√（r2－a2）の微小高さdzの円柱が重なっていると考えて、V＝∫π(r2 － z2) dz、
ここで積分範囲は、 球欠の高さhを使うと、－（h－r）からrなので、見やすい形、V＝πh2(3r － h)/3 となるのね」
「うん。そうじゃな。
ここで、h＝2rとすると、おなじみの、4πr3/3が得られる。
次は、重心じゃな」
「これは、微小高さの円柱の体積×z×密度（＝1）を上記の範囲で積分し、全質量（この場合は、体積V）で割れば、求められる。
Z＝3(√(r2 － a2) － r)2/(4(2r － √(r2 － a2)))＝3(h － 2r)2/(4(3r － h)) 」
「特に半球の場合は、a＝rとすると、Z＝3r/8 となって、公式集などに載っている値と一致するので、一安心じゃな」
※式の導出の一部で、h<rのケースを考慮していない部分がありましたので、当該部分を修正しました。（2012/9/19）
「斜面上の球欠を考えよう。静止摩擦係数が大きいとして、球欠は、斜面上を滑らない状態を仮定しようか」
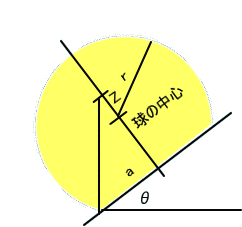
「限界角度は、重心から下ろした垂線が切断面の角にちょうど一致する角度を求めればいいわね。
上図から、限界角度をθとして、tanθ＝a/（Z+h－r）。ここで、Zは、重心の位置を示し、球の中心から上方、Zの位置にある。
a＝k×rとして、無次元パラメータkを導入して、計算すると、θ＝ATAN(4a(h － 3r)/(h(h － 4r))) ＝ ATAN(4(√(1
－ k2) － 2)(2√(1 － k2) － k2 － 2)/(k(k2 + 8)))」
「DERIVEで、グラフにすると、このようになるの。角度は、θ×180/πとして、単位を度に直してある」
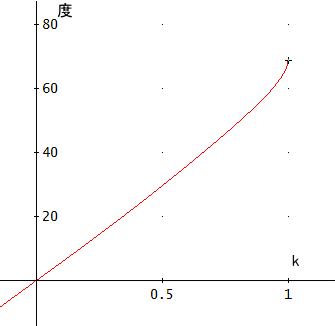
「kが小さいときは、θ≒k+k3/6じゃな。（ラジアン単位）
今回は、a すなわち、kが小さいときに関心がある。k＝0.2のときまで、kを0.05刻みでθを計算してみると、単位を度として、
[θ=0, θ = 2.865980625, θ = 5.739063049, θ = 8.626110763, θ = 11.53352125]となる。最初から、k＝0、0.05、0.1、0.15、0.2の場合のθじゃ。
たとえば、球の半径r＝4mとして、aがその10分の1が0.1の場合じゃから、a＝40cmのときに限界角度は、約5.7度となる。」
「こういう場合は、数式処理ソフト DERIVE（デライブ）の解析メニューの数列の作成で近似値を選べばいいのね」
「そうじゃな。このところ、DERIVEでの説明がおろそかになっているが、そういうことじゃ」
「では、次に回転楕円体について、同様の計算をしてみようかの。球の場合と紛らわしいので、「楕円体球欠」と呼ぶことにしよう。
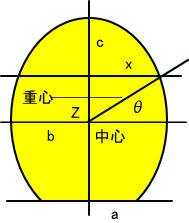
上の図は、回転楕円体を輪切りにしたところじゃな。中心を通る水平面の半径をb、垂直面を通る半径をcとしている。
球の場合と同様に中心を原点にして考える。上方、zのところの水平面の半径をxとおく。x2＝b2（1－z2/c2）なので、面積 πx2をz＝－（h－c）からhまで、定積分すると、体積が求められる。
結果は、V＝πb2h2(3c － h)/(3c2) となる。ここで、hは、楕円体球欠の高さ 。
では、重心位置を求めてご覧」
「球の場合と同じね。πx2×zを同じ積分区間で積分した値をさっきの体積の式で割れば、求められる。
Z＝3(h － 2c)2/(4(3c － h)) となる。
ここで、c＝bとすると、結果は、球の場合に一致することが分かる」
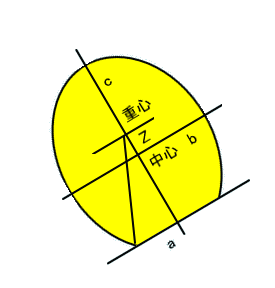
「そうね。球の場合と同様に図を元に考える。限界角度をθとして、tanθ＝a/（Z+h－c）なので、
tanθ＝4ab(2b － √(b2 － a2))/(c(2b√(b2 － a2) + a2 + 2b2))、さらに、a＝k×b、c＝m×bとして、無次元パラメータkとmを使うと、
tanθ＝4k(2 － √(1 － k2))/(m(2√(1 － k2) + k2 + 2)) と簡単化される。ここで、m＝1のときは、4k(2 － √(1 － k^2))/(2√(1 － k^2) + k^2 + 2) と球の場合と一見、異なるように見えるけど、分母を有理化すると、4(√(1
－ k^2) － 2)(2√(1 － k^2) － k^2 － 2)/(k(k^2 + 8)) となるので、同一であることが分かるわ」
「そうだの。グラフにしてみるとじゃ。m＝0.5、1、1.5、2、2.5、3の場合にそれぞれ、限界角度をkの関数として表してみた。
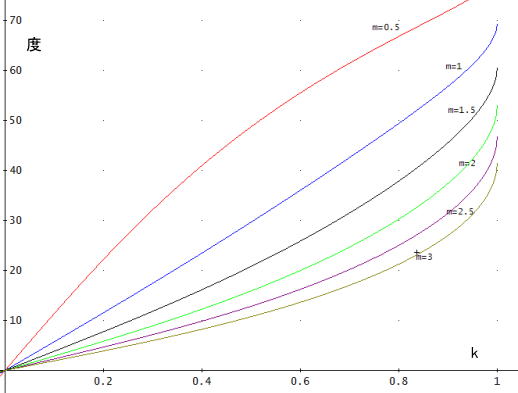
kの小さいときは、概ね、θ＝k/m + k3(3m2 － 2)/(6m3)、と近似できる（ラジアン単位）」
「でも、楕円体の場合は、球と違って、下図のように、斜めに切断したときが、まだ、検討していないわね」
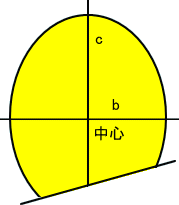
「うん、そうじゃな。球の場合は、平面で切断すれば、どのように切断しても、切り口は、円じゃな、楕円体の場合は、斜めに切断することが可能で、そのようなケースの方が斜面に置いたときの安定性が高いと考えられるが、計算が面倒になるので、後日の宿題ということにしたいの」
※斜めに切断した場合については、第74回『石の安定性（球欠・楕円体球欠）（2）』で取り上げました。
初掲載日 2008/4/20：最終更新日 2012/9/19
