数式処理ソフト DERIVE（デライブ） de ドライブ
８３．常微分方程式の数値解法（アダムス法）（1）
（1）多段階法
「これまで、数式処理ソフト DERIVE（デライブ）で、常微分方程式の数値解法として、オイラー法、改良オイラー法、テイラー展開法、ルンゲ・クッタ法などを取り上げてきた。
これらは、いずれも、一つ手前の分点での［x(n)，y(x(n))］の値から次の分点の値を求める、という意味で、「1段階法」と呼ばれるものじゃ。
ここで、刻み幅を一定として、その大きさを h とするとき、オイラー法（元祖）の精度は、h の一次、改良オイラー法は、2次、テイラー展開法は、任意次数、DERIVEのルンゲ・クッタ法関数は、4次じゃった。
これらの一段階法に対して、「多段階法」というものがある。
これは、［x(n+1)，y(x(n+1))］の値を求めるのに、直前の［x(n)，y(x(n))］以前の分点の関数値を必要とするものじゃ。
そのため、初期値も、あらかじめ、（何らかの方法で）、複数個の値を求めておかなくてはならないのが面倒ではある。
一方、ルンゲ・クッタ法に比較して、次数を高めた公式を容易に求めることができるという利点もある。
ここでは、代表的な多段階法である「アダムス法」を取り上げることにしよう」
「アダムスさんというのは、どこの国の人なのかな？」
「ともちゃん。おはよう。
だいぶ、過ごしやすい季節になったのう。
アダムス氏は、ウィキの日本語版によれば、ジョン・クーチ・アダムズ（John Couth Adams）、イギリスの数学者・天文学者、1819年～1892年。
天王星の軌道の乱れから新天体の存在を推定し1843年10月に海王星の位置を予測したことで有名とのことじゃ。
常微分方程式の解法の「アダムス法」（「アダムズ法」ともいう）や数学の「アダムズ賞」に名前が残る。
英語のウィキには、情報が豊富。（https://en.wikipedia.org/wiki/John_Couch_Adams）
なるほど、そう言われれば、海王星の発見物語は、何かで読んだ記憶があるのう。
イギリスとフランスのどちらが最初に発見するかを争った話もな」
「そのフランス人とは、リビリエ（ルヴェリエ）さん達ね。
太陽系の惑星は、水・金・地・火・木・土・天・海・冥、だったんだけど、2006年に国際天文学連合（IAU）の決定で、冥王星は、準惑星になった。
なるほど、アダムス法の開発は、天文学に利用しようという意図があったのか」
「古典力学は、ニュートンによって創始され、太陽と地球、地球と月、のような「2体問題」は、鮮やかに解き明かされたが、3体以上になるとうまくいかないのだな。
3体では、特別な配置（直線解、正三角形解等）以外は、解析的に閉じた解を得られなかったが、近年、コンピューターを使って、追いかけっこする配置が可能であることが見いだされてはいる。
しかし、実際の惑星・人工衛星・人工惑星の軌道は、コンピューターを使って、微分方程式を積分し、その時間変化を追跡するというのが、一般的じゃ。
その際、精度が低いと（精度だけではないが）当然ながら、真の軌道とずれていってしまう」
「天体の位置計算であれば、観測した時系列の（複数の）位置を初期条件として、軌道計算に含めるのが可能なので、むしろ、多段階法の方が自然。
小惑星ケレス（Ceres セレスとも言われる。1801年に発見）の軌道計算は、かのガウスが行ったことで有名ね。
その際に「最小二乗法」を発明したことでも有名な話だもの。
誰が一番速く発見するかを争うのは、古今東西、変わらない」
「ケレスは、今は、「準惑星」と呼ばれているようじゃが、科学の発展にそのような「功名心」が大きく寄与していることは、事実じゃと思う。
ちなみに、海王星の代表的な5つの環には、下のように、海王星の発見に寄与した人たちの名前が付けられている。（理科年表 2014年版）
Gallea（仏 ガレ）、Leverrier（仏 リベリエ）、Lassell（英 ラッセル）、Arago（仏 アラゴ）、Adams（英 アダムス）。
では、次節で、アダムス法を勉強してみよう」
（2）アダムスの陽的解法
「直前以前の分点も考慮して、未知関数の値を計算するのが多段階法じゃ。
となると、まずは、1階の常微分方程式を考える。
方程式が、正規形、y ' (x)=f(x，y)、とであるとき、具体的にどのように計算すればよいかということじゃな。
そこで、登場するのが、第82回で登場した「補間法」なのだ。
ニュートンの後退補間公式、刻み幅 h を一定として、任意の関数 g(x)、をx=x0で展開するとき、
g(x)=Σ（j=0～m）▽^j g(0)（t＋j－1｜j）、じゃった。
ここで、t=（x－x(0)）/h、また、（t＋j－1｜j）は、「一般化二項係数」で、t(t＋1)(t＋2)・・(t＋j－1)/ j !、である。
ただし、（t｜0)=1、と約束する。
m=0の場合は、y ' (x)=f(x，y) の両辺を、x=x0～x1の間で積分すると、
左辺は、y1－y0となる。（以下、y(x0＋h)) をy1、y(x=x0)をy0、などと略記する。）
一方、右辺は、∫f(x，y) dx、であるが、f(x，y)=y ' (x)、の y ' (x)、を g(x) と見なして、後退補間公式の初項までとると、
∫y ' (0) dx=∫f(x0，y0)dx=f(x0，y0)×h、となるので、
よって、y2=y1＋h×f(x0，y0)、が得られる。これは、オイラー法（元祖）と（結果的に）同じとなる。
同様に、m=1、の場合は、y ' (x)=f(x，y) を x=x1～x2の間で積分をすると、
左辺は、y2－y1、となる。
右辺は、f(x，y)=y ' (x)、のy ' (x) をg(x) と見なして、後退補間公式の第2項まで求めると、
∫y' (1)＋▽y ' (1)×t dx=h∫（t=0～1）（y '(1)＋（y '(1)－y '(0)） t dt、となるので、
h（y ' (1)＋（y '(1)－y '(0)）(1/2)）=（h/2)（3 y ' (1)－y ' (0)）、
よって、y2=y1＋（h/2)（3 y ' (1)－y ' (0)）=y1＋（h/2)（3 f(x1，y1)－f(x0，y0)）、となる。
ともちゃん、第72回に出てきた、y'=x＋y、を例にして、この近似公式を比較検討してみてくれないかな」
「えーと、第72回の「常微分方程式の数値解法（初期値問題）（1）」に出てくる例ね。
厳密解が、y(x)=exp(x)－x－1、で、初期値が、x=0、y=0、の場合。
| x |
厳密解 |
2段階法 |
絶対誤差 |
1次のオイラー法 |
絶対誤差 |
2次のテイラー展開法 |
絶対誤差 |
| 1 |
0.7182818284 |
0.7181703868 |
－0.0001114416584 |
0.7048138294 |
－0.013467999 |
0.7182368625 |
－ 4.496595831×10^(－5) |
| 5 |
142.4131591 |
142.3824920 |
－0.03066710276 |
138.7727724 |
－3.640386670 |
142.4008842 |
－0.01227490259 |
| 10 |
2.201546579×10^4 |
2.200635478·10^4 |
－9.111014862 |
2.094815563×10^4 |
－1067.310156 |
2.201182244×10^4 |
－3.643354861 |
刻み幅を、第72回の場合と同一のh=0.01、とし、初期値［x=0，y(0)=0，y(h)=5.016708332·10^(－5)］として計算し、上の表に「2段階法」と記載した。
なお、2段階法では、x0、y0の他に、x1、y1の値も必要となる。
x1は、x0＋hであるが、y1=y(h)は、厳密解、exp(x)－x－1、において、x=hとした値を使用した。
比較のために、一次のオイラー法と2次のテイラー展開法を並べて表示している。
2段階法は、2次のテイラー展開法には、やや及ばないものの、1次のオイラー法よりは、はるかに精度が高い。
この計算には、DERIVEのユーザー定義関数として、Adams2_user(r, v, v0, h, n)、を次のように定義し、使用した。
rは、y'=f(x，y)の右辺のf(x，y)、vは、rに使用した変数名と関数名、この例では、［x，y］、v0は、初期値［x0，y0，y1］、
hは、刻み幅、nは、計算回数。
Adams2_user := PROG(f_ ≔ DifAdms_user(r, x0_, x1_, y0_, y1_, h, n),
g_ ≔ ITERATES([w_↓1 + h, w_↓3, w_↓3 + LIM(f_, [x0_, x1_, y0_, y1_], [w_↓1, w_↓1 + h, w_↓2, w_↓3])], w_, v0, n),
VECTOR([g_↓k_↓1, g_↓k_↓2], k_, 1, n + 1))、
この中で、使っている、DifAdms_user関数は、2段階法に特化しているので、暫定的なんだけど、次の通り。
DifAdms_user(r, x0_, x1_, y0_, y1_, h, m)
:= PROG(IF(m = 2, RETURN h/2·(3·LIM(r, [x, y], [x1_, y1_]) － LIM(r, [x, y], [x0_, y0_]))))」
「このように微分方程式を解いていくのが、「アダムスの陽的解法」と呼ばれるものじゃ。
「陽的」というのは、直前の分点を含めて、手前の分点のみ値から、直ちに、現在の分点上の関数値を求められる方法のことだな。
陽的に対して、「陰的」というものもある。これについては、今回は、触れないことにしよう。
ともちゃんが書いてくれた関数の3行目のVector関数は、［x，y］のみを表示するためのものじゃな。
では、わしが、m段のr の近似式を返す、DifAdams_user 関数を次のように書いてみた。
DifAdams_user(r_, v_, v0_, h, m_)
:=∑(
∑(
COMB(j_, l_)·(－1)^(j_ － l_)·LIM(r_, v_, [v0_↓1 + (m_ － j_ + l_)·h,
v0_↓(m_ － j_ + l_ + 2)]), l_, 0, j_)
×∫(COMB(t_ + j_ － 1, j_), t_, 0, 1), j_, 0, m_)、
これは、m>=0の任意の整数について、rの近似式を求めるためのものじゃ。
DifAdams_user(g(x,y),[x,y],v0,h,m) にこのように引数をセットして、計算させると、
m=0では、g(v0↓1，v0↓2) 、
m=1では、(1/2)（3g(v0↓1＋h，v0↓3)－g(v0↓1，v0↓2)、
などをを返す。（m=1では、x0をv0↓1、x1をv0↓2、y0をv0↓3、y1をv0↓4と返す）
この関数では、h を掛けていないので、呼び出し側で、hを乗じる必要がある。
さて、この関数を使えば、ともちゃんが定義してくれた、アダムス法の2段階版は、
Adams2_user（r，v，v0，h，n）
:=PROG(
f_ ≔ DifAdams_user(r, v, v0_, h, 1),
g_ ≔ ITERATES([w_↓1 + h, w_↓3, w_↓3 + h·LIM(f_, v0_, [w_↓1, w_↓2,
w_↓3])], w_, v0, n),
VECTOR([g_↓k_↓1, g_↓k_↓2], k_, 1, n + 1))、と定義できる」
「なるほど。
じゃ、あたしは、Adams2_userを少し変更して、3段階法 Adams3_user 関数を作ってみた。
Adamas3_user（r，v，v0，h，n）
:=PROG(
f_ ≔ DifAdams_user(r, v, v0_, h, 2),
g_ ≔ ITERATES([w_↓1 + h, w_↓3, w_↓4, w_↓4 + h·LIM(f_, v0_, [w_↓1,
w_↓2, w_↓3, w_↓4])], w_, v0, n),
VECTOR([g_↓k_↓1, g_↓k_↓2], k_, 1, n + 1))、
でも、あれね、段数を増やすと、（1）節に書かれているように、初期値を別途、計算するというのが、面倒になるわね」
「では、初期値を、ルンゲ・クッタ法で、計算するようにして、Adams4_user 関数を作ってみてご覧。
ただし、初期値を求める個所は、標準の刻み幅 hの1/40に小さくする。そして、y1の値を11番目の計算値とするなどと考えればよい」
「わかったわ。
こんな感じになるわね。
Adams4_user(r, v, v0, h, n)
:=PROG(
h_ ≔ RK([r], v, v0, h/10, 40),
u0_ ≔ [v0↓1, v0↓2, h_↓11↓2, h_↓21↓2, h_↓31↓2, h_↓41↓2],
f_ ≔ DifAdams_user(r, v, v0_, h, 3),
g_ ≔ ITERATES([w_↓1 + h, w_↓3, w_↓4, w_↓5, w_↓5 + h·LIM(f_, v0_, [w_↓1,
w_↓2, w_↓3, w_↓4, w_↓5])], w_, u0_, n),
VECTOR([g_↓k_↓1, g_↓k_↓2], k_, 1, n + 1))、
上で、v0ベクトルは、［x0，y0］とする。（これまでは、y1、y2、y3も必要であった）
作業用ベクトル h_にルンゲ・クッタ法（刻み幅 h/40）で計算した計算値を代入する。
その計算値の一部を利用して、関数内の作業用ベクトルu0_ に、［x0，y0，y1，y2，y3，y4］の値を代入。
f_は、m=3の場合の、rの近似式を代入しておく仮の関数。
そして、本命の計算の繰り返し処理の結果を作業用配列g_に代入する。
最後に、g_の1列目（x(n)）と2列目の値（y(n))の値の2つを配列として出力することにしている」
「ようできましたな。
では、m=5 のAdams6_user関数を作るが、より精度が高まったことを考慮して、初期値の算出で、h/100 の刻み幅として、計600回の計算を行うようにした。
Adams6_user（(r, v, v0, h, n)
PROG(
h_ ≔ RK([r], v, v0, h/100, 600),
u0_ ≔ [v0↓1, v0↓2, h_↓101↓2, h_↓201↓2, h_↓301↓2, h_↓401↓2, h_↓501↓2,
h_↓601↓2],
f_ ≔ DifAdams_user(r, v, v0_, h, 5),
g_ ≔ ITERATES([w_↓1 + h, w_↓3, w_↓4, w_↓5, w_↓6, w_↓7, w_↓7 + h·LIM(f_,
v0_, [w_↓1, w_↓2, w_↓3, w_↓4, w_↓5, w_↓6, w_↓7])], w_, u0_, n),
VECTOR([g_↓k_↓1, g_↓k_↓2], k_, 1, n + 1))、
ま、プログラムとしてみた場合は、少し、物足りない点は残っている。
一つは、m の違いにより、プログラムを別にした点じゃが、実用上は、あまり問題ではない。
もう一つは、組み込み関数のルンゲ・クッタ法やわしらの作った、任意次数までのオイラー展開法では、連立1階常微分方程式に対応できるんじゃが、今回、記載した2つの関数は、対応できない。
次回、この点を解決したいと思う。
さて、次節では、アダムス法の精度を簡単に比較してみよう」
（3）アダムスの陽的解法の精度（実例）
「何度も登場しているが、y '=x+y、初期値は、［0，0］で比較してみよう。
厳密解は、exp(x)－x－1、じゃ」
「Adams4_user と Adams6_user 関数と厳密解を比較してみたよ。
比較は、LN（｜計算値－厳密解｜）をグラフにした。
計算範囲は、x=0～10まで、刻み幅は、h=0.01、とした。（計算精度10桁）
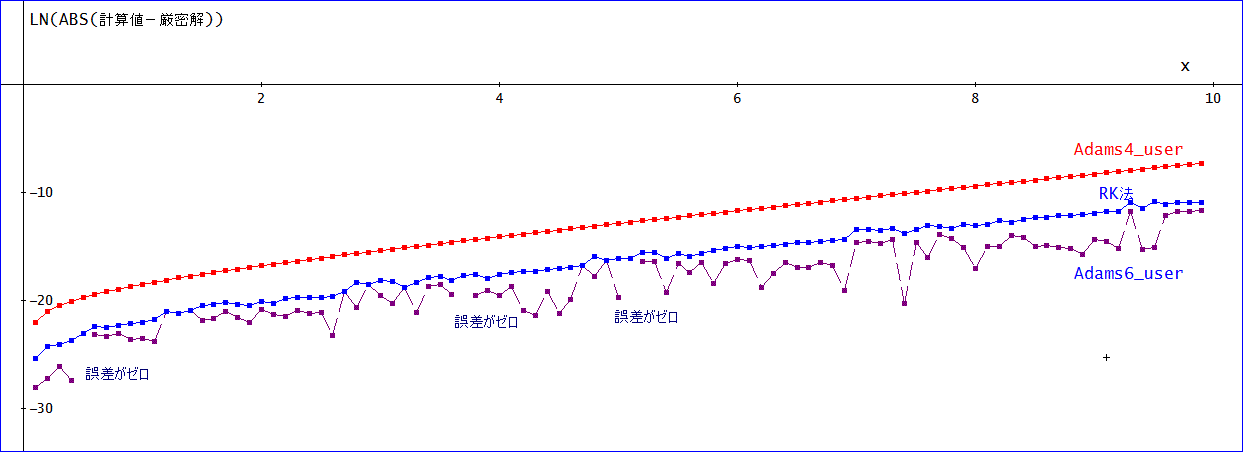
上のグラフでは、下方向ほど、絶対誤差が小さいことを示す。
Adams4_user や RK法と比較すると、Adams6_user では、絶対誤差の変動が大きい。
では、計算精度を20桁として、Adams6_user のみを再度計算してみた。
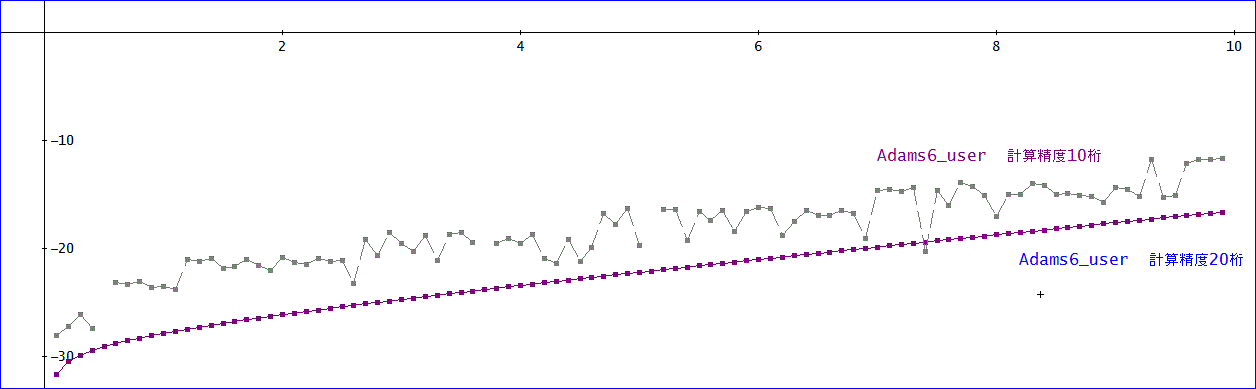
上の図は、Adams6_user でDERIVE の計算精度を10桁とした場合と20桁とした場合を比較している。
明らかに、20桁とした場合の結果が安定している。
これは、6次のオイラー展開法でも、同様の傾向となった。
6次のオイラー展開法やAdams6_user の打ち切り誤差は、h=0.01の6乗程度、この場合は、1×10^(－12)に達するので、計算精度が10桁では、まずかったことが分かるわ」
「なるほどのう。
興味深い現象じゃったな。
今回は、このあたりにしておこうかの」
最終更新日 2016/5/12
