数式処理ソフト DERIVE(デライブ) de ドライブ
84.道中双六の問題(補筆1)
目次
『道中双六の問題』の過去記事を振り返る
はじめに
宿場数1の場合
宿場数が2の場合
宿場数が3の場合
宿場数が一般で、p=1/2の場合
宿場数が一般の場合の差分方程式
偏微分方程式で近似
ζ(3,1/4)-ζ(3,3/4) の値は?
フルヴィッツのツェータ(ゼータ)関数による数値計算といくつかの数値的予想
リーマンのツェータ(ゼータ)関数とその定積分表示
フルヴィッツのツェータ(ゼータ)関数とその定積分表示
フルヴィッツのツェータ(ゼータ)関数の関数等式によるζ(3,1/4)-ζ(3,3/4) の値の導出
宿場数が4の場合の上がる確率の予想 (2017/1/23追記)
宿場数が一般の場合の上がる確率の予想 (2017/1/23追記)
『道中双六の問題』の過去記事を振り返る
はじめに
「『道中双六の問題』については、『今月のご挨拶』で3回にわたって取り上げたのじゃった。
以下が、過去の記事へのリンクじゃな。
・ 道中双六の問題 (2014年1月)
・ 道中双六の問題(続) (2014年2月)
・ 道中双六の問題(続々) (2016年4月)
初めて、今回の記事をご覧になる方は、上に掲げた道中双六の問題(続々) をお読みいただくだくとよいじゃろう」

「2014年が午年だったから、最初の記事から、3年になるのね。
記事の冒頭の寅さん的口上が面白かったな。
下に引用しますね。
『さあ、寄ってらっしゃい、見てらっしゃい。昔懐かしい「道中双六」だよ。
日本橋を振り出しに東海道最初の宿場は、品川宿。間を端折って、五十三個目が大津宿、上がりは花の都は京の三条大橋だ。
今年は午年、馬と宿場は縁があるんだ。元は駅と言っていた。電車じゃないのよ。停まるのは。
昔、中国で馬を置き通信の便にあてそれを驛と言った。驛の字が馬偏だ。簡単に言えば、馬の乗り継ぎ所。五十三「次」や「駅伝」にいわれが残る。
 なに、この双六は、宿場の数が少ないとな。なんと、賢い、お客様。お客様は神様だ。
なに、この双六は、宿場の数が少ないとな。なんと、賢い、お客様。お客様は神様だ。
ここからが肝心だ。急に難しくなっちゃうよ。
この双六の宿場では、確率 Pで一つ進み、確率(1-P)で一つ戻る。
振り出しは常に一つ進み、上がりは双六から消えちゃうよ。
さあ、そうすると、どうなるか。ドウと鳴らなきゃ、カンと鳴る。カントは、ドイツの哲学者。
P=1ならば宿場毎に1日を費やすと最短で宿場の数に一を加えた日数だ。
P=0ならば、上がらない。誰もやらないよ。つまらないから。
しかれども、その刻遅く、彼の刻早く、
Pが0と1の間の値を取ったなら、平均、最短の何倍で上がれるかが問題と、言ってるそばから日が暮れる。
蕎麦は長いが日は短い。カラスと一緒に帰ります。
続きは、ウェブにてと、向後万端よろしくお願い申し上げます。』」
「ともちゃん。
『DERIVE de ドライブ』を半年以上、お休みしてしまったが、これからも、よろしくお願いしますよ。
道中双六の問題は、ともちゃんが冒頭の部分を引用してくれたように、元々は、2014年の年賀状の題材として、考えたものじゃったな。
さて、双六のルールを簡単に再掲しておこう。
絵双六で駒を振り出しから進める。
振り出しから、上がりまでの間に宿場が少なくとも、1つ以上ある。
1.駒は、振り出しから、必ず、1番目の宿場に進める。
2.駒は、各宿場で、確率 pで、次の宿場に進み、確率 (1-p) で1つ戻るものとする。
3.駒が最後の宿場から上がりに進んだときは、双六上から消える。(上がりから戻ることはない)
4.駒どおしの関係は、無いものとする。
5.振り出しから、1番目の宿場まで、及び、各宿場間、並びに、最後の宿場と上がりまでの所要時間は、同一とし、1(日)と勘定する
テーマは、平均何日で上がれるか?、
だが、なかなか難しくて、計3回にわたって、取り上げることになってしまったというわけじゃ。
なお、2015年2月の「宿題を片付けよう!?」でも、宿題の一つとして載せている。
これまでに得られた結果をまとめてみよう。
最短日数=宿場数+1=c、これは、明らかじゃ。
ここで、宿場数+1≡c とおいている」
目次に戻る
宿場数1の場合
「宿場数=1の場合は、最短日数は、2(日)となる。
上がりまでの日数をm、その確率をf(m)で表し、m=0~、の整数として、
f(2m+2)=p(1-p)^m、
これから、平均上がり日数は、Σ(m=0~n)m×f(m)=Σ(m=0~n)(2m+2)p(1-p)^m=2/p - 2(1 - p)^(n
+ 1)(n·p + p + 1)/p 、
最後に、n->∞、の極限をとると、値は、2/p、となる。
この平均日数を最短日数で割ると、1/p、また、特に、p=1/2の場合は、この値が 2 (平均日数は4日)となる事に注意して欲しいのう」
目次に戻る
宿場数が2の場合
 「じゃ、私は、宿場数が2の場合ね。
「じゃ、私は、宿場数が2の場合ね。
最短日数は、3日となる。
宿場数が1の場合にならって、
上がりまでの日数をm、その確率をf(m)で表し、m=0~、の整数として、
f(2m+3)=p^2×(1-p)^m×(1+p)^m=p^2×(1-p^2)^m、と書けることがわかったのね。
そこで、平均日数は、Σ(m=0~n)m×f(m)=Σ(m=0~n)(2m+3)×p^2×(1-p^2)^m=(p^2 + 2)/p^2 - (1 - p^2)^(n + 1)·(2·n·p^2 + 3·p^2 + 2)/p^2、
nを無限大に近づけると、平均日数は、1+2/p^2、となり、
平均日数/最短日数=(2+p^2)/(3p^2)、特に、p=1/2の場合は、3 (平均日数は9日)となることが分かるわ」
目次に戻る
宿場数が3の場合
「3回目の記事では、宿場数が3の場合について、宿場数が1、2の場合のように厳密に計算してみたのじゃった。
mを0以上の整数として、2m+4日目に上がる確率は、下の式になることが分かった。
f(2m+4)=(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))、
ここで、A、B、Cは、0以上の整数、Comb関数は、組み合わせ数を計算するDERIVEの関数じゃ。
従って、平均日数=Σ(m=0~n)(2m+4)f(2m+4)、
しかし、残念ながら、上の式をこれ以上簡単化できなかったので、数値的に計算してみた。
n=100、として近似計算してみると、p=1/2の場合、平均日数≒15.9999、これは、最短日数^2=4^2=16に極めて近いじゃろう」
| p |
平均日数のn=100の近似値 |
Excelで計算した平均日数 |
確率の和(Excelの計算) |
| 0.1 |
10.6385 |
1,837.5580 |
0.999866 |
| 0.2 |
53.7451 |
220.0000 |
1 |
| 0.3 |
54.9580 |
65.1851 |
1 |
| 0.4 |
28.6685 |
28.7500 |
1 |
| 0.5 |
15.9999 |
16.0000 |
1 |
| 0.6 |
10.3703 |
10.3703 |
1 |
| 0.7 |
7.4635 |
7.4635 |
1 |
| 0.8 |
5.7812 |
5.7812 |
1 |
| 0.9 |
4.7187 |
4.7187 |
1 |
 「けれど、p=0.3以下では、Excelで計算した結果の方が、真値に近いと考えられるわね。
「けれど、p=0.3以下では、Excelで計算した結果の方が、真値に近いと考えられるわね。
上の表の黄色、赤色の枠よ」
「DERIVEの計算では、変数 a、b、c、を0~mまで変化させて、平均日数を計算させるのじゃが、
H(a,b,c,m)=IF(a+b+c=m,1,0)と定義して、a+b+c<>m の場合は、H=0となるので、実質的な和の計算に含めないようにした。
また、a、b、c は、すべて、m=0~nとしてしまうと計算量が増えるので、変域をずらして、計算量を減らす工夫をしている。
平均日数=Σ(m=0~n)(2m+4)×Σa=0~m(Σb=0~m-a(Σc=0~m-a-b(・・・)))、
ここで、・・・は、p^(m - a)·COMB(a + b, a)·COMB(b + c, b)×(1-p)^m×H(a,b,c,m)、
しかし、この方法でも、n=100の場合の計算時間は、約150秒、(変域を制限しないと、約1300秒必要)じやった。
nをこれ以上増やすと、計算時間が飛躍的に増えてしまった」
「あ! おじぃさん。
その計算式のΣが一つ多いわ!
関数 H も必要ない。
変数 m、a、b、c の間に、m=a+b+c、の関係があるんだから、c=m-a-b、として」
「おっと、これは、うっかりしていたな。
余分な計算時間がかかっていたな。(第3回目の記事に記載した平均日数の値には影響しない)
あらためて、ともちゃんのリマークを生かすと、
平均日数=Σ(m=0~n)(2m+4)×(Σa=0~m(Σb=0~m-a(p^(m - a)·COMB(a + b, a)·COMB(m-a, b)×(1-p)^m)))、で十分じゃった。
p=1/2の場合は、n=100として、約8秒の計算時間で、平均日数≒15.99997458、が求められた。
p=0.3の場合は、n=100として、約105秒の計算時間で、平均日数≒54.9580、と求められたが、この値は、Excelの計算値(65.1851 )に比較して、かなり少ない値である。
計算時間が短縮できたので、n=400と増やして計算が可能となり、平均日数≒65.18315987、有効数字4桁まで、Excelの計算値に一致してきた。
ただし、計算時間は、約1200秒(20分)とかなり必要となってしまったがな」
※赤字の(2m+4)は、f(2m+4)と書かれていましたが、正しくは、上記の通り、(2m+4)でした。(2017/2/14訂正)
目次に戻る
宿場数が一般で、p=1/2の場合
 「これらの計算結果から、
「これらの計算結果から、
p=1/2の場合は、平均日数=最短日数の2乗=(宿場数+1)^2、と表せるのではないかと予想したという訳ね」
「ま、この程度の計算結果なので、偶然かも知れないと思ったがの。
そこで、ともちゃんが Excel表による数値計算『道中双六の問題(続)』によって、宿場数が5、と、53 の場合を計算してくれたんじゃったな。
そのExcel表による数値計算は、労作じゃった。(結果を下に再掲した)」
|
宿場数=5 |
宿場数=53 |
| P |
平均日数/最短日数 |
| 0.1 |
|
|
| 0.2 |
568.7 |
|
| 0.3 |
67.67 |
|
| 0.4 |
15.78 |
|
| 0.5 |
6 |
53.56 |
| 0.6 |
3.18 |
4.77 |
| 0.7 |
2.065 |
2.45 |
| 0.8 |
1.519 |
1.65 |
| 0.9 |
1.203 |
1.24 |
| 1 |
1 |
1 |
「たしかに。Excelの力を久々に実感できたわ。(実物をご覧になりたい方は、自作もののページにアップしてあるのでよろしくね)
この結果を見ると、
宿場数=5の場合、p=1/2、では、平均日数/最短日数が6となり、最短日数=宿場数+1=6、とあわせてみれば、平均日数=最短日数^2=c^2、となっていることが分かる。
この最後の式で、c=宿場数+1=最短日数、よ。
同様に、
宿場数が53の場合も、p=1/2、では、平均日数/最短日数≒53.56、となり、平均日数≒2892、これは、最短日数^2=54^2=2915、に非常に近いことが分かった」
「上の表の空欄は、約16000個ほどのセルを使っても、確率の和が十分に1に近くならないため、信頼性の高い数字が得られなかったpの値に対応する。、
当然、宿場数が大きくなると、同じpでも、より多数のセルを計算に使う必要が出てくる。
この計算結果を見て、宿場数に限らず、p=1/2の場合、平均日数=最短日数^2、という予想は、かなり正しいと思うたな」
目次に戻る
宿場数が一般の場合の差分方程式
 「2014年2月のご挨拶『道中双六の問題(続)』で扱った差分方程式については、次のようね。
「2014年2月のご挨拶『道中双六の問題(続)』で扱った差分方程式については、次のようね。
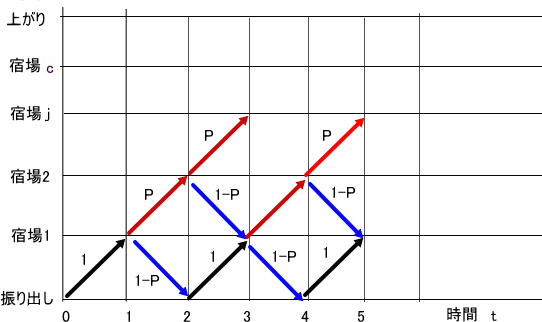
時間をtで、振り出しから上がりまでをj(0~c)で表す。
ただし、各宿場に至る確率をf(j,t)とし、上がり c=宿場数+1、
(1)f(0,0)=1
(2)t<j → f(j,t)=0
(3)j>c → f(j,t)=0
(3)f(0,t)=(1-p)×f(1,t-1)
(4)f(1,t)=f(0,t-1)
(5)j<c-1 → f(j,t)=(1-p)×f(j+1,t-1)+p×f(j-1,t-1)
(6)上記以外は、f(j,t)=p×f(j-1,t-1)」
「そうじゃったな。
ともちゃんがDERIVEで定義してくれたf(i,j)の関数を使って、宿場数が、小さいときは、各項が厳密に求められた。
これは、宿場数が3の場合を検討する際に非常に役立ったのう」
目次に戻る
偏微分方程式で近似
「宿場数が3以上では、差分方程式の一般解を求めることが難しかったので、差分を微分で置き換えて、偏微分方程式として扱ったのじゃった。
位置 x、時間 t を連続量と考えて、時刻 t における f(x,t)を双六上の駒の確率密度関数とする。
直感的には、駒よりも旅人と考えると、わかりやすいじゃろう。
f(x,t)dx は、時刻 t において、位置 x~x+dx にいる旅人の人数の密度と考えればよい。
t=0では、全区間(x=0~c)の旅人の密度は、x=0、すなわち、振り出しで1、以外はゼロである。
f(x,t+1)=p×f(x-1,t)+(1-p)×f(x+1,t)、を得る。
ここで、f(x,t+1)≒f+∂(f,t)、
f(x-1,t)≒f-∂(f,x)+(1/2)∂(f,x,2)、
f(x+1,t)≒f+∂(f,x)+(1/2)∂(f,x,2)、
と差分を微分で近似する。
なお、∂(f,x)は、f(x,t)のxに関する1階の偏導関数、∂(f,x,2)は、f(x,t)のxに関する2階の偏導関数を表す。
∂(f,t)=(1-2p)∂(f,x)+(1/2)∂(f,x,2)、
p=1/2の場合は、第1項が消えるので、熱伝導などを表す偏微分方程式に一致する。
このとき、忘れてはいけないのが、初期条件と境界条件じゃが、
t=0では、f(x,t)=δ(t)、
x=0では、∂(f,x)=0、(断熱条件)
x=cでは、f(x=c,t)=0、(放熱条件)
放熱条件は、p=1/2の場合の数値実験から、Excel表での数値計算結果にあわせるためには、
x=cで、∂(f,x)=-∞、という境界条件を与えれば、一致度合いがよいことから、決めたものじゃ。
これらにより、
f(x,t)=Σ2/c×cos(λ√2 x)×exp(-λ^2 t)、
λ√2 c=(k-1/2)π、と求められた。
ここで、k=1~∞、を動く整数じゃ」
 「そうだったわね。
「そうだったわね。
そして、肝心の平均日数は、∫(t=0~∞)t×f(c,t) dt、で計算できなかったのよね」
「そのとおり。
f(x,t)は、差分方程式の時とは違うので、x=c という一点の値を元に計算する意味がない。
まして、境界条件から、f(x=c,t)は、ゼロと置いているのだから、∫(0~∞)t×f(x=c,t) dt、とすると、ゼロとなってしまう。
そこで、H(t)=∫(x=0~c)f(x,t) dx、という関数を考える。
f が確率密度というのを忘れて、旅人の人数(の密度)と考える。
このH(t)は、時刻 t における全区間(x=0~c)に残っている旅人の合計人数(の密度)じゃ。
反対に考えると、1-H(t)が、時刻 t で、すでに全区間の外に出て行った人数(の密度)となる。
とすると、t=t~t=t+dtの間に、出て行く人数(の密度)は、-∂(H(t),t)dt。
負号を付けているのは、正の値とするためだな。
この出て行く人達のそれまでに費やした時間は、t なので、平均日数は、∫t×(-∂(H(t),t))dt、となる。
よって、平均日数=∫(t=0~∞)H(t) dt、と求められる。
ここで、部分積分を使ったが、H(∞)→ ゼロ、を仮定している。(x=cが放熱条件であれば、これは、満たされている)」
「従って、p=1/2 の具体的な表式に適用すると、k=1~の整数として、
平均日数=Σ2 sin(cλ√2)/(c √2 λ^3)、λ√2 c=(k-1/2)π、と変形出来る。
そして、DERIVEの数値計算では、平均日数=c^2、と見なしてよいことが示されたのね」
「その点、少し、疑問が残ったのじゃ。
今、s>1、z>0の実数として、ζ(s,α)=Σ(k=0~∞)1/(k+α)^s、は、『フルヴィッツのツェータ(ゼータ)関数』と言われるものじゃ。
DERIVEのこの記法により、
平均日数=c^2×(-ζ(3,3/4)+ζ(3,1/4))/(2 π^3)、と書けるので、
平均日数=c^2、であるためには、
-ζ(3,3/4)+ζ(3,1/4)=2π^3、が成立していればよいのじゃな。
これについては、もう一度、次節で考えてみよう」
「なるほど。
こうやって見て来たところ、
p=1/2の場合については、いろいろな結果が得られてきたな、という気がするわね。
だけど、p が1/2に等しくない場合は、まだ、不十分な気がする」
「まったくじゃな。
解くべき方程式は、
∂(f,t)=(1-2p)∂(f,x)+(1/2)∂(f,x,2)、
ここで、v=2p-1、と置き、当面、p>1/2 と仮定すると、v>0、である。
∂(f,t)=(1/2)∂(f,x,2)-v ∂(f,x)、
f(x,t)=exp(v(x-vt/2))×w(x,t)、とおくと、
w(x,t)については、p=1/2の場合と同じ形の方程式に変換されるというのが、2016年4月の結果じゃった。
そこで問題となったのは、初期条件と境界条件だった。
その際、初期条件は、とりあえず、
w(x,0)=δ(x)、とする。
x=0では、∂(f,t)=0、から、(∂(w,x)+v w)=0、となり、
∂(w,x)=-v w(x=0,t)、
x=cでは、f(x=c,t)=0、から、
w(x=c,t)=0、
とおいて、
c3(k)=(4λ^2/(c(v^2 + 2λ^2) - v))、と係数、c3(k)を定めると、
w(x,t)=Σc3(k)(-v /√2λ×sin(√2λx)+cos(λ√2 x))exp(-λ^2 t)、
ここで、λは、tan(√2 cλ)=√2λ/v から決まる。
となって、まあ、こんな感じで解けたかなと思ったのじゃったがな」
「そうなのよね。
だけど、c=54(宿場数=53)の場合を数値計算してみると、Excelなどで計算した結果と合わないのよ。
また、宿場数が小さい場合については、時間不足で、そもそも、計算できていないし、なんか、すっきりとしないわ」
「まったくじゃ。
そこで、これまで、長々と振り返ってきたが、検証不足や未検討事項を今回と次回以降、取り上げてゆくとしよう」
目次に戻る
ζ(3,1/4)-ζ(3,3/4) の値は?
フルヴィッツのツェータ(ゼータ)関数による数値計算といくつかの数値的予想
「前節に記載したように、差分方程式を偏微分方程式で近似すると、
p=1/2の場合は、ζ(3,1/4)-ζ(3,3/4)の値が、2π^3、であれば、平均日数がc^2、であることが証明されたことになろう。
ここで、ζ(s,α)=Σ(k=0~∞)1/(k+α)^s、で定義される、『フルヴィッツのツェータ(ゼータ)関数』(フルヴィッツのツェータ(ゼータ)関数:Hurwitz zeta function)と言われるものじゃ。
当面は、2つの変数は、実数で、s>1、α>0、とする。
また、c=宿場数+1、と置いていることにも注意して欲しいのう」
 「ところで、
「ところで、
リーマンのツェータ(ゼータ)関数は、s>1 においては、ζ(s)=Σ(k=1~∞)1/k^s、と定義されているので、フルヴィッツのツェータ(ゼータ)関数は、その拡張とも言えるのね。
今回は、sが3で、αが特別な値、1/4と3/4、におけるのその関数の値の差が問題となっている。
それについて、s=2~10、のように、1つずつ変化させて計算してみた。
計算したのは、ζ(s,1/4)-ζ(s,3/4)、の値で、s=2~10、の範囲ね。(DERIVEの計算精度は、10桁とした)
ζ(2,1/4)-ζ(2,3/4)≒ 14.6554495;
ζ(3,1/4)-ζ(3,3/4)≒ 62.01255336;
ζ(4,1/4)-ζ(4,3/4)≒ 253.1698052;
ζ(5,1/4)-ζ(5,3/4)≒ 1020.065615;
ζ(6,1/4)-ζ(6,3/4)≒ 4090.61467;
ζ(7,1/4)-ζ(7,3/4)≒ 1.637670105·10^4;
ζ(8,1/4)-ζ(8,3/4)≒ 6.552616896·10^4;
ζ(9,1/4)-ζ(9,3/4)≒2.6213081·10^5;
ζ(10,1/4)-ζ(10,3/4)≒1.048558346·10^6、となったわ。
さてと、s=3のときは、予想によれば、2π^3、と書けるので、2π^3≒62.01255336、となり、上の数字は、計算的には、一致している。
s=5の場合は、どうかと思って、有理数×π^5、と仮定して、未知の有理数の値を求めると、
ζ(5,1/4)-ζ(5,3/4)=10/3×π^5≒1020.065615、であろうことが分かった。
以下、同様に、s=7、9の場合は、
ζ(7,1/4)-ζ(7,3/4)=244/45×π^7≒1.637670105×10^4、
ζ(9,1/4)-ζ(9,3/4)=554/63×π^9≒2.621308100·10^5、であろうことが分かったわ」
目次に戻る
リーマンのツェータ(ゼータ)関数とその定積分表示
「よ、ともちゃん。大活躍じゃったな。
ところで、フルヴィッツのツェータ(ゼータ)関数 ζ(s,α)において、s>1、かつ、αが1の場合は、リーマンのツェータ(ゼータ)関数になる。
リーマンのツェータ(ゼータ)関数は、ζ(s)は、s>1で、ζ(s)=Σ(k=1~∞)1/k^s、と定義されるからな。
ここで、s=2m、ここで、m=1、2、~の整数とすると、
ζ(2m)=(2π)^2m/(2(2m!))×(-1)^(m+1)×B(2m)、と書けることが知られている。(岩波数学辞典第4版 付録公式)、
ただし、B(2m)は、ベルヌイ(ベルヌーイ)数じゃ。
ベルヌイ数については、第52回の『数値積分(1)(台形公式とベルヌイ数)』で扱っている。
n次のベルヌイ数を B(n)と書くと、x/(exp(x)-1)=Σ(n=0~∞)B(n)xn/n! の係数とするのが母関数による定義じゃ。
なお、母関数のxは、不定元とも言われるもので、□、でも○でもよい。
しかし、この定義を元に直接、計算すると、DERIVEでも、B(9)ぐらいまでで、それより大きい次数は、うまく計算できなかったのじゃったな。
そこで、漸化式を求めた。
B(n)=-1/(n+1)Σ(k=0~n-1)comb(n+1,k)×B(k) 、というものじゃ。
この漸化式を元に計算してみた。
具体的には、n=0~50番目までの計算結果を再掲すると、
[1, - 1/2, 1/6, 0, - 1/30, 0, 1/42, 0, - 1/30, 0, 5/66, 0, - 691/2730, 0, 7/6, 0, - 3617/510, 0, 43867/798, 0, - 174611/330,
0, 854513/138, 0, - 236364091/2730, 0, 8553103/6, 0, - 23749461029/870, 0, 8615841276005/14322,
0, - 7709321041217/510, 0, 2577687858367/6, 0, - 26315271553053477373/1919190,
0, 2929993913841559/6, 0, - 261082718496449122051/13530,
0,1520097643918070802691/1806, 0, - 27833269579301024235023/690, 0, 596451111593912163277961/282,
0,
- 5609403368997817686249127547/46410, 0, 495057205241079648212477525/66]、
ただし、赤字は、10番目毎を表す、のようになった。
従って、ζ(2)=(2π)^2/4×B(2)=π^2×(1/6)=π^2/6、
また、ζ(4)=(2π)^4/(2(4!))×(-1)×B(4)=16π^4/48×-B(4)=π^4/3×(1/30)=π^4/90、など。
このように、リーマンのツェータ(ゼータ)関数では、sが偶整数の場合の値は、πのべき乗×有理数、と書けるのじゃ。
一方、奇整数の場合については、このような簡単な式では書けないことが広く知られている」
 「なるほどね。
「なるほどね。
ζ(2)=Σ(k=1~∞)1/k^2=π^2/6、
のわりあい簡単な求め方は、いろいろあるようね。
『物理学への数学的序説』(荒木源太郎 著:みすず書房)では、x^2 をx=-π~π、でフーリエ級数に展開した式、
x~2=π^2/3+4×Σ(k=1~∞)((-1)^k/k^2×cos(kx))、において、
x=πとおけば、
π^2=π^2/3+4×Σ1/k^2、
よって、ζ(2)=π^2/6、と求められることが紹介されていた」
「そうじゃのう。
『MATHEMATICAL METHODS OF PHYSICS』(Second Edition)(JON MATHEWS、R. L.WALKER 著)では、
もう少し、取り付きやすい方法として、
f(x)=x+x^2/4+x^3/9+x^4/16+・・・、とおいたとき、
xで微分すると、f '=1+x/2+x^2/3+・・
上の式の右辺が、=-(1/x)×LN(1-x)、であることに注意すれば、
f(x)に関する1階の微分方程式としてとらえて、初期条件 f(0)=0、と併せ考えると、
f(x)=-∫(t=0~x)(1/t)×LN(1-t) dt、と書ける。
ここで、x=1と置けば、
f(1)=ζ(2)=-∫(t=0~1)(1/t)×LN(1-t) dt、
よって、
ζ(2)=∫(t=0~∞)(t/(exp(t)-1)dt、と定積分で表示できることが分かるじゃろう」
「なるほど。
ではと、ζ(2)以外のリーマンのツェータ(ゼータ)関数の積分表示を得るために、
∫(t=0~∞)(t^β/(exp(t)-1)dt、を考えてみるよ。
与式は、∫(t^βexp(-t)/(1-exp(-t))dt、と書き換えられるので、t>0では、|exp(-t)|<1、に注意して、
項別に展開すると、∫t^β×exp(-t)(1+exp(-t)+exp(-2t)+exp(3t)+・・)dt、
ここで、ガンマ関数の定義式、Γ(x+1)=∫(t=0~∞)t^x×exp(-t) dt、を思い出せば、
与式は、Σ(k=1~∞)Γ(β+1)(1/1^(β+1)+1/2^(β+1)+1/3^(β+1)+・・)、
この右辺は、Γ(β+1)×ζ(β+1)、であるので、
結局、
ζ(β+1)=(1/Γ(β+1))×∫(t=0~∞)(t^β/(exp(t)-1)dt、のように、リーマンのツェータ(ゼータ)関数の値を定積分で表示できる。
たとえば、
β=3とおけば、Γ(4)=3!=6に注意して、
ζ(4)=(1/6)×(t^3/(exp(t)-1)dt=(1/6)×(π^4/15)=π^4/90、と先に求めた値と一致する。
これと似たようなことをすると、フルヴィッツのツェータ(ゼータ)関数も定積分で表示できると思う」
目次に戻る
フルヴィッツのツェータ(ゼータ)関数とその定積分表示
「よくできましたな。
では、わしも、ともちゃんに負けないように、
∫(t=0~∞)(t^β/(exp(t)-1)dt=∫(t^β×exp(-t)/(1-exp(-t))dt、を拡張して、
∫t^β×exp(-αt)(1+exp(-t)+exp(-2t)+exp(3t)+・・)dt、を考えてみよう。
与式の各項は、k=0~、として、
∫t^β×exp(-(α+k)t) dt、であることから、
(α+k)t=uと置けば、
(1/(α+k)^(β+1))∫(u=0~∞)u^β×exp(-u)du=Γ(β+1)×(1/(α+k)^(β+1))、
よって、フルヴィッツのツェータ(ゼータ)関数を、
ζ(β+1,α)=(1/Γ(β+1))×∫(t^β×exp(-αt)/(1-exp(-t))dt、と表すことができた。(β>0、α>0)
試しに、
β=2、α=1/4、では、
ζ(3,1/4)=1/Γ(3)×∫(t^2×exp(-t/4)/(1-exp(-t))dt≒64.66386996、
DERIVEで、直接、ζ(3,1/4)を求めた結果と一致する。
同様に、
β=2、α=3/4、では、
ζ(3,3/4)=1/Γ(3)×∫(t^2×exp(-3t/4)/(1-exp(-t))dt≒2.651316608、
結果、
ζ(3,1/4)-ζ(3,3/4)≒62.01255335、
一方、2π^3≒62.01255336、となり、最後の桁が1異なるだけじゃ。
有効数字を20桁として計算すると、
ζ(3,1/4)≒64.663869968768460135、
ζ(3,3/4)≒2.6513166081688198116、
差し引き、ζ(3,1/4)-ζ(3,3/4)≒62.012553360599640323、
一方、2π^3≒62.012553360599640350、なので、有効数字18桁まで一致している。
しかし、多少違いがあるのが気になるのう。
有効数字を30桁として、計算してみたところ、
ζ(3,1/4)-ζ(3,3/4)≒62.0125533605996403509526297788、
2π^3≒62.0125533605996403509526301342、
となり、24桁程度まで、一致していることが分かったが、約430秒と計算時間がかかった」
 「DERIVEの組み込み関数のζ関数により、有効数字50桁で、直接、計算したところ、一瞬で、
「DERIVEの組み込み関数のζ関数により、有効数字50桁で、直接、計算したところ、一瞬で、
ζ(3,1/4)-ζ(3,3/4)≒62.012553360599640350952630134202790404450577131770、が求められた。
一方、2π^3≒62.012553360599640350952630134202790404450577131770、
となって、両者が全桁一致していることが分かったわ。
これで、フルヴィッツのツェータ(ゼータ)関数について、定積分により、DERIVEで数値計算すると多少の誤差は、出ることは、分かったけど、
そもそもの問題のζ(3,1/4)-ζ(3,3/4)は、2π^3、に等しいことは、ほぼ、確実なようね」
目次に戻る
フルヴィッツのツェータ(ゼータ)関数の関数等式によるζ(3,1/4)-ζ(3,3/4) の値の導出
「これまでは、リーマンのツェータ(ゼータ)関数やフルヴィッツのツェータ(ゼータ)関数も引数が実数と考えてきていたのじゃな。
その場合、たとえば、リーマンのツェータ(ゼータ)関数、ζ(s)=Σ(k=1~∞)1/k^s、において、
右辺が収束するためには、s>1でないと、いけなかったのじゃ。
リーマンは、sを複素数まで広げて、ツェータ(ゼータ)関数の定義を拡張した。(このような方法を『解析接続』と呼ぶ)
そうして、次の関数等式を導いたのじゃ。
sを1以外の複素数として、
ζ(s)=2^s×π^(s-1)× sin(πs/2)×Γ(1-s)×ζ(1-s)、
これを負数の場合にも適用できるツェータ(ゼータ)関数の定義だと思い直せば、
たとえば、ζ(-1)=(1/2)×(1/π^2)×(-1)×Γ(2)×ζ(2)、
このときの右辺は、Γ(2)=1、ζ(2)=π^2/6、に注意すると、ζ(-1)=-1/12、となる」
 「ああ、それが、1+2+3+・・・=-1/12、と偶に書かれたりするのね。
「ああ、それが、1+2+3+・・・=-1/12、と偶に書かれたりするのね。
もちろん、左辺の表記と右辺の -1/12、が文字通り、等しいと言っているのじゃないのね」
「そのとおり。
ζ(s)を無限級数 Σ(k=1~∞)1/k^s、の形で定義できるのは、Re(s)>1、でないといけない。
ここで、Re( )は、sの実部を取り出す関数じゃ。
なので、あくまでも、1+2+3+・・・=-1/12、の左辺は、ζ(-1)の簡易表記と考える必要があるのじゃな。
なお、sが負の偶数の場合、s=-2m、(m=1~)とおけば、
ζ(-2m)=0となることが分かる。(sin(πs/2)の因子が入っているのでな)」
「リーマンのツェータ(ゼータ)関数の関数等式は、導くのが大変でしょうね」
「確かにな。
このDERIVE de ドライブの複素関数は、第51回の『複素関数(6)(留数定理の応用)』で終わっているからな。
解析接続に踏み込んでおらん。というか、踏み込めんかったと言うべきかな。
なので、今回、そこは、端折っておこう。
さて、フルヴィッツのツェータ(ゼータ)関数についても、次の関数関係が知られている。
整数、m、nを 1=<m=<n、であるとすると、s<>1、の複素数について、
ζ(1-s,m/n)=2Γ(s)/(2πn)^s×Σ(k=1~n)(cos(πs/2-2πk m/n)×ζ(s,k/n)、の関係がある。
これは、たとえば、ウィキペディアの『フルヴィッツのゼータ函数』の項にある。
また、Souichiro Ikebe 氏の『特殊関数 グラフィックスライブラリー』
(http://math-functions-1.watson.jp/index.html)の『Hurwizのツェータ(ゼータ)関数』の項にも記載されている。
他に、次の特徴的な関係がある。
ζ(s,α)=Σ(k=0~∞)1/(k+α)^s、において、両辺をαで微分した場合、
∂(ζ(s,α),α)=-s×ζ(s+1,α)、が成り立つことが分かる,」
「先に出てきた関数等式は、複雑な式ね。
ζ(1-s,m/n)=2Γ(s)/(2πn)^s×Σ(k=1~n)(cos(πs/2-2πk m/n)×ζ(s,k/n)、
でも、s=3、m=1、n=4、とおけば、
左辺は、ζ(-2,1/4)、
右辺は、2Γ(3)/(8π)^3×(cos(3π/2-π/2)ζ(3,1/4)+cos(3π/2-π)ζ(3,1/2)+cos(3π/2-3π/2)ζ(3,3/4)+cos(3π/2-2π)ζ(3,1))、
赤字の項がゼロとなるので、Γ(3)=2!=2、を使って、
右辺は、1/(128π^3)×(-ζ(3,1/4)+ζ(3,3/4))、となる。
ここで、ζ(-2,1/4)の値が、-1/64、ならば、問題の式、ζ(3,1/4)-ζ(3,3/4) の値が、2π^3、となるんだけど」
「うん。
今は、うまく説明できないのじゃが、DERIVEの計算によれば、ζ(0,α)=1/2-α、と書けるのじゃな。
※ 次のHPを参照すると上の値が正しいことが分かる。
http://mathworld.wolfram.com/HurwitzZetaFunction.html 2017/4/7追記
さて、∂(ζ(s,α),α)=-s×ζ(s+1,α)、が成り立つとして、両辺をαで積分すると、
※ 上式は、s=0、1 以外では、成立する。http://mathworld・・ 、に記載されている。2017/4/7追記
ζ(s,α)=-s ×∫ζ(s+1,α)dα+const、
ここで、s=-1、α=1 とおけば、
左辺=ζ(0,1)=-1/12、
右辺=(∫(1/2-α)dα+cons)t=α/2-α^2/2=0+const、
従って、const=-1/12、
これにより、ζ(-1,α)=α/2-α^2/2-1/12、
同様に、s=-2、とおけば、
ζ(-2,α)=2×(-α^3/6+α^2/4-α/12)+const=-α^3/3+α^2/2-α/6+const、
ここで、α=1と置けば、ζ(-2,1)=0、である。
なぜなら、フルヴィッツのツェータ(ゼータ)関数の先の関係等式で、s=3、m=n=1、と置くことにより、
ζ(-2,1)=2Γ(3)/(2π)^3 ×cos(3π/2-2π/1)=0であるからじゃな。
よって、const=0、である必要がある。
これより、ζ(-2,α)=-α^3/3+α^2/2-α/6、であることが分かるのじゃ。
従って、α=1/4、と置くことにより、
ζ(-2,1/4)=-1/64、であることがわかった」
「なるほどね。
その結果が正しければ、
1/(128π^3)×(-ζ(3,1/4)+ζ(3,3/4))=ζ(-2,1/4)、の右辺を-1/64、と置くことにより、
-ζ(3,1/4)+ζ(3,3/4)=2π^3、であることが証明された。
じゃ、同じように、
s=5、n=4、m=1、と置くことにより、フルヴィッツのツェータ(ゼータ)関数の関係等式より、
ζ(-4,1/4)=2Γ(5)/(8π)^3×(cos(5π/2-π/2)ζ(5,1/4)+cos(5π/2-3π/2)ζ(7,1/4))、
なお、右辺では、ゼロとなる項を省略して書いたわよ。
左辺は、前述のように計算するか、DERIVEの計算に従えば、
ζ(-4,1/4)=5/1024、であることが分かる。
右辺は、3/(2048π^5)(ζ(5,1/4)-ζ(5,3/4))、
よって、
ζ(5,1/4)-ζ(5,3/4)=(10/3)π^5、
これは、数値計算で予想した結果と同じになったわ。
同様に、s=7、n=4、m=1、と置くことにより、
ζ(-6,1/4)=-45/(65536π^7)(ζ(7,1/4)-ζ(7,3/4))、
これから、
ζ(7,1/4)-ζ(7,3/4)=-ζ(-6,1/4)×65536π^7/45、
ここで、ζ(-6,1/4)=-61/16384、から、
ζ(7,1/4)-ζ(7,3/4)=(244/45)π^7、
これも、数値計算で予想した結果と同じになったわ。
同様に、s=9、n=4、m=1、と置くことにより、
ζ(-8,1/4)=315/(524288π^9)(ζ(9,1/4)-ζ(9,3/4))、
これから、
ζ(9,1/4)-ζ(9,3/4)=ζ(-8,1/4)×524288π^9/315、
ここで、ζ(-8,1/4)=1385/262144、から、
ζ(9,1/4)-ζ(9,3/4)=(554/63)π^9、
これも、数値計算で予想した結果と同じになったわ」
「よーできたな。
さて、今回の結果をまとめると、
フルヴィッツのツェータ(ゼータ)関数の関数等式、
ζ(0,α)=1/2-α、
∂(ζ(s,α),α)=-s×ζ(s+1,α)の関係が s=0、1 以外のすべてのsにおいて成立することを前提とすると、
『道中双六の問題』の偏微分方程式による近似において、p=1/2の場合、
平均日数=(宿場数+1)^2、であることが証明された。
なお、宿場数が1、2、と小さい場合でも、平均日数=(宿場数+1)^2、が厳密に成立していることを考え合わせると、
偏微分方程式で近似する前の差分方程式においても、このことが厳密に成り立っているのではないかと予想される。
いや、しかし、こんなところで、ツェータ(ゼータ)関数の関数等式にお目にかかるとは、思いがけなかったがな。
ツェータ(ゼータ)関数は、深掘りすると、切りが無いが、長くなったので、懸案となっている p<>1/2 の場合の再検討については、次に回すことにしよう」
目次に戻る
宿場数が4の場合の上がる確率の予想 (2017/1/23追記)
宿場数が3の場合の上がる確率の式から類推して、宿場数が4の場合、次式を予想しました。
mを0以上の整数として、2m+5日目に上がる確率は、
f(2m+5)=(1-p)^m p^4 Σ(a+b+c+d=m)(p^(m-a)Comb(a+b,a) Comb(b+c,b)Comb(c+d,c))、
ここで、a、b、c、d は、0以上の整数、Comb関数は、組み合わせ数を計算するDERIVEの関数。
上式をもとに、m=0~9まで計算したところ、『道中双六の問題(続)』で、差分方程式を基に計算した結果と下表の通り一致しました。
| m |
道中双六の問題(続) s=4の場合 |
(1-p)^m p^4 Σ(a+b+c+d=m)(p^(m-a)Comb(a+b,a) Comb(b+c,b)Comb(c+d,c)) |
備考 |
| 0 |
p^4 |
(p^4) |
一致 |
| 1 |
p^4(1 - p)(3p + 1), |
(p^4·(1 - p)·(3·p + 1)) |
一致 |
| 2 |
p^4(p - 1)^2(8p^2 + 4p + 1), |
(p^4·(p - 1)^2·(8·p^2 + 4·p + 1)) |
一致 |
| 3 |
p^4(1 - p)^3(3p + 1)(7p^2 + 2p + 1) |
(p^4·(1 - p)^3·(21·p^3 + 13·p^2 + 5·p + 1)) |
一致 |
| 4 |
p^4(p - 1)^4(55p^4 + 40p^3 + 19p^2 + 6p + 1) |
(p^4·(p - 1)^4·(55·p^4 + 40·p^3 + 19·p^2 + 6·p + 1)) |
一致 |
| 5 |
p^4(1 - p)^5(3p + 1)(6p^2 + 1)(8p^2 + 4p + 1) |
(p^4·(1 - p)^5·(144·p^5 + 120·p^4 + 66·p^3 + 26·p^2 + 7·p + 1)) |
一致※ |
| 6 |
p^4(p - 1)^6(377p^6 + 354p^5 + 219p^4 + 100p^3 + 34p^2 + 8p + 1) |
(p^4·(p - 1)^6·(377·p^6 + 354·p^5 + 219·p^4 + 100·p^3 + 34·p^2 + 8·p +
1)) |
一致 |
| 7 |
p^4(1 - p)^7(3p + 1)(7p^2 + 2p + 1)(47p^4 + 20p^3 + 10p^2 + 4p + 1) |
(p^4·(1 - p)^7·(987·p^7 + 1031·p^6 + 705·p^5 + 361·p^4 + 143·p^3 + 43·p^2
+ 9·p + 1)) |
一致※ |
| 8 |
p^4(p - 1)^8(8p^2 + 4p + 1)(323p^6 + 210p^5 + 132p^4 + 64p^3 + 21p^2 +
6p + 1), |
(p^4·(p - 1)^8·(2584·p^8 + 2972·p^7 + 2219·p^6 + 1250·p^5 + 556·p^4 + 196·p^3
+ 53·p^2 + 10·p + 1)) |
一致※ |
| 9 |
p^4(1 - p)^9(3p + 1)(41p^4 + 8p^3 + 9p^2 + 2p + 1)(55p^4 + 40p^3 + 19p^2
+ 6p + 1) |
(p^4·(1 - p)^9·(6765·p^9 + 8495·p^8 + 6862·p^7 + 4198·p^6 + 2053·p^5 +
815·p^4 + 260·p^3 + 64·p^2 + 11·p + 1)) |
一致※ |
上表で、備考欄に「一致※」と、※印の表示は、予想式では、完全に因数分解されていない場合で、差分方程式から計算した結果と一目で、一致しているとは判断できないものです。
しかし、たとえば、m=9の(p^4·(1 - p)^9·(6765·p^9 + 8495·p^8 + 6862·p^7 + 4198·p^6 + 2053·p^5 + 815·p^4 + 260·p^3 + 64·p^2 + 11·p + 1)) は、
(p^4·(1 - p)^9·(3p+1)(2255·p^8 + 2080·p^7 + 1594·p^6 + 868·p^5 + 395·p^4
+ 140·p^3 + 40·p^2 + 8·p + 1)、であり、
更に、41p^4 + 8p^3 + 9p^2 + 2p + 1、55p^4 + 40p^3 + 19p^2 + 6p + 1、の2つの式の積であることが分かります。
従って、両者は、一致しています。
ちなみに、平均日数=Σ(m=0~n)(2m+5)f(2m+5)、となるので、
n=100として数値計算した結果、平均日数≒(24.99052493)、
これは、平均日数=5^2=25、(最短日数5の2乗)に極めて近いことも、予想式が正しいと思われる理由です。
目次に戻る
宿場数が一般の場合の上がる確率の予想 (2017/1/23追記)
前節の予想を更に一般化して次式を得ました。
宿場数+1≡c、と置いて、
mを0以上の整数として、2m+c日目に上がる確率は、
f(2m+c)=(1-p)^m p^(c-1) Σ(k1+k2+・・+kc-1=m)(p^(m-k1)Comb(k1+k2,k1) Comb(k2+k3,k2)・・Comb(kc-2+kc-1,kc-2))、
ここで、k1、k2、k3等 は、0以上の整数、Comb関数は、組み合わせ数を計算するDERIVEの関数。
と想定されます。
上式をもとに、c=6、(宿場数=5)の場合を、m=0~9までの確率を計算しました。
| m |
道中双六の問題(続) s=5の場合 |
f(2m+6)予想式 |
備考 |
| 0 |
p^5 |
(p^5) |
一致 |
| 1 |
p^5(1 - p)(4p + 1) |
(p^5·(1 - p)·(4·p + 1)) |
一致 |
| 2 |
p^5(p - 1)^2(13p^2 + 5p + 1) |
(p^5·(p - 1)^2·(13·p^2 + 5·p + 1)) |
一致 |
| 3 |
p^5(1 - p)^3(40p^3 + 19p^2 + 6p + 1) |
(p^5·(1 - p)^3·(40·p^3 + 19·p^2 + 6·p + 1)) |
一致 |
| 4 |
p^5(p - 1)^4(121p^4 + 66p^3 + 26p^2 + 7p + 1) |
(p^5·(p - 1)^4·(121·p^4 + 66·p^3 + 26·p^2 + 7·p + 1)) |
一致 |
| 5 |
p^5(1 - p)^5(364p^5 + 221p^4 + 100p^3 + 34p^2 + 8p + 1) |
(p^5·(1 - p)^5·(364·p^5 + 221·p^4 + 100·p^3 + 34·p^2 + 8·p + 1)) |
一致 |
| 6 |
p^5(p - 1)^6(1093p^6 + 727p^5 + 364p^4 + 143p^3 + 43p^2 + 9p + 1) |
(p^5·(p - 1)^6·(1093·p^6 + 727·p^5 + 364·p^4 + 143·p^3 + 43·p^2 + 9·p + 1)) |
一致 |
| 7 |
p^5(1 - p)^7(3280p^7 + 2367p^6 + 1286p^5 + 560p^4 + 196p^3 + 53p^2 + 10p
+ 1) |
(p^5·(1 - p)^7·(3280·p^7 + 2367·p^6 + 1286·p^5 + 560·p^4 + 196·p^3 + 53·p^2
+ 10·p + 1)) |
一致 |
| 8 |
p^5(p - 1)^8(9841p^8 + 7652p^7 + 4459p^6 + 2105p^5 + 820p^4 + 260p^3 +
64p^2 + 11p + 1) |
(p^5·(p - 1)^8·(9841·p^8 + 7652·p^7 + 4459·p^6 + 2105·p^5 + 820·p^4 + 260·p^3 + 64·p^2 + 11·p + 1)) |
一致 |
| 9 |
p^5(1 - p)^9(29524p^9 + 24601p^8 + 15256p^7 + 7705p^6 + 3260p^5 + 1156p^4
+ 336p^3 + 76p^2 + 12p + 1) |
(p^5·(1 - p)^9·(29524·p^9 + 24601·p^8 + 15256·p^7 + 7705·p^6 + 3260·p^5
+ 1156·p^4 + 336·p^3 + 76·p^2 + 12·p + 1)) |
一致 |
宿場数が5の場合、上表のように、『道中双六の問題(続)』で、差分方程式を基に計算した結果と予想式は、一致していることが分かりました。
また、平均日数をm=0~100まで変化させて、計算したところ、(35.76778393)、となりました(計算時間≒3200秒あまり)。
以前に記載したように、Excel表での計算値は、36なので、宿場数が4の場合よりも近似度合いは悪いものの、予想式が正しいことを感じさせる値になっています。
目次に戻る
最終更新日 2017/2/14
一部追記 2017/4/7
ゼータ関数をツェータ(ゼータ)関数と変更:2023/11/24




 なに、この双六は、宿場の数が少ないとな。なんと、賢い、お客様。お客様は神様だ。
なに、この双六は、宿場の数が少ないとな。なんと、賢い、お客様。お客様は神様だ。
