
2015年2月の「宿題を片付けよう!?」に記載のリストの最初に掲げている宿題です。今回で、3回目となりました。
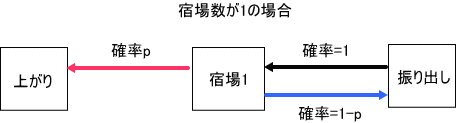
(1)宿場数が1及び2のケースのおさらい
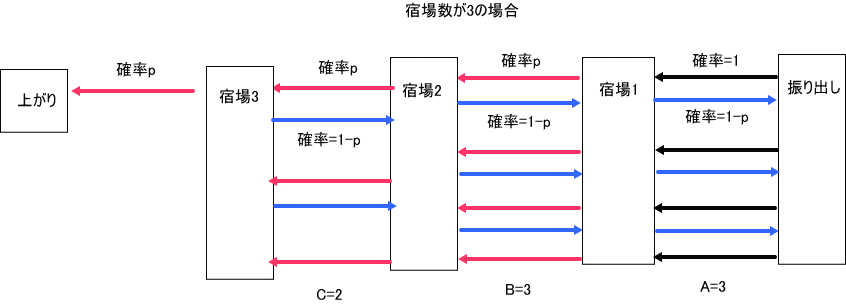
(2)宿場数が3の場合
(3)宿場数が3の場合をExcelで計算する
(4)偏微分方程式で解析(1)(初期条件、境界条件等)
(5)偏微分方程式で解析(2)(p=1/2の場合)
(6)偏微分方程式で解析(3)(オイラー変換の利用)
(7)偏微分方程式で解析(4)(pが一般の場合)
(8)終わりにあたって
「だいぶ時間が経ってしまった。
道中双六の問題を再度振り返ってみようということじゃ」
 「たしかにね。
「たしかにね。
最初が2014年の1月「道中双六の問題」、次いで、翌月の2014年の2月の「道中双六の問題(続)」だったもの。
元々が2014年の午年にちなんだ問題だったんだけど、もう2年前のことでしょ。
例の宿題リスト「宿題を片付けよう!?」の1番目に載っているし、そろそろ、決着を付けないとね」
「そのとおりじゃのう。
まずは、簡単に問題を説明しよう。
絵双六で駒を振り出しから進める。
上がりまでの間に宿場がs 個ある。(s>0)
1.駒は、振り出しから、必ず、1番目の宿場に進める。
2.駒は、各宿場で、確率 Pで、次の宿場に進み、確率 (1-P)で1つ戻るものとする。
3.駒が最後の宿場から上がりに進んだときは、双六上から消える。(上がりから戻ることはない)
4.駒どおしの関係は、無いものとする。
5.振り出しから、1番目の宿場まで、及び、各宿場間、並びに、最後の宿場と上がりまでの所要時間は、同一とし、1日と勘定する。
というようなルールで行うと仮定したゲームで、平均何日で上がれるかを計算したかったという訳じゃ。
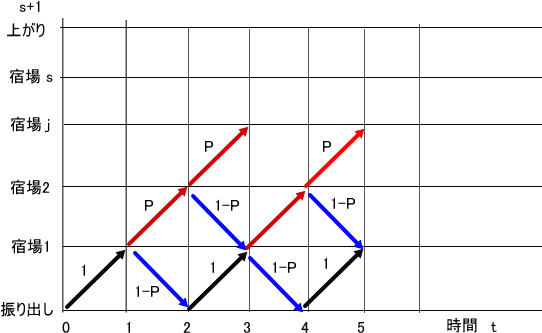
振り出しから上がりまでの位置をj で表し、j=0 を振り出し、j=s+1 を上がりとする。
宿場数 s=1の場合は、上の図のようになる。
上がりまでの日数をm、その確率をf(m)で表すと、m=0~、の整数として、最速日数である2日の確率 f(2)=p、はすぐに分かる。
f(3)はゼロで、f(4)=p(1-p)、以下同様に、f(2m+2)=p(1-p)^m、である。
従って、平均日数は、Σm×f(m)=Σ(2m+2)p(1-p)^m=lim n->∞{2/p - 2(1 - p)^(n + 1)(n·p
+ p + 1)/p }、
0=<p<=1。なので、右辺の極限値は、2/p となるのじゃな」
「そうだったわね。
s=2の場合は、下図のようになる。
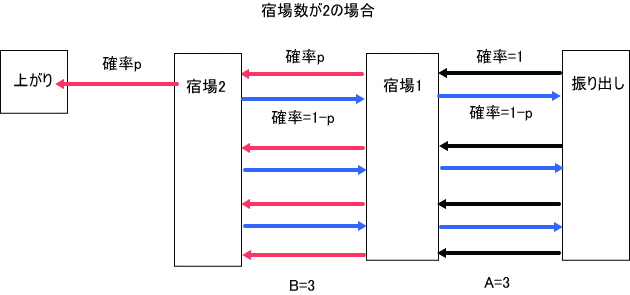
今度は、少し難しくなったんだけど、振り出しと宿場1の間の折り返しの組数をA、宿場1と宿場2の間の折り返しの組数をBとしたとき、
振り出しから上がりまでの日数は、2m+3 日(m=0、1、・・)である。
上の図では、A=3、B=3、の場合を示している。
ここで、2m+3=3+2A+2B、が成り立つことに注意すると、A+B=m。
f(2m+3)=Σ(A+B=m)(1-p)^A×(1-p)^B×p^(B+1)×p、となるのね。
f(2m+3)=Σ(A=0~m)Comb(m,A)(1-p)^(A+B)×p^(B+2)=Σ(A=0~m)Comb(m,A)(1-p)^m×p^(m-A+2)、
ここで、Comb(m,A)=m!/(A!(m-A)!) は、2項係数を表す。
一方、(1+p)^m=Σ(A=0~m)Comb(m,A)p^(m-A)、であるので、
f(2m+3)=p^2×(1-p)^m×(1+p)^m=p^2×(1-p^2)^m、と簡単化される。
これから、平均日数は、
Σ(2m+3)×p^2×(1-p^2)^m=lim n→∞ {(p^2 + 2)/p^2 - (1 - p^2)^(n + 1)·(2·n·p^2 + 3·p^2 + 2)/p^2}、となるので、
平均日数は、1+2/p^2、となることが分かる」
「宿場数が1及び2では、p=1/2 において、平均日数=(宿場数+1)^2の関係があることに注意する。
前回、これを一般化して、p=1/2では、平均日数/(宿場数+1)=宿場数+1、すなわち、平均日数=(宿場数+1)^2、を予想している。
Excel表による数値計算では、この予想を支持する結果が得られている。
次節で、宿場数が3について、取り上げよう」
「宿場数が2の場合に準じて考えると、下図を参照して、2m+4 日で上がる確率は、
f(2m+4)=Σ(A+B+C=m)((1-p)^A (1-p)^(B+1) p^(B+1) (1-p)^C p^(C+1) p)、m=0~・・。
すなわち、f(2m+4)=(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A))、と書けるのではないか、と思うじゃろう。
しかし、それは、少し違うのじゃな」
 「2014年2月の「道中双六の問題(続)」を見ると、宿場数が3の場合は、m=0~9について、f(2m+4)が次のようになると書かれているわ。
「2014年2月の「道中双六の問題(続)」を見ると、宿場数が3の場合は、m=0~9について、f(2m+4)が次のようになると書かれているわ。
※2月のご挨拶では、f(s+1,s+2m-1)、m=1、2・・と記載しているが、s=3と固定した場合は、m の初期値が違うだけで本質的には同じ。
s=3の場合、m=0~9までで、
([p^3, p^3(1 - p)(2p + 1), p^3(p - 1)^2(4p^2 + 3p + 1), p^3(1 - p)^3(2p + 1)(4p^2 + 2p + 1), p^3(p - 1)^4(16p^4 + 20p^3 + 13p^2 + 5p + 1), p^3(1 - p)^5(2p + 1)(4p^2 + p + 1)(4p^2 + 3p + 1), p^3(p - 1)^6(64p^6 + 112p^5 + 104p^4 + 63p^3 + 26p^2 + 7p + 1), p^3(1 - p)^7(2p + 1)(4p^2 + 2p + 1)(16p^4 + 16p^3 + 10p^2 + 4p + 1), p^3(p - 1)^8(4p^2 + 3p + 1)(64p^6 + 96p^5 + 84p^4 + 51p^3 + 21p^2 + 6p + 1), p^3(1 - p)^9(2p + 1)(16p^4 + 12p^3 + 9p^2 + 3p + 1)(16p^4 + 20p^3 + 13p^2 + 5p + 1)])、となっている。
おじさんが書いた上の式と比較してみると、m=0、1、2の時、次の表のようになった。
| m | f(2m+4)2014年2月のご挨拶 | (1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)) | 備考 |
| 0 | p^3 | p^3 | 一致 |
| 1 | p^3(1 - p)(2p + 1) | A=0:B=0:C=1:p^3(1-p)p+ A=0:B=1:C=0:p^3(1-p)p+ A=1:B=C=0:p^3(1-p) =p^3(1 - p)(2p + 1)、 |
一致 |
| 2 | p^3(p - 1)^2(4p^2 + 3p + 1) | A,B,C=0,1,1:p^3(1-p)^2 p^2+ 0,0,2:p^3(1-p)^2 p^2+ 0,2,0:p^3(1-p)^2 p^2+ 2,0,0:p^3(1-p)^2 + 1,0,1:p^3(1-p)^2 p+ 1,1,0:p^3(1-p)^2 p =p^3(1-p)^2 (3p^2+2p+1) |
不一致 |
これを見ると、すでに、m=2の時、赤字で示した数字が違っているわ」
「一見すると、2014年2月の方が間違っているのではないかと思うかも知れん。
ところが、子細に考えると、たとえば、A=B=1、C=0 では、次のような2つのケースを1つとして勘定してしまっていることに気がつく。
ここで、丸付き数字は、時間的順序を表す。
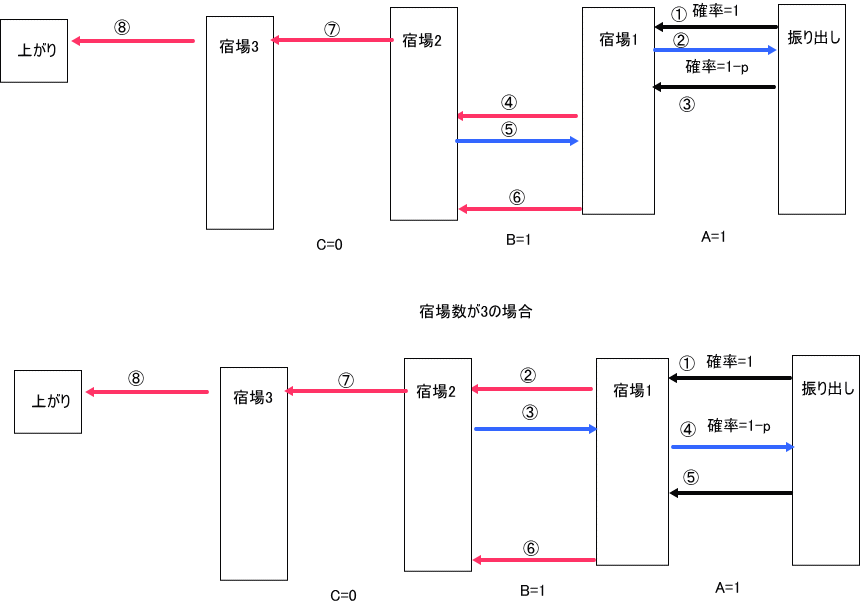
同様に、A=0、B=C=1、についても、下図のように2通りあることが分かる。
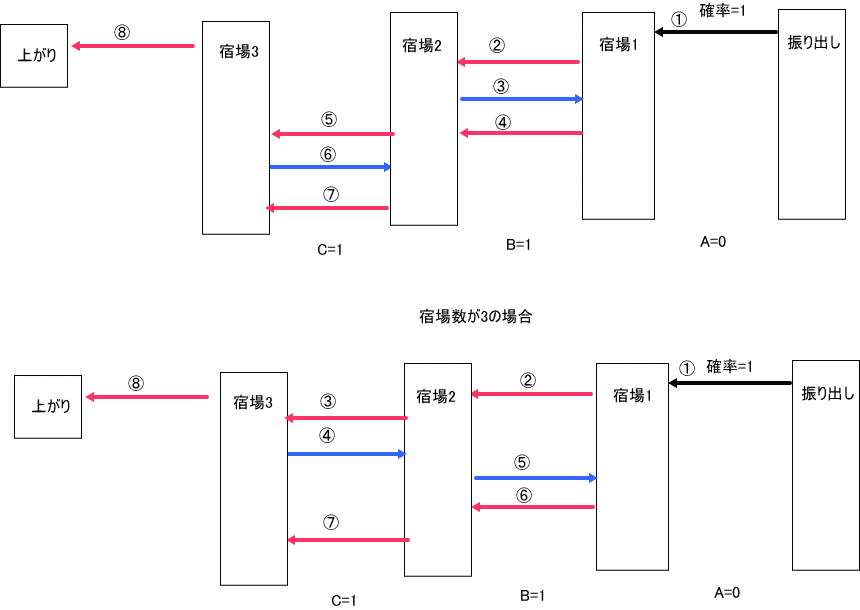
従って、m=2の場合、p^3(1-p)^2 (3p^2+2p+1)ではなくて、p^3(1-p)^2 (4p^2+3p+1)、が正しい。
そこで、今回、改良した式として、
f(2m+4)=(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))、を考える。
| m | f(2m+4)2014年2月のご挨拶 | (1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B)) | 備考 |
| 0 | p^3 | 0,0,0,:p^3 | 一致 |
| 1 | p^3(1 - p)(2p + 1) | 0,0,1:p^3(1-p)p+ 0,1,0:p^3(1-p)p+ 1,0,0:p^3(1-p) =p^3(1 - p)(2p + 1)、 |
一致 |
| 2 | p^3(p - 1)^2(4p^2 + 3p + 1) | 0,1,1:2p^3(1-p)^2 p^2+ 0,0,2:p^3(1-p)^2 p^2+ 0,2,0:p^3(1-p)^2 p^2+ 2,0,0:p^3(1-p)^2 + 1,0,1:p^3(1-p)^2 p+ 1,1,0:2p^3(1-p)^2 p =p^3(1-p)^2 (4p^2+3p+1) |
一致 |
| 3 | p^3(1 - p)^3(2p + 1)(4p^2 + 2p + 1) | 0,0,3:(1-p)^3 p^3 p^3+ 0,3,0:(1-p)^3 p^3 p^3+ 3,0,0:(1-p)^3 p^3 + 0,1,2:3(1-p)^3 p^3 p^3+ 0,2,1:3(1-p)^3 p^3 p^3+ 1,0,2:(1-p)^3 p^3 p^2+ 1,2,0:3(1-p)^3 p^3 p^2+ 1,1,1:4(1-p)^3 p^3 p^2+ 2,1,0:3(1-p)^3 p^3 p+ 2,0,1:(1-p)^3 p^3 p+ =(1-p)^3 p^3(2p + 1)(4p^2 + 2p + 1) |
一致 |
| 4 | p^3(p - 1)^4(16p^4 + 20p^3 + 13p^2 + 5p + 1) | p^3·(1 - p)^4·(16·p^4 + 20·p^3 + 13·p^2 + 5·p + 1) | 一致 |
| 5 | p^3(1 - p)^5(2p + 1)(4p^2 + p + 1)(4p^2 + 3p + 1) | p^3·(1 - p)^5(2·p + 1)·(4·p^2 + p + 1)(4·p^2 + 3·p + 1) | 一致 |
| 6 | p^3(p - 1)^6(64p^6 + 112p^5 + 104p^4 + 63p^3 + 26p^2 + 7p + 1) | p^3·(1 - p)^6·(64·p^6 + 112·p^5 + 104·p^4 + 63·p^3 + 26·p^2 + 7·p + 1) | 一致 |
| 7 | p^3(1 - p)^7(2p + 1)(4p^2 + 2p + 1)(16p^4 + 16p^3 + 10p^2 + 4p + 1) | p^3·(1 - p)^7·(2·p + 1)·(4·p^2 + 2·p + 1)·(16·p^4 + 16·p^3 + 10·p^2 + 4·p + 1) | 一致 |
| 8 | p^3(p - 1)^8(4p^2 + 3p + 1)(64p^6 + 96p^5 + 84p^4 + 51p^3 + 21p^2 + 6p + 1), | p^3·(1 - p)^8·(4·p^2 + 3·p + 1)·(64·p^6 + 96·p^5 + 84·p^4 + 51·p^3 + 21·p^2 + 6·p + 1) | 一致 |
| 9 | p^3(1 - p)^9(2p + 1)(16p^4 + 12p^3 + 9p^2 + 3p + 1)(16p^4 + 20p^3 + 13p^2 + 5p + 1) | p^3·(1 - p)^9·(2·p + 1)·(16·p^4 + 12·p^3 + 9·p^2 + 3·p + 1)·(16·p^4 + 20·p^3 + 13·p^2 + 5·p + 1) | 一致 |
以上を見てみると、宿場数が3 の場合の改良した予想式、
f(2m+4)=(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))、は、正しいようじゃな。
この場合、上がりまでの平均日数は、m=0~100までとって数値計算すると、p=1/2の場合、15.99997458・・、となる。
前回の予想では、平均上がり日数は、最短日数の、s+1(宿場数+1=4)倍と考えているので、4日×4=16、となり、p=1/2の計算値は、ほぼ予想通りじゃ」
「f(2m+4)=(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))の具体的な計算はどうやったの?」
「これは、簡単じゃ。
関数 K(a,b,c,m)を次のように定義する。
K(a,b,c,m)=IF(a + b + c = m, p^(m - a)·COMB(a + b, a)·COMB(b + c, b), 0)、
そして、g(m,p)=∑(∑(∑((1 - p)^m·p^3·K(a, b, c, m), a, 0, m), b, 0, m), c, 0, m)、とすれば、f(2m+4)=g(m, p)、となる。
関数 Kは、a+b+c=m の場合だけ、ゼロでない値を返すので、実質的には、a+b+c=m についてのみ計算するのと同じ結果となる。
関数g(m,p)は、a=0~m、b=0~m、c=0~mについて、(1-p)^m p^3 ×K(a,b,c,m)、を計算してその和を求めている」
「でも、それだと、mが大きくなると、m^3の手間がかかるから、
Σa=0~m(Σb=0~m-a(Σc=0~m-a-b(・・・)))、のようにすれば、手間は減るでしょ」
「確かにな。
ただし、ともちゃんの書いた式をそのまま計算すると、無駄がある。
それは、a+b+c=m、の3つの数について、Σa=0~m(Σb=0~m-a(Σc=0~m-a-b(・・・)))、と計算すると、
a,b,cがすべてゼロから始まるが、m>0では、たとえば、m=1であれば、a,b,cのすべてがゼロというケースはない。
mが大きくなれば、その違いは、大きくなるので計算の無駄も増えてしまうと言うことだ。
しかし、無駄なケースを省こうとすると、面倒になるばかりなので、
H(a,b,c,m)=IF(a+b+c=m,1,0)と定義して、
f(2m+4)=Σa=0~m(Σb=0~m-a(Σc=0~m-a-b(・・・)))、
ここで、・・・は、p^(m - a)·COMB(a + b, a)·COMB(b + c, b)×(1-p)^m×H(a,b,c,m)、とすれば、それなりに高速化はなされるようじゃ」
「なるほどね。
初期値を、(m/3)の小数点以下切り捨てた値とすればよいかとも思ったけど、a,b,cのうち、一つがmで、残りがゼロという組み合わせも排除できないので、結局、そういった関数(H(a,b,c,m))を使う方が簡単ね。
試しに、m=0~29まで計算させてみると、Σa=0~m(Σb=0~m(Σc=0~m(・・・)))、と計算した場合は、10.5秒、
Σa=0~m(Σb=0~m-a(Σc=0~m-a-b(・・・)))と計算した場合は、約1.9秒程度、とかなり短縮はされる。
ちなみに、m=0~100までとった平均上がり日数の計算は、改良した方法では、約145秒と大幅に短縮された。(改良前の方法では、約1300秒)。
そこで、pの代表的な数値を元に平均日数を表にしてみた。(m=0~100まで変化させて計算。計算精度は、10桁)」
| p | 平均日数 | m=0~100の確率の和 | 備考 |
| 0.1 | 10.6385 | (0.1030790020) | ? |
| 0.2 | 53.7451 | (0.6020985751) | ? |
| 0.3 | 54.9580 | (0.9604109680) | |
| 0.4 | 28.6685 | (0.9996174989) | |
| 0.5 | 15.9999 | (0.9999998632) | 最短日数4日の4倍 |
| 0.6 | 10.3703 | 1 | |
| 0.7 | 7.4635 | 1 | |
| 0.8 | 5.7812 | 1 | |
| 0.9 | 4.7187 | 1 |
「p=0.1、及び p=0.2 の場合の上がりまでの平均日数がp=0.3 の時の値より減少しているのは気になるな。
pが小さいと、次の宿場に行くより振り出し側に戻されてしまう確率が大きくなるのだから、常識的には、上がりにくくなる。
すなわち、平均日数は大きくなると考えるのが妥当じゃ。
宿場数が1及び2の場合は、そうなっていた」
「表の3列目に、m=0~100までの確率の和を追加してみたけど、p=0.1と0.2の場合は、1より相当小さいので、mの上限を100としたんでは、圧倒的に足りないことが分かる。
とはいえ、mの上限を100から200にすると、計算が現実的な時間内に収まらないのよ」
「ともちゃんがExcelで計算してくれた2014年2月の「道中双六の問題(続)」にならってみたらどうかな」
 「Excel表で計算するか。
「Excel表で計算するか。
こいつは、うっかり、忘れていたわね。
Excelで計算すると言っても、VBAを使うわけじゃなくて、確率に関する式をベターとコピーしていくだけなので、簡単。
「Dochusugoroku.xlsx」として、「自作ものコーナー」からダウンロードできます。
作り方を説明しますね。
上の表(部分)は、宿場数が3の場合の例よ。
B2~B4は、宿場数と確率p、及び、1-pを置いておくセル。
(B2とB3のみを入力。ただし、シート毎に宿場数を固定しているのでB2は、メモ的なものね)
B20をゼロとしてXFD20までは、日数を表す。(オートフィルで作成)
A19~A15は、振り出し(A19は、ゼロ)から上がり(A15は、上がりで宿場数+1の4)までの位置を表す。
B19は、確率の初期分布であるので、1である。
以下、(1)節のルールに従って、各セルの確率の値をB19~XFD15の範囲で下図の規則で計算する。
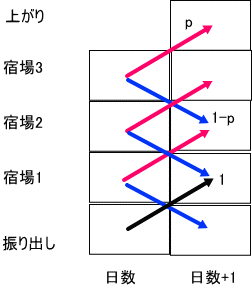
今、各セルの値を、F(x,t)で表す。x=0~4は、位置(0が振り出し、4が上がり)。
t は、時間(日数)。
15行目:F(4,t+1)=p×F(4,t)、
16行目:F(3,t+1)=p×F(2,t)、
17行目:F(2,t+1)=p×F(1,t)+(1-p)×F(3,t)、
18行目:F(1,t+1)=1×F(0,t)+(1-p)×F(2,t)、
19行目:F(0,t+1)=(1-p)×F(1,t)、
あとは、オートフィル機能またはコピーして貼り付けを使って、XFD列までコピーするだけ。
13行目:x=0~3までのFの和、すなわち、振り出しから宿場3までに残っている確率の和。
22行目:15行目の上がる確率F(4,日数)×20行目の日数を書けた値
A22:22行目の値の和で平均日数を表す。
A23:15行目の上がりの確率の和
B25:A23と同じ。
B26:A22と同じ。
B27:宿場数 B3+1で最短日数
B28:平均日数を最短日数で割った値。
前節の表の一部を再掲して、Excelの計算結果を追加してみた」
| p | (2)節で計算した宿場数が3の平均日数 | Excelで計算した平均日数 | 確率の和(Excelの計算) |
| 0.1 | 10.6385 | 1,837.5580 | 0.999866 |
| 0.2 | 53.7451 | 220.0000 | 1 |
| 0.3 | 54.9580 | 65.1851 | 1 |
| 0.4 | 28.6685 | 28.7500 | 1 |
| 0.5 | 15.9999 | 16.0000 | 1 |
| 0.6 | 10.3703 | 10.3703 | 1 |
| 0.7 | 7.4635 | 7.4635 | 1 |
| 0.8 | 5.7812 | 5.7812 | 1 |
| 0.9 | 4.7187 | 4.7187 | 1 |
「なるほど。
やはり、p=0.1~0.3までの平均日数は、正しい値からは、だいぶん遠いものじゃったことが分かる。
それにしても、p=0.1では、なんと1837日≒5年以上とは驚きじゃのう。
しかし、Excel の威力は、たいしたものじゃ。
pを変化させても、関係するセルの計算は、ほぼ一瞬(1秒以下)で求められるものな。
また、計算の対象日数は、最大16382日だから、宿場数が3では、p=0.1の場合でも、確率の和は、99.98%以上となっている」
「とは言っても、Excel表でも、宿場数が多くなると、p<0.5 では、16000列を使っても、確率の和が低くなってしまう。
たとえば、宿場数が5では、p=0.1は、確率の和が1割程度、宿場数が53では、p=0.4 ですでに不十分となる。
Excel表を横長ではなくて、縦長にすれば、行数も大幅に増やせるのでかなり改善されると思うけどね」
「下のグラフを見ると納得じゃな。
なお、近似曲線の式表示で、x とあるのは、確率 p、縦軸 y は、平均日数の自然対数じゃ。
また、近似式は、たとえば、s=3では、y=-2.649 LN(x)+1.0928、となっているが、LN(平均日数)=-2.649 LN(p)+1.0928、という意味になる。
このため、平均日数≒3×p^(-2.65)、となり、p=0.5では、近似値として18.7日を与える。計算結果では、16日なので、ほぼ正しい。
同様に、s=5の場合は、平均日数≒3.5×p^(-3.88)、s=53の場合は、平均日数≒36×p^(-4.46)、となる。
※Excel 2013のグラフで近似式が正しい値を与えるのは、グラフの種類が「散布図」の場合に限られる。
(折れ線グラフ等でも近似曲線そのものは、正しく引かれる)
次節では、宿場数が大きい場合を偏微分方程式で解析してみよう」
「ここからが本題じゃ。
位置 x、時間 t を連続量と考えて、時刻 t における f(x,t)を双六上の駒の確率密度関数とする。
直感的には、駒よりも旅人と考えると、わかりやすいじゃろう。
f(x,t)dx は、時刻 t において、位置 x~x+dx にいる旅人の人数の密度と考えればよい。
t=0では、全区間(x=0~c)の旅人の密度は、x=0、すなわち、振り出しで1、以外はゼロである。
前節の F(2,t+1)=p×F(1,t)+(1-p)×F(3,t)の2をx、1をx-1、3をx+1と置き換えて、
f(x,t+1)=p×f(x-1,t)+(1-p)×f(x+1,t)、を得る。
ここで、f(x,t+1)≒f+∂(f,t)、
f(x-1,t)≒f-∂(f,x)+(1/2)∂(f,x,2)、
f(x+1,t)≒f+∂(f,x)+(1/2)∂(f,x,2)、
と差分を微分で近似する。
なお、∂(f,x)は、f(x,t)のxに関する1階の偏導関数、∂(f,x,2)は、f(x,t)のxに関する2階の偏導関数を表す。
∂(f,t)=(1-2p)∂(f,x)+(1/2)∂(f,x,2)、
これが、2014年2月の「道中双六の問題(続)」の中で導いた式じゃな」
 「そうだったわね。
「そうだったわね。
特に、p=1/2の場合は、右辺の第1項が消えて、典型的な(一次元の)熱伝導方程式に一致するんだった。
だけど、境界条件をどうしたらよいかが、はっきりしなかったので、具体的な解を求めるには至らなかったのよね」
「そこで、まず、初期条件じゃが、f(x,0)は、デルタ関数とする。
f(x,0)=δ(x)。これは、もっともな仮定じゃろう。
次にx=0の境界条件を考える。
xに関する勾配がゼロと置く。
すなわち、x=0で、∂(f,x)=0、(熱伝導方程式では、「断熱条件」と言われる。)
一方、x=c 、の境界条件をどうするかが難しかったのじゃな。
当初は、f(c+1,t)-f(c,t)=0-f(c,t)、これを、∂(f,x)、と等しいと置き、
∂(f,x)=-f(c,t)、ただし、左辺は、x=cでの値。(外部をゼロとした場合の放熱条件に相当)と考えた。
本稿を書く前に、これらを初期条件、境界条件として、p=1/2について、計算してみたのじゃ。
ところが、先回りして言ってしまうと、たとえば、宿場数が53の場合にExcel表を使った数値計算より小さい値を与えた。
そこで、∂(f,x)=-αf(c,t)、と置き、αを1より大きい方向に変化させて試行してみたのじゃ。
結局、α→∞のとき、前回の予想、p=1/2では、平均日数/(宿場数+1)=宿場数+1、となり、宿場数が53の場合は、平均日数は、54^2=2916 と予想される。
∂(f,x)=-∞になるように変更すると、この予想と一致することが分かった。
そこで、あらためて、x=cの境界条件を次のように仮定する。
f(x=c,t)=0、(f の解がxに関してcos関数なので、∂(f,x)/f(c,t)=-α、において、∂(f,x)は、-sin関数、よって、f(x=c,t)がゼロであれば、右辺、-αは、-∞、になる)
次節では、特別ではあるけれど、典型的なケースである、p=1/2の場合を解析しよう」
「解くべき方程式は、
∂(f,t)=(1/2)∂(f,x,2)、
これは、2階、2変数、定数係数、線形で放物型、かつ、同次の「偏微分方程式」である。
以下では、c=宿場数+1 を使う。(前節まで使用していた宿場数 s は、以下、使用しない)
xの変域は、x=0~cとなる。
初期条件及び境界条件(同次境界条件)は、
f(x,0)=δ(x)、
x=0で、∂(f,x)=0、(関数の導関数の値を指定している:ノイマン条件)
x=cで、 f(c,t)=0、(関数の値を指定している:ディリクレ条件)
となる。
方程式を変数分離法で解くために、f=X(x)×T(t)と置いて、与式に代入してごらん」
 「そうね。
「そうね。
T '/T=(1/2)X '' /X、となる。この式の値は、x、t に依存しない「定数」に等しいので、
この「定数」を、-λ^2 と置くと、
∂(T,t)=-λ^2 T
∂(X,x,2)=-2λ^2 X、
という2つの常微分方程式が得られる」
「そうじゃな。
なお、「定数」が正の場合は、t→∞で発散するので、適さない。
また、「定数」がゼロは、時間によらない一定値が解となる場合で、今回は、適切でない。
さて、
第1式から、T=c1×exp(-λ^2 t)、
第2式から、X=c2×sin(λ√2 x)+c3×cos(λ√2 x)、となる。
元の方程式は線形で、かつ、同次なので、T×Xの任意定数(c1、c2、c3)に関する和やλに関する積分も方程式を満たす。
よって、形式的に、f(x,t)∝ Σ/∫(c2×sin(λ√2 x)+c3×cos(λ√2 x))exp(-λ^2 t)、と表される。
まず、x=0の境界条件を満たすためには、
∂(f,x)==(λ√2 c2×cos(λ√2 x)-λ√2 c3×sin(λ√2 x))exp(-λ^2 t)、であるから、
x=0の時に ∂(f,x)=0とするには、c2=0が必要。
また、
x=cの境界条件は、x=cの時のf(x=c,t)=0、から、c3×cos(λ√2 c)exp(-λ^2 t)=0、
cos(λ√2 c)=0、となるので、λ√2 c=(k-1/2)π、k=1、2、・・。とλがとびとびの値をとることが分かる。
このλを固有値という。
では、初期条件からc3(k)を決定してみてごらん」
「f(x,t)=Σ(c3(k)×cos(λk √2 x)×exp(-λk^2 t)、ここで、c3(k)は、k番目の固有値に対応する係数とする。
ただし、固有値のλは、λ√2 c=(k-1/2)π、k=1、2、・・。
t=0の初期条件は、f(x,0)=δ(x)なので、
Σc3(k)×cos(λk √2 x)=δ(x)、から係数を決めることを試みる。
両辺にcos(λj √2 x)をかけて、x=0~cで積分すると、右辺は、∫δ(x)dx=1 となる。
左辺は、√2·SIN(c·(√2·λ - √2·μ))/(4·(λ - μ)) + √2·SIN(c·(√2·λ + √2·μ))/(4·(λ + μ))、となる。
ここで、λk をλ、λj をμと書いた。
μ=λでは、c/2+(√2sin( cλ√2)cos(cλ√2))/4λ となることが分かる。
また、μがλと等しくないときは、λ√2 c=(k-1/2)π、μ√2 c=(m-1/2)π、を使うと、ゼロとなる。
従って、c3(k)×(c/2+(√2 sin(cλk√2 )cos(cλk√2 )/(4λk)))、となる。
更に、λ√2 c=(k-1/2)πから、
かっこ内の第2項がゼロとなるので、c3(k)=2/c、が得られる。
このc3(k)を使って、f は、次のように表される。(k=1~∞)、λの下添え字を略する。
f(x,t)=Σ2/c×cos(λ√2 x)×exp(-λ^2 t)、λ√2 c=(k-1/2)π、となる」
「さてと、こうして求まった f(x,t)から、振り出しから上がりまでの平均日数を計算するには、どうしたらよいかの?」
「平均日数=∫(0~∞)t×f(x=c,t) dt、でいいんじゃないの?」
「そうではないんじゃな。
わしも、最初は、そう思った。
しかし、f(x,t)は、差分方程式の時とは違って、x=c という一点の値を元に計算するのは意味がない。
まして、境界条件から、f(x=c,t)は、ゼロと置いているのだから、∫(0~∞)t×f(x=c,t) dt、とすると、ゼロとなってしまう。
そこで、H(t)=∫(x=0~c)f(x,t) dx、という関数を考える。
f が確率密度というのを忘れて、前に言ったように、旅人の人数(の密度)と考える。
このH(t)は、時刻 t における全区間(x=0~c)に残っている旅人の合計人数(の密度)じゃ。
反対に考えると、1-H(t)が、時刻 t で、すでに全区間の外に出て行った人数(の密度)となる。
とすると、t=t~t=t+dtの間に、出て行く人数(の密度)は、-∂(H(t),t)dt。
負号を付けているのは、正の値とするためだな。
この出て行く人達のそれまでに費やした時間は、t なので、平均日数は、∫t×(-∂(H(t),t))dt、となる。
ここで、部分積分を使うと、平均日数=∫(0~∞)H(t)dt、となることが分かる。
なお、t×H(t)が、t→∞でゼロになることを使った。(H(t) に定数項がないときに限る。両端が断熱条件では、この例外が起きる)、
一方、f(x,t)=Σ2/c×cos(λ√2 x)×exp(-λ^2 t)、なので、
H(t)=Σ√2 ×sin(cλ√2)/(cλ)、から、
平均日数=Σ2 sin(cλ√2)/(c √2 λ^3)、と求められるのじゃ」
「な~るほど。
cλ√2=(k-1/2)πを使うと、
平均日数=Σ(k=1~n)32c^2·(-1)^k/(π^3(1 - 2k)^3)、と級数で表示できる。
ところで、c=54に対して、n=100として計算すると、2915 を与える。
こいつは、Excel表の計算結果、2892余りにかなり近い」
「上々の結果じゃ。
しかし、ともちゃんには、54^2=2916、に気がついて欲しかったがの。
Excel表での計算、c=54 、p=1/2では、平均日数=約2892のときの確率の和が0.99875・・、であり、セル数(約16000個)の制約から、2892は、真値に若干不足している感があった。
Σ(k=1~n)32c^2·(-1)^k/(π^3(1 - 2k)^3)において、nを10000、とすると平均日数は、2916 、となり、これは、54×54である。
n=∞としたときの平均日数の式に現れる無限級数は、絶対収束するので、
kが、偶数、k=2mの和は、- c^2×(3, 3/4)/(2·^3)、と、奇数の和は、c^2×(3, 1/4)/(2·^3)、と別々に求めてもよい。
ここで、ζ(s,z)=Σ(k=0~∞)1/(k+z)^s、とDERIVEで定義されているリーマンのツェータ関数じゃ。
両者の和は、DERIVEの計算的には、c^2×1となる」
「すごい、びっりぽんやね。
平均日数=c^2=(宿場数+1)^2、であることが分かったんだから。
それはそうと、f(x,t)=Σ(2/c)×cos(λ√2 x)×exp(-λ^2 t)、ただし、cλ√2=(k-1/2)π。
このf の時間変化のグラフを下に描いてみたよ。
c=54、時刻 t=1、6、10、100、1000、の時点の様子。(t=0は、δ関数なのでちょっと描けない)」
また、H(t)=∫f(x,t) dx、x=0~c、のグラフは、下図の通り」
「老婆心(おっと、老爺心かな)ながら、ご注意を。
ここに現れる無限級数は、交代級数なので、そのまま計算すると収束が遅いのじゃな。
こんなときこそ、オイラー変換の出番じゃ。
次節で、その点を触れておこう」
 「オイラー変換は、DERIVE de ドライブの「66.再帰関数(5)(オイラー変換、差分、和分)」で扱ったのが最後だったわね。
「オイラー変換は、DERIVE de ドライブの「66.再帰関数(5)(オイラー変換、差分、和分)」で扱ったのが最後だったわね。
無限級数の第n_項がa(n_)で外部で定義されているとき、
ユーザー定義した関数 S(n,m)は、k=0~n-1項まで、正直に和を計算し、k=n~は、第m階差まで使って計算する。
s(n_, m_) ≔ ∑(a(k_), k_, 0, n_ - 1) + SIGN(a(n_))·∑((-1)^k_·2^(- (k_ + 1))·∑(ABS(a(n_ + k_ - j_))·COMB(k_, j_)·(-1)^j_, j_, 0, k_, 1), k_, 0, m_)、
ここで、青色の第1項が正直に計算しているところで、赤色の第2項がオイラー変換部分になるの。
詳しくは、上のページを読んでくださいね。
試しに、a(k):=(-1)^k/(k+1)、k=0、1、・・。
で計算してみる。
Σ(k=0~∞)a(k)=LN(2)≒0.69314718055994530941・・、である。
s(20,20)=(0.69314718055994530938)、となり、計算精度20桁で、青字個所が一致している。
これは、正直計算で20項しかとっていないにもかかわらず、驚きの精度。
さて、今回の級数は、a(k)=32·c^2·(-1)^k/(^3·(2·k + 1)^3)、である。
ただし、上で定義しているオイラー変換による和の関数 s(n,m)は、項の添え字kを0から使用しているため、前節のkをk+1で置き換えていることに注意してね。
s(20,20)で、c^2、となる。
これは、無限級数部分を1と計算できたってこと」
「s(n,m)の階差を表す、mが大まかに有効数字に等しいので、たとえば、有効数字 6桁で十分ならば、s(20,6)でも(0.99999999999815918256·c^2)、と計算できる。
このように、オイラー変換は、今回、非常に有効じゃが、なにも有効なのは、平均日数の計算だけではないぞ。
f(x,t)=Σ(2/c)×cos(λ√2 x)×exp(-λ^2 t)、ただし、cλ√2=(k+1/2)π、k=0、1・・。
の計算でも役に立つ。
また、λが陽に表示できない場合、たとえば、今回、境界条件として、x=cで、∂(f,x)=-αf(x=c,t)、が課せられたときは、λが次のような方程式の根となる。
√2λtan(√2 cλ)=α、
ここで、u=√2 cλとおけば、u/c tan(u)=α、よって、uは、u sin(u)-αc cos(u)=0、の方程式の根(解)である。
このuから、λ=u/(c√2)と求められる。
uは、tan(u)とαc/u、の曲線の交点から得ることかできる。
下図にc=54 で、α=2及びα=1/2の例を示す。横軸がu。
グラフからも明らかじゃが、uが大きくなると、根は、(k+1/2)πに漸近する。
つまり、根は、おおむね 周期 πで並ぶことになる。
従って、ニュートン法と数列の作成を組み合わせることにより、次のようにすると、いっぺんに多くの根を求めることができる。
VECTOR(NEWTON(u·SIN(u) - α·c·COS(u), u, (k -1/2), 6), k, 1, 100, 1)、
c=54、α=2の場合、100個の根が0.5秒以下で求められた。
この場合のc3(k)は、c3(k)×(c/2+(√2sin( cλ√2)cos(cλ√2))/4λ)=1、から決まる。
これを使って、f(x,t)=Σc3(k)cos(√2 λx)exp(-λ^2 t)、
また、H(t)=∫(x=0~c)f(x,t)dx=Σc3(k)sin(√2 λc)/(λ√2)×exp(-λ^2 t)、
さらに、平均日数=Σc3(k)sin(√2 λc)/(√2 λ^3)、となる。
このように、λが明示的に式表示できない場合は、具体的にはどのように計算したらよいかな?」
「そのときは、ベクトルをv として、いっぺんに計算したu の値を元に、λ=u/(c√2)をベクトルVのk番目(k=1~)の要素として代入する。
この v をλとして計算式で使えばいいでしょ。
ただし、ここで使っているオイラー変換の定義式では、各項の添え字をゼロから始めていることを忘れてはいけないわ。
なので、a(k):=、の右辺に現れる v ↓k のk をk+1に変える必要がある。
c3(k)の具体的な形は、次の通り。
c3(k)=2(α^2 + 2·λ^2)/(c(α^2 + 2·λ^2) + 1)、
f(x,t)=Σ(k=1~)c3(k)cos(√2 λx)exp(-λ^2 t)、
さらに、c=54、α=2の場合は、
a(k):= 2·(2^2 + 2·v↓(k + 1)^2)/(54·(2^2 + 2·v↓(k + 1)^2) + 1)·(COS(v↓(k + 1)·√2·x)·EXP(- v↓(k + 1)^2·t))、となる。
この v↓(k+1)は、VECTOR(NEWTON(u·SIN(u) - α·c·COS(u), u, (k -1/2), 6), k,
1, 100, 1)で計算したuをλ=u/(c√2)として、v↓k、に格納したものを使用する。
s(60,20)とすると、f(x,t)の近似式が表示される。(ここに貼り付けるのはあまりに無駄なので略す)
これを元に、f(x,t)のグラフを描いてみた。
前節では、級数の収束が遅く計算時間がかかるので、なめらかなグラフを描くのは、面倒だったので、xのとびとびの点を結んだ。
今回は、t の値を代入してグラフを描かせるだけで下図のようななめらかなグラフを描くことができた。
なお、s(n,m)の引数が小さいときは、t=1のときの、下図のs(20,20)やs(40,20)のようにf が正負で交代する区間がでる。その場合は、n、m
を増やす必要がある。
ただし、n+m が v の次元 100未満でないといけない。
また、H(t)は、a(k):= 2·(2^2 + 2·v↓(k + 1)^2)/(54·(2^2 + 2·v↓(k + 1)^2) + 1)·(√2·^(-
t·v↓(k + 1)^2)·SIN(54·√2·v↓(k + 1))/(2·v↓(k + 1)))、
と置くことで、s(60,20)として計算できる。
グラフは、下図の通り。
最後に、平均日数は、
a(k):= √2·SIN(54·√2·v↓(k + 1))/(2·v↓(k + 1)^3)·(2·(2^2 + 2·v↓(k + 1)^2)/(54·(2^2
+ 2·v↓(k + 1)^2) + 1))、と定義して、
s(60,20)として、平均日数≒2984 と求められた」
「お疲れさんじゃった。
x=cの境界条件が、∂(f,x)=-2 f(x=54,t)、の場合、宿場数が53の平均日数は、2984日というわけだ。
これが、(4)節で書いた境界条件を変更する試行の一つじゃ。
なお、p=1/2の場合は、既出のように、λが明示的に得られるので、このようにベクトルを使う必要は無かった。
しかし、p が1/2に等しくない場合、今回、ともちゃんにやってもらった点が重要になると思う」
「さてと、p=1/2を含めて、0<p<1、の場合を考えてみよう。
解くべき方程式は、
∂(f,t)=(1-2p)∂(f,x)+(1/2)∂(f,x,2)、
xの変域は、x=0~cとなる。(c=宿場数+1)
初期条件及び境界条件は、p=1/2 と同じとする。
f(x,0)=δ(x)、
x=0で、∂(f,x)=0、
x=cで、f(x=c,t)=0、
とする。
ここで、v=2p-1、と置き、当面、p>1/2 と仮定すると、v>0、である。
∂(f,t)=(1/2)∂(f,x,2)-v ∂(f,x)、
p=1/2 の場合と大きく違っているのは、-v ∂(f,x,1)が追加されている点じゃ。
手元の参考書「偏微分方程式(科学者・技術者のための使い方と解き方)」(スタンリー・ファロウ著:伊理正夫・伊理由美 訳)(朝倉書店:2015年6月新版第17刷)に従って、f を次のように分解する。
f(x,t)=exp(v(x-vt/2))×w(x,t)、
まずは、ここから、スタートしてごらん」
 「変換術ね。
「変換術ね。
∂(f,t)=exp(v(x-vt/2))×(∂(w,t)-v^2 w/2)、
∂(f,x)=exp(v(x-vt/2))×(∂(w,x)+v w)、
∂(f,x,2)=exp(v(x-vt/2))×(∂(w,x,2)+v(2∂(w,x)+v w)、
上の3つの数式を元の方程式に代入すると、
∂(f,t)=(1/2)∂(f,x,2)-v ∂(f,x)、は、w に関する方程式としては、p=1/2 のときに扱った、
∂(w,t)=(1/2)∂(w,x,2)、が得られる」
「今度は、w(x,t)の初期条件と境界条件じゃな。
初期条件は、とりあえず、
w(x,0)=δ(x)、とする。(あとで見直すことになる)
x=0では、∂(f,t)=0、から、(∂(w,x)+v w)=0、となり、
∂(w,x)=-v w(x=0,t)、
x=cでは、f(x=c,t)=0、から、
w(x=c,t)=0、
では、これらの条件を基にw(x,t)を求めてご覧」
「wに関する方程式は、∂(w,t)=(1/2)∂(w,x,2)、でこれは、p=1/2のときの、f と同じ形。
だから、w(x,t)∝ Σ/∫(c2×sin(λ√2 x)+c3×cos(λ√2 x))exp(-λ^2 t)、と表される。
これから、∂(w,x)∝Σ/∫(√2λc2×cos(λ√2 x)-√2λc3×sin(λ√2 x))exp(-λ^2 t)、
x=0の条件は、∂(w,x)=-v w(x=0,t)、から、c2 λ√2 =-v c3、
これより、c2=-c3×v /λ√2、
x=cの条件は、w(c,t)=0、から、c2×sin(λ√2 c)+c3×cos(λ√2 c)=0、
これから、tan(√2 cλ)=√2λ/v、の関係が得られる。
よって、w(x,t)=Σc3(k)(-v /√2λ×sin(√2λx)+cos(λ√2 x))exp(-λ^2 t)、
最後に初期条件、w(x,t=0)=δ(x)、より、
Σc3(k)(-v /√2λ×sin(√2λx)+cos(λ√2 x))=δ(x)、
両辺に、(-v /√2μ×sin(√2μx)+cos(√2μx))をかけて、x=0~c で積分する。
右辺は、1、である。
左辺は、μがλに等しくない場合、ゼロになることが確認できる。
一方、μ=λの場合、tan(√2 cλ)=√2λ/v、を使うと、添え字を略して、
c3(k)((c·(v^2 + 2·λ^2) - v)/(4·λ^2))=1、となり、
c3(k)=(4·λ^2/(c·(v^2 + 2·λ^2) - v))、と求められた」
「ようできましたな。
これらは、スツルム・リウビウ系境界問題として知られている。
今回の問題では、g''+λ^2g=0、であった。
g(x,λ)=g1、g(x,μ)=g2、などと略記すれば、
g1''+λ^2g1=0、両辺にg2をかけて、x=a~bで積分すると、
∫g1'' g2 dx+λ^2∫g1 g2 dx=0、
同様に、g2''+μ^2g2=0、の両辺にg1をかけて積分すると、
∫g2''g1 dx+μ^2∫g1 g2 dx=0、
この2つの式を引き算すると、
(λ^2-μ^2)∫g1 g2 dx+∫(g1'' g2-g2'' g1)dx=0、となる。
第2項を部分積分により、簡単化すれば、
(λ^2-μ^2)∫g1 g2 dx+g1'(b)g2(b)-g1'(a)g2(a)-g2'(b)g1(b)+g2'(a)g1(a)=0、となることが分かる。
ここで、境界における条件を使うと、g1'(b)=-δg1(b)/γ、などとなり、g 'の項をgの項に置き換えられる。
こうすると、第1項以外は、打ち消し合って、ゼロとなり、(λ^2-μ^2)∫g1 g2 dx=0、が得られる。
これは、異なる固有値に属する固有関数同士の定積分は、ゼロとなることを示している。
というようなわけで、(-v /√2μ×sin(√2μx)+cos(√2μx))をかけて、x=0~c で積分すると、μがλに等しくないときは、定積分はゼロとなるのじゃ。
さて、こうして、c3(k)を求めてもらったので、f(x,t)を構成してごらん」
「f(x,t)=exp(v(x-vt/2))×w(x,t)、により、f は、
f(x,t)=exp(vx-v^2t/2)Σc3(k)(-v /√2λ×sin(√2λx)+cos(λ√2 x))exp(-λ^2 t)、となる。
ここで、c3(k)=(4·λ^2/(c·(v^2 + 2·λ^2) - v))、
また、λは、tan(√2 cλ)=√2 λ/v、の根である。
もし、vがゼロの場合は、tan(√2 cλ)が無限大になるので、λ=(k-1/2)π、であり、また、v→0で、c3(k)→ 2/c、
f(x,t)=Σc3(k)cos(λ√2 x)exp(-λ^2 t)、となって、p=1/2の場合の解に一致することが分かる。
ところで、ここまでは、v=2p-1、を正と考えてきたが、exp(vx-v^2t/2)の因子は、vが負の場合も、t が無限大で発散はしないので、負の場合にも適用することができると思われる」
「一応そうなのじゃが、ここで難題じゃ。
f(x,t)の初期条件は、δ(x)、なので、実は、w(x,t)の初期条件は、w(x,t=0)=exp(-vx)δ(x)、なのだ。
今得られた、c3(k)により、δ(x)=Σc3(k)R(k)、と展開できる。
ただし、R(k)=(-v /√2λ×sin(√2λx)+cos(λ√2 x))exp(-λ^2 t)、λは、k番目の固有値。
よって、
正しいc3(k)をd3(k)と書けば、Σ(k=1~)d3(k)R(k)=exp(-vx)Σ(j=1~)c3(j)R(j)、となる。
両辺に、R(k)を掛けて、x=0~cで積分すると、
d3(k)×∫R(k)^2 dx =Σ(j=1~)c3(j) ∫R(k)R(j)exp(-vx)dx、
このようにして求めた、d3(k)を使って、
f(x,t)=exp(vx-v^2t/2)Σd3(k)(-v /√2λ×sin(√2λx)+cos(λ√2 x))exp(-λ^2 t)、と書けるのではないかと思われる。
なお、H(t)を計算して、t=0が1でない場合は、H(0)により、正規化して平均日数を計算する必要があるかも知れない。
と考えてきたが、今月は、時間切れじゃな。
p が一般の場合の具体的な計算と検証は、後日、DERIVE de ドライブに譲ることにしよう。
また、簡易的な近似計算の方法がありそうじゃが、別の機会に検討する。
以上、3回にわたっておつきあいいただきました「道中双六の問題」は、ひとまず、これで、終わりにしようと思います」
今回は、 ご覧いただきありがとうございました。
では、次回も、本欄で元気にお会いできますことを願っています。
(1)「道中双六の問題」 2014年1月
(2)「道中双六の問題(続)」 2014年2月
(3)「道中双六の問題(続々)」 2016年4月) (本稿です)
(4)「道中双六の問題(補筆1)」2017年1月)「DERIVE de ドライブ」第84回
(5)「道中双六の問題(補筆2)」2017年2月)「DERIVE de ドライブ」第85回
(6)「道中双六の問題(補筆3)」2018年1月)「DERIVE de ドライブ」第87回
(7)「マルコフ過程(1)(非対称型道中双六:宿場数=3~5)」2018年4月「DERIVE de ドライブ」第88回
(8)「マルコフ過程(2)(非対称型道中双六:差分法1)」2018年4月「DERIVE de ドライブ」第89回
(9)「マルコフ過程(3)(非対称型道中双六:平均日数計算公式)」2018年5月「DERIVE de ドライブ」第90回
(10)「マルコフ過程(4)(非対称型道中双六:固有方程式の漸化式)」2018年6月「DERIVE de ドライブ」第91回
(11)「マルコフ過程(5)(非対称型道中双六:固有方程式の一般形)」2018年7月「DERIVE de ドライブ」第92回
(12)「マルコフ過程(6)(非対称型道中双六:平均日数と対称式)」2019年8月「DERIVE de ドライブ」第93回
(13)「マルコフ過程(7)(非対称型道中双六:宿場数=8の平均日数)」2020年7月「DERIVE de ドライブ」第95回
(14)「マルコフ過程(8)(非対称型道中双六:基本対称式の概2次形式)」2020年8月「DERIVE de ドライブ」第96回
最終更新日 2017/2/10
リンクを追加 2018/1/21、2018/4/5、2018/4/15
リンクを追加 2018/5/21、2018/6/16、2018/7/9、2019/10/21
リンク追加 2020/7/24
リンク追加 2020/9/4