1.概要
2.平均日数(c=奇数)
(1)計算式
(2)c=5(宿場数=4)
(3)c=7(宿場数=6)
(4)c=9(宿場数=8)
3.対称式Ψの予想
(1)Ψの基本対称式による表現
(2)Ψの基本対称式による予想式
(3)Ψの予想式に基づく平均日数の計算
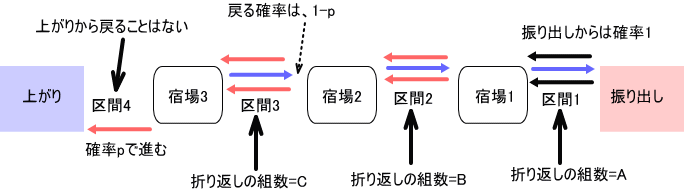
『非対称型道中双六』におきまして、c=宿場数+1、とすれば、c=2~10のうち、振り出しから、上がりまでに要する日数(宿場間の移動=1日)の平均(以下『平均日数』という)は、c=9を除き、厳密解が得られています。
なお、c=9につきましては、2018年4月にさかのぼりますが、第88回「マルコフ過程(1)(非対称型道中双六:宿場数=3~9)」において、数値計算を元に推定した平均日数として下式を得ました。
平均日数=(p^8+20p^6-40p^5+60p^4-56p^3+34p^2-12p+2)/p^8、
ここで、pは、推移確率行列(マルコフ行列)に含まれる推移確率です。
下の図は、宿場が3つ(c=4)の非対称型道中双六。(参考)

今回は、第90回で導いた平均日数公式から得られる多項式を第93回「マルコフ過程(6)(非対称型道中双六:平均日数と対称式)」で紹介した基本対称式に分解する手法を用いて、c=5、7、は、これまでの結果を再検証し、c=9、は、はじめて、前掲の推定式が正しいことを確認できました。
これにより、c=2~10のすべての平均日数の厳密解が得られたことになりましたので、あらためて、下表にまとめました。
| 宿場数 | c | 平均日数 |
| 1 | 2 | 2/p |
| 2 | 3 | (p^2+2)/p^2 |
| 3 | 4 | (4p^2-2p+2)/p^3 |
| 4 | 5 | (p^4+6p^2-4p+2)/p^4 |
| 5 | 6 | (6p^4-6p^3+10p^2-6p+2)/p^5 |
| 6 | 7 | (p^6+12p^4-16p^3+16p^2-8p+2)/p^6 |
| 7 | 8 | (8p^6-12p^5+28p^4-32p^3+24p^2-10p+2)/p^7 |
| 8 | 9 | (p^8+20p^6-40p^5+60p^4-56p^3+34p^2-12p+2)/p^8 |
| 9 | 10 | (10p^8-20p^7+60p^6-100p^5+116p^4-90p^3+46p^2-14p+2)/p^9 |
また、平均日数を構成する対称式を「基本対称式」で表しますと、基本対称式の2次形式(定数項、1次項を含む)と表せるのではないかという新たな予想が浮かんできました。今のところ、証明できていない予想ですが、これが正しいと仮定すると対称式を、より容易に基本対称式に分解でき、平均日数を計算できる範囲が広がると思われます。これについては、第3章で触れました。
目次へ戻る
「第93回がc(=宿場数+1)が偶数の場合が中心だったので、今回は、cが奇数の場合にスポットを当てていく。
奇数の場合の平均日数公式は、次の通りだ。
※公式については、第90回「マルコフ過程(3)(非対称型道中双六:平均日数計算公式)」をご参照ください。
cを奇数として、c=2s+1、ただし、s=1、2、3・・、と書くと、
これにより、平均日数は、pを推移確率、xiを推移確率行列Aの固有値の2乗として、
と与えられる。
また、係数diは、次の2つの関係式から求めることができる。
なお、Uは、[U1(t),U2(t),・・,U2s+1(t)](の転置)という状態ベクトル。(かっこ内の数字は、日数=0、1,2、・・を表す)
添え字の1が振り出しを、c=2s+1が上がり直前にある最後の宿場を表す。
t=0の初期状態は、[1,0,0,・・・0](の転置)、m=0~s-1とする」
 「前回の第94回は、フィボナッチ数列だったけど、今回は、非対称型道中双六のc=9の方を先にやるつもりなのね?」
「前回の第94回は、フィボナッチ数列だったけど、今回は、非対称型道中双六のc=9の方を先にやるつもりなのね?」
「ともちゃんも暑いところ、ご苦労様じゃ。フィボナッチ数列の続きで、数列の母関数を取り上げようと準備していたんじゃが、やはり、その前に済ませておいた方が良いと思ったのでな。まずは、復習と言うことで、次節でc=5を取り上げてみよう」
目次へ戻る
「c=5の場合は、下図のような場合だ。

c=5は、c=2s+1、から、s=2のケースであり、前節の2番目の式から、m=0、1と置くことにより、
というdiに関する2元連立方程式が得られる。
ここで、x1等は、推移確率行列Aの固有方程式で、λを固有値とするとき、
(-λ(λ^4+λ^2(p-1)(3p+1)+p(p+2)(p-1)^2))=0、
ここで、λ<>0として、固有値λの2乗をxと置いた式、
φ(x)=(x^2+x(p-1)(3p+1)+p(p+2)(p-1)^2)=0、から決まる。
※固有方程式は、一般に固有値λの2s+1次式となるが、非対称型道中双六では、特別な初期状態のため、λ×(λ^2のs次式)の形を取る。
今回は、λ×(λ^2の2次式)となるので、(λ^2の2次式)のλ^2=x、と置けば、その2根がx1とx2となる」
 「特別な初期状態とは、U(0)=[1,0,0,0,0](の転置)、のことよ。t=0では、全札が振り出しにいて、途中の宿場には、ひとつの札もない状態が『特別な初期状態』ということね。ま、道中双六(絵双六)としては、すっごく、あたりまえだけどね。
「特別な初期状態とは、U(0)=[1,0,0,0,0](の転置)、のことよ。t=0では、全札が振り出しにいて、途中の宿場には、ひとつの札もない状態が『特別な初期状態』ということね。ま、道中双六(絵双六)としては、すっごく、あたりまえだけどね。
一方、Aは、下図の通りね。

また、U5(4)等は、前節の3番目の式から、
となるので、
U5(4)=p^3≡u4、
U5(6)=p^3(1-p)(3p+1)≡u6、
とそれぞれ、略して書く約束にしたのだったわね」
「その通りじゃ。平均日数は、前掲の以下の式で、
s=2とおいて、次のように表される。
これを展開すると、
となる。
分母は、φ(1)=(1-x1)(1-x2)、の2乗に等しい。
第93回の『平均日数公式の分母』の節から、cが奇数の場合は、φ(1)^2=p^(2c-2)、となるため、c=5では、分母=p^8、となるのじゃな」
「そうなるわね。
問題は、分子の方、(あ!これは、「ぶんしのほう」よ。「ふんこのかた」ではないわ)
おじぃさんが言うように、分母がp^8、なので、平均日数=ψ(x1,x2)/p^7、と書くことができる。
ここで、
となるx1、x2の関数をΨと書いている。これが、対称式となっていることを利用するというのが第93回で得た結果。つまり、固有方程式を解かずに対称式を基本対称式に分解することで、Ψの値を決定するところがポイントなのね。もっとも、今回の場合は、2次方程式なので、根を求めて、計算した方が早いと思うかも知れないけど、3次、4次では、かなり面倒で、5次以上では、できないからよ」
「そういうことじゃ。未知のd1、d2は、
から、連立方程式を解いて、
d1=(u4x2-u6)/(x2-x1)
d2=(u4x1-u6)/(x1-x2)
となるので、Ψの式に代入すると、
Ψ=(-3u4x1^2x2+5u4x1^2-3u4x1x2^2+x1x2(11u4+3u6)-5x1(2u4+u6)+5u4x2^2-x2(10u4+5u6)+5u4+7u6)、
となる」
「対称式を基本対称式に分解するウェアリングの方法を実行するのは、手計算では、とっても面倒だけど、第63回で定義したDERIVEのユーザー定義関数、Fg(多項式,第1項,変数の個数)を使うと比較的簡単なのね。まずは、Freset(2)を実行すると、
(vs≔[x1+x2,x1x2])と表示されて、基本対称式の組がx1+x2とx1x2であると明示される。このとき、変数等の初期化も同時に行われている。
この後、Fg(Ψ,-3u4x1^2x2,2)を実行する。ここで、2つ目の引数は、Ψをx1、x2で展開したとき、最大次数となる第1項を入れる。また、3つ目の引数は、変数の個数なので、2に固定する。
Fgの演算結果として、
([1,-3s1s2u4,5u4x1^2+x1x2(11u4+3u6)-5x1(2u4+u6)+5u4x2^2-5x2(2u4+u6)+5u4+7u6])が返る。
再び、Fgを実行するけど、そのときは、Fg(残差(青い式),残差の第1項=5u4x1^2,2)と入力・実行する。
繰り返し、続けること、5回目で、([5,5u4+7u6,0])が返る。第3項の残差がゼロなので、終了ね。
最後に、Σ(k=1~5)vg↓k、を使って、演算結果の第2項を足し合わせて、Ψを再構築すると、
Ψ=5s1^2u4-3s1s2u4-5s1(2u4+u6)+s2(u4+3u6)+5u4+7u6、
と基本対称式、s1、s2の多項式として、求められた。
一方、固有多項式からは、
φ(x)=x^2+x(p-1)(3p+1)+p(p+2)(p-1)^2、なので、
これを、φ=x^2+a1x+a0=0、と書けば、基本対称式、s1、s2は、2次方程式の根と係数の関係から、
s1=x1+x2=-a1、
s2=x1x2=a0、
の関係があるので、
a1=(p-1)(3p+1)
a0=p(p+2)(p-1)^2
から、s1、s2の値が、
s1=-a1=(1-p)(3p+1)
s2=a0=p(p+2)(p-1)^2
となるのね」
「そこで、s1、s2をΨに代入すると、
Ψ=9p^6u4-6p^5u4+p^4(16u4+3u6)-24p^3u4+p^2(14u4+6u6)-4p(u4+u6)+2u6、
となる。
あとは、u4とu6は、前述の
u4=U5(4)=p^3、
u6=U5(6)=p^3(1-p)(3p+1)、
を使えば、
Ψ=p^3(p^4+6p^2-4p+2)、
となるので、このΨをp^7で割れば、平均日数が、
平均日数=Ψ/p^7=(p^4+6p^2-4p+2)/p^4
と求められるという訳じゃ。
この結果は、たとえば、第90回で再検証した結果とも一致することが確認できるじゃろう」
「たしかに。ちなみに、第90回では、固有方程式の2根の値を求めて、平均日数を計算していたわね」
目次へ戻る
「宿場数=6、すなわち、c=7の場合は、c=2s+1と書いたとき、s=3に相当する。以下、前節のc=5と流れは、同一なので、シンプルに記載していこう。固有方程式は、λを固有値として、
(-λ(λ^6+λ^4(p-1)(5p+1)+2pλ^2(p-1)^2(3p+2)+p^2(p+3)(p-1)^3))=0、となるが、λ<>0として、λ^2=xと変換して、φ(x)=0、と書けば、
φ(x)=x^3+x^2(5p^2-4p-1)+2px(3p^3-4p^2-p+2)+p^2(p^4-6p^2+8p-3)、である。
平均日数の公式から、
であるが、s=3とすれば、
を得るのじゃ」
 「ここで、d1等を求める式は、
「ここで、d1等を求める式は、
において、1番目の式で、s=3と置くことにより、
が得られる。
この中のU7(6)は、7次元の状態ベクトル、Uの7番目の要素U7の日数=6の値を示すのね。以下では、煩雑なので、U7(6)=u6などと置き換える。
また、それらの値は、推移確率行列Aを使って、上の図の2番目の式から決定される。Aは、下図の通り。
U7(6)=u6=p^5、
U7(8)=u8=p^5(1-p)(5p+1)、
U7(10)=u10=p^5(p-1)^2(19p^2+6p+1)、
とね」
「そうじゃな。
ここで、固有方程式を、φ(x)=x^3+a2x^2+a1x+a0、と書いたとき、
φ(x)=x^3+x^2(5p^2-4p-1)+2px(3p^3-4p^2-p+2)+p^2(p^4-6p^2+8p-3)、から。
a0=p^2(p^4-6p^2+8p-3)、
a1=2p(3p^3-4p^2-p+2)、
a2=(5p^2-4p-1)、
である。
一方、3次方程式の根と係数の関係から、
a0=-x1x2x3
a1=(x1x2+x1x3+x2x3)
a2=-(x1+x2+x3)、が成り立つことに注意する。
さて、平均日数の式の分母は、p^(2c-2)=p^12、である。
また、ψ(x1,x2,x3)=Σdk(7-5xk)(1-xk+1)^2(1-xk+2)^2、と書いて
ここで、下添え字kは、3を法として、1から3まで動くものとすれば、
平均日数=ψ/p^11、である。(分子のpと分母のp^12を勘案)
以下、具体的にΨを計算しよう」
「そのためには、d1等に関する3元連立方程式を解いて、
d1=(x2(u6x3-u8)-u8x3+u10)/((x1-x2)(x1-x3))、
d2=(x1(u6x3-u8)-u8x3+u10)/((x1-x2)(x3-x2))、
d3=(x1(u6x2-u8)-u8x2+u10)/((x1-x3)(x2-x3))、
これらをΨの式、
ψ=d1(7-5x1)(1-x2)^2(1-x3)^2+d2(7-5x2)(1-x1)^2(1-x3)^2+d3(7-5x3)(1-x1)^2(1-x2)^2、
に代入して展開すると、少し長くなるんだけど、
Ψ=(-5u6x1^2x2^2x3+7u6x1^2x2^2-5u6x1^2x2x3^2+x1^2x2x3(17u6+5u8)-7x1^2x2(2u6+u8)+7u6x1^2x3^2-7x1^2x3(2u6+u8)+x1^2(7u6+9u8)-5u6x1x2^2x3^2+x1x2^2x3(17u6+5u8)-7x1x2^2(2u6+u8)+x1x2x3^2(17u6+5u8)-x1x2x3(5u10+43u6+24u8)+x1x2(7u10+28u6+23u8)-7x1x3^2(2u6+u8)+x1x3(7u10+28u6+23u8)-x1(9u10+2(7u6+9u8))+7u6x2^2x3^2-7x2^2x3(2u6+u8)+x2^2(7u6+9u8)-7x2x3^2(2u6+u8)+x2x3(7u10+28u6+23u8)-x2(9u10+2(7u6+9u8))+x3^2(7u6+9u8)-x3(9u10+2(7u6+9u8))+11u10+7u6+9u8)、
となる。このあたり、もう、手計算では、大変だと思うよ。
このΨをウエアリングの方法で基本対称式に分解する。
そのために、第93回で定義した、DERIVEのユーザー定義関数、Freset(3)を実行すると、
(vs≔[x1+x2+x3,x1(x2+x3)+x2x3,x1x2x3])が返り、基本対称式の3つの組が明示される。
あとは、前節と同様にユーザー定義関数、Fgを繰り返し実行します。ただし、変数の個数は、3とする。
すると、9回目の実行結果が[9,11u10+7u6+9u8,0]となり、
戻り値のベクトルの第3項目の要素がゼロとなるので、残差がなくなって、完了したことが分かる。
Σ(k=1~9)vg↓k、を計算すれば、Ψの再構築が行われ、
Ψ=(s1^2(7u6+9u8)-7s1s2(2u6+u8)+s1s3(3u6+5u8)-s1(9u10+2(7u6+9u8))+7s2^2u6-5s2s3u6+s2(7u10+14u6+5u8)-s3(5u10+u6+3u8)+11u10+7u6+9u8)
と基本対称式(s1、s2、s3)の多項式として、Ψを表すことができたわ」
「よっしゃ。あとは、s1等やu6等を下の表に従い、pの式で置き換えれば良い。
| 値 | |
| u6 | p^5 |
| u8 | p^5(1-p)(5p+1) |
| u10 | p^5(p-1)^2(19p^2+6p+1) |
| s1 | -(5p^2-4p-1) |
| s2 | 2p(3p^3-4p^2-p+2) |
| s3 | -p^2(p^4-6p^2+8p-3) |
そうすると、
Ψ=p^5(p^6+12p^4-16p^3+16p^2-8p+2)、
となる。平均日数は、これをp^11で除して、
平均日数=(p^6+12p^4-16p^3+16p^2-8p+2)/p^6
これは、第90回の「cが奇数の例2 宿場数=6 (c=7)」で計算した値と一致する。
第90回では、3次方程式を解いて、その根を平均日数の公式に代入し計算したので、実は、かなり苦労したのじゃった」
目次へ戻る
「前節までは、すでに厳密解が得られているケースじゃった。c=9は、まだ、厳密解を得られていないケースじゃな。とは言え、方法は、前節までと同様なので、簡潔に記載しよう。宿場数=8、すなわち、c=9、は、c=2s+1から、s=4のケースとなる。
固有方程式は、λを固有値として、
(-λ(λ^8+λ^6(p-1)(7p+1)+3pλ^4(p-1)^2(5p+2)+10p^2λ^2(p+1)(p-1)^3+p^3(p+4)(p-1)^4))=0、
であるが、λ<>0として、λ^2=xと置き換えた式は、
φ(x)=(x^4+x^3(7p^2-6p-1)+3px^2(5p^3-8p^2+p+2)+10p^2x(p^4-2p^3+2p-1)+p^3(p^5-10p^3+20p^2-15p+4))=0
である。
ここで、平均日数は、
において、s=4と置いて、
と与えられる」
 「ここで、d1等を求める式は、
「ここで、d1等を求める式は、
において、1番目の式で、s=4と置くことにより、
が得られる。
この中のU9(8)は、9次元の状態ベクトル、Uの9番目の要素U9の日数=8の値を示すのね。以下では、煩雑なので、U9(8)=u8などと置き換える。
また、それらの値は、推移確率行列Aを使って、上の図の2番目の式から決定される。Aは、下図の通り。
U9(8)=u8=p^7
U9(10)=u10=p^7(1-p)(7p+1)
U9(12)=u12=p^7(p-1)^2(34p^2+8p+1)
U9(14)=u14=p^7(1-p)^3(143p^3+43p^2+9p+1)
、とね」
「そうじゃな。ここで、固有方程式、φ(x)=x^4+a3x^3+a2x^2+a1x+a0、と書いたとき、
φ(x)=x^4+x^3(7p^2-6p-1)+3px^2(5p^3-8p^2+p+2)+10p^2x(p^4-2p^3+2p-1)+p^3(p^5-10p^3+20p^2-15p+4)=0、
から。
a0=p^3(p^5-10p^3+20p^2-15p+4)、
a1=10p^2(p^4-2p^3+2p-1)、
a2=3p(5p^3-8p^2+p+2)、
a3=(7p^2-6p–1)、
である。
4次方程式の根と係数の関係から、
3次項の係数=a3=-(x1+x2+x3+x4)、
2次項の係数=a2=(x1x2+x1x3+x1x4+x2x3+x2x4+x3x4)、
1次項の係数=a1=-(x1x2x3+x1x2x4+x1x3x4+x2x3x4)、
定数項=a0=(x1x2x3x4)、
が成り立つことに注意する。
さて、平均日数の式の分母は、p^(2c-2)=p^16、である。
また、ψ(x1,x2,x3)=ψ(x1,x2,x3,x4)=Σdk(9-7xk)(1-xk+1)^2(1-xk+2)^2(1-xk+3)^2、
と書いて、下添え字kは、4を法として、1から4まで動くものとすれば、
平均日数=ψ/p^15、である。(分子のpと分母のp^16を勘案)
以下、具体的にΨを計算しよう」
「そのためには、d1等に関する4元連立方程式、
を解いて、
d1=(x2(x3(u10-u8x4)+u10x4-u12)+x3(u10x4-u12)-u12x4+u14)/((x1-x4)(x1-x2)(x1-x3))
d2=(x1(x3(u10-u8x4)+u10x4-u12)+x3(u10x4-u12)-u12x4+u14)/((x4-x2)(x1-x2)(x2-x3))
d3=(x1(x2(u10-u8x4)+u10x4-u12)+x2(u10x4-u12)-u12x4+u14)/((x1-x3)(x2-x3)(x3-x4))
d4=(x1(x2(u8x3-u10)-u10x3+u12)+x2(u12-u10x3)+u12x3-u14)/((x1-x4)(x2-x4)(x3-x4)))
となる。
そこで、これらをΨの式、
ψ=(d1(9-7x1)(1-x2)^2(1-x3)^2(1-x4)^2+d2(9-7x2)(1-x1)^2(1-x3)^2(1-x4)^2+d3(9-7x3)(1-x2)^2(1-x1)^2(1-x4)^2+d4(9-7x4)(1-x2)^2(1-x3)^2(1-x1)^2)、
に代入して展開すると、とっても長くなるんだけど、ごめんなさいね。
Ψ=
(-7u8x1^2x2^2x3^2x4+9u8x1^2x2^2x3^2-7u8x1^2x2^2x3x4^2+x1^2x2^2x3x4(7u10+23u8)-9x1^2x2^2x3(u10+2u8)+9u8x1^2x2^2x4^2-9x1^2x2^2x4(u10+2u8)+x1^2x2^2(11u10+9u8)-7u8x1^2x2x3^2x4^2+x1^2x2x3^2x4(7u10+23u8)-9x1^2x2x3^2(u10+2u8)+x1^2x2x3x4^2(7u10+23u8)-x1^2x2x3x4(32u10+7u12+57u8)+x1^2x2x3(29u10+9(u12+4u8))-9x1^2x2x4^2(u10+2u8)+x1^2x2x4(29u10+9(u12+4u8))-x1^2x2(22u10+11u12+18u8)+9u8x1^2x3^2x4^2-9x1^2x3^2x4(u10+2u8)+x1^2x3^2(11u10+9u8)-9x1^2x3x4^2(u10+2u8)+x1^2x3x4(29u10+9(u12+4u8))-x1^2x3(22u10+11u12+18u8)+x1^2x4^2(11u10+9u8)-x1^2x4(22u10+11u12+18u8)+x1^2(11u10+13u12+9u8)-7u8x1x2^2x3^2x4^2+x1x2^2x3^2x4(7u10+23u8)-9x1x2^2x3^2(u10+2u8)+x1x2^2x3x4^2(7u10+23u8)-x1x2^2x3x4(32u10+7u12+57u8)+x1x2^2x3(29u10+9(u12+4u8))-9x1x2^2x4^2(u10+2u8)+x1x2^2x4(29u10+9(u12+4u8))-x1x2^2(22u10+11u12+18u8)+x1x2x3^2x4^2(7u10+23u8)-x1x2x3^2x4(32u10+7u12+57u8)+x1x2x3^2(29u10+9(u12+4u8))-x1x2x3x4^2(32u10+7u12+57u8)+x1x2x3x4(97u10+41u12+7u14+127u8)-x1x2x3(71u10+40u12+9(u14+8u8))+x1x2x4^2(29u10+9(u12+4u8))-x1x2x4(71u10+40u12+9(u14+8u8))+x1x2(44u10+35u12+11u14+36u8)-9x1x3^2x4^2(u10+2u8)+x1x3^2x4(29u10+9(u12+4u8))-x1x3^2(22u10+11u12+18u8)+x1x3x4^2(29u10+9(u12+4u8))-x1x3x4(71u10+40u12+9(u14+8u8))+x1x3(44u10+35u12+11u14+36u8)-x1x4^2(22u10+11u12+18u8)+x1x4(44u10+35u12+11u14+36u8)-x1(22u10+26u12+13u14+18u8)+9u8x2^2x3^2x4^2-9x2^2x3^2x4(u10+2u8)+x2^2x3^2(11u10+9u8)-9x2^2x3x4^2(u10+2u8)+x2^2x3x4(29u10+9(u12+4u8))-x2^2x3(22u10+11u12+18u8)+x2^2x4^2(11u10+9u8)-x2^2x4(22u10+11u12+18u8)+x2^2(11u10+13u12+9u8)-9x2x3^2x4^2(u10+2u8)+x2x3^2x4(29u10+9(u12+4u8))-x2x3^2(22u10+11u12+18u8)+x2x3x4^2(29u10+9u12+36u8)-x2x3x4(71u10+40u12+9(u14+8u8))+x2x3(44u10+35u12+11u14+36u8)-x2x4^2(22u10+11u12+18u8)+x2x4(44u10+35u12+11u14+36u8)-x2(22u10+26u12+13u14+18u8)+x3^2x4^2(11u10+9u8)-x3^2x4(22u10+11u12+18u8)+x3^2(11u10+13u12+9u8)-x3x4^2(22u10+11u12+18u8)+x3x4(44u10+35u12+11u14+36u8)-x3(22u10+26u12+13u14+18u8)+x4^2(11u10+13u12+9u8)-x4(22u10+26u12+13u14+18u8)+11u10+13u12+3(5u14+3u8))
となる。うんざりでしょ。手計算では、とうてい無理だわ。
このΨをウエアリングの方法で基本対称式に分解する。
そのために、第93回で定義した、DERIVEのユーザー定義関数、Freset(4)を実行すると、
(vs≔[x1+x2+x3+x4,x1(x2+x3+x4)+x2(x3+x4)+x3x4,x1(x2(x3+x4)+x3x4)+x2x3x4,x1x2x3x4])、と基本対称式の4つの組が明示される。
この後、前節と同様に、ユーザー定義関数、Fgを繰り返し、実行します。ただし、変数の個数は、4とする。
すると、14回目でFg関数の実行結果が([14,11u10+13u12+3(5u14+3u8),0])となり、戻り値のベクトルの第3項目の要素がゼロとなるので、完了が分かる。
Σ(k=1~14)vg↓k、を計算すれば、
Ψ=(s1^2(11u10+13u12+9u8)-s1s2(22u10+11u12+18u8)+s1s3(7u10+9(u12+2u8))-s1s4(5u10+7u12+3u8)-s1(22u10+26u12+13u14+18u8)+s2^2(11u10+9u8)-9s2s3(u10+2u8)+s2s4(7u10+5u8)+s2(22u10+9u12+11u14+18u8)+9s3^2u8-7s3s4u8-s3(5u10+7u12+9(u14+2u8))+s4(3u10+5u12+7u14+u8)+11u10+13u12+3(5u14+3u8))
と基本対称式(s1、s2、s3,s4)の多項式として、Ψを表すことができたわ」
「よっしゃ。ここからは、s1等やu8等を以下の表に従って、pの式で置き換えるだけだ。
| 値 | |
| u8 | p^7 |
| u10 | p^7(1-p)(7p+1) |
| u12 | p^7(p-1)^2(34p^2+8p+1) |
| u14 | p^7(1-p)^3(143p^3+43p^2+9p+1) |
| s1=-a3 | -(7p^2-6p-1) |
| s2=a2 | 3p(5p^3-8p^2+p+2) |
| s3=-a1 | -(10p^2(p^4-2p^3+2p-1)) |
| s4=a0 | p^3(p^5-10p^3+20p^2-15p+4) |
そうすると、
Ψ=p^7(p^8+20p^6-40p^5+60p^4-56p^3+34p^2-12p+2)、
となるので、平均日数は、これをp^15で除して、
平均日数=(p^8+20p^6-40p^5+60p^4-56p^3+34p^2-12p+2)/p^8
これは、第88回の「宿場数=8(c=9)の平均日数」で推定した以下の式と一致することが分かる。
平均日数の予想式=(p^8+20p^6-40p^5+60p^4-56p^3+34p^2-12p+2)/p^8、
なお、第88回では、平均日数の関数形に関する仮定の下に数値計算により、9つの係数を決定していたのじゃった」
「これで、c=2~10までの平均日数が計算できたわ。平均日数の計算途中は、複雑になるけど、平均日数のpの関数形は、かなりシンプルなので、漸化式が求められても良さそうだけどね」
「ま、分母は、p^(c-1)、分子の定数項は、2とか、cが違う式の係数間の関係などいろいろ、あるんじゃが、cが増えると、項数が増えるので、それまで得られている式からは、簡単には、見通せない項が現れるのじゃな。
一方、p=1のときは、最短日数なので、平均日数=c、また、p=1/2では、平均日数=c^2、を満たすと考えられるので、係数間に2つの関係式がある。だが、これらを考慮しても、項の少なくとも1つは、係数が不明となるのじゃ。もう少し、考えてみよう。また、次回じゃ」
目次へ戻る
c=宿場数+1としたとき、
平均日数=Ψ/p^(2c-3)、c=2s、s=1、2、・・。と書く。
※cが偶数の場合、以前のΨの定義の2倍を新しいΨとしているのでご注意願います。2020/8/7追記。
下表に、c=2~10までのΨの基本対称式による表現を整理した。
| c | s | 新しいΨの基本対称式による表現 | 備考 |
| 2 | 1 | -2u1s1+2u1 | s1^2はない |
| 3 | 1 | -u2s1+3u2 | s1^2はない |
| 4 | 2 | 4·s1^2·u3-2·s1·s2·u3-4·s1·(2·u3+u5)+2·s2·u5+2·(2·u3+3·u5) | s2^2はない |
| 5 | 2 | 5s1^2u4-3s1s2u4-5s1(2u4+u6)+s2(u4+3u6)+5u4+7u6 | s2^2はない |
| 6 | 3 | 2·s1^2·(3·u5+4·u7)-6·s1·s2·(2·u5+u7)+2·s1·(s3·(u5+2·u7)-6·u5-8·u7-4·u9)+6·s2^2·u5-2·s2·(2·s3·u5-6·u5-2·u7-3·u9)-2·(s3·(u7+2·u9)-3·u5-4·u7-5·u9) | s3^2はない |
| 7 | 3 | s1^2(7u6+9u8)-7s1s2(2u6+u8)+s1s3(3u6+5u8)-s1(9u10+2(7u6+9u8))+7s2^2u6-5s2s3u6+s2(7u10+14u6+5u8)-s3(5u10+u6+3u8)+11u10+7u6+9u8 | s3^2はない |
| 8 | 4 | 2·s1^2·(6·u11+4·u7+5·u9)-2·s1·s2·(5·u11+8·u7+10·u9)+2·s1·s3·(4·u11+8·u7+3·u9)-2·s1·s4·(3·u11+u7+2·u9)-4·s1·(6·u11+3·u13+4·u7+5·u9)+2·s2^2·(4·u7+5·u9)-8·s2·s3·(2·u7+u9)+2·s2·s4·(2·u7+3·u9)+2·s2·(4·u11+5·u13+8·u7+10·u9)+8·s3^2·u7-6·s3·s4·u7-2·s3·(3·u11+4·u13+8·u7+2·u9)+2·s4·(2·u11+3·u13+u9)+2·(6·u11+7·u13+4·u7+5·u9) | s4^2はない |
| 9 | 4 | s1^2(11u10+13u12+9u8)-s1s2(22u10+11u12+18u8)+s1s3(7u10+9(u12+2u8))-s1s4(5u10+7u12+3u8)-s1(22u10+26u12+13u14+18u8)+s2^2(11u10+9u8)-9s2s3(u10+2u8)+s2s4(7u10+5u8)+s2(22u10+9u12+11u14+18u8)+9s3^2u8-7s3s4u8-s3(5u10+7u12+9(u14+2u8))+s4(3u10+5u12+7u14+u8)+11u10+13u12+3(5u14+3u8) | s4^2はない |
| 10 | 5 | 2·s1^2·(6·u11+7·u13+8·u15+5·u9)-2·s1·s2·(12·u11+14·u13+7·u15+10·u9)+2·s1·s3·(12·u11+5·u13+2·(3·u15+5·u9))-2·s1·s4·(3·u11+4·u13+5·(u15+2·u9))+2·s1·s5·(2·u11+3·u13+4·u15+u9)-4·s1·(6·u11+7·u13+8·u15+4·u17+5·u9)+2·s2^2·(6·u11+7·u13+5·u9)-4·s2·s3·(6·u11+3·u13+5·u9)+2·s2·s4·(4·u11+5·(u13+2·u9))-2·s2·s5·(3·u11+2·(2·u13+u9))+2·s2·(12·u11+14·u13+6·u15+7·u17+10·u9)+2·s3^2·(6·u11+5·u9)-10·s3·s4·(u11+2·u9)+2·s3·s5·(4·u11+3·u9)-2·s3·(12·u11+4·u13+5·u15+2·(3·u17+5·u9))+10·s4^2·u9-8·s4·s5·u9+2·s4·(2·u11+3·u13+4·u15+5·(u17+2·u9))-2·s5·(u11+2·u13+3·u15+4·u17)+2·(6·u11+7·u13+8·u15+9·u17+5·u9) | s5^2はない |
※ 上の表で、u1、u2等は、下図のUc(k)をukと略記したもの。
ここで、c=偶数のとき、k=2m+2s-1、奇数の時、k=2m+2s、
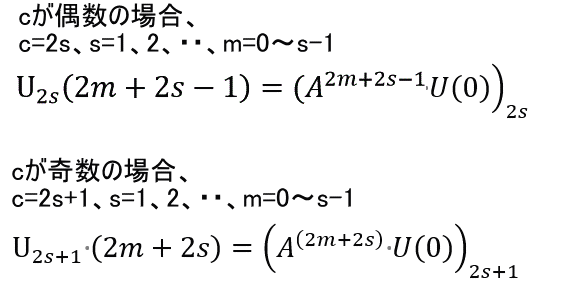
ただし、U(0)は、c次元の状態ベクトル、Uの初期値で、[1,0,0,・・・0](の転置)
目次へ戻る
cの偶奇に関わらず、平均日数=Ψ/p^(2c-3)、c=2s、s=1、2、・・。と書いたとき、
分子の対称式Ψ(x1,x2,・・,xs)について、基本対称式をsi(i=1~s)としたとき、前節の計算例から、
Φ(予想)=Σ(i=1~s-1)(α(i)×si^2)+2×Σ(i=1~s-1、j=i+1~s)(β(i,j)×si×sj)+Σ(i=1~s)(γ(i)×si)+δ、
である。
※ Φの式の赤字部分の記号等を変更しました。2020/8/7追記
目次へ戻る
Φの係数を求める際は、xiが固有方程式の根であることは、忘れて、任意の数の組を与え、ΦとΨの双方で計算を行って決定すれば良い。たとえば、定数項、δは、Ψ(すべてのxi⇒0)=Φ(すべてのsi⇒0)の関係から決定できる。
α、β、γについては、適切な値のxiの組を与えて計算した結果から、連立方程式を解いて決定できる。
また、x1等に関する2階の偏微分と適切なxiの与え方により現れる変数の数を低下させる工夫をしたい。2020/8/7追記
付け加えれば、予想が正しければ、目標である五十三次のc=54においては、Ψが27次27変数の対称式となるが、それを基本対称式に変換するのは、非常な困難が伴うと想像される。それと比較すれば、今回の予想に基づく係数の決定は、はるかに容易だと思われる。今後、あらためて、この予想の真偽とその帰結について、再考することにしたい。
目次へ戻る
作成日:2020/7/24
語句を一部修正2020/7/25
第3章を追記2020/8/1
第3章のΨの定義及び予想式の記法等を変更2020/8/7