数式処理ソフト DERIVE(デライブ) de ドライブ
88.マルコフ過程(1)(非対称型道中双六:宿場数=3~9)
目次
はじめに
(1)推移確率行列
非対称型道中双六と対称型道中双六
マルコフ過程
推移確率行列
宿場数=1(c=2)の平均日数
(2)宿場数=2(c=3)の平均日数
初期状態ベクトル、推移確率行列 A
固有値
固有ベクトル
変換行列 R
平均日数
(3)宿場数=3(c=4)の平均日数
初期状態ベクトル、推移確率行列 A
固有値
固有ベクトル
変換行列 R
平均日数
平均日数の式の確認
(4)宿場数=4及び5の平均日数(予想)
宿場数=4 (c=5)の平均日数
宿場数=5 (c=6)の平均日数
(5)宿場数=6~9の平均日数(予想) 2018/4/6追記
宿場数=6(c=7)の平均日数
宿場数=7(c=8)の平均日数
宿場数=8(c=9)の平均日数
宿場数=9(c=10)の平均日数
(6)宿場数=1~9(c=2~10)の平均日数(まとめ) 2018/4/6追記
はじめに
「第87回『道中双六の問題(補筆3)(今後の課題)』の末尾で、『マルコフ過程』について、今後、勉強することを『課題5』として挙げました。
そこで、今回、『確率過程超!入門』(松原 望 著:東京図書:2011年10月第1刷)を入手して、(少し)勉強してみました。

これにより、同書に記載の『推移確率行列』の考え方を使って、以下に述べましたように、『非対称型道中双六』の宿場数=3の場合の平均日数の厳密解を求めることができました。
得られた結果は、平均日数=(4p^2-2p+2)/p^3、となりました。
従来は、平均日数に関する確率 pに関して閉じた関数形を求めることができず、2m+4 日目に上がる確率を f(2m+4) とするとき、mをm=0~の整数として、
f(2m+4)=(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))、
ただし、A、B、Cは、0以上の整数、は、得られていましたので、
平均日数=Σ(m=0~n)(2m+4)f(2m+4)、n⇒大 として、数値計算で求めていたものです。
また、宿場数=4並びに5の場合も、宿場数=1~3までの結果と数値計算を併せて検討したところ、これらの平均日数の厳密解(の予想式)を得ましたので、それらも記載しました。
なお、今回述べた方法だけでは、五十三次(宿場数=53)のように大きい宿場数の場合の一般解を得ることは、難しいと思われますが、以前に考えていたよりも、平均日数の関数形が簡単な可能性が高くなったことにより、今後、より広い範囲で厳密解が求められるのではないかと考えています。
※宿場数=6~9について、予想式を追加しました。(2018/4/6 追記)
目次へ戻る
(1)推移確率行列
非対称型道中双六と対称型道中双六
「これまで、何回も説明してきたので、読者の方がいい加減うんざりされるじゃろう。
ここでは、必要なことだけをごく簡単に説明しよう。
詳しくお知りになりたい方は、第87回の『道中双六の問題の概要』などをご覧ください。
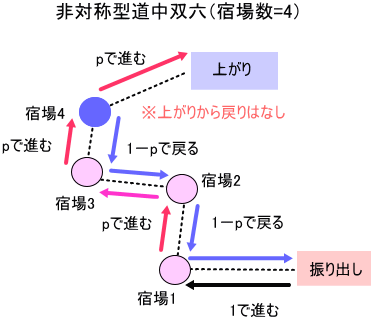
1.駒は、振り出しから、確率1で、1番目の宿場に進むことができる。
2.駒は、各宿場で、確率 pで、次の宿場に進み、確率 (1-p)で1つ戻るものとする。
3.駒が最後の宿場から上がりに進んだときは、双六上から消える。(上がりから戻ることはない)
4.駒どおしの関係は、無いものとする。
5.振り出しから宿場まで、各宿場間、最後の宿場と上がりまでの所要時間は、同一とし、1(日)と勘定する。
というルールに従って、駒を進めるとき、平均何日で上がれるかという問題じゃ」
 「えーと、読者の方に、わたしから説明するけど、
「えーと、読者の方に、わたしから説明するけど、
おじぃさんが『非対称型道中双六の問題』と、わざわざ、『非対称型』と断っている訳はね、
前回で『対称型道中双六』について、今後の課題としてあげたからなの。
ちなみに、対称型というのは、こんな感じね。
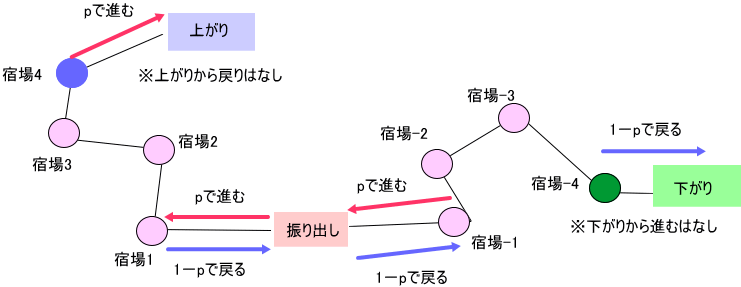
どこが違うかっていうと、対称型でも駒は、振り出しからスタートするけど、上がり方向だけでなく、下がり方向にも戻ることができるのね。
それと、非対称型では、振り出しから進む確率は、1だったんだけど、対称型では、進む確率は、p、戻る確率は、1-p、というように振り出しが普通の宿場と同じになっている点が違うのよ」
「お銀さんかい。
上掲の本のおかげで、ようやく、胸のつかえがとれましたな。
宿場数=3の場合の平均日数(の厳密解)が分かりましたぞ」
目次へ戻る
マルコフ過程
 「あんたは、水戸黄門かいな。
「あんたは、水戸黄門かいな。
それより、マルコフ過程の『マルコフ』というのは、人の名前かしら?」
「おお、ともちゃんかい。
マルコフ過程のマルコフとは、ロシアの数学者、アンドレイ・マルコフ氏(1856年~1922年)のことじゃ。
同氏の生涯・業績のあらましは、ウィキペディアを参照して欲しい。
上掲の本に書かれているように、
『マルコフ過程』とは、現在のシステムの状態が一つ前の時刻(連続時間では、微少時間前)における状態にのみ陽に依存する場合のシステムの推移(遷移)を(調べることを)指すようじゃ。
なお、時間がとびとび(離散的)の場合を特に『マルコフ連鎖』とも言う。
ただし、広い意味では、1つ前だけでなく、それ以前の状態にも陽に依存するケースも含めることがあるそうじゃが、ここでは、狭い意味のマルコフ過程を考えていこう」
「その、システムの状態というのは、道中双六で言うと、何を指すのかしら?」
「道中双六の問題で、差分方程式を立てたことがあったのを覚えておるじゃろう。
それを振り出しの位置をゼロからではなく1から数えることにして、振り出しを1とし、最後の宿場をc、上がりをc+1、とする。
ここで、c=宿場数+1、である。
例えば、宿場数が4の場合(c=5)では、振り出しを1、最初の宿場を2、最後の宿場を5、上がりを6とする。
さて、一般に、日数をtで表し、t日経過後の各位置にいる駒の確率密度をf(j,t)とすると、t=0、1、2、・・に対して、
(1) f(1,0)=1、初期条件
(2) f(1,t)=(1-p)×f(2,t-1)、振り出し
(3) f(2,t)=f(1,t-1)、最初の宿場
(4) f(c,,t)=p×f(c-1,t-1)、最後の宿場、
(5) f(c+1,,t)=p×f(c,t-1)、上がり、
(6) f(j,t)=(1-p)×f(j+1,t-1)+p×f(j-1,t-1)、j= 2~c-2の宿場、
が成立している。
ただし、
宿場数が1(c=2)では、最初の宿場が最後の宿場であるため、(4)及び(6)を使わない、
宿場数が2(c=3)では、(6)を使わないことに注意するようにな」
「DERIVEで平均日数を計算する関数を作るときには、こんな図を書いて、調べたわね。
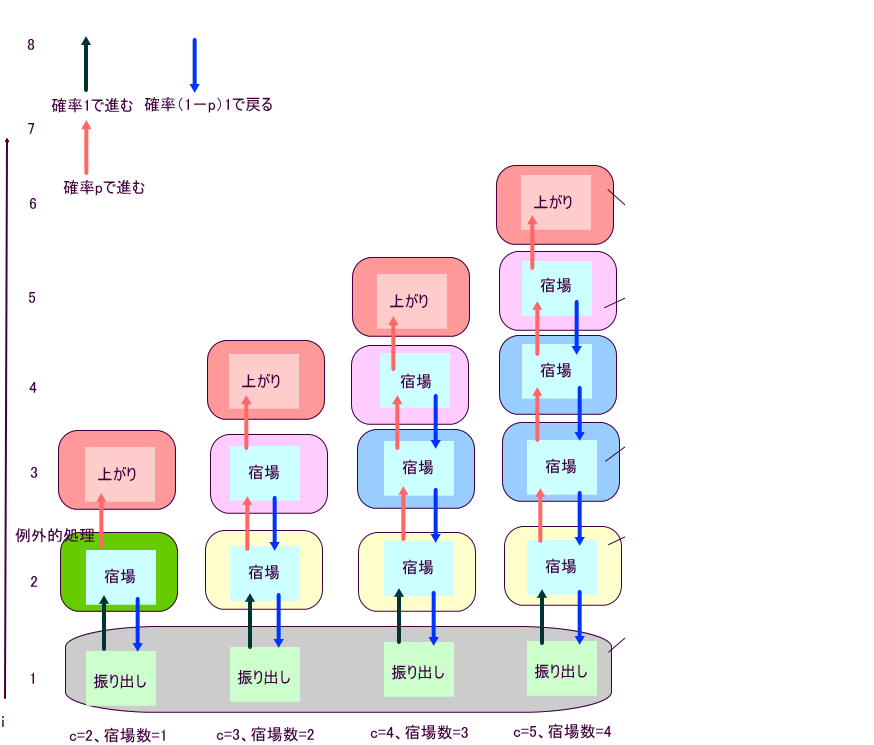
上の図は、第85回の『道中双六の問題(補筆2)』に表れたもので、余分な説明を省いたものよ」
「そうじゃったな。
今回は、確率密度関数を次のようなベクトルで表す。
初期状態 t=0、
U0=[f(1,0),f(2,0),f(3,0),f(4,0),f(5,0)]、これは、c=4、宿場数が3の例、
一般には、U0=[f(1,0),f(2,0),f(3,0),f(4,0),f(5,0),・・・,f(c,0),f(c+1,0)]、
一方、t=m日後の状態は、
Um=[f(1,m),f(2,m),f(3,m),f(4,m),f(5,m)]、これは、c=4、宿場数が3の例、
一般には、Um=[f(1,m),f(2,m),f(3,m),f(4,m),f(5,m),・・・,f(c,m),f(c+1,m)]、
などと書くことにしよう」
「なるほど。
ベクトルと行列を使おうという訳ね」
目次へ戻る
推移確率行列
「その通りじゃ。
U0から1日後の状態は、宿場数が3(c=4)の例でどうなるか考えてみよう。
なお、状態を表すベクトルは、上の例では、横ベクトルとしているが、左から行列を掛ける普通の記法に合わせると本来は縦ベクトルする必要がある。
しかし、HP上では、縦ベクトルを書きにくいので、横ベクトルのように書いている。
すると、
0日後では、U0=[1,0,0,0,,0]、初期状態
1日後では、U1=[0,1,0,0,,0]、
2日後では、U2=[1-p,0,p,0,,0]、
3日後では、U3=[0,(1-p)^2,0,p^2,,0]、
4日後では、U4=[(p - 1)(p^2 - 1), 0, - p(2p^2 - p - 1), 0, p^3]、最初の上がりの日、
などとなる。
ここで使われているのが、推移確率行列 A じゃ。
U1=A×U0、などと計算する。
Aは、DERIVE画面では、こんなかんじじゃな。
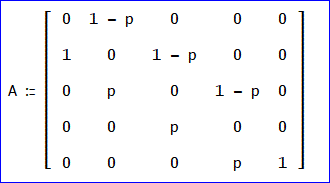
行列の要素をA(i,j)で表し、状態ベクトルをU、要素をU(k)、k=1~c+1、で表すとき、
A*Uのk番目の要素は、
Σ(j=1~c+1)A(k,j)×U(j)、であることは、行列×ベクトルの計算の基本じゃ。
上で掲げた推移確率ベクトルは、これを見ると、
j 列目の要素から i 行目の要素に至る確率とする必要がある。
A(2,1)=1、
1番目(振り出し)から2番目(最初の宿場)には、確率1で進む、
A(j,j+1)=1-p、j=1~c-1、
j+1番目からj番目には、1-pで戻る
A(j+2,j+1)=p、j=1~c、
j+1番目からj+2番目には、pで進む
A(c+1,c+1)=1、
c+1番目の要素は、以前の値を保持(してそれに加算する)。
わかりやすく説明を加えると、次のような図解となる」
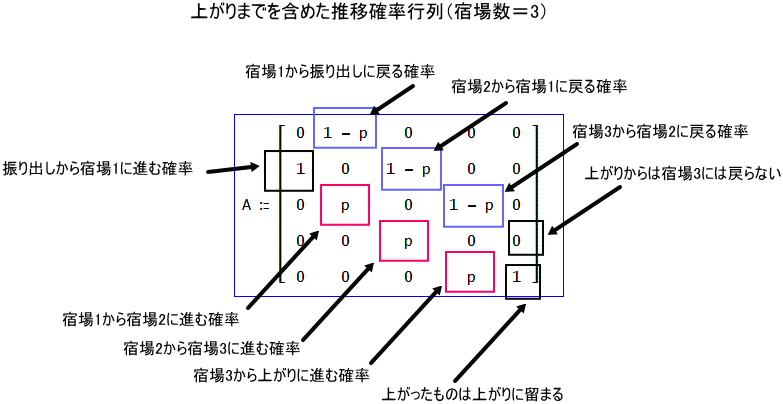
 「すると、2m+4日後の状態は、mを0以上の整数として、
「すると、2m+4日後の状態は、mを0以上の整数として、
A^(2m+4)×U0 で与えられるということね。
でも、Aは、行列よね。
そのべき乗の計算は、面倒でしょ?」
「さすがは、ともちゃん。
まさに、一を聞いて十を知る女子じゃな。
そこで、行列の固有値と対角化を使おうということじゃ。
なお、一つご注意を。
上の状態では、ベクトルの要素の和が常に1となっているが、上がりを状態ベクトルのc+1個目の要素としているためじゃ。
たとえば、宿場数が3の場合では、c=4であり、上の説明では、状態ベクトルと行列の次元は、c+1=5となる。
しかし、今回のテーマである平均値等の計算では、最後の宿場までであればよい。
これは、上がりの一つ手前の要素にpを乗じたものが2m+4日後に上がる勘定となることから、
3日後の最後の要素の値(p^2)にpを乗じて、p^3を作れば、これが最初に、上がりに加算される量となる。
従って、平均日数=Σ(2m+4)×p×(2m+3日後の状態ベクトルの最後の要素)、で計算できる。
すなわち、ベクトルと行列の次元は、c=4でいいことになる。
上の図解を使えば、次のようになる。
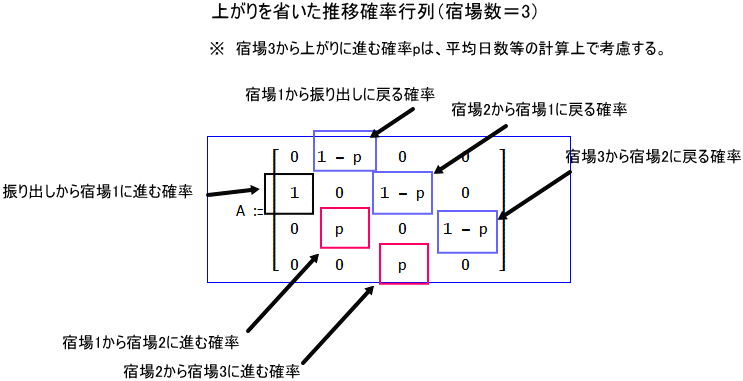
次節で、宿場数1の場合で具体的に説明しよう」
目次へ戻る
宿場数=1(c=2)の平均日数
「前節の最後の注意によれば、状態ベクトルは、2次元で、[振り出し,宿場]、
すなわち、初期状態ベクトル U0=[1,0]となる。
では、ともちゃん、推移確率行列 A は、どうなるかな」
 「宿場数が1の場合は、平均日数が2/p となった例ね。
「宿場数が1の場合は、平均日数が2/p となった例ね。
ちなみに、上がるまでの日数は、2m+2、m=0~の整数、が必要。
さて、推移確率行列をAと書けば、

となるわ」
「では、推移確率行列 Aの固有値と固有ベクトルを求めて欲しい」
「行列の固有値と固有ベクトルについては、第63回『再帰関数(2)(数列の母関数、固有値のべき乗法)』で取り上げたことがある。
固有値は、数式処理ソフト DERIVEでは、
EIGENVALUES(行列,(変数名))で求めることができる。(変数名は、省略可)
また、固有ベクトルは、
EXACT_EIGENVECTOR(行列,厳密な固有値)で縦ベクトルとして、求めることができる。
今回の固有値は、EIGENVALUES(A))により、([√(1 - p), - √(1- p)])の2つであることが分かる。
一つ目の固有ベクトルは、EXACT_EIGENVECTOR(A, √(1 - p))から、
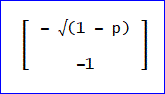
と求められた。
2つめも同様に、EXACT_EIGENVECTOR(A, -√(1 - p))から、
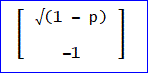
と求められる」
「2つの固有ベクトルから、推移確率行列 Aを対角化する変換行列をRと書くとき、対角化された行列をBとすると、
B=R^(-1) ×A×R、と求められる。(R^(-1) は、Rの逆行列)
この変換行列Rは、固有ベクトルを並べれば、得られるが、ベクトル同士を結合する必要がある。
そのために、DERIVEでは、ファイルメニューから、ユーティリティファイルを読み込む必要がある。
Program Files (x86)\TI Education\Derive 6\Math\VectorMatrixFunctions.mth、
これにより、APPEND(ベクトル,ベクトル,・・)でベクトルを結合できる。
※APPEND関数は、DOS版でも同様の機能を持つ関数があるが名称が変わったので注意。
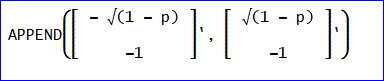
ただし、元になっている固有ベクトルの表示が縦ベクトルなので、転置(右上のアポストロフィ)により横ベクトルに変換している。
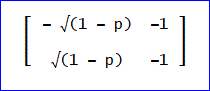
こうして得られた行列を再度、転置すると、下図のRが得られる。
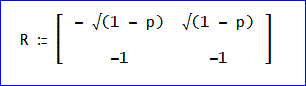
では、これが変換行列になっていることを確かめてご覧」
「Rの逆行列は、R^(-1)なので、
R^(-1)×A×Rを作ると、
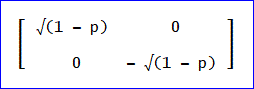
となって、確かに、対角化されていることが分かるわ」
「これで準備が整ったな。
まず、対角化された行列 Bの(2m+2-1)=(2m+1)乗を求める。
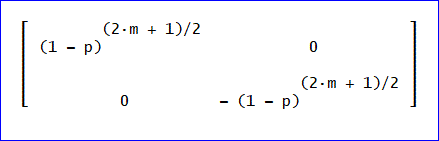
これが、B^(2m+1)、だな。
次に、R×B^(2m+1)×R^-1、を作る。
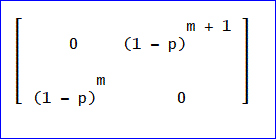
最後に、[1,0]’を右から掛けると、(初期状態ベクトルU0を転置して縦ベクトルとしている)

これは、[振り出し,宿場]なので、最後の要素は、確率pで上がりに進む。
そこで、最後の要素を取り出して、p×(2m+2)を掛けて、m=0~nまで加えると、平均日数が得られる。
平均日数=Σ(m=0~n)(2m+2)×p×(1-p)^m、
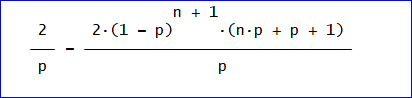
ここで、n→∞とすれば、
平均日数=2/p、の式が得られるという訳じゃ」
「なるほど。
これまでの回では、極限をとる前の式は、
平均日数=2/p - 2(1 - p)^(n + 1)(np + p + 1)/p 、だったので、
上の結果との差し引きすると、下図のようにゼロになるため同じ結果であることが分かった」
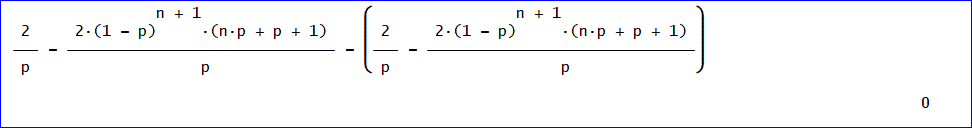
「DERIVEを使う際、2つほど注意するところがある。
変数 pの範囲を0<p<1、
変数mの範囲を正の整数とする。
これは、「入力」メニューから変数の変域から行う。
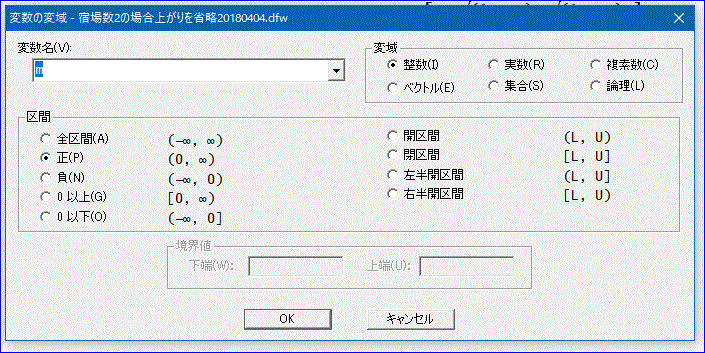
上の図は、mを正の整数としているところじゃ。
さて、次節では、宿場数が2の場合を計算してみよう」
※ 上記のように、n次正則行列を対角化可能なのは、一次独立なn個の固有ベクトルが得られる場合です。(2018/4/9 追記)
目次へ戻る
(2)宿場数=2 (c=3)の平均日数
前節と基本的な内容は同じなので、項目毎に結果のみを示すことにします。
初期状態ベクトル、推移確率行列 A
初期状態ベクトルは、3次元なので、[振り出し,宿場1,宿場2]、となり、
転置をつけた状態で、U0=([1, 0, 0]`)、と表せます。
推移確率行列 A は、上がりを省略した状態では、3次行列となり、
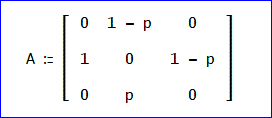
となりました。
目次へ戻る
固有値
Aの固有値は、3つあり、
([0, √((p + 1)(1 - p)), - √((p + 1)(1 - p))])、でした。

目次へ戻る
固有ベクトル
3つの固有値に対応した固有ベクトルは、次の通りです。
ゼロに対しては、
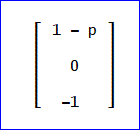
残りの2つに対しては、
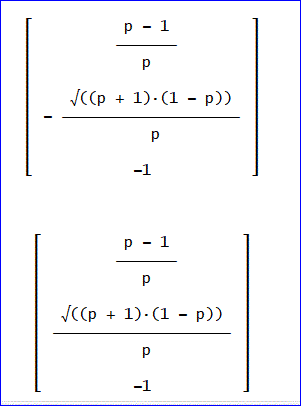
が得られました。
目次へ戻る
変換行列 R
B=R^-1 ×A×R、ここで、Bは、対角化された推移行列とする変換行列は、
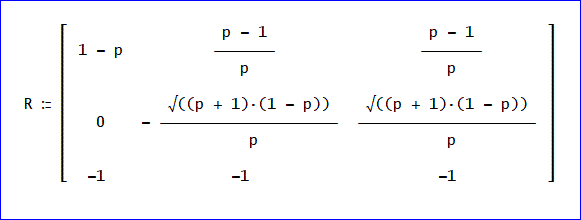
と求められました。
確認のため、R^-1 ×A×R を計算すると、
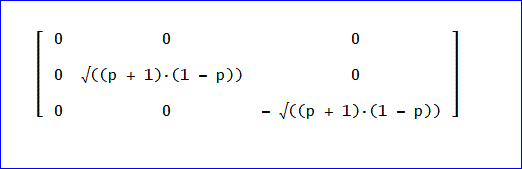
と確かに対角化されていることが分かります。
目次へ戻る
平均日数
平均日数=Σ(m=0~n)(2m+3)×p×((R×B^(2m+2)×R^(-1))×U0の最後の要素)、
上の式で、宿場数1の例と比較して、2m+1 → 2m+2、2m+2→ 2m+3、と変わっていることに注意してください。
まず、B^(2m+2)は、
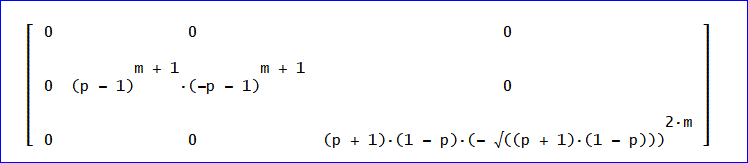
となる。
((R×B^(2m+2)×R^(-1))×U0の最後の要素は、
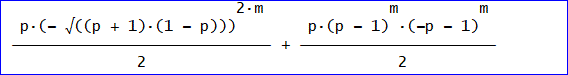
となるので、
平均日数=∑(p^2(2m + 3)(- √((p + 1)(1 - p)))^(2m)/2 + p^2(p - 1)^m(2m + 3)(-p
- 1)^m/2、
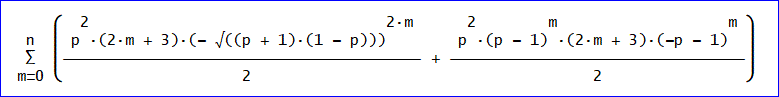
これは、(- (2np^2 + 3p^2 + 2)((p + 1)(1 - p))^(n + 1)/p^2)、であり、
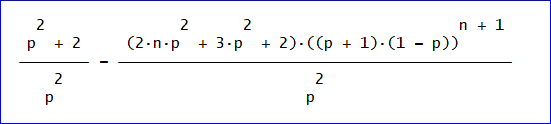
最後に、n→∞とすれば、
平均日数=1+2/p^2、が得られました。
これは、以前に求めていた平均日数の式と等しいことが分かります。
目次へ戻る
(3)宿場数=3 (c=4)の平均日数
宿場数が3(c=4)の場合の平均日数は、これまで、pに関し閉じた表式が得られていなかったものです。
この節では、前節の宿場数=2に準じた形で、結果のみを記載します。
初期状態ベクトル、推移確率行列 A
状態ベクトルは、[振り出し,宿場1,宿場2,宿場3]までで4次元です。
U0=([1, 0, 0, 0]`)、ただし、転置をつけて縦ベクトルとしています。
また、推移確率行列 Aは、
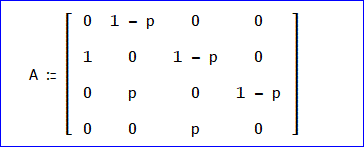
と4次行列となります。
目次へ戻る
固有値
推移確率行列 Aの固有値は、次の通りです。
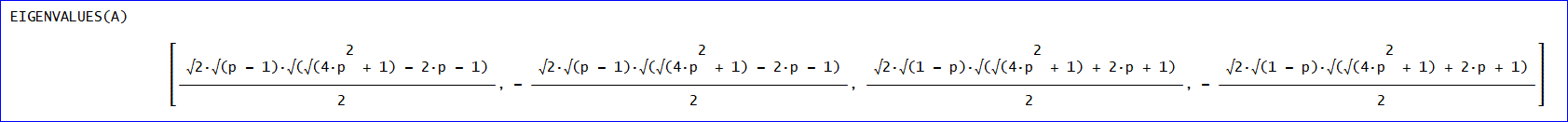
([√2√(p - 1)√(√(4p^2 + 1) - 2p - 1)/2, - √2√(p - 1)√(√(4p^2 + 1) - 2p
- 1)/2, √2√(1 - p)√(√(4p^2 + 1) + 2p + 1)/2, - √2√(1 - p)√(√(4p^2 + 1)
+ 2p + 1)/2])
目次へ戻る
固有ベクトル
4つの固有ベクトルは、次の通りです。
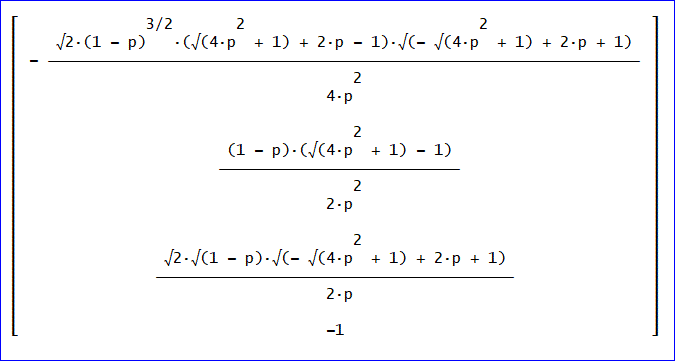

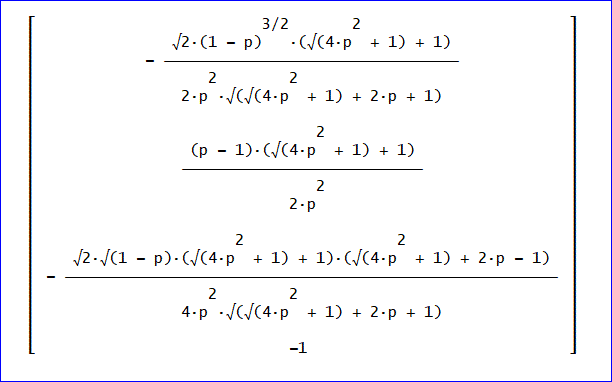
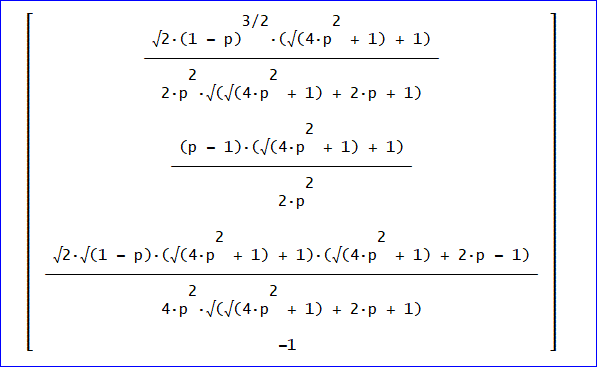
変換行列 R
B=R^-1 ×A×R、ここで、Bは、対角化された推移行列とする変換行列 R は、
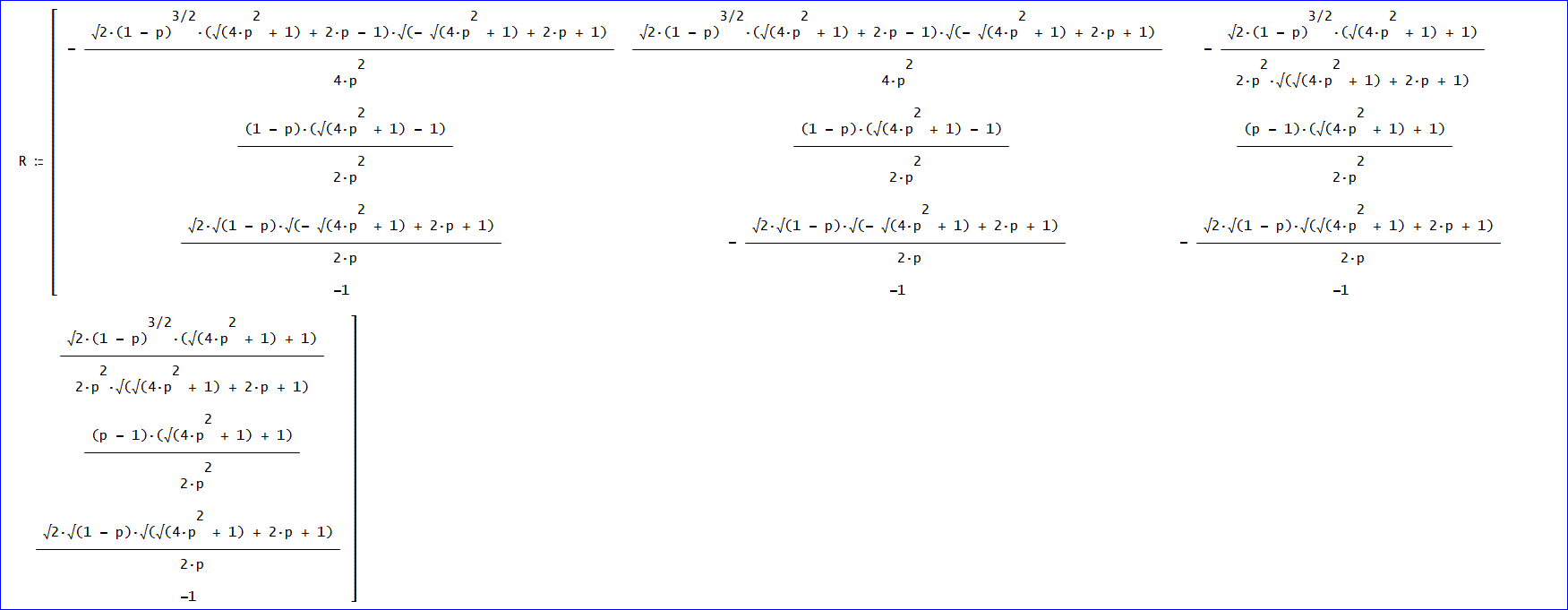
また、対角化された行列、B、を下図に示します。

目次へ戻る
平均日数
平均日数=Σ(m=0~n)(2m+4)×p×((R×B^(2m+3)×R^(-1))×U0の最後の要素)、
まず、B^(2m+3)は、対角化されたBの対角項を(2m+3)乗したものです。
(R×B^(2m+4)×R^(-1))×U0の最後の要素は、
(p^2(1 - p)^M((√(4p^2 + 1) + 2p + 1)/2)^(M + 1)/√(4p^2 + 1) - p^2(1 -
p)^M(- (√(4p^2 + 1) - 2p - 1)/2)^(M + 1)/√(4p^2 + 1))、
※いくつかの式では、mの代わりにMと表示されていますが、同じものです。
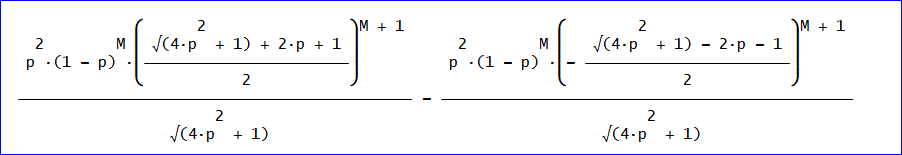
上の式に p×(2m+4)を乗じて、m=0~nまで加えると、
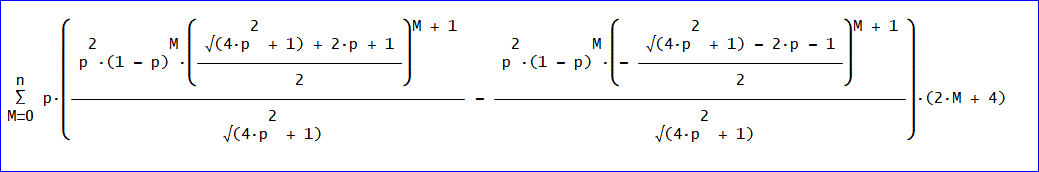

ここで、n→∞の極限をとると、
平均日数=2(2p^2 - p + 1)/p^3、が得られました。
目次へ戻る
平均日数の式の確認
宿場数=3の場合の平均日数は、p=1の場合の 4、p=1/2の場合の4^2=16を除くと、
pの他の点での平均日数は、数値計算に頼っていました。そこで、両者を比較してみました。
今回の厳密解 平均日数=2(2p^2 - p + 1)/p^3、を基にp=0.1~1まで、0.1刻みで計算した結果は、次の通りです。
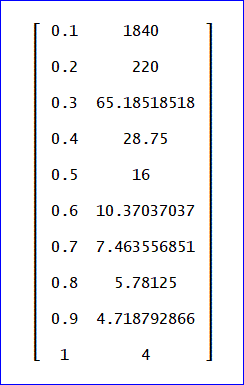
一方、Excelで計算した値は、次の通り。(第84回『道中双六の問題(補筆1)』)
| p |
Excelで計算した平均日数 |
確率の和(Excelの計算) |
| 0.1 |
1,837.5580 |
0.999866 |
| 0.2 |
220.0000 |
1 |
| 0.3 |
65.1851 |
1 |
| 0.4 |
28.7500 |
1 |
| 0.5 |
16.0000 |
1 |
| 0.6 |
10.3703 |
1 |
| 0.7 |
7.4635 |
1 |
| 0.8 |
5.7812 |
1 |
| 0.9 |
4.7187 |
1 |
これを比較すると、p=0.1の場合を除き、両者の一致は、良好です。
唯一、一致しないp=0.1では、今回の計算式では、1840、となったのに対して、Excelの計算では、1837.558、となっていました。
しかし、Excelの16000列余りのセルを駆使した計算でも、足し合わせた項の確率の和は、0.999866 と1より小さいため、平均日数は、このときの
1837よりも大きいものと思われ、今回の計算式で得られた、1840の方がより正確な値であると考えられます。
目次へ戻る
(4)宿場数=4及び5の平均日数(予想)
宿場数が4以上になると、状態ベクトルと推移確率行列の次元が5以上となります。
固有方程式が5次以上になると固有値等の厳密解が一般には求められません。
もちろん、具体的なpの数値を元にして、固有値等を数値的に求めて平均日数を計算することは、可能ですが、それでは、厳密解を得ることは、できません。
そのため、以下では、これまでに得られた平均日数の式を観察して、過去の数値計算と併せて、平均日数の厳密解を予想しました。
※ なお、少なくとも、宿場数4及び5については、複雑な式にはなりますが、固有値は、厳密に求められます。
※ その後、c=4~7について、p=0.1の場合の値を前節までの方法で数値的に計算しました。
計算値と予想式のp=0.1 における値との一致は、極めて良好でした。
しかし、c=8~10では、推移確率行列を対角化するための一次独立な固有ベクトルがc個未満となり、対角化できません。
そのため、前節までの方法でp=0.1の場合の数値計算を実行して比較することができませんでした。(2018/4/9追記)
宿場数=4 (c=5)の平均日数
これまでのところ、平均日数の厳密解は、
宿場数1、c=2 の場合が、2/p、
宿場数2、c=3 の場合が、1+2/p^2、
宿場数3、c=3 の場合が、(4p^2-2p+2)/p^3、でした。
宿場数4、c=4 の場合が、 ?、
これを元に宿場数が4の場合の厳密解を次のように予想しました。
※以下の式中のcは、未知のパラメーターの一つであり、宿場数+1のcではありません。
平均日数=(ap^4 + bp^3 + cp^2 + dp + e)/p^4、と予想します。
Excelで宿場数が4の場合をシミュレートした結果とともに以下のようにDERIVEの行列を作成しました。

行列は、1行目が、確率 p と 推定式、
2行目以降は、[pの値,計算値]となります。(2行目以降の順番は、不定です)
2行目以降のデータの数は、予想式に含まれる未知パラメーター、a、b、c、d、e の総数である5以上が必要です。
今回は、上記のように9個のデータを使用しました。
DERIVEでは、これらのデータから最小2乗法で予想式の未知パラメーターを計算することができます。
そのためには、FIT(行列)、を計算をします。
結果は、次の通りでした。
2.514695037·10^(-7)/p + 6/p^2 - 4/p^3 + 2/p^4 + 0.9999999197、
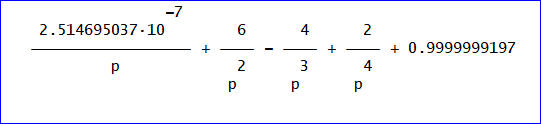
そこで、上記の結果から、宿場数4の場合の平均日数を次のように推定しました。
平均日数(予想)=(p^4 + 6p^2 - 4p + 2)/p^4、
また、予想式を基にp=0.1~1まで数値計算したところ、下記を得ました。
p=0.1, 1.6601·10^4、
p= 0.2, 901、
p= 0.3, 166.4320987、
p=0.4, 54.125、
p= 0.5, 25、
p=0.6, 14.58024691、
p=0.7, 9.912952936、
p=0.8, 7.4453125、
p=0.9, 5.968754762、
p=1, 5、
数値計算との一致は、調べた範囲では、良好です。
目次へ戻る
宿場数=5 (c=6)の平均日数
これまでのところ、平均日数の厳密解と予想式は、
宿場数1、c=2 の場合が、2/p、
宿場数2、c=3 の場合が、1+2/p^2、
宿場数3、c=3 の場合が、(4p^2-2p+2)/p^3、
宿場数4、c=4 の場合が、(p^4 + 6p^2 - 4p + 2)/p^4、(予想)、
となりました。
前節と同様に、宿場数=5の場合の平均日数を表す式を次のように予想しました。
(ap^5 + bp^4 + cp^3 + dp^2 + ep + f)/p^5、(p^6をp^5に修正:2018/4/6)
※以下の式中のcは、未知のパラメーターの一つであり、宿場数+1のcではありません。
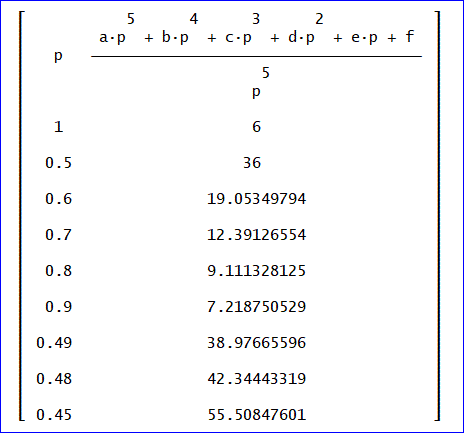
データの個数は、9個です。
未知パラメーターの個数は、6個と1つ増えています。
9組のデータを使って、FIT関数により得た予想式は、次の通りでした。(図を2つ差し替えました。:2018/4/6)
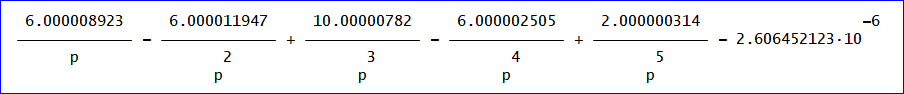
これを元に宿場数が5の場合の平均日数の厳密解を次のように予想しました。
平均日数=2(3p^4 - 3p^3 + 5p^2 - 3p + 1)/p^5、(本式は、変更ありません:2018/4/6)
また、上の予想式を基に平均日数をp=0.1~1まで0.1刻みで計算したものは、次の通りです。
p=0.1, 1.4946·10^5、
p=0.2, 3630、
p=0.3, 406.0082304、
p=0.4, 94.6875、
p=0.5, 36、
p=0.6, 19.05349794、
p=0.7, 12.39126554、
p=0.8, 9.111328125、
p=0.9, 7.218750529、
p=1, 6、
数値計算の結果は、良好です。
目次へ戻る
(5)宿場数=6~9の平均日数(予想) 2018/4/6追記
(4)節の結果を元に更に、計算を進めて、宿場数=6~9(c=7~10)に対する平均日数の予想式を計算しました。
方法は、前節と同様ですが、数値データは、DERIVEで計算させたものです。
宿場数=6(c=7)の平均日数
簡単のために、説明を省略して、予想式とデータのセット、最小2乗法による予想式とそれを書き改めたものを下記に示します。

※予想式の未知パラメーターにfの次にrが出ていますが、g、h、が別の用途で使用中のためです。
他意はありません。以下同様です。
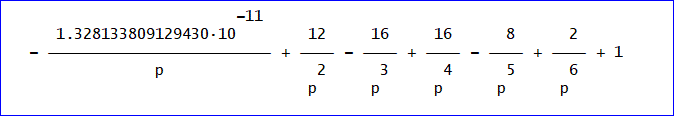
平均日数=(p^6 + 12p^4 - 16p^3 + 16p^2 - 8p + 2)/p^6、(予想式)
予想式を基にした計算値
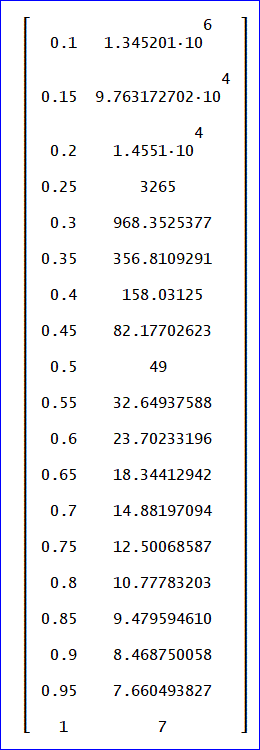
下記は、計算したデータです。
([0.1, 1.345201·10^6; 0.15, 9.763172702·10^4; 0.2, 1.4551·10^4; 0.25,
3265; 0.3, 968.3525377; 0.35, 356.8109291; 0.4, 158.03125; 0.45, 82.17702623;
0.5, 49; 0.55, 32.64937588; 0.6, 23.70233196; 0.65, 18.34412942; 0.7, 14.88197094;
0.75, 12.50068587; 0.8, 10.77783203; 0.85, 9.479594610; 0.9, 8.468750058;
0.95, 7.660493827; 1, 7])
目次へ戻る
宿場数=7(c=8)の平均日数
結果だけを示します。

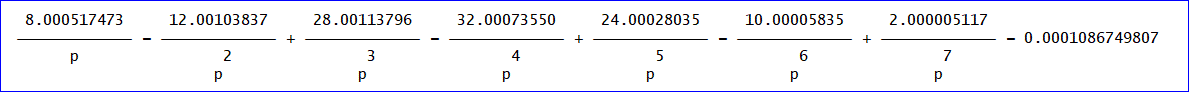
平均日数=2(4p^6 - 6p^5 + 14p^4 - 16p^3 + 12p^2 - 5p + 1)/p^7、(予想式)
予想式を基にした平均日数の計算値は、次の通りです。
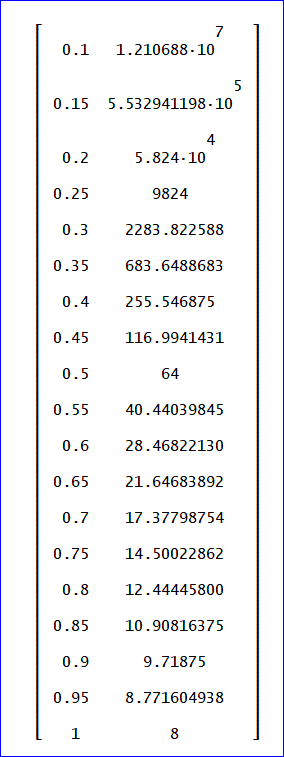
([0.1, 1.210688·10^7; 0.15, 5.532941198·10^5; 0.2, 5.824·10^4; 0.25, 9824;
0.3, 2283.822588; 0.35, 683.6488683; 0.4, 255.546875; 0.45, 116.9941431;
0.5, 64; 0.55, 40.44039845; 0.6, 28.46822130; 0.65, 21.64683892; 0.7, 17.37798754;
0.75, 14.50022862; 0.8, 12.44445800; 0.85, 10.90816375; 0.9, 9.71875; 0.95,
8.771604938; 1, 8])
目次へ戻る
宿場数=8(c=9)の平均日数
結果だけを示します。


平均日数=(p^8 + 20p^6 - 40p^5 + 60p^4 - 56p^3 + 34p^2 - 12p + 2)/p^8、(予想式)
予想式に基づく計算値は、次の通りです。
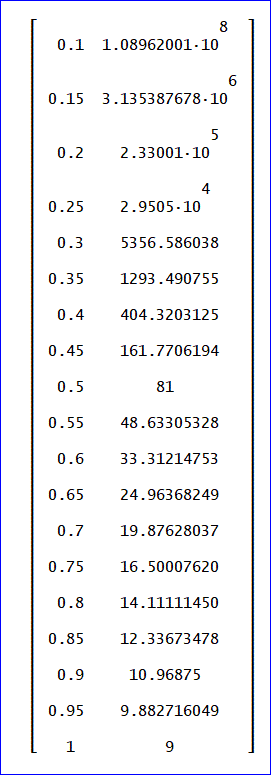
([0.1, 1.08962001·10^8; 0.15, 3.135387678·10^6; 0.2, 2.33001·10^5; 0.25,
2.9505·10^4; 0.3, 5356.586038; 0.35, 1293.490755; 0.4, 404.3203125; 0.45,
161.7706194; 0.5, 81; 0.55, 48.63305328; 0.6, 33.31214753; 0.65, 24.96368249;
0.7, 19.87628037; 0.75, 16.50007620; 0.8, 14.11111450; 0.85, 12.33673478;
0.9, 10.96875; 0.95, 9.882716049; 1, 9])
目次へ戻る
宿場数=9(c=10)の平均日数
結果だけを示します。


平均日数=2(5p^8 - 10p^7 + 30p^6 - 50p^5 + 58p^4 - 45p^3 + 23p^2 - 7p + 1)/p^9、(予想式)
予想式に基づく計算結果を次に示します。
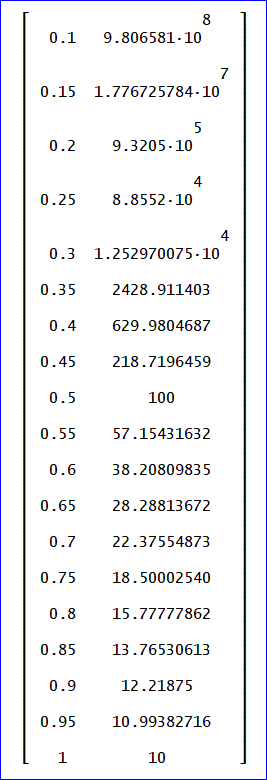
([0.1, 9.806581·10^8; 0.15, 1.776725784·10^7; 0.2, 9.3205·10^5; 0.25,
8.8552·10^4; 0.3, 1.252970075·10^4; 0.35, 2428.911403; 0.4, 629.9804687;
0.45, 218.7196459; 0.5, 100; 0.55, 57.15431632; 0.6, 38.20809835; 0.65,
28.28813672; 0.7, 22.37554873; 0.75, 18.50002540; 0.8, 15.77777862; 0.85,
13.76530613; 0.9, 12.21875; 0.95, 10.99382716; 1, 10])
目次へ戻る
(6)宿場数=1~9(c=2~10)の平均日数(まとめ)
これまで、宿場数が1から9までの平均日数の厳密解または予想式を求めてきました。
なお、当然ながら、予想式は、cが大きいケースほど、係数等が今後、変わる可能性は、あります。
| 宿場数 |
c=宿場数+1 |
平均日数 |
備考 |
| 1 |
2 |
2/p |
厳密解 |
| 2 |
3 |
(p^2+2)/p^2 |
厳密解 |
| 3 |
4 |
(4p^2-2p+2)/p^3 |
厳密解 |
| 4 |
5 |
(p^4 + 6p^2 - 4p + 2)/p^4 |
予想(確実性高い) |
| 5 |
6 |
(6p^4 - 6p^3 + 10p^2 - 6p + 2)/p^5 |
予想(確実性高い) |
| 6 |
7 |
(p^6 + 12p^4 - 16p^3 + 16p^2 - 8p + 2)/p^6 |
予想(確実性高い) |
| 7 |
8 |
(8p^6 - 12p^5 + 28p^4 - 32p^3 + 24p^2 - 10p + 2)/p^7 |
予想(確実性やや低い) |
| 8 |
9 |
(p^8 + 20p^6 - 40p^5 + 60p^4 - 56p^3 + 34p^2 - 12p + 2)/p^8 |
予想(確実性やや低い) |
| 9 |
10 |
(10p^8 - 20p^7 + 60p^6 - 100p^5 + 116p^4 - 90p^3 + 46p^2 - 14p +
2)/p^9 |
予想(確実性やや低い) |
※ 予想式のうち、c=5~7につきましては、
p=0.1の場合について、厳密に解析したところ、平均日数が予想式と末尾まで一致しましたので、予想式の確実性は、高いと推定されます。
これに対して、c=8~10の予想式は、係数の一部が異なる可能性が、やや高いと思われます。(2018/4/7修正)
※ c=8~10では、推移確率行列を対角化するための一次独立な固有ベクトルがc個未満となり、対角化できません。
そのため、前節までの方法でp=0.1の場合の数値計算を実行して比較することができませんでした。
この意味で、予想式の確実を、やや低い、と記載しています。(2018/4/9追記)
※ 厳密解及び予想式の係数について、観察・計算したところ、次のことが分かりました。(2018/4/9追記)
(1) c=宿場数+1としたとき、平均日数の式は、『有理関数』であり、その分母は、p^(c-1)、である。
(2) 平均日数の式の分子は、pの整数係数の多項式であり、
cが偶数の場合は、pの(c-2)次の多項式、
cが奇数の場合は、(c-1)次の多項式で、(c-1)次の係数は、1である。
(3) 分子の定数項は、2である。
(4) c>=3、分子の p^1の係数は、-2(c-3)、
(5) c>=4、分子の p^2の係数は、c^2-7c+16、
(6) c>=5、分子の p^3の係数は、-(c-5)(c^2-7c+24)/3、
(7) c>=6、分子の p^4の係数は、-(c^4-18c^3+143c^2-606c+1152)/12、
(8) c>=7、分子の p^5の係数は、(c-7)(c^4-18c^3+159c^2-782c+1920)/60、
平均日数と確率のグラフです。
ただし、縦軸は、平均日数の対数値 Ln(平均日数)を表します。
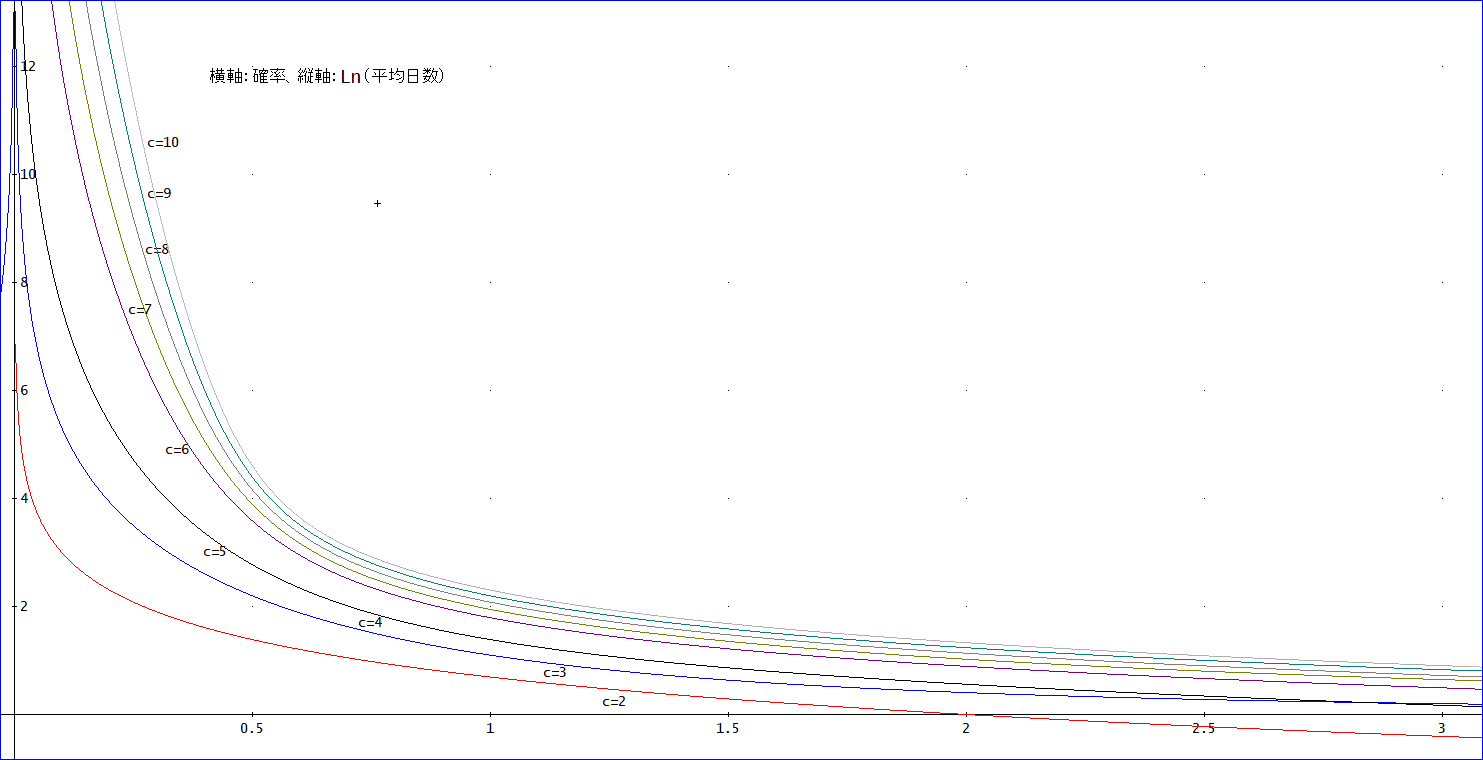
下の図は、横軸にc(=宿場数+1)、縦軸は、Ln(平均日数)を描いたものです。
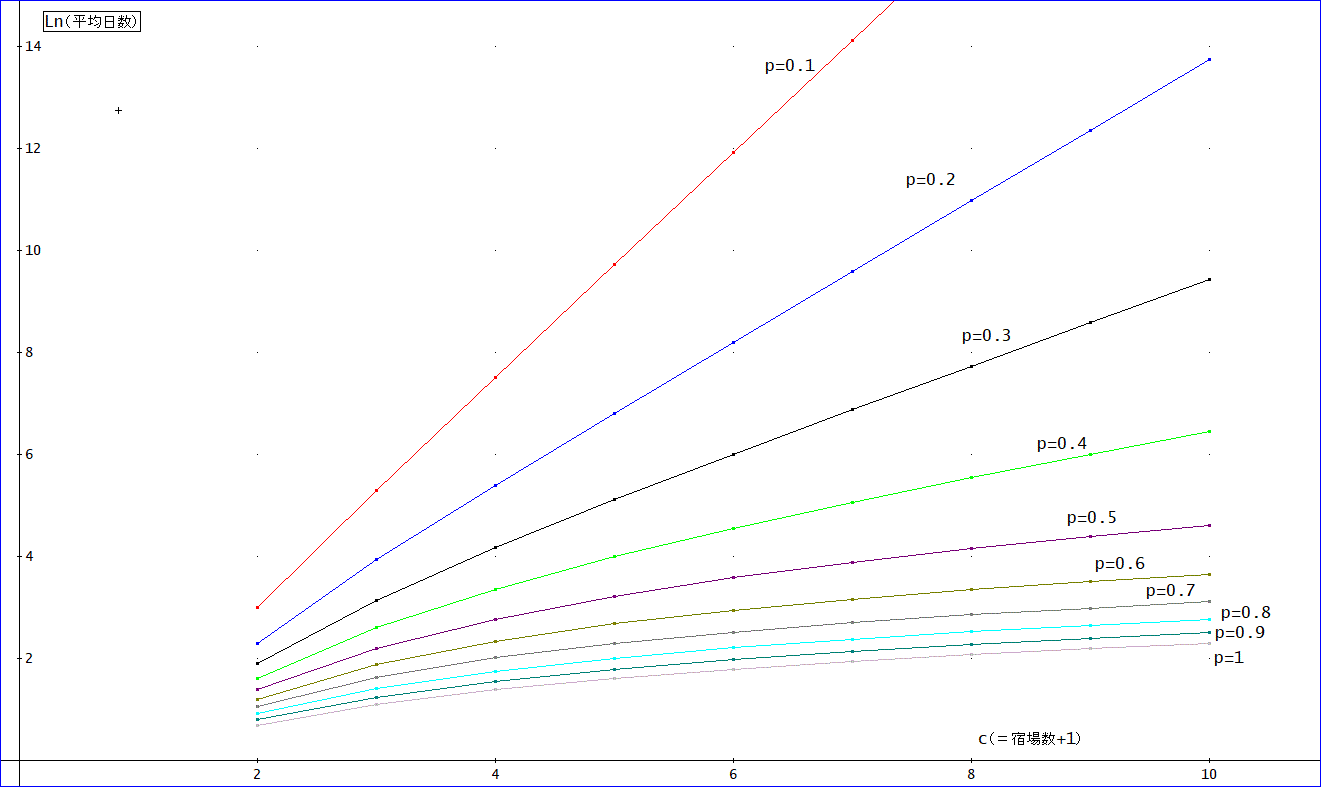
※上図のc=7の場合が誤っていましたので、図を差し替え、説明を削除しました。(2018/4/7)
目次へ戻る
最終更新日 2018/4/5 一部修正・追記 2018/4/6、 2018/4/7、2018/4/9、文章を微修正 2018/9/23、大きすぎる画像を小さく
2019/6/22~6/26





 「えーと、読者の方に、わたしから説明するけど、
「えーと、読者の方に、わたしから説明するけど、



