数式処理ソフト DERIVE(デライブ) de ドライブ
89.マルコフ過程(2)(非対称型道中双六:差分法1)
目次
はじめに
前回の概要
今回の概要
(1)宿場数=1 (c=2)
(2)宿場数=2 (c=3)
(3)宿場数=3 (c=4)
(4)宿場数=4 (c=5)
(5)宿場数=5 (c=6)
(※cは、宿場数+1 で最短で上がれる日数です)
はじめに
前回の概要
第88回『マルコフ過程(1)非対称型道中双六:宿場数=3~9)』においては、『確率過程超!入門』(松原 望 著:東京図書:2011年10月第1刷)に表れる『推移確率行列』の考え方に基づき、『非対称型道中双六』の宿場数=1~3の場合の推移確率
p に関して閉じた平均日数の厳密解を求めました。
また、宿場数が4~9の場合は、宿場数=1~3の厳密解の形と(pに関して閉じていない厳密解を基にした)計算値から、最小2乗法に基づき厳密解の係数を推定しました。
こうして得た予想式は、推移確率行列に基づく方法(以下『行列法』と略記します)にて、 p=0.1 の場合を計算し、その一致度合いを確認しました。
それによりますと、宿場数が4~6では、予想式と行列法に基づく確率 p=0.1の計算値は、その末尾までが一致しました。
一方、宿場数=7では、行列法での対角化が困難になる現象が発生し、行列法による検証は、実行できませんでした。
目次へ戻る
今回の概要
今回は、第84回『道中双六の問題(補筆1)』で再掲した『差分方程式』を解く方法(以下『差分法』と略記します)を試みました。
宿場数=1~3につきましては、差分法により、上がる確率や平均日数の厳密解を導き、行列法による結果と当然ながら一致することを確認しました。
宿場数=4につきましては、新たに平均日数等の厳密解を導き、平均日数については、前回、予想した式と一致することを確かめました。
一方、宿場数=5では、厳密解を一般的な形では、導出できませんでしたが、p=0.1~1まで0.1刻みで計算し、予想式と数値が一致することを確かめました。(※その後、式の変形を工夫することにより、完全に一致する結果を導出しました。2018/5/11 追記)
なお、宿場数=5以上で起きる差分法による困難は、有限和の極限値をとる過程で発生しているもので、原理的なものではないと推察されます。
差分法では、推移確率行列、状態ベクトル、固有方程式、固有値は、使いますが、固有ベクトルと行列の対角化は、必要としません。
これは、(上がりを除いた)状態ベクトルの各要素間の連立差分方程式を最終要素について解き、その解(t=2m+c-1)に(2m+c)×p を掛けたものを足し合わせる方法です。(m=0~整数。2m+c
は、上がりに至る日数)
連立差分方程式から最終要素に関する高階差分方程式を求める過程は、推移確率行列の固有方程式を求める場合と同じになるため、固有方程式が求められれば、あらためて、手間を掛ける必要がありません。
こうして得られた(最終要素に関する)高階差分方程式は、その解を、最終要素=Σ 定数×固有値^t、と仮定して解きます。
ここに現れる 高々 c 個の定数は、最終要素に関する最初の方の計算値と一致するように定数間の連立方程式を解くことにより求めます。
はっきりとは証明していませんが、『非対称型道中双六』の推移確率行列の固有方程式は、どうやら、変数の高々4次か、または、変数^2等を新変数と見なすことにより、4次または3次方程式に還元できるように思われます。
これは、非対称型道中双六の推移確率行列がゼロ要素が多く帯行列であることによるのでしょう。
※ 上記の取り消し線部分を 2018/5/4 に取り消しました。
なお、宿場数=6~9 (c=7~10 )の場合は、時間の関係で、次回に回します。
目次へ戻る
(1)宿場数=1 (c=2)
「というわけで、まずは、簡単な例で再確認してみようと思うのじゃ」
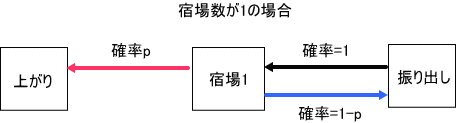
 「非対称型道中双六では、宿場が1 (c=2)が一番簡単な例なのね。
「非対称型道中双六では、宿場が1 (c=2)が一番簡単な例なのね。
図で書くと、こんな感じ。
cは、宿場数+1で、最短で上がれる日数でもあるのよ。
この場合は、2日ね」
「c=2では、行列法での(上がりを除いた)推移確率行列の次元が2となる。
一般に、非対称型道中双六の問題の差分方程式は、振り出し位置を1、宿場1を2などとした場合、
日数をtで表し、t日経過後の各位置にいる駒の確率密度を f(j,t)とすると、t=0、1、2、・・に対して、
(1) f(1,0)=1、初期条件
(2) f(1,t)=(1-p)×f(2,t-1)、振り出し
(3) f(2,t)=f(1,t-1)、最初の宿場
(4) f(c,,t)=p×f(c-1,t-1)、最後の宿場、
(5) f(c+1,,t)=p×f(c,t-1)、上がり、
(6) f(j,t)=(1-p)×f(j+1,t-1)+p×f(j-1,t-1)、j= 2~c-2の宿場、
という差分方程式で表すことができた。
これは、『道中双六の問題(続)』(2014年2月のご挨拶)で初めて導出した。
その後、DERIVE de ドライブの第84回『道中双六の問題(補筆1)』)で再掲している。
さて、行列法での、c=2 の場合は、
t日後の状態ベクトルを、上がりを省略して書いた場合、2次元となり、
U=[振り出し,宿場]、これは、[f(1,t),f(2,t)]である。
推移確率行列を A と書けば、下図のようになり、

t+1日後の状態ベクトル=A ×t日後の状態ベクトルである。
※ 状態ベクトルは、横ベクトルのように書いているが、計算の際は、縦ベクトルになるように転置を行う。(以下、断らないことにする)
具体的には、
0日後では、[1,0]、初期状態、
1日後では、[0,1]、
2日後では、[1-p,0]、最初の上がりの日、
などとなることは、前回確認してきた。
以下では、分かりやすくするために、記法を次のように少し変えてみよう。
状態ベクトル U の各要素を、U1、U2、とする。
その中身は、確率密度関数 f(j,t)なんだが、略して、Uj (t) と書くことにしたい。
※ 一般のcについては、j=1~c となる
すなわち、U の右側の数字は、ベクトルの要素の番号を示し、時間は、(t)で表すということじゃ。
(t) は、式全体で同じ場合のように誤解が起きない場合は、省略してもよいとしよう。
ところで、数列のずらし演算子(シフト演算子)をEと書くとき、
ここで、Eは、時間変数に対して働くものとして、
E U1(t)=U1(t+1)、などと表すことができる。
※ ずらし演算子は、第53回の『数値積分(2)(Euler-Maclaurin展開とその応用)』に表れる。
ともちゃん、このような記法を使って、今回の差分方程式を書いてみて欲しい」
「そうね。
q ≡1-p と置けば、
U1 (t+1)=E U1(t)なので、
差分方程式は、
E U1(t)=q×U2(t)、
E U2(t)=U1 (t)、
のような2元連立差分方程式になる。
2番目の式にEを左から掛けると、
E^2 U2(t)=E U1 (t)、
右辺は、1番目の式から、q×U2(t) なので、
結局、
E^2 U2(t)=q×U2(t)、となるわ」
「そうじゃな。
上がりに至る確率等を求める立場からすれば、
上がるのは、m=0~の整数として、t=2m+2 なので、その1日前の、t=2m+1 のU2(t) を知りたい。
さすれば、平均日数=Σ(m=0~∞)(2m+2)×p×U2(2m+1)、
と計算可能となる。
なお、U2の値にpを掛けているのは、(最後の)宿場から上がりに進む確率は、p だからじゃな。
では、ともちゃん、t=2m+1 のU2(t)は、どう表したらいいかな」
「E^2 U2(t)=q×U2(t)、は、2階の線形差分方程式なので、
U2(t)=λ^t、と置いて特解を求めると、
λ=±√q、となることは、明らかなので、
U2(t)=C1×(√q)^t+C2×(-1)^t×(√q)^t、と一般解を表せる。
パラメーター C1、C2、は、2つの条件、
U2(0)=0、
U2(1)=1、から分かるので、
U2=q^(t/2)(1/(2√q) - (-1)^t/(2√q))、と求められる。
従って、t=2m+1 では、簡単になって、
U2(2m+1)=q^m、となる」
「なるほどな。
t=2m+2日に上がる確率は、U2(2m+1)×p なので、
上がる確率は、p×q^m=p×(1-p)^m、である。
m=0~10までを表にしてみると図のようになる。
 これは、2014年2月の『道中双六の問題(続)』で計算した s(宿場数)=1の場合と一致していることが分かる。
これは、2014年2月の『道中双六の問題(続)』で計算した s(宿場数)=1の場合と一致していることが分かる。
また、当然ながら、第84回『道中双六の問題(補筆1)』で取り上げた式、p(1-p)^m とも一致する。
さて、平均日数=Σ(m=0~∞)(2m+2)×p×U2(2m+1)、から、
平均日数=∑(2·p·(1 - p)^m·(m + 1))=2/p、となって、
これまでの結果と合致することが分かる。
で、特に注目すべきは、λを求める方程式じゃ。
ともちゃんが解いてくれたように、U2(t)=λ^t、と置いて、
与式に代入すると、λ^2=q、を得た。
一方、前回の行列法では、推移確率行列の固有値を求めたが、
推移確率行列 Aの固有方程式は、変数をzと書いて、
z^2-q=0、となる。
移項すると、
z^2=q、となって、同じ形じゃ」
「へー。
不思議な感じね。
みなさん、DERIVEでは、行列の固有方程式は、
CHARPOLY(行列,[変数名])で求められますよ。(変数名は、省略可能)
実際、
z^2+p-1、となります。
(=0は、省略されて表示される)
この方程式の解は、z=±√q、となる」
「では、次節では、宿場数=2 (c=3)について、確認していこう」
目次へ戻る
(2)宿場数=2 (c=3)
「c=2では、簡単すぎて、行列法と差分法との違いや類似点が分かりにくかったかも知れない。
この節では、宿場数が2つ(c=3)の場合を考えてみよう。
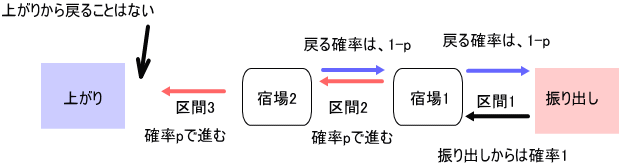
上の図のような感じじゃな」
 「この場合の行列法での上がりを省略した推移確率行列 Aは、次の通りね。
「この場合の行列法での上がりを省略した推移確率行列 Aは、次の通りね。
3次行列となる。
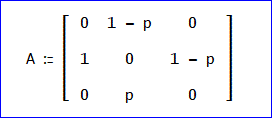
一方、状態ベクトルは、
U=[振り出し,宿場1,宿場2]として、
前節のように、状態ベクトルの各要素を、U1(t)、U2(t)、U3(t) とする。
このとき、U の時間変化は、
[U1(t),U2(t),U3(t)]= A^t ×[U1(0),U2(0),U3(0)] で求められる。
差分方程式と見なす立場からは、3元連立差分方程式となる。
で、前節のように、それを解いて、U3(t)を求めるんだけど、
そのプロセスは、固有方程式とその解を求めることで置き換えられるので、省略するわよ。
さて、固有方程式は、変数をzとしたとき、
z·(z^2 + (p + 1)·(p - 1))=0、となる。
移項して、zで除すと、
z^2=(1-p^2)、
前節にならうと、U3(t) に関する式を求めたいので、
上の式のzをずらし演算子 E と見なして、
E^2 U3(t)=(1-p^2) U3(t)、とすればいいんじゃないかな」
「そうじゃな。
固有方程式は、z=0が解の一つになっている。
なので、見かけ上は、3階の差分方程式に見えたが、実は、2階ということになる。
ゼロ以外の固有値は、z=±√(1-p^2)、であるので、
U3(t)の一般解は、
U3(t)=C1×(√(1-p^2))^t+C2×(-1)^t×(√(1-p^2))^t、となる。
ここで、上がりに至る日数は、t=2m+3 であることから、最後の宿場である宿場2では、
t=2m+2でゼロでない値が発生する。(m=0~の整数)
状態ベクトルの推移を調べると、
([1, 0, 0]`)が初期状態ベクトル、
A×[1, 0, 0]`が t=1なので、U3(1)は、3つ目の要素である、0、
A^2×[1, 0, 0]`が t=2、なので、U3(2)は、3つ目の要素である、p、
よって、
C1 = p/(2·(p + 1)·(1 - p))、
C2=p/(2·(p + 1)·(1 - p))、とパラメーターが決定できる。
注意する点は、t=1から、値が入ると考えて、パラメーターを決める際、U3(0)、U3(1)ではなくて、U3(1)とU3(2)を元にする。
ここで、あらためて、t=2m+2 とおけば、
U3(2m+2)=p·((p + 1)·(1 - p))^m、となる。
2m+3日目に上がる確率は、
p×p·((p + 1)·(1 - p))^m=p^2×(1-p^2)^m、となり、m=0~10までを表にしてみると図のようになる。
これは、2014年2月の『道中双六の問題(続)』で計算した s(宿場数)=2の場合と一致していることが分かる。
また、当然ながら、第84回『道中双六の問題(補筆1)』で取り上げた式、p^2×(1-p^2)^m とも一致する。
よって、平均日数=Σ(m=0~∞)(2m+3)×p×p·((p + 1)·(1 - p))^m、を計算すれば、
平均日数=(p^2+2)/p^2、とこれまでと同じ結果が得られる」
「その、t=0のところだけど、U3(t)の式のままだと、
U3(0)がゼロでない値になってしまうんだけど、それで良いのかな?」
「う~ん。今のところ、
t=0では、U3(0)=0、
t>0では、U3(2m+1)=0、U3(2m+2)=p·((p + 1)·(1 - p))^m、と考えておこう」
目次へ戻る
(3)宿場数=3 (c=4)
「宿場数=3 (c=4)の場合を考えてみよう。
下図がこの場合の図解じゃな」
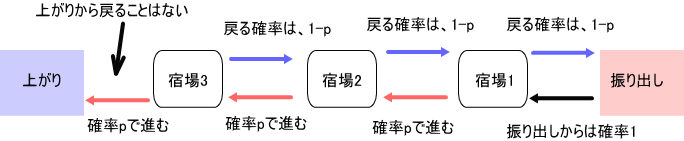
 「第88回で初めて、厳密解が計算できたケースね。
「第88回で初めて、厳密解が計算できたケースね。
それまでは、t=2m+4 で上がる確率は、A、B、C をゼロ以上の整数としたとき、
(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))、と理論的には、求められていたので、
平均日数=Σ(m=0~大きい整数)(2m+4)×上掲の確率、というように、
最終的には、概数を数値計算で求めてきたんだけどね。
※ Comb(a,b)関数は、a C b であり、組み合わせ数を求めるDERIVEの関数。
結局、第88回で、行列法により、平均日数=(4p^2 - 2p + 2)/p^3、と厳密に求められた訳」
「行列法の推移確率行列 Aは、下図のように、なっていた。
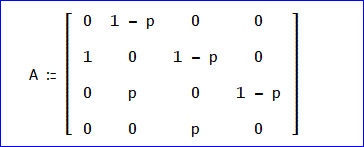
一方、状態ベクトルは、上がりを省略して、
U=[振り出し,宿場1,宿場2,宿場3]とし、
各要素は、U1(t)、U2(t)、U3(t) 、U4(t) と書くことにする。
Uの時間変化は、
[U1(t),U2(t),U3(t),U4(t)]= A^t ×[U1(0),U2(0),U3(0),U4(0)] で求められる。
状態ベクトルの最初の6つの具体的な値は、次のようになる。
t=0 [1, 0, 0, 0] 初期状態、
t=1 [0, 1, 0, 0]
t=2 [1 - p, 0, p, 0]
t=3 [0, 1 - p^2, 0, p^2]、
t=4 [(p - 1)·(p^2 - 1), 0, - p·(2·p^2 - p - 1), 0]
t=5 [0, (p - 1)·(2·p^3 - p - 1), 0, - p^2·(2·p^2 - p - 1)]
3つめの宿場のU4(t)を求めるためのパラメーターを決定する条件は、
U4(2)=0、U4(3)=p^2、U4(4)=0、U4(5)=-p^2(2p^2-p-1)の4つ。
一方、固有方程式は、次の通り。
z^4= z^2·(1-2·p^2 + p) - p·(p - 1)^2、
zをずらし演算子と見なして、解くべき、差分方程式は、
E^4 U4(t)=·(1-2·p^2 + p) E^2 U4(t)-p(p-1)^2 U4(t)、となる。
この一般解は、U4(t)=Σ定数×固有値^t、と表される。
その固有値は、前回求めていたが、
z=±(√2·√(p - 1)·√(√(4·p^2 + 1) - 2·p - 1)/2)、
z=±(√2·√(1 - p)·√(√(4·p^2 + 1) + 2·p + 1)/2)、
の4つとなる。
そこで、λ=(√2·√(p - 1)·√(√(4·p^2 + 1) - 2·p - 1)/2、
μ=(√2·√(1 - p)·√(√(4·p^2 + 1) + 2·p + 1)/2、と置けば、
残りは、-λ、-μ、となる。
では、ともちゃん、U4(t)を求めてご覧」
「途中の計算は、複雑にはなるけど、
U4(t)= C1·λ^t + C2·(-λ)^t + C3·μ^t + C4·(-μ)^t、として、
C1~C4の係数を決めることができたわ。
C1=(√2·p^2/(2·(p - 1)^(3/2)·√(√(4·p^2 + 1) - 2·p - 1)·√(4·p^2 + 1)))
C2=(√2·(((2·p + 1)·√(4·p^2 + 1) - 4·p^2 - 2·p - 1)^2·((2·p + 1)·√(4·p^2 + 1)·(4·p^2 + p + 1) + 16·p^4 + 12·p^3 + 8·p^2 + 3·p + 1) - 4·p^2·√(4·p^2 + 1)·(√(4·p^2 + 1)·(8·p^2 + 5·p + 2) - 16·p^3 - 10·p^2 - 5·p - 2))·((2·p + 1)·√(4·p^2 + 1) + 4·p^2 + 2·p + 1)/(32·p^2·(p - 1)^(3/2)·(√(4·p^2 + 1) - 2·p - 1)^(3/2)·(4·p^2 + 1)))
C3=(- √2·((2·p + 1)·√(4·p^2 + 1) - 4·p^2 - 2·p - 1)·((2·p + 1)·√(4·p^2
+ 1)·(4·p^2 + p + 1) + 16·p^4 + 12·p^3 + 8·p^2 + 3·p + 1)/(4·(1 - p)^(3/2)·(√(4·p^2
+ 1) + 2·p + 1)^(3/2)·(4·p^2 + 1)))
C4=(√2·p^2·((p - 1)·(2·p + 1)·√(4·p^2 + 1) + 4·p^3 - 4·p^2 + p - 1)/(2·(1
- p)^(5/2)·(√(4·p^2 + 1) + 2·p + 1)^(3/2)·(4·p^2 + 1)))、
t=2m+4日後に上がる確率は、U4(2m+3)×p となり、次式のようにかなり簡単に表される。
2m+4日後に上がる確率=p^3·(1 - p)^m·((2·p^2 + p + 1)^(m + 1) - (p·(1 - 2·p))^(m
+ 1))/(4·p^2 + 1)、
m=0~10までを表にしてみると下図のようになる。
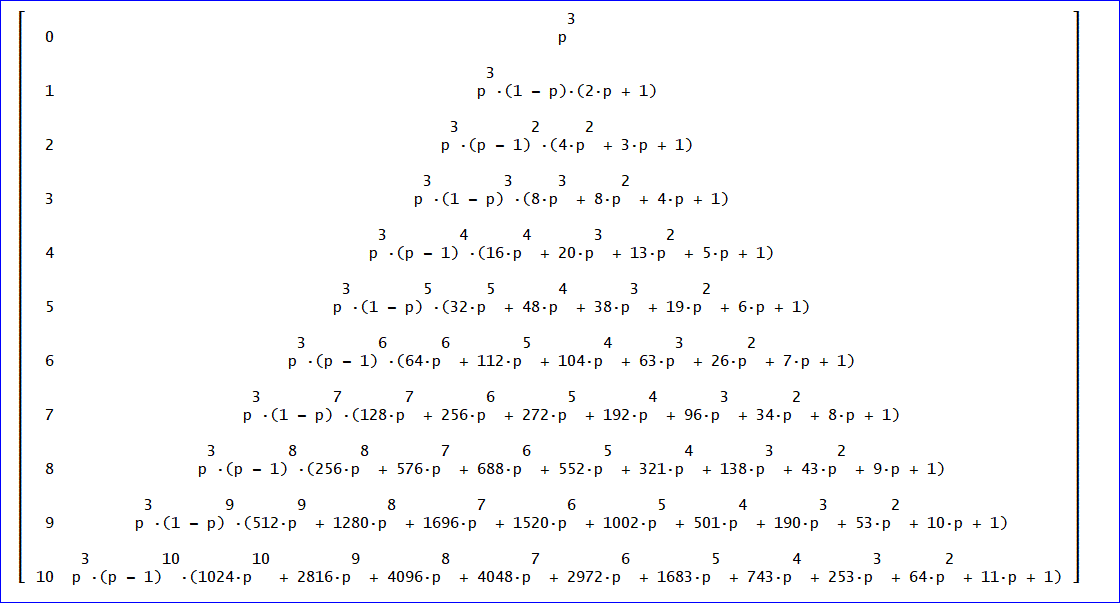
これは、2014年2月の『道中双六の問題(続)』で計算した s(宿場数)=3の場合と一致していることが分かるのね。
一方、平均日数は、2m+4で上がることから、上掲の確率に(2m+4)を掛けて無限和を求めると、
平均日数=(4·p^2 - 2p + 2)/p^3、と求められた」
「2014年2月の記事では、s(宿場数)=3の場合、次のようになっていた。
m=0~9で、
p^3,
p^3(1 - p)(2p + 1),
p^3(p - 1)^2(4p^2 + 3p + 1),
p^3(1 - p)^3(2p + 1)(4p^2 + 2p + 1),
p^3(p - 1)^4(16p^4 + 20p^3 + 13p^2 + 5p + 1),
p^3(1 - p)^5(2p + 1)(4p^2 + p + 1)(4p^2 + 3p + 1),
p^3(p - 1)^6(64p^6 + 112p^5 + 104p^4 + 63p^3 + 26p^2 + 7p + 1),
p^3(1 - p)^7(2p + 1)(4p^2 + 2p + 1)(16p^4 + 16p^3 + 10p^2 + 4p + 1),
p^3(p - 1)^8(4p^2 + 3p + 1)(64p^6 + 96p^5 + 84p^4 + 51p^3 + 21p^2 + 6p
+ 1),
p^3(1 - p)^9(2p + 1)(16p^4 + 12p^3 + 9p^2 + 3p + 1)(16p^4 + 20p^3 + 13p^2
+ 5p + 1)
だった。
一見すると、例えば、m=9では、双方の結果が異なるように見えるけれども、
今回求めた式でのm=9の値は、
(p^3·(1 - p)^9·(512·p^9 + 1280·p^8 + 1696·p^7 + 1520·p^6 + 1002·p^5 +
501·p^4 + 190·p^3 + 53·p^2 + 10·p + 1))
は、次のように因数分解できる。
(p^3·(1 - p)^9·(2·p + 1)·(16·p^4 + 12·p^3 + 9·p^2 + 3·p + 1)·(16·p^4 +
20·p^3 + 13·p^2 + 5·p + 1))、
この青字は、赤字で示した従来の値と一致しているのじゃな。
ところで、t=2m+4、で上がる確率は、A、B、C をゼロ以上の整数としたとき、
(1-p)^m p^3 Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))、だった。
これと、前述の2m+4日後に上がる確率、
(2^(-m - 1)·p^3·(1 - p)^m·((√(4·p^2 + 1) + 2·p + 1)^(m + 1) - (- √(4·p^2 + 1) + 2·p + 1)^(m + 1))/√(4·p^2 + 1))、
とを等しいと置けば、
Σ(A+B+C=m)(p^(m-A)Comb(A+B,A) Comb(B+C,B))
=2^(-m - 1)·((√(4·p^2 + 1) + 2·p + 1)^(m + 1) - (- √(4·p^2 + 1) + 2·p +
1)^(m + 1))/√(4·p^2 + 1)、
が示されたことになる」
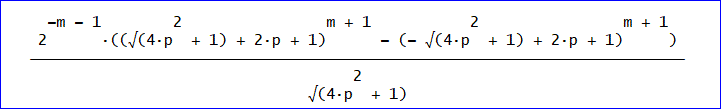
※ 上の青文字の式を修正し、正しい式の図を追加しました。(2018/4/18)
「c=2~4の場合を差分方程式を解く方法で、平均日数を求めてきたんだけど、
差分方程式を解くときに利用するパラメーターの値を決定するための条件は、次のようになった。
Uc(t) の値は、t=(c-2)~(2c-3)の区間の値が必要だった」
「逆に言えば、t<(c-2)では、Uc(t)は、ゼロと考えるということだな」
目次へ戻る
(4)宿場数=4 (c=5)
「前回は、cが5~10では、予想式を求めた。
本節では、c=5の場合を前節と同様に計算してみよう。
全体は、こんな図解となる。

ただ、解法は、ほぼ前節までと同じ流れになるので、状態ベクトルの定義などは、繰り返さないことにしよう。
推移確率行列は、下図のようになる。

固有方程式は、
(- z^5 + z^3·(1 - p)·(3·p + 1) - p·z·(p + 2)·(p - 1)^2)=0、だが、
c=3の場合と同様に、z=0があるので、
z^4 = z^2·(1-p)·(3·p + 1) - p·(p + 2)·(p - 1)^2、と z について4次式になる。
z=0 以外の固有値は、次の4つ。
±(√2·√(p - 1)·√(√(5·p^2 - 2·p + 1) - 3·p - 1)/2)、
±(√2·√(1 - p)·√(√(5·p^2 - 2·p + 1) + 3·p + 1)/2)、
では、ともちゃん、状態ベクトルの最初の方を挙げてもらえないかな」
 「分かったわ。
「分かったわ。
前節では、必要なベクトルは、t=c-2~2c-3、の範囲だったので、
今回の場合に当てはめると、t=3~7 となる。
だけど、ついでなので、t=0~7までを挙げるわよ。
なお、必要なものは、U5(t)だけなので、状態ベクトルのc番目の(ここでは5つめ)の要素のみを取り出して表示する。
t=0~2までは、ゼロ。
t=3 0、
t=4 p^3、
t=5 0、
t=6 p^3·(1 - p)·(3·p + 1)、
t=7 0、
となっているわ」
「ご苦労さんじゃった。
c=5では、上がりに至るのは、t=2m+5 ということになっている。
U5(t)= C1·λ^t + C2·(-λ)^t + C3·μ^t + C4·(-μ)^t、と置いてみる。
ここで、λ、μは、ともちゃんが書いてくれている4つの固有値のうち、プラス符号のものを表すことにしよう。
t=3~6までの値を使って、C1等を求めると、次のようになった。
c1 = p^3·(3·p^2 - 2·p + μ^2 - 1)/(2·λ^4·(λ + μ)·(μ - λ))、
c2 = p^3·(3·p^2 - 2·p + μ^2 - 1)/(2·λ^4·(λ + μ)·(μ - λ)) 、
c3 = p^3·(3·p^2 - 2·p + λ^2 - 1)/(2·μ^4·(λ^2 - μ^2)) 、
c4 = p^3·(3·p^2 - 2·p + λ^2 - 1)/(2·μ^4·(λ^2 - μ^2))、
そして、λ、μに先の値を代入するとやや複雑な式となるが、
t=2m+4を代入すると、(これは、上がる日数=2m+5 の1日前)
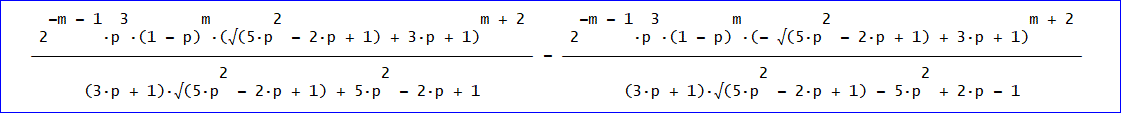
上図の式にpを掛けたものが、2m+5日後に上がる確率だ。
U5(2m+4)×p
=2^(-m - 1)·p^4·(1 - p)^m·((√(5·p^2 - 2·p + 1) + 3·p + 1)^(m + 1) - (-
√(5·p^2 - 2·p + 1) + 3·p + 1)^(m + 1))/√(5·p^2 - 2·p + 1)、)
そして、上の確率の式に(2m+5)を掛けて、m=0~nまでを加えてから、n→∞、にすれば、
平均日数=(p^4 + 6·p^2 - 4·p + 2)/p^4、が得られた」
「よかったわ。
第88回で予想した式と同じだったわ」
「わしも一安心じゃ。
一方、以前に得られていた、c=cの場合の2m+c日で上がる確率は、一般に次式で示される。
(1-p)^m p^(c-1) Σ(k1+k2+・・+kc-1=m)(p^(m-k1)Comb(k1+k2,k1) Comb(k2+k3,k2)・・Comb(kc-2+kc-1,kc-2))、
※ Comb関数は、組み合わせ数を表すDERIVEの関数。
この式で、c=5 の場合、
(1-p)^m p^4 Σ(k1+k2+k3+k4=m)(p^(m-k1)Comb(k1+k2,k1) Comb(k2+k3,k2)Comb(k3+k4,k3))、であるが、
今回導いた確率の式と比較すると、
Σ(k1+k2+k3+k4=m)(p^(m-k1)Comb(k1+k2,k1) Comb(k2+k3,k2)Comb(k3+k4,k3))
=2^(-m - 1)··((√(5·p^2 - 2·p + 1) + 3·p + 1)^(m + 1) - (- √(5·p^2 - 2·p + 1) + 3·p + 1)^(m + 1))/√(5·p^2 - 2·p + 1))、
となることが分かる」
目次へ戻る
(5)宿場数=5 (c=6)
「前回は、cが5~10では、予想式を求めた。
本節では、c=6の場合を前節と同様に計算してみよう。
全体の図解は、下の図のような感じじゃな。

ほぼ、これまでと、同じ流れになるので、状態ベクトルの定義などは、繰り返さないことにしよう。
推移確率行列は、下図のようになる。

固有方程式は、6次式となるが、
(z^6 + z^4·(4·p^2 - 3·p - 1) + 3·p·z^2·(p + 1)·(p - 1)^2 + p^2·(p - 1)^3)=0、なので、
z^2 について、3次式となり、固有値は、厳密に求めることができる。
その固有値は、次の6つ。
±λ=±(√3·√(1 - p)·√(- 2·√(7·p^2 - p + 1)·SIN(ASIN (w)/3) + 4·p + 1)/3)、
±μ=±(√3·√(1 - p)·√(√3·√(7·p^2 - p + 1)·COS(ASIN (w)/3) + √(7·p^2 - p + 1)·SIN(ASIN (w)/3) + 4·p + 1)/3)、
±ν=±(√3·√(1 - p)·√(- √3·√(7·p^2 - p + 1)·COS(ASIN (w)/3) + √(7·p^2 - p + 1)·SIN(ASIN (w)/3) + 4·p + 1)/3)、
ただし、w=(20·p^3 - 12·p^2 - 3·p + 2)/(2·(7·p^2 - p + 1)^(3/2))、
一方、状態ベクトルは、6次元となり、その6つめの要素をU6(t)と書くと、
u6(t) ≔ c1·λ^t + c2·μ^t + c3·ν^t + c4·(-λ)^t + c5·(-μ)^t + c6·(-ν)^t、
となる。
ここで。c1~c6は、パラメーター、λ、μ、νは、前掲の固有値。
では、ともちゃん。
このパラメーターを決めて欲しい」
 「U6(t) の値は、t=(c-2)~(2c-3)の範囲で求めると、
「U6(t) の値は、t=(c-2)~(2c-3)の範囲で求めると、
U6(4)=0、
U6(5)=p^4、
U6(6)=0,
U6(7)=p^4·(4·p^2 - 3·p - 1)、
U6(8)=0、
U6(9)=p^4·(13·p^4 - 21·p^3 + 4·p^2 + 3·p + 1)、
の6つあれば、c1~c6を決めることができる。
途中の計算を略すと、
c1 = p^4·(13·p^4 - 21·p^3 + 4·p^2·(μ^2 + ν^2 + 1) - 3·p·(μ^2 + ν^2 - 1) + (μ^2 - 1)·(ν^2 - 1))/(2·λ^5·(λ + μ)·(λ - μ)·(λ + ν)·(λ - ν)) 、
c2 = p^4·(13·p^4 - 21·p^3 + 4·p^2·(λ^2 + ν^2 + 1) - 3·p·(λ^2 + ν^2 - 1)
+ (λ^2 - 1)·(ν^2 - 1))/(2·μ^5·(λ + μ)·(λ - μ)·(μ + ν)·(ν - μ)) 、
c3 = p^4·(13·p^4 - 21·p^3 + 4·p^2·(λ^2 + μ^2 + 1) - 3·p·(λ^2 + μ^2 - 1) + (λ^2 - 1)·(μ^2 - 1))/(2·ν^5·(λ + ν)·(λ - ν)·(μ + ν)·(μ - ν)) 、
c4 = p^4·(13·p^4 - 21·p^3 + 4·p^2·(μ^2 + ν^2 + 1) - 3·p·(μ^2 + ν^2 - 1)
+ (μ^2 - 1)·(ν^2 - 1))/(2·λ^5·(λ + μ)·(λ - μ)·(λ + ν)·(ν - λ)) 、
c5 = p^4·(13·p^4 - 21·p^3 + 4·p^2·(λ^2 + ν^2 + 1) - 3·p·(λ^2 + ν^2 - 1) + (λ^2 - 1)·(ν^2 - 1))/(2·μ^5·(λ + μ)·(λ - μ)·(μ + ν)·(μ - ν)) 、
c6 = p^4·(13·p^4 - 21·p^3 + 4·p^2·(λ^2 + μ^2 + 1) - 3·p·(λ^2 + μ^2 - 1)
+ (λ^2 - 1)·(μ^2 - 1))/(2·ν^5·(λ^2 - ν^2)·(μ + ν)·(ν - μ))、
と、決定できた。
そして、U6(t)の式にc1等を代入して、t=2m+5の値にpを掛けたものが、t=2m+6 で上がる確率なのね。
これは、すごく長い式なので、無駄な感じもあるけど、一応、貼り付けるわよ。
(p^5·((μ + ν)·(μ - ν)·(13·p^4 - 21·p^3 + 4·p^2·(μ^2 + ν^2 + 1) - 3·p·(μ^2
+ ν^2 - 1) + (μ^2 - 1)·(ν^2 - 1))·(-λ)^(2·m) + λ^(2·m)·(μ + ν)·(μ - ν)·(13·p^4
- 21·p^3 + 4·p^2·(μ^2 + ν^2 + 1) - 3·p·(μ^2 + ν^2 - 1) + (μ^2 - 1)·(ν^2
- 1)) + (λ + ν)·(ν - λ)·(13·p^4 - 21·p^3 + 4·p^2·(λ^2 + ν^2 + 1) - 3·p·(λ^2
+ ν^2 - 1) + (λ^2 - 1)·(ν^2 - 1))·(-μ)^(2·m) + μ^(2·m)·(ν^2 - λ^2)·(13·p^4
- 21·p^3 + 4·p^2·(λ^2 + ν^2 + 1) - 3·p·(λ^2 + ν^2 - 1) + (λ^2 - 1)·(ν^2
- 1)) + (λ + μ)·(λ - μ)·(13·p^4 - 21·p^3 + 4·p^2·(λ^2 + μ^2 + 1) - 3·p·(λ^2
+ μ^2 - 1) + (λ^2 - 1)·(μ^2 - 1))·((-ν)^(2·m) + ν^(2·m)))/(2·(λ + μ)·(λ
- μ)·(λ + ν)·(λ - ν)·(μ + ν)·(μ - ν)))、
で、本当は、この式のλ、μ、ν、に前述の固有値の式を代入して、式を簡単化したいな、と思ったんだけど、到底、簡単になりそうもないわ」
「三角関数や逆三角関数が複雑に入っているのでな。
ここでは、離散的なpの数値を使って、第88回で予想した式との比較を行ってみよう。
まず、wの値をp=0.1~1まで厳密に計算すると、下図のようになる。

1列目がp、2列目が wの値じゃ。
次にこのwを基にして、Σ(m=0~∞)(2m+6)×U6(2m+5)×p、を計算する。
| 確率 p |
平均日数(今回計算値) |
予想式 2(3p^4 - 3p^3 + 5p^2 - 3p + 1)/p^5 |
| 0.1 |
1.4946·10^5 |
1.4946·10^5 |
| 0.2 |
3630 |
3630 |
| 0.3 |
406.0082304 |
406.0082304 |
| 0.4 |
94.6875 |
94.6875 |
| 0.5 |
36 |
36 |
| 0.6 |
19.05349794 |
19.05349794 |
| 0.7 |
12.39126554 |
12.39126554 |
| 0.8 |
9.111328125 |
9.111328125 |
| 0.9 |
7.218750529 |
7.218750529 |
| 1 |
|
6 |
実際の手順は、
平均日数=U6(2m+5)×p×(2m+6) をλ、μ、ν のまま、計算し、m=0~nまでを合計する。
次に、先に計算してある、λ、μ、νの式を代入する。
3番目に、その式に、p と wの値を代入する。
ここまでは、厳密に計算可能じゃ。
最後に、n→∞、とした後に、得られた式を概数で評価する。
赤字の計算は、各 p について、繰り返す」
「両者の結果は、文句なしに一致するけど、固有値に、逆三角関数や三角関数が入ってくると、難しくなってしまうわね。
残念ながら、100% 満足は、していないけど」
「確かにな。何か、工夫があると思うんじゃがな。
後日、考えてみよう。※
ただ、そうは言うものの、前回得た予想式は、式の形を類推し、その係数を最小2乗法で得たものだ。
そもそも、元にした平均日数の計算式自体は、厳密なものじゃが、それによる計算は、有限和までで打ち切る必要がある。
一方、今回は、式の形は、予想せず、また、有限和ではなく、無限和を取っている点が違う。
手間さえいとわなければ、任意のpの値に対する平均日数が厳密に計算可能だ。
そこの重みは、違うと思うのう」
「それは、そうね。
前節とあわせて言えば、c=4 及び c=5の場合の平均日数の予想式の確実性には疑いがなくなったわ」
※ 平均日数の式とその後の式の変形を工夫したところ、厳密解の予想式と完全に一致する結果が得られました。
詳細は、第90回に記載する予定です。(2018/5/11追記)
目次へ戻る
最終更新日 2018/4/15、図を追加 2018/4/16、(3)節末尾の式を修正 2018/4/18、『今回の概要』末尾の一部を取消 2018/5/4、
(5)節に追記(2018/5/11)、タイトルを変更 2018/5/23、文章を微修正 2018/9/23



 「非対称型道中双六では、宿場が1 (c=2)が一番簡単な例なのね。
「非対称型道中双六では、宿場が1 (c=2)が一番簡単な例なのね。




