数式処理ソフト DERIVE(デライブ) de ドライブ
90.マルコフ過程(3)(非対称型道中双六:平均日数計算公式)
目次
(1)概要
(2)差分法の応用
数式作成ツールの利用
記号等の説明
差分法による平均日数等の計算原理
状態ベクトルの計算(最後から最初に進む)宿場数=3 (c=4)の例
状態ベクトルの計算(最初から最後に進む)宿場数=3 (c=4)の例
(3)差分法による状態ベクトルと平均日数
宿場数=3 (c=4)を例にして定式化
一般化 c が偶数の場合
一般化 c が奇数の場合
(4)差分法による平均日数等の計算式の簡素化
c が偶数の場合の簡素化
c が偶数の例 宿場数=5 (c =6)
c が奇数の場合の簡素化
c が奇数の例 宿場数=4 (c=5)
c が奇数の例 宿場数=6 (c=7)
(※cは、宿場数+1で、上がりに至る最短日数です)
(1)概要
第89回の『マルコフ過程(2)(非対称型道中双六:差分法)』の続きとして、差分法に基づき平均日数を計算する式を導き、具体的な例で検証します。
ちなみに、第88回、第89回における平均日数の計算結果は、次のようになっています。
| 宿場数 |
c=宿場数+1 |
平均日数 |
備考 |
今回 |
| 1 |
2 |
2/p |
厳密解 |
|
| 2 |
3 |
(p^2+2)/p^2 |
厳密解 |
|
| 3 |
4 |
(4p^2-2p+2)/p^3 |
厳密解 |
再検証 |
| 4 |
5 |
(p^4+6p^2-4p+2)/p^4 |
厳密解 |
再検証 |
| 5 |
6 |
(6p^4-6p^3+10p^2-6p+2)/p^5 |
厳密解 |
再検証 |
| 6 |
7 |
(p^6+12p^4-16p^3+16p^2-8p+2)/p^6 |
予想(確実性高) |
厳密解 |
| 7 |
8 |
(8p^6-12p^5+28p^4-32p^3+24p^2-10p+2)/p^7 |
予想(確実性中) |
厳密解※1 |
| 8 |
9 |
(p^8+20p^6-40p^5+60p^4-56p^3+34p^2-12p+2)/p^8 |
予想(確実性中) |
厳密解※2 |
| 9 |
10 |
(10p^8-20p^7+60p^6-100p^5+116p^4-90p^3+46p^2-14p+2)/p^9 |
予想(確実性中) |
厳密解※1 |
上表で『再検証』は、過去に得た結果と同一の結果を、今回、得たこととを示します。
また、『厳密解』は、今回、初めて、前回までの予想式を厳密に検証したことを示します。
さらに、『厳密解※1』は、第93回「マルコフ過程(6)(非対称型道中双六:平均日数と対称式」で厳密解と確認しました。
また、『厳密解※2』は、第95回「マルコフ過程(7)(非対称道中双六:宿場数=8の平均日数)」で厳密解と確認しました。
宿場数=4、(c=5)の場合
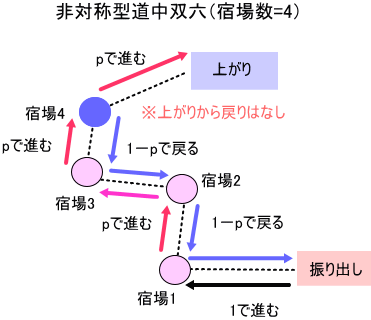
以下では、これまでの習慣に従い、c=宿場数+1、と書くことにします。
上図のような『非対称型道中双六』の問題において、振り出しを1とし、最後の宿場をcで表すとき、
1~cまでの場所に駒が存在する確率を表す『状態ベクトル』 を、t を離散的な時間として、
U(t)=[U1(t),U2(t),・・,Uc(t)]、とします。
※ Uは、横ベクトルのように書いています。DERIVEで、A×U とするときに、Uの転置をとる必要があります。
ただ、煩雑なので、HP上では、省略しています。
このとき、Uのt=0の初期ベクトルは、[1,0,0,・・,0]です。
ここで、推移確率行列 A とすると、U(t+1)=A×U(t) と書くことができました。
pは、推移確率行列 A に現れる確率で、下図は、c=5の場合のAです。

さて、今回、導いた平均日数の式は、c の偶・奇により、多少、形が変わります。
いま、sを s=1、2,・・の自然数として、
cが偶数、すなわち、c=2s、では、平均日数は、次式で与えられます。
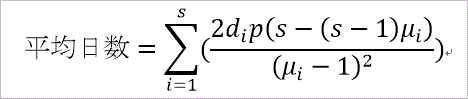
ここで、Aの固有方程式 は、2s次ですが、Φ(λ^2)=0、となる(と期待される)ことから、
λ^2=μと置けば、s次となり、その根をμi と書きます。
また、di は、μi、Uc(t) と次の2つの関係式を満たす係数です。
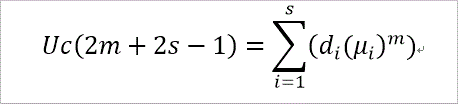
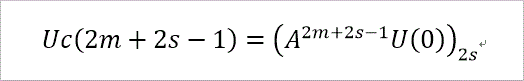
ここで、mは、m=0~s-1、までを動きます。
一方、cが奇数、c=2s+1、では、平均日数は、次式で与えられます。
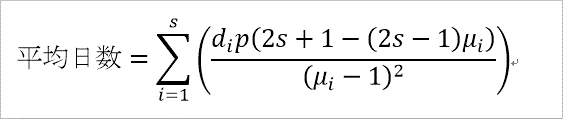
μは、Aの固有方程式 は、2s+1次ですが、λ×Φ(λ^2)=0、と分解できる(と期待される)ことから、
Φにおいて、λ^2=μと置けば、s次となり、その根をμi と書きます。
また、di は、μi、Uc(t) と次の2つの関係式を満たす係数です。
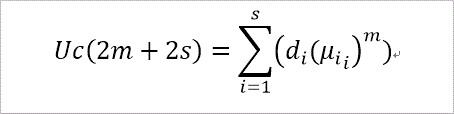
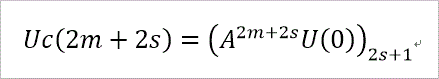
ここで、mは、m=0~s-1、までを動きます。
以下では、これらの式の導出方法や適用例について、主として、取り上げていきます。
※ 上記の式は、これまで取り上げてきた『非対称道中双六』問題に即したものです。
双六上の駒は、前後1つしか移動できず、結果、最後の宿場からのみ上がれるケースです。
しかし、一般の双六の駒は、前後だけでなく、2つ以上離れた位置に移動する可能性もあります。
その場合、推移確率行列の固有方程式、Φ(λ)=0、が λ^2の関数とは必ずしもならないため、上記の式は、根 λに関する式となります。
従って、解くべき固有方程式の次数や係数を求めるための連立方程式の次元が上記の2倍になります。
また、最後の宿場以外の場所からも上がれる場合は、より複雑となります。
これらのケースは、これまでと同様に本稿では、触れないことにします。
目次へ戻る
(2)差分法の応用
数式作成ツールについて
「今回、式の一部をWordの数式ツールで作り、ホームページに画像として貼り付けてみたんじゃ」
 「数式ツールは、2018年5月の今月のご挨拶『数式作成機能・ソフト』で紹介しているOfficeの機能ね。
「数式ツールは、2018年5月の今月のご挨拶『数式作成機能・ソフト』で紹介しているOfficeの機能ね。
Wordだけでなく、Office 2007 以降の PowerPoint、Excel でも使えるものでしょ」
「ともちゃん、今回もご苦労さんじゃのう。
これまでは、式の画像は、DERIVEの画面コピーを使ってきたんじゃった。
Word を選んだのは、下書きも兼ねさせるためじゃな」
「へー。
おじぃさん、今まで、下書きは、作っていなかったんじゃないの?」
「たしかに『今月のご挨拶』などの下書きは、作ってこんかった。
過去の『DERIVE de ドライブ』でも、DERIVEのファイルを元にして書いただけじゃった。
しかし、
・ DERIVEのグラフは、保存されないので、HP作成時に再度、描く必要がある。
・ HPに使う、あるいは使った、DERIVEのファイルがなかなか見つからない。
そこで、Word のファイルに、DERIVEの計算結果やグラフの画像を貼り付けておけば、後日、探し回る手間が減るということだ。
数式作成ツールを利用して、DERIVEの画面コピーよりもきれいな数式も作れるしな」
「まさに、一石三鳥、ということね」
目次へ戻る
記号等の説明
「例によって、『非対称型道中双六』の問題の図解と記号等の説明を簡単にしておこう。
下の図は、『非対称型道中双六』で宿場数=5(c=6)の図解じゃ。

あらためて、言うまでもないが、概要の注釈に書いたように、
双六上の駒は、前後1つしか移動できず、最後の宿場からのみ上がることができることに注意じゃ」
 「なるほどね。
「なるほどね。
一般の双六では、下図のように、2つ以上飛んでしまう場合があるものね」
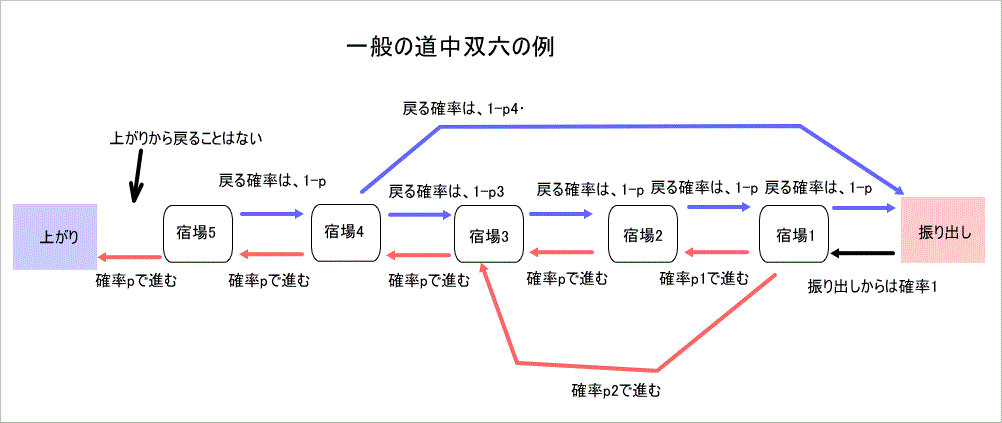
「その通りじゃ。
1回お休み、のように、同じ宿場に留まる可能性もある。
まして、最後の宿場以外から上がりに至る確率がゼロでないケースまでを考えると、これまで、計算の基礎としてきた、最後の宿場からのみ上がるという前提が崩れてしまうからな。
平均日数の計算式がいたずらに複雑になってしまう」
「ま、ゲームとしても、振り出しなどから、いきなり、上がるというのは、つまらないでしょうね」
「そういうことじゃ。
さてと、記号等を説明しよう。
まず、一般の c(>=2)についてじゃ。
推移確率行列(の上がりを省略したもの)をAで表す。
振り出し以外の宿場から次の宿場または上がりに進む確率をp、
振り出しから最初の宿場に進む確率を1
振り出し及び上がり以外の宿場から一つ手前の宿場に戻る確率を1-p、
なお、1-pは、qと書く場合がある。
いま、振り出しを1とし、最後の宿場をcで表すとき、
1~cまでの場所に駒が存在する確率を表す『状態ベクトル』 (上がりは、省略している)、
U(t)=[U1(t),U2(t),・・,Uc(t)]、とする。t=0の初期ベクトルは、[1,0,0,・・,0]、じゃ。
ここで、推移確率行列 A と書けば、U(t+1)=A×U(t) と書くことができる」
「状態ベクトル U(t)、推移確率行列 Aは、いずれも、上がりを省略して考えてることに注意してね。
つまり、上がり(c+1番目)は、現れていないの。
それと、状態ベクトル U は、横ベクトルで書いているので、A×U を計算する際は、Uの転置をとって、A×U ’ と縦ベクトルとする必要がある事ね」
「ともちゃん、補足、ありがとさん。
ところで、平均日数を計算する際、前述のように、最後の宿場からのみ上がりに至ることに注意することが大切じゃ。
これにより、最後の宿場である c から上がりに至る確率が p であることから、知りたいのは、Uc(t)である。
これが分かると、t=2m+c に上がる確率は、直前の時刻のc の位置の Uc(2m+c-1)に p を乗ずることで求められるからだな。
さて、U(t+1)=AU(t)から、U(2m+c-1)=A^(2m+c-1)×U(0) となる。(U(0)は、初期状態ベクトル)
右辺の行列Aのべき乗の中身を知るために、第88回『マルコフ過程(1)(非対称型道中双六)』では、行列の対角化を行った。
対角化は、c=7までは、pを数値に置き換えると実行可能じゃった。
しかし、c=8では、固有値は、求められたが、一次独立な8個の固有値ベクトルを得ることができず、行列の対角化ができんかった。
そこで、前回で、差分法を使ってみたわけじゃ。
以下では、その原理と一般化を説明しよう」
目次へ戻る
差分法による平均日数等の計算原理
「差分方程式としての、道中双六の問題は、次のようじゃった。
初期条件:U1(0)=1、Uj(0)=0、(2=<j<=c)
振り出し:U1(t+1)=q×U2(t)、
最初の宿場:U2(t+1)=U1(t)+q×U2(t)、
途中の宿場:Uj(t+1)=q×U(j+1)(t)+p×U(j-1)(t)、
最後の宿場:Uc(t+1)=p×U(c-1)(t)、
上がり:p×Uc(t)、」
 「そうね。
「そうね。
差分方程式は、2014年2月の『道中双六の問題(続)』で、初めて取り上げたものね。
ただし、
c=2のときは、最初の宿場の右辺の第2項q×U2(t)はなく、また、途中の宿場もない。
c=3のときは、途中の宿場はない。
という注意が必要ね。
それと、下付き添え字がHPでは、書きにくいので、Uc と書いているが、本当は、U↓c のこと。
ただし、DERIVEで、計算させる際、Uc は、1つの変数名として書いているの。
これ以外にも、係数 d1 など、d1 という変数で書いて、計算しているなど、融通無碍のところがあるので、心得ておいてくださいな」
「たしかに、その通りじゃ。
さて、差分法では、時間に関するずらし演算子をEで表し、Uj(t+1)=EUj(t)のような働きをするものとする。
上の方程式から、
U1(t+1)=EU1(t)=q×U2(t)、
U2(t+1)=EU2(t)=U1(t)、
Uj(t+1)=EUj(t)=q×U(j+1)(t)+p×U(j-1)(t)、
Uc(t+1)=EUc(t)=p×U(c-1)(t)、
が得られる。
c=4の場合に具体的に行列を使って書き下ろすと、次のようになるじゃろう。
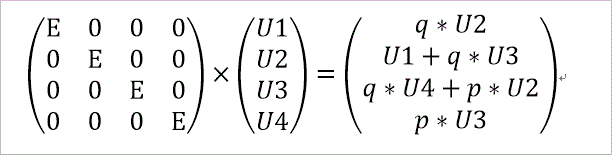
これは、E×I×U(t)=U(t+1)、と表される。(q=1-p)
ここで、Iは、単位行列。
一方、AU(t)=U(t+1)は、下図の関係。

これらから、AU(t)=E×I×U(t)、であることが分かる。
書き直すと、(A-E×I)U(t)=ゼロ行列、
ゼロでないU(t)が存在するためには、Aの固有方程式を Φ(λ)=0と書くとき、
EがΦ(E)=0を満たす必要がある。
これより、Φ(E)Uj(t)=0、
もし、Φ(λ)=0の方程式の根が単根であるならば、固有値をλi として、パラメ-タ-をci(j)で表すと、
Uj(t)=ΣCi(j)×(λi)^t と表すことができる。(i、j=1~c)」
「じゃ、宿場数が3、すなわち、c=4の場合を具体的に計算してみるよ」
目次へ戻る
状態ベクトルの計算(最後から最初に進む)宿場数=3 (c=4)の例
 「c=4の場合は、宿場数=3 で、第88回で初めて、厳密解が計算できたケースね。
「c=4の場合は、宿場数=3 で、第88回で初めて、厳密解が計算できたケースね。
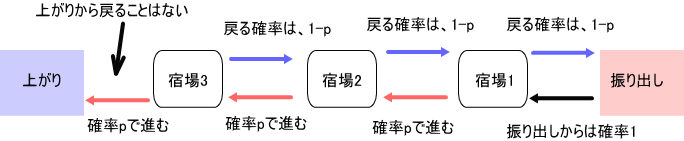
状態ベクトル U=[U1,U2,U3,U4]として、(tを省略して書く)
推移確率行列 Aは、
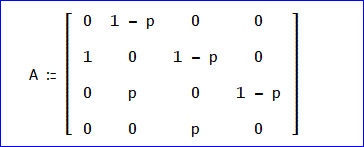
固有方程式は、f(E)=E^4-E^2q(2p+1)+pq^2=0である。
なお、第89回では、j=cとして、Uc(t)=ΣCi(c)×λi^tと仮定して、Ciを決定した。
この場合、Uc以外の要素が、どう表されるかも考えてみたわ。
Uc(t)=ΣCi×λi^tとすれば、
EU4=pU3から、
U3=(1/p)EU4(t)=(1/p)EΣCi×λi^t=(1/p)ΣCi×λi^(t+1)、と求められる。
U2は、EU3=pU2+qU4、から、U2=(1/p)(EU3-qU4)
U1は、EU2=qU3+U1、から、U1=EU2-qU3
と芋づる式に求められるわね」
「なるほど。
では、わしは、U1を先に求めることを考えてみよう。
U1(t)=ΣCi(1)×λi^tと仮定して、係数Ci(1)を決定したとする。
U2は、EU1=qU2、から、
U2=(1/q)EU1、が得られる。
※EU1=ΣCi(1)×λi^(t+1)、と計算する。
U3は、EU2=qU3+U1から、
U3=(1/q)(EU2-U1)が求められる。
最後に、U4は、
EU3=pU2+qU4から、
U4=(1/q)(EU3-pU2)、が得られる」
「たしかに、平均日数の計算のためには、Ucを得ることが大切だったので、U1ではなく、Ucを解いた。
U1を先に求めた場合は、Ucを求めるまでに、U2~Uc-1も、余分に計算する必要があるので、手間が少し多くなるわね」
「それは、そうじゃ。
じゃが、係数Ciを決定する手間は、どうじゃろうか。
これをc=4の場合について比較してみよう。
なお、cが偶数の場合、固有方程式は、Φ(λ^2)=0、のようにλ^2の式となる。
また、奇数の場合でも、λ×Φ(λ^2)=0、となるので、λ=0を除くと、ほぼ、cが偶数の場合と同じように扱うことができる。
c=4では、固有方程式の解は、±λ1、±λ2と4つの根がある。
λ^4-λ^2q(2p+1)+pq^2=0
λの正の方は、そのまま表記し、負の方に、-を付けるとすると、U4、または、U1のいずれを求めるとしても、
Uj=C1(λ1)^t+C2(-λ1)^t+C3(λ2)^t+C4(-λ2)^t、とおけるじゃろう」
「じゃ、U4を先に求めてみるわ。
今、c=4と偶数なので、
U4は、時刻が奇数の場合にゼロでない値を持つ。
そこで、t=2m+3、と置くと、
U4=D1(λ1)^(2m+3)+D2(λ2)^(2m+3)、(m=0~の整数)、
ただし、ここで、D1=C1-C2、D2=C3-C4、
一方、時刻が偶数の場合は、U4は、ゼロなので、
C1+C2=0、C3+C4=0、である。
従って、D1、D2が求まれば、
C1=D1/2、C2=-C1、C3=D2/2、C4=-C3、である。
D1、D2は、
U4(3)=p^2、
U4(5)=p^2q(2p+1)
以上の2つの式から、
D1=p^2 (2 p q+q-λ2^2)/(λ1^3 (λ1^2-λ2^2))、
D2=p^2 (2 p q+q-λ1^2)/(λ2^3 (λ2^2-λ1^2))、
と定まる。
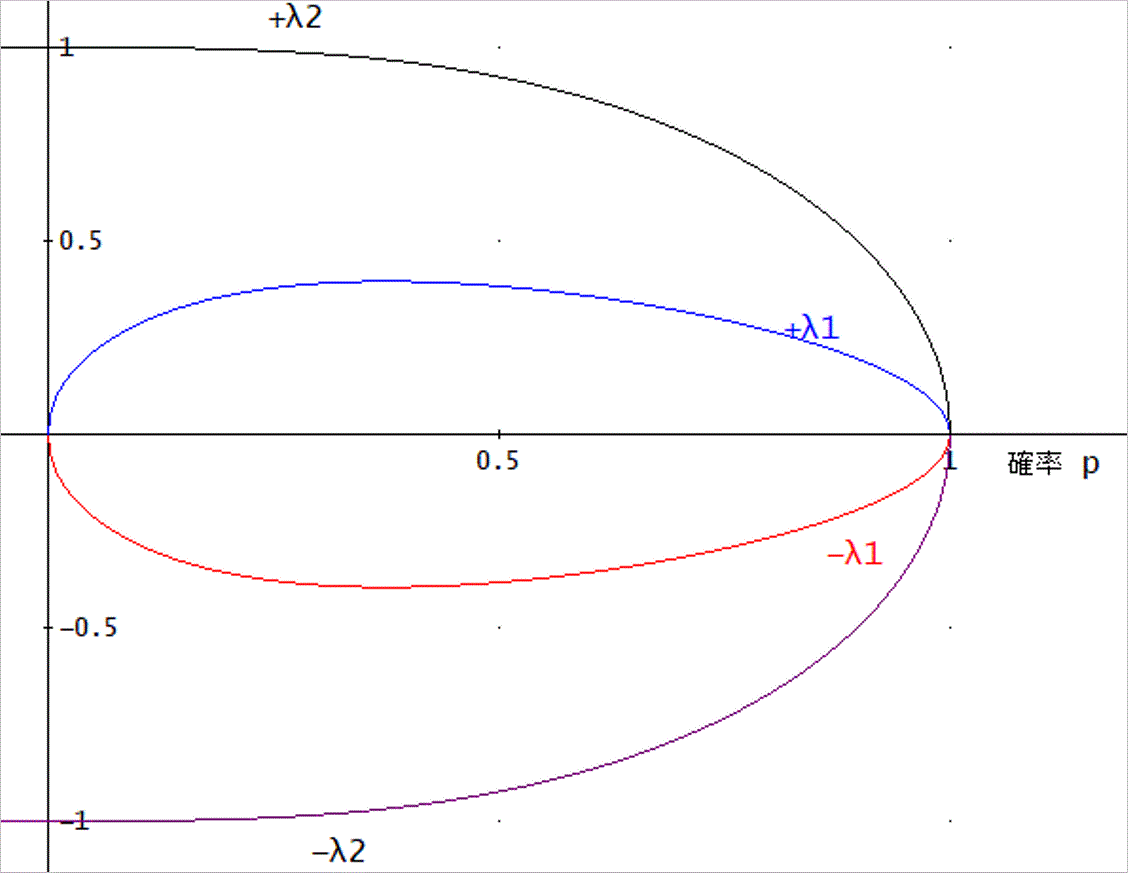
λ^4-λ^2q(2p+1)+pq^2=0、の解は、上図の通り。
横軸は、確率 p、
λ1=(√2 √(q) √(-√(4 p^2+1)+2 p+1)/2)、
λ2=(√2 √(q) √(√(4 p^2+1)+2 p+1)/2)
D1、D2の式に代入すると、
D1=√2 p^2 (√(4 p^2+1)-2 p-1)/((1-p)^(3/2) √(4 p^2+1) (-√(4 p^2+1)+2 p+1)^(3/2))、
D2=√2 p^2/((1-p)^(3/2) √(√(4 p^2+1)+2 p+1) √(4 p^2+1))、
よって、U4は、
U4(t)=(D1/2)×(λ1)^t-(D1/2)×(-λ1)^t+(D2/2)×(λ2)^t-(D2/2)×(-λ2)^t、
と定まる。
U4(2m+3)=(p^2 (1-p)^m ((√(4 p^2+1)+2 p+1)/2)^(m+1)/√(4 p^2+1)-p^2 (1-p)^m
(-(√(4 p^2+1)-2 p-1)/2)^(m+1)/√(4 p^2+1))
Wordの数式ツ-ルを使うと、こんな感じね」
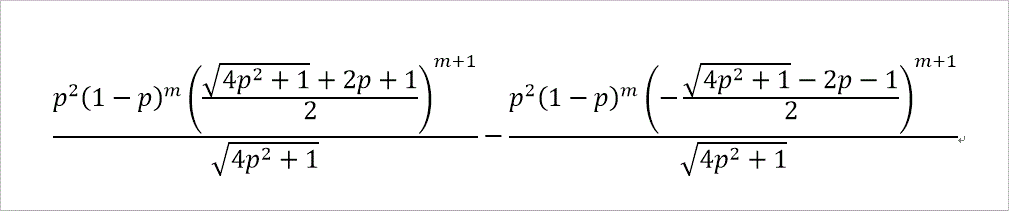
U4(2m+3)でm=0~5まで。
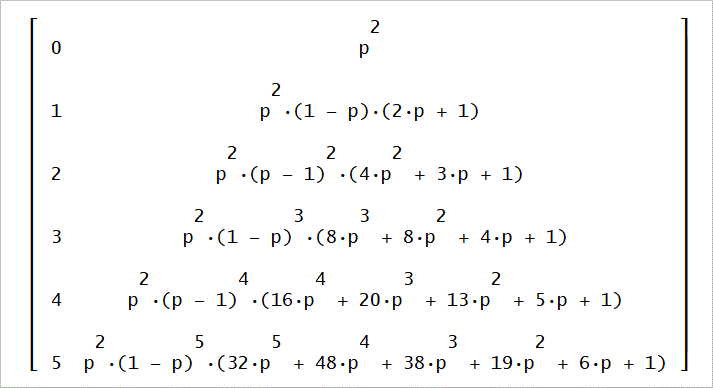
「では、その続きをわしがやってみよう。
まずは、U3を求めてみよう。
U3=(1/p)EU4(t)、より、
U3(t)=(1/p)U4(t+1)、
U3(t)=(1/p)U4(t+1)、t=2m+2とおいて、U3(2m+2)=(1/p)U4(2m+3)から、
U3(2m+2)でm=0~5の値。
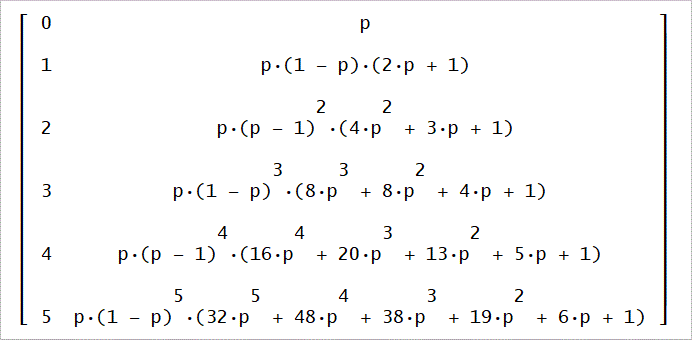
U2は、U2=(1/p)(EU3-qU4)から、
U2(t)=(1/p)(EU3(t)-qU4(t))=(1/p)(U3(t+1)-qU4(t))
U2(2m+1)=(1/p)((1/p)U4(2m+3)-qU4(2m+1))、
ただし、U4(1)=0とする。
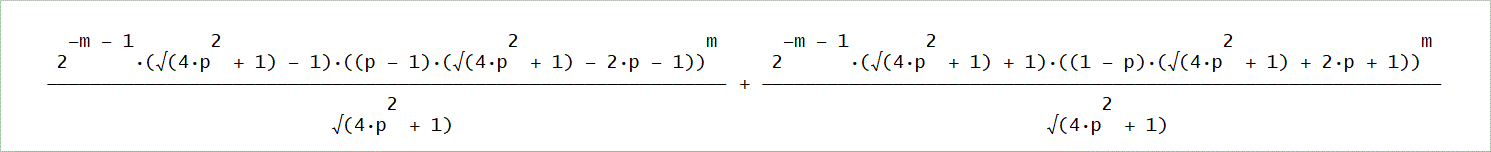
U2(2m+1)でm=0~5まで。
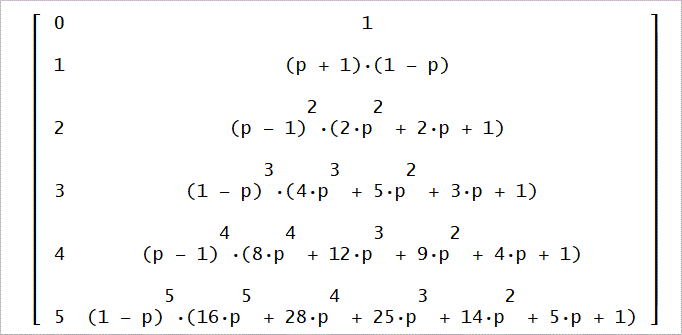
U1は、U1=EU2-qU3から、
U1(t)=U2(t+1)-qU3(t)、
U1(2m)=U2(2m+1)-qU3(2m)=(1/p)((1/p)U4(2m+3)-qU4(2m+1))-(q/p)U4(2m+1)、
ただし、U4(1)=0とする。
U1(2m)=(2^(-m - 1)·(√(4·p^2 + 1) + 2·p - 1)·((p - 1)·(√(4·p^2 + 1) - 2·p
- 1))^m/√(4·p^2 + 1) + 2^(-m - 1)·(√(4·p^2 + 1) - 2·p + 1)·((1 - p)·(√(4·p^2
+ 1) + 2·p + 1))^m/√(4·p^2 + 1))
U1(2m)のm=0~5までは、次のようになる」
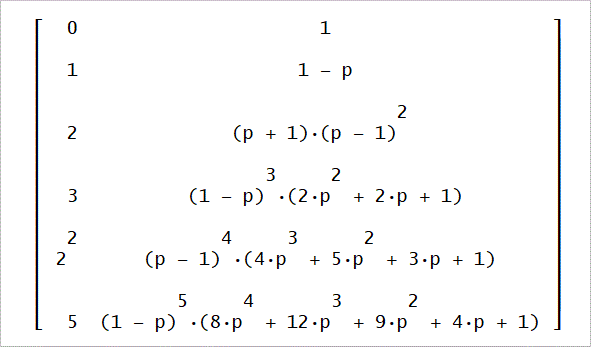
目次へ戻る
状態ベクトルの計算(最初から最後に進む)宿場数=3 (c=4)の例
 「今度は、逆に、U1(t)を先に求めてみるわね。
「今度は、逆に、U1(t)を先に求めてみるわね。
U1=C1(λ1)^t+C2(-λ1)^t+C3(λ2)^t+C4(-λ2)^t、である。
U1では、tが偶数の時にゼロでない値をとるため、(cの偶・奇に関わらない)
D3=C1+C2、D4=C3+C4とすれば、
U1=D3(λ1)^t+D4(λ2)^tである。
U1は、t が奇数の際にゼロとなることから、C1-C2=0、C3-C4=0、である。
これにより、
C1=D3/2、C2=C1、C3=D3/2、となる。
U1=(D3/2)(λ1)^t+(D3/2)(-λ1)^t+(D4/2)(λ2)^t+(D4/2)(-λ2)^t、と表される。
D3とD4は、
t=0とt=2の時のU1の値、
U1(0)=1、
U1(2)=1-p、
から、決定できる。
D3=(p+λ2^2-1)/(λ2^2-λ1^2)、
D4=(p+λ1^2-1)/(λ1^2-λ2^2)、 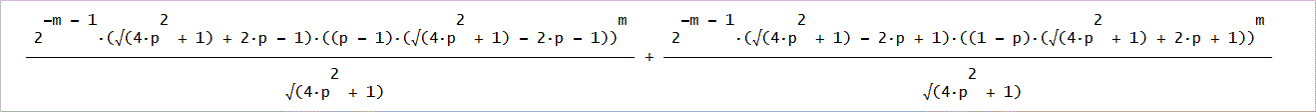
U1(2m)、m=0~5までの値。
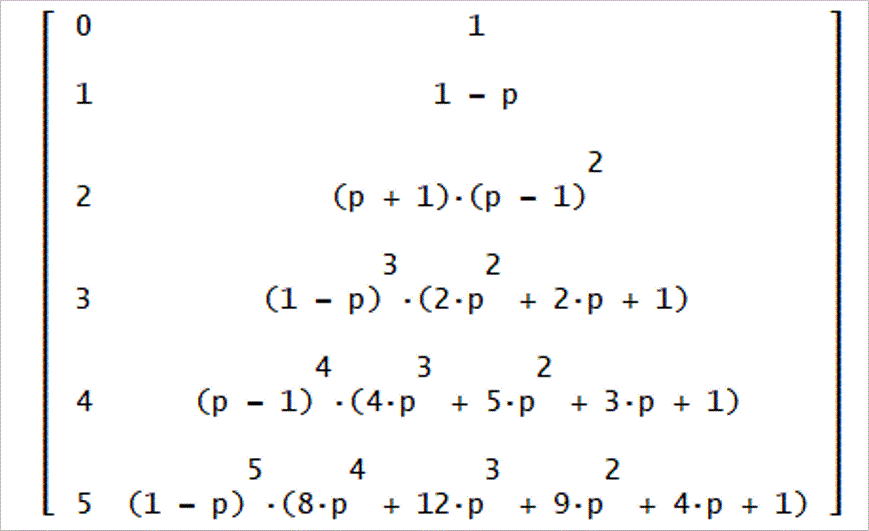
U1(t)から、U2(t)を求める。
U2は、EU1=qU2、から、
U2=(1/q)EU1、が得られる。 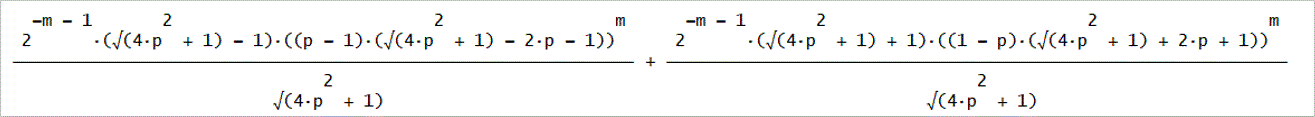
U2(2m+1)、m=0~5までで、
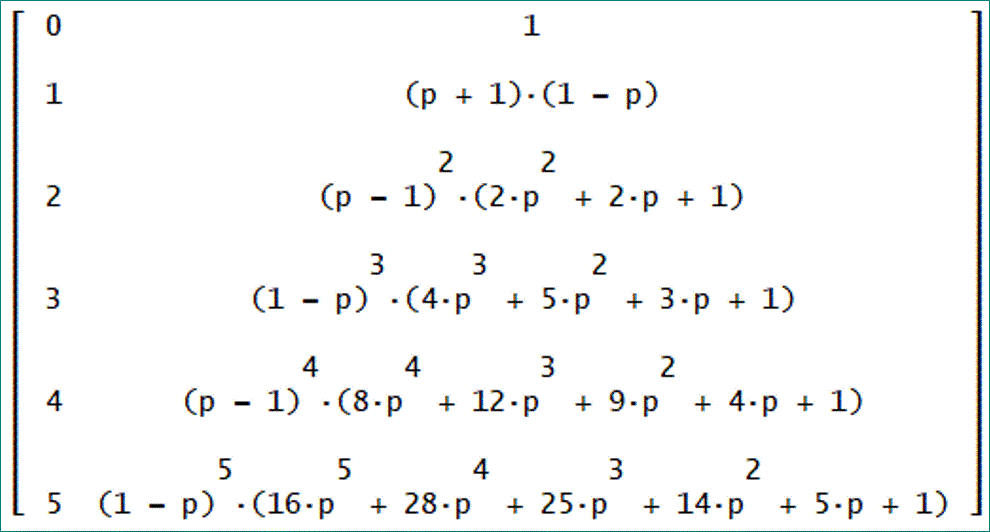
U3は、
U3=(1/q)(EU2-U1)として、 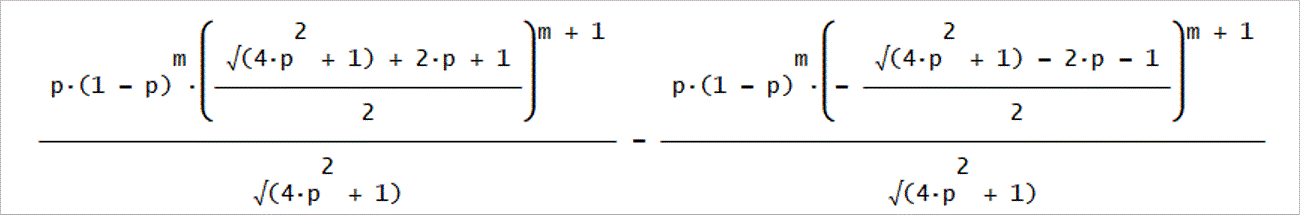
U3(2m+2)、m=0~5までで、
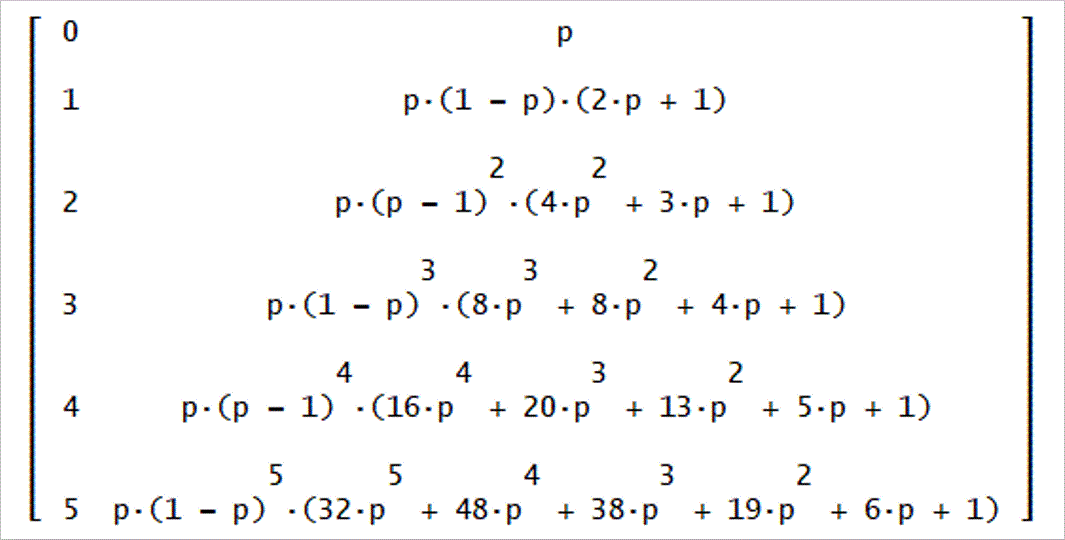
最後に、U4は、
U4=(1/q)(EU3-pU2)、として、
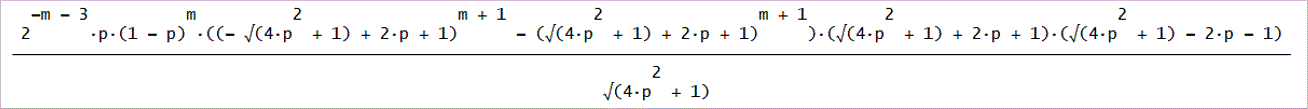
見た目は、U4から先に求めた場合と異なるように見えるが、実際は、同じである。
U4(2m+3)、m=0~5までで、下図の通り」
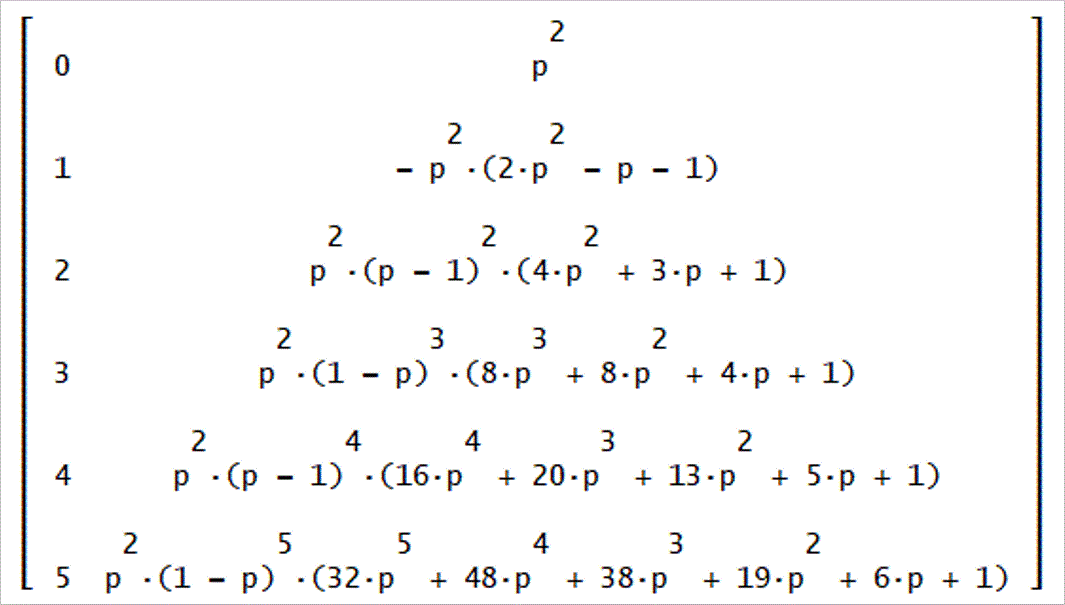
「このように、U1から求めていってもU4から求めても、状態ベクトルの計算結果は、当然ながら同一になるのじゃな。
C1等の係数計算は、U1から求めた方が簡単である。
しかし、その際は、U1を求めた後、U2、U3、を経て、U4に至る必要があるので、c が大きくなると面倒ではある。
ただし、最後の宿場以外の場所の状態ベクトルの値をすべて求める必要があれば、U1から順に求めていく方が容易だと思うのう。
今は、必ず、最後の宿場から上がるルールなので、平均日数の計算は、これまで通り、Uc のみを求めるようにしよう。
次節では、本稿のメインの平均日数の定式化について考えてみよう」
目次へ戻る
(3)差分法による状態ベクトルと平均日数
宿場数=3 (c=4)を例にして定式化
「これまでは、平均日数を求める場合、毎回、最初から計算を始めたが、手間を省くために、定式化を試みてみよう。
わしらの『非対称型道中双六』の問題では、平均日数の計算を、状態ベクトルの最後の要素の値を基にして計算を行う。
前節で調べたように、最後の宿場から求めても、最初の宿場から最後の宿場に進めても、同じなので、最後の宿場の値を求めるとして進める。
これは、t=2m+cの1つ手前の時刻、t=2m+c-1、の際の cの場所 の値、Uc(2m+c-1)である。
(m=0,1,・・の整数)、また、c=宿場数+1じゃ」
 「c=4の場合を例にとって、次のように計算してみたよ。
「c=4の場合を例にとって、次のように計算してみたよ。

U=[振り出し,宿場1,宿場2,宿場3]とし、
各要素を、U1(t)、U2(t)、U3(t) 、U4(t) と書くことにする。
Uの時間変化は、
[U1(t),U2(t),U3(t),U4(t)]= A^t ×[U1(0),U2(0),U3(0),U4(0)] で求められる。
状態ベクトルの最初の6つの具体的な値は、次のようになる。
t=0 [1, 0, 0, 0] 初期状態、
t=1 [0, 1, 0, 0]
t=2 [1 - p, 0, p, 0]
t=3 [0, 1 - p^2, 0, p^2]、
t=4 [(p - 1)·(p^2 - 1), 0, - p·(2·p^2 - p - 1), 0]
t=5 [0, (p - 1)·(2·p^3 - p - 1), 0, - p^2·(2·p^2 - p - 1)]
U4から先に求める場合、
U4(t)=(D1/2)×(λ1)^t-(D1/2)×(-λ1)^t+(D2/2)×(λ2)^t-(D2/2)×(-λ2)^t、
D1=√2 p^2 (√(4 p^2+1)-2 p-1)/((1-p)^(3/2) √(4 p^2+1) (-√(4 p^2+1)+2 p+1)^(3/2))、
D2=√2 p^2/((1-p)^(3/2) √(√(4 p^2+1)+2 p+1) √(4 p^2+1))、
平均日数=Σ(2m+4)×p×U4(2m+3)、で求めることができる。
和の計算を、m=0~nまで行うと、
(2 D1 p λ1^(2 n+5) (n (λ1^2-1)+2 λ1^2-3)/(λ1^2-1)^2+2 D2 p λ2^(2 n+5)
(n (λ2^2-1)+2 λ2^2-3)/(λ2^2-1)^2+2 D1 p λ1^3 (2-λ1^2)/(λ1^2-1)^2+2 D2 p
λ2^3 (2-λ2^2)/(λ2^2-1)^2)、
ここで、固有値 λ1、λ2が1より小さいことを使うと、
平均日数=(2 D1 p λ1^3 (2-λ1^2)/(λ1^2-1)^2+2 D2 p λ2^3 (2-λ2^2)/(λ2^2-1)^2)
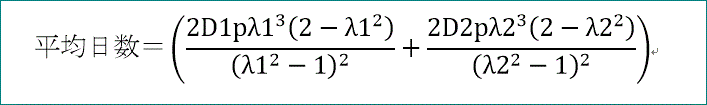
D1、D2、λ1、λ2を代入すると、
平均日数=2 (2 p^2-p+1)/p^3、となって、以前に求めた値と一致することが分かるわ」
「なるほど。
一般に、行列の要素が正またはゼロで、A^k がk → ∞、で、A^k → ゼロ行列が成り立つ場合、固有値は、1より小さいことが知られている。
(『行列と行列式』(古屋茂 著:培風館:1970年3月 増補第20版) 「元素が正数または0である行列の性質」)
これは、p が正ならば、十分な時間が経過後、すべての駒が上がるので、状態ベクトルのすべての要素がゼロになることから、成り立つじゃろう。
次節で、cの偶・奇により場合を分けて、平均日数の式を一般化してみよう」
目次へ戻る
一般化 c が偶数の場合
「 cが偶数の一般の場合について、平均日数を計算する式を導くとしよう。
以下では、c=2s、s=1~の自然数とする。
Uc(t)=Σ(i=1~2s)Ciλi^t、とする。
このとき、推移確率行列 Aの固有方程式、Φ(λ)=0は、2s次方程式である。
しかし、この方程式は、λ^2を新変数と置くことでs次方程式に変換できる(と予想)。
この方程式の根は、±λi、i=1~s、であり、すべて単根と仮定する。
すると、
Uc(t)=Σ(i=1~s)(C2i-1λi^t+C2i(-λi)^t)、となる。
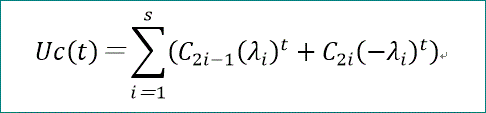
t=2m+c-1=2m+2s-1、の時のUcの値がゼロでないので、
(c=4の場合ならば、s=2なので、2m+3となる)
Uc(2m+2s-1)=Σ(i=1~s)(C2i-1λi^(2m+2s-1)+C2i(-λi)^(2m+2s-1))、となる。
C2i-1-C2i=Diと書き直すと、
Uc(2m+2s-1)=Σ(i=1~s)(Diλi^(2m+2s-1))、となる。
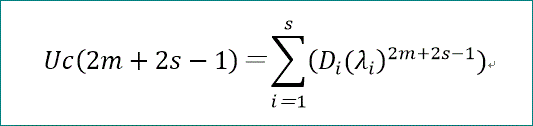
Diは、m=0~s-1、のs個の関係式から求めることができる。
具体的には、
Uc(2m+2s-1)=(A^(2m+2s-1)U(0))↓(2s)、(下向きの矢印は、要素の番号を示す。この場合は、最後の場所)
じゃな」
 「では、わたしは、平均日数の計算を一般化してみるよ。
「では、わたしは、平均日数の計算を一般化してみるよ。
平均日数は、
Uc(2m+2s-1)に上がる確率p及び日数(2m+2s)を掛けて、m=0~nまで集計すると、
Σ(2 Di p λi^(2 n+2 s+1) (n (λi^2-1)+s (λi^2-1)-1)/(λi^2-1)^2+2 Di p λi^(2
s-1) (λi^2-s (λi^2-1))/(λi^2-1)^2)、
n→∞の極限をとると、固有値が1より小さいことを考慮して、
平均日数=Σ(2 Di p λi^(2 s-1) (λi^2-s (λi^2-1))/(λi^2-1)^2)、となる。
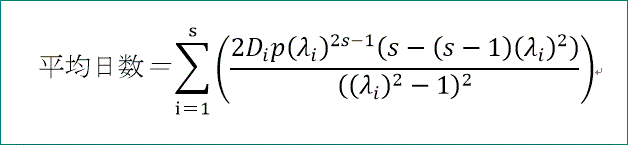
宿場数=3、c=4という具体的な例に適用してみると、
c=4、すなわちs=2なので、
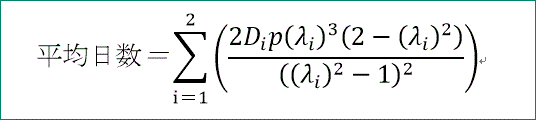
前節で導いた式は、次の通り。
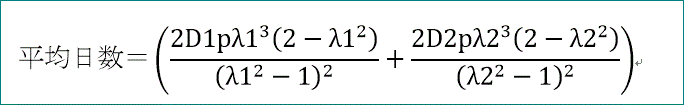
比較すると、一致していることが分かるわ」
「では、次の節では、c が奇数の場合を考えてみよう」
目次へ戻る
一般化 c が奇数の場合
 「cが奇数の場合を偶数の場合にならって、考えてみたわ。
「cが奇数の場合を偶数の場合にならって、考えてみたわ。
以下では、c=2s+1、s=1~の自然数ね。
Uc(t)=Σ(i=1~2s)Ciλi^t、とする。
このとき、推移確率行列Aの固有方程式は、2s+1次の方程式なんだけど、
これまでの経験では、λ×Φ(λ^2)=0、という形となっている。
Φ(λ^2)=0は、λ^2を新変数と置くことで、s次の方程式に変換できる(と予想)。
この方程式の根は、±λi、i=1~s、であり、すべて単根と仮定する。
すると、
Uc(t)=Σ(i=1~s)(C2i-1λi^t+C2i(-λi)^t)、となる。
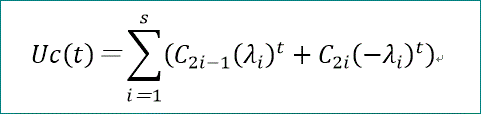
t=2m+c-1=2m+2s、の時のUcの値がゼロでないので、
(c=5の場合ならば、s=2なので、2m+4となる)
Uc(2m+2s)=Σ(i=1~s)(C2i-1λi^(2m+2s)+C2i(-λi)^(2m+2s))、となる。
C2i-1+C2i=Diと書き直すと、
Uc(2m+2s)=Σ(i=1~s)(Diλi^(2m+2s))、となる。
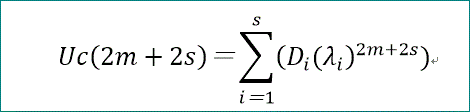
Diは、m=0~s-1、のs個の関係式から求めることができる。
具体的には、
Uc(2m+2s)=(A^(2m+2s)U(0))↓(2s+1)、である。
(下向きの矢印は、要素の番号を示す。この場合は、最後の場所)」
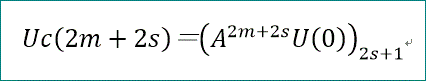
「では、わしが、平均日数の方を計算してみよう。
平均日数は、
Uc(2m+2s)に上がる確率p及び日数(2m+2s+1)を掛けて、m=0~nまで集計すると、
Σ(Di p λi^(2 (n+s+1)) (2 n (λi^2-1)+2 s (λi^2-1)+λi^2-3)/(λi^2-1)^2-Di
p λi^(2 s) (2 s (λi^2-1)-λi^2-1)/(λi^2-1)^2)
n→∞の極限をとると、固有値が1より小さいことを考慮して、
平均日数=Σ(Di p λi^(2 s) (λi^2+1-2 s (λi^2-1))/(λi^2-1)^2)、となる。
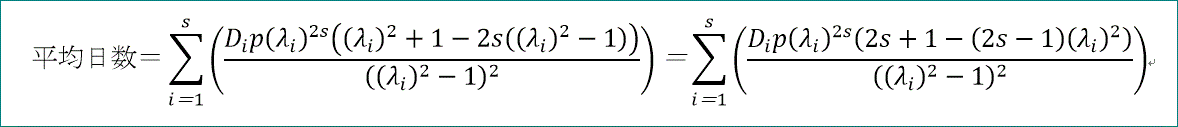
具体的な例として、c=5の場合、
c=2s+1、と書いたとき、s=2、の場合を試してみる。

推移確率行列 Aは、下図のようになる。

固有方程式は、
(-λ (λ^4+λ^2 (p-1) (3 p+1)+p (p+2) (p-1)^2))=0、
λ=0以外の根は、4つあるが、それらは、
±(√2 √(1-p) √(-√(5 p^2-2 p+1)+3 p+1)/2)=±λ1、
±(√2 √(1-p) √(√(5 p^2-2 p+1)+3 p+1)/2)=±λ2、
である。
Diは、次の関係から決まる。
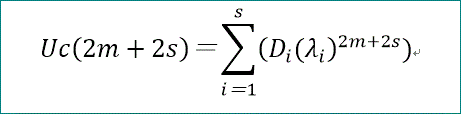
D1とD2を決める式は、
Uc(2m+2s)=(A^(2m+2s)U(0))↓(2s+1)
s=2なので、
Uc(2m+4)=(A^(2m+4)U(0))↓(5)
ここで、m=0、m=1、の2つのケ-スについて、計算すると、
Uc(4)=p^3、
Uc(6)=p^3 (1-p) (3 p+1)、
よって、
D1=p^3 (3 p^2-2 p+λ2^2-1)/(λ1^4 (λ2^2-λ1^2))、
D2=p^3 (3 p^2-2 p+λ1^2-1)/(λ2^4 (λ1^2-λ2^2))、
平均日数の式は、
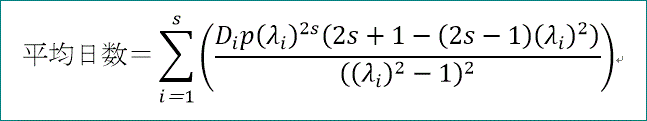
であるので、
平均日数=(p^4 (3 λ1^2-5) (3 p^2-2 p+λ2^2-1)/((λ1^2-1)^2 (λ1^2-λ2^2)))+(p^4
(5-3 λ2^2) (3 p^2-2 p+λ1^2-1)/((λ1^2-λ2^2) (λ2^2-1)^2))
=((p^4+6 p^2-4 p+2)/p^4)、
となった。
これは、第89回で導いた宿場数=4(c=5)の場合の平均日数と一致しているのが分かるじゃろう。
新しい節で、平均日数等の計算をもう少し、簡素にする方法を調べよう」
目次へ戻る
(4)差分法による平均日数等の計算式の簡素化
c が偶数の場合の簡素化
「cが偶数の場合(c=2s)の下式をもう少し簡素化する。
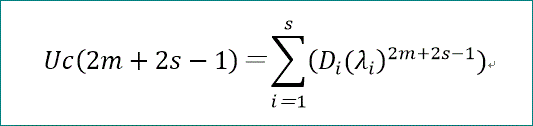
上の式で、di=Di(λi^(2s-1))、と置くと、
Uc(2m+2s-1)=Σ(i=1~s)(diλi^(2m))、となる。
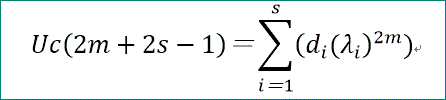
diは、m=0~s-1、のs個の関係式から求めることができる。
具体的には、
Uc(2m+2s-1)=(A^(2m+2s-1)U(0))↓(2s)、
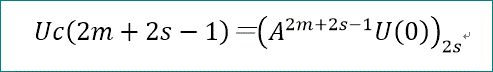
じゃな」
 「ここで、読者のみなさんにお知らせですよ。
「ここで、読者のみなさんにお知らせですよ。
DERIVEの標準では、
・ 大文字と小文字を区別しない、
・ 1文字は1変数と見なす、
が有効となっているのね。
だから、今までもそうだったんだけど、
DERIVEのオプションからモード設定で、
以下のように、設定を変更しておかないと、D と d が同一視されたり、D2がD×2の意味になってしまうわよ。
だけど、こうしたときは、関数名を、必ず、大文字で書かないと正しく解釈されないので注意。
たとえば、平方根を表す関数は、通常は、sqrt(x) と書いても、Sqrt(x)、と書いても、自由なんだけど、
上図のように設定を変更した場合は、SQRT(x)と書く必要があるのね。
もちろん、変数間のかけ算は、アスタリスク * を必ず使用する習慣を付けておく必要がある。
そうしないと、xa は、x×aではなく、xa という1つの変数になってしまう。
ああ、だけど、かっこを使っている場合は、x*(a+b)、と書かなくても、x(a+b)でも差し支えないわ」
「おっと、ともちゃん、その注意は、助かるな。
さて、平均日数は、
平均日数=Σ(m=0~∞)(p(2m+2s)Σ(i=1~s)(diλi^(2m)))、
=Σ(i=1~s)((2dip(λi^2-s(λi^2-1))/(λi^2-1)^2))
更に、μi≡λi^2、と置けば、
Uc(2m+2s-1)=Σ(i=1~s)(di μi^(m))、となる。
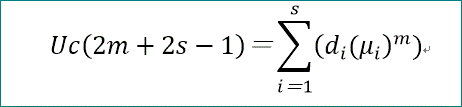
一方、前節で一般化した平均日数は、
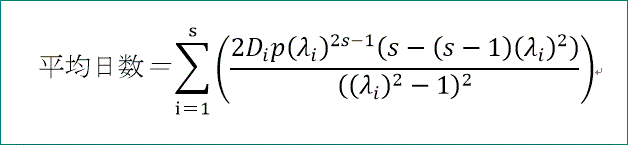
だったので、λ^2 をμに置き換えることで、
平均日数=Σ(i=1~s)(2dip(s-(s-1)μi)/((μi-1)^2))、
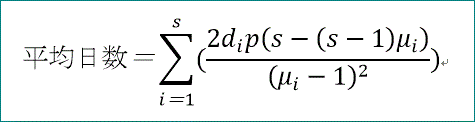
と簡素化されたことが分かるじゃろう。
なお、di の計算では、次のように工夫すると、見通しが良い。
例えば、c=8の場合、s=4なので、
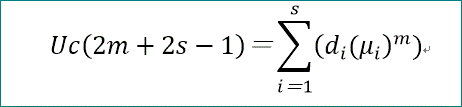
上式は、次のような行列で表現できるじゃろう。
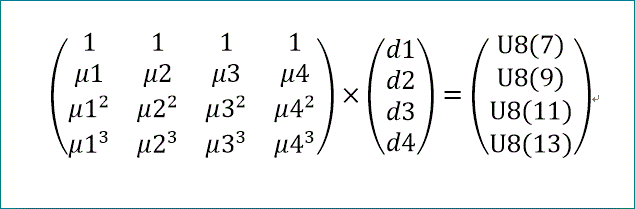
ここで、右辺の縦ベクトルは、U8(2m+2s-1)、m=0~3を動く。
(A^(2m+2s-1)×U(0)’)↓(2s) 、で、その具体的な値は、求められる」
目次へ戻る
c が偶数の例 宿場数=5 (c =6)
 「じゃ、c=6(宿場数=5)について、検証してみるよ。
「じゃ、c=6(宿場数=5)について、検証してみるよ。

ちなみに、推移確率行列は、下図のようになる。

c=6なので、c=2sとしたときの、s=3の場合ね。
U6(5)=(A^(5)U(0))↓(6)=p^4=Σdi
U6(7)=(A^(7)U(0))↓(6)=p^4 q (4 p+1)=Σdi μi
U6(9)=(A^(9)U(0))↓(6)=p^4 q^2 (13 p^2+5 p+1)=Σdi μi^2
から、
d1=p^4 (13 p^4-21 p^3+4 p^2 (μ2+μ3+1)-3 p (μ2+μ3-1)+(μ2-1) (μ3-1))/((μ1-μ2) (μ1-μ3))、
d2=p^4 (13 p^4-21 p^3+4 p^2 (μ1+μ3+1)-3 p (μ1+μ3-1)+(μ1-1) (μ3-1))/((μ1-μ2)
(μ3-μ2))、
d3=p^4 (13 p^4-21 p^3+4 p^2 (μ1+μ2+1)-3 p (μ1+μ2-1)+(μ1-1) (μ2-1))/((μ1-μ3) (μ2-μ3))、
と係数が求められた。
平均日数の式は、
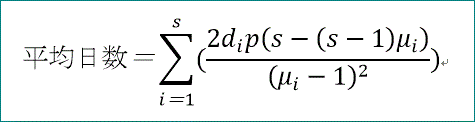
そこで、
平均日数=(2·d1·p·(3 - 2·μ1)/(μ1 - 1)^2 + 2·d2·p·(3 - 2·μ2)/(μ2 - 1)^2 + 2·d3·p·(3
- 2·μ3)/(μ3 - 1)^2)、
ここに、d1等の式を代入すると、
平均日数=分子/分母、の形に整理できる。
分母=(μ1 - 1)^2·(μ2 - 1)^2·(μ3 - 1)^2、
分子=(- 2·p^5·(13·p^4·(μ1·(μ2·(2·μ3 - 3) - 3·μ3 + 4) + μ2·(4 - 3·μ3) + 4·μ3
- 5) - 21·p^3·(μ1·(μ2·(2·μ3 - 3) - 3·μ3 + 4) + μ2·(4 - 3·μ3) + 4·μ3 - 5)
+ 4·p^2·(μ1^2·(μ2·(2·μ3 - 3) - 3·μ3 + 4) + μ1·(μ2 + μ3 - 1)·(μ2·(2·μ3 -
3) - 3·μ3 + 4) + μ2^2·(4 - 3·μ3) - μ2·(3·μ3^2 - 7·μ3 + 4) + 4·μ3^2 - 4·μ3
- 1) - 3·p·(μ1^2·(μ2·(2·μ3 - 3) - 3·μ3 + 4) + μ1·(μ2 + μ3 - 3)·(μ2·(2·μ3
- 3) - 3·μ3 + 4) + μ2^2·(4 - 3·μ3) - μ2·(3·μ3^2 - 13·μ3 + 12) + 4·μ3^2
- 12·μ3 + 9) + μ1^2·(μ2^2·(2·μ3 - 3) + μ2·(μ3 - 3)·(2·μ3 - 3) - 3·μ3^2
+ 9·μ3 - 7) + μ1·(μ2^2·(μ3 - 3)·(2·μ3 - 3) - μ2·(9·μ3^2 - 30·μ3 + 25) +
9·μ3^2 - 25·μ3 + 18) - μ2^2·(3·μ3^2 - 9·μ3 + 7) + μ2·(9·μ3^2 - 25·μ3 +
18) - 7·μ3^2 + 18·μ3 - 12))、
ここで、固有方程式、は、6次で、
λ^6 + λ^4·(4·p^2 - 3·p - 1) + 3·pλ^2·(p + 1)·(p - 1)^2 + p^2·(p - 1)^3)=0、
の6つの根 λ、から、μ=λ^2、を使うと、
μ1=(p - 1)·(√3·√(7·p^2 - 2·p + 1)·COS(θ) - √(7·p^2 - 2·p + 1)·SIN(θ) -
5·p - 1)/3、
μ2=√3·(1 - p)·√(7·p^2 - 2·p + 1)·COS(θ)/3 + (1 - p)·√(7·p^2 - 2·p + 1)·SIN(θ)/3
+ (1 - p)·(5·p + 1)/3、
μ3=(p - 1)·(2·√(7·p^2 - 2·p + 1)·SIN(θ) - 5·p - 1)/3、
なお、θは、
前掲の分子の式にμ1、μ2、μ3を代入すると、
θ=(ASIN((20 p^3-12 p^2-3 p+2)/(2 (7 p^2-p+1)^(3/2)))/3)、を使って、
分子=(2·p^5·(3·p^4 - 3·p^3 + 5·p^2 - 3·p + 1))、と簡単化される。
一方、
分母=((μ1 - 1)^2·(μ2 - 1)^2·(μ3 - 1)^2)、
ここで、(μ1 - 1)·(μ2 - 1)·(μ3 - 1) を計算すると、-p^5となるので、
分母=(-p^5)^2=p^10、であることが分かる。
結局、平均日数=(2 (3 p^4-3 p^3+5 p^2-3 p+1)/p^5)、と厳密解の予想式と一致することが分かった」
「なかなか、大変じゃったな。
とは言え、第89回の宿題を1つ解決できた。
それと、ワンポイントアドバイスじゃが、分母は、簡単に計算できるぞ。
λ^6 + λ^4·(4·p^2 - 3·p - 1) + 3·pλ^2·(p + 1)·(p - 1)^2 + p^2·(p - 1)^3)=0、
において、λ^2=μと置き換えた方程式は、
Φ(μ)=μ^3+μ^2·(4·p^2 - 3·p - 1) + 3·pμ·(p + 1)·(p - 1)^2 + p^2·(p - 1)^3、
ここで、Φが、根 μi を使って、Φ=(μ-μ1)(μ-μ2)(μ-μ3)、と表示できることに注意すれば、
分母=((μ1 - 1)^2·(μ2 - 1)^2·(μ3 - 1)^2)=(Φ(1))^2=(-p^5)^2=p^10、となるんだな」
「あ、確かに!
固有値を使った計算は、分子だけで良かったのね」
目次へ戻る
c が奇数の場合の簡素化
「では、cが奇数の場合じゃ。
実は、偶数とまったく同じには、ならないんじゃな。
c=2s+1、s=1~の自然数とすると、
Uc(t)=Σ(i=1~2s)Ciλi^t、と仮定すれば、
このとき、推移確率行列Aの固有方程式f(λ)=0は、2s+1次方程式であるが、
実際は、λ×Φ(λ^2)=0、という形となる。
Φ(λ^2)=0は、λ^2を新変数と置くことでs次方程式に変換できる。
この方程式の根は、±λi、i=1~s、であり、すべて単根と仮定すると、
Uc(t)=Σ(i=1~s)(C2i-1(λi)^t+C2i (-λi)^t)、となる。
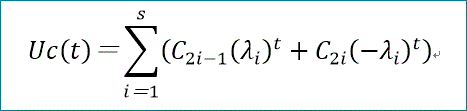
cが奇数では、
t=2m+c-1=2m+2s、の時のUcの値がゼロでないので、
(c=5の場合ならば、s=2なので、2m+4となる)
Uc(2m+2s)=Σ(i=1~s)(C2i-1λi^(2m+2s)+C2i(-λi)^(2m+2s))、となる。
C2i-1+C2i=Diと書き直すと、
Uc(2m+2s)=Σ(i=1~s)(Diλi^(2m+2s))、となる。
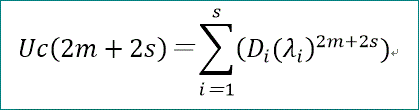
さらに、di=Di(λi^(2s))、と置くと、
Uc(2m+2s)=Σ(i=1~s)(di λi^(2m))、と書ける。
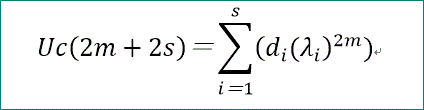
diは、m=0~s-1、のs個の関係式から求めることができる。
具体的には、
Uc(2m+2s)=(A^(2m+2s)U(0))↓(2s+1)
である。
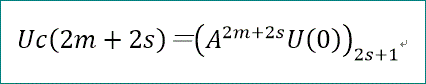
更に、μi=λi^2、と置くことにより、
Uc(2m+2s)=Σ(i=1~s)(di μi^(m))、と書ける」
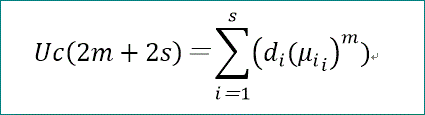
 「では、わたくしが、平均日数を計算してみるね。
「では、わたくしが、平均日数を計算してみるね。
Uc(2m+2s)に上がる確率p及び日数(2m+2s+1)を掛けて、m=0~nまで集計すると、
(di p μi^(n+1) (2 n (μi-1)+2 s (μi-1)+μi-3)/(μi-1)^2-di p (2 s (μi-1)-μi-1)/(μi-1)^2)
n→∞にて、固有値が1より小さいことを考慮して、
平均日数=Σ(di p (2 s+1-(2s-1)μi)/(μi-1)^2)、
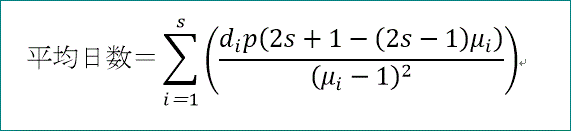
と簡素化された平均日数の式が求められたわ」
「では、c=5、(宿場数=4)、及び c=7、(宿場数=6)、という2つの例で計算し、確認してみよう」
目次へ戻る
c が奇数の例1 宿場数=4 (c=5)
「宿場数=4,すなわち、c=5の場合は、
c=2s+1、において、s=2 に相当するので、奇数の場合の簡素化された公式を試してみよう。

推移確率行列 Aは、下図のようになる。

固有方程式は、
(-λ (λ^4+λ^2 (p-1) (3 p+1)+p (p+2) (p-1)^2))=0、となるので、
λ=0を除くと、4次式であるが、λ^2=μと置き換えると、
μ1=λ1^2=((p-1) (√(5 p^2-2 p+1)-3 p-1)/2)、
μ2=λ2^2=((1-p) (√(5 p^2-2 p+1)+3 p+1)/2)、
d1とd2を決める式は、
Uc(2m+2s)=Σ(i=1~s)(di μi^(m))、から、
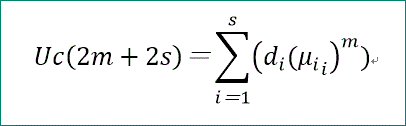
上式で、s=2なので、
Uc(2m+4)=(A^(2m+4)U(0))↓(5)
ここで、m=0、m=1、の2つのケ-スについて、計算すると、
Uc(4)=p^3=d1+d2、
Uc(6)=p^3 (1-p) (3 p+1)=d1μ1+d2μ2、
よって、
d1=p^3 (3 p^2-2 p+μ2-1)/(μ2-μ1)、
d2=p^3 (3 p^2-2 p+μ1-1)/(μ1-μ2)、
では、平均日数は、お銀さん、お願いしますよ」
 「あんたは、黄門様かいな。
「あんたは、黄門様かいな。
えーと、平均日数は、
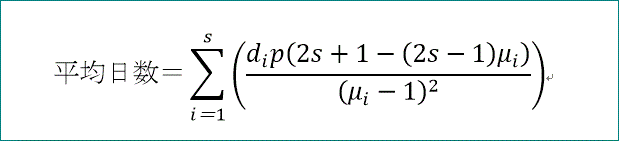
s=2の場合なので、
平均日数=(-p^4 (3 p^2 (μ1 (3 μ2-5)-5 μ2+7)-2 p (μ1 (3 μ2-5)-5 μ2+7)+μ1^2 (3
μ2-5)+μ1 (μ2-3) (3 μ2-5)-5 μ2^2+15 μ2-12)/((μ1-1)^2 (μ2-1)^2))、
ここで、μ1、μ2を代入すると、
平均日数=((p^4+6 p^2-4 p+2)/p^4)、となり、以前導いた結果と一致することが分かったわ」
「どれどれ、2次方程式の根では、三角関数が出てこないので、そのまま代入すれば、十分じゃな。
では、節を変えて、宿場数=6、すなわち、c=7の場合をやってみよう」
目次へ戻る
c が奇数の例2 宿場数=6 (c=7)
「宿場数=6,すなわち、c=7の場合は、
c=2s+1、において、s=3 に相当するので、奇数の場合の簡素化された公式を試してみよう。
固有方程式は、
(-λ (λ^6+λ^4 (p-1) (5 p+1)+2 p λ^2 (p-1)^2 (3 p+2)+p^2 (p+3) (p-1)^3))、
λ=0以外の根は、6つあるが、
±√3 √(1-p) √(-√3 √(7 p^2-2 p+1) COS(θ)+√(7 p^2-2 p+1) SIN(θ)+5 p+1)/3
±√3 √(1-p) √(√3 √(7 p^2-2 p+1) COS(θ)+√(7 p^2-2 p+1) SIN(θ)+5 p+1)/3、
±√3 √(1-p) √(√3 √(7 p^2-2 p+1) COS(θ)+√(7 p^2-2 p+1) SIN(θ)+5 p+1)/3、
である。
θは、θ=ASIN((7 p^3-3 p^2-6 p+2)/(2 (7 p^2-2 p+1)^(3/2)))/3、
従って、μ=λ^2は、
μ1=((p-1) (√3 √(7 p^2-2 p+1) COS(θ)-√(7 p^2-2 p+1) SIN(θ)-5 p-1)/3)、
μ2=(√3 (1-p) √(7 p^2-2 p+1) COS(θ)/3+(1-p) √(7 p^2-2 p+1) SIN(θ)/3+(1-p)
(5 p+1)/3)、
μ3=((p-1) (2 √(7 p^2-2 p+1) SIN(θ)-5 p-1)/3)
となる。
一方、d1、d2、d3を決める式は、
Uc(2m+2s)=Σ(i=1~s)(diμi^(m))、
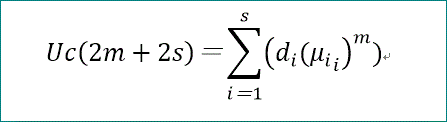
上式で、s=3の場合なので、
Uc(6)=p^5=Σdi、
Uc(8)=(p^5 (1-p) (5 p+1))=Σdiμi、
Uc(10)=(p^5 (p-1)^2 (19 p^2+6 p+1))=Σdiμi^2、
から、
d1=p^5 (19 p^4-32 p^3+p^2 (5 μ2+5 μ3+8)-4 p (μ2+μ3-1)+(μ2-1) (μ3-1))/((μ1-μ2)
(μ1-μ3))、
d2=p^5 (19 p^4-32 p^3+p^2 (5 μ1+5 μ3+8)-4 p (μ1+μ3-1)+(μ1-1) (μ3-1))/((μ1-μ2) (μ3-μ2))、
d3=p^5 (19 p^4-32 p^3+p^2 (5 μ1+5 μ2+8)-4 p (μ1+μ2-1)+(μ1-1) (μ2-1))/((μ1-μ3)
(μ2-μ3))、
ここは、わしが平均日数まで、求めてしまおう。
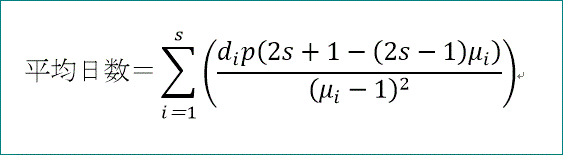
s=3の場合なので、
平均日数=(-27 p^6 (2 (p-1)^3 (7 p^2-2 p+1)^(3/2) SIN(3 θ)+20 p^6+24 p^5+300
p^4-436 p^3+453 p^2-228 p+56)/(2 (p-1)^6 (7 p^2-2 p+1)^3 COS(6 θ)+4 (1-p)^3
(5 p^2-4 p+2) (7 p^2-2 p+1)^(3/2) (4 p^4+8 p^3-4 p+1) SIN(3 θ)-3 (362 p^12-1248
p^11+4632 p^10-8936 p^9+10458 p^8-8208 p^7+4800 p^6-2376 p^5+1089 p^4-440
p^3+132 p^2-24 p+2)))、
ここで、θを置き換えると、
平均日数=(p^6+12 p^4-16 p^3+16 p^2-8 p+2)/p^6、
となり、これは、第88回で予想していた厳密解であることが分かった」
 「ご隠居様、お疲れ様でした。
「ご隠居様、お疲れ様でした。
これで、c=2~7までは、厳密解が得られたことになるわね。
c=8、では、どうかしら?」
「そろそろ、厳密解という意味では、限界に来ているかのう。
固有方程式の解は、p を数値として与えて、固有値も数値で求めるしかなくなるじゃろう。
ところで、大分、分量が多くなったので、今回は、このくらいにしておこう。
いや、ともちゃんも、お疲れさんじゃった」
目次へ戻る
最終更新日 2018/5/22
タイトルを変更 2018/5/23
文章の一部を微修正 2018/5/27、2018/9/23
c=8、10の結果を概要に追記 2020/7/15




 「数式ツールは、2018年5月の今月のご挨拶『
「数式ツールは、2018年5月の今月のご挨拶『


