数式処理ソフト DERIVE(デライブ) de ドライブ
91.マルコフ過程(4)(非対称型道中双六:固有方程式の漸化式)
目次
(1)概要
(2)固有方程式の漸化式
まえがき
用語の話
c が奇数の場合の固有方程式
c が偶数の場合の固有方程式
固有方程式の書き下ろし
(3)λ^2の多項式の理由
(4)固有方程式の判別式
判別式のご利益と定義
2次方程式の判別式
3次方程式の判別式
4次方程式の判別式
4次方程式の判別式の応用
5次方程式の判別式
(※cは、宿場数+1で、上がりに至る最短日数です)
(1)概要
『DERIVE de ドライブ』の第91回では、非対称型道中双六の問題の固有方程式を帰納的再帰関数として求めました。
これで、推移確率行列を経由しなくても、固有方程式を計算できるようになりました。
c=宿場数+1、としたとき、c =2~25、c=30 の場合の固有方程式(の左辺の多項式)を書き下ろしました。
また、cが偶数では、方程式が、(固有値^2の多項式)であること、並びに、
c が奇数では、固有値×(固有値^2の多項式)であること、について、証明しました。
なお、その理由についても、考察しました。
確率 pが、0<p<1 の間で、固有方程式の根が単根であることに関連して、代数方程式(2次~5次)の判別式について、少し、調べて見ました。
判別式は、方程式の根を使って定義されますが、実際は、方程式の係数のみで書き直すことができます。
前回導いた、平均日数の計算公式も固有方程式の根を含んでいますが、これが方程式の係数のみで書き表すことができるかどうかも、今後の検討課題です。
目次へ戻る
(2)固有方程式の漸化式
まえがき
「非対称型道中双六の固有方程式を漸化式の形で求めてみよう。
漸化式を求める目的は、
(1)推移確率行列を経由しなくても、固有方程式を書き下ろせること、
(2)c を宿場数+1とおいたとき、c=奇数では、固有方程式が、λ×(λ^2の多項式)=0、となることを示す、
(3)c =偶数では、固有方程式が、(λ^2の多項式)=0、であることを示す、
の3つじゃな」
 「なるほど。
「なるほど。
えーと、読者の皆様に、ちょっとだけ、説明しますね。
おじぃさんが言っている『非対称型道中双六』は、この『DERIVE de ドライブ』では、何度も登場しているのね。
図で書くと、こんな感じの双六。
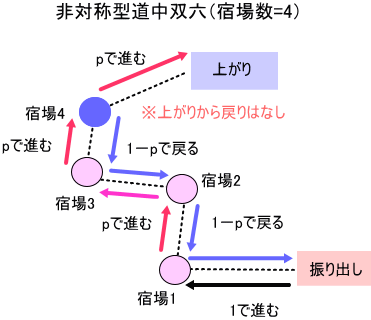
更に詳しい説明は、第88回の『マルコフ過程(1)(非対称型道中双六:宿場数=3~9)』をお読み下さいな。
なお、推移確率行列は、上がりを(わざと)除いているので、注意して下さい。
従って、上の図では、振り出しから上がりの直前の宿場まで、5つの場所があるとして、
この推移確率行列 A は、下図のようになります。

Aの固有値を求める固有方程式は、|A-λI|=0、となるので、一般に λの5次方程式となるはずでしょ。
※λは、固有方程式の変数名、I は、単位行列です。
ところが、これまで、実際に計算した c=2~10 では、
c が奇数では、固有方程式が、λ×(λ^2の多項式)=0、
また、c が偶数では、固有方程式が、(λ^2の多項式)=0、となるのね。
そこで、第90回『マルコフ過程(3)(非対称型道中双六:平均日数計算公式)』では、これらを仮定して、平均日数の計算式を導いてる。
今回、それを一般的に証明してみようということなの」
「お、ともちゃん、今回もお世話になりますよ。
ま、実際は、(2)、(3)を証明しようとする過程で、固有方程式の漸化式が得られたので、副産物として、(1)もできることになったということじゃ。
本当は、第90回に書きたかったのじゃが、行列式の演算は、とんと、忘れてしまっていたので、取り上げられなんだ。
行列式の演算など、面倒なことは、DERIVE さんにお任せしてきたので、『一般には・・』という証明は、ちょと、弱ることがあるんだな。
そこで、次回、ともちゃんに、行列式とはなんぞや、から、行列式の展開方法を復習してもらえんかのう」
目次へ戻る
用語の話
 「分かりやした。
「分かりやした。
行列・行列式関係のDERIVEの関数もご紹介しますよ。
ところで、これまで、固有方程式が、λ^2の関数、というような表現があった思うけど、正確には、λ^2に関する(実数係数の)多項式と言うのが正しいと思う。
もちろん、多項式も関数だから、まったくの間違いと言うのではないけども。
ま、読者の皆様には、その意図するところは、伝わっているとは思うけどね」
「たしかにな。
ついでなので、言い訳しておくとじゃな、前にも書いたことがあるが、方程式の『根』は、現代数学では、『解』と書くのが一般的なようだ。
なので、実根は、実数解、(純)虚根は、(純)虚数解、複素根は、複素数解、などと書くべきなんじゃ。
つい、習慣で、根、根と言ってしまう」
「コン、コン、とは、まるで、お狐さんのようね。

私も、合わせて、いきますよ。
ついでに言えば、『同次』、あるいは、『斉次』も分かりにくい。
数学では、普通、同じ意味で利用されているようね。
同次や斉次は、そのまま読めば、次数が等しいことなので、x^2+a 2xy+b y^2 、のように、考えている変数 x,y について、同じ次数を意味する。
ただ、dy/dx=h(y/x)、のように、関数/変数を新変数に置き換えると、新変数の方程式に変換できるものも『同次形』と呼ばれる。
同次と斉次では、斉次の方が昔から使われている用語かも知れないわ。
日常生活でも、『一斉に・・』とか『斉唱』などに使われるけど、最近は、あまり見ない気がする。
それは、『斉』が常用漢字ではあるけど、中学校までに習う漢字には、入っていないからでしょうね」
「ま、振り返ると、『方程式』は、式=0、の全体を指すんじゃが、方程式の左辺の部分を、方程式と書いている個所もあると思う。
いちいち、『方程式の左辺は、・・』など書くのは、冗長すぎる気がするのでな。
更に言えば、『整次式』という用語も、自分では、次数が整数の多項式、のようなつもりで書いたことがあったと思う。
じゃが、あらためて、Googleで検索してみると、ともちゃんが挙げてくれた『斉次式』は、あるが、『整次式』は、ヒットしない。
これらを含めて、全体の文脈で読者が混乱することはないと思うが、気をつけていこう」
目次へ戻る
c が奇数の場合の固有方程式:λ×(λ^2の多項式)=0
「例によって、前置きが長くなってしまったのう。
c=5の場合について、証明の手順を説明しよう。
これは、容易に、c が一般の奇数の場合に適用できる。
さて、c=5の固有方程式を、Φ(λ,5) と書くことにしよう。
※引数のλは、固有値の変数名を明確にしているだけで、計算方法には、無関係。
固有方程式は、一般に、|A-λI|=0、であり、( I は、単位行列)
Φ(λ,5)は、具体的には、次のようじゃ。

※上の図で、q は、1-p を表す。
行列式を1行目について展開して、(行列式の展開などは、次回、ともちゃんが説明します。以下同様)
Φ(λ,5)=-λ×(1,1余因子行列式) + q×(-1)(1,2余因子行列式)、
ここで、( i , j 余因子行列式)は、元の行列式の i 行及び j 列を除いた行列式。
すなわち、(1,1余因子行列式)は、下図の行列式から青い破線の行と列を除いた行列式で、

次のように、1つ次元が低い4次行列式で表される。
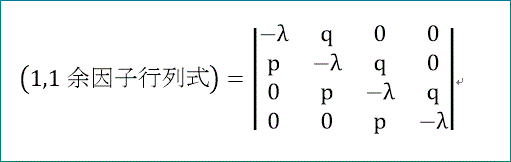
今、ここで、f(λ,2)を次式で定義すると、
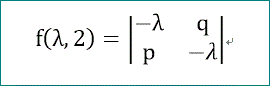
同じ構造を持つ (1,1余因子行列式)を、f(λ,4) と書くことができるじゃろう。
これは、後に、固有方程式の漸化式の1つの要素となる。
一方、(1,2余因子行列式)は、下図の行列式から青い横線の行と赤い縦線の列を除いた行列式で、
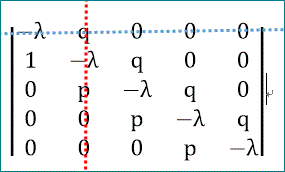
次のように、次元が1つ低い4次行列式で表される。
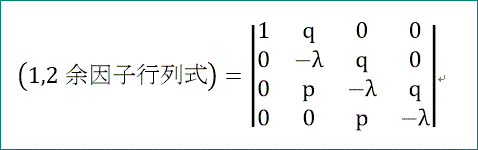
この(1,2余因子行列式)は、行列式の性質を使うと次のように変形することができる。
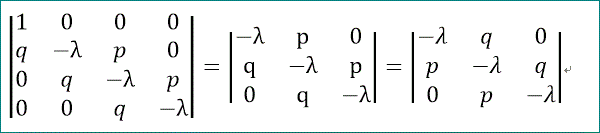
ここで、先のf(λ,2)にならって、g(λ,3)を下の式で表せば、
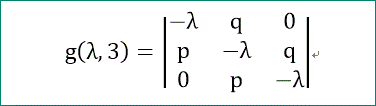
(1,2余因子行列式)は、g(λ,3)、で置き換えることができる訳じゃ。
このg() も漸化式のもう一つの要素となる。
よって、Φ(λ,5)=-λ×(1,1余因子行列式)+q×(-1)(1,2余因子行列式)、は、
Φ(λ,5)=-λ×f (λ,4)-q×g (λ,3)、と展開される。
青字の右辺第1項は、あきらかに、λ×(λの4次多項式)だが、赤字の右辺第2項は、このままでは、定かではない。
そこで、g(λ,3)を1行目で展開する。(3次行列式の公式を使っても良いが)、
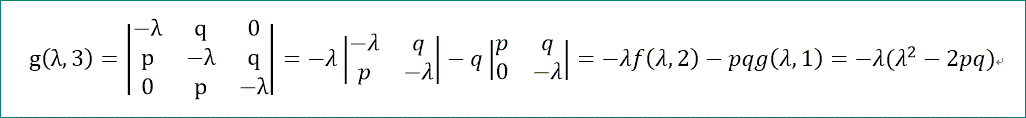
g(λ,3)は、-λ(λ^2-2pq)、となり、λ×(λ^2の多項式)であることが分かる。
なお、ここで、g(λ,1) =-λ、と g の範囲を拡張している。
よって、
Φ(λ,5)=-λ×f(λ,4)-q×g(λ,3)=-λ×f(λ,4) + q×λ(λ^2-2pq)、であり、
Φ(λ,5)=λ×(λの4次多項式)は、証明された。
しかし、まだ、青字の第2項は、λ^2の多項式かどうかが明らかではないので、f(λ,4)がλ^2の関数であることを証明しよう。
f(λ,4)を第1行によって展開すると、
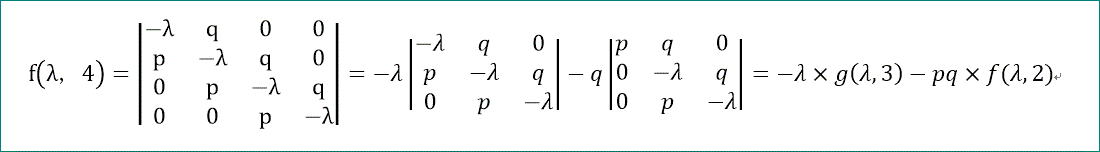
と変形することができるじゃろう。
また、f(λ,2)は、前述のように、
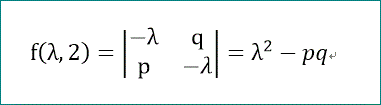
なので、これらから、
f(λ,4)=-λ×(-λ(λ^2-2pq))-pq(λ^2-pq)=p^2·q^2 - 3·p·q·λ^2 + λ^4、
よって、
Φ(λ,5)=-λ(f(λ,4)-q×(λ^2-2pq))
=- λ·(λ^4 - λ^2·(3·p·q + q) + p^2·q^2 + 2·p·q^2))、
となり、Φ(λ,5)がλ×(λ^2の多項式)が証明できた思うがどうじゃな」
 「どれどれ。
「どれどれ。
まずは、計算ミスがないか、どうかだね。
検算も兼ねて、DERIVEで、f (λ,n) と g(λ,m) の2つの帰納的関数を定義するよ。
この2つの関数は、おじぃさんが、c=5の場合の固有方程式Φ(λ,5)を計算するために定義したものなの。
その際は、f (λ,4) を計算したのだけど、簡単に一般化できるので、
n を偶数として、
f (λ,n) =-λ×g(λ,n-1)-p q×f (λ,n-2)、
f (λ,0) = 1、
と帰納的再帰関数の形に整理できる。
ただし、おじぃさんの元の定義では、f (λ,2) = λ^2-pq 、としていたけど、
f (λ,n) =-λ×g(λ,n-1)-p q×f (λ,n-2) の式で、n=2とすれば、
左辺は、λ^2-pq で、右辺は、-λ×(-λ)-pq×f(λ,0)、となる。
左辺=右辺となるためには、f (λ,0) = 1、と定義すれば可能。
なので、f (λ,0) = 1、として始めることにした訳よ。
DERIVEで、IF関数を利用すれば、
f(λ_, n_) ≔ IF(n_ = 0, 1, - λ_·g(λ_, n_ - 1) - p·q·f(λ_, n_ - 2))、
と帰納的に定義できる。
なお、上の関数の定義では、引数に λ_ 、n_ と引数にアンダーバーを付けている。
これは、ローカル変数を意味するマイルールなの。
残念ながら、DERIVEでは、ローカル変数とグローバル変数の区別がないので、誤って外部で引数の値を変更しないようにあたし達でやっていること。
それ以外のp、q やg( ) は、外部で定義されているという前提ね。
※f の定義をする前に、g を関数として定義しておかないと、f の関数定義でエラーになります。
しかし、g の定義の中に、f があるので、このままだと循環エラー!!
そこで、最初に、g(λ_,m_):=
と書いて、g を関数と定義してから、f の定義をちゃんと書き、その後で、gの関数定義を修正すればいいのよ。
次は、g(λ,m) ね。
c=5の例では、g(λ,3)=-λ×f(λ,2)-p q×g(λ,1)、だった。
そこで、これを一般化して、mを奇数とすれば、
g(λ,m)=-λ×f (λ,m-1)-p q×g(λ,m-2)、
g(λ,1)=-λ、が初期値となる。(これは、おじぃさんが定義したのと同じ)
DERIVEでは、
g(λ_, m_) ≔ IF(m_ = 1, -λ_, - λ_·f(λ_, m_ - 1) - p·q·g(λ_, m_ - 2))、
なお、gでは、引数をm_ としているけど、これは、分かりやすいように使い分けただけで、n_ でも一向に差し支えないの。
ホントは、sは、自然数、として、g(λ,2s+1):=のように定義したいんだけど、DERIVEの関数定義では、許されません。
いったん、上の青い式のように定義した後、g(λ,2s+1) などを計算させるのは、まったく問題はないんだけどね。
これで、f や g を自由に計算できるようになったので、
試しに、DERIVEで、
f(λ,4)を計算させると、
f(λ,4)=p^2·q^2 - 3·p·q·λ^2 + λ^4、となって、正しいことが分かります。
また、f(λ,8)では、
f(λ,8)=(λ^8 - 7·p·q·λ^6 + 15·p^2·q^2·λ^4 - 10·p^3·q^3·λ^2 + p^4·q^4) となる。
これは、下図のような行列の行列式を直接、計算したものと一致します。

更に、g(λ,3)は、
g(λ,3)=λ·(2·p·q - λ^2) となり、これも正しく計算されている。
念のため、g(λ,9)を計算すると、
g(λ,9)=- λ·(λ^8 - 8·p·q·λ^6 + 21·p^2·q^2·λ^4 - 20·p^3·q^3·λ^2 + 5·p^4·q^4)、
となりますが、
これは、

上の図のように9次行列の行列式の計算結果、すなわち、
- λ·(λ^8 - 8·p·q·λ^6 + 21·p^2·q^2·λ^4 - 20·p^3·q^3·λ^2 + 5·p^4·q^4)、と一致します。
さてと、もう少しね、
元の行列式の1行目での展開に戻ると、
Φ(λ,5)=-λ×f(λ,4)-q×g(λ,3) 、だったので、
これにならって、Φ(λ,n) を次のように定義する。
n を3以上の奇数として、
Φ(λ,n)=-λ×f (λ,n-1)-q×g (λ,n-2)、
DERIVEでは、
Φ(λ_, n_) ≔ - λ_·f(λ_, n_ - 1) - q·g(λ_, n_ - 2)、
これを使えば、
Φ(λ,5)=- λ·(λ^4 - λ^2·(3·p·q + q) + p^2·q^2 + 2·p·q^2)、
と正しく計算できた」
「やー、これは、良かった。
ちなみに、c=11の場合の固有方程式を計算してみると、
上の図のような推移確率行列から固有値を計算するためのDET( A-λI)の計算結果は、
- λ·(λ^10 - q·λ^8·(9·p + 1) + 4·p·q^2·λ^6·(7·p + 2) - 7·p^2·q^3·λ^4·(5·p + 3) + 5·p^3·q^4·λ^2·(3·p + 4) - p^4·q^5·(p + 5))、
一方、ともちゃんが作ってくれた漸化式を利用すると、
Φ(λ,11)=- λ·(λ^10 - q·λ^8·(9·p + 1) + 4·p·q^2·λ^6·(7·p + 2) - 7·p^2·q^3·λ^4·(5·p + 3) + 5·p^3·q^4·λ^2·(3·p + 4) - p^4·q^5·(p + 5))、
となって、目の子でも分かるが、DERIVEで差し引きして、両者が一致することが分かったのう」
「今度は、c が偶数の場合ね」
目次へ戻る
c が偶数の場合の固有方程式:(λ^2の多項式)=0
「宿場数+1がcであるが、cが偶数の場合の固有方程式を求めてみよう。
奇数の場合にならい、c=6 の場合を例にとって、計算する。
これも、c が一般の偶数の場合に容易に適用できる。
さて、cが6の場合の固有方程式をψ(λ,6)と書けば、

ψ(λ,6)は、上の図のようになるので、
cが奇数の場合と同様に1行目で行列式を展開すると、
ψ(λ,6)=-λ×(1,1余因子行列式)+q×(-1)(1,2余因子行列式)となる。

(1,1余因子行列式)は、上の図の青い破線の行・列を除いた行列式なので、
前節の記号を使えば、これは、g(λ,5)である。
一方、(1,2余因子行列式)は、
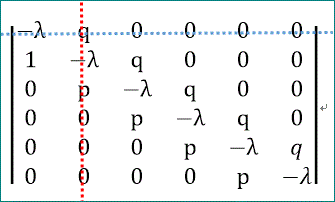
上の図の青い横線の行と赤い縦線の列を除いた行列式なので、

となるので、これが前節で定義したf(λ,4)であることがわかるのじゃな。
従って、ψ(λ,6)=-λ×(1,1余因子行列式)+q×(-1)(1,2余因子行列式)は、
ψ(λ,6)=-λ×g(λ,5)-q×f(λ,4)、
となった」
 「奇数の場合に定義した関数が使えて良かったわ。
「奇数の場合に定義した関数が使えて良かったわ。
ψ(λ,6)=-λ×g(λ,5)-q×f(λ,4) を一般化して、
n を偶数とすれば、
ψ(λ,n)=-λ×g(λ,n-1)-q×f(λ,n-2)、となる。
DERIVEでは、
ψ(λ, n) ≔ -λ·g(λ, n-1)-q·f(λ, n-2)、と定義すれば、
nが偶数の場合の固有方程式を作り出すことができる。
試しに、Ψ(λ,6)は、
Ψ(λ,6)=λ^6 - q·λ^4·(4·p + 1) + 3·p·q^2·λ^2·(p + 1) - p^2·q^3、
となるわ。
一方、下図のように、直接、

6次の行列式を計算すると、
(λ^6 - q·λ^4·(4·p + 1) + 3·p·q^2·λ^2·(p + 1) - p^2·q^3) 、となり、
先ほどのψ(λ,6)と一致することが分かった」
「前節で定義した Φ(λ,c=奇数)、
本節で定義した ψ(λ,c=偶数)、は、一つにまとめることもできる。
DERIVEでは、
整数かどうか → INTEGER?(c) で、true が戻れば、c は、整数である。
また、整数の場合の偶・奇については、
偶数かどうか → EVEN?(c)、
奇数かどうか → ODD?(c)、
によって、それぞれ、true 、false が戻れば、真偽を確認できる。(整数でなくても答えは返るが意味のある答えでない)
今、ひとつにまとめるために、Φの方を修正すると、次のようになる。

Φ(λ_, n_) ≔
PROG(
IF(INTEGER?(n_) = false, RETURN "Not Integer"),
IF(n_ < 2, RETURN "Number < 2"),
IF(ODD?(n_),
- λ_·f(λ_, n_ - 1) - q·g(λ_, n_ - 2),
- λ_·g(λ_, n_ - 1) - q·f(λ_, n_ - 2)))、
引数のn_ が整数でない場合は、Not Integer、とエラーメッセージが返る。
また、整数でも、2未満の場合は、Number < 2、とエラーが返る。
それ以外は、n_の偶奇により、それぞれの固有方程式(の左辺の多項式)が返ることになる」
「なるほどね。
おじぃさんの書き換えたΦ(λ,c) では、Prog と Return 関数が使われているのね。
いずれも、第69回『方程式の数値解法(4)(ハレー法、DERIVEのPROGとRETURN)』の後半で解説しているわよ。
ここでは、整数であるか、奇数か などの判定をするためのDERIVEの関数をいくつか挙げておきましょう。
整数か? → INTEGER? ( )
偶数か? → EVEN? ()
奇数か? → ODD? ()
数値か? → NUMBER? ()
文字か? → STRING? ()
循環小数か? → RATIONAL? ()
変数か? → VARIABLE? ()
ベクトルか? → VECTOR? ()
行列か? → MATRIX? ()
他にもあるけど、あとは、DERIVEのヘルプを参照して下さいな」
「ともちゃん。
ご苦労さんじゃった。
なお、上のΦ(λ,c)、再帰関数では、c が20程度までは、ほぼ瞬時に計算できるが、30以上になると、極端に時間がかかる。
※ 次節に固有方程式の計算結果を表にして記載した。
これは、以前、フィボナッチ数の計算のところでも、出てきた問題じゃ。
そのときは、ベクトルを使って、計算速度を上げることができた。
今回の漸化式は、f と g と2つの関数が入っているので、まだ、試してはいない。
いずれ、c=54 の五十三次の平均日数を計算するまでに、計算速度が改善されるように、ともちゃんにお願いすることにしよう。
(3)節では、なぜ固有方程式がλ^2の多項式になるのか?、という点を補足しておきたい」
目次へ戻る
固有方程式の書き下ろし結果(c=2~25,30)
固有方程式の左辺の多項式を書き下ろしました。
計算範囲は、c=2~25、c=30です。
なお、計算速度向上のために、f 、g 、Φ、の定義中の q を1-p に置き換えた以下の3つの再帰関数を使用しています。
計算時間は、目安です。
f(λ_, n_) ≔ IF(n_ = 0, 1, - λ_·g(λ_, n_ - 1) - p·(1 - p)·f(λ_, n_ - 2))、
g(λ_, m_) ≔ IF(m_ = 1, -λ_, - λ_·f(λ_, m_ - 1) - p·(1 - p)·g(λ_, m_ -
2))、
Φ(λ_, n_) ≔ PROG(
IF(INTEGER?(n_) = false, RETURN "Not Integer"),
IF(n_ < 2, RETURN "Number < 2"),
IF(ODD?(n_), - λ_·f(λ_, n_ - 1) - (1 - p)·g(λ_, n_ - 2),
- λ_·g(λ_, n_ - 1) - (1 - p)·f(λ_, n_ - 2)) )
| c |
固有方程式:Φ(z,c) 、q=1-p と置き換えてあります。 |
計算時間 |
| 2 |
(z^2 + p - 1) |
~0 |
| 3 |
(- z·(z^2 + (p + 1)·(p - 1))) |
~0 |
| 4 |
(z^4 + z^2·(2·p^2 - p - 1) + p·(p - 1)^2) |
~0 |
| 5 |
(- z·(z^4 + z^2·(p - 1)·(3·p + 1) + p·(p + 2)·(p - 1)^2)) |
~0 |
| 6 |
(z^6 + z^4·(4·p^2 - 3·p - 1) + 3·p·z^2·(p + 1)·(p - 1)^2 + p^2·(p - 1)^3) |
~0 |
| 7 |
(- z·(z^6 + z^4·(p - 1)·(5·p + 1) + 2·p·z^2·(p - 1)^2·(3·p + 2) + p^2·(p
+ 3)·(p - 1)^3)) |
~0 |
| 8 |
(z^8 + z^6·(6·p^2 - 5·p - 1) + 5·p·z^4·(p - 1)^2·(2·p + 1) + 2·p^2·z^2·(p
- 1)^3·(2·p + 3) + p^3·(p - 1)^4) |
~0 |
| 9 |
(- z·(z^8 + z^6·(p - 1)·(7·p + 1) + 3·p·z^4·(p - 1)^2·(5·p + 2) + 10·p^2·z^2·(p
+ 1)·(p - 1)^3 + p^3·(p + 4)·(p - 1)^4)) |
~0 |
| 10 |
(z^10 + z^8·(8·p^2 - 7·p - 1) + 7·p·z^6·(p - 1)^2·(3·p + 1) + 5·p^2·z^4·(p
- 1)^3·(4·p + 3) + 5·p^3·z^2·(p + 2)·(p - 1)^4 + p^4·(p - 1)^5) |
~0 |
| 11 |
(- z·(z^10 + z^8·(p - 1)·(9·p + 1) + 4·p·z^6·(p - 1)^2·(7·p + 2) + 7·p^2·z^4·(p
- 1)^3·(5·p + 3) + 5·p^3·z^2·(p - 1)^4·(3·p + 4) + p^4·(p + 5)·(p - 1)^5)) |
0.01 s |
| 12 |
(z^12 + z^10·(10·p^2 - 9·p - 1) + 9·p·z^8·(p - 1)^2·(4·p + 1) + 28·p^2·z^6·(p
- 1)^3·(2·p + 1) + 35·p^3·z^4·(p + 1)·(p - 1)^4 + 3·p^4·z^2·(p - 1)^5·(2·p
+ 5) + p^5·(p - 1)^6) |
0.01 s |
| 13 |
(- z·(z^12 + z^10·(p - 1)·(11·p + 1) + 5·p·z^8·(p - 1)^2·(9·p + 2) + 12·p^2·z^6·(p
- 1)^3·(7·p + 3) + 14·p^3·z^4·(p - 1)^4·(5·p + 4) + 7·p^4·z^2·(p - 1)^5·(3·p
+ 5) + p^5·(p + 6)·(p - 1)^6)) |
0.01 s |
| 14 |
(z^14 + z^12·(12·p^2 - 11·p - 1) + 11·p·z^10·(p - 1)^2·(5·p + 1) + 15·p^2·z^8·(p
- 1)^3·(8·p + 3) + 42·p^3·z^6·(p - 1)^4·(3·p + 2) + 14·p^4·z^4·(p - 1)^5·(4·p
+ 5) + 7·p^5·z^2·(p + 3)·(p - 1)^6 + p^6·(p - 1)^7) |
0.03 s |
| 15 |
(- z·(z^14 + z^12·(p - 1)·(13·p + 1) + 6·p·z^10·(p - 1)^2·(11·p + 2) +
55·p^2·z^8·(p - 1)^3·(3·p + 1) + 30·p^3·z^6·(p - 1)^4·(7·p + 4) + 126·p^4·z^4·(p
+ 1)·(p - 1)^5 + 28·p^5·z^2·(p + 2)·(p - 1)^6 + p^6·(p + 7)·(p - 1)^7)) |
0.06 s |
| 16 |
(z^16 + z^14·(14·p^2 - 13·p - 1) + 13·p·z^12·(p - 1)^2·(6·p + 1) + 22·p^2·z^10·(p
- 1)^3·(10·p + 3) + 165·p^3·z^8·(p - 1)^4·(2·p + 1) + 42·p^4·z^6·(p - 1)^5·(6·p
+ 5) + 42·p^5·z^4·(p - 1)^6·(2·p + 3) + 4·p^6·z^2·(p - 1)^7·(2·p + 7) +
p^7·(p - 1)^8) |
0.09 s |
| 17 |
(- z·(z^16 + z^14·(p - 1)·(15·p + 1) + 7·p·z^12·(p - 1)^2·(13·p + 2) +
26·p^2·z^10·(p - 1)^3·(11·p + 3) + 55·p^3·z^8·(p - 1)^4·(9·p + 4) + 66·p^4·z^6·(p
- 1)^5·(7·p + 5) + 42·p^5·z^4·(p - 1)^6·(5·p + 6) + 12·p^6·z^2·(p - 1)^7·(3·p
+ 7) + p^7·(p + 8)·(p - 1)^8)) |
0.14 s |
| 18 |
(z^18 + z^16·(16·p^2 - 15·p - 1) + 15·p·z^14·(p - 1)^2·(7·p + 1) + 91·p^2·z^12·(p
- 1)^3·(4·p + 1) + 143·p^3·z^10·(p - 1)^4·(5·p + 2) + 99·p^4·z^8·(p - 1)^5·(8·p
+ 5) + 462·p^5·z^6·(p + 1)·(p - 1)^6 + 30·p^6·z^4·(p - 1)^7·(4·p + 7) +
9·p^7·z^2·(p + 4)·(p - 1)^8 + p^8·(p - 1)^9) |
0.21 s |
| 19 |
(- z·(z^18 + z^16·(p - 1)·(17·p + 1) + 8·p·z^14·(p - 1)^2·(15·p + 2) +
35·p^2·z^12·(p - 1)^3·(13·p + 3) + 91·p^3·z^10·(p - 1)^4·(11·p + 4) + 143·p^4·z^8·(p
- 1)^5·(9·p + 5) + 132·p^5·z^6·(p - 1)^6·(7·p + 6) + 66·p^6·z^4·(p - 1)^7·(5·p
+ 7) + 15·p^7·z^2·(p - 1)^8·(3·p + 8) + p^8·(p + 9)·(p - 1)^9)) |
0.34 s |
| 20 |
(z^20 + z^18·(18·p^2 - 17·p - 1) + 17·p·z^16·(p - 1)^2·(8·p + 1) + 40·p^2·z^14·(p
- 1)^3·(14·p + 3) + 455·p^3·z^12·(p - 1)^4·(3·p + 1) + 1001·p^4·z^10·(p
- 1)^5·(2·p + 1) + 429·p^5·z^8·(p - 1)^6·(4·p + 3) + 132·p^6·z^6·(p - 1)^7·(6·p
+ 7) + 165·p^7·z^4·(p + 2)·(p - 1)^8 + 5·p^8·z^2·(p - 1)^9·(2·p + 9) +
p^9·(p - 1)^10) |
0.56 s |
| 21 |
(- z·(z^20 + z^18·(p - 1)·(19·p + 1) + 9·p·z^16·(p - 1)^2·(17·p + 2) +
136·p^2·z^14·(p - 1)^3·(5·p + 1) + 140·p^3·z^12·(p - 1)^4·(13·p + 4) +
273·p^4·z^10·(p - 1)^5·(11·p + 5) + 1001·p^5·z^8·(p - 1)^6·(3·p + 2) +
1716·p^6·z^6·(p + 1)·(p - 1)^7 + 99·p^7·z^4·(p - 1)^8·(5·p + 8) + 55·p^8·z^2·(p
+ 3)·(p - 1)^9 + p^9·(p + 10)·(p - 1)^10)) |
0.9 s |
| 22 |
(z^22 + z^20·(20·p^2 - 19·p - 1) + 19·p·z^18·(p - 1)^2·(9·p + 1) + 51·p^2·z^16·(p
- 1)^3·(16·p + 3) + 340·p^3·z^14·(p - 1)^4·(7·p + 2) + 364·p^4·z^12·(p
- 1)^5·(12·p + 5) + 1001·p^5·z^10·(p - 1)^6·(5·p + 3) + 429·p^6·z^8·(p
- 1)^7·(8·p + 7) + 429·p^7·z^6·(p - 1)^8·(3·p + 4) + 55·p^8·z^4·(p - 1)^9·(4·p
+ 9) + 11·p^9·z^2·(p + 5)·(p - 1)^10 + p^10·(p - 1)^11) |
1.5 s |
| 23 |
(- z·(z^22 + z^20·(p - 1)·(21·p + 1) + 10·p·z^18·(p - 1)^2·(19·p + 2) +
57·p^2·z^16·(p - 1)^3·(17·p + 3) + 204·p^3·z^14·(p - 1)^4·(15·p + 4) +
476·p^4·z^12·(p - 1)^5·(13·p + 5) + 728·p^5·z^10·(p - 1)^6·(11·p + 6) +
715·p^6·z^8·(p - 1)^7·(9·p + 7) + 429·p^7·z^6·(p - 1)^8·(7·p + 8) + 143·p^8·z^4·(p
- 1)^9·(5·p + 9) + 22·p^9·z^2·(p - 1)^10·(3·p + 10) + p^10·(p + 11)·(p
- 1)^11)) |
2.4 s |
| 24 |
(z^24 + z^22·(22·p^2 - 21·p - 1) + 21·p·z^20·(p - 1)^2·(10·p + 1) + 190·p^2·z^18·(p
- 1)^3·(6·p + 1) + 969·p^3·z^16·(p - 1)^4·(4·p + 1) + 612·p^4·z^14·(p -
1)^5·(14·p + 5) + 6188·p^5·z^12·(p - 1)^6·(2·p + 1) + 1144·p^6·z^10·(p
- 1)^7·(10·p + 7) + 6435·p^7·z^8·(p + 1)·(p - 1)^8 + 1001·p^8·z^6·(p -
1)^9·(2·p + 3) + 143·p^9·z^4·(p - 1)^10·(2·p + 5) + 6·p^10·z^2·(p - 1)^11·(2·p
+ 11) + p^11·(p - 1)^12) |
3.9 s |
| 25 |
(- z·(z^24 + z^22·(p - 1)·(23·p + 1) + 11·p·z^20·(p - 1)^2·(21·p + 2) +
70·p^2·z^18·(p - 1)^3·(19·p + 3) + 285·p^3·z^16·(p - 1)^4·(17·p + 4) +
3876·p^4·z^14·(p - 1)^5·(3·p + 1) + 1428·p^5·z^12·(p - 1)^6·(13·p + 6)
+ 1768·p^6·z^10·(p - 1)^7·(11·p + 7) + 1430·p^7·z^8·(p - 1)^8·(9·p + 8)
+ 715·p^8·z^6·(p - 1)^9·(7·p + 9) + 1001·p^9·z^4·(p + 2)·(p - 1)^10 + 26·p^10·z^2·(p
- 1)^11·(3·p + 11) + p^11·(p + 12)·(p - 1)^12)) |
6.3 s |
| 30 |
(z^30 + z^28·(28·p^2 - 27·p - 1) + 27·p·z^26·(p - 1)^2·(13·p + 1) + 325·p^2·z^24·(p
- 1)^3·(8·p + 1) + 1150·p^3·z^22·(p - 1)^4·(11·p + 2) + 10626·p^4·z^20·(p
- 1)^5·(4·p + 1) + 33649·p^5·z^18·(p - 1)^6·(3·p + 1) + 10659·p^6·z^16·(p
- 1)^7·(16·p + 7) + 29070·p^7·z^14·(p - 1)^8·(7·p + 4) + 41990·p^8·z^12·(p
- 1)^9·(4·p + 3) + 92378·p^9·z^10·(p + 1)·(p - 1)^10 + 3978·p^10·z^8·(p
- 1)^11·(8·p + 11) + 6188·p^11·z^6·(p + 2)·(p - 1)^12 + 140·p^12·z^4·(p
- 1)^13·(4·p + 13) + 15·p^13·z^2·(p + 7)·(p - 1)^14 + p^14·(p - 1)^15) |
69.9 s |
目次へ戻る
(3)固有方程式がλ^2の多項式を含む理由
「(2)節では、推移確率行列から作られる行列式を展開することで、方程式がλ^2の多項式になることを明らかにした。
この節では、状態ベクトルの特徴を基にして、それを調べて見よう。
非対称型道中双六の問題の状態ベクトルをU(t)=[U1(t),U2(t),・・,Uc(t)]とする。
この問題では、初期条件として、U1(0)=1、その他の場所のUj(0)=0としている。
また、t=t+1 に進む際、駒は、前後の宿場(振り出し、上がりを含む)に移動するだけで、t=tの時点にいた宿場に留まることはない。
この2つの前提により、j=1~cの場所において、
Uj(t)<>0 ならば、Uj(t+1)=0、かつ、Uj(t+2)<>0、が成り立つ。
なお、jの場所で、最初に、その値が0でなくなるのは、t=jの時である。
この後、t>=j では、時間周期=2で、Uj(t)の値は、ゼロとなる。
今、固有方程式の根が単根であると仮定すれば、
Uj(t)は、C1×λ1^t+C2×λ2^t+・・、と表される。
C1等は、jによって、異なる係数である。
場所により、tは、異なるものの、
下記の第1式が成立すれば、第2式以降も成立する。
C1×λ1^t+C2×λ2^t+・・=0、
C1×λ1^(t+2) +C2×λ2^(t+2)+・・=0、
cが偶数の場合を考えると、λ1等は、c個ある。
C1、C2等がゼロでない場合にこれらの式が成立するためには、2つずつのλの組毎に
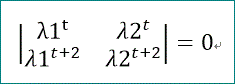
の関係があることが必要だ。
左辺は、
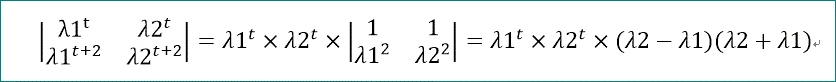
と変形できるので、根がゼロでなければ、
単根の仮定により、λ1=-λ2、となる必要性がある。
これは、固有方程式が、λ^2 の多項式であることを示す。
ちなみに、cが3の倍数でもあるとき、λ1~λ3までの3つずつの組で同様のことができるかを見てみる。
C1~C3がゼロでない場合は、
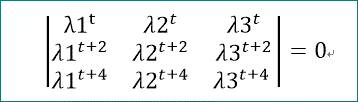
が必要だが、変形すると、
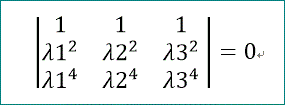
これは、
(λ1 + λ2)·(λ1 - λ2)·(λ1 + λ3)·(λ1 - λ3)·(λ2 + λ3)·(λ3 - λ2)=0
である。
これから、λ1~λ3は、符号を含めて同一(=重根、3重根)か、または、異符号で絶対値は、同じであることが必要と分かる。
単根の仮定から、前者ではないので、後者とすると、
たとえば、λ1=-λ2、ならば、λ3は、このλ1とλ2ともいずれとも異符号である必要があるが不可能である。
4つ以上の組も同様に成り立たない。
すなわち、時間周期=2で、ゼロと非ゼロを繰り返すためには、c個の単根の2つずつが絶対値が等しく、異符号である必要がある。
これは、固有方程式がλ^2の多項式であることを示している。
と、まあ、このように考えていたんじゃがな」
 「ちょっと、おかしい気がするわね。
「ちょっと、おかしい気がするわね。
なぜって、(2)節で推移確率行列から固有値を求めるための行列式を変形して、
c が偶数の場合は、λ^2の多項式であることを導いている。
その際、初期分布については、何も仮定していない。
しかし、おじぃさんの議論では、初期分布がデルタ分布であることから、状態ベクトルの任意の要素の値がゼロと非ゼロを時間周期=2で繰り返す性質を使っている。
初期分布がデルタ分布でない場合は、状態ベクトルの値がゼロと非ゼロを繰り返すことは、ないでしょうね。
なので、一般の初期分布に対しては、こういう論法は、成り立たないと思うわ」
「そうなんじゃな。
わしも、書いてから、そう思った。
ま、t=0で、振り出し以外に駒が置かれているという状況は、普通の双六では、あり得ないとは、思ったがの。
ただ、双六と離れて、マルコフ連鎖の問題として、考えると、ともちゃんが指摘している点は、もっともじゃ。
わしも、デルタ分布以外で同様の論法が成り立たないかと考えてみたんじゃが、それは、推移確率行列による状態ベクトルの変化の計算に戻る。
結局、一般の初期分布の場合、(2)節で導いたように固有方程式を漸化式の形に書いて、λ^2の多項式が含まれることを説明するしかないのかな。
固有値を求める行列式のλを-λに置き換えた行列式の値が置き換え前と符号を除いて、一致することを言ってもよいと思うが、その手間は、漸化式を導くのと大きな差がないように思える。
さて、次節では、固有方程式の判別式に触れて見よう」
目次へ戻る
(4)固有方程式の判別式
判別式のご利益と定義
 「判別式ね。
「判別式ね。
比較的、最近では、2階の線形同次偏微分方程式の判別式、という話題を取り上げたわね。
※第86回『偏微分方程式の解法(1)(関数変換、変数変換、積分変換)』の変数変換のヒント、を参照。
そこでは、2次方程式、Az^2+Bz+C=0 の判別式、D=B^2-4AC、が登場する。
けれど、3次以上の代数方程式の判別式については、これまで、取り上げてこなかったと思うわ」
「さすが、DERIVE の女、ともちゃんじゃな。
取り上げてこなかった理由は、3次以上の判別式の計算は、手間がかかるためでもある。
2n-1 次行列式の計算が必要となる。(n=2で、3次、n=3で、5次、・・)
行列式の計算は、行列の要素がすべて数であれば、それほどの困難はないものの、行列にパラメーターが含まれていると大変だ。
異なるパラメーターが多くなればなるほど、判別式の計算は、途方もないことになる。
更に言えば、判別式のご利益が限定的なためかの」
「えーと、判別式のご利益は、解(根)の分類に役立つということでしょ?」
「確かに、2次方程式の判別式 D では、
D>0 → 異なる2実根、
D=0 → 実数の2重根、
D<0 → 複素根、
というように、判別式で、きれいに分類できた。
なお、D=0 の2重根は、実数であって、虚数部がゼロではない複素数ではない。
これは、複素根では、必ず、その共役複素数も根になるためだ。
つまり、下のzに関する方程式の一つの根をz1=α+β#i とすれば、共役複素数である z2=α-β#i もまた、根となる。
すなわち、
(z-z1)(z-z2)=z^2-(z1+z2) z +z1 z2=z^2-2αz+(α^2-β^2)=0、において、
判別式 D=4α^2-4(α^2-β^2)=4β^2、となり、D=0 とβ=0 とは、同値じゃ。
ところが、3次では、判別式だけでは、2次の場合ほどは、きれいに分類できない。
まして、4次以上となると、判別式だけでは、いっそう漠然としてくる」
「じゃ、判別式のご利益は、何なのかしら?」
「次数が高い場合を含めて言えば、判別式からすぐに分かることは、重根があるかどうかじゃろう。
一般の(最高次の係数を1とした場合の)代数方程式の判別式の定義は、z i を根として、
D=Π(zi-zj)^2、ただし、i < j となるすべての根について動く。
つまり、定義を見るとすぐに分かるのは、zi=zj となる根が1組でもあると、D=0 となることだ。
ただし、それが2重根なのか、あるいは、3重根等の多重根なのか、といった細かい点は、これだけでは、分からない」
「つまり、
判別式=0、ならば、少なくとも一組以上の重根がある。
逆に、判別式がゼロでなければ、単根だけということね」
「そうじゃな。
判別式の大きさ、あるいは、判別式の2乗の値により、複数の根のまとまり具合も分かることがあるじゃろう。
※ 4次方程式の判別式を参照、この値が小さいほど、根が集中している。
なお、誤解のないように言うておくと、判別式の正負からも、次のことが分かる。
ウィキペディアの『判別式』によれば、
D>0 → 0=< k <= n/4 の整数 k として、複素根の組(複素根と共役複素根)が2k 個、n-4k 個の実根がある。
D<0 → 0=< k <=(n-2)/4の整数 kとして、複素根の組(複素根と共役複素根)が2k+1 個、n-4k-2 個の実根がある。
ただ、上の表現から分かるように、nが大きいと判別式の正負から得られる情報は、ある幅を持った限定的なものとなる」
目次へ戻る
2次方程式の判別式
「まずは、2次方程式を考えてみよう。
係数を簡単にするために、今後、方程式の最高次の係数は、1とする。
別の言い方をすれば、最高次の係数で、他の係数を割ったものを新しい係数と考える。
2次方程式を、z^2 + a1 z + a0=0、と書くことにしよう。
※ 以下では、2次方程式を含めて、 z^k の項の係数を ak とおく。(ただし、k=0~n-1)
ここで、2つの根を z1、z2 とおけば、方程式は、
(z-z1)(z-z2)=0、となり、展開すると、z^2-(z1+z2)z+z1z2=0、
ここで、前の表式と見比べて、根とa1やa0との関係は、
1次項の係数=a1=-(z1+z2)、
定数項=a0=z1 z2、
であり、これが、2次方程式の『根と係数の関係』と呼ばれているのは、わしが言うまでもないじゃろう。
さて、前節でも出てきた、2次方程式の判別式は、最高次の係数が1の場合は、
今の係数の記法に従うと、
D=a1^2-4×a0である。
このDを根と係数の関係を使って置き換えると、
D=(z1+z2)^2-4z1z2
=z1^2-2z1z2+z2^2
=(z1-z2)^2、となる。
これは、前節で定義された判別式 D=Π (zi-zj)^2、と一致することが分かるじゃろう」
 「なるほど。
「なるほど。
でも、本当は、順序が逆よね。
z^2 + a1 z + a0=0、の根は、
(z = (√(a1^2 - 4·a0) - a1)/2 ∨ z = - (√(a1^2 - 4·a0) + a1)/2)、となるので、
z1=√(a1^2 - 4·a0) - a1)/2、
z2=√(a1^2 - 4·a0) + a1)/2、
とおけば、判別式、D=Π (zi-zj)^2=(z1-z2)^2、は、
D=(z1-z2)^2=a1^2-4a0、であることが分かる、ということでしょう」
「ま、2次方程式では、その説明がもっとも簡明な方法ではある。
しかし、3次、4次、と次数が高くなるにつれて、難しくなる。
5次以上では、根の一般解を与える公式がないので、根を求めて、判別式の定義に当てはめるという方法は、できんのじゃ。
そこで、別の方法があるのじゃ。
ともちゃん、2次関数のグラフで、判別式を説明してご覧」
「これは、簡単ね。
下の図の3つが代表的なグラフでしょう。
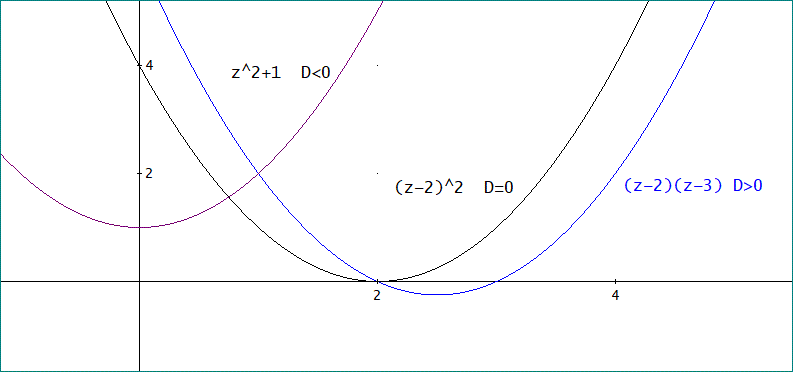
Dの正負とゼロも書き添えているから、すぐ分かると思うの」
「うん。
その通りだな。
ヒントは、D=0 のグラフだな。
そのグラフは、z=2で横軸に接しているじゃろう。
ということは、z=2での微分係数がゼロ、と言うことじゃ。
一般的に言えば、方程式が f(z)=0、のとき、
z=重根であれば、
f(z)=0、の他に、f ' (z)=0、なんだな」
「なるほど。
f(z)=z^2+a1 z+a0=0、のときに、その左辺の1階微分、
f ' (z)=2z+a1=0、も、また、ゼロになるzが重根という訳ね。
でも、普通に考えると、2つ目の式から、zを求めて、1番目の式に代入する。
これでは、結局、2次方程式を解くことと同じになってしまうよ」
「そのとおりじゃ。
そこで、f(z)が2次式で、3つの項(2次、1次、定数項)があることを考えて、
もう一つ、式を増やして、3つの式を行列間の関係として表すことを考える。
f(z)は、2次式で、f ' (z)は、1次式なので、f ' (z) にzを掛けて、2次式を作る。
z^2+a1 z+a0=0、
2z^2+a1 z=0、
2z+a1=0、
この3組の関係を行列で書き表すと、
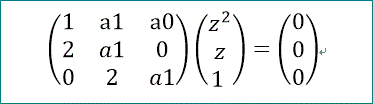
上の関係が成り立つためには、z の任意性により、
左辺の3次行列の行列式がゼロとなることが必要だ。
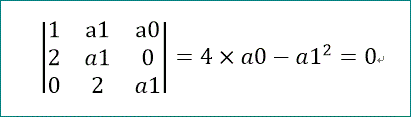
※方程式の次数、n に対して、符号を (-1)^(n(n-1))/2 とすれば、先に定義した判別式と同一となる。(次回解説予定)
今回は、n=2、なので、-1を掛けて、
D=a1^2-4a0、が得られる。
この考え方は、3次方程式以降でも有効なんじゃ」
「へー。
式の数を増やすとは、思いつかないわね」
「ずっと以前に、3次方程式の解法として、タルタリア(あるいはカルダノ)の方法を紹介した。(第12回『3次方程式』参照)
この中で、一般の3次方程式を y^3+m*y+n=0、に変換した後に、
y=u+v、と置いて解く方法を説明している。
未知数 y が不明なのに、それを u + vとおいて、1つだった未知数をu、v の2つに増やしている。
数学における『秘術』とも言えるじゃろう」
目次へ戻る
3次方程式の判別式
「では、わしが、3次方程式の根を元にして、判別式を計算してみよう。
3次方程式は、z^3+a2 z^2+a1 z+ a0=0、とする。
この3次式方程式は、z1、z2、z3という根を使って書けば
(z-z1)(z-z2)(z-z3)=0、であり、展開すると、
z^3 - z^2·(z1 + z2 + z3) + z·(z1z2 + z1z3 + z2·z3) - z1·z2·z3=0、である。
2次項の係数=a2=-(z1 + z2 + z3)、
1次項の係数=a1=(z1z2 + z1z3 + z2·z3)、
0次項の係数=a0=-z1·z2·z3、
という3組の3次方程式の『根と係数の関係』が得られる。
さて、判別式の定義から、
D=(z1-z2)^2 (z2-z3)^2 (z3-z1)^2、であるが、
このD内のz1~z3を上述の3つの根と係数の関係で表せば、Dを係数、a2、a1、a0 のみで書き表すことができる。
前述のように、5次方程式以上では、解の公式がないので、一般性がない方法ではある。
しかし、あえて、3次方程式の解の公式を使って、Dのz1等をa0等で置き換えてみよう。
途中の計算をDERIVEに任せて、その詳細を略すると、(無駄に画面を占有されるのでな・・)
D=- 27·a0^2 + 18·a0·a1·a2 - 4·a0·a2^3 - 4·a1^3 + a1^2·a2^2、
と表されることが分かる」
 「じゃ、わたしは、行列を使う方法を試してみるわ。
「じゃ、わたしは、行列を使う方法を試してみるわ。
もし、重根があれば、
f(z)=z^3+a2 z^2+a1 z+a0=0、
f ' (z)=3z^2+2 a2 z+a1=0、
となるが、f(z)は、zの0次~3次まで4つの項があるので、4つの式が必要となる。
しかし、最高次を z^3 であるとすれば、追加可能なのは、f ' ×z だけ。
これ以上、式を追加できないわね」
「そこで、zの4次まで許すことにする。
その代わり、5つの式を作ることを考える。
そうなると、方程式が3つ足りないので、
f(z)にzを掛けたもの、
f ' (z) にz及びz^2を掛けたもの、という 3つの方程式を追加する。
少し、順番を整理して、
z×f(z)=0、
f(z)=0、
z^2×f ' (z)=0,
z×f ' (z)=0,
f ' (z)=0,
という順にすると、
z^4+a2 z^3+a1 z^2+a0 z+0=0、
0 z^4+z^3+a2 z^2+a1 z+a0=0、
3z^4+2 a2 z^3+a1z^2+0z+0=0、
0z^4+3z^3+2 a2 z^2+a1z+0=0、
0z^4+0z^3+3z^2+2 a2 z+a1=0、
となる。
2次の場合と同様に重根がある条件を行列式の形で書き出すと、

となる。
左辺は、(27·a0^2 - 18·a0·a1·a2 + 4·a0·a2^3 + 4·a1^3 - a1^2·a2^2)、となる。
符号は、n=3では、(-1)^(n(n-1))/2=-1,より、-1を掛けたものとなるので、
判別式は、
D=-(27·a0^2 - 18·a0·a1·a2 + 4·a0·a2^3 + 4·a1^3 - a1^2·a2^2)、となる。
これは、前掲の判別式、
D=- 27·a0^2 + 18·a0·a1·a2 - 4·a0·a2^3 - 4·a1^3 + a1^2·a2^2、
と同一であることが分かる。
ただ、行列式は、行の入れ替えによって、符号のみが変わる。
先の5つの方程式の順番が入れ替わる可能性はあるので、符号が不確かな場合は、根が分かっている例で計算して、
符号が、+、なのか、-、なのかを確かめてみれば、良い。
たとえば、3次方程式であれば、z^3+1=0,とすると、
これは、a2=0、a1=0,a0=1、の場合にあたる。
このとき、(27·a0^2 - 18·a0·a1·a2 + 4·a0·a2^3 + 4·a1^3 - a1^2·a2^2)=27、である。
しかし、z^3+1=0、の根は、複素根1組と実根1つなので、D<0、となる。
従って、符号は、マイナスとなるべきで、
D=-(27·a0^2 - 18·a0·a1·a2 + 4·a0·a2^3 + 4·a1^3 - a1^2·a2^2)、が正しいことを再確認できる。
ちなみに、3次方程式の判別式については、次のことが知られている。
Dがゼロでは、2重根と単根、または、3重根、
Dが正の場合は、3つの実根、
Dが負の場合は、1組の複素根と1つの実根
のように、D=0では、2つのいずれであるかは、分からない。
区別するためには、別の判別式が必要となる。
3次の場合は、
D2=-2 a2^3+9 a2 a1-27 a0、として、
・D>0 → 異なる3つの実根、
・D=0、かつ、D2<>0 → 3つの実根(単根1と2重根)
・D=D2=0 →(当然ながら実数の)3重根、
・D<0 → 複素根1組と実根1つ、
と分類される」
「3次方程式のグラフを追加しておきますよ。
(1) 3実根がある場合。
f(z)=(z - 2)·(z - 3)·(z - 1)、
D=(z1 - z2)^2·(z2 - z3)^2·(z3 - z1)^2=4、
f ' (z)=3z^2-12z+11

3実根がある場合で、f(z)=(z - 2)·(z - 3)·(z - 1)のときのグラフね。
z=1、2、3 という根がある。
f(z)の微分は、青いグラフの2次曲線となり、実軸とは、2個所で交わっているが、赤いf(z)の実軸上の交点とは異なっている。
すなわち、f '(z)=0は、2根を持つものの、f(z)との共通の根では、ないことが見て取れる。
なお、f'(z)=0、の2根は、何かというと、f(z)のグラフが極値を取る2点のzを表す。
(2) 実数の2重根がある場合。
f(z)=(z-1)^2 (z-3)、
f ' (z)=(z-1)(3z-7)、
D=(z1 - z2)^2·(z2 - z3)^2·(z3 - z1)^2=0、

明らかに、f(z)とf ' (z) の実軸上の交点がz=1の一個所で一致している。
f'(z)=0のもう1つの根は、f(z)のグラフが極値を取るzの値を表す。
(3) 実数の3重根がある場合
f(z)=(z-1)^3、
f ' (z)=3(z-1)^2、
D=(z1 - z2)^2·(z2 - z3)^2·(z3 - z1)^2=0
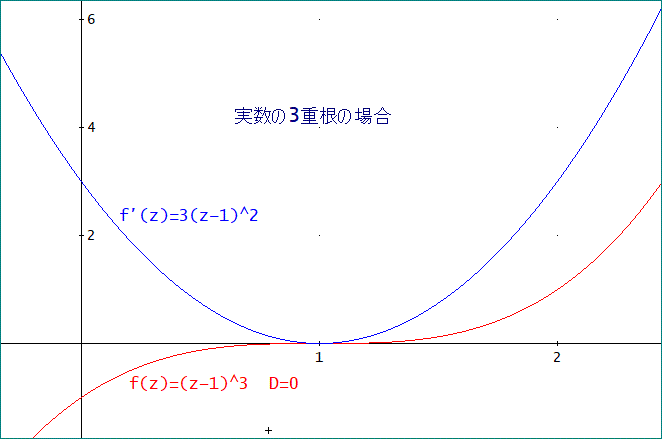
これは、z=1が3重根となっている例ね。
(4) 1実根と1組の複素根の場合
f(z)=(z-1)(z^2+2)、根は、z=1、z=1±2#i、
f ' (z)=3z^2-2+2、
D=(z1 - z2)^2·(z2 - z3)^2·(z3 - z1)^2=-256、
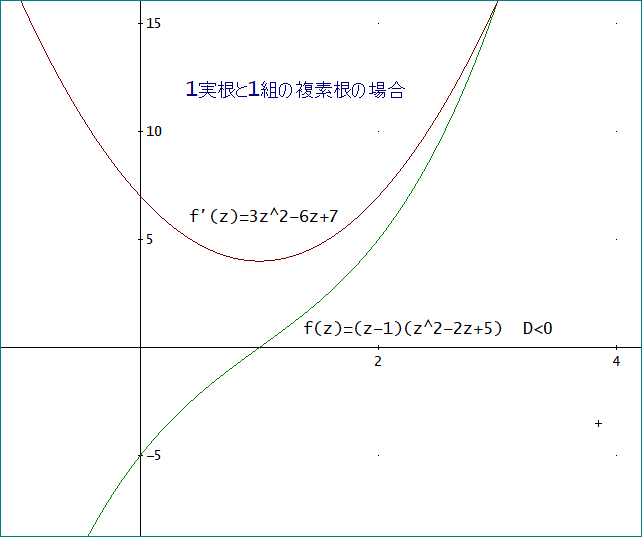
よく知られているように、3次方程式には、少なくとも1つの実根があるということが分かるわね」
目次へ戻る
4次方程式の判別式
 「では、3次の次は、4次と言うことで、前節のおじぃさんのようにやってみましょう。
「では、3次の次は、4次と言うことで、前節のおじぃさんのようにやってみましょう。
4次方程式は、z^4 + a3 z^3 + a2 z^2 + a1 z + a0=0、とする。
この4次式方程式は、z1、z2、z3、z4 という根を使って書けば
(z-z1)(z-z2)(z-z3)(z-z4)=0、であり、展開すると、
z^4 - z^3·(z1 + z2 + z3 + z4) + z^2·(z1·(z2 + z3 + z4) + z2·(z3 + z4)
+ z3·z4) - z·(z1·(z2·(z3 + z4) + z3·z4) + z2·z3·z4) + z1·z2·z3·z4、である。
先ほどの式と比較すると、4次方程式の根と係数の関係は、
3次項の係数=a3=-(z1 + z2 + z3 + z4)、
2次項の係数=a2=(z1·z2 + z1·z3 + z1·z4 + z2·z3 + z2·z4 + z3·z4)、
1次項の係数=a1=-(z1·z2·z3 + z1·z2·z4 + z1·z3·z4 + z2·z3·z4)、
定数項=a0=(z1·z2·z3·z4)、
となる。
一方、判別式を計算するために、
f(z)=z^4 + a3 z^3 + a2 z^2 + a1 z + a0、とおいて、
左辺の微分を作ると、
f ' (z)=4z^3 + 3 a3 z^2 + 2 a2 z + a1=0、がもう一つの式となるのね。
3次の場合は、2×3-1=5つの式が必要だったので、4次では、2×4-1=7つの式が必要となるでしょう。
具体的には、z^6 までを許して、
z^2×f(z)=0、
z×f(z)=0、
f(z)=0,
z^3×f ' (z)=0,
z^2×f ' (z)=0、
z×f ' (z)=0、
f ' (z)=0、
となる。
3次の場合のように行列式で重根となる条件を表すと、
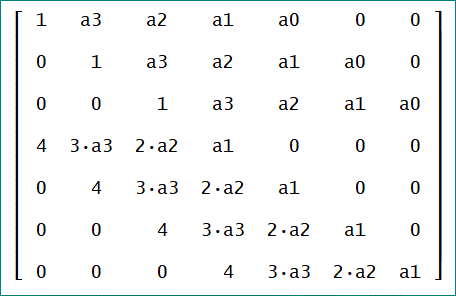
となる。
行列式を計算すると、
(256·a0^3 - 192·a0^2·a1·a3 - 128·a0^2·a2^2 + 144·a0^2·a2·a3^2 - 27·a0^2·a3^4
+ 144·a0·a1^2·a2 - 6·a0·a1^2·a3^2 - 80·a0·a1·a2^2·a3 + 18·a0·a1·a2·a3^3
+ 16·a0·a2^4 - 4·a0·a2^3·a3^2 - 27·a1^4 + 18·a1^3·a2·a3 - 4·a1^3·a3^3 -
4·a1^2·a2^3 + a1^2·a2^2·a3^2)、である。
前述のように、n=4では、(-1)^(n(n-1))/2=1,より、符号は変わらず、
判別式、Dは、
D=256·a0^3 - 192·a0^2·a1·a3 - 128·a0^2·a2^2 + 144·a0^2·a2·a3^2 - 27·a0^2·a3^4
+ 144·a0·a1^2·a2 - 6·a0·a1^2·a3^2 - 80·a0·a1·a2^2·a3 + 18·a0·a1·a2·a3^3
+ 16·a0·a2^4 - 4·a0·a2^3·a3^2 - 27·a1^4 + 18·a1^3·a2·a3 - 4·a1^3·a3^3 -
4·a1^2·a2^3 + a1^2·a2^2·a3^2、
となったわね」
「どれどれ、ようできたな。
念のため、符号を確認してみよう。
f(z)=(z-1)(z-2)(z-3)(z-4)とおけば、
a3=-10、a2=35、a1=-50、a0=24、なので、
ともちゃんが計算してくれたDは、144、となる。
一方、下のように判別式の定義、
D=Π(zi-zj)^2、から計算すると、
D=(1-2)^2(1-3)^2(1-4)^2(2-3)^2(2-4)^2(3-4)^2=144、となり、両者が一致することが分かった。
このように、5次以上では、更に複雑になる。
しかも、問題は、少し、次数が増えるだけで、判別式の計算自体が加速度的に煩雑になることじゃな。
判別式の計算の手間は、自由なパラメ-タ-の数に大きく依存する。
自由なパラメ-タ-が多い場合は、17次方程式程度でも、パソコン程度では、到底、計算できない時間と計算結果を格納するための記録容量を要する。
※今回の道中双六の問題のように、固有方程式の係数 a0、a1、等が、ただ1つのパラメ-タ- p の式である場合は、比較的、手間が少ない」
目次へ戻る
4次方程式の判別式の応用
 「じゃ、折角、4次方程式の判別式が得られたので、c=4の場合で。重根がないことを確認してみましょう。
「じゃ、折角、4次方程式の判別式が得られたので、c=4の場合で。重根がないことを確認してみましょう。
実際問題としては、4次方程式を解いてしまっているので、すべて単根であることは、確認済みなんだけどね。
今回、求めた漸化式では、
Φ(z,4)=z^4 - z^2·(2·p·q + q) + p·q^2=z^4 + z^2·(2·p^2 - p - 1) + p·(p - 1)^2、
ここで、q=1-p、この解は、4つあり、
z1 = - √2·√(1 - p)·√(- √(4·p^2 + 1) + 2·p + 1)/2、
z2= √2·√(1 - p)·√(- √(4·p^2 + 1) + 2·p + 1)/2、
z3= - √2·√(1 - p)·√(√(4·p^2 + 1) + 2·p + 1)/2、
z4= √2·√(1 - p)·√(√(4·p^2 + 1) + 2·p + 1)/2、
である。
グラフは、下図のとおり。
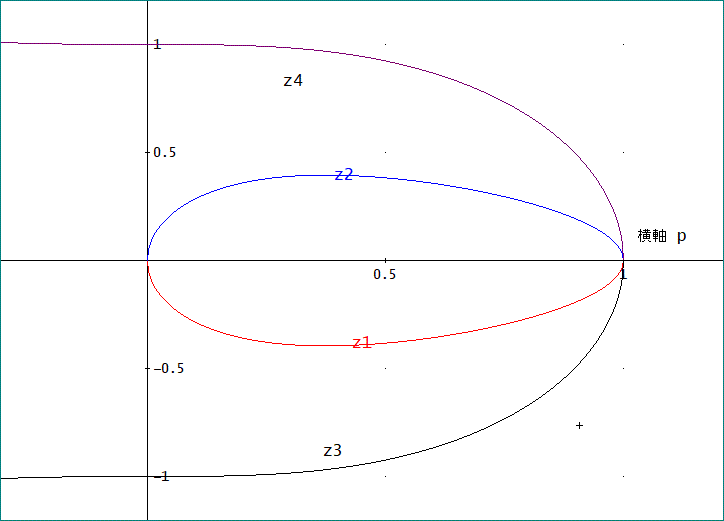
これにより、
p=0では、z1とz2がいずれもゼロとなり、2重根、
p=1では、z1~z4までがゼロに一致し、4重根となることが分かる。
すなわち、0<p<1、の範囲のp では、単根であることが分かるわね。
問題は、判別式の値は、どうなるか」
「では、それは、わしが計算してみよう。
f(z)=z^4 + z^2·(2·p^2 - p - 1) + p·(p - 1)^2、から、
a3=0、a2=·(2·p^2 - p - 1) 、a0=p(1-p)^2、なので、
D=16·p·(p - 1)^2·(16·p^8 - 64·p^7 + 104·p^6 - 96·p^5 + 65·p^4 - 36·p^3
+ 14·p^2 - 4·p + 1)、
=16p(1-p)^2×((p - 1)^4·(4·p^2 + 1)^2)、
よって、
D=16·p·(1 - p)^6 ·(4·p^2 + 1)^2、である。
判別式、Dのグラフは、下図のようだ。
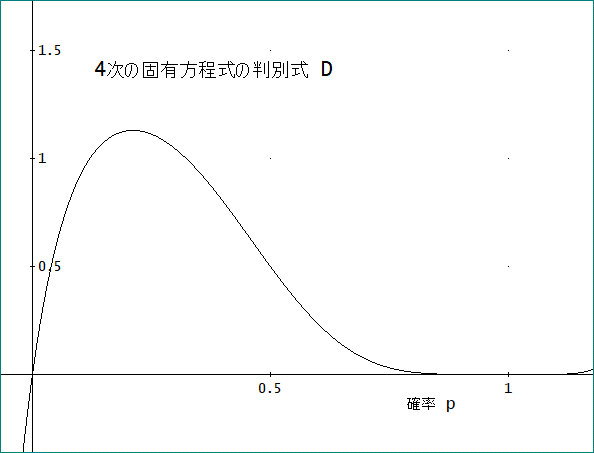
当然ながら、根から直接、得られた結果と同じではある。
ただ、一つ言えることは、p=1の近傍で、Dがゼロにかなり早く近づくことだ。
Dに(1-p)^6が含まれているからな。
判別式の大きさ(2乗でも良い)は、方程式の根がどの程度、同じ値に集まっているかを知る目安になると思う」
「なるほど。
根と係数の関係で、方程式の定数項は、z1z2・・zn ね。
似ている感じね。
今回の場合は、それは、a0=p(1-p)^2、なので、
a0^2 のグラフを描いてみると、下図の通り。
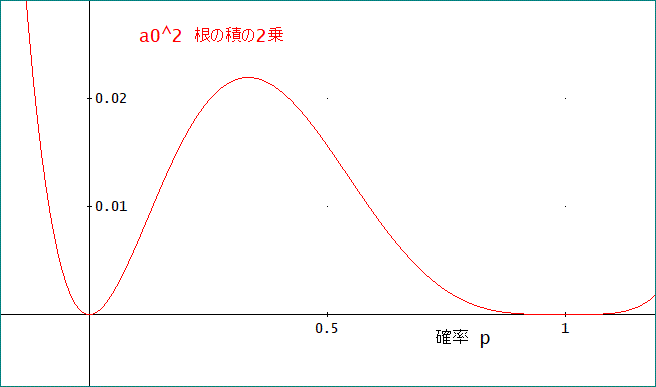
一方、判別式^2は、下図のようになる。。
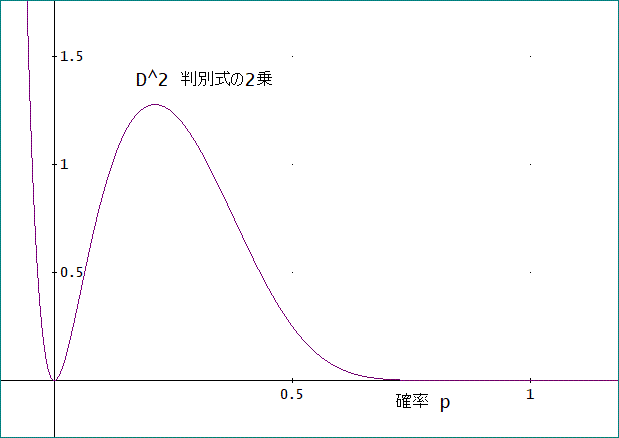
縦軸のスケールは、違うものの、両者が、この場合は、かなり似通った振る舞いをしていることが分かる」
「うん、これは、面白いのう。
そういえば、第68回の『方程式の数値解法(3)(解の重心と範囲、DKA法)』で根の平均値、という話題が登場している。
それは、根と係数の関係から出る、コンな簡単な式、
根の平均値=(z1+z2+・・・+zn)/n=-(an-1 )/n、で計算できることじゃ。
ここで、an-1 は、n-1 次項の係数じゃ」
「思い出したわ。
確か、この平均値を使って、n-1次項を消去できるので、その変換は、2次方程式~4次方程式の解法で大活躍したのね。
第68回では、解の最大値の見積についても、テーマにしていた。
そして、ワイエルシュトラス法又はDKA法(デュラン・カーナー・アバースの公式)につないでいったんだった。
懐かしいわね」
「その点から言えば、判別式の2乗は、判別式が根同士の差の2乗の積じゃから、原点の移動の影響を受けないので、ある程度の価値は、あるかも知れんな。
ただ、根の絶対値の大きさは、様々なので、根の最大値なり平均値なりで規格化しないと、他との比較は、しにくい。
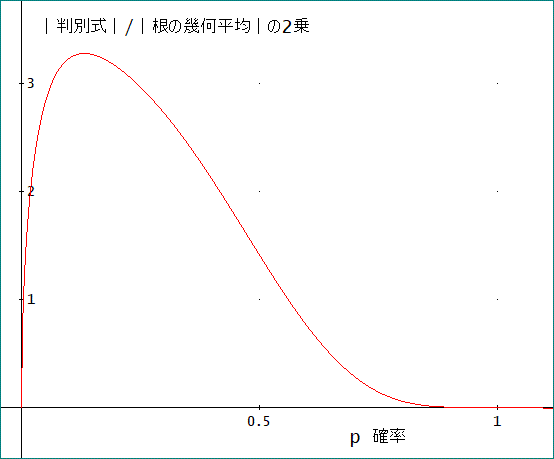
その意味で、|判別式|/(|根の幾何平均|)^2、のようなものが良いかも知れない。
4つの根の積は、a0=p(1-p)^2、この4乗根(=幾何平均)の2乗は、(1-p)√p、となるので、
|判別式|/(|根の幾何平均|)^2=(16·√p·(1 - p)^5·(4·p^2 + 1)^2)、
グラフは、下図のようになる」
目次へ戻る
5次方程式の判別式
 「では、4次の場合に続いて、5次方程式の判別式を求めてみましょう。
「では、4次の場合に続いて、5次方程式の判別式を求めてみましょう。
5次方程式は、z^5 + a4 z^4 + a3 z^3 + a2 z^2 + a1 z + a0=0、とする。
この5次式方程式は、z1、z2、z3、z4、z5 という根を使って書けば
(z-z1)(z-z2)(z-z3)(z-z4)(z-z5)=0、であり、展開すると、
z^4 - z^3·(z1 + z2 + z3 + z4+z5) + z^3(z1·(z2 + z3 + z4 + z5) + z2·(z3
+ z4 + z5) + z3·(z4 + z5) + z4·z5)-z^2(z1·(z2·(z3 + z4 + z5) + z3·(z4 +
z5) + z4·z5) + z2·(z3·(z4 + z5) + z4·z5) + z3·z4·z5)+z(z1·(z2·(z3·(z4 +
z5) + z4·z5) + z3·z4·z5) + z2·z3·z4·z5)-(z1·z2·z3·z4·z5)=0、と大分長くなります。
先ほどの式と比較すると、5次方程式の根と係数の関係は、
4次項の係数=a4=-(z1 + z2 + z3 + z4 + z5)、
3次項の係数=a3=(z1·z2 + z1·z3 + z1·z4 + z1·z5 + z2·z3 + z2·z4 + z2·z5 + z3·z4
+ z3·z5 + z4·z5)、
2次項の係数=a2=-(z1·z2·z3 + z1·z2·z4 + z1·z2·z5 + z1·z3·z4 + z1·z3·z5 + z1·z4·z5
+ z2·z3·z4 + z2·z3·z5 + z2·z4·z5 + z3·z4·z5)、
1次項の係数=a1=(z1·z2·z3·z4 + z1·z2·z3·z5 + z1·z2·z4·z5 + z1·z3·z4·z5 + z2·z3·z4·z5)、
定数項=a0=-(z1·z2·z3·z4·z5)、
となる。
一方、判別式を計算するために、
f(z)=z^5 + a4 z^4 + a3 z^3 + a2 z^2 + a1 z + a0、とおいて、
左辺の微分を作ると、
f ' (z)=5 z^4 + 4 a4 z^3 + 3 a3 z^2 + 2 a2 z + a1=0、がもう一つの式となるのね。
4次の場合は、2×4-1=7つの式が必要だったので、5次では、2×5-1=9つの式が必要となるでしょう。
具体的には、z^8 までを許して、
z^3×f(z)=0、
z^2×f(z)=0、
z×f(z)=0、
f(z)=0,
z^4×f ' (z)=0,
z^3×f ' (z)=0,
z^2×f ' (z)=0、
z×f ' (z)=0、
f ' (z)=0、
となる。
そこで、上の9つの式から、4次の場合のように行列式で重根となる条件を表すと、
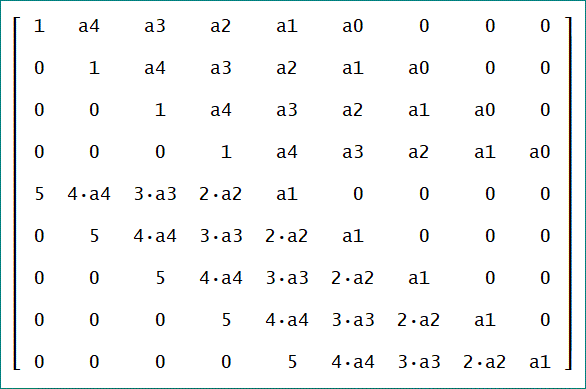
となる。
符号は、n=5では、(-1)^(n(n-1))/2=1,より、符号は変わらず、
5次方程式の判別式、Dは、
D=(3125·a0^4 - 2500·a0^3·a1·a4 - 3750·a0^3·a2·a3 + 2000·a0^3·a2·a4^2 +
2250·a0^3·a3^2·a4 - 1600·a0^3·a3·a4^3 + 256·a0^3·a4^5 + 2000·a0^2·a1^2·a3
- 50·a0^2·a1^2·a4^2 + 2250·a0^2·a1·a2^2 - 2050·a0^2·a1·a2·a3·a4 + 160·a0^2·a1·a2·a4^3
- 900·a0^2·a1·a3^3 + 1020·a0^2·a1·a3^2·a4^2 - 192·a0^2·a1·a3·a4^4 - 900·a0^2·a2^3·a4
+ 825·a0^2·a2^2·a3^2 + 560·a0^2·a2^2·a3·a4^2 - 128·a0^2·a2^2·a4^4 - 630·a0^2·a2·a3^3·a4
+ 144·a0^2·a2·a3^2·a4^3 + 108·a0^2·a3^5 - 27·a0^2·a3^4·a4^2 - 1600·a0·a1^3·a2
+ 160·a0·a1^3·a3·a4 - 36·a0·a1^3·a4^3 + 1020·a0·a1^2·a2^2·a4 + 560·a0·a1^2·a2·a3^2
- 746·a0·a1^2·a2·a3·a4^2 + 144·a0·a1^2·a2·a4^4 + 24·a0·a1^2·a3^3·a4 - 6·a0·a1^2·a3^2·a4^3
- 630·a0·a1·a2^3·a3 + 24·a0·a1·a2^3·a4^2 + 356·a0·a1·a2^2·a3^2·a4 - 80·a0·a1·a2^2·a3·a4^3
- 72·a0·a1·a2·a3^4 + 18·a0·a1·a2·a3^3·a4^2 + 108·a0·a2^5 - 72·a0·a2^4·a3·a4
+ 16·a0·a2^4·a4^3 + 16·a0·a2^3·a3^3 - 4·a0·a2^3·a3^2·a4^2 + 256·a1^5 -
192·a1^4·a2·a4 - 128·a1^4·a3^2 + 144·a1^4·a3·a4^2 - 27·a1^4·a4^4 + 144·a1^3·a2^2·a3
- 6·a1^3·a2^2·a4^2 - 80·a1^3·a2·a3^2·a4 + 18·a1^3·a2·a3·a4^3 + 16·a1^3·a3^4
- 4·a1^3·a3^3·a4^2 - 27·a1^2·a2^4 + 18·a1^2·a2^3·a3·a4 - 4·a1^2·a2^3·a4^3
- 4·a1^2·a2^2·a3^3 + a1^2·a2^2·a3^2·a4^2)、
となりました」
「いやいや、やはり長い式になるのう。
符号の検算をしてみよう。
f(z)=(z + 1)·(z - 1)·(z + 2)·(z - 2)·(z - 3)=z^5 - 3·z^4 - 5·z^3 + 15·z^2
+ 4·z - 12、
D=((z1-z2)(z1-z3)(z1-z4)(z1-z5)(z2-z3)(z2-z4)(z2-z5)(z3-z4)(z3-z5)(z4-z5))^2
=8294400、
一方、ともちゃんが書いてくれた式では、
a4=-3、a3=-5、a2=15、a1=4、a0=-12、と置けば、
8294400、となって、一致した。
ま、試みに、判別式の計算をやってみたんじゃが、5次方程式あたりで、すでに、うんざりしてきたの。
わしらの目的は、平均日数を計算することじゃ。
c=10 以上では、(固有方程式がλ^2の多項式として5以上の次数となり)、代数式として根を求められない。
そこで、確率 p を数値として与えて、固有方程式を近似的に解いて、根をすべて求める。
近似的にせよ、根を求めてしまうので、単根であることを含めて、根の性質がほぼ分かってしまう。
なので、判別式の出番がない」
「ななな。
それは、あまりな」
「判別式の定義は、方程式の根を使って書かれていたが、実際の計算では、方程式の係数のみで、判別式を表すことができた。
第90回で導いた、わしらの平均日数の計算式も、方程式の根が含まれているが、ひょっとすると、係数のみで書くことができるかもしれん。
ともちゃんに、行列式を講習してもらうんじゃから、そのあたりも検討してもらいたいなと思ったのでな。
では、次回、よろしゅうお願いしますよ」
「・・・」
目次へ戻る
最終更新日 2018/6/15、(2)に節を追加 2018/6/16、文章を微修正 2018/6/17、2018/9/23



 「なるほど。
「なるほど。
