数式処理ソフト　DERIVE（デライブ） de ドライブ

８６．偏微分方程式の解法（1）（関数変換、変数変換、積分変換）

目次

　（0）はじめに
　（1）偏微分方程式の解法
　（2）関数変換
　　1階偏微分方程式の例
　　2階偏微分方程式の例
　（3）変数変換
　　2次曲線の変換のおさらい
　　変数のアフィン変換
　　1階偏微分方程式の例
　　2階偏微分方程式の例
　　変数変換のヒント
　　極座標
　（4）積分変換
　（5）ラプラス変換
　　ラプラス変換と逆変換
　　1階偏微分方程式の例
　　2階偏微分方程式の例
　（6）ラプラス逆変換
　　逆変換と複素関数
　　留数の利用
　　ヘビサイドの展開定理
　　F(s)=1/s の場合の逆変換の計算例（2017/3/26追記）

（0）はじめに

「これまでも、『偏微分方程式』については、このシリーズや『今月のご挨拶』などで、何回か、触れてはきた。
　じゃが、DERIVEでは、代数方程式や常微分方程式の場合とは違って、偏微分方程式の解を直接求めることはできない。
　そのため、偏微分方程式、そのものについては、扱ってこんかったのじゃな」

「けれど、例の『道中双六の問題』をきっかけにして、どうしても、やる必要が出てきたということかしら？」

「ともちゃんかい。
　ようやっと、3月になって、日差しのぬくもりが感じられるようになったのう。
　さて、ともちゃんが言うように、『道中双六の問題（補筆2）』では、新たに偏微分方程式の『判別式』や『双曲型』などの用語が出てきた。
　偏微分方程式は、もう少し、先に取り扱う心づもりじゃったのだが、一連の流れを受けて、関数の変換、変数の変換等を利用した解法を調べることにしよう。
　今回扱うのは、1階または2階の線形偏微分方程式で、独立変数が2つ、未知関数が1つの場合に限ることにする。
　最初に、参考書を挙げておこうかの。
　手頃のものとして、『理工系数学のキーポイント』の『偏微分方程式』（河村哲也 著：岩波書店：2013年10月第13刷）がある」
　「えーと、その他、
　2016年4月の今月のご挨拶『道中双六の問題（続々）』で紹介していた本もあったね」

「ちょっと、厚い本じゃが、『偏微分方程式 科学者・技術者のための使い方と解き方』（スタンリー・ファロウ著：伊理正夫・伊理由美 訳）（朝倉書店：2015年6月新版第17刷）のことじゃな。
　また、『自然科学者のための数学概論（増訂版）』（寺沢寛一 著：岩波書店：2014年12月第34刷）は、昔から定評のある本じゃ。
　
　以前にも紹介した『演算子法』（近藤次郎 著：培風館：昭和45年6月30日）、は、だいぶ前の本なので、手に入りづらいじゃろう。　
最近のものでは、『数学のかんどころシリーズ』の『ラプラス変換』（國分雅敏 著：共立出版：2012年7月初版第1刷）、
　『技術者のための高等数学』シリーズの『フーリエ解析と偏微分方程式』（E.クライツィグ 著：阿部寛治 訳：近藤次郎・堀 素夫 監訳：培風館：2015年10月第8版第16刷）などがある。後者は、フーリエ解析と・・、なっているが、ラプラス変換も解説されている。

　
　ま、いきなり、難しい本に取り付くのは、挫折の元ともなりかねない。
　わしが思うには、小説などと違って、こういった専門書は、一部の方を除き、ぱらぱらと読み進むことが難しい。
　見かけが薄手じゃからと言って、中身が易しいとも限らん。
　なので、実際に買い求めるにあたっては、本の初めの方を読んでみて、平易すぎる程度がちょうどよいと思うのう。
　分厚い本は、必要に応じて、辞書のように、拾い読みをするような使い方ではないかな」

「なるほどね。
　で、最初に偏微分方程式の例や用語などを挙げてもらえると助かるわ」

「ま、必要なんじゃが、数学の本のように、定義、定理、証明などが並んでいると、それだけで、読む気がなくなってしまうじゃろう。
　最低限必要な用語や記号を説明して、あとは、順次、紹介していこうかの。
　以下では、（独立）変数をx、y、（あるいは、x，t）、また、それらの未知関数を f 、F、などで表す。
　数学や物理の問題には、変数の数が3以上、また、未知関数も複数の場合も出てくるわけじゃが、2変数、1関数の場合に限ることにしよう。
　また、ホームページでは、添え字を書くのに手間がかかるので、f のxに関する偏微分（偏導関数ともかく） fxを f x などと略記する。
　これらは、DERIVEでは、∂（f，x）、であらわすので、本文中でも、同じ表現をすることがあるじゃろう。
　簡単な例じゃが、未知関数 F(x, y) に関する、
　Fx－Fy＋F=0、がある。（DERIVEの記法では、∂（F(x, 　y)，x）－∂（F(x, 　y)，y）＋F（x，y）=0、じゃ）
　この一般解は、後ほど、求めるが、F=Exp(－x）×φ（x＋y）、じゃ、（φは、任意関数）。
　ざっくりと言えば、偏微分方程式は、このように、未知関数とその偏導関数を含む方程式のことだな。
　なお、1階などの『階数』とは、関数の導関数の最高階の階数を指す。
　上の例、Fx－Fy＋F=0、は、1階じゃ。
　また、F t=(1/2) Fxx、は、t に関しては、1階じゃが、xに関しては、2階じゃ。よって、これは、2階の方程式となる。
　最後に、線形、というのは、（未知）関数及びその導関数について1次であることを言う。
　つまり、F^3、とか、(Fx)^2、などを含まないことことじゃな」

「あと、常微分方程式の時も出てきたんだけど、同次、という用語があるわね。
　同次っていうのは、方程式に、関数とその導関数以外の項が含まれていない場合よ。
　上の例や、y Fx＋x Fy＋2F=0、のようなのは、同次、ね。
　逆に、非同次というのは、Fx－Fy=2、とか、Fx－x Fy=y^2、とかよ」

「方程式が線形、かつ、同次の場合は、解の重ね合わせが可能じゃ。
　すなわち、方程式の解が、φ(x, 　y）及びψ(x, 　y) のとき、c1×φ＋c2×ψ もまた、解になるということじゃな。
　ここで、c1、c2は、定数。
　解の重ね合わせは、方程式が線形であっても、同次でないと、一般には成り立たん。
　このあたりも、常微分方程式の場合と似ているな。
　また、当然ながら、
　線形よりも、非線形の方が、定数係数よりも変数係数の方が、同次よりも、非同次の方が、それぞれ、難易度が高くなる。

　以前に、取り上げた偏微分方程式の例をいくつか挙げてみよう。
　　1次元の波動方程式：Ft t = Fxx、
　解法としては、『変数分離法』を紹介している。固有値も登場した。
　これらは、『今月のご挨拶』の『光と音は兄と妹（1）』に掲載。
　　1次元の熱伝導方程式：F t=(1/2) Fxx、
　これは、『今月のご挨拶』の『道中双六の問題』以降、何回か取り上げてきた。
　解法として、変数分離法を使った。固有値も登場した。
　　複素関数論の中では、∂u/∂x＝∂v/∂y、∂u/∂y＝－∂v/∂x、というコーシー・リーマンの方程式が顔を出した。
　『複素関数論（1）』（コーシー・リーマンの関係式、コーシーの積分定理）』
　このような関係式を満たすu(x, 　y)は、楕円型の偏微分方程式、
　A Uxx＋C Uyy＋F U＋G(x, y)=0、を満たす。（『楕円型』の標準形。G(x, y)=0、の場合は同次）
　ただ、この解を具体的に調べることは、しておらんがな。
　また、1階常微分方程式（正規形：dy/dx=r(x, 　y)）は、書き換えると、P(x, 　y)dx＋Q(x, 　y)dy=0、となる。
　これは、『完全微分方程式』であるか、または、（原理的には）完全微分方程式に変換できるものじゃ。
　完全微分方程式では、∂（P（x, 　y）, 　y）=∂（Q（x, 　y）, 　x） が必要であることを学んだのう。
　『1階常微分方程式の解法（2）』、
　そこでは、方程式が完全微分方程式でない場合、両辺に掛ける『積分因子』、λ(x, 　y)の条件として、
　　Q∂（λ, 　x）－P∂（λ, 　y）＋λ（∂（Q, 　x）－∂（P, 　y）=0、
　という偏微分方程式が現れた。
　P、Q が特別な場合は、実際に積分因子λ(x, y)を求めることができ、常微分方程式の解を求めることができたな」

「非線形の偏微分方程式には、どんなものがあるのかしら？」

「流体力学の『ナヴィエ・ストークスの方程式』、『KdV方程式』、光学の『アイコナール方程式』、あるいは、アインシュタインの一般相対論に現れる重力場の方程式なども非線形じゃ。
　こういった非線形方程式は、解析的には、通常は、なんらかの（線形）近似解法により、解かれる。
　もっとも、KdV方程式は、戸田先生他により、楕円関数を使った厳密解（ソリトン解）が求められたことで、大きな話題になった。
　その後、似た非線形方程式の厳密解が求められたりしているとのことじゃ」
　目次へ戻る

（1）偏微分方程式の解法

「このシリーズ、DERIVE de ドライブの大きなテーマに、『方程式を解く』ことがあることは、分かるじゃろう。
　方程式は、1次方程式から始まって、常微分方程式まで、これまで、いろいろな方程式と解法が登場してきたのう。
　一般に方程式の解法は、『解析的解法』と『数値的解法』という2つの大きなグループに分かれる。
　代数方程式や常微分方程式の場合と異なり、DERIVEでは、偏微分方程式を直接解く方法が用意されていない。
　そのため、解析的解法をサポートする手段が中心になる。（※DERIVEは、偏微分方程式の数値解法には、向かない）
　
　冒頭に触れた『偏微分方程式 科学者・技術者のための使い方と解き方』の最初の方のページに主な解法が10個ほどに分類・整理されていた。
　その中から、今回に関連する内容を4つごく簡単に紹介しよう。

　1．変数分離
　偏微分方程式を複数の常微分方程式に変える。
　未知関数を F(x, 　y) を、X(x)×Y(y)、の形に置いて、方程式に代入し、変数を分離可能であれば、2つの常微分方程式に分解できる。
　前節で紹介した1次元の波動方程式や道中双六の問題に現れた熱伝導方程式で、この方法を使った。
　初期条件や境界条件を満たす解をどうやって構成するかがポイントじゃな。

　2．関数変換
　方程式が複雑で、いきなり変数分離ができない場合は、式を簡単化したい。
　未知関数 F(x, 　y) を新らしい未知関数 G と補助関数φの積、F=G(x, 　y)×φ(x, 　y) と定義し、G(x, 　y) に関する方程式に変換する。
　補助関数φ（通常、未知のパラメーターを含む）の選択により、Gに関する方程式が、F のそれよりも簡単になる場合がある。

　3．変数変換
　現在の変数［x，y］などから導かれる新しい変数［u，v］などで方程式を書き換える。
　今回は、変数の1次変換（u=αx＋βy、など）を使ったが、座標系に極座標を使う方法も変数変換に含まれる。

　4．積分変換
　ラプラス変換、フーリエ変換などを使って、偏微分方程式の変数を減らす。
　2変数の2階偏微分方程式、特に定数係数の場合は、常微分方程式に変換できる。
　その常微分方程式の解析解が得られれば、逆変換により、元の方程式の解が得られる。
　なお、この常微分方程式は、場合により、再度、積分変換し、代数方程式に還元して解くことも可能な場合がある」

「それ以外には、どんな方法があるのかな？」

「上記と『数値的解法』以外には、摂動法、インパルス応答法、積分方程式に変換、変分法、固有関数展開法などが挙げられていた。
　摂動法というのは、方程式に微少なパラメーターが含まれる場合、そのパラメーターに関して展開して、近似解を構成する方法じゃな。
　固有関数展開法は、非同次方程式の右辺をゼロとした（同次随伴方程式の）解を基にした級数により、元の方程式の解を組み立てる方法じゃ。
　有限区間のフーリエ級数や無限区間のフーリエ変換を使って非同次方程式の解を得るのは、固有関数展開の代表的な例じゃ。
　変分法は、未知関数を含む定積分の変分を取ると偏微分方程式が導かれる定積分を構成して、その積分の値を極小にするような近似解を見いだす方法じゃ。
　なお、同書でも、これらのすべてが網羅的に解説されているわけではないので注意して欲しい」

「偏微分方程式では、初期条件以外に境界条件が重要よね」

「おお、そうじゃな。
　常微分方程式では、初期値問題が中心じゃった。
　常微分方程式の境界値問題も考えられるが、初期値問題の変形として扱うことができる。（この件は、まだ扱っておらんがの）
　一方、偏微分方程式では、領域の縁（無限遠では、無限遠）での関数の条件を決めないと具体的な関数が分からない。
　たとえば、Fx－Fy=0、の一般解は、任意関数をφ（t）として、 F =φ（x＋y）である。
　なぜならば、Fx=∂（φ，x）=φ’、同様に、Fy=∂（φ，y）=φ’、なのでな。
　任意関数の中身は、（定義域内で偏微分可能な関数であれば）何でも差し支えない。
　たとえば、φ(t)=SIN（t）、φ(t)=t^2＋2t＋3、のように。
　偏微分方程式の一般解の範囲は、途方もなく広い。
　なので、一般解のままでは、具体的な問題と比較しようがない。
　境界条件には、縁の関数の値を指定（ディリクレ条件）、導関数の値を指定（ノイマン条件）、両方（混合条件）、がある。
　常微分方程式では、たいていの初期値に対して解があった。
　しかし、偏微分方程式では、特定の初期条件や境界条件を満たす解が存在しないこともある。
　境界条件や初期条件などをまとめて『制約条件』と呼ぶこともあるのじゃ
　なお、複素係数の方程式では、1階の方程式の中にも、全く解を持たないものがあることが知られている」

「なるほど。
　φ(t)=t^2＋2t＋3、は、Fx－Fy=0、の解か。
　DERIVEで、計算させても、方程式を満たしているね。
　φ(t) ≔ 2·t^2 + 2·t + 3、とφを定義してから、
　f(x, 　 y) ≔ φ(x + y)、を定義すると、
　∂(f(x, 　 y), 　 x) － ∂(f(x, 　 y), 　 y) の計算結果は、当然ながら、ゼロとなった。
　ものすごい広い範囲の関数が解となっているのが実感されるわね」

「今の場合は、式が特に簡単だったので、DERIVEに頼ることもないがの。
　しかし、式が少し煩雑になると、変数が多い分、検算や変数変換、関数変換などで計算を間違えやすい。
　その意味で、DERIVE、などの数式処理ソフトの利用は、大いに便利だと思う」

「Fx－Fy=0を満たす3つの関数、f=x+y、f=sin(x+y)、f=（x＋y）^2、のグラフを下図に描いてみたわ。
　ただし、縦軸は、z 軸。また、灰色の平面は、z=0 を表します」　

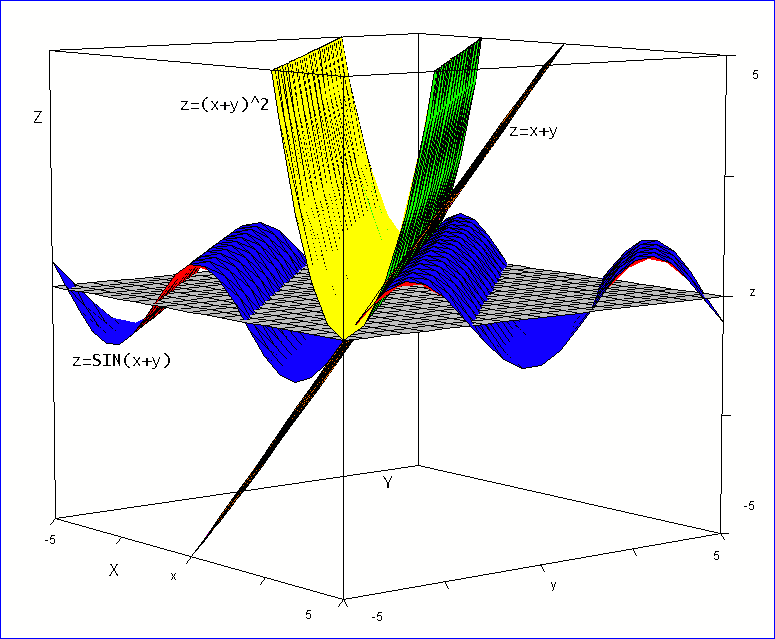
　目次へ戻る

（2）関数変換

「関数変換による解法を説明しよう。
　今、未知関数 f(x, 　y)に関する偏微分方程式があるとして、
　補助関数を、たとえば、φ=Exp（λx）として、f=φ×G(x, 　y)、とし、 G(x, 　y) と未知のパラメータ λの方程式に変換する方法じゃ。
　具体的に説明するために、独立変数 x，y、未知関数 f に関する以下の2階線形同次偏微分方程式を考えよう。
　A fxx＋B fxy＋C fyy＋D fx＋E fy＋F f=0、じゃ。
　ここに、A～Fは、一般的には、x、yの関数と考えてもよいが、以下では、定数の場合を例にとる。
　このA～Fの係数を6次元のベクトルとしてとらえ、関数変換後の新しい係数ベクトルを計算するためのDERIVEの関数を作った。
　FPDE2（A_，v_，φ_）がそれじゃ。


　ここで、関数内部の、x_、wx_ などのバー付きの変数は、いわゆるローカル変数を表す。
　DERIVEでは、ローカル変数とグローバル変数の区別がないので、このように分けておくのがよい。
　第1引数 A_は、現在の方程式の係数ベクトル（［A，B，C，D，E，F］）だ。
　第2引数 v_は、［x，y］のように変数名を与えるためのベクトル。
　v_ により現在の変数名を与えているので、［x，t］とか［r，θ］のように［x，y］でない変数名でも利用可能だ。
　第3引数 φ_は、補助関数（普通は、未知なるパラメーターを含める）じゃな。
　関数の中身は、手計算で行うのとほぼ同じなので、特に解説は、せんがの」

「これは、便利ね。
　手計算だと間違えやすいもの。
　確認してみるよ。
　A fxx＋B fxy＋C fyy＋D fx＋E fy＋F f=0、は、
　A_=［A，B，C，D，E，F］、
　v_=［x，y］、
　とする。
　一方、補助関数を φ=Exp(λx）とする場合、すなわち、新しい未知関数をgとして、f=g×φと置く場合、
　FPDE2([A, 　 B, 　 C, 　 D, 　 E, 　 F], 　 [x, 　 y], 　 EXP(λ·x))、を計算するのね。
　[A·^(λ·x), 　 B·^(λ·x), 　 C·^(λ·x), 　 ^(λ·x)·(2·A·λ + D), 　 ^(λ·x)·(B·λ + E), 　 ^(λ·x)·(A·λ^2 + D·λ + F)]、が返ってくる。
　このベクトルをExp(λx)で割れば、（これは、以下でも繰り返し現れるので、今後は、一々断らないわよ）
　[A, 　 B, 　 C, 　 2·A·λ + D, 　 B·λ + E, 　 A·λ^2 + D·λ + F]、が得られる。
　これを見ると、2階の項、A、B、C は、変わらないことが分かる。
　一方、1階（赤字）とゼロ階（青字）の係数には、λが含まれている。
　これを利用すれば、1階またはゼロ階の項を消去など可能となるわね」　
　目次へ戻る

1階偏微分方程式の例

「Fx－Fy＋F=0、を例にとって、使い方を説明しよう。
　補助関数 φ=Exp(λx）、として、F=φ×G(x, y)、と考え、
　FPDE2([0, 　 0, 　 0, 　 1, 　 －1, 　 1], 　 [x, 　 y], 　 EXP(λ·x))、を計算すると、
　G(x, 　y)に関する新方程式の係数は、
　[0, 　 0, 　 0, 　 1, 　 －1, 　 λ + 1]、が求められる。
　ここで、λ=－1、と置けば、ゼロ階の項は、消去できるので、新しい方程式は、
　Gx－Gy=0、となり、この解は、容易に、G=ψ（x＋y）、ここで、ψは、任意関数、と求められる。
　従って、原方程式の解、F=Exp(－x)×ψ（x＋y）、となることが分かるじゃろう。
　実際、検算してみると、
　Fx－Fy＋F=(^(－x)·ψ'(x + y) － ^(－x)·ψ(x + y) － ^(－x)·ψ'(x + y) + f(x, 　 y))=0、となるのでな」

「なるほどね。
　でも、F=Exp（y）×ψ（x＋y）も、解ね。
　これは、なぜだか、皆さんも分かるでしょ？」　
　目次へ戻る

2階偏微分方程式の例

「では、『道中双六の問題』の方程式、『道中双六の問題（補筆2）』から、2階の場合を取り上げてみるよ。
　∂(f(x, 　 t), 　 x, 　 2)/2 ＋(2p － 1)∂(∂(f(x, 　 t), 　 t), 　 x)＋(1 － 2p)∂(f(x, 　 t), 　 x) －∂(f(x, 　 t), 　 t)=0、
　この方程式は、q=2p－1、と置いて、（p<>1/2と考えているので、q<>0）
　(1/2)fxx＋q fxt－q fx－f t=0、と書き表されるのね。
　係数ベクトルは、[1/2, 　q, 　0, 　－q, 　－1, 　0]、
　関数変換の補助関数をφ=EXP(λx+μt)として、
　FPDE2(([1/2, 　 q, 　 0, 　 －q, 　 －1, 　 0]), 　[x, 　t], 　EXP(λx+μt))、を計算すると、
　新係数は、([1/2, 　 q, 　 0, 　 q·(μ － 1) + λ, 　 q·λ － 1, 　 q·λ·(μ － 1) + λ^2/2 － μ])、となる。
　1階の項を消去するために、
　λ=1/q、
　μ=(q^2 － 1)/q^2、と定めれば、
　新係数は、([1/2, 　 q, 　 0, 　 0, 　 0, 　 1/(2·q^2) － 1])となり、
　(1/2)Gxx＋q Gxt＋（1/(2q^2)－1）G=0、と簡単化される」

「ともちゃんがやってくれた道中双六の方程式では、変数名として、［x，t］を使っていることに注意して欲しい。
　今回紹介した関数は、補助関数や係数に、［x，y］以外の変数が使用されていても、正しい結果が得られるようにできている。
　これは、現在の変数名を第2引数で与え、関数内で、現在の変数名の変数を一時変数に置き換え、最後に元の変数名に戻しているためじゃ。
　なお、ともちゃんがやってくれた例では、1階の項を消去したが、場合により、ゼロ階の項を消去することもできる。
　ただし、EXP（λx＋μt）のような補助関数では、前述のように、2階の係数は、変えられないので、本方程式を標準形、Gxt=係数×G、に変えることはできない。
　2階の項を変えるためには、次に述べる変数変換が有効じゃ。
　一方、変数変換により、2階の項を変更した際、1階の項が現れることがあるので、それを消去するときに関数変換を利用するのが便利じゃな」
　目次へ戻る

（3）変数変換

2次曲線の変換のおさらい

「変数変換か。
　『キーポイント 偏微分方程式』にも出てくる、u=u(x, 　y)、v=v(x, 　y)として、独立変数を変更する方法ね。
　だけど、どうやって、変換関数を見つけるかが問題」

「2階の方程式、A fxx＋B fxy＋C fyy＋D fx＋E fy＋F f=0、の係数を『定数』として、
　x－y平面上の2次曲線の方程式と対比して考えてみよう。
　A x^2＋B xy＋C y^2＋D x＋E y＋F=0、
　変数変換 ［x，y］⇒［u，v］、ここでは、x=u+a 、 y=v+b により、曲線を『平行移動』すれば、
　A·u^2＋B·u·v ＋C·v^2 + u·(2·A·a + B·b + D) ＋v·(B·a + 2·C·b + E) + A·a^2 + B·a·b + C·b^2 + D·a + E·b + F = 0、
　x、yの一次項を消去するためには、B^2－4AC<>0 であれば、a、bが下記のように求められる。
　a = (B·E － 2·C·D)/(4·A·C － B^2)、
　b = (B·D － 2·A·E)/(4·A·C － B^2)、
　このとき、u、vの1次の項は、消去されて方程式は、次のようになる。
　A·u^2·(4·A·C － B^2) ＋B·u·v·(4·A·C － B^2) + C·v^2·(4·A·C － B^2) + A·(4·C·F － E^2) － B^2·F + B·D·E － C·D^2=0、となる。
　また、B^2－4AC=0のときは、
　（1）B=0のとき、
　　　a=b=0として、
　　　①　A=0 かつ C<>0、の場合
　　　　　u = － (C·v^2 + E·v + F)/D、ただし、D<>0
　　　　　これは、放物線となる。
　　　　　なお、もし、D=0ならば、C·v^2 + E·v + F = 0、から決まる、v=一定で表される2直線。（重根の場合は、1直線）、
　　　②　C=0、かつ、A<>0 の場合
　　　　　v = － (A·u^2 + D·u + F)/E、ただし、E<>0、
　　　　　これは、放物線となる。
　　　　　なお、もし、D=0ならば、A·u^2 + D·u + F = 0、から決まる、u=一定で表される2直線。（重根の場合は、1直線）、
　　　③　A=C=0の場合
　　　　　D·u + E·v + F = 0、で決まる1直線。
　（2）B<>0のとき、
　　　A<>0、かつ、C<>0 が必要。
　　　このとき、B=±2√（AC）、なお、AとCは、同符号でないといけない。
　　　(a·(b + v) + b·u + u·v)·√(A·C) + A·(a^2 + 2·a·u + u^2) + C·(b^2 + 2·b·v + v^2) + D·(a + u) + E·(b + v) + F = 0、
　　　一次項を消去する条件は、
　　　((2·A·a + D) + b·√(A·C) = 0)、(2·C·b + E)+(a·√(A·C))=0、
　　　これらから、
　　　([b = (C·D － 2·E·√(A·C))·√(A·C)/(3·A·C^2) ∧ a = (E·√(A·C) － 2·C·D)/(3·A·C)])
　　　従って、
　　　3·A·u^2 +3·u·v·√(A·C) + 3·C·v^2 +D·E/√(A·C) + (A·(3·C·F － E^2) － C·D^2)/(A·C) = 0、
　こうして、直線となる場合を除くと、A' u^2＋B' uv＋C' v^2 ＋F'=0、と変換できる。
　なお、新しい係数に’を付けている。
　ここで、u=ξcos(s)＋ηsin(s)、v=－ξsin(s)＋ηcos(s)、と更に曲線を『回転』すれば、
　楕円、双曲線、または、放物線、場合により、2直線（特殊なときは1直線や点）となるのは、分かるじゃろう」

「だいぶ昔にやった『アフィン変換』を思い出すわね。
　2007年4月頃。懐かしい♪
　第28回『変数変換と座標変換』、第30回『座標変換（2）』で扱っているわ」

「並進、回転、と出たんじゃが、これに『伸縮』を付け足すと、ともちゃんが指摘してくれた『アフィン変換』じゃな。
　伸縮は、変数の定数倍となるだけではあるが、伸縮により、方程式の無次元化が可能となることがあるので重要だ。
　結局、平行移動、伸縮、回転を含めて、
　新変数［u，v］に対して、
　uをαx＋βy、vをγx＋δy、などと変換すれば、よいことになる。
　アフィン変換では、楕円が真円に変わることはあっても、双曲線に変わったり、放物線になったりすることはない。
　ただし、u とv が一次従属関係になってはいけない。
　すなわち、αδ－βγ（ロンスキー行列式：下記注参照）がゼロとならぬよう、パラメーターの値を選ぶ必要がある。
　なお、念のため、座標系の考え方を付け加えておこう。
　新座標［u，v］は、本来、元の座標系［x，y］の中で考えていることじゃ。
　u、v と変数名を変えているのは、後で、変数の内容をx，y に戻すための、いわば、便宜上のことじゃな。
　すなわち、新しい座標系を立てたのではなく、図形自体を移動、回転、伸縮しただけじゃ。
　もちろん、座標系が新しくなったと考えてもよいが、その際は、元と同じ直交座標系であると思わないといけない」

　

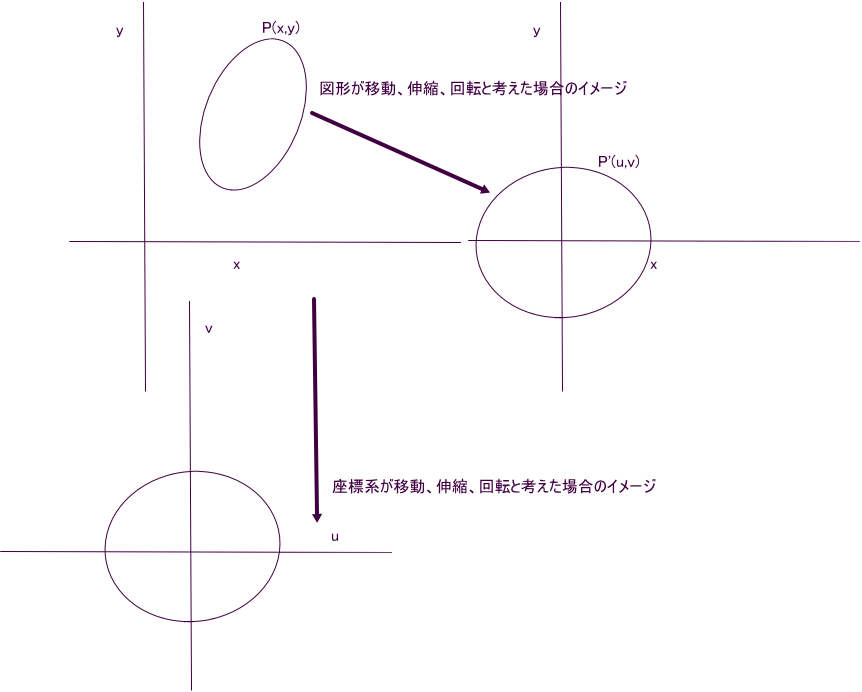
「えーと。
　そこんところ、ちょっと分かりづらいんだけど」

「つまり、アフィン変換により、x－y平面の図形が同じ平面内にあって変形（移動、伸縮、回転）したと考えてもよいし、新しいu－v平面に写る（写像）と考えてもよい。
　このとき、図形は、延ばされたり、縮んだりして写ることもあるわけじゃな。
　しかし、後者のu－v座標系の座標軸は、直交している。（斜交座標や一般の曲線座標ではない）
　以上は、2次曲線の変換のことじゃったが、2階の、特に定数係数の線形偏微分方程式に対して、変数のアフィン変換が有効じゃ。
　次節で確認していこう」　

　注：ロンスキー行列式
　u=u(x, y)、v=v(x, y)、の場合、行列、
　［［∂u/∂x，∂v/∂x］，［∂u/∂y，∂v/∂y］］、この行列式がゼロとなる場合は、uとvの間に一次従属関係がある。
　3変数以上でも、同様の関係式が成り立つ。この行列式を『ロンスキー行列式』という。
　目次へ戻る

変数のアフィン変換

「変数の変換のために、（2）節の『関数変換』の場合と同様に、DERIVEで新しい関数を定義してみた。
　対象は、関数変換と同様に、2変数の2階線形同次偏微分方程式だ、
　A fxx＋B fxy＋C fyy＋D fx＋E fy＋F f=0、じゃな。
　ここに、A～Fは、一般的には、x、yの関数と考えてもよいが、以下では、定数の場合を取り上げる。
　このA～Fの係数を6次元のベクトルとしてとらえて、第1引数 A_とする。
　第2引数の変数名ベクトル、v_は、現在の変数名、［x，y］、
　第3引数のvn_は、新変数名を現在の変数名で表した式を入れる。
　もし、u=αx＋βy、v=γx＋δy、とする場合、u，vをx，yについて、解いた、
　［(u·δ － v·β)/(α·δ － β·γ))，(u·γ － v·α)/(β·γ － α·δ)］、を第3引数に入れる。
　ただし、空のベクトル、［］、を入力し、省略も可能だ。省略した場合は、現在の変数名のままとなる。
　第4引数の変換関数ベクトル、w_は、新変数を現在の変数名で表したものを入れる。
　たとえば、uをαx＋βy、vをγx＋δy、とする場合、［α·x + β·y, 　 γ·x + δ·y］と置く。
　これが、FPDE1（A_，v_，vn_，w_）、じゃ。
　なお、極座標に変換したい場合も可能だ。（後述）
　実行すると、新しい係数ベクトルを返す。　
　

　実際、
　FPDE1([A, 　 B, 　 C, 　 D, 　 E, 　 F], 　 [x, 　 y], ［］， [α·x + β·y, 　 γ·x + δ·y])、として、計算させると、
　新しい係数ベクトルとして、
　[A·α^2 + B·α·β + C·β^2, 　 2·A·α·γ + B·(α·δ + β·γ) + 2·C·β·δ, 　 A·γ^2 + B·γ·δ + C·δ^2, 　 D·α + E·β, 　 D·γ + E·δ, 　 F]、が返る」
　目次へ戻る

1階偏微分方程式の例

「なるほど。
　では、（2）節でも取り上げた、Fx－Fy＋F=0、の例をやってみるよ。
　FPDE1([0, 　 0, 　 0, 　 1, 　 －1, 　 1], 　 [x, 　 y]，［］， [α·x + β·y, 　 γ·x + δ·y])、を計算させると、
　[0, 　 0, 　 0, 　 α － β, 　 γ － δ, 　 1]、が戻る。
　もし、α=2、β=1、γ=δ=1、とすれば、（ロンスキー行列式：αδ－βγ=2×1－1×1=1<>0）
　[0, 　 0, 　 0, 　 1, 　 0, 　 1]、となることが分かるので、
　新方程式は、Fu＋F=0、
　これから、F=φ(v)×Exp（－u)、ただし、φ(v)は、vの任意関数。
　u=αx＋βy=2x＋y、
　v=γx＋δy=x＋y、
　により、元の変数に戻すと、
　F=φ(x＋y)×Exp（－(2x+y)）、
　これは、（2）節の結果、F=Exp(－x)×ψ（x＋y）とは、違って見える。
　だけど、等値してみると、
　φ(x＋y)×Exp（－(2x+y)）=Exp(－x)×ψ（x＋y）、
　これから、ψ（x+y）=φ（x+y）×Exp（－(x+y)）、であれば、満たされることが、ψは、任意関数なので、このように置くことができる。
　よって、この節の方法による解も同一であることが分かるわ」

「そのとおりじゃな。
　もっとも、この例では、関数変換を使った（2）節の方法が分かりやすかったかもしれんがの」
　目次へ戻る

2階偏微分方程式の例

「道中双六の問題の方程式、『道中双六の問題（補筆2）』から、2階の例じゃ。
　∂(f(x, 　 t), 　 x, 　 2)/2 ＋(2p － 1)∂(∂(f(x, 　 t), 　 t), 　 x)＋(1 － 2p)∂(f(x, 　 t), 　 x) －∂(f(x, 　 t), 　 t)=0、
　この方程式において、q=2p－1、と置き、（p<>1/2と考えているので、q<>0）
　(1/2)fxx＋q fxt－q fx－f t=0、を考えてみよう。
　u=αx＋βt、v=γt、と変換して、（こうすれば、uとvが一次従属になるおそれはない）
　FPDE1([1/2, 　q, 　0, 　－q, 　－1, 　0], 　[x, 　t], 　［］，[αx+βt, 　γt])、を計算すると、
　[q·α·β + α^2/2, 　 q·α·γ, 　 0, 　 － q·α － β, 　 －γ, 　 0]、が返る。
　第1項を消去するために、β=－α/(2q)、とすると、
　[0, 　 q·α·γ, 　 0, 　 α/(2·q) － q·α, 　 －γ, 　 0]、となる。
　簡単化のために、α=2q、γ=1と置くと、β=－1、
　すなわち、u=2qx－t、v=t、と変数を変換したことになり、新係数は、
　[0, 　 2·q^2, 　 0, 　 1 － 2·q^2, 　 －1, 　 0]、となる。
　これは、
　2q^2 F u v＋（1－2q^2）Fu－Fv=0、じゃな。
　ともちゃん、（2）節の関数変換を使って1階の項を消去してご覧」

「関数変換のための補助関数を、φ=EXP（λu＋μv）として、
　FPDE2([0, 　 2·q^2, 　 0, 　 1 － 2·q^2, 　 －1, 　 0], 　 [u, 　 v], 　 EXP(λ·u + μ·v))、を計算すると、
　[0, 　 2·q^2, 　 0, 　 q^2·(2·μ － 2) + 1, 　 2·q^2·λ － 1, 　 2·q^2·λ·(μ － 1) + λ － μ]、となる。
　1階の項を消去するため、
　q^2·(2·μ － 2) + 1 = 0、及び、2·q^2·λ － 1 = 0、を使うと、
　λ=1/(2q^2)、
　μ=1－1/(2q^2)、
　とパラメーター、λ、μが決定できる。
　このとき、係数ベクトルは、
　[0, 　 2·q^2, 　 0, 　 0, 　 0, 　 (1 － 2·q^2)/(2·q^2)]、となり、
　双曲型の偏微分方程式の『標準形』である、
　G u v=τ G、となる。
　ただし、τ=－1/(4q^4)＋1/(2q^2)、F=G（u，v）×Exp（λu＋μv）、よ」

「そうじゃな。
　付け加えると、双曲型の偏微分方程式の標準形は、もう一つあるそうだ。
　それは、G(u, 　v) に関する方程式を、ξ=u＋v、η=u－v、と更に変数変換することだ。
　FPDE1([0, 2·q^2, 0, 0, 0, (1 － 2·q^2)/(2·q^2)], [u, v], [(ξ + η)/2, (ξ － η)/2], [u + v, u － v])、として計算すると、
　この新しい変数［ξ，η］に関する方程式の係数は、
　[2·q^2, 　 0, 　 － 2·q^2, 　 0, 　 0, 　 (1 － 2·q^2)/(2·q^2)]、となり、
　これは、すなわち、
　G ξξ－ G ηη－τ G=0、を表す。
　ここで、τ=－1/(4q^4)＋1/(2q^2)、また、G ξξなどは、∂（∂（G，ξ），ξ）などを意味するので注意して欲しいのう」

「G u v=τ G、τ=－1/(4q^4)＋1/(2q^2)、
　ただし、q=2p－1、であるので、－1 =< q =< 1、である。（ただし、p=1/2、すなわち、q=0は、除く）
　グラフは、下図ね。横軸は、q、縦軸は、τ。
　
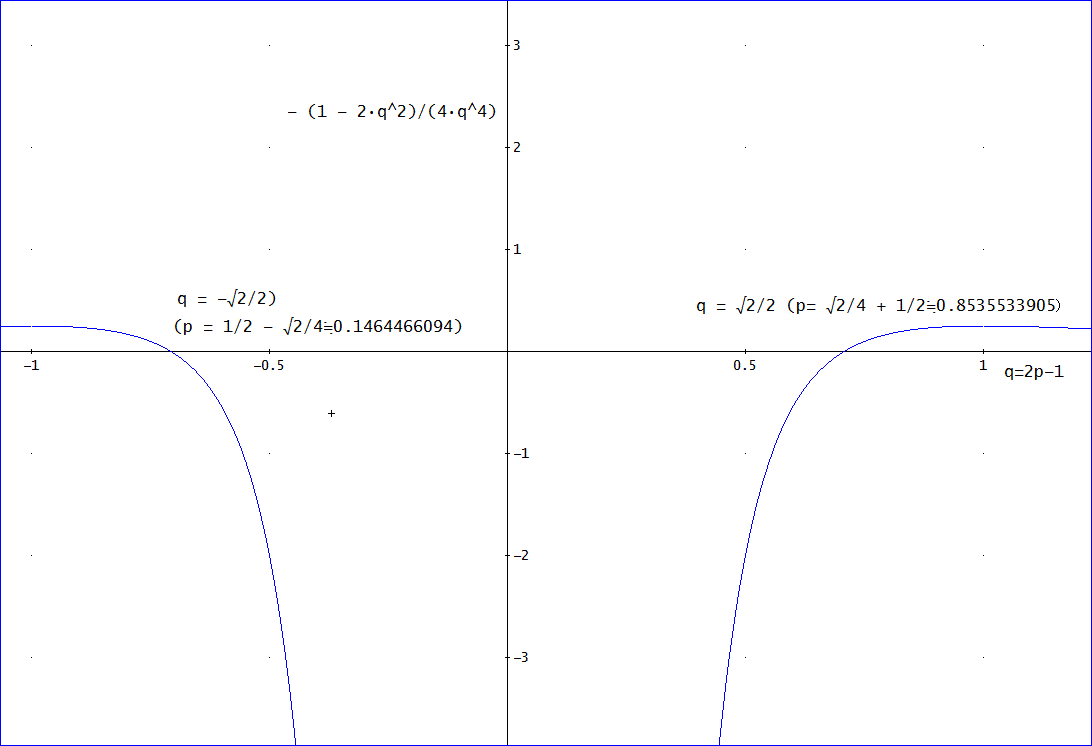
　qの正負の範囲に、τの符号が反転する点があるのが面白いわね」

「双曲型の（第1）標準形、G u v=τ G、の解は、
　τ>0 ならば、a Sinh(τu+v)＋b Cosh(τu＋v)、の a，b等の級数または積分、
　τ=0 ならば、φ(u)＋ψ(v)、（φ、ψは、任意関数）、
　τ<0 ならば、a Sin（｜τ｜u＋v）＋b Cos（｜τ｜u＋v）、の a，b等の級数または積分、
　ただ、道中双六の問題に即して解くためには、もう少し準備が必要なので、次回に回すことにしよう」　
　目次へ戻る

変数変換のヒント

「2階の線形同次偏微分方程式を例にして説明しよう。
　解こうとする方程式が、A Fxx＋B Fxy＋C Fyy=0、であったとする。
　左辺の偏微分を、∂/∂x を偏微分演算子 Dx、などで表すことにすれば、A<>0のとき、
　（Dx^2＋B/A Dx Dy ＋C/A Dy^2）F=0、とも書き直すことができるじゃろう。
　このとき、左辺が、因数分解できて、
　（Dx＋αDy）（Dx＋βDy）F=（Dx^2＋（α＋β）Dx Dy＋αβDy^2）、
　これから、もし、α＋β=B、αβ=Cとなる、α、βがあれば、
　（Dx＋α Dy）φ=0、
　（Dx＋β Dy）φ=0、
　の2つの方程式の解は、元の方程式の解でもあると考えられる」

「α＋β=B/A、αβ=C/A、なる α、βは、2次方程式（変数 tには、特に意味はない）、
　t^2－B/A t＋C/A=0、の2根、t=（1/2A)（B±√（B^2－4AC））ね。
　根号内のB^2－4AC が正またはゼロであれば、実根がある。
　ここで、ようやく、2階の偏微分方程式の判別式が出てきたわ。
　判別式、B^2－4AC、がゼロの場合が『放物型』、正の場合が、『双曲型』、負の場合が『楕円型』というわけね。
　ところで、（Dx＋αDy）φ=0、つまり、φx＋αφy=0、の解は、φ=ξ（αx－y）、
　同様に、（Dx＋βDy）φ=0、の解は、φ=η（βx－y）、
　元の方程式の解であるかは、f=ξ（αx－y）、を 元の方程式の左辺に代入すると、
　A α^2ξ' '－B αξ' '＋C ξ' '=（α^2－B/A α＋C/A）ξ' '、となるんだけど、
　このかっこ内は、ゼロになるので、ξ（αx－y）は、元の方程式を満たしていることが分かる」

「A Fxx＋B Fxy＋C Fyy=0、の一般解は、ξ（αx－y）＋η（βx－y）、となるのじゃな。
　なお、B^2－4AC<0の場合は、α、βが複素数になるが、適宜、変数と関数を変換すれば、よいじゃろう。
　さて、A fxx＋B fxy＋C fyy＋D fx＋E fy＋F f=0、のような一般の2階線形同次偏微分方程式の場合は、このようには、分解できない。
　しかし、2階部分の係数が定数であれば、α、βを求めて、u=αx－y、v=βx－y、のように変数を変換することは、効果的であると考えられる。
　たとえば、道中双六の問題の方程式は、
　∂(f(x, 　 t), 　 x, 　 2)/2 ＋(2p － 1)∂(∂(f(x, 　 t), 　 t), 　 x)＋(1 － 2p)∂(f(x, 　 t), 　 x) －∂(f(x, 　 t), 　 t)=0、
　q=2p－1、と置いて、（p<>1/2と考えているので、q<>0）
　(1/2)f xx＋q f xt－q f x－f t=0、であった。
　2階部分は、A=1/2、B=q、C=0、である。
　これから、α、β=（1/2A)（B±√（B^2－4AC））=q±q=2q、または、ゼロ、が得られるので、
　u=2qx－t、v=－t、と変換するのが効果的ということになる。
　実際、
　FPDE1(([1/2, 　 q, 　 0, 　 －q, 　 －1, 　 0]), 　[x, 　t], 　[2*q*x－t, 　－t])、を計算してみると、
　[0, 　 － 2·q^2, 　 0, 　 1 － 2·q^2, 　 1, 　 0]、となり、
　すなわち、
　－2q^2 f u v＋（1－2q^2）f u＋f=0、となる。
　更に、関数変換、
　FPDE2(([0, 　 － 2·q^2, 　 0, 　 1 － 2·q^2, 　 1, 　 0]), 　[u, 　v], 　EXP(λ*u+μ*v))、を計算してみると、
　[0, 　 － 2·q^2, 　 0, 　 1 － 2·q^2·(μ + 1), 　 1 － 2·q^2·λ, 　 － 2·q^2·λ·(μ + 1) + λ + μ]、
　1階の係数をゼロとするためには、(1 － 2·q^2·λ)=0、(1 － 2·q^2·(μ + 1) = 0)、が必要なので、
　λ=1/(2·q^2)、
　μ=(1 － 2·q^2)/(2·q^2)、
　結局、係数行列は、
　[0, 　 － 2·q^2, 　 0, 　 0, 　 0, 　 (1 － 2·q^2)/(2·q^2)]、
　すなわち、
　－2q^2 G u v＋（1/(2q^2)－1）G=0、
　移項すると、
　G u v=（1/(4q^4)－1/(2q^2)）G、
　ここで、f=G(u, 　v)×Exp（λu＋μv）、となるのだな」

「前の節で求めた方程式と符号が違っちゃっているわね？
　前の節のは、F=G（u，v）×Exp（λu＋μv）、
　u=2qx－t、
　v=t、
　λ=1/(2q^2)、
　μ=1－1/(2q^2)、
　G u v=－（1/(4q^4)－1/(2q^2)）G、だった。
　今回のを’を付けて区別すると、
　u '=2qx－t、
　v '=－t、
　λ’=1/(2·q^2)、
　μ’=(1 － 2·q^2)/(2·q^2)、
　G u ' v '=（1/(4q^4)－1/(2q^2)）G、
　比べると、下の赤い2個所が異なっていることが分かる。
　u：u '、
　v：－v '、
　λ：λ'、
　μ：－μ'
　しかし、方程式は、vの符号が逆なので、それを勘案すると同じね。
　一方、f=G×Exp（λu＋μv）、の指数関数内のμv も、μとvの符号が同様に逆になっているから、同一。
　まとめると、今回の方法は、少なくとも、双曲型の問題については、有効であると思うわ」

「極座標を使う場合について、次の節で、少し補足しておこう。
　なお、変数係数の場合の変換関数の選択については、参考書の『特性曲線』などの項目の内容を確認して欲しい」　
　目次へ戻る

極座標

「今回は、2変数の場合としているので、極座標を使う場合というと、楕円型の偏微分方程式、あるいは、Ft または F tt の項が位置座標 x，y のFxx、Fxy 等の項と分離されている方程式に限定されてしまうが、どのように、FPDE1 関数を使ったらよいかを説明しよう。
　ともちゃん、直交座標 ［x，y］から極座標 ［r，s］へ変換した場合、Fx、Fy 等の偏微分係数は、どのように変わるかの」

「いつも、頭を悩まされる問題よね。それは。
　x=r COS(s)、
　y=r SIN(s)、
　このとき、F(x，y)の偏微分係数、Fxは、
　Fx=Fr dr/dx＋Fs ds/dx、などと表されるので、
　x=r COS(s)、の両辺を、rで偏微分して、dx/dr=COS(s)、
　同様に、sで偏微分して、dx/ds=r SIN(s)、
　よって、Fx=Fr (1/COS(s))＋Fs (1/(r SIN(s))、だったかしら。
　でも、なんか違うみたいね」

「それは、だれも陥りやすい点じゃな。前にわしも、やってしまったのう。
　常微分の場合と違って、偏微分の ∂x/∂r と ∂r/∂x は、片方をひっくり返して、等しくおくことはできないのじゃ。
　なぜならば、F(r＋Δr，s＋Δs）－F(r，s) = Fr Δr＋Fs Δs＋・・2次以上の微少量、であるから、
　ΔF=Fr Δr＋Fs Δs、これから、
　ΔF/Δr=Fr＋Fs Δs/Δr、と右辺に第2項があるためじゃな。
　そこで、Fx、Fy を ［r，s］で表すには、2通りの方法があると思うが、分かりやすいのは、次の方法じゃろう。
　以下では、∂F/∂rなどを、dF/dr などと略記する。
　dF/dr=dF/dx dx/dr＋dF/dy dy/dr、
　dF/ds=dF/dx dx/ds＋dF/dy dy/ds、
　と逆に考えてから、
　x=r COS(s)、y=r SIN(s)、の両辺をrで偏微分して、
　dx/dr=COS(s)、dy/dr=SIN(s)、
　同様に、
　x=r COS(s)、y=r SIN(s)、の両辺をsで偏微分して、
　先ほどの2式の右辺の赤字の部分に代入して、
　dF/dr=COS(s) dF/dx＋SIN(s) dF/dy、
　dF/ds=－r SIN(s) dF/dx＋r COS(s) dF/dy、を得る。
　これらの2つの連立方程式から、Fx、Fy を求める。
　Fx=COS(s) dF/dr－(SIN(s)/r) dF/ds、
　Fy= SIN(s) dF/dr＋(COS(s)/r) dF/ds、が得られる」

「なるほど。
　わたしの出発点になった下の2式は、合ってたので、
　Fx=Fr dr/dx＋Fs ds/dx、
　Fy=Fr dr/dy＋Fs ds/dy、
　一方、x=r COS(s)、y=r SIN(s)、から、r=√（x^2+y^2）、TAN(s)=y/x、の関係があるので、
　dr/dx、ds/dx などを、dr/dx=COS(s)、dr/dy=SIN(s)、
　また、SEC(s)^2 ds/dx=－y/x^2=－(r SIN(s))/(r COS(s))^2、
　よって、ds/dx=－SIN(s)/r、ds/dy=COS(s)/r、
　Fx=Fr dr/dx＋Fs ds/dx=Fr COS(s)－Fs SIN(s)/r、
　Fy=Fr dr/dy＋Fs ds/dy=Fr SIN(s) ＋Fs COS(s)/r、
　とすれば、よかったのね」

「ま、それはそれで、正しいが、3次元の場合は、前の方法の方が、分かりやすいと思うのう。
　Fxx、Fxy、などは、上のFx、Fy を演算子的に掛け合わせることで求められる。
　とは言え、面倒な上に、符号などをうっかりと間違えやすい。
　FPDE1で計算してみよう。
　まず、Fx を極座標であらわしてみよう。
　FPDE1([0, 0, 0, 1, 0, 0], [x, y], [r·COS(s), r·SIN(s)], [√(x^2 + y^2), ATAN(y/x)])、を計算する。
　これまで、空ベクトルとしていた第3引数のvn_ に [r·COS(s), r·SIN(s)] と入れている点に注意して欲しい。
　これは、第2引数のv_ として指定している現在の変数名［x，y］を極座標の変数名［r，s］で表したものじゃ。
　[0, 0, 0, COS(s), － SIN(s)/r, 0]、となるが、これは、
　Fx=Fr COS(s)－Fs SIN(s)/r、を意味するので、上で導いた結果を検算できるじゃろう」

「なるほど、
　じゃ、Fyは、
　FPDE1([0, 0, 0, 0, 1, 0], [x, y], [r·COS(s), r·SIN(s)], [√(x^2 + y^2), ATAN(y/x)])、から、
　[0, 0, 0, SIN(s), COS(s)/r, 0]、が得られるので、
　Fy=Fr SIN(s)＋Fs COS(s)/r、
　また、Fxxは、
　FPDE1([1, 0, 0, 0, 0, 0], [x, y], [r·COS(s), r·SIN(s)], [√(x^2 + y^2), ATAN(y/x)])、から、
　[COS(s)^2, － 2·SIN(s)·COS(s)/r, SIN(s)^2/r^2, SIN(s)^2/r, 2·SIN(s)·COS(s)/r^2, 0]、となるので、
　Fxx=(COS(s))^2 Frr－2SIN(s)COS(s)/r Frs＋(SIN(s))^2/r^2 Fss＋(SIN(s))^2 /r Fr＋2SIN(s)COS(s)/r^2 Fs、
　同様に、
　Fyy=SIN(s)^2 Frr＋2·SIN(s)·COS(s)/r Frs＋ COS(s)^2/r^2 Fss＋ COS(s)^2/r Fr－ 2·SIN(s)·COS(s)/r^2 Fs、
　Fxy=SIN(s)·COS(s) Frr＋ （2·COS(s)^2/r － 1/r）Frs － SIN(s)·COS(s)/r^2 Fss － SIN(s)·COS(s)/r Fr＋（1/r^2 － 2·COS(s)^2/r^2）Fs、
　となったわ。
　まとめると、
　Fx=Fr COS(s)－Fs SIN(s)/r、
　Fy=Fr SIN(s)＋Fs COS(s)/r、
　Fxx=(COS(s))^2 Frr－2SIN(s)COS(s)/r Frs＋(SIN(s))^2/r^2 Fss＋(SIN(s))^2 /r Fr＋2SIN(s)COS(s)/r^2 Fs、
　Fyy=SIN(s)^2 Frr＋2·SIN(s)·COS(s)/r Frs＋ COS(s)^2/r^2 Fss＋ COS(s)^2/r Fr－ 2·SIN(s)·COS(s)/r^2 Fs、
　Fxy=SIN(s)·COS(s) Frr＋ （2·COS(s)^2/r － 1/r）Frs － SIN(s)·COS(s)/r^2 Fss － SIN(s)·COS(s)/r Fr＋（1/r^2 － 2·COS(s)^2/r^2）Fs、
　となりました」

「逆に、極座標の式を直交座標に変換することもできる。
　たとえば、Fx=Fr COS(s)－Fs SIN(s)/r、を逆変換するには、
　FPDE1([0, 0, 0, COS(s), － SIN(s)/r, 0], [r, s], [√(x^2 + y^2), ATAN(y/x)], [r·COS(s), r·SIN(s)])、を計算すると、
　[0, 0, 0, 1, 0, 0]を得る。これは、Fx じゃ。
　また、
　Fxx=(COS(s))^2 Frr－2SIN(s)COS(s)/r Frs＋(SIN(s))^2/r^2 Fss＋(SIN(s))^2 /r Fr＋2SIN(s)COS(s)/r^2 Fs、
　の逆変換は、
　FPDE1(([COS(s)^2, － 2·SIN(s)·COS(s)/r, SIN(s)^2/r^2, SIN(s)^2/r, 2·SIN(s)·COS(s)/r^2, 0]), [r, s], [√(x^2 + y^2), ATAN(y/x)], [r·COS(s), r·SIN(s)])、
　から、
　[1, 0, 0, 0, 0, 0]、を得ることができる。これは、Fxx じゃ。
　ま、こういった計算は、何回かは、手作業で経験してみて、納得したら、あとは、機械に任せた方が正確な結果を得るということじゃな。
　次節では、積分変換、具体的には、ラプラス変換を紹介しよう」　　
　目次へ戻る

（4）積分変換

「積分変換とは、前出の『演算子法』（近藤次郎 著：培風館）によれば、
　g(p)=∫（t=a～b）K(t，p) f(t) dt、と書いたとき、これを関数 f(t) の積分変換と呼ぶ。
　f(t)が原関数、g(p)が像関数、K(p，t)は、変換の核、p は、変換のパラメーターと呼ばれている。
　積分変換は、関数の和の像関数は、個別に変換した像関数の和となり、線形性を持つ変換じゃ。
　さて、像関数から原関数を求める操作は、逆変換と呼ばれ、
　f(t)=∫（p=a～b）G(p，t) dp、と原理的には、書けることが知られている。
　しかし、任意のKに対しては、 G を解析的に求められない場合も多く、また、求められても、複雑になる場合は、実用にならない。
　『岩波数学辞典』（第4版）の『積分変換』によれば、変換の核は、K(t，p)=K(t×p)、あるいは、K(t－p)、の形で与えられる関数が多いそうじゃ。
　よく知られている『フーリエ変換』は、K(t，p)=K(t×p) の形であり、
　K=Sin(u t)、a=0、b=＋∞ の場合、F(u)=∫（t=0～∞）Sin(u t) f(t) dt、は、フーリエ正弦変換、
　同様に、K=Cos(u t)、の場合は、F(u)=∫（t=0～∞）Cos(u t) f(t) dt、は、フーリエ余弦変換、という。
　逆変換は、それぞれ、
　f(t)=2/π×∫（u=0～∞）Sin(u t) F(u) du、
　f(t)=2/π×∫（u=0～∞）Cos(u t) F(u) du、となる。（書籍により、変換と逆変換の係数に違いがあるので注意）
　なお、フーリエ変換で積分区間が有限でパラメーターuがとびとびの場合は、有限フーリエ変換（いわゆる『フーリエ級数』）になる」　

「フーリエ変換以外には、どんな変換があるのかしら？」

「上述の岩波の数学辞典によれば、代表的なものとしては、
　ラプラス変換（K=Exp(－st)、a=0、b=＋∞）、（これは、次節で説明）
　Hankel（ハンケル）変換（K=√(xy)J ν(xy)、a=0、b=＋∞）、J νは、ν次のベッセル関数。、
　ヒルベルト変換（K=1/(x－y)、a=－∞、b=＋∞）、
　Mellin（メリン）変換（K=x^(y－1)、a=0、b=＋∞）、
　Stieltjes（スティルチェス）変換（K=（x＋y)^ρ、a=0、b=＋∞、ρ>0 ）、
　など、数多くあるそうじゃ」
　目次へ戻る

（5）ラプラス変換

ラプラス変換と逆変換

「ラプラス変換については、このシリーズでは、
　第33回『演算子法』、
　第44回『積分（4）（高速ラプラス逆変換）』、
　第45回『積分（5）（高速ラプラス逆変換２）』、
　第70回『1階常微分方程式の解法（2）』、でそれぞれ、少しずつ触れては、きておる。
　さて、ラプラス変換は、前節の積分変換の核 Kを、K=Exp(－s t)、a=0、b=＋∞、とした場合に相当する。
　原関数 f(t)、像関数 F(s) と書いたとき、
　F(s)=∫（t=0～∞）f(t) Exp(－st) dt、　ここで、一般に、sは、複素数のパラメーターとなる。
　この逆変換は、f(t)=1/(2π#i)×∫（Br=ブロムイッチ積分路）F(s) Exp(st) ds、となる。
　ただし、#i は、虚数単位。
　
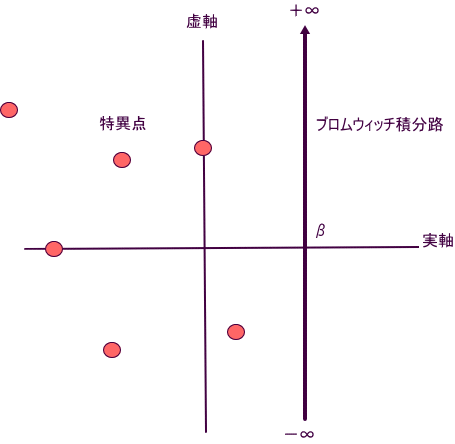
　ブロムウィッチ積分路は、上図のように、F(s)のすべての特異点よりも、右側の、s=β－∞#i～β＋∞ #iの虚軸に平行な直線上となる。
　なお、上のような複素関数論を使った逆変換は、これまで説明してこなかったので、後述しよう
　次節では、ラプラス変換を偏微分方程式の解法に応用する。
　（1）節で説明したように、2変数の方程式では、どちらか片方の変数について、ラプラス変換を行うことができれば、偏微分方程式は、常微分方程式になる。
　その解を逆変換することにより、元の方程式の解を得られるというものじゃ」
　目次へ戻る

1階偏微分方程式の例

「見かけは、簡単じゃが、基本的な内容が含まれている次の例で説明しよう。
　f x－f t=0、
　これは、今回、最初の方で説明したもので、一般解 f=φ（x＋t）、ただし、φは、任意関数、じゃった。
　さて、今、f(x，t)に関する上記の方程式が x=0～、t=0～∞、で成り立っているとする。
　初期条件　f(x，0）= Sin(x)、境界条件　f(0，t)=Sin(t)、
　f(x, 　t)のtに関するラプラス変換後の関数をF(x, s)、と書くことにする。
　ラプラス変換は、F(x, 　s)=∫（t=0～∞）f(x, 　t)×Exp(－st) dt、
　これを簡単に、記号 ⊃、⊂ を使って、
　変換は、f ⊃ F、と書き、
　逆変換は、F ⊂ f、と書くことにしよう。
　ところで、与式は、ラプラス変換の基本性質により、
　f t ⊃ s F－f(x，0)、から、
　初期条件より、f(x，0)=Sin(x)、を使って、方程式は、
　dF/dx－（s F－Sin(x)）=0、と変換される。
　移項して、
　dF/dx－s F=－Sin(x)、
　右辺=0の場合の同次方程式の一般解は、
　F=c×Exp（sx）、
　非同次方程式の解を求めるために、定数変化法を使うと、
　（－∫（y=0～x）Sin(y) exp(－sy) dy）×Exp（sx）、が得られるので、
　一般解は、同次方程式の一般解とこの特解を加えたものなので、
　F=c×Exp（sx）＋（－∫（y=0～x）Sin(y) exp(－sy) dy）×Exp（sx）、
　具体的に計算すると、
　F=(^(s·x)·(c － 1/(s^2 + 1)) + (COS(x) + s·SIN(x))/(s^2 + 1))、
　と求められる。
　一方、未定の積分定数 cは、x=0で、F=c、となることと、
　境界条件 x=0で、f=Sin(t)⊃F(0，s)=1/(s^2+1)、となることから、
　c=1/(s^2+1)、と決定できる。
　よって、F(x，s)=(COS(x) + s·SIN(x))/(s^2 + 1)、
　ここで、逆変換のために、ラプラス変換の変換表を見て、
　1/(s^2+1)⊂Sin(t)、及び
　s/(s^2+1)⊂Cos(t)、の関係を使うと、
　f(x，t)=Sin（t）Cos(x)＋Cos(t) Sin(x)=Sin（t＋x）、
　結局、f=φ（x＋t）、において、φ=正弦関数としたのと同じになったじゃろう」

「常微分方程式、dF/dx－s F=－Sin(x)、は、
　第70回『1階常微分方程式の解法（2）』で解説した線形微分方程式なので、DERIVEで解いてもいいのよ。
　その際は、あらかじめ、DERIVEのユーティリティファイル『FirstOrderODE.mth』を読み込んでおくのを忘れないこと。
　y'＋p(x)y=q(x)、としたとき、LINEAR1（p，q，x，y，x0，y0）、と引数を入れる必要があるので、
　今回は、y=F、p=－s、q=－Sin(x)、x0=0、y0=1/(s^2+1)、と当てはめて、
　LINEAR1(－s, － SIN(x), x, f, 0, 1/(s^2 + 1))、を計算すると、
　F = (COS(x) ＋ s·SIN(x))/(s^2 + 1)、が直ちに得られる。
　なお、逆変換は、逆変換表を引くか、DERIVEのユーザーファイルの『LaplaceTransform.dfw』を開いて、
　INVLaplace((COS(x) ＋ s·SIN(x))/(s^2 + 1))、を計算すると、
　f=SIN(t)·COS(x) ＋ COS(t)·SIN(x)=Sin(x＋t)、が求められた。
　グラフは、下のような感じ。
　灰色の平面は、z=0の面を表します」
　

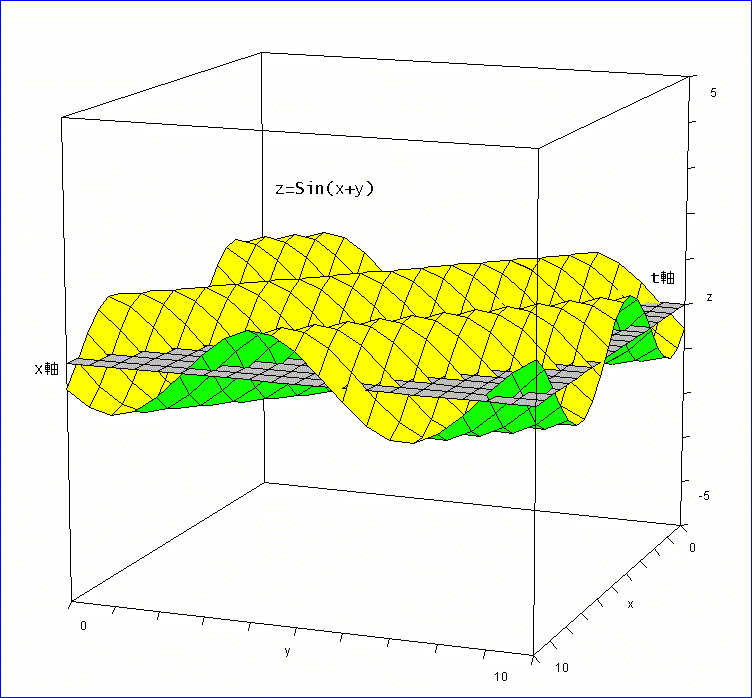
「上出来じゃな。
　次は、2階の例をやってみよう」
　目次へ戻る

2階偏微分方程式の例

「1次元の波動方程式じゃな。
　f t t=v^2 f x x、（v>0）
　ただし、t=0～、また、xの範囲は、x=0～π とする。
　また、両端は、固定されていて、f=0、である。
　初期条件は、f(x，0)=Sin(x)、f t (x, 0)=0、とする。（これは、境界条件を満たしている）
　f(x, 　t) ⊃ F(x, 　s)、として、t に関するラプラス変換を行うと、
　s^2 F－s Sin(x)=v^2 Fxx、となり、移項して、
　Fxx－（s/v)^2 F=－（s/v^2）Sin(x)、が得られる。
　先の1階の例と同じように、右辺がゼロの場合の同次方程式、
　Fxx－（s/v)^2 F=0、の一般解を見つける。
　一般解は、Exp(sx/v)及びExp(－sx/v)の一次結合であるが、
　双曲線関数を使って、F=A Cosh(sx/v)＋B Sinh(sx/v)、とも書くことができる。
　次いで、非同次方程式の解を求めるのじゃが、目の子で、
　α Sin(x)と置いて方程式に代入してみると、
　α=s/(s^2＋v^2)、のとき満たされていることが分かる。
　よって、方程式の一般解は、同次方程式の一般解とこの特解を加えた、
　F=A Cosh(sx/v)＋B Sinh(sx/v)＋s/(s^2＋v^2)×Sin(x)、となる。
　ところで、境界条件を思い出すと、
　x=0でF=0なので、A=0、
　また、x=πでF=0、から、B Sinh(sx/v)=0、
　よって、B=0、結果として、
　F=s/(s^2＋v^2)×Sin(x)、
　これをsに関して、逆変換すると、
　s/(s^2＋a^2)⊂Cos(at)、を使って、
　f=Cos(v t)×Sin(x)、と解が求められた」

「なるほど。
　じゃ、わたしは、t のラプラス変換後のxに関する常微分方程式を解くところから始めてみるね。
　Fxx－（s/v)^2 F=－（s/v^2）Sin(x)、
　この常微分方程式を、xに関して、更に、ラプラス変換して解いてみるわ。
　f(0，t)=0、
　f x(0，t)　これは不明なのね。（後で境界条件から決まる）
　f(π，t)=0、
　F(x，s)⊃G(σ，s)、をxに関するラプラス変換関数（xの変換後の変数をσ）とすると、
　σ^2G－Fx(0，s)－(s/v)^2×G=－（s/v^2）/(σ^2＋1)、
　G=Fx(0，s)/（σ^2－(s/v)^2）－（s/v^2）/（（σ^2＋1）（σ^2－(s/v)^2））、とG が求められる。
　ところで、σに関してxに逆変換するには、
　1/(σ^2－a^2)⊂(1/a)Sinh(ax)、
　第1項⊂Fx(0，s)×(v/s) Sinh(sx/v)、
　第2項⊂－ v·^(s·x/v)/(2·(s^2 + v^2)) + v·^(－ s·x/v)/(2·(s^2 + v^2)) + s·SIN(x)/(s^2 + v^2)、
　（第2項は、面倒なので、InvLaplace関数に頼ったけど）
　ともあれ、求まって、
　F=Fx(0，s)×(v/s) Sinh((sx/v)(－ v^3·^(s·x/v)/(2·s·(s^2 + v^2)) + v^3·^(－ s·x/v)/(2·s·(s^2 + v^2)) + v^2·SIN(x)/(s^2 + v^2))、
　ここで、境界条件、x=πで、f=0、を使うと、
　Fx(0，s)=s/(s^2＋v^2)、であることが分かる。
　よって、Fの式に代入して、
　F=s·SIN(x)/(s^2 + v^2)、となることが分かった。
　これを s に関してtに逆変換すると、
　f=Sin(x)×Cos(v t)、であ～る。
　ああ、しんど。
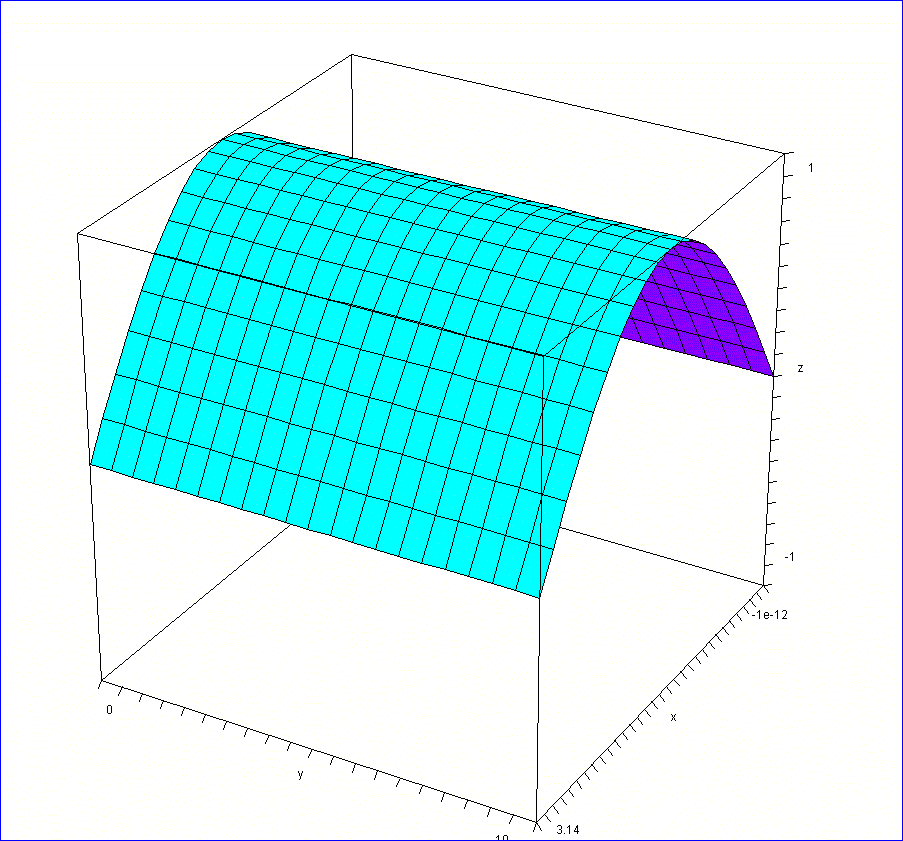
　最後に、
　v=1として、グラフを描いてみた。下図が、t=0の関数、Sin(x)、
　

　下図が、Cos(t) Sin(x)のグラフ。（v=1としている）」
　

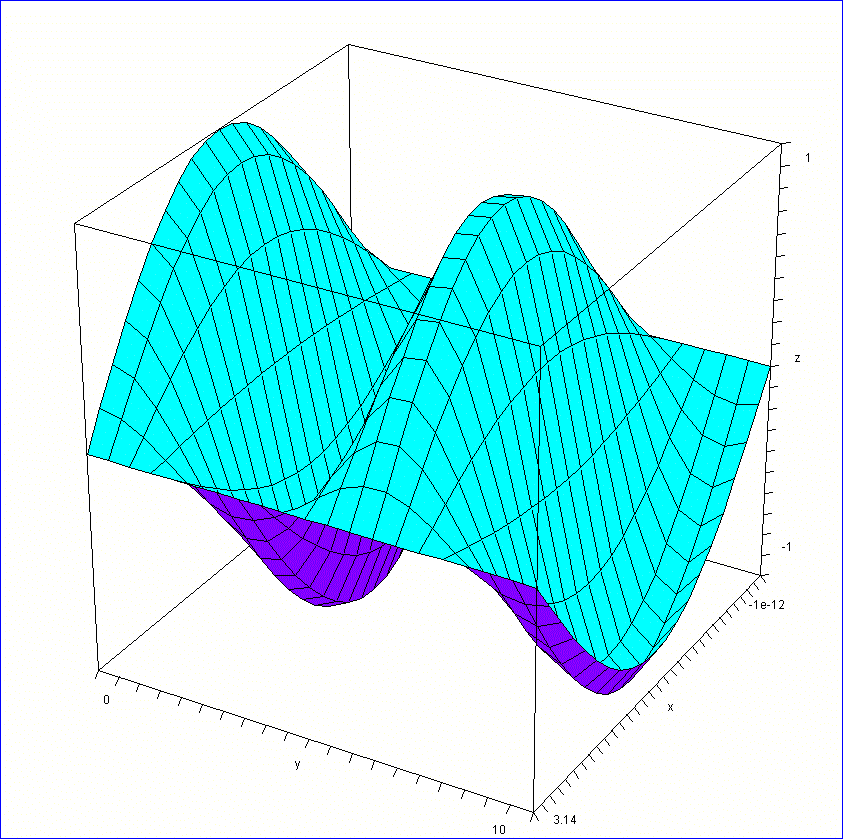
「当然じゃが、同じ結果となった。
　f=Cos(v t) Sin(x) が、方程式、f t t=v^2 f x x、を満たしていて、初期条件と境界条件も満たしていることは、すぐ分かるじゃろう。
　上の例題は、『演算子法』（近藤次郎 著：培風館：昭和45年6月30日初版第13刷）の141～142ページに記載されている例を簡単化したものじゃ。
　同書によれば、xの範囲を、0～L、初期条件をf(x，0)=g(x)、両端固定と初期速度ゼロは、本例と同じとしたとき、
　f(x，t)=Σ（n=1～∞）（2/L）（∫（ξ=0～L）g(ξ)×Sin(n πξ/L）dξ）Sin(nπx/L）Cos(nπv t/L））、
　となる。（フーリエ級数による解）
　本例では、初期条件 g=Sin(x)、と、区間の長さ L=πのおかげで、
　解の級数内の定積分が、n>1、では、ゼロとなり、無限和がn=1の1項のみとなって、とりわけ、簡単になったのじゃな。
　ラプラス変換により偏微分方程式を解くのは、代数方程式や常微分方程式の場合に比し、必ずしも容易でないことが分かる。
　一般にラプラス変換を使う場合、前半の変換とそれを解くところまでは、なんとかできても、後半の逆変換で立ち往生することが多い。
　特に、偏微分方程式の場合、逆変換する関数は、常微分方程式の解なので、すでに数式が複雑になっていて、逆変換がより難しい。
　なお、逆変換が解析的に実行できない場合は、数値的に逆変換できる場合がある。
　それが以前に書いた『ラプラス高速逆変換』で紹介した方法じゃ。
　数値的に求めるのであれば、偏微分方程式を数値的に解くのと、同じとも考えられるじゃろうが、常微分方程式の解が解析的に求められていれば、それを元に数値的に逆変換する方法は、特に制約条件に敏感な（固い）問題に対して効果があると思われる。
　今回は、だいぶ長くなってきたので、これまで、説明してこなかった『ラプラス逆変換』の複素関数論との関係について触れて終わりにしよう」　
　目次へ戻る

（6）ラプラス逆変換

逆変換と複素関数

「ラプラス変換を使って解を求める際、逆変換が難しくなり勝ちという話をしてきた。
　さて、原関数を f(t)、ラプラス変換後の関数（像関数）を F(s) と書く。
　F(s)=∫（t=0～∞）f(t)×Exp(－st) dt、であることは、何度も触れた。
　逆変換については、逆変換表や変換表を使う、変換の規則を応用するという方法以外は、説明してこんかった。
　しかし、このシリーズでも、途中までとは言え複素関数論をやってきたので、そろそろ、書いてもよいじゃろう。
　s を複素変数と見なし、複素平面で考えて、
　f(t)=1/(2π#i)×∫（Br=ブロムイッチ積分路）F(s) Exp(st) ds、が逆変換の公式じゃ。
　右辺の積分を『ブロムウィッチ積分』と呼んでいる。
※F(s)=1/s の場合の逆変換の計算例を参考に示す。（2017/3/26 追加）

　
　なお、s→∞の時に｜F(s)｜→0、となる F(s)であれば、
　f(t)=(1/2π#i）∫（F(s)のすべての特異点を囲む閉曲線内）F(s)×Exp(st) ds、とも書ける。
　特異点とは、F(s) が発散する（Lim s→α ｜F(s)｜→∞、となる）点、s=α のことじゃな。
　たとえば、1/s、1/(s－α)^2、などの s=0、s=αなどは、孤立特異点（そのまわりは、『正則点』）といわれておる」

「複素関数は、このシリーズでは、以下の6回取り上げてきたわね。
　第46回の『複素関数（1）（コーシー・リーマンの関係式、コーシーの積分定理』、
　第47回の『複素関数（2）（正則、特異点、極、コーシーの積分公式）』、
　第48回の『複素関数（3）（テイラー展開、ガンマ関数）』、
　第49回の『複素関数（4）（ガンマ関数、ローラン展開）』、
　第50回の『複素関数（5）（留数、留数定理とその応用）』、
　第51回の『複素関数（６）（留数定理の応用）』、
　今回の『正則』は、第46回、47回に出てきているわね。
　ちょっと、繰り返すけど、正則点というのは、微分係数が1つに定まる点のことね。
　複素平面では、関数上の特定の点に任意の方向から接近することができるでしょ。
　どんな方向から近づいても、微分係数が同じになるのが正則点ということ。
　また、正則関数というのは、複素平面の全部または一部で正則点を持つ関数のことよ。
　ところで、複素関数 F(s)で、dF/ds が1つに決まるためには、
　s=s＋α＋β#i、と置いて、（以前、複素変数を z で表してきたけど、ラプラス変換に合わせて s で表します）
　Lim （α→0，β→0） （F(s＋α)－F(s)）/（α＋β#i）、と、
　Lim （β→0，α→0） （F(s＋α)－F(s)）/（α＋β#i）、が等しい必要があるの。（α、βは、実数、#iは、虚数単位）
　F(s)=u（x，y）＋#i v（x，y）と書いたとき、（複素平面上の点 s=x＋y #i と書いている）
　lim（α→0、β→0）（u（x＋α，y＋β）－u（x，y））＋#i （v（x＋α，y＋β）－v（x，y））/（α＋β #i））
　lim（α→0、β→0）（（αu（x＋α，y＋β）－αu（x，y）＋βv（x＋α，y＋β）－βv（x，y））－#i（βu（x＋α，y＋β）－βu（x，y）＋αv（x＋α，y＋β）－αv（x，y））/（α2＋β2）、
　ここで、lim（β→0→α→0）与式＝（α∂u/∂x×α＋#i α∂v/∂x×α）/（α2）＝∂u/∂x＋#i ∂v/∂x
　また、同様に、lim（α→0→β→0）与式＝∂v/∂y－#i ∂u/∂y となる。
　このとき、F(s)がsで正則ならば、双方が等しい必要があるので、
　∂u/∂x＝∂v/∂y
　∂u/∂y＝－∂v/∂x
　これが『コーシー・リーマンの関係式（方程式）』と呼ばれているものだったわね」

「そうじゃな。
　複素関数は、だいぶ前にやったので、忘れてしまっていることがある。
　少し、重複するかも知れんが、逆変換に関係することは、重ねて触れていこう。
　以下では、αは、複素数とする。
　さて、αが特異点の場合、F(s)×(s－α)^n、が初めて特異点でなくなる整数 n があるとき、αをn位の極と呼ぶ。
　このとき、αは、除去可能な特異点とも呼ばれる。
　F(s)=1/s、のs=0などは、1位の極、あるいは、単極という。
　また、1/s^2、1/(s－α)^2 などの、s=0やs=αは、2位の極と言われる。
　一方、－Ln(s－α) のs=α は、(s－α)^n のnをどれほど大きくとっても、Lim s→α（(s－α)^n ×（－Ln(s－α)）、が収束しない。
　このような特異点を『真性特異点』という。
　※F(s)が真性特異点を含んでいても逆変換できる場合がある。
　　たとえば、F(s)=Ln(s)/s の逆変換は、f(t)=－Ln(t)－γ、ここで、γは、オイラーの定数」
　目次へ戻る

留数の利用

「ところで、s→∞の時に｜F(s)｜→0、となる F(s)であれば、
　逆変換の式で、右辺は、『留数』（Res( ) ）を使うと、f(t)=Σ（すべての特異点）Res（Exp(st)×F(s)）、となる。
　『留数』は、第50回『複素関数（5）（留数、留数定理とその応用）』で出てきた用語じゃったが、ともちゃんは、覚えていてくれたかのう。
　この場合の留数とは、平たく言えば、
　F(s) Exp(st) を特異点s=αでローラン展開した場合の 1/(s－α) の項の係数のことじゃ。
　たとえば、F(s)=1/s、の場合は、
　1/s×Exp(st)=1/s＋t＋s(t)^2/2!＋・・、であるので、1/sの係数は、1ということじゃ。
　これは、F(s)=1/s、の逆変換は、f(t)=1、（=単位関数）を意味している。
　単極の場合は、ローラン展開を意識せずに、次のように計算すれば、よいことは、すぐに分かる。
　φ(s)=(s－α)×F(s)、とすると、s=α、において、φ(s)は、正則関数となる。
　正則関数は、正則点において、無限回、微分可能（コーシーの積分公式参照）なので、
　正則点では、テイラー展開が可能である。
　φ(s)=φ(α)＋φ'(α)(s－α)＋φ''(α)(s－α)^2/2!＋・・、となる。（整関数の場合、ある次数の項以上はゼロとなるが）
　一方、Exp(st)も、正則なので、
　Exp(st)=Exp(αt)（1＋t (s－α)＋t^2 (s－α)^2/2!＋・・）、（こちらは、無限級数）
　よって、φ×Exp(st)、のs=α、における展開の(s－α)のゼロ乗の項は、
　φ(α)×Exp(αt)、となる。
　こごで、本来のF(s)×Exp(st)、の留数の計算に戻れば、この(s－α)のゼロ次の項が、留数なので、
　留数は、赤字の項同士を掛け合わせて、Lim s→α（φ(s)×Exp(st)）、と求められる。
　たとえば、F(s)=1/（(s－1)(s＋3)）、であれば、
　s=1及びs=－3が単極なので、それぞれの留数を計算して加え合わせると、
　f(t)を得ることができるという寸法じゃ。
　実際、
　Lim s→1（(s－1)×F(s)×Exp(st))=Exp(t)/4、
　同様に、s=－3からは、－Exp(－3t)/4、
　結局、f(t)=Exp(t)/4－Exp(－3t)/4、
　念のため、f(t)をラプラス変換して、確認してみると、
　第1項は、(1/4)×1/(s－1)、
　第2項は、－(1/4)×1/(s＋3)、
　足し合わせて、
　F(S)=1/（(s－1)(s＋3)）、となるのが確認できる。
　ただし、第1項のラプラス変換では、
　一般に、h(t)×Exp(at)⊃H(s－a)、であることを使っている。
　ここで、h(t)は、ラプラス変換可能な任意関数、H(s)は、その像関数じゃ。
　※f(t)⊃F(s) は、ラプラス変換、F(s)⊂f(t) は、逆変換の関係をそれぞれ示す」

「前節で登場した、F(s)=s/(s^2+v^2)、で試してみるよ。
　F(s)×Exp(st)の特異点は、s=±v #i、これは、単極なので、
　Lim s→#i　(s－v #i) F(s)×Exp(st)=^(·t·v)/2、
　同様に、
　Lim s→#i　(s＋v #i) F(s)×Exp(st)=^(－ ·t·v)/2、
　よって、両者を加えて、
　(1/2) Exp(vt #i)＋(1/2) Exp(－vt #i)=Cos(v t)、であることが分かったわ」

「そうじゃな。
　今度は、s=αが2重根の場合を考えてみよう。
　φ(s)=(s－α)^2×F(s)、とすると、s=α、において、φ(s) は、正則関数となる。
　正則点では、テイラー展開が可能なので、φ(s) は、
　φ(s)=φ(α)＋φ'(α)(s－α)＋φ''(α)(s－α)^2/2!＋・・、となる。
　一方、Exp(st)も、正則なので、
　Exp(st)=Exp(αt)（1＋t (s－α)＋t^2 (s－α)^2/2!＋・・）、
　よって、φ×Exp(st)、のs=α、における展開の(s－α)の1次の項は、
　赤字の2項同士を掛けあせた、
　φ(α)×t Exp(αt)＋φ'(α)×Exp(αt)、である。
　この項が本来のF(s)×Exp(st)、の1/(s－α)、の係数=留数、となるのは、分かるじゃろう。
　よって、s=αが2重根の場合の留数は、
　Lim s→α　（φ'(s)×1＋φ(s)×t）Exp(st)）、（2つの項があることに注意）
　たとえば、F(s)=s/(s＋1)^2、は、s=－1が、2重根じゃ。
　φ=s、なので、
　f(t)=Lim s→－1　（φ'(s)×1＋φ(s)×t）Exp(st)）=Exp(－t)×（1－t)、となるが、
　確かめてみると、正しいことが分かる。
　では、ともちゃん。
　s=αがn重根の場合は、どのように計算したらよいかを考えて欲しい」

「s=αがn重根の場合は、単根や2重根の場合の方法にならうと、
　φ(s)=Σ（k=0～∞）φ(k)(α)(s－α)^k/k!、
　Exp(st)=Σ（m=0～∞）（t^m）Exp(αt)(s－α)^m/m!、とそれぞれs=αでテイラー展開して、
　掛け合わせると、
　Σ（k=0～∞）Σ（m=0～∞）（φ(k)(α)(s－α)^(k＋m)×t^m/(k! m!)、となる。
　ここで、φ×Exp(st)の無限級数の、(s－α)^(n－1)、の項を取り出すと、これが、s=αの留数になるので、
　k＋m=n－1、から、m=n－k－1、及び、k=0～n－1、までの有限和であることから、
　s=αがn重根の場合の留数は、
　Σ（k=0～n－1）（φ(k)(α)×t^(n－k－1)/(k!( n－k－1)!)×Exp(αt)、となるでしょう」

「では、次の例を計算してみよう。（『演算子法』（近藤次郎 著）の例題より）
　F(s)=(2·s^7 + 2·s^6 + 9·s^5 + 11·s^4 + 11·s^3 + 5·s^2 + 2·s + 2)/(s^3·(s + 1)·(s^2 + 1)^2)、
　s=0が3重根、s=±#i が2重根、s=－1、が単根じゃが、結構、計算が面倒である。
　そこで、DERIVEで、次の関数を定義してみた。
　h(f_, v_, n_, a_):=
　PROG(g_ ≔ (s_ － a_)^n_·LIM(f_, v_↓1, s_), w_ ≔ LIM(∑(∂(g_, s_, n_ － k_ － 1)·(t_^k_·EXP(a_·t_)/((n_ － k_ － 1)!·k_!)), k_, 0, n_ － 2), s_, a_) + LIM(g_, s_, a_)·(t_^(n_ － 1)·EXP(a_·t_)/(n_ － 1)!), w_ ≔ LIM(w_, [s_, t_], v_), w_)、
　第1引数：F(s)、
　第2引数：ラプラス変換の変数名。通常は、［s，t］、
　第3引数：n重根のn、
　第4引数：特異点の値（一般には、複素数。虚数単位は、#i）、
　具体的には、α=0、n=3、であれば、
　h(f(s), [s, t], 3, 0)、から、t^2＋1、
　同様に、2重根のs=±#i、では、
　h(F(s)，［s，t］，2，#i）＋h(F(s)，［s，t］，2，－#i）、を計算し、
　(t + 3)·SIN(t) － 2·t·COS(t)、を得る。
　最後に、1重根のs=－1、では、
　h(F(s)，［s，t］，2，#i）＋h(F(s)，［s，t］，1，－1）、より、
　 Exp(－t)、
　これらを加え合わせて、
　f(t)=^(－t) － 2·t·COS(t) + (t + 3)·SIN(t) + t^2 + 1、
　念のため、変換し直してみると、
　f(t)⊃(2·s^7 + 2·s^6 + 9·s^5 + 11·s^4 + 11·s^3 + 5·s^2 + 2·s + 2)/(s^3·(s + 1)·(s^2 + 1)^2)、となり、
　正しく、逆変換されていたことが分かるじゃろう」

「じゃ、わたしは、従来の部分分数に展開する方法で、検算してみるよ。
　F(s)=2·s/(s^2 + 1)^2 + 4/(s^2 + 1)^2 + 1/(s^2 + 1) + 1/(s + 1) + 2/s^3 + 1/s、
　逆変換表を参照すると、
　2·s/(s^2 + 1)^2 ⊂2×t Sin(t×1)/(2×1)=t×Sin(t)、
　4/(s^2 + 1)^2　⊂ 4×(1/(2×1^3))（Sin(t×1)－t×1× Cos(t×1)）=2×（Sin(t)－t×Cos(t)）、
　1/(s^2 + 1) 　　⊂ 1×(1/1)Sin(1×t)=Sin(t)、
　1/(s + 1) 　　　 ⊂ Exp(－1×t)=Exp(－t)、
　2/s^3 　　　　　 ⊂ 2×t^(3－1)/(3－1)!=t^2、
　1/s　　　　　　　⊂ 1、
　よって、
　f(t)=^(－t) － 2·t·COS(t) + (t + 3)·SIN(t) + t^2 + 1、と求められた。
　確かに、合っているわね」

「上記のことをまとめたのが、『ヘビサイドの展開定理』と言われるものじゃ。
　次節で取り上げよう」
－－－－－　補注－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
・ コーシーの積分公式とテイラー展開
　F(s)=1/(2π#i)∫（s=s の回りの反時計回りの1周積分）F(z) / (z－s) dz、と書くことができる。
　ただし、s は、正則点。これを『コーシーの積分公式』という。
　また、F(s)のn階微分は、上記より、
　F(n)(s)=n! / (2π#i)∫（s=s の回りの反時計回りの周回積分）F(z) / (z－s)(n+1) dz、となる。
　例：F(s)=s^2、では、s^2=1/(2π#i)∫z^2 / (z－s) dz、
　ここで、z=s＋r×Exp(#iθ）と置けば、
　定積分は、∫(－ 2·r^2·SIN(θ)·COS(θ) － 2·r·s·SIN(θ) + ·(2·r^2·COS(θ)^2 + 2·r·s·COS(θ) － r^2 + s^2), θ, 0, 2·)、
　結果は、2π#i s^2、となるので、2π#iで割れば、s^2、となる。
　F(s)=s^2、の3回以上の微分は、ゼロとなるが、周回積分による表現は、可能なので、正則点で無限回テイラー展開可能と表現する。

・ ローラン展開と留数
　特異点の回りの正則、かつ、一価関数となる領域で、
　F(s)は、一般には、正・負べきの項を持つ級数、ローラン級数に展開できる。
　これをローラン展開という。
　F(s)=Σ（n=－∞～∞）a n×（s－α）^n、
　このとき、係数 a n は、n の負の場合は、a －n と書き表すことにすれば、
　a n= 1 / (2π#i)∫（s=αの回り周回積分）F(z) / (z－α)(n+1) dz、で与えられる。
　留数は、F(s)=Σ（n=－∞～∞）a n×（s－α）^n、、のように展開できている場合、
　∫F(s) ds、ただし、積分は、s=α、を中心とした周回積分、を作ると、
　右辺の、第n項を代表に考えれば、
　a n ∫（s－α）^n ds、ここで、s=α＋r exp(#i θ）、と置いて、積分すると、
　a n ×#i×r^(n+1) ∫（θ=0～2π）Exp(#i(n＋1)θ) dθ、となるが、
　これは、n=－1、の場合は、a－1×#i×1×2π=2π#i ×a－1、となる。
　しかし、nが－1、でない場合は、ゼロとなることが容易に分かる。
　すなわち、ローラン展開されているとき、特異点αの回りのF(s)の周回積分でゼロとならないのは、n=－1、の項のみである。
　これが留まる数、留数、という語源のようだ。
　例：F(s)=1/(s^2＋1)、
　
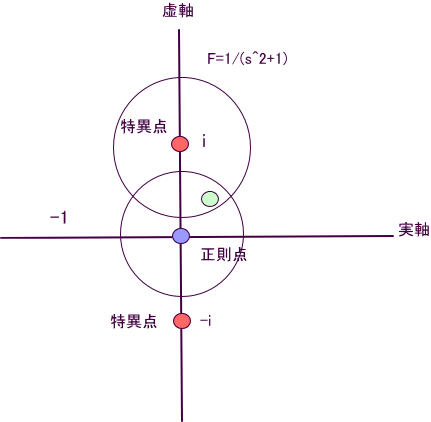
　正則点のs=0、でテイラー展開すると、
　F(s)=1－s^2＋s^4－＋・・・、
　上式は、初項 1、公比 －s^2 の無限級数なので、｜s｜<1、のとき、収束し、無限和は、1/(s^2＋1)、である。
　実数で考えれば、1/(x^2+1)、は、x=－∞～∞、で有界で、収束半径が1であるとは思えない。
　しかし、1/(s^2＋1)の s を複素数と見なすと、s=±#i、の極があるため、s=0 でのテイラー展開の収束半径の 1が理解できる。
　一方、s=#i、を中心としたローラン展開は、
　F=1/(s^2+1)=1/(s－#i)－1/(s＋#i)、と部分分数に展開できる。
　第1項は、すでに、s=#i、でのローラン展開になっている。
　第2項、－1/(s＋#i)、は、実は、s=#i で正則関数であり、s=#i でテイラー展開可能である、、
　－1/(s＋#i)=－（ 1/(2#i)＋1/4 (s－#i)－(1/8#i)(s－#i)^2＋・・）、
　よって、F=1/(s－#i) －（ 1/(2#i)＋1/4 (s－#i)－(1/8#i)(s－#i)^2＋・・）、収束半径は、1。
　まとめると、
　s=0 でのテイラー展開：F1=F(s)=1－s^2＋s^4－＋・・・、、
　s=#i でのローラン展開：F2=1/(s－#i) －（ 1/(2#i)＋1/4 (s－#i)－(1/8#i)(s－#i)^2＋・・）、
　ここで、どちらの展開式でも、カバーされている、s=(1/2＋#i/2)のF(s)の値を計算してみる。、
　正確な値は、F(1/2＋#i/2)=4/5 － 2·/5≒0.8 － 0.4·、
　s=0でテイラー展開した式で、F(s)をF1と書くと、第n＋1項までの和は、
　F1=s^(2·(n + 1))·COS(·n)/(s^2 + 1) + 1/(s^2 + 1)、であり、
　F1(1＋#i/2)≒0.80078125 － 0.400390625·、（10項の和）、
　F1(1＋#i/2)≒0.8 － 0.4·、（30項の和）、となる。
　一方、s=#iでローラン展開した式で、F(s)をF2と書くと、第n＋1項までの和は、
　F2=(1/(s － ) － ∑((s － )^k·(－1)^k·(2·)^(－k － 1), k, 0, n))·(1/(2·))、
　F2（1＋#i/2)≒0.8000030517 － 0.4000091552·、（10項の和）、
　F2（1＋#i/2)≒0.8 － 0.4·、（30項の和）、となる。　
　※F(s)=1/(s^2＋1) は、s=0でのテイラー展開の収束半径は、1であるが、z=1/s と置き、
　z=0 でテイラー展開してから、sに置き換えれば、
　F(s)=1/s^2－1/s^4＋1/s^6－＋・・、となる。この収束半径は、｜s｜>1 となる。　
　この右辺は、F(s)のs=無限遠点でのテイラー展開と見なすことができる。
　目次へ戻る

ヘビサイドの展開定理

「逆変換を求められる関数は、たいてい、F(s)=G(s) / H(s)、の形をしている。
　ここで、H(s)、G(s)は、sの整次式で、Gの方がsより低次のsの整式とすれば、s→∞で、｜F(s)｜→0、となる。
　このとき、F(s)の極は、H(s)=0、の根であるじゃろう。
　H(s)の零点（ゼロ点）、すなわち、H(s)=0、の根が単根だけとして、それをs=α1、α2、・・・、とする。
　任意のs=α、で考えた時、H(s)=(s－α)K(s)、と書ける。（以下、添え字を省略）
　ここで、K(s)は、(s－α)を含まない部分を表す。
　H(s)をsで微分すると、
　H'(s)=K(s)＋(s－α)×K'(s)、となる。
　従って、
　Lim s→α H'(s)=Lim s→α　K(s)＋(s－α)×K'(s)=Lim s→α　K(s)、となることが分かる。
　前節で、F(s)が単極を持つ場合は、その留数は、
　Lim s→α (s－α)×F(s)×Exp(st)、、だったことを思い出すと、
　Lim s→α　(s－α)×G(s)/H(s)×Exp(st)、
　(s－α)/H(s)、の部分を、上述のように、Lim s→αH'(s)、で置き換えることができる。
　これにより、
　Lim　s→α　G(s)Exp(st) / H'(s)=G(α)Exp(αt) / H'(α)、が、αでの留数の値であり、
　すべてのαjについて、加えると、
　f(t)=Σ（j=1～）G(αj)Exp(αj t) / H'(αj)、
　この式が F(s) の逆変換を与える。
　これを、（単極の場合の）『ヘビサイドの展開定理』と呼ぶ」　

「2重根の場合も同じよう考えてみると、
　分母の方は、H(s)=(s－α)^2 K(s)、と置いて、
　Hを2回微分すると、K(s)=H''(s)/2、が得られるので、
　2重根の部分から、f(t)への逆変換の項は、
　Σ2×（G(α) t＋G'(α)） Exp(αt) / H''(α)、となると思う」

「残念じゃが、単純には、そうは、ならないのだな。
　まず、K(s)=H''(s)/2 ではない。
　正しくは、K(α)=Lim s→α H''(s)/2、であることに注意じゃ。
　左辺は、K(α)であって、K(s) ではないのじゃな。
　次に、前段で、多重根の公式を導いてくれた。、
　Σ（k=0～n－1）（φ(k)(α)×t^(n－k－1)/(k!( n－k－1)!)×Exp(αt)、
　これは、正しいのじゃな。
　ここで、φ=(s－α）^n F(s)、また、nは、多重度数。
　2重根の場合は、φ= G(s) / （H(s) / (s－α)^2）、
　K(s)=（H(s) / (s－α)^2）、
　φ=G/K、から、上の公式の第1項は、Exp(αt)を除き、
　φ(α) t ＋φ'(α) 、
　となるので、
　第1項は、φ(α) =Lim s→α G(s)/K(s)、
　K(α)=Lim s→α (1/2) H''(s) = (1/2) H''(α)、とみなすと、
　φ(α) =G(α)/K(α)=2 G(α) / H''(α)、となるので、ともちゃんの式と同じじゃ。
　しかし、第2項は、
　φ' =（G' K－G K'）/ K^2=G' / K－G K' / K^2、
　ここで、K(α)=Lim s→α H''(s)/2を使うと、
　φ' (α)=2G '(α) / H ''(α)－4 G(α) K'(α) / H''(α) となる。
　この赤字で示した項がともちゃんが書いてくれた式には、抜けているのじゃな」

「えー、そうなんだ。
　K'(α)、が、必要なんだ！」

「そうなんじゃな。
　K'(α) をH(α)及びその導関数だけで、簡単には、表せない。
　H(s)が無限級数でなければ、φ(s)=G(s)(s－α)^2 / H(s)、を計算してから、
　ΣExp(αt) （φ(α) t ＋Φ'(s)）を求める方が現実的のようじゃ。
　ヘビサイドの展開定理については、もう少し触れたかったが、あまりに分量が増えてしもうた。
　次回以降に延期しよう。
　特に、F(s)に平方根号（√s）を含む数式が出ることがある。
　簡単な例では、F(s)=1/√s、この逆変換は、f(t)=1/√（πt）、となる。
　f(t)⊃1/√s、は、容易に変換できるが、√s は、2価関数なので、逆変換の説明には、準備が必要じゃ」

「そうね。
　わたしも、前から、その点が疑問なのよね」
　目次へ戻る

F(s)=1/s の場合の逆変換の計算例（2017/3/26追記）

F(s)=1/s、の場合は、s=0 が単極なので、容易に、原関数は、f(t)=1、と求められる。
　しかし、ここでは、あくまでも、元々のブロムウィッチ積分を実行してみる。
　f(t)=(1/2π#i)∫（s=α－β#i～α＋β#i）F(s) Exp(st) ds、において、Lim β→∞。
　αは、F(s)の極（ここでは、s=0）よりも右側の実数であれば、なんでもいいので、ここでは、α=1とする。
　s=1＋y #i、と変数を変更すると、
　(1/2π)∫（y=－∞～∞）（Exp(t) Exp(y t #i) / (1＋y #i) dy、となるので、分母・分子に、1－y #i を掛けて、実数部と虚数部とに整理する。
　虚数部は、奇関数なので、その定積分は、ゼロとなり、偶関数の実部の定積分のみ残り、
　f(t)=　(Exp(t) /π)∫（y=0～∞）（Cos(y t) / (1＋y^2) dy ＋　(Exp(t) /π)∫（y=0～∞）（y Sin(y t) / (1＋y^2) dy 、となる。
　右辺の2つの異常積分は、『フーリエ変換』の変換表を見ると、
　Exp(－t) = (2/π)∫（u=0～∞）1/(1＋u)^2 ×Cos(u t) du、
　Exp(－t) = (2/π)∫（u=0～∞）u/(1＋u)^2 ×Sin(u t) du、が掲載されているので、知ることができる。
　あるいは、第50回の複素関数の留数の応用による定積分の計算例を参照してもよい。
　いずれにしても、
　f(t)=(Exp(t) /π)×（Exp(－t)×π/2）＋(Exp(t) /π)×（Exp(－t)×π/2）=1/2＋1/2=1、
　となる。
　これは、1/s ⊂ 1、（単位関数（t<0 では、ゼロ、t>=0で、1となる関数））であることを示している。
　なお、数値計算で求める場合は、三角関数により正負が周期的に変化する級数となるので、オイラー変換を利用しないと実用的ではない。
　この点については、高速ラプラス逆変換の続きとして、機会があれば、触れる予定です。
　目次へ戻る

最終更新日　2017/3/26　一部追記 2017/4/6、文章を微修正 2018/9/23